1. Introduction
Let B denote the set of all analytic functions 
defined on the unit disk 
having the property that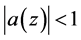 
for all 
A logharmonic mapping defined on the unit disk 
is a solution of the nonlinear elliptic partial differential equation
(1.1)
where the second dilatation function
. Because 
the Jacobian
is positive and hence, non-constant logharmonic mappings are sense-preserving and open on U. If f is a nonconstant logharmonic mapping of 
and vanishes at 
but has no other zeros in U, then f admits the following representation
(1.2)
where m is a nonnegative integer, 
and, 
and 
are analytic functions in 
with 
and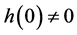 
([1] ). The exponent 
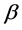in (1.2) depends only on 
and can be expressed by
Note that 
if and only if 
and that a univalent logharmonic mapping on 
vanish at the origin if and only if
. Thus, a univalent logharmonic mappings on 
which vanishes at the origin will be of the form
where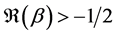 
and 
and have been studied extensively in the recent years, see [1] -[7] . In this case, it follows that 
are univalent harmonic mappings of the half-plane
a detail study of univalent harmonic mappings to be found in [8] -[14] . Such mappings are closely related to the theory of minimal surfaces, see [15] [16] .
Let 
be a univalent logharmonic mapping. We say that 
is starlike logharmonic mapping if
for all
. Denote by 
the set of all starlike logharmonic mappings, and by 
the set of all starlike analytic mappings. It was shown in [4] that
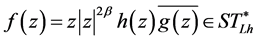if and only if 
It is rather a natural question to ask whether there exists a linkage between the starlikeness of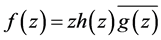 
and 
In Section 2, we determine the radius of starlikeness for the logharmonic mapping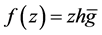 
where 
A distortion theorem and an upper bound for the arclength of these mappings will be included.
In Section 3, we discuss the integral means for logharmonic mappings associated to starlike analytic mappings.
2. Basic Properties of Mappings from 
We start this section by establishing a linkage between the starlikeness of 
and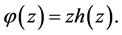 
Theorem 1 a) Let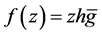 
be a logharmonic mapping where 
Then f maps the disk
, where 
onto a starlike domain.
b) If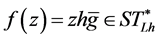
. Then 
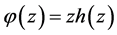maps the disk
, where 
onto a starlike domain.
Proof. a) Let 
be a logharmonic mapping with respect to 
and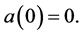 
Suppose that 
Then 
can be written in the form
(2.1)
A simple calculations leads to
where 
Since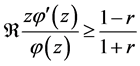 
and 
we obtain
This gives
Thus 
if 
Therefore, the radius of starlikeness 
is the smallest positive root (less than 1) of 
which is 
We conclude that f is univalent in 
and maps the disk 
onto a starlike domain.
b) Let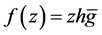 
be a starlike logharmonic mapping defined on the unit disk 
with respect to 
with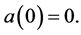 
Then by [4] 
and also,
Hence,
and then simple calculations give that
Thus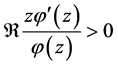 
if 
Therefore, the radius of starlikeness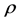 
is the smallest positive root (less than 1) of 
which is 
We conclude that 
is univalent in 
and maps the disk 
onto a starlike domain.
Our next result is a distortion theorem for the set of all logharmonic mappings 
where 
Theorem 2 Let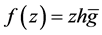 
be a logharmonic mapping defined on the unit disk U where
then for 
i) 
ii)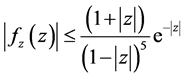 
iii)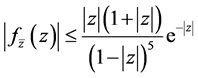 
Equality holds for the right hand side if and only if 
and 
which leads to
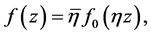where
Proof. i) Let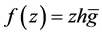 
be a logharmonic mapping with respect to 
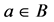with 
Suppose that 
Then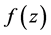 
can be written in the form
(2.2)
For 
we have
(2.3)
and
(2.4)
Combining (2.2), (2.3) and (2.4), we get
Equality holds for the right hand side if and only if 
and 
which leads to
For the left hand side inequality, we have
ii) and iii) Differentiation 
in (2.2) with respect to 
and 
respectively leads to
(2.5)
and
(2.6)
The result follows from substituting from Theorem 2(i), (2.3) and (2.4) into (2.5) and (2.6).
In the next theorem we establish an upper bound for the arclength of the set of all logharmonic mappings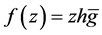 
where 
Theorem 3 Let 
be a logharmonic mapping defined on the unit disk U where
Suppose that for 
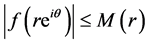then
Proof. Let 
denote the closed curve which is the image of the circle 
under the mapping
. Then
Now using (2.5) and (2.6) we have
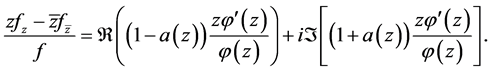
Therefore,
(2.7)
(2.8)
Since 
is harmonic, and by the mean value theorem for harmonic functions, 
Also,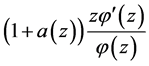 
is subordinate to
therefore, we have
Substituting the bounds for 
and 
in (2.8), we get
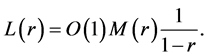
3. Integral Means
Theorem 4 of this section is an applications of the Baerstein star functions to the class of logharmonic mappings 
defined on the unit disk 
where
. Star function was first introduced and properties were derived by Baerstein [17] [18] , [Chapter 7]. The first application was the remarkable result, if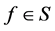 
then
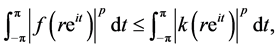(3.1)
where
, 
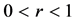and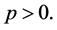 
If 
is a real 
function in an annulus 
then the definition of the star function of
, 
is
One important property is that when 
is symmetric (even) re-arrangement then
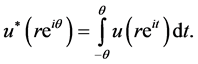(3.2)
Other properties [18] , [Chapter 7] are that the star-function is sub-additive and star respects subordination. Respect means that the star of the subordinate function is less than or equal to the star of the function. In addition, it was also shown that star-function is additive when functions are symmetric re-arrangements. Here is a lemma, quoted in [18] , [Chapter 7] which we will use later.
Lemma 1 For 
real and 
on 
the following are equivalent a) For every convex non-decreasing function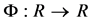 
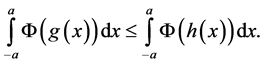
b) For every 
c) For every 
Our main result of this section is the following theorem.
Theorem 4 If 
be a logharmonic mapping defined on the unit disk U where 
then for each fixed 
and as a function of 
Equality occurs if and only if 
is one of the functions of the form
, 
, where
Proof. Let
, then by (2.2), we have
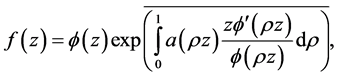
where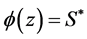 
and 
Then
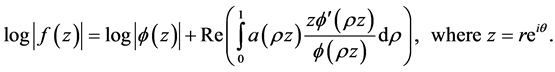(3.3)
Write 
where 
is analytic, 
and 
(see [9] ).
As the star-function is sub-additive,
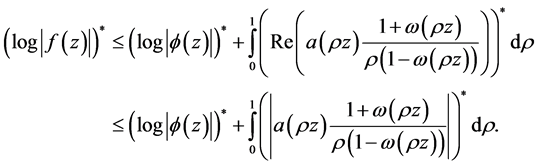(3.4)
But since
each is subharmonic. 
is subordinate to 
and 
is subordinate to
Hence
and
Then,
Thus,
It follows that
(3.5)
Consequently, by combining (3.4), (3.5) and using the fact that star-functions respect subordination, it follows that
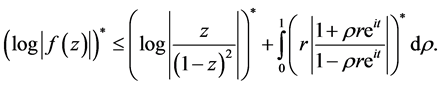
Hence, as star-functions are additive when functions are symmetric re-arrangements,
(3.6)
Now by using Theorem 4 we have Corollary 1 If 
be a logharmonic mapping defined on the unit disk U where 
then 
and
the later implies that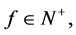 
hence 
has radial limits.
Proof. Let 
this is non-decreasing convex function .The first integral mean can be obtained using part (a) of Lemma 1 and Theorem 4. Moreover, the choice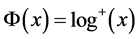 
yields the second integral mean.