1. Introduction
The theory of rough sets, proposed by Pawlak [1] [2] , is an extension of the set theory for the study of intelligent systems characterized by insufficient and incomplete information. Using the concepts of the lower and the upper approximations from the rough set theory, knowledge hidden in information systems may be unraveled and expressed in the form of decision rules [2] [3] .
The classical rough approximations are based on equivalence relations, but this requirement is not satisfied in some situations. Thus the classical rough approximations have been extended to the similarity relation based rough sets [4] [5] , the tolerance relation based rough sets [6] , the dominance relation based rough sets [7] , the arbitrary binary relation based rough sets [8] -[10] and the covering-based rough sets [11] -[13] .
An interesting and natural research topic in rough set theory is to study rough set theory via topology. Indeed, Polkowski [14] pointed: topological aspects of rough set theory were recognized early in the framework of topology of partitions. Skowron [15] and Wiweger [16] separately discussed this topic for classical rough set theory in 1988. Polkowski [17] constructed and characterized topological spaces from rough sets based on information systems. Kortelainen [18] considered relationships between modified sets, topological spaces and rough sets based on a pre-order. Skowron et al. [6] [19] generalized the classical approximation spaces to tolerance approximation spaces, and discussed the problems of attribute reduction in these spaces (also see [20] ). Lashin et al. [21] introduced the topology generated by a subbase, also defined a topological rough membership function by the subbase of the topology. In addition, connections between fuzzy rough set theory and fuzzy topology were also investigated (see [22] -[24] ).
General topology has been considered as the entrance to understanding topology science, moreover the base of general topology is the topological space, which has been considered as a representation of universal space in general, and geometric shape in special, also the mathematical analysis concepts. The general topology has become the appropriated frame for every collection connected by relations. Topology is also a mathematical tool to study information systems and rough sets [15] [21] .
General topology has applications in the theory of image processed by exhibiting algorithms, which apply current knowledge of digital topology (i.e., the study of the geometric and topological properties of digital images [25] ). The problems that might arise are, for example finding connected components, set boundaries or any other operations which are needed in image processing. The well-known digital Jordan curve theorem is proved by using topological approach [26] -[28] . The theorem is important in the theory of computer graphics.
The basic building block of the digital n-space is the digital line or the so called Khalimsky line [26] [29] -[31] . This is the set of the integers, Z, equipped with the topology K, generated by 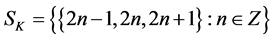 as a subbase. Thus a set U is open in K if and only if whenever
as a subbase. Thus a set U is open in K if and only if whenever  is an even integer, then
is an even integer, then . Nowadays, this topology, called the Khalimsky topology, is one of the most important concepts of the digital topology. It has been studied and used by many authors, e.g., [26] -[37] .
. Nowadays, this topology, called the Khalimsky topology, is one of the most important concepts of the digital topology. It has been studied and used by many authors, e.g., [26] -[37] .
The remainder of this paper is organized as follows. In Section 2, we present the fundamental concepts and properties of Pawlak’s rough set theory, general topology and digital topology. Section 3 presents the classifications of topologies in rough sets using the properties of the binary relations. In addition, we use the upper approximation operator to obtain the digital line, which is the basic building block of the digital spaces in Section 4 to try to describe the link between rough sets and digital topology. This paper concludes in Section 5.
2. Preliminaries
In this section, we introduce a review of some basic concepts of topological space and Pawlak approximation space.
A topological space is a pair  consisting of a set U and family τ of subset of U satisfying the following conditions:
consisting of a set U and family τ of subset of U satisfying the following conditions:
(T1)  and
and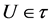 .
.
(T2) τ is closed under arbitrary union.
(T3) τ is closed under finite intersection.
The pair  is called a space, the elements of U are called points of the space, the subsets of U belonging to τ are called open sets in the space, and their complement are called closed sets in the space; the family τ of open subsets of U is also called a topology for U [38] .
is called a space, the elements of U are called points of the space, the subsets of U belonging to τ are called open sets in the space, and their complement are called closed sets in the space; the family τ of open subsets of U is also called a topology for U [38] .
Definition 2.1. [39] A topology τ on the set U is called an Alexandroff topology if the intersection of arbitrarily many open sets is still open, or equivalently, the union of arbitrarily many closed sets is still closed.
Definition 2.2. [37] Let U be a nonempty set and cl:  be a function. The space
be a function. The space  is called Smyth space if the following conditions hold.
is called Smyth space if the following conditions hold.
1)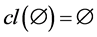 2)
2) 3)
3) .
.
Definition 2.3. For the set of integer Z we have:
(1) In Z the 2-neighbors of x is (2) In Z2 the 4-neighbors of
(2) In Z2 the 4-neighbors of  is
is 
(3) In Z2 the 8-neighbors of  is
is
 .
.
Definition 2.4. Let X be a nonempty set. Then the following are defined.
1) A relation R on a set X is reflexive if and only if xRx for all x in X.
2) A relation R on a set X is symmetric if and only if xRy implies yRx.
3) A relation R on a set X is transitive if xRy, yRz, then xRz.
A relation R on a set X is called an equivalence relation if it is reflexive, symmetric and transitive.
Definition 2.5. [2] Let R be an equivalence relation on a nonempty set U. For any subset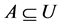 , the lower and upper approximations of A according to R are then defined as
, the lower and upper approximations of A according to R are then defined as

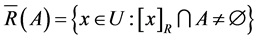 where [x]R is called an equivalence class of
where [x]R is called an equivalence class of .
.
Yao [37] extended the Pawlak’s definitions of a rough set to any binary relation R as follows:
Definition 2.6. For the pair , the set xR is defined as
, the set xR is defined as  called the right neighborhood of an element
called the right neighborhood of an element .
.
Definition 2.7. Let R be any binary relation on a nonempty set U. For any subset , the lower and the upper approximations of A according to R are then defined as
, the lower and the upper approximations of A according to R are then defined as 

Obviously, if R is an equivalence relation,  and these definitions are equivalent to the original Pawlak’s definitions.
and these definitions are equivalent to the original Pawlak’s definitions.
We list the properties that are of interest in the theory of rough sets, let :
:
L1. , where AC denotes the complementation of A in U.
, where AC denotes the complementation of A in U.
L2. .
.
L3.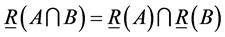 .
.
L4.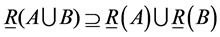 .
.
L5. .
.
L6. .
.
L7.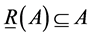 .
.
L8. .
.
L9. .
.
L10. .
.
U1. .
.
U2. .
.
U3. .
.
U4. .
.
U5. 
U6. 
U7. .
.
U8. .
.
U9. 
U10. .
.
Properties L1 and U1 state that two approximations are dual to each other. Hence, properties with the same numbers may be regarded as dual properties. Properties L9, L10, U9 and U10 are expressed in terms of set inclusion. The standard version using set equality can be derived from L1 - L10 and U1 - U10. For example, it follows from L7 and L9 that . It should also be noted that these properties are not independent.
. It should also be noted that these properties are not independent.
We can find the basic axioms for extended topological spaces in Table 1.
3. Topology Classifications Based on Rough Sets
In this section, we discuss the classification of topologies in the theory of rough sets.
Proposition 3.1. For any relation R on a nonempty set U and for every  the properties L1 - L5 and U1 - U5 hold according to Definition 2.7.
the properties L1 - L5 and U1 - U5 hold according to Definition 2.7.
Proof. See [9] .
Example 3.1. Let  be a relation on a nonempty set
be a relation on a nonempty set . Then
. Then ,
,  ,
, 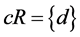 and
and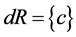 . Then
. Then  is not a topology on U.
is not a topology on U.
Theorem 3.1. Suppose that  is a rough approximation space. If
is a rough approximation space. If  satisfies the properties L1 - L5 and U1 - U5, then
satisfies the properties L1 - L5 and U1 - U5, then  is a Smyth space [37] .
is a Smyth space [37] .
Proposition 3.2. For any reflexive relation R on a nonempty set U and for every  the properties L1 - L7 and U1 - U7 hold according to Definition 2.7.
the properties L1 - L7 and U1 - U7 hold according to Definition 2.7.
Proof. See [9] .
Example 3.2. Let  be a reflexive relation on a nonempty set
be a reflexive relation on a nonempty set . Then
. Then  and
and . Then
. Then 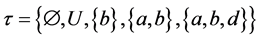 is a topology on U.
is a topology on U.
Theorem 3.2. If  satisfies the properties L1 - L7 and U1 - U7, then
satisfies the properties L1 - L7 and U1 - U7, then  is a pre-topology or Čech closure space.
is a pre-topology or Čech closure space.
Proposition 3.3. For any reflexive and symmetric relation R on a nonempty set U and for every  the properties L1 - L8 and U1 - U8 hold according to Definition 2.7.
the properties L1 - L8 and U1 - U8 hold according to Definition 2.7.
Proof. See [9] .
Example 3.3. Let 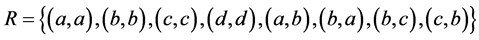 be a reflexive and symmetric relation on a nonempty set
be a reflexive and symmetric relation on a nonempty set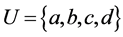 . Then
. Then 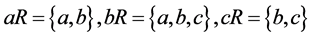 and
and . Then
. Then  is a topology on U in which each open (closed) set is also closed (open) set.
is a topology on U in which each open (closed) set is also closed (open) set.
Theorem 3.3. If  satisfies the properties L1 - L8 and U1 - U8, then
satisfies the properties L1 - L8 and U1 - U8, then 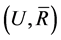 is a pre-topology or Čech closure space in which each open (closed) set is also closed (open).
is a pre-topology or Čech closure space in which each open (closed) set is also closed (open).
Proposition 3.4. For any reflexive and transitive relation R on a nonempty set U and for every 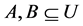 the properties L1 - L7, L9, U1 - U8 and U9 hold according to Definition 2.7.
the properties L1 - L7, L9, U1 - U8 and U9 hold according to Definition 2.7.
Proof. See [9] .
Example 3.4. Let  be a reflexive and transitive relation on a nonempty set
be a reflexive and transitive relation on a nonempty set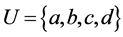 . Then
. Then  and
and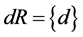 . Then
. Then 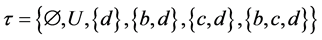 is an Alexandroff topology on U.
is an Alexandroff topology on U.
Birkhoff [40] showed that there exists a one-to-one correspondence between the set of all reflexive and transi

Table 1. The basic axioms for extended topological spaces.
tive binary relations and Alexandroff topologies.
Theorem 3.4. If 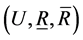 satisfies the properties L1 - L7, L9, U1 - U7 and U9, then
satisfies the properties L1 - L7, L9, U1 - U7 and U9, then 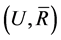 is an Alexandroff topological space.
is an Alexandroff topological space.
Proposition 3.5. For any equivalence relation R on a nonempty set U and for every  the properties L1 - L10 and U1 - U10 hold according to Definition 2.7.
the properties L1 - L10 and U1 - U10 hold according to Definition 2.7.
Proof. See [9] .
Example 3.5. Let  be an equivalence relation on a nonempty set
be an equivalence relation on a nonempty set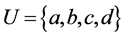 . Then
. Then  and
and . Then
. Then  is a topology on U in which each open (closed) set is also closed (open) set, and socalled clo-open topology.
is a topology on U in which each open (closed) set is also closed (open) set, and socalled clo-open topology.
Theorem 3.5. If  satisfies the properties L1 - L10 and U1 - U10, then
satisfies the properties L1 - L10 and U1 - U10, then  is an Alexandroff topological space in which each open (closed) set is also closed (open) set, and so-called clo-open space.
is an Alexandroff topological space in which each open (closed) set is also closed (open) set, and so-called clo-open space.
We summarize these results in Table 2, which indicates the generalized topological spaces depending on the properties of rough sets.
4. Connecting Digital Topology and Rough Sets
In this section, we try to get the structure of digital topology from the concepts of the theory of rough sets (the upper approximate operator).
Definition 4.1. Let R be any relation on a set of integer Z. We define another relation R' on Z as follows:

on the other hand, we can write the relation R′ in an equivalent form as follows:

Theorem 4.1. 1) The relation R on Z is reflexive if and only if R′ is also reflexive.
2) The relation R on Z is transitive if and only if R′ is also transitive.
Proof. 1) Let R be a reflexive relation on  is reflexive.
is reflexive.
2) Assume that xR′y and yR′z, then 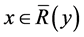 and
and 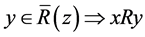 and yRz, hence by transitivity of R we get xRz, thus
and yRz, hence by transitivity of R we get xRz, thus , that implies xR′z. Therefore R′ is transitive. Conversely, suppose that xRy and yRz, then
, that implies xR′z. Therefore R′ is transitive. Conversely, suppose that xRy and yRz, then  and
and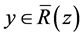 , that implies xR′y and yR′z, hence by transitivity of R′ we get xR′z, thus
, that implies xR′y and yR′z, hence by transitivity of R′ we get xR′z, thus , so that xRz. Therefore R is transitive.
, so that xRz. Therefore R is transitive.
The following conditions hold on Z using the relation →1) if two points  are 2-neighbors, then either x → y or y → x2) if two points
are 2-neighbors, then either x → y or y → x2) if two points 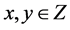 are not 2-neighbors, then both x → y and y → x not hold.
are not 2-neighbors, then both x → y and y → x not hold.
Lemma 4.1. If  such that
such that  and
and , then we have either
, then we have either  or
or .
.
Proof. By condition (1) we have either  or
or . Let
. Let . By condition (1) either
. By condition (1) either  or
or . If
. If , then by transitivity
, then by transitivity  which contradiction to condition (2). Hence
which contradiction to condition (2). Hence .
.
Then by Lemma 4.1 we can draw the graph of the relation → as follows (Figure 1).
Note that, in the line → ○ ← is equivalent to the open set containing the element “○” and ← □ → is equivalent to the closed set containing the element “□”, also the digital line is an Alexandroff topology.
Now, if we consider R is a relation on Z2, then the following conditions hold:
a) If two points 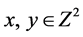 are 4-neighbors, then either x → y or y → x,
are 4-neighbors, then either x → y or y → x,

Table 2. Generalized topological spaces defining axioms are indicated by٭.
b) If two points  are not 8-neighbors, then both x → y and y → x not hold.
are not 8-neighbors, then both x → y and y → x not hold.
Lemma 4.2. If  which are in the same horizontal or vertical gride line of Z2 such that
which are in the same horizontal or vertical gride line of Z2 such that  and
and , then we have either
, then we have either  or
or  on a gride line.
on a gride line.
Proof. By condition a) we have either  or
or . Let
. Let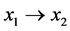 . Also, by condition a) either
. Also, by condition a) either  or
or . If
. If , then by transitivity
, then by transitivity  which contradiction to condition b). Hence
which contradiction to condition b). Hence .
.
In the plane note that, the element “○” is equivalent to the open-open, the element “□” is equivalent to the closed-closed, and the element “●” is called the mixed point and equivalent to the open-closed or the closedopen.
We must note that, there are two topologies on Z2 which satisfy the conditions 1 and 2, one of them was described in Khalimsky et al. [26] and the other was introduced by Marcus et al. [41] .
Figure 2 describe the topology in [26] . Furthermore, if there is no mixed point, then we have the topology in [41] , which described in Figure 3.

Figure 2. Khalimsky topology in the plane.
5. Conclusions
In short, topology is a branch of mathematics, whose concepts are fundamental not only to all branches of mathematics, but also in real life applications. Image plays important role in real life. In the past the process of image analysis took place via various mathematical models with an acceptable amount of error. Digital topology is a new accurate approach.
So we use the theory of rough sets to generate the digital spaces, in order to narrow the gap between rough sets and digital topology.