Parameter Dependence in Stochastic Modeling—Multivariate Distributions ()
1. Introduction
This paper can be viewed as an extension of our previous work (Filus and Filus [1] ) on the bivariate Gaussian pdf structure’s genesis of wide classes of newly constructed bivariate probability distributions. These distributions we constructed in our papers since 2000 up to recently (see, Filus and Filus [1] -[6] , also see Kotz, Balakrishnan and Johnson [7] pp. 217-218). Here, our explanations concerning the relation of our models to the bivariate normal were modified and we extended the topic to higher dimensional models and to the relation between our “parameter dependence method” of models construction and the multivariate normal paradigm.
It is a well-known fact that among existing multivariate probability distributions, there are no more than a few classes that are widely and successfully applied in practical stochastic modeling procedures. Typically, the underlying random variables are assumed to be independent or having an “approximately Gaussian” bivariate or multivariate distribution. The normality often is assumed even when corresponding data hardly agree with that mathematical model (showing asymmetry, for example). On the other hand, from all the multivariate distributions used in applications, the normal seems to be “the best”. The reason for this is that the Gaussian models catch the stochastic relationship (mainly by a regression function) between its marginal random variables in the most natural way. We first analyze and interpret the specific way the multivariate normal density of the random vector  relates to the marginal quantities
relates to the marginal quantities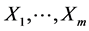 . Next we extend the “Gaussian pattern” to more general classes of bivariate and multivariate distributions including cases with non-Gaussian marginals. First of all we show that the common “mechanism” of the stochastic dependences both in the Gaussian distributions structure and the structure of the distributions we define, relies on the same way of conditioning. Namely, in all the considered cases, the conditional density of one random variable, say,
. Next we extend the “Gaussian pattern” to more general classes of bivariate and multivariate distributions including cases with non-Gaussian marginals. First of all we show that the common “mechanism” of the stochastic dependences both in the Gaussian distributions structure and the structure of the distributions we define, relies on the same way of conditioning. Namely, in all the considered cases, the conditional density of one random variable, say,  , given realizations, say,
, given realizations, say,  , of the marginal random variables
, of the marginal random variables  can be obtained by setting (often arbitrarily) an “initially constant” parameter, say, qj of the density of Xj to be any continuous function
can be obtained by setting (often arbitrarily) an “initially constant” parameter, say, qj of the density of Xj to be any continuous function  of the realizations. In this way the conditional pdf of Xj, given
of the realizations. In this way the conditional pdf of Xj, given  is defined, which stands for the “source” of the stochastic dependences.
is defined, which stands for the “source” of the stochastic dependences.
Pursuing this method successively for  we always arrive at a unique model. This manner, however, is characteristic for the m-variate normal where we turn an “original” normal N(mj, σj) density of Xj into the conditional density by setting a new value
we always arrive at a unique model. This manner, however, is characteristic for the m-variate normal where we turn an “original” normal N(mj, σj) density of Xj into the conditional density by setting a new value  of the “affected old parameter mj” to be the following (linear regression) function:
of the “affected old parameter mj” to be the following (linear regression) function: . Our main contribution is to generalize the latter function to any, not necessarily linear, function and consider not only the parameter mj but also any other parameter of any probability density to define the corresponding conditional distributions. This is the essence of the socalled parameter dependence method. Specifically in this paper, our task will be showing more closely relation of this method to the multivariate Gaussian model construction.
. Our main contribution is to generalize the latter function to any, not necessarily linear, function and consider not only the parameter mj but also any other parameter of any probability density to define the corresponding conditional distributions. This is the essence of the socalled parameter dependence method. Specifically in this paper, our task will be showing more closely relation of this method to the multivariate Gaussian model construction.
In Section 2, we analyze the stochastic dependences between marginal random variables of the bivariate normal in order to point out the original version of the parameter dependence pattern next extending to other constructed bivariate probability densities. The explanation as well as the example of applications of the bivariate normal is different from that in Filus and Filus [1] . In Section 3 we present the extension of the bivariate normal pdf to the bivariate FF-normal (formerly called “pseudonormal”). In Section 4 we apply the parameter dependence method to construct the bivariate FF-Weibull (formerly “pseudo-Weibull”) density in reliability framework of joint density of parallel system components life times. Comparison with other, similar, methods in the literature is presented in Section 5. In Section 6 we extend the constructions from bivariate to multivariate probability densities, first showing their relation with the multivariate normal dependences structure. Examples of the construction of multivariate FF-normal and multivariate FF-exponential (“pseudo-exponential”) densities are given.
In Section 7, we point out that the “method of parameter dependence” is used in some more areas of reliability theory for different situations than we are considering. This is a part of the accelerated life testing theory where the dependence of life time distribution’s parameter from a given (high) stress is investigated.
Another (fairly new) area is the “load optimization theory” sometimes associated with the load sharing phenomena analysis that we sketch in Subsection 7.2. The differences between these approaches and our theory are pointed out in 7.2.
2. The Bivariate Normal Case
We start with the following situation. Suppose the normally distributed random variable X2 describes an attribute of a physical or biological object, say u. Consider the (stochastic) behavior of the object u in two distinct “physical” situations. In the first situation, u is exposed to some random stress whose magnitude is described by a normally distributed random variable X1. In the second situation we assume there is no such a stress present or the stress takes on a fixed predetermined value. The usual task here is to determine the joint distribution of X1, X2. Let the densities of X1, X2 be normal, i.e.,  ,
, . [It is clear that we must assume that the value (m2 – kσ2) is positive for at least k = 3, in order to assure approximate positivity of the normal life-time X2].
. [It is clear that we must assume that the value (m2 – kσ2) is positive for at least k = 3, in order to assure approximate positivity of the normal life-time X2].
2.1. Simplified Biomedical Example
Imagine the following fictitious experiment whose goal is to establish the possible stochastic impact of a medication’s dose change on some cancer treatment results. Suppose a person of a certain fixed age, was diagnosed with a kind of cancer. Assume that one of the significant characteristics of that kind of cancer is a tumor with a size X2. During a given time period T after the patient was diagnosed, a specific medication was administered. Also suppose that this medication was routinely administered in the past, and that the average dose is estimated (or fixed) to be m1 milligrams per kilo of weight daily. Assume that, originally, the known (either measured or estimated) average size of the tumor is, say, m2 millimeters and after the period T of treatment the tumor size X2 is measured again and its negative or positive increment  is statistcally confronted with the dose X1 of the medication administered.
is statistcally confronted with the dose X1 of the medication administered.
We assume that the goal of the underlying experiment is to make a prediction on effect  of the treatment when the dose is changed from its “original level”
of the treatment when the dose is changed from its “original level”  to a level
to a level . Randomness of the doze X1 may be justified when only “historical data” are analyzed and then extrapolated for a larger population of cases not yet recorded. In the case of extrapolation of historical data for a larger population we assume that the only information one possess on the applied in the past dose X1 is its probability distribution, which is the Gaussian
. Randomness of the doze X1 may be justified when only “historical data” are analyzed and then extrapolated for a larger population of cases not yet recorded. In the case of extrapolation of historical data for a larger population we assume that the only information one possess on the applied in the past dose X1 is its probability distribution, which is the Gaussian  with given values for both the parameters m1, σ1. Also, for
with given values for both the parameters m1, σ1. Also, for  the tumor size X2 (after the treatment) is assumed to be a random variable having a normal
the tumor size X2 (after the treatment) is assumed to be a random variable having a normal 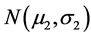 density, where
density, where  is the value of the tumor “increment” under the treatment characterized by the dose level m1. For any other applied doze X1 = x1 the, associated with a single patient, value (x1 – m1) statistically affects the change in the tumor size X2 – m2 i.e., the treatment result. The word “statistically” here means that the impact of a nonzero quantity (x1 – m1) (“the dose is not the standard one”) on the (former) probability density N(m2, σ2) of the tumor size X2 realizes through affecting the value of the mean m2 rather than directly affecting the numerical value x2 of X2.
is the value of the tumor “increment” under the treatment characterized by the dose level m1. For any other applied doze X1 = x1 the, associated with a single patient, value (x1 – m1) statistically affects the change in the tumor size X2 – m2 i.e., the treatment result. The word “statistically” here means that the impact of a nonzero quantity (x1 – m1) (“the dose is not the standard one”) on the (former) probability density N(m2, σ2) of the tumor size X2 realizes through affecting the value of the mean m2 rather than directly affecting the numerical value x2 of X2.
If we were interested in finding the joint probability distribution of X1, X2 it is enough to determine the conditional density g2(x2|x1) of X2|X1, since the marginal density of X1 is not changing.
In accordance with the “linear regression rule”, the dependence of the (new) expected value 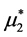 (so new probability density
(so new probability density ) of the tumor size X2 on the event X1 = x1, is determined by the familiar functional relationship:
) of the tumor size X2 on the event X1 = x1, is determined by the familiar functional relationship:
 (1)
(1)
where a = r(σ2/σ1) and r is the (linear) correlation coefficient of the variables X1, X2 .
This approach directly leads to the determination of the conditional density of the random variable X2 given any realization X1 = x1. It is a well-known fact that the conditional density g2(x2|x1) is, again, normal and
 , (2)
, (2)
i.e., the  density in x2.
density in x2.
The joint density g(x1,x2) of the random variables X1, X2 is given by the usual arithmetic product g2(x2|x1)g1(x1) .
2.2. Remark
In the example above, one can reinterpret the “response random variable” X2 to be for example the patient’s “residual life-time”, or blood pressure, or level of some important chemical in the blood (such as cholesterol). In such cases the mathematics of the problem would remain the same.
Note the obvious fact that the tumor size X2 does not have a physical influence on the medication dose X1 so that the original marginal pdf g1(x1) remains the same. However, the stochastic dependence between X1, X2 is mutual, since, in general, g1(x1|x2) ≠ g1(x1).
It is well known that the actual problem with the bivariate normal density construction is to get to the conditional density (2), which fully represents the underlying stochastic dependence of random variable X2 on X1.
Our claim is that the above paradigm for the stochastic dependence (characteristic for the bivariate Gaussians) can be extended to other classes of bivariate and multivariate distributions (see Filus and Filus [3] [4] ).
3. The FF-Normal (Pseudonormal) Extension
Historically, people relied on the nice symmetry in the stochastic dependence of X1 and X2 when using their joint bivariate normal distribution. This kind of symmetry (i.e., both marginal and both conditional distributions are normal and both sides regression functions are linear) can only be achieved with the linear regression functions as described above (1). However, are linear regression functions really the only functions that one can successfully apply within this framework? Assuming that the function m2(X1) is any continuous function in X1, one obtains a wide and interesting extension of the class of bivariate normal densities. We called this class FF-normal (previously named “pseudonormal”, see [2] and also [7] ). In this case the parameter σ2 can as well become a continuous function of the stress X1 (X1 may have a “stress” interpretation in a very wide sense). This stress may change the parameter σ2 of the (normal) density of, say, the “life-time” X2 into another value  that depends on the particular realization x1 of the random variable X1. The price for such a wide generalization is loss of the, mentioned above, symmetry (the marginal of X2 ceases to be normal) but the gains are considerable. Anyway, the bivariate normal remains to be a special cases of the FF-normals.
that depends on the particular realization x1 of the random variable X1. The price for such a wide generalization is loss of the, mentioned above, symmetry (the marginal of X2 ceases to be normal) but the gains are considerable. Anyway, the bivariate normal remains to be a special cases of the FF-normals.
With the bivariate FF-normal densities of (X1, X2) we can use general continuous m2(x1) and σ2(x1) functions, and, performing similar calculations as above, we find, rather surprisingly, that g2(x2|x1) is once more a regular normal density in x2.
Consider now the following situation with a bivariate FF-normal distribution in which the “physical” interpretation of the underlying random variables can now be more general than above. Let u1, u2 be two objects (or phenomena) which are characterized by the random variables X1, X2 respectively. If the objects are physically separated then the random variables X1, X2 are assumed to be independent, having normal pdfs  and
and  respectively. When the objects physically interact (or rather only u1 physically impacts u2), then the corresponding joint FF-normal density g(x1, x2) of the random vector (X1, X2) is given by the usual product formula:
respectively. When the objects physically interact (or rather only u1 physically impacts u2), then the corresponding joint FF-normal density g(x1, x2) of the random vector (X1, X2) is given by the usual product formula:
 with the invariant marginal density
with the invariant marginal density .
.
For the conditional density of X2|x1 we have: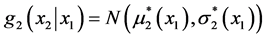 .
.
The functions  are “formed” from the “no-stress” parameters m2, σ2 of X2’s density.
are “formed” from the “no-stress” parameters m2, σ2 of X2’s density.
More explicitly, one obtains the bivariate FF-normal pdf in the form:

where 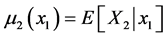 is the (in general, nonlinear) “regression function”, and
is the (in general, nonlinear) “regression function”, and  is the conditional variance obtained from the “previous” variance
is the conditional variance obtained from the “previous” variance .
.
In particular, one may consider the “nonlinear regression function”

with arbitrary real parameters  and A,
and A,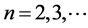 .
.
Realize that in the case A = 0 and  we obtain the regular bivariate Gaussian density. The coefficient A of the term
we obtain the regular bivariate Gaussian density. The coefficient A of the term  may be considered as a nonlinear “correction” of the regular Gaussian (linear) regression. The main purpose of that correction is to enhance the accuracy in various modeling procedures. For some type of asymmetric data, especially interesting may be the “non-symmetric” “quadratic” case n = 2.
may be considered as a nonlinear “correction” of the regular Gaussian (linear) regression. The main purpose of that correction is to enhance the accuracy in various modeling procedures. For some type of asymmetric data, especially interesting may be the “non-symmetric” “quadratic” case n = 2.
Equally important is the “symmetric” “cubic” case when n = 3. Also interesting is the case where a
* = 0 and A ≠ 0. Here, the linear correlation coefficient is zero, while the (nonlinear) dependence may be quite “heavy”. Another interesting case (which may be combined with those above) is when we choose the standard deviation function as belonging to the “parametric class” of “quadratic functions” defined by

with k positive real. It is rather obvious that the idea of the construction of bivariate normal (and FF-normal as well) can be extended to other probability distributions such as exponential, gamma, Weibull, lognormal, etc.
Generally speaking, the essence of the construction method is that for any pair of (“initially independent”) random variables X1 and X2 with given probability densities  and
and  respectively, one can simply “declare” some parameter (or a vector parameter), say Θ, of the density
respectively, one can simply “declare” some parameter (or a vector parameter), say Θ, of the density  to be dependent on the values of the other random variable X1. This means that when X1 = x1 we may assume that
to be dependent on the values of the other random variable X1. This means that when X1 = x1 we may assume that 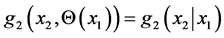 is the “affected by x1” distribution of the random variable X2 (given the event X1 = x1 occurred, with probability density g1(x1) ).
is the “affected by x1” distribution of the random variable X2 (given the event X1 = x1 occurred, with probability density g1(x1) ).
Then the joint density of the pair (X1, X2) is always .
.
This situation is especially natural if we consider X2 to be the life-time of an object and X1 is the stress put on it.
Roughly, one can say that the construction method of bivariate distributions, presented above is an extension of the method used in the construction of the bivariate normal.
4. Reliability Example
Consider a 2-component (say u1, u2) parallel system reliability setting in which X1, X2 represent the components’ life-times (see Barlow and Proschan [8] ). We start with the situation where the system’s components act separately. We call that pattern the “laboratory conditions”. In this latter case the components are physically separated and consequently their life-times (represented by the, statistically estimated, “baseline probability densities” g1(x1) and g2(x2) respectively), are stochastically independent. When the two components are installed into the system, they start to interact. Assume that during that interaction some irregularities in the work of component u1 cause corresponding changes in u2’s inner physical structure. This increases the hazard rate of that physically affected component u2. Such physical phenomena are then “responsible” for the occurrence of stochastic dependence in the “in-system” component life-times X1 and X2.
One can also imagine this situation as follows. During the two components’ “in-system” performance, component u1 creates a situation in which component u2 is “constantly bombarded” by a string of harmful “micro-shocks” (see Filus and Filus [5] ). Each such micro-shock causes a corresponding “micro-damage” in the affected component u2’s physical constitution. We also assume that these micro-damages in component u2’s inner physical structure “cause” some corresponding “micro-changes in the original (baseline) failure rate” (and, in parallel, in the corresponding probability distribution) of its life-time X2. After a, possibly long, time period X1 of such interaction all these micro-damages cumulate their effects. As a result of this accumulation, the overall change in the corresponding “hazard rate function” will become significant. To describe formally the change in the hazard rate function we have chosen to consider corresponding changes in its parameter(s). In what follows we present a particular bivariate model for a 2-component system reliability which we called FF-Weibullian (formerly “pseudo-Weibullian” in Filus and Filus [4] ).
Suppose the lifetimes of the components u1 and u2 in “laboratory conditions” are independent and distributed according to the Weibull density random variables X1 and X2.
Let  be the pdf of Xk (k = 1, 2).
be the pdf of Xk (k = 1, 2).
Here, for k = 1, 2, we have the “vector parameter”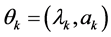 .
.
Next consider the components u1 and u2 as acting within the system. Let the resulting (changed) values ,
,  of the parameters of the (original) pdf g2(x2; l2, a2) be determined by the following continuous functions of x1:
of the parameters of the (original) pdf g2(x2; l2, a2) be determined by the following continuous functions of x1:
 and
and .
.
One then obtains the wide class of bivariate FF-Weibullian densities:
 (3)
(3)
where, for ease of computation, we recommend to apply as “sub-model” the following family of “parameter functions”:
 and
and  with parameters A, r, s positive reals.
with parameters A, r, s positive reals.
In particular, s may depend on x1.
Another analytically interesting “sub-model” is given by:
 with A and r real, and
with A and r real, and  with s > 0, c ³ 0.
with s > 0, c ³ 0.
Note that both factors g1(x1) and g2(x2|x1) of the joint density g(x1, x2) given by (3) are Weibullian densities. In particular, g2(x2|x1) is Weibullian with respect to the argument x2 alone.
For the simpler FF-exponential example, see [1] .
5. Notice on Similar Investigations in the Literature
A parallel and basically independent path of investigation, which also has its roots in the bivariate normal distribution’s dependence paradigm, is present in the literature under the key word “conditioning”.
This method, used in the construction of numerous multivariate probability distributions, was extensively developed mostly since around 1987. See, for example, Arnold, Castillo and Sarabia [9] with citations. Also consider Castillo and Galambos [10] .
The underlying method (by numerous authors called the “conditioning method”) relies on imposing conditional structure X|Y and Y|X on, given in advance, “baseline” probability densities f(x; A) and g(y; B) of some (“initially independent”) random variables X and Y respectively, where A and B are scalar or vector parameters. The two conditional densities are defined as we did above, i.e.
g(y|x) = g(y; B(x)) and f(x|y) = f(x; A(y))
where A(y) and B(x) are continuous functions of realizations of the random variables Y, X respectively.
In this case the task is to find two proper (unknown) marginal densities for the bivariate probability distribution of (X, Y) which are, as a rule, not unique and sometimes do not exist.
Despite similarities this method essentially differs from ours. In our case, instead of the two conditional densities g(y|x) and f(x|y), we define only one, say, g(y|x), but together with the marginal f(x).
Pursuing this way we always directly obtain a unique model simply as the product of the two (known) densities.
In such a way, we have obtained a wide class of bivariate densities which is essentially disjoint from the class obtained by that alternative method. Also, the physical interpretation of the, so defined, conditional densities differs in the two approaches. However, both approaches are devoted to the same purpose which is to extend of the paradigm of the bivariate normal in stochastic modeling. Nevertheless, using the conditioning method it is very difficult to construct the multivariate distributions of any higher than two dimensions.
Practically that method reduces to the bivariate cases while the method we present has a remarkable easiness of construction of probability distributions of, actually, arbitrary finite dimension. There is, namely, a recurrence procedure which allows to construct any j-th dimensional pdf based on corresponding (j – 1)-th dimensional pdf  constructed “at an earlier stage”. That procedure was also used in Filus and Filus [11] for the construction of discrete time stochastic processes.
constructed “at an earlier stage”. That procedure was also used in Filus and Filus [11] for the construction of discrete time stochastic processes.
The next section is devoted to the construction of multivariate distributions for any arbitrary finite dimension.
6. Method of Parameter Dependence for Multivariate Probability Distributions Construction
For the construction, mentioned in the title, we successively use the simple recurrence method that yields the j-th dimensional probability density, given the (j – 1)-th one. Realize, that (for j = 3) we have already defined the 2- dimensional densities g2(x1, x2) by means of the products g1(x1)g2(x2|x1), where each underlying conditional density was given by g2(x2|x1) = g2(x2, q2(x1)).
So the “first step” is already done. Suppose now that we have at our disposal the (j – 1)-th dimensional (j ³ 3) pdf, say  of the random vector
of the random vector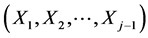 . The task of obtaining the joint density
. The task of obtaining the joint density  of the random vector
of the random vector 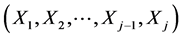 always reduces to defining the conditional density
always reduces to defining the conditional density , given any univariate baseline pdf
, given any univariate baseline pdf  by the method of parameter dependence. Assuming that originally qj is a constant parameter, we define the conditional pdf
by the method of parameter dependence. Assuming that originally qj is a constant parameter, we define the conditional pdf  by setting (according to the new physical situation of “being in the system” together with the other j – 1 objects):
by setting (according to the new physical situation of “being in the system” together with the other j – 1 objects):

Now, the “new” value  of the parameter is a continuous function of the realizations (“multi-stresses”)
of the parameter is a continuous function of the realizations (“multi-stresses”)  of the random vector
of the random vector .
.
The j-dimensional pdf of the random vector  one obtains simply as the product:
one obtains simply as the product:

The latter pdf becomes the basis for identical construction of the (j + 1)-dimensional pdf and so on.
We then stop the procedure once j + 1 = m, where m is the total dimension of the considered (maximal) random vector, say, .
.
Since the analogy with the construction of each j-dimensional normal pdf  is not as straightforward as in the bivariate case, we found it beneficial to show this analogy closer, by reducing the normal’s construction to the “diagonal case”. Let us start with recalling that any normally distributed random vector, say,
is not as straightforward as in the bivariate case, we found it beneficial to show this analogy closer, by reducing the normal’s construction to the “diagonal case”. Let us start with recalling that any normally distributed random vector, say, 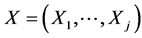 ,
,  is obtainable from the random vector
is obtainable from the random vector  by an affine transformation
by an affine transformation
 , (4)
, (4)
where the random variables  are independent and each having the standard normal N(0, 1) pdf. A is an arbitrary j × j matrix with real entries (here, without losing generality, we restrict ourselves to nonsingular matrices A, only) and
are independent and each having the standard normal N(0, 1) pdf. A is an arbitrary j × j matrix with real entries (here, without losing generality, we restrict ourselves to nonsingular matrices A, only) and  is an arbitrary fixed vector in Rj. The symbolT denotes the usual matrix transpose. Recall that every matrix A can be decomposed as
is an arbitrary fixed vector in Rj. The symbolT denotes the usual matrix transpose. Recall that every matrix A can be decomposed as
 , (5)
, (5)
where B is a lower triangular and M is an orthogonal matrix. From (5) we obtain that any nonsingular lower triangular matrix B can be represented as the product:
 , (6)
, (6)
where A is an arbitrary nonsingular matrix. If we replace representation (4) of the random normal vector X by the following representation
 , (7)
, (7)
then we replace the arbitrary random vector X by an arbitrary “triangular” random vector Y related to X by:
 , (8)
, (8)
where MT is an arbitrary orthogonal transformation.
Since the two zero-expectation random vectors X – µ, Y – µ are obtained one from another by an isometry (here, rotation) MT in the Euclidean space Rj, they may be considered as representing the same “stochastic data” expressed in two different (but still rectangular) coordinate systems. So from a stochastic viewpoint the “difference” between the random vectors X and Y is inessential and we can consider the random vector Y as an “arbitrary normal” (“with accuracy to the rotation” MT).
Collecting all the above, we will consider the normal random vector Y, given by (7), where matrix B is any lower triangular matrix and Z is the standard normal j-vector. Write (7) in the form:
 (7*)
(7*)
where m ³ j is the actual dimension of the constructed (final) random vector, say  (if m = ¥, one defines, in effect, a stochastic process with time j).
(if m = ¥, one defines, in effect, a stochastic process with time j).
Considering the first –1 lines in (7*) as a system of linear equations, one obtains all  as linear combinations of
as linear combinations of . Substituting these solutions back into (7*) one obtains the following form:
. Substituting these solutions back into (7*) one obtains the following form:
 (9)
(9)
Realize that transformation (9) is easily reversible.
Assuming that realizations  of the random variables
of the random variables  are known, we obtain for each
are known, we obtain for each :
:
 (10)
(10)
where from the above assumed nonsingularity we have ckk ≠ 0. From (10) it follows that the conditional density of each Yk, given the values , is normal and for the corresponding conditional expectation we have
, is normal and for the corresponding conditional expectation we have

while for the (constant) conditional variance we obtain

To adopt the above procedure to our concept of “baseline” Tj versus “in system” Yj random variables, replace in (9) the independent standard random variables 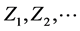 by independent random variables, say,
by independent random variables, say,  where each Tk has the (“baseline”) normal N(µk, sk) pdf
where each Tk has the (“baseline”) normal N(µk, sk) pdf .
.
Replace transformation (7) by
 , (11)
, (11)
where . Using this change, (10) will be replaced by the following inverse transformation:
. Using this change, (10) will be replaced by the following inverse transformation:
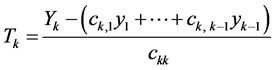 (10*)
(10*)
This yields the conditional pdf of 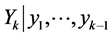 to be the normal
to be the normal

Finally, the general pattern of “creation” of any successive j-variate normal pdf can be explained as follows.
Given are the first j – 1 lines of transformation (11) in the form:
 (12)
(12)
for some . (Realize that the joint normal pdf
. (Realize that the joint normal pdf  of the random vector
of the random vector 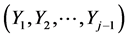 was defined in j – 1 “previous” steps. In particular for j – 1 = 1, it is the univariate normal N(µ1, |c11|s1) density of the variable Y1.)
was defined in j – 1 “previous” steps. In particular for j – 1 = 1, it is the univariate normal N(µ1, |c11|s1) density of the variable Y1.)
We may assume that the next baseline random variable Tj, originally having the N(µj, sj) pdf, is incorporated to the “system” by transforming

This transformation is thought of as adding to (12) the following j-th line:
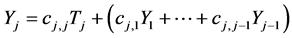 (13)
(13)
[“Physically” this could mean that the variables  “become” explanatory (“stresses”) for the “new” variable Yj obtained from Tj that (originally) was independent from these stresses].
“become” explanatory (“stresses”) for the “new” variable Yj obtained from Tj that (originally) was independent from these stresses].
From (13) one can determine the conditional pdf of Yj, given any realization  of the random vector
of the random vector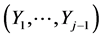 , as the following normal pdf in yj:
, as the following normal pdf in yj:
 .
.
Thus, as the j-th “object” (originally independent from the “system” and characterized by the random quantity Tj) was “put into the system” the quantity Tj turns to the quantity Yj and, in parallel, the parameters µj and sj of its normal density are turned into  and
and , respectively, while normality is preserved.
, respectively, while normality is preserved.
Clearly, the new value  of the (conditional) expectation became the continuous (here linear) function
of the (conditional) expectation became the continuous (here linear) function

of realizations  while unfortunately the new value of the standard deviation does not depend on
while unfortunately the new value of the standard deviation does not depend on 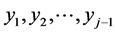 but remains constant even if multiplied by the specific, determined by the “system”, number cjj. This can be “made up” if we allow the number cjj in (13) to be dependent on
but remains constant even if multiplied by the specific, determined by the “system”, number cjj. This can be “made up” if we allow the number cjj in (13) to be dependent on , but then the so obtained multivariate FF-normal distribution ceases to be normal since (13) ceases to be linear.
, but then the so obtained multivariate FF-normal distribution ceases to be normal since (13) ceases to be linear.
As we have shown also in multivariate cases, the origin of the “parameter dependence method for the construction”, lies in the construction of the multivariate normal distributions. Recall that having defined the conditional pdf  and the joint pdf
and the joint pdf 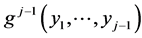 we automatically have the joint pdf
we automatically have the joint pdf  as the simple arithmetic product of the two. In the case just considered, all the densities
as the simple arithmetic product of the two. In the case just considered, all the densities  are (arbitrary with the accuracy to the rotations in Rj ) multivariate normal.
are (arbitrary with the accuracy to the rotations in Rj ) multivariate normal.
Preserving the general spirit of the multivariate normal pdf derivation, let us extend all the Equations (13) for  by allowing the translations
by allowing the translations  to be any nonlinear continuous function of
to be any nonlinear continuous function of  and replacing the constant cj,j by any continuous function of the same variables. Now, for any
and replacing the constant cj,j by any continuous function of the same variables. Now, for any  (13) may be rewritten into the following “triangular” (see Filus, Filus and Arnold [12] ) form:
(13) may be rewritten into the following “triangular” (see Filus, Filus and Arnold [12] ) form:
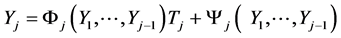 (13*)
(13*)
where Fj() and Yj() are arbitrary continuous functions and .
.
From (13*) we obtain its inverse:
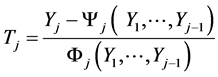 (13**)
(13**)
and then for each observation  of
of  the conditional pdf of
the conditional pdf of 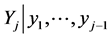 as follows:
as follows:
 (14)
(14)
It is clear that the sequence of the densities (14)  together with the normal initial density g1(y1) of Y1 uniquely determines the m-variate FF-normal pdf
together with the normal initial density g1(y1) of Y1 uniquely determines the m-variate FF-normal pdf  of the random vector
of the random vector . Remarkably, this non-normal density has its natural representation as the product of m normal densities:
. Remarkably, this non-normal density has its natural representation as the product of m normal densities:
 (15)
(15)
However, the marginal pdfs of  are not normal anymore.
are not normal anymore.
The main conclusion which follows the considerations in Sections 6.2 - 6.4 may be stated as: There is a generic relationship that associates the construction method of the parameter dependence with the stochastic dependence structure present within the multivariate normal distribution of any dimension.
As an example of this relationship realize that the transformations (13) and (13*), when applied to the independent normal random variables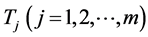 , define multivariate normal and FF-normal pdfs respectively. They produce other m-variate probability distributions if the normality assumption for Tj is dropped.
, define multivariate normal and FF-normal pdfs respectively. They produce other m-variate probability distributions if the normality assumption for Tj is dropped.
Let now  be independent random variables all having the standard exponential pdf:
be independent random variables all having the standard exponential pdf:
 .
.
Applying to the random vector  transformation (13*) and then (13**) for
transformation (13*) and then (13**) for , one obtains the joint density
, one obtains the joint density  of the resulting random vector
of the resulting random vector  to be given by the product of m factors (15), where according to first row of (12) we have
to be given by the product of m factors (15), where according to first row of (12) we have  and according to (13**)
and according to (13**)

where the latter is the two parameter exponential density with respect to yj for .
.
Another interesting case of the m-variate FF-Weibullian pdf can be obtained by applying transformations (13*) to m independent Weibullian random variables. An even more general class of FF-Weibullians one obtains using the pseudopower transformations (see Filus and Filus [4] ) instead of the pseudoaffine (13*) which actually is a special case of the pseudopower.
All these distributions (including the m-variate normal) can as well be obtained by direct use of the “parameter dependence pattern” which produces more m-variate models than the considered above transformations. On the other hand existence of the defining transformations facilitates an underlying statistical analysis and simulations.
7. Other Parameter Dependence Paradigms in the Literature
Some paradigms, applied in the reliability literature, are exactly those of the “parameter dependence” that we describe in this paper. However, in most of the cases they are not directly related to the problem of construction of multivariate probability distributions (so, also are different from the “conditioning” procedures in [9] [10] ; see above, Section 5). There are two such subjects that we discuss in the following.
7.1. The Accelerated Life Testing
When testing the life times of some high reliability products, the stresses usually encountered such as temperature, humidity, voltage sometimes are kept on significantly higher than usual levels in order to make the life times shorter than they are in normal conditions. The so obtained data (a “sample”) is then extrapolated into those (hypothetical) life times that would, possibly, be obtained under the regular values of the stresses. Existence of rules, that associate the products’ life times with values of the stresses applied, is necessary for performing proper extrapolations. Several such rules, typically known as the Arrhenius or Eyring (see, Meeker and Escobar [13] , Nelson [14] and [15] an internet source) relationships, are based on physical and chemical considerations on the rates of some chemical reactions that give rise to a given unit’s failure. The obtained models, in general, allow determining the ratio of life times of the same product under higher and under normal temperature or, in the case of the Eyring model, some other physical quantities that play the role of the stresses (see, [13] , formula (18.5) page 476). Methods like that (i.e., the so called SAFT models [13] ) directly relate the (life) times by means of a simple coefficient called the “acceleration factor”.
Unfortunately, with this method the simplicity often comes along with inaccuracy of the predictions. Other methods apply the “Proportional Hazards Relationships” known also as Cox Model (see Cox [16] ) which instead of times relate hazard rates.
More recently ([15] ), the relationships between the life times under different stresses are related indirectly through their probability distributions via distribution’s parameter in that way that considers distribution’s parameter as a function of a given stress (mostly temperature, humidity, pressure, voltage). Those relationships, even if considered in a different context, obey the same paradigm (of the parameter dependence) as that considered in this paper in association with the construction of the multivariate probability distributions.
In what follows we discuss the differences.
1) The generality of the “parameter dependence theory” we built in this paper, is significantly higher than the very special case applied to the accelerated life testing theory. There are three reasons for that.
Firstly, in our approach the subject of constructing conditional probability distributions is not limited to the life testing, and not even to the “stress-life time” pattern only. The range of applications of our theory is very wide, including many biomedical (see, Collett [17] ) and econometric relationships, (see, Filus and Filus [11] also Filus, Filus and Krysiak [18] ).
Secondly, in the paradigm we consider, the relation between a parameter and stress (or any other random quantity) is given by an arbitrary continuous function, while the number of such functions applied in association with the accelerated life time testing is very limited. Actually, the functions are restricted to few “models” such as the Arrhenius, Eyrie, inverse power law, log-linear, and not many more (see, for example, the Eyring-Weibull model in [15] , Section 5). Those models were obtained from physical and chemical considerations that are only valid for some simple failure (degradation) mechanisms while very often real failure mechanism is too complicated to be analyzed that way.
Our idea is to omit the complicated physical or chemical phenomena that often are poorly understood and to apply two steps purely empirical approach.
Speaking roughly, the first step is an “educated guess” (for choice of a proper function) and the second is statistical verification of this guess.
Thirdly, in our theory we may consider an arbitrary parameter of an arbitrary probability distribution as a stress dependent, while, according to our knowledge (see, for example, [15] ), the only life time distributions so far considered in the accelerated life testing are exponential, Weibullian, and lognormal (normal), and for each the distribution only one parameter is taken under consideration.
2) Besides the generality (of the constructed conditional distributions) our concept also differs with regard to the purpose. Namely, independently of the conditional distributions construction, we also have the construction of bivariate and multivariate probability distributions such as the FF-normal, FF-exponential, FF-Weibullian, FF-gamma and other (for comparison with similar “conditioning methods” of construction present in the literature, see Section 5).
The construction of high dimension multivariate distributions based on parameter dependence can easily be extended to Markovian and non-Markovian (still simple!) stochastic processes (see Filus and Filus [11] ). The latter constructions seem to be rather unique in the literature.
7.2. Load Control and Load Sharing
1) Other than the accelerated life testing subject, where the “parameter dependence paradigm” is applied, is a set of problems centered around the notion of “load optimization” (see Filus [19] [20] , Levitin and Amari [21] , Nourelfath and Yalaoui [22] and others). This relatively new topic can be described as follows. Some working systems, such as cargo transporting trucks, trains, electric power lines, highways, computer processors, or other systems supporting varying amounts of load, require control of that load. On the one hand more load yields more gain, but, on the other hand, load (as stress) increment yields a corresponding increment of the system’s failure rate which, in turn, depends on certain parameters [20] . The optimization problem can be formulated in several ways ([20] [21] ) but, in all cases, the main idea is to balance between an expected gain that follows a good (load) transportation and the loss in reliability of the transporting medium which decreases the overall gain. Thus, for some (optimal) value of the load to be found, the pure expected gain earned by the system is maximal. In this framework the relationship between stress (the load) and some parameters of the system life time probability distribution (failure rate) is vital for finding a proper model. As examples of such relations, the power and exponential functions of the load were chosen in [20] .
2) Similar application of the parameter dependence pattern also occurs when “load sharing phenomena” takes place. Suppose that we have a parallel system supporting a load such as several engines aircraft or two electric power lines. Failure of any system’s component may cause the total load to be redistributed among fewer components, so that the load on each of them increases by some predictable value. Now we may encounter either the load optimization problem [21] or simply the task of determination of system’s life time probability distribution (see Freund [23] for the exponential case as well as Lu [24] and Filus [25] for Weibullian and lognormal cases). In all these cases the parameter dependence pattern is involved or it is desirable to apply it to get a deeper insight into the underlying stochastic phenomena.
Remark. As a final remark, let me mention the relationship between the parameter dependence presented in this paper, and the stochastic dependence based on models initiated in 1961 by Freund [23] . Besides some similarity the most basic difference lies in the fact that in the Freund scheme the system components act independently until the first failure. In general, the components successive failures cause the total load to be shared by fewer and fewer remaining components, affecting their failure rates (via the parameters).
Quite opposite to that, in the models we introduce, the component interactions take place only when the components work. Any failure of a system component stops its influence on the remaining components’ life times. Therefore, the two paradigms, the “Freund’s load sharing” and our “parameter dependence”, are “disjoint” and in a sense “complementary”. In reality, both (physical) phenomena may take place at the same time and it seems to be quite possible in the future to construct stochastic models (i.e., multivariate probability distributions) that would obey both paradigms.
Nevertheless, we stress the generic relation of all the multivariate probability distributions based on the parameter dependence with the multivariate Gaussians.