1. Introduction
In last few decades, to reduce greenhouse gases emissions and fossil fuels dependence, numerous renewable energy technologies have been studied. Amidst all of the various environmental friendly solutions, fuel cell systems are one of the promising energy technologies. Fuel cells are electrochemical devices that generate electrical energy from chemical reactants continuously. Due to its high efficiency, fast power response, high power density, low operation temperature and ease of maintenance [1] -[3] , the proton exchange membrane fuel cell (PEMFC) appears as a suitable clean energy generator technology for a wide range of applications. However, several bolts, especially related to its control, still remain to be removed to improve the overall system performance. Indeed, global efficiency improvement, optimal hydrogen and air consumption, and reliable and accurate power response remain challenging control goals.
In the literature, numerous control strategies ranging from PID controllers, state feedback linearizing approaches, dynamic neural network controllers, linear quadratic Gaussian (LG) controllers, to model predictive control (MPC) strategies, have been reported regarding PEMFC control. An indicative only review of the various approaches follows. Huang et al. [4] designed a fuzzy PID controller to regulate hydrogen flow rate, resulting in an optimization of hydrogen consumption. Wang and Ko [5] proposed a multivariable robust PID controller, based on a classical PID approach combined to the merits of robust control, to regulate air and hydrogen flow rates. Results obtained showed good performance in terms of stability and efficiency using a simple control structure. Methekar et al. [6] considered the fuel cell as a MIMO system and proposed two PID control strategies. Using a steady-state relative gain array (RGA) analysis, these authors showed that hydrogen and coolant inlet flow rates are suitable manipulated variables to control the output power and the temperature of a PEMFC, respectively. Li et al. [7] proposed a nonlinear robust control of a PEMFC based on a state feedback linearizing approach. This well-known nonlinear approach allows obtaining a nonlinear control law directly from the dynamic nonlinear model of the process. To improve the robustness of the controller, the authors proposed to add a H∞ robust control strategy to the state feedback control law. Hatti et al. [8] designed a dynamic neural network controller based on the Quasi-Newton-Levemberg-Marquardt algorithm. The authors proposed a setpoint tracking of the reactive power demand considering hydrogen flow as control variable. Hasikos et al. [9] proposed an optimization methodology to minimize the hydrogen consumption. This methodology is based on a neural network model including in a Non-Linear Programming optimization problem. Shokuhi-Rad et al. [10] developed an approximate predictive control (APC) approach based on a neural network model. At each sample time, a linear model is extracted from the neural network model and a linear controller is designed. In this case, performance of the approach has been evaluated in simulation environment. Wu et al. [11] designed a multi-loop nonlinear predictive control scheme using a reduced order model to regulate stack temperature and oxygen excess ratio of the fuel cell in a hybrid energy system. However, the controller has only been tested in simulation environment, and authors underlined that some devices and design have not been taken into account (e.g. hydrogen storage, power management and inverters). Gruber et al. [12] developed a model based predictive controller to control the oxygen excess ratio using the compressor motor. Experimental results showed that the proposed strategy stabilized the oxygen excess ratio around the desired value five times faster than the built-in controller. Ziogou et al. [13] proposed a nonlinear model-based predictive control (NMPC) approach to track a variable load demands while avoiding oxygen starvation and minimizing hydrogen consumption. To achieve on-line application, the authors developed a tailor-made optimization strategy that discretizes control variables and state variables. The proposed approach has been experimentally tested and exhibited good performance in terms of computational time efficiency and setpoint tracking accuracy. Damour et al. [14] proposed a fast NMPC scheme, based on a particular parameterization of the control actions, to decrease the optimization problem dimension and achieve real-time implementation. The proposed strategy, tested in simulation environment, turned out to be a promising candidate to achieve on-line implementation.
Regarding advanced control strategies, the modeling step remains essential and mandatory for the control design. In the literature, a wide variety of models, either mechanistic or black-box, with different levels of complexity, can be consulted. Regarding mechanistic approaches, numerous one-dimensional and multi-dimensional models have been proposed [15] -[27] . However, due to their complexity and heavy computation, most of these models are not suitable for real-time control purposes. In this context, black-box approaches appear as a hopeful alternative. Among the various black-box models solutions, artificial neural network model turns out to be a promising candidate to model PEMFC systems. Saengrung et al. [28] investigated the relevance of ANN as predictive models of a commercial PEMFC system (1.2 kW). The authors developed and compared the performance of back-propagation (BP) and radial basis function (RBF) algorithms in terms of speed and accuracy to predict stack voltage and current, using air flow rate and stack temperature measurements as inputs. Sisworahardjo et al. [29] developed an ANN model of a portable PEMFC (100 W) considering stack temperature and current as inputs, and hydrogen flow rate, stack voltage and power as outputs. The authors reported that, except the transient voltage response of the ANN model, which is faster than the actual fuel cell, the performance of the ANN model in terms of speed and accuracy is quite satisfactory. In Chavez-Ramirez et al. [30] , the authors proposed an ANN model of a high power PEMFC (5 kW) using seven inputs to predict cell voltage and cathode temperature. The authors reported a maximum prediction error of 9.4% in the stack voltage and 5.6% in the stack temperature measurements.
In this paper, a neural model-based self-tuning PID controller is developed to control the output voltage of a PEMFC. Controller parameters are updated on-line, at each sampling time, based on an instantaneous linearization of an ANN model of the process and a General Minimum Variance (GMV) control law. Combining GMV control design with instantaneous linearization allows managing nonlinearities of the process, while avoiding heavy computations. To confirm the reliability and the relevance of this approach, the controller is implemented on-line and experimentally tested on a real fuel cell system. The rest of this paper is organized as follows: Section 2 provides a description of the experimental setup of the fuel cell unit. Section 3 is dedicated to control design—a real-time implementable self-tuning PID algorithm dedicated to the PEMFC output voltage control is detailed, and an ANN model of the PEMFC, dedicated to control purposes, is designed and experimentally validated. In Section 4, the performance of the proposed control strategy, in terms of setpoint tracking accuracy and robustness against plant/model mismatch, is experimentally demonstrated. Eventually, conclusions and prospects are drawn in Section 5.
2. Fuel Cell System Description
In the present work, a 50 cm2 single home fuel cell assembling, with a commercial membrane electrode assembly (MEA) from Paxitech, is used. The fuel cell is assembled with Teflon glass fiber as seal joints and clamped at 11 Nm bolt torque. Details about the fuel cell assembling optimization can be consulted in a previous work [31] . MEA used for this work is composed of symmetric electrodes (0.5 mgPt∙cm−2, Pt 40 wt%/C) with a Nafion® N115 membrane. All experiments are performed on a Fuel Cell Test Station (FCTS) manufactured by Fuel Cell Technologies, Inc. (Figure 1).
The FCTS provides control of flow, temperature, humidity, and pressure for both anode and cathode gases. The station incorporates a programmable DC electronic load and an AC-Impedance measurement system (Figure 2). Inlet gas flow rates are controlled using two mass flow controllers, located before the humidifier. Fuel cell temperatures and humidification temperatures are controlled using temperature controllers. Reactant gases are humidified through external water tanks, and desired gas humidification value is reached through the regulation of the water temperature in the humidifiers. An electronic load measures cell output voltage and current. The automatic backpressure systems have two main parts: The first is a diaphragm type regulator that mechanically positions itself to provide the desired backpressure. The second is a transducer that provides the gas to the regulator. The transducer is controlled using the software through a LabJack interface unit that provides a 0 - 5 voltage. This range of voltage corresponds to a 0 - 400 kPa backpressure. The automation of the FCTS is based on a Supervisory Control and Data Acquisition (SCDA) system developed on LabViewTM-software. The SCDA system allows to acquire and monitor all available data, and to manipulate all system actuators. All measured data are written in a file and can be accessed in real-time, and actuators can be manipulated on-line.
In this study, pure hydrogen and air are used as fuel and oxidant, respectively.
3. Self-Tuning PID Controller Design
3.1. Self-Tuning PID Algorithm
The basic feature of the proposed approach consists in an instantaneous linearization of an ANN model combines with a GMV control law. At each sampling time, coefficients are extracted from the nonlinear ANN using instantaneous linearization to obtain a linearized ANN. Parameters of the PID controller are updated using the previous extracted coefficients and a GMV control law. This strategy allows managing nonlinear behaviors of the process while avoiding heavy computations.
The proposed strategy is based on a classical PID control law:
 (1)
(1)
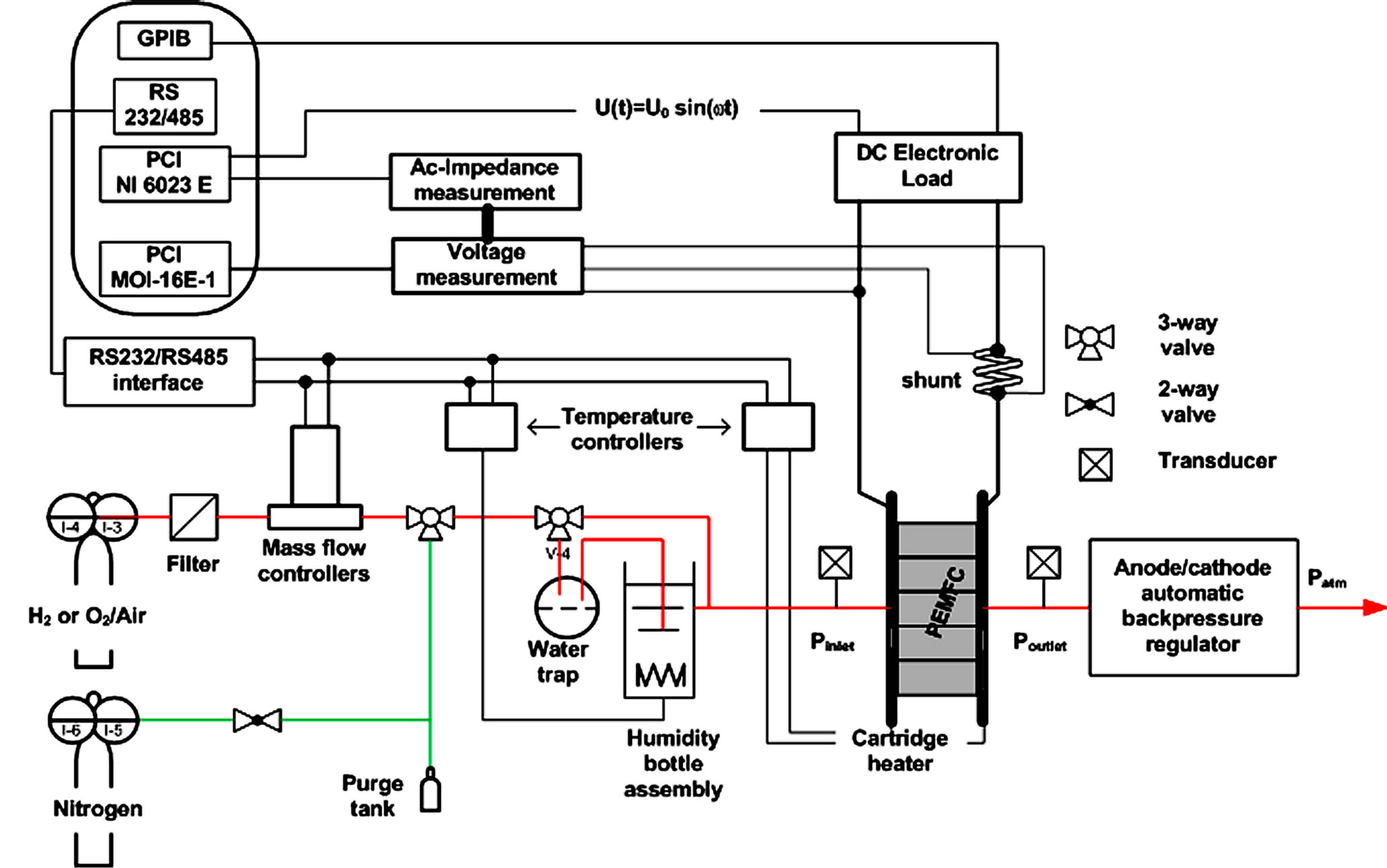
Figure 2. Simplified process and instrumentation diagram of the FCTS system.
where  is the trajectory tracking error.
is the trajectory tracking error.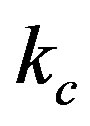 ,
, 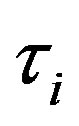 and
and  are the proportional gain, the integral time constant and the derivative time constant, respectively.
are the proportional gain, the integral time constant and the derivative time constant, respectively.
A velocity form of the discrete PID controller can be written as:
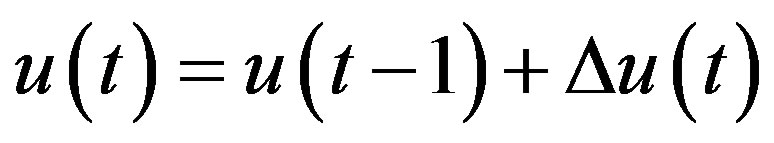 (2)
(2)
where u(t) is the control action at time t and 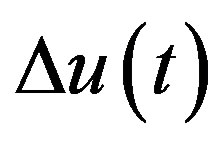 is written as:
is written as:
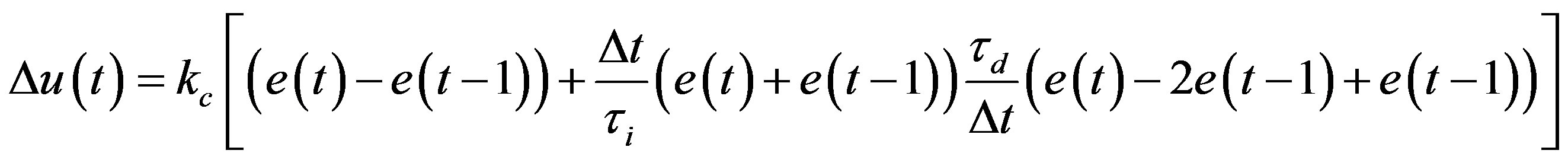 (3)
(3)
where 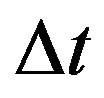 is the sampling period,
is the sampling period, 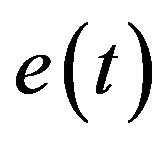 the trajectory tracking error at time t, and the integral action is computing using trapezoidal approximation.
the trajectory tracking error at time t, and the integral action is computing using trapezoidal approximation.
Rearranging the previous equation, the discrete PID control law can be rewritten:
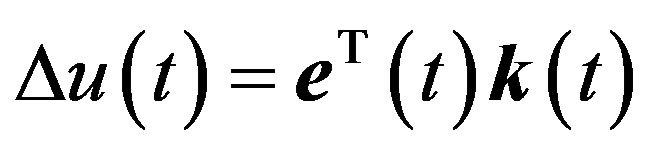 (4)
(4)
where ,
, 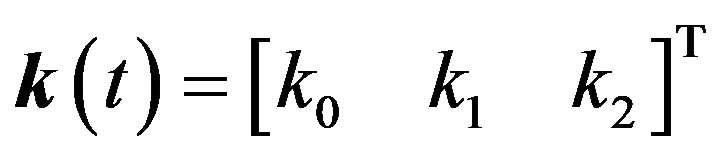 and with
and with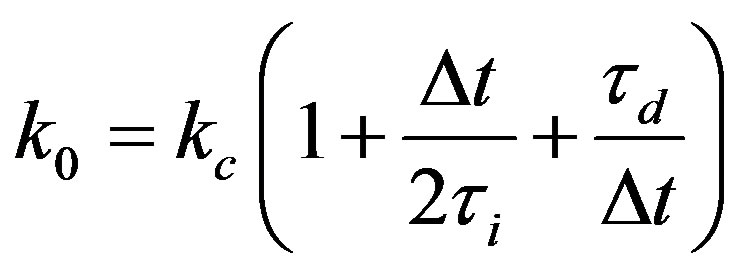 ,
, 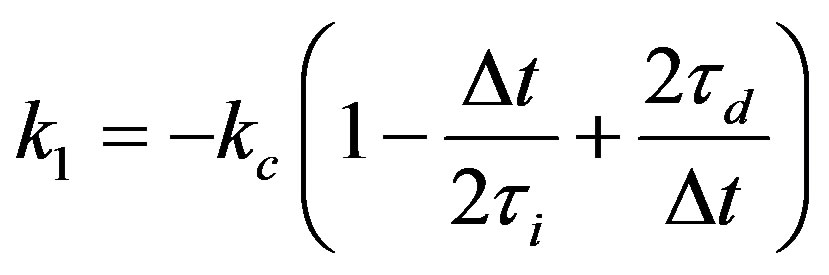 and
and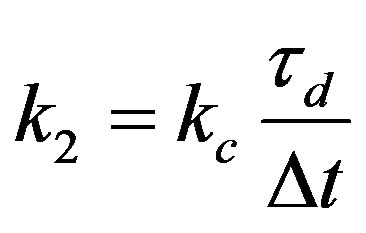 .
.
In the proposed methodology, the optimization problem is written as:
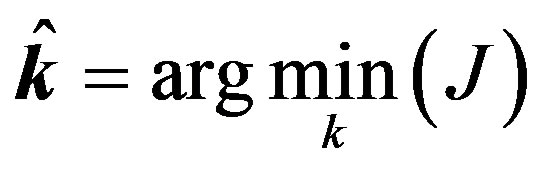 (5)
(5)
where the optimal solution 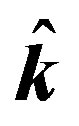 is the set of parameters that minimizes the cost function
is the set of parameters that minimizes the cost function 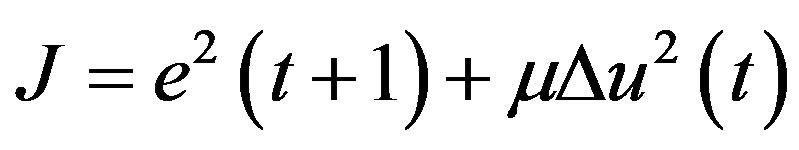 and
and 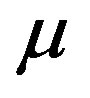 is a weighting penalty parameter.
is a weighting penalty parameter.
However, since 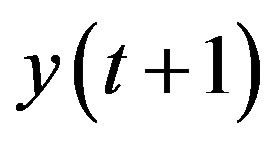 is not available at time t,
is not available at time t, 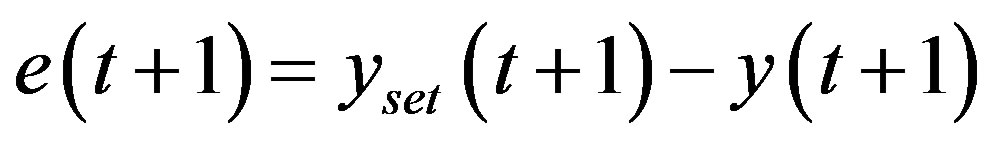 cannot be calculated. To overcome this limitation,
cannot be calculated. To overcome this limitation, 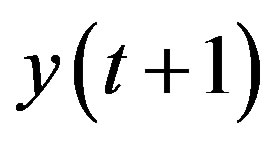 is estimated using the linearized ANN model. Therefore, the cost function J can be approximated by the cost function L:
is estimated using the linearized ANN model. Therefore, the cost function J can be approximated by the cost function L:
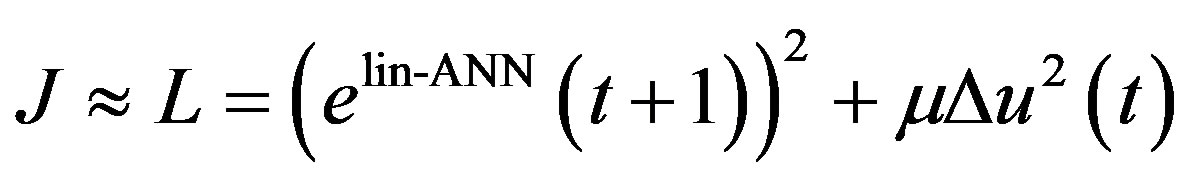 (6)
(6)
where 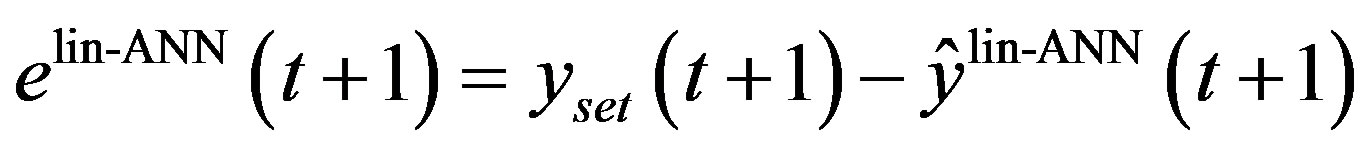 is the estimated trajectory tracking error and
is the estimated trajectory tracking error and 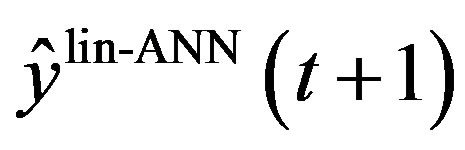 is the output estimated using the linearized ANN model.
is the output estimated using the linearized ANN model.
It can be demonstrated that the minimization of the cost function L can be achieved using a not iterative procedure. Instantaneous linearization of the ANN and minimization of the cost function are fully detailed in [32] [33] .
Finally, PID controller parameters are updated at each sampling time using:
 (7)
(7)
3.2. PEMFC ANN Model
This section is dedicated to the PEMFC ANN model design. This model is expected to predict the output voltage of the PEMFC one step ahead once the load current is available.
In this aim, various network architectures have been investigated to determine which one will provide the best prediction in terms of computational speed and accuracy. After comparing several architectures, a fully connected three layers feed forward network is retained. The input layer consists of one input, namely load current. The hidden layer has five neurons with tangential sigmoid activation function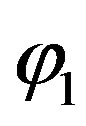 . The output layer, composed of 1 neuron with linear activation function
. The output layer, composed of 1 neuron with linear activation function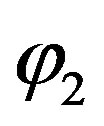 , provides the cell output voltage.
, provides the cell output voltage.
Regarding ANN model identification, the choice of the training data set is a quite important feature. Indeed, since ANN model performs better in interpolation than in extrapolation the training data set needs to cover a large range of operating conditions from minimum inputs/outputs values to maximum inputs/outputs values.
In the following, two sets of experimental data, sampled with a 3-second period and collected from the PEMFC system described in Section 2, are used. The training phase is performed on the first set using Levenberg-Marquardt algorithm with an error goal of 0.001, whereas the validation step is based on the second one (Figure 3).
Prediction performance of the ANN model is investigated using three criteria: the root mean squared error (RMSE), the absolute mean error (AME) and the absolute maximal error (AE¥). RMSE and AME are used to evaluate the model accuracy, whereas AE¥ represents the worst case in terms of prediction accuracy:
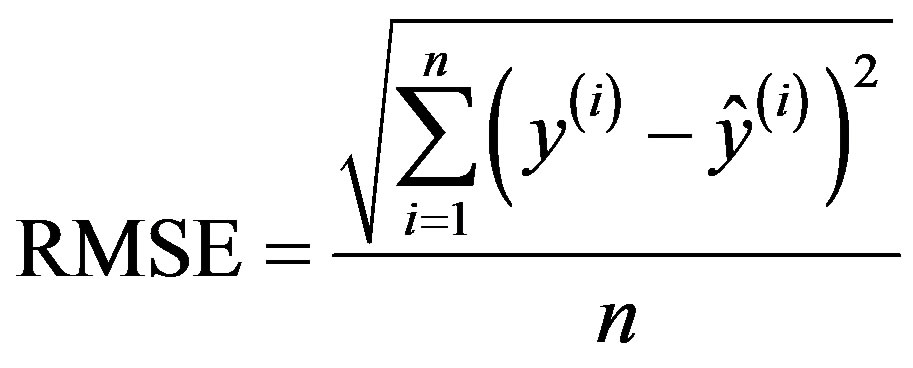 (8)
(8)
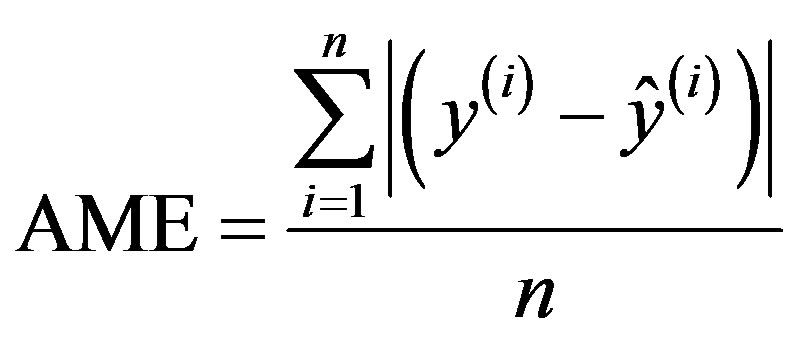 (9)
(9)
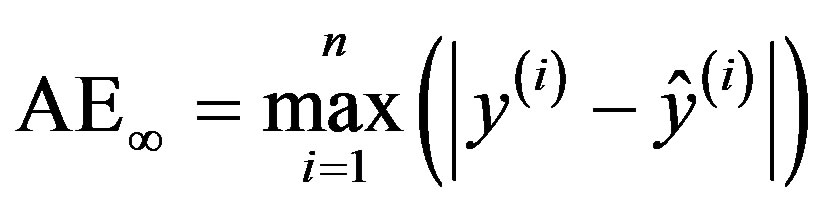 (10)
(10)
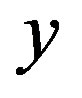 represents the experimental values,
represents the experimental values, 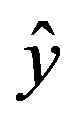 is the simulated data obtained using the ANN model and n is the number of data.
is the simulated data obtained using the ANN model and n is the number of data.
Prediction accuracy results of the proposed ANN model are summarized in Table 1.
Considering that the ANN model is dedicated to control purposes, the prediction accuracy performance is considered quite satisfactory.

Table 1. Training and validation results.
3.3. PEMFC control Scheme
The proposed self-tuning PID controller is used to regulate the output voltage of the PEMFC system (y) using the load current as manipulated variable (u) (Figure 4).
yset is the PEMFC output voltage setpoint, nu and ny are the number of past inputs and outputs used for determining the prediction. In the present work, nu and ny are both set to one. It is important to notice that the optimization problem that leads to optimal controller parameters is solved using a not iterative procedure, which is an important advantage to achieve real-time implementation, especially when dealing with fast dynamic systems.
4. On-Line Implementation and Experimental Results
To evaluate the applicability, efficiency and robustness of the proposed self-tuning PID control scheme several experiments, based on varying control scenarios and several output voltage profiles, are carried out. In this aim, the original built-in controller is overridden and the PID controller is implemented externally. The PID control strategy, implemented in Matlab® environment, is executed on-line and communicates with the SCDA system of the fuel cell.
In the sequel, load current is considered as manipulated variable, whereas output voltage is the controlled variable. The cell temperature and the sampling period are set to 70˚C and 3 s, respectively. It should be pointed out that an operating fuel cell plant requires the regulation of other variables, to avoid for instance oxygen starvation or membrane flooding or dehydration. It is assumed these variables have already been well controlled.
Performance of the proposed control strategy, especially in terms of setpoint tracking accuracy, is investigated on a typical output voltage profile (Figure 5) using the root mean squared error criteria. To evaluate the effect of the weighting penalty parameter 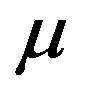 on the self-tuning PID controller performance, 3 cases are considered: case 1:
on the self-tuning PID controller performance, 3 cases are considered: case 1: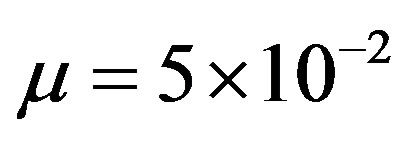 , case 2:
, case 2: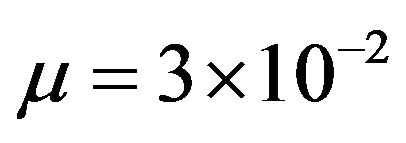 , and case 3:
, and case 3: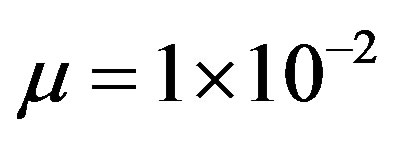 .
.
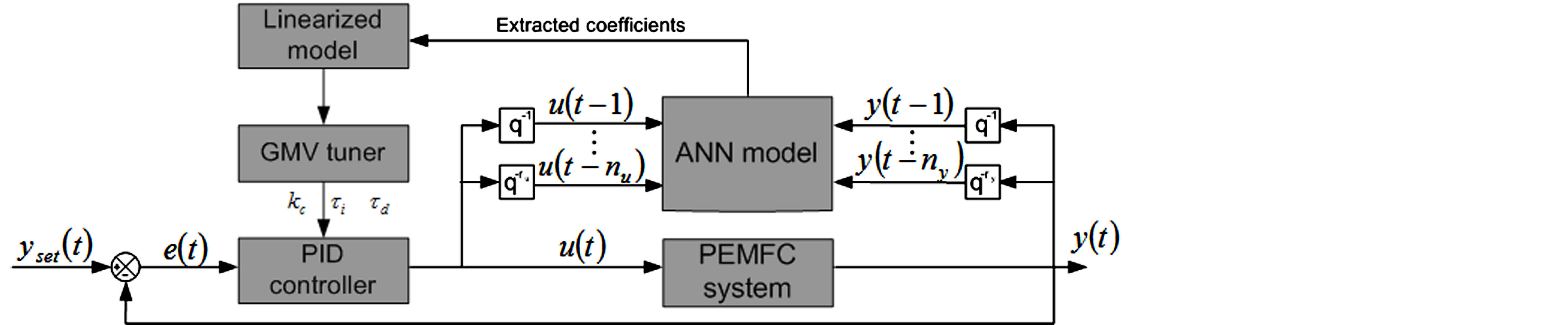
Figure 4. Control scheme of the PEMFC system based on self-tuning PID controller.
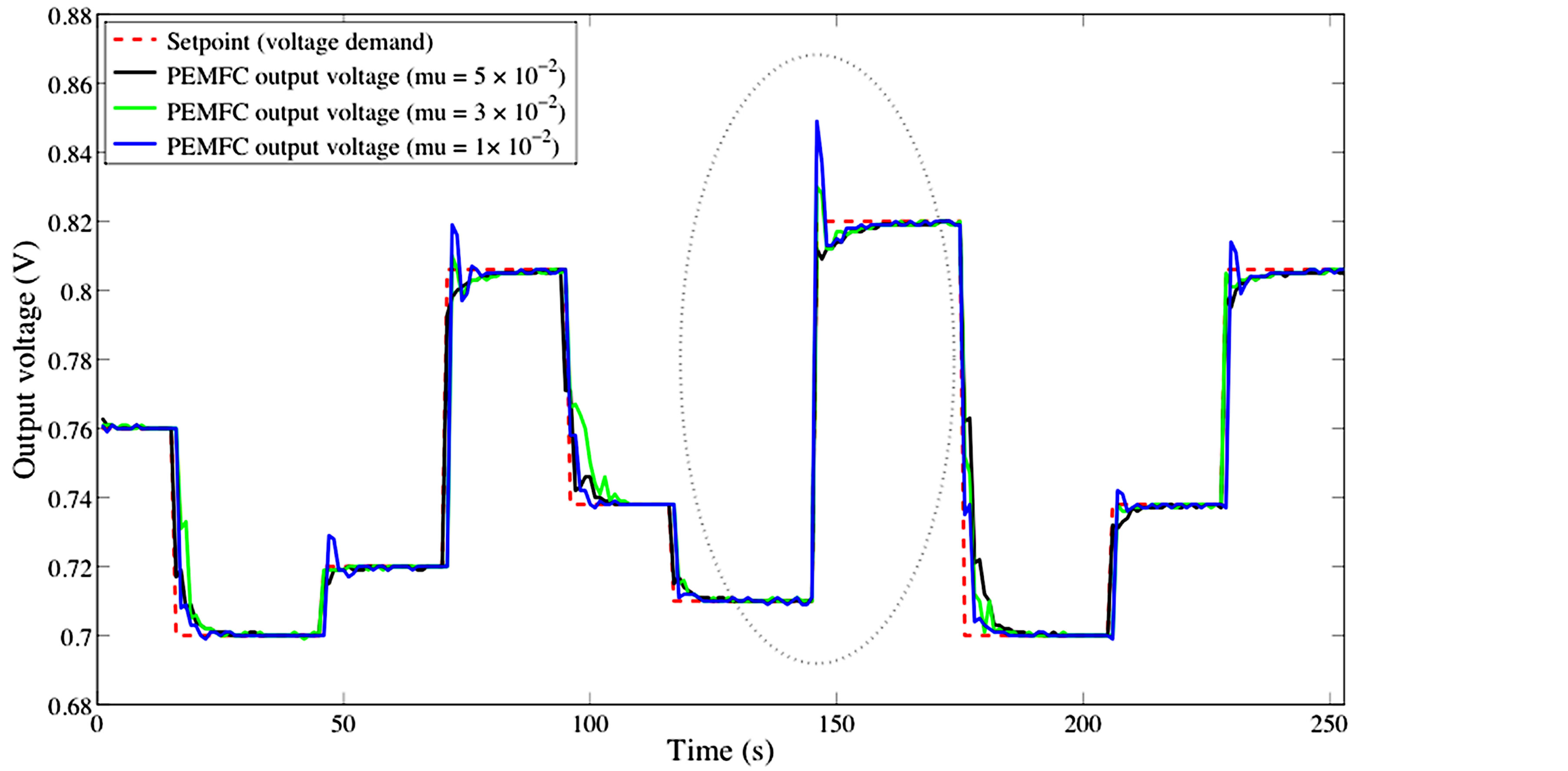
Figure 5. PEMFC output voltage setpoint tracking using self-tuning PID controller.

Table 2. Experimental setpoint tracking performance of the proposed PID controller.
Figure 5 and Table 2 illustrate the control effectiveness of the self-tuning PID controller for different values of . The proposed control strategy shows excellent accuracy in voltage setpoint tracking regardless of the value of the
. The proposed control strategy shows excellent accuracy in voltage setpoint tracking regardless of the value of the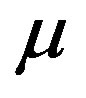 , which emphasizes among other things its robustness against plant/model mismatch.
, which emphasizes among other things its robustness against plant/model mismatch.
However, even if the overall setpoint tracking accuracy remains the same whatever the value of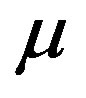 , it is important to notice that the value of
, it is important to notice that the value of 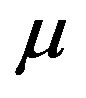 is strongly correlated with the overshoot. As illustrates on Figure 6, a decrease of the value of
is strongly correlated with the overshoot. As illustrates on Figure 6, a decrease of the value of  involves an increase of the overshoot.
involves an increase of the overshoot.
5. Conclusion and Prospects
In this work, a neural model-based self-tuning PID controller has been designed and experimentally tested online to control the output voltage of a PEMFC. Controller parameters have been updated on-line, at each sampling time, based on a linearized ANN model and a GMV control law. Combining GMV control design with instantaneous linearization allowed managing nonlinearities of the process, while avoiding heavy computations.
In a first stage, an artificial neural network model, expected to predict output voltage of the PMEFC, has been designed and experimentally validated. In a second stage, the performance of the proposed strategy has been evaluated through several experiments. In this aim, the original built-in controller has been overridden and the self-tuning PID controller has been implemented externally and executed on-line. Experimental results demonstrated the efficiency of the proposed approach in terms of setpoint tracking accuracy and robustness against plant/model mismatch.
Regarding fast dynamic nonlinear systems, such as PEMFC, the proposed self-tuning PID strategy turned out to be a promising alternative to heavy computation nonlinear control strategies and not optimal linear control strategies.