Natural Convective Boundary Layer Flow over a Horizontal Plate Embedded in a Porous Medium Saturated with a Nanofluid ()
1. Introduction
The study of convective heat transfer in nanofluids is gaining a lot of attention. The nanofluids have many applications in the industry since materials of nanometer size have unique physical and chemical properties. Nanofluids are solid-liquid composite materials consisting of solid nanoparticles or nanofibers with sizes typically of 1-100 nm suspended in liquid. Nanofluids have attracted great interest recently because of reports of greatly enhanced thermal properties. For example, a small amount (<1% volume fraction) of Cu nanoparticles or carbon nanotubes dispersed in ethylene glycol or oil is reported to increase the inherently poor thermal conductivity of the liquid by 40% and 150%, respectively [1,2]. Conventional particle-liquid suspensions require high concentrations (>10%) of particles to achieve such enhancement. However, problems of rheology and stability are amplified at high concentrations, precluding the widespread use of conventional slurries as heat transfer fluids. In some cases, the observed enhancement in thermal conductivity of nanofluids is orders of magnitude larger than predicted by well-established theories. Other perplexing results in this rapidly evolving field include a surprisingly strong temperature dependence of the thermal conductivity [3] and a three-fold higher critical heat flux compared with the base fluids [4,5]. These enhanced thermal properties are not merely of academic interest. If confirmed and found consistent, they would make nanofluids promising for applications in thermal management. Furthermore, suspensions of metal nanoparticles are also being developed for other purposes, such as medical applications including cancer therapy. The interdisciplinary nature of nanofluid research presents a great opportunity for exploration and discovery at the frontiers of nanotechnology.
Porous media heat transfer problems have several engineering applications such as geothermal energy recovery, crude oil extraction, ground water pollution, thermal energy storage and flow through filtering media. Cheng and Minkowycz [6] presented similarity solutions for free convective heat transfer from a vertical plate in a fluid-saturated porous medium. Gorla and co-workers [7,8] solved the nonsimilar problem of free convective heat transfer from a vertical plate embedded in a saturated porous medium with an arbitrarily varying surface temperature or heat flux. Chen and Chen [9] and Mehta and Rao [10] presented similarity solutions for free convection of non-Newtonian fluids over horizontal surfaces in porous media. Nakayama and Koyama [11] studied the natural convection over a non-isothermal body of arbitrary geometry placed in a porous medium. All these studies were concerned with Newtonian fluid flows. The boundary layer flows in nano fluids have been analyzed recently by Nield and Kuznetsov and Kuznetsov [12] and Nield and Kuznetsov [13]. A clear picture about the nanofluid boundary layer flows is still to emerge.
The present work has been undertaken in order to analyze the natural convection past an isothermal horizontal plate in a porous medium saturated by a nanofluid. The effects of Brownian motion and thermophoresis are included for the nanofluid. Numerical solutions of the boundary layer equations are obtained and discussion is provided for several values of the nanofluid parameters governing the problem.
2. Analysis
We consider the steady free convection boundary layer flow past a horizontal plate placed in a nano-fluid saturated porous medium. The co-ordinate system is selected such that x-axis is in the horizontal direction. We consider the two-dimensional problem. Figure 1 shows the coordinate system and flow model. At the surface, the temperature T and the nano-particle fraction take constant values TW and ϕW, respectively. The ambient values, attained as y tends to infinity, of T and are denoted by T∞ and ϕ∞, respectively.
The Oberbeck-Boussinesq approximation is employed and the homogeneity and local thermal equilibrium in the porous medium are assumed. We consider the porous medium whose porosity is denoted by ε and permeability by K. The Darcy velocity is denoted by 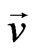 . The following four field equations embody the conservation of total mass, momentum, thermal energy, and nano-particles, respectively. The field variables are the Darcy velocity
. The following four field equations embody the conservation of total mass, momentum, thermal energy, and nano-particles, respectively. The field variables are the Darcy velocity , the temperature T and the nano-particle volume fraction.
, the temperature T and the nano-particle volume fraction.
 (1)
(1)
 (2)
(2)
 (3)
(3)

Figure 1. Coordinate system and flow model.
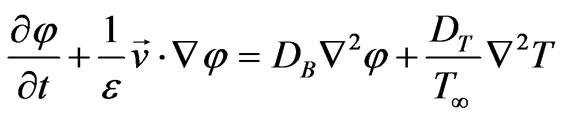 (4)
(4)
We write .
.
Here , μ and β are the density, viscosity and volumetric volume expansion coefficient of the fluid;
, μ and β are the density, viscosity and volumetric volume expansion coefficient of the fluid; 
the density of the particles; g the gravitational acceleration;  the effective heat capacity and km effective thermal conductivity of the porous medium and DB the Brownian diffusion coefficient and DT the thermophoretic diffusion coefficient. The flow is assumed to be slow so that an advective term and a Forchheimer quadratic drag term do not appear in the momentum equation.
the effective heat capacity and km effective thermal conductivity of the porous medium and DB the Brownian diffusion coefficient and DT the thermophoretic diffusion coefficient. The flow is assumed to be slow so that an advective term and a Forchheimer quadratic drag term do not appear in the momentum equation.
The boundary conditions are taken to be
 (5)
(5)
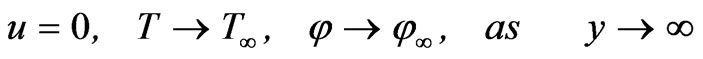 (6)
(6)
We consider the steady state flow. In keeping with the Oberbeck-Boussinesq approximation and an assumption that the nano-particle concentration is dilute, the momentum equation may be written as:
 (7)
(7)
We now make the standard boundary layer approximation based on a scale analysis and write the governing equations.
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
where
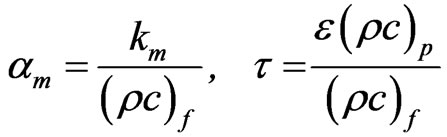 (13)
(13)
One can eliminate P from Equations (9) and (10) by cross-differentiation. At the same time one can introduce a stream line function ψ such that the continuity is automatically satisfied:
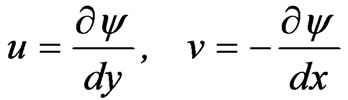 (14)
(14)
We are then left with the following three equations.
 (15)
(15)
 (16)
(16)
 (17)
(17)
Proceeding with the analysis we introduce the following dimensionless variables:




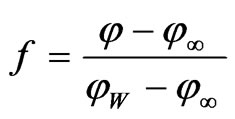 (18)
(18)
We assume that Tw and  are constants.
are constants.
Substituting the expressions in Equation (18) into the governing Equations (15)-(17) we obtain the following transformed equations:
 (19)
(19)
 (20)
(20)
 (21)
(21)
where the four parameters are defined as:
 ,
,
 ,
,
 ,
,
 (22)
(22)
The transformed boundary conditions are:
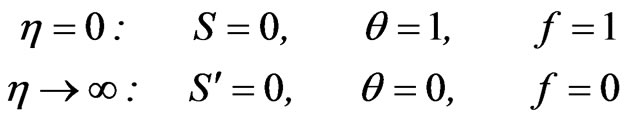 (23)
(23)
The local friction factor may be written as
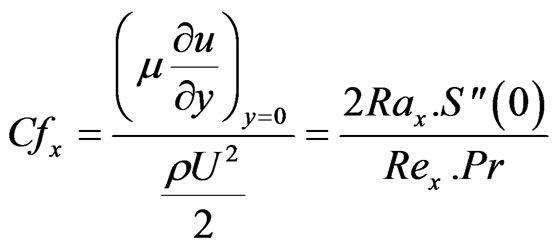
The heat transfer rate at the surface is given by:
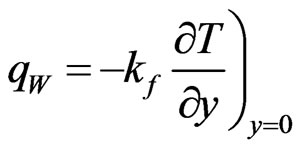
The heat transfer coefficient is given by:

Local Nusselt number is given by:
 (24)
(24)
The mass transfer rate at the surface is given by:

where  = mass transfer coefficientThe local Sherwood number is given by:
= mass transfer coefficientThe local Sherwood number is given by:
 (25)
(25)
3. Results and Discussion
3.1. Numerical Method
The system of Equations (19)-(21) with the boundary conditions (23) is solved numerically by means of an efficient, iterative, tri-diagonal implicit finite-difference method discussed previously by Blottner [13]. Equations (19)-(21) are discretized using three-point central difference formulae with  replaced by another variable V. The h direction is divided into 196 nodal points and a variable step size is used to account for the sharp changes in the variables in the region close to the surface where viscous effects dominate. The initial step size used is
replaced by another variable V. The h direction is divided into 196 nodal points and a variable step size is used to account for the sharp changes in the variables in the region close to the surface where viscous effects dominate. The initial step size used is 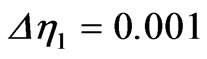 and the growth factor
and the growth factor  such that
such that  (where the subscript n is the number of nodes minus one). This gives
(where the subscript n is the number of nodes minus one). This gives ≈ 35 which represents the edge of the boundary layer at infinity. The ordinary differential equations are then converted into linear algebraic equations that are solved by the Thomas algorithm discussed by Blottner [14]. Iteration is employed to deal with the nonlinear nature of the governing equations. The convergence criterion employed in this work was based on the relative difference between the current and the previous iterations. When this difference or error reached 10-5, the solution was assumed converged and the iteration process was terminated.
≈ 35 which represents the edge of the boundary layer at infinity. The ordinary differential equations are then converted into linear algebraic equations that are solved by the Thomas algorithm discussed by Blottner [14]. Iteration is employed to deal with the nonlinear nature of the governing equations. The convergence criterion employed in this work was based on the relative difference between the current and the previous iterations. When this difference or error reached 10-5, the solution was assumed converged and the iteration process was terminated.
Equations (19)-(21) were solved numerically to satisfy the boundary conditions (23) for parametric values of Le, Nr (buoyancy ratio number), Nb (Brownian motion parameter) and Nt (thermophoresis parameter) using finite difference method. Tables 1-5 indicate results for wall values for the gradients of velocity, temperature and concentration functions which are proportional to the friction factor, Nusselt number and Sherwood numberrespectively. From Tables 1-3, we notice that as Nr and Nt increase, the friction factor increases whereas the heat transfer rate (Nusselt number) and mass transfer rate (Sherwood number) decrease. As Nb increases, the fric-

Table 1. Effects of Nr on S"(0), −θ'(0) and −f'(0) for Nb = 0.3, Nt = 0.1 and Le = 10.
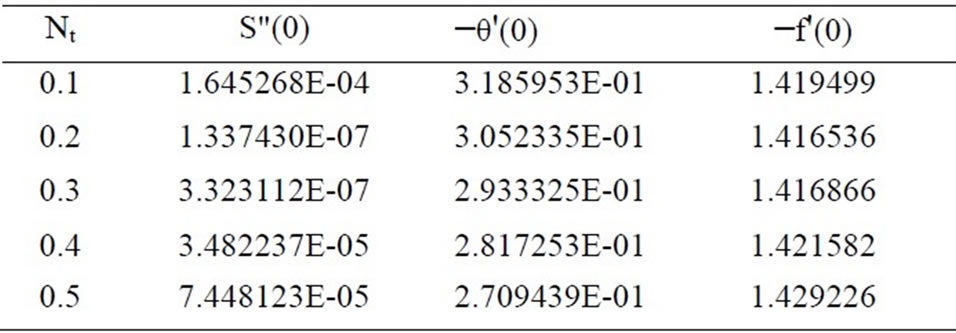
Table 2. Effects of Nt on S"(0), −θ'(0) and −f'(0) for Nb = 0.3, Nr = 0.5 and Le = 10.
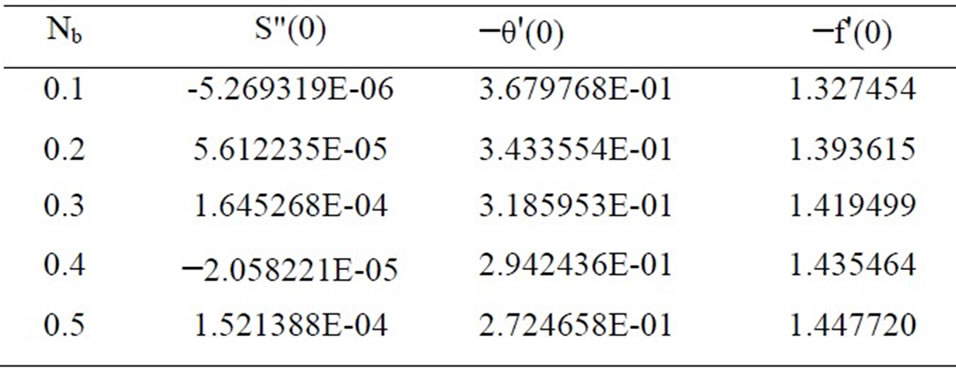
Table 3. Effects of Nb on S"(0), −θ'(0) and −f'(0) for Nr=0.5, Nt=0.1 and Le=10.
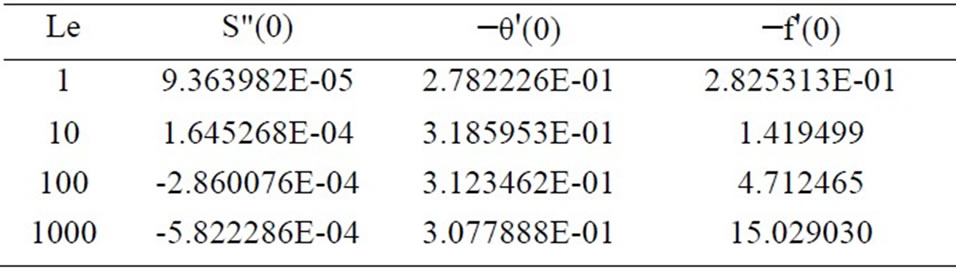
Table 4. Effects of Le on S"(0), −θ'(0) and −f'(0) for Nb=0.3, Nr = 0.5, and Nt = 0.1.

Table 5. Effects of Le on S"(0), −θ'(0) and −f'(0) for Nb = 0, Nr = 0, and Nt = 0.
tion factor and surface mass transfer rates increase whereas the surface heat transfer rate decreases. Results from Table 4 indicate that as Le increases, the heat and mass transfer rates increase. From Table 5, we observe that the nano fluids display drag reducing and heat and mass transfer rate reducing characteristics.
Figures 2-4 indicate that as Nr increases, the velocity decreases and the temperature and concentration increase. Similar effects are observed from Figures 5-10 as Nt and Nb vary.
Figure 11 illustrates the variation of velocity within the boundary layer as Le increases. The velocity increases as Le increases. From Figures 12 and 13, we observe that as Le increases, the temperature and concentration within the boundary layer decrease and the thermal and concentration boundary later thicknesses decrease.
The influence of nanoparticles on natural convection is modeled by accounting for Brownian motion and thermophoresis as well as non-isothermal boundary conditions. The thickness of the boundary layer for the mass fraction is smaller than the thermal boundary layer thickness for Large values of Lewis number Le. The contribution of Nt to heat and mass transfer does not depend on the value of Le. The Brownian motion and thermophoresis of nano particles increases the effective thermal conductivity of the nanofluid. Both Brownian diffusion and thermophoresis give rise to cross diffusion terms that are similar to the familiar Soret and Dufour cross diffusion terms that arise with a binary fluid discussed by Lakshmi Narayana et al. [15].
4. Concluding Remarks
In this paper, we presented a boundary layer analysis for
the natural convection past a non-isothermal vertical
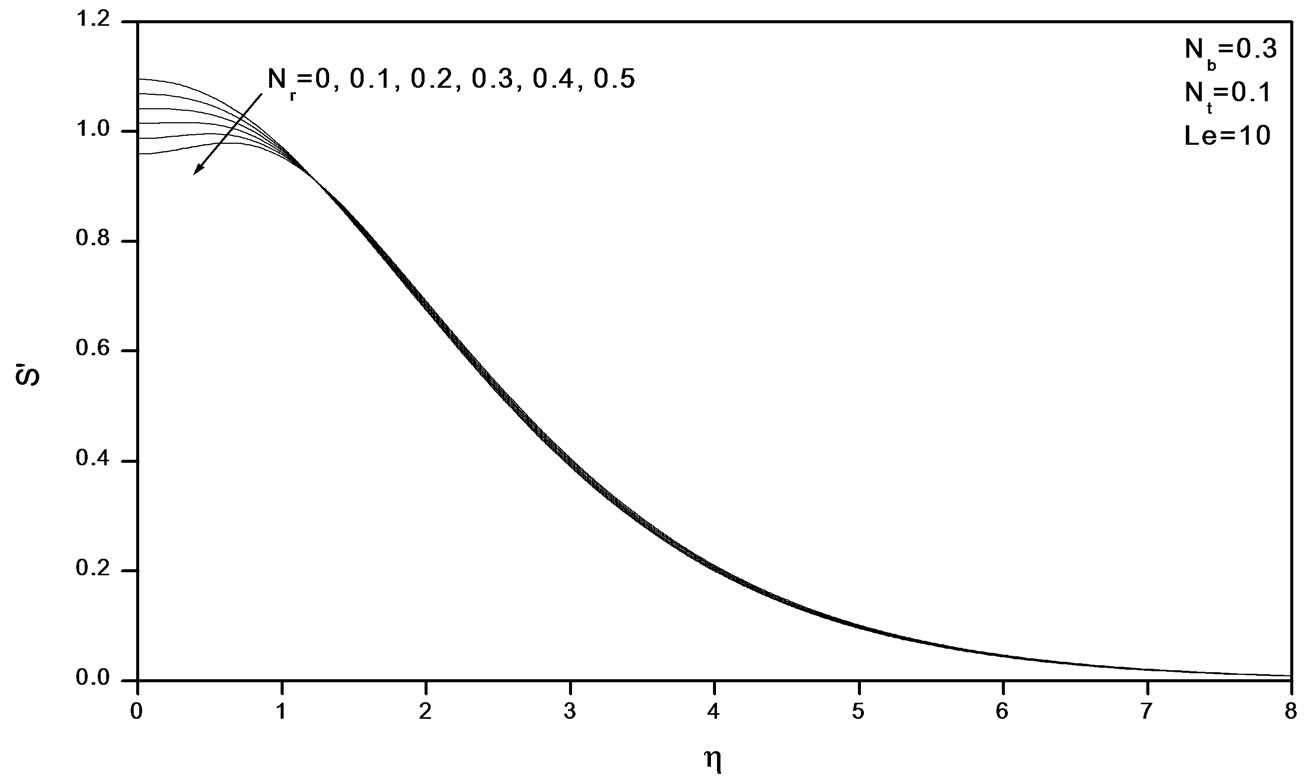
Figure 2. Effects of Nr on velocity profiles.

Figure 3. Effects of Nr on temperature profiles.

Figure 4. Effects of Nr on volume fraction profiles.

Figure 5. Effects of Nt on velocity profiles.
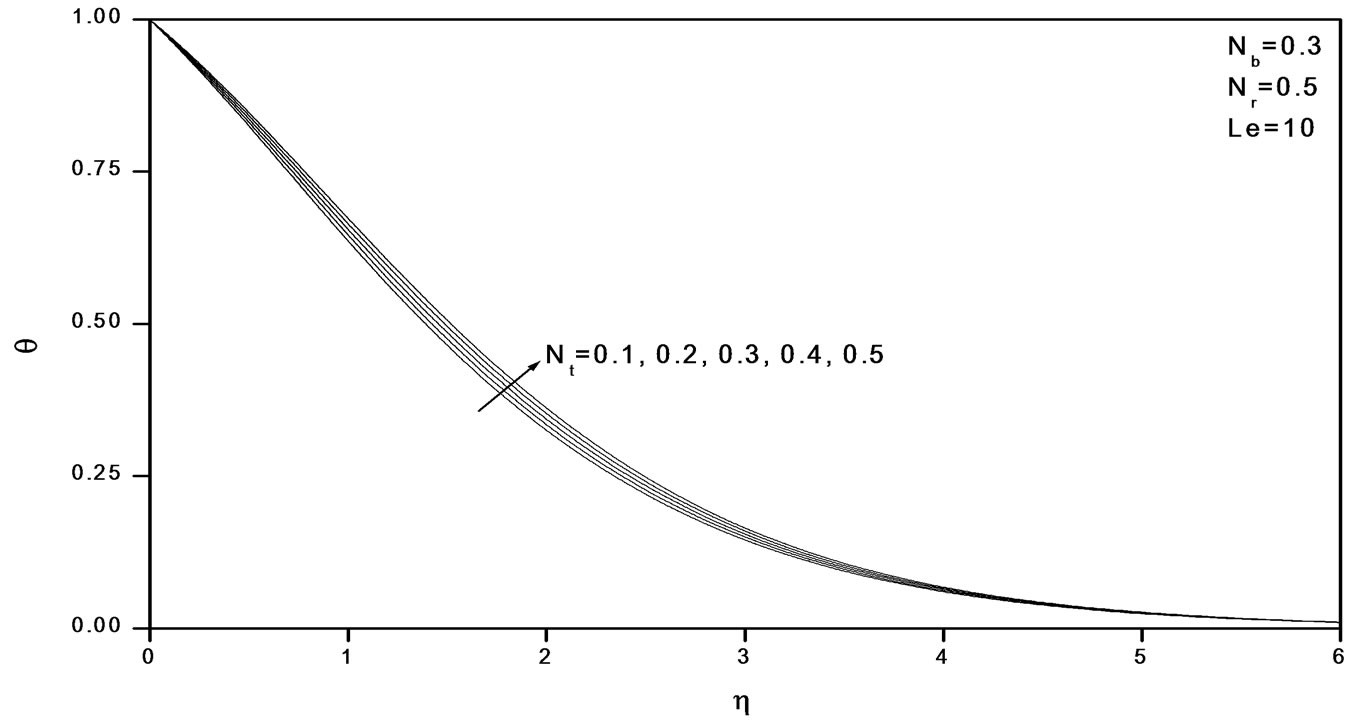
Figure 6. Effects of Nt on temperature profiles.

Figure 7. Effects of Nt on volume fraction profiles.

Figure 8. Effects of Nb on velocity profiles.

Figure 9. Effects of Nb on temperature profiles.

Figure 10. Effects of Nb on volume fraction profiles.

Figure 11. Effects of Le on velocity profiles.

Figure 12. Effects of Le on temperature profiles.

Figure 13. Effects of Le on volume fraction profiles.
plate in a porous medium saturated with a nano fluid. Numerical results for friction factor, surface heat transfer rate and mass transfer rate have been presented for parametric variations of the buoyancy ratio parameter Nr, Brownian motion parameter Nb, thermophoresis parameter Nt and Lewis number Le. The results indicate that as Nr and Nt increase, the friction factor increases whereas the heat transfer rate (Nusselt number) and mass transfer rate (Sherwood number) decrease. As Nb increases, the friction factor and surface mass transfer rates increase whereas the surface heat transfer rate decreases. As Le increases, the heat and mass transfer rates increase. Nano fluids display drag reducing and heat and mass transfer rate reducing characteristics.