2. Literature Review
2.1. Kuratowski Closure Operator
A closure operator is an arbitrary set-valued, set-function  where
where  is the power set of a non-void set
is the power set of a non-void set  that satisfies some closure axioms [1]. Consequently, various combinations of the following axioms have been used in the past in an attempt to define closure operators [2]. Let
that satisfies some closure axioms [1]. Consequently, various combinations of the following axioms have been used in the past in an attempt to define closure operators [2]. Let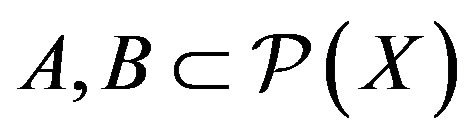 .
.
1) Grounded: 
2) Expansive: 
3) Sub-additive: . This axiom implies the Isotony axiom:
. This axiom implies the Isotony axiom: implies
implies 
4) Idempotent: 
The structure , where
, where 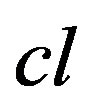 satisfies the first three axioms is called a closure space [2].
satisfies the first three axioms is called a closure space [2].
2.2. Isotonic Space
A closure space  satisfying only the grounded and the Isotony closure axioms is called an isotonic space [3]. This is the space of interest in this study and clearly, it is more general than a closure space.
satisfying only the grounded and the Isotony closure axioms is called an isotonic space [3]. This is the space of interest in this study and clearly, it is more general than a closure space.
In a dual formulation, a space  is isotonic if and only if the interior function
is isotonic if and only if the interior function satisfies;
satisfies;
1)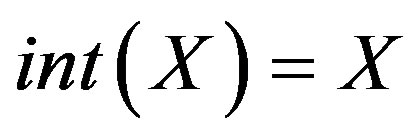 .
.
2)  implies
implies 
2.3. Category
A category has objects  and arrows
and arrows  such that
such that , i.e.
, i.e. 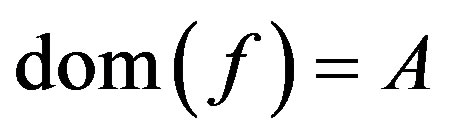 and
and . Two arrows
. Two arrows  and
and 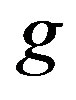 such that
such that  are said to be composable [4].
are said to be composable [4].
Axioms of a Category
According to [5], the following are the axioms of a category;
1) If  and
and  are composable, then they must have a composite which is the arrow shown
are composable, then they must have a composite which is the arrow shown  shown in the diagram below
shown in the diagram below

The arrow  goes from the
goes from the  to the
to the  such that
such that 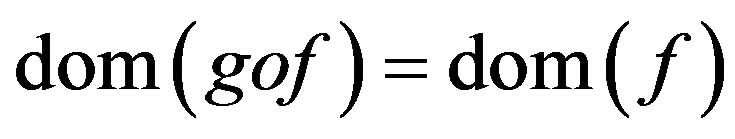 and the
and the

1) For every object  there exists the identity arrow
there exists the identity arrow .
.
2) Composition is associative. This can be represented in as shown below;

3. Main Results
3.1. Quasi-Isotone Space
A closure space  with a closure operator
with a closure operator 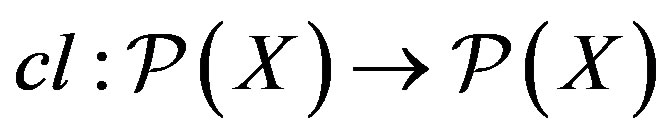 is called a quasi-isotone space if the closure operator satisfies the following three Kuratowski closure axioms 1)
is called a quasi-isotone space if the closure operator satisfies the following three Kuratowski closure axioms 1) 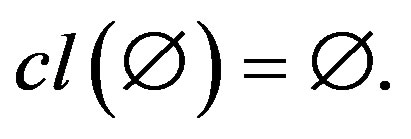
2) For 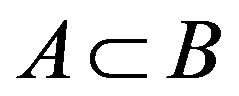 implies
implies 
3)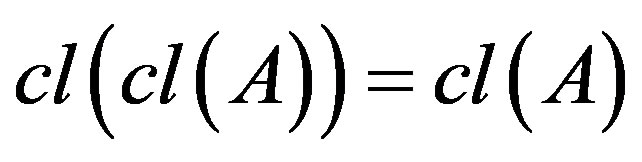 .
.
The third axiom is called the idempotent axiom. It will become very useful while defining the pseudo-category on the quasi-isotone space.
3.2. Pseudo-Category
To define a pseudo-category on the class of quasi-isotone space, we firstly need to identify the objects and morphisms on this class of spaces. The objects are the closure operators  such that they obey the three Kuratowski axioms above.
such that they obey the three Kuratowski axioms above.
Next is to define the morphisms on the category. The arrows linking the objects together are  such that
such that . More explicitly, the arrow
. More explicitly, the arrow 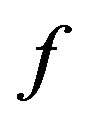 may be represented diagrammatically by;
may be represented diagrammatically by;

Therefore, the pseudo-category on quasi-isotone space has as objects the closure operators  and
and  such that
such that 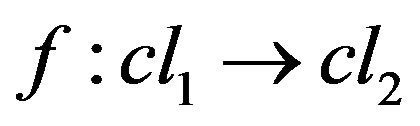 as the morphisms. Of course two arrows
as the morphisms. Of course two arrows  and
and  such that
such that  are said to be composable
are said to be composable
Axioms of the Pseudo-Category
1) If  and
and 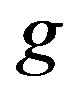 are composable, then they must have a composite which is the arrow
are composable, then they must have a composite which is the arrow  shown in the diagram below
shown in the diagram below

The arrow  goes from the
goes from the  to the
to the  such that
such that  and the
and the
 .
.
2) For every object  there exists the identity arrow
there exists the identity arrow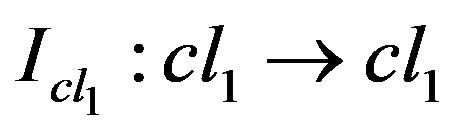 . The existence of this identity arrow is guaranteed by the idempotent axiom defined on the quasi-isotone axiom. Indeed, the name pseudo-category for this structure is adopted since the idempotent axiom is not exactly an identity function.
. The existence of this identity arrow is guaranteed by the idempotent axiom defined on the quasi-isotone axiom. Indeed, the name pseudo-category for this structure is adopted since the idempotent axiom is not exactly an identity function.
3) Composition is associative. This can be representedas in the diagram below:

4. Remark
Other notions of a category may also be defined on the pseudo-category of quasi-isotone spaces. They include functors, natural transformations, adjunctions among others.
5. Conclusion
On a space defined by the Kuratowski closure axioms, it is possible to define a category-like structure in a very natural and straightforward way. This will enable some mathematical analysis to be extended onto closure spaces.
[1] W. J. Thron, “What Results Are Valid on Cech-Closure Spaces,” Topology Proceedings, Vol. 6, No. 3, 1981, pp. 135-158.
[2] T. A Sunitha, “A Study of Cech Closure Spaces,” Doctor of Philosophy Thesis, School of Mathematical Sciences, Cochin University of Science and Technology, Cochin, 1994.
[3] A. K. Elzenati and E. D. Habil, “Connectedness in Isotonic Spaces,” Turkish Journal of Mathematics, Vol. 30, No. 3, 2006, pp. 247-262.
[4] C. McLarty, “Elementary Categories, Elementary Toposes,” Oxford University Press, Oxford, 1992.
[5] S. MacLane, “Category for the Working Mathematician,” 2nd Edition, Springer-Verlag Inc., New York, 1998.