1) A two-way lunar ranging precision measurement at Apache Point Lunar Laser-ranging Operation (APOLLO) facility of the velocity of light has been finding the latter’s tabular value c = 2.99792458 × 108 m·s−1 to exceed by 200 ± 10 m·s−1 [1];
2) The Oscillation Project with Emulsion tRacking Apparatus (OPERA) at the underground Gran Sasso Laboratory (LNGS) has measured the (one-way) velocity of neutrinos from the CERN CNGS over a base line of 731 km and has out of more than 16,000 events been finding an earlier arrival time of the latter with respect to c by (60.7 ± 6.9 (stat.) ± 7.4 (sys.)) ns, which corresponds to (vv − c)/c ≈ 2.5 × 10−5 and, thus, vv > c, where vv denotes velocity of neutrino [2];
3) Other than OPERA in # 2) has the Imaging Cosmic And Rare Underground Signals (ICARUS) Collaboration over the same base line of 731 km from CERN, with their detector in direct neighborhood to OPERA, out of seven beam-associated events the time of flight difference between the speed of light and the arriving neutrino events been finding (vv − c)/c = 0, i.e. simultaneous arrival of all events with equal speed, the one of light [3]. And very recently CERN announced that now all four experiments situated at Gran Sasso, including OPERA, measure a neutrino time of flight consistent with the speed of light (press release 2012-06-08);
4) Most recently for the LVD (Large Volume Detector) Collaboration and OPERA as well has been announced proof against superluminal neutrinos without the need of knowing the CERN-LNGS distance 731 km by comparison of timing at OPERA and LVD using the cosmic ray muons traversing both experiments due to a geologic anomaly of the mountainous terrain from the same direction as the CERN neutrinos roughly [4,5];
5) Position measuring of pulsar B 1951 + 32 relative to background radio sources at four epochs between 1989 and 2000 revealed pulsar age of ≈ 64 ± 18 kyr, considerably less than its characteristic age of 107 kyr, considered to approximate its true age [6];
6) Proper motions of optical filaments of the Crab nebula with a base line > 50 yr projected backward indicate the mean date of the supernova event as A. D. 1130 22 ± 16 yr in comparison to the authentic historical date A. D. 1054, implying that since the latter the outward velocity of the nebula has accelerated (e.g. [7]);
7) The lightcurves of over 800 quasars in different areas of the sky on time scales up to 28 years at distances between 6 × 109 ly and 10 × 109 ly have been found to exhibit no effect of cosmological time dilation 1 + z [8];
8) Contrary and in contrast to # 7) in a study of the redhift of seven supernovae (SN) at redshifts between z = 0.35 and 0.46, the majority of the lightcurves have been found generally to be broadened as expected from the big bang model in the order of 1 + z; i.e. the latter broadening of the lightcurves’ width is attributed to the cosmological time dilation associated with the expanding Universe [9]. In two more recent works this result has been confirmed by studying the broadening of the latter width of several hundred SN in the redshift—range z = 0.3 to 0.7 [10] and in the case of the Type Ia SN 1997ex with redshift z = 0.361 [11];
9) From the fractional counting rates of diverse nuclides has been found the respective decay constant of the latter to be modulated annually in the order of ≈3 × 10−3, and, as it seems, about in phase with the varying distance squared of the Earth to the Sun in the course of the year. Thereby have been measured higher counts or a faster decay rate in the period January and slower counts in the summer period July, respectively (e.g. [12] and [13]);
10) An analysis of the combined data of cosmic ray muons from MACRO, LVD and Borexino experiment at the LNGS, gathered over a time period of 20 years, has revealed the muon flux to exhibit a large amplitude fluctuation with a period of one year and a phase of half a year. Especially has been found this annual modulation to have a peak in the summer of the northern hemisphere and the lowest value in winter [14].
11) The interaction-radius and total cross section in collisions of elementary particles (hadrons) have been found to increase steadily with higher velocity of the latter, i.e. rising energy of the beam, from √s = 5 GeV up to 7 TeV, where √s denotes total center-of-mass energy (e.g. [15] and [16]);
12) The mean-free-paths of ultra relativistic particles (nucleii) traversing different material media have been found to shrink in dependence on (center-of-mass) energy (e.g. [17]).
As widely known, special relativity rests on two premises:
1) The invariance of the physical laws for all observers, independently of the state of inertial motion (Galileian principle of relativity);
2) The constancy of the velocity of light in a frame of rest independently of the velocity of the source (Einsteinian extension of 1)), implying the former velocity to be the upper bound of velocity in vacuo.
Therefrom, on the grounds of a two-way gedanken experiment, the Lorentz transformation results automatically. Notably, the latter establishes symmetry between inertial frames in such a way that the transformation from the state of rest to the one of motion be identical to its inverse, implying that the latter states are indistinguishable one from another physically, i.e. they are Lorentz-invariant. But one should notice that originally the principle of relativity has been introduced into the kinematical theory on a mere hypothetical basis (Copernicus, Galilei, Poincaré, Einstein).
A reconsideration of the kinematics of special relativity by rigidly differentiating between state of motion and state of rest will result in proposing a novel definition of the concept of velocity between any two inertial frames of reference and a modification of the Lorentz transformation. In some aspects, the predictions of this proposed novel kinematical notion markedly deviate from canonical special relativity, especially at velocities near that of light and, thus, will explain the previously mentioned experimentally verified but seemingly unrelated and, as already mentioned, partly even contradictionary physical phenomena both qualitatively and quantitatively commonly being of special relativistic origin. Furthermore, up to now, the only hypothetical principle of relativity will be derivated theoretically.
2. SYMMETRY OF SPACETIME
2.1. Is Inertial Motion Quantized?
Consider a system S2 (x2, y2, z2, t2) moving inertially at constant uniform speed “w” parallelly to a system Σ (x, y, z, t) and the latter moving at the velocity “v” relative to an observer resting in the coordinate source of a system S1 (x1, y1, z1, t1) “at rest”, according to the principle of relativity.
1) It will be demonstrated that the resulting relativistically composite velocity  of S2 - as observed from S1—is variable, dependent on the respective value of v and w, but where
of S2 - as observed from S1—is variable, dependent on the respective value of v and w, but where 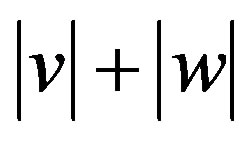 is always constant. Einstein considered
is always constant. Einstein considered
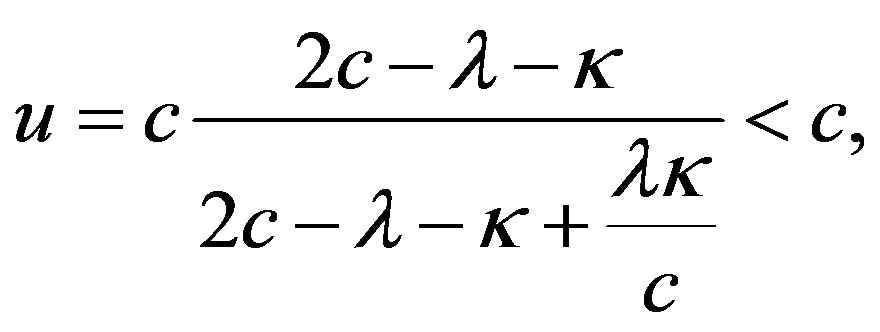 (1)
(1)
in order to prove the relativistic sum of two velocities which are slower than light always to result in a velocity slower than light [18]. We posit v = c − λ, w = c − κ and λmax = λ + κ, whereby always λmax > (λmax − λ) > 0. From Eq.1 follows

if the postulates are satisfied: 0 < (λmax = const) ≤ 2c, λ ≤ c, κ ≤ c. Clearly u reaches a maximum value if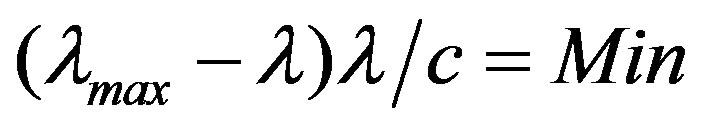 . This is the case if (λmax − λ), or λ, reaches its maximum value. The composite velocity u reaches its minimum value if λ = κ and λmax = 2λ = 2κ:
. This is the case if (λmax − λ), or λ, reaches its maximum value. The composite velocity u reaches its minimum value if λ = κ and λmax = 2λ = 2κ:
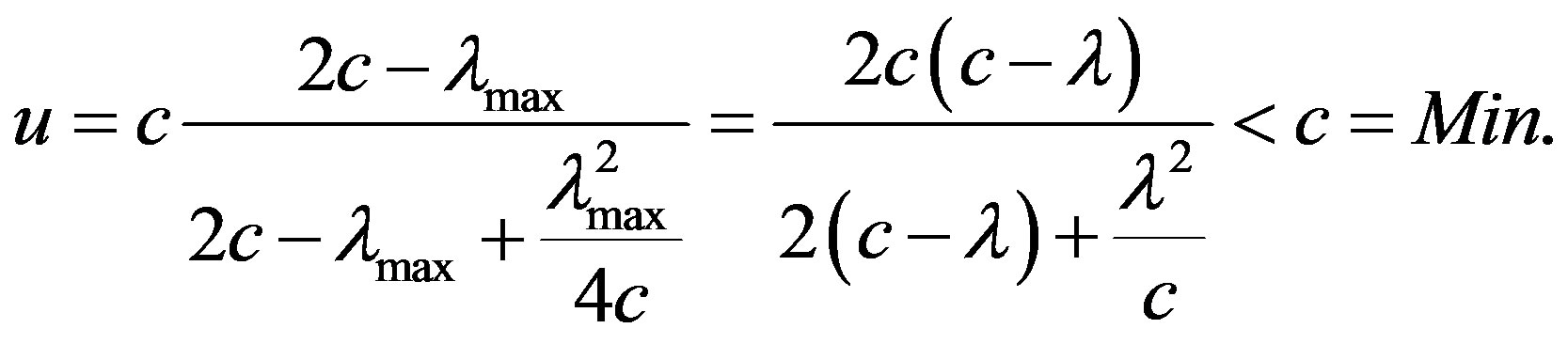
which attains the form
 (2)
(2)
if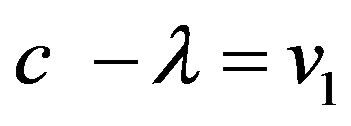 .
.
2) If vice versa u = const it seems clear that any points Σ could simultaneously exist (can be thought of or physically realized) between S1 and S2 so that any relativistic sum (v + w)/(1 + vw/c2) = const conceivably would yield u with |v| + |w| = Max. = 2v1> u if (2) is valid and |v| + |w| = Min. = u < 2v1 if Σ coincides with S1 or S2. Thus—considering the extremes only—apparently the following is valid:
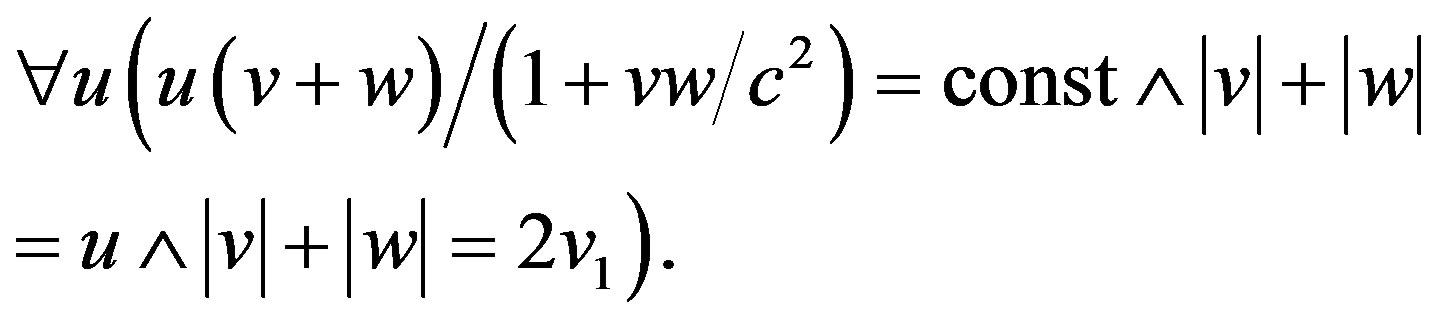
3) Now we maintain that the symmetrically composite velocity (2) is the only existing proper velocity of S2 relative to S1 implying both systems to move symmetrically at equal but oppositely directed velocity v1 relative to a point in spacetime considered to be at rest, now designated Σ0:
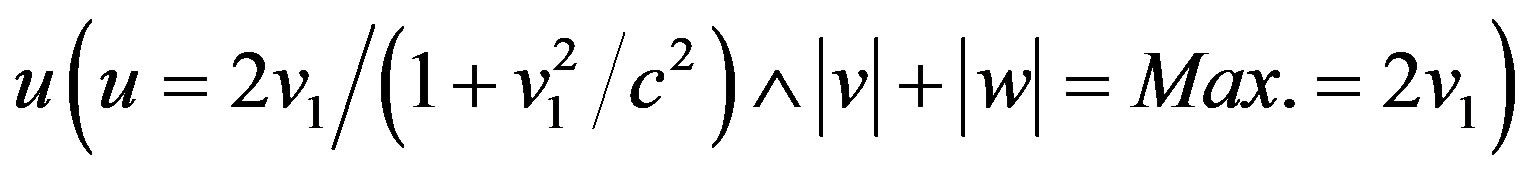 .
.
4) Consider 2) to be true. In this case the velocity of Σ0 relative to S1 will be v1 and the distance S1S2, as observed from Σ0, for reasons of symmetry 2v1 × Δt0. Thus, it must be valid
 (2a)
(2a)
whereby u in the left-hand member according to 2) apparently could be non-composite and simultaneously composite. If a light signal is transmitted from S2 to S1 via Σ0 it shall travel the distance between those systems in the time
 (2b)
(2b)
The light signal must in any case propagate via Σ0. A non-composite u does not exist in the space time of Σ0, respectively contains Σ0. This requires u in the left-hand member to be symmetrically composite. Thus, u to be non-composite is ruled out as well as any other composite velocity with no point Σ0. Therefore, 2) must be false and 3) true so that (2b) attains the only possible form
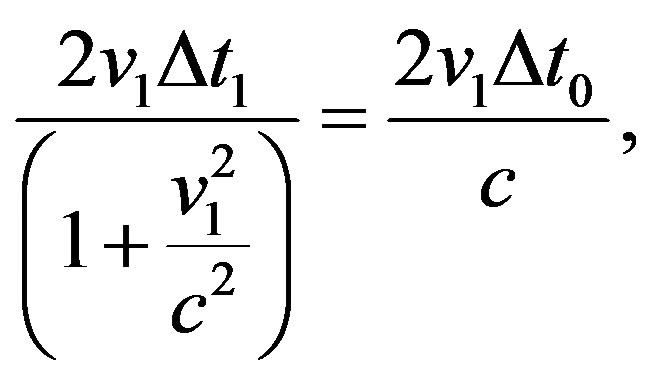 (2c)
(2c)
which guarantees the light signal to propagate via Σ0.
5) Hence, between any two inertial frames of reference S1 and S2, moving relative to each other with constant uniform speed, an inherent preferred reference point Σ0 always exists at rest—for the time of the translational motion—relative to S1 and S2 implying their velocity relative to Σ0 to be symmetrically equal and oppositely directed such that relative to another the relativistic sum (2) must be valid.
The chain of evidence and the result that any velocity u be symmetrically composite is also valid for the velocities “v1”, “v2” etc. Thus, a point Σ1 must exist also between Σ0 and S2, a point Σ2 between Σ0 and Σ1, Σ1 and S1, or S2 and so forth. This leads to
 (3)
(3)
where . Hence, the relative translational motion between any two inertial systems S1 and S2 must be the relativistic sum of 2n quanta of velocity. Therefrom follows that the following must be valid:
. Hence, the relative translational motion between any two inertial systems S1 and S2 must be the relativistic sum of 2n quanta of velocity. Therefrom follows that the following must be valid:
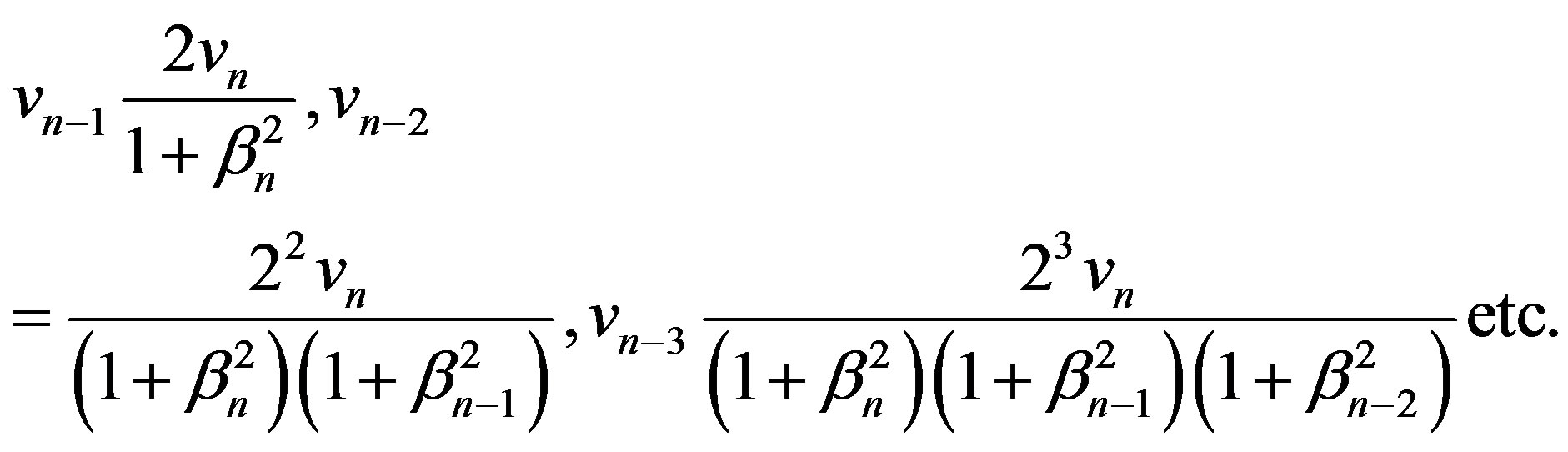
resulting in the product
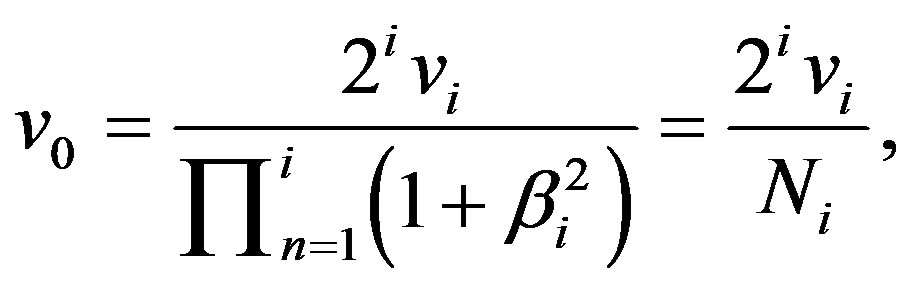 (4)
(4)
where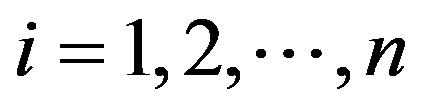 . Henceforth, v0 designates naturally composite velocity in the sense of the latter formula and it is clear that this form of velocity quantization maintains the group property of spacetime. It follows that if 2n = Nn, this implies v0 = c.
. Henceforth, v0 designates naturally composite velocity in the sense of the latter formula and it is clear that this form of velocity quantization maintains the group property of spacetime. It follows that if 2n = Nn, this implies v0 = c.
The result that every velocity is quantized in the order of Eq.3 and all elements of (4) without any exception have a common attribute , where
, where , implies the laws of well-arranged sets to be applicable, or, with other words: Eq.3 is a well-arranged set. The well-known definition of well-arranged sets applied on Eq.4 implies that a first minimum composite velocity “vmin” different from zero exists. Furthermore, it follows that product (4) is finite and
, implies the laws of well-arranged sets to be applicable, or, with other words: Eq.3 is a well-arranged set. The well-known definition of well-arranged sets applied on Eq.4 implies that a first minimum composite velocity “vmin” different from zero exists. Furthermore, it follows that product (4) is finite and  or
or
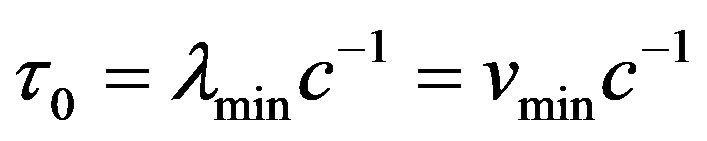 (5)
(5)
where “ ” denotes quantum of time and λmin quantum of length.
” denotes quantum of time and λmin quantum of length.
Thus, velocity is always composite according to (4), which usually falsely is taken to be non-composite. It is clear that even in the ultra relativistic region, where v0 → c, direct measurements would unveil no difference to the classical apparently non composite velocity “v”. But this cannot be true for measurements of momentum or energy, which are based on the electron Volt (eV). A protron (antiprotron), accelerated in an electrical field with the potential difference of one eV, would reach the subrelativistic velocity . Thus, with rising energy or momentum a systematic deviation of the correct composite value according to (4) from the special relativistic one of the order of magnitude
. Thus, with rising energy or momentum a systematic deviation of the correct composite value according to (4) from the special relativistic one of the order of magnitude
 (6)
(6)
must be taken into consideration, where “n” denotes any number (multiplicity) of eV, p0 momentum on the strength of naturally composite velocity according to (4), p special relativistic momentum based on the non-composite concept of velocity, m rest mass, v conventional non-composite velocity, γ and γ0 Lorentz factor on the strength of the conventional and the composite concept of velocity, respectively. The latter effect should principally be perceptible in high energy collisions (see paragraph 4.5 below).
According to (4) must be valid  if v0→ c such that Ni successively will take the values
if v0→ c such that Ni successively will take the values
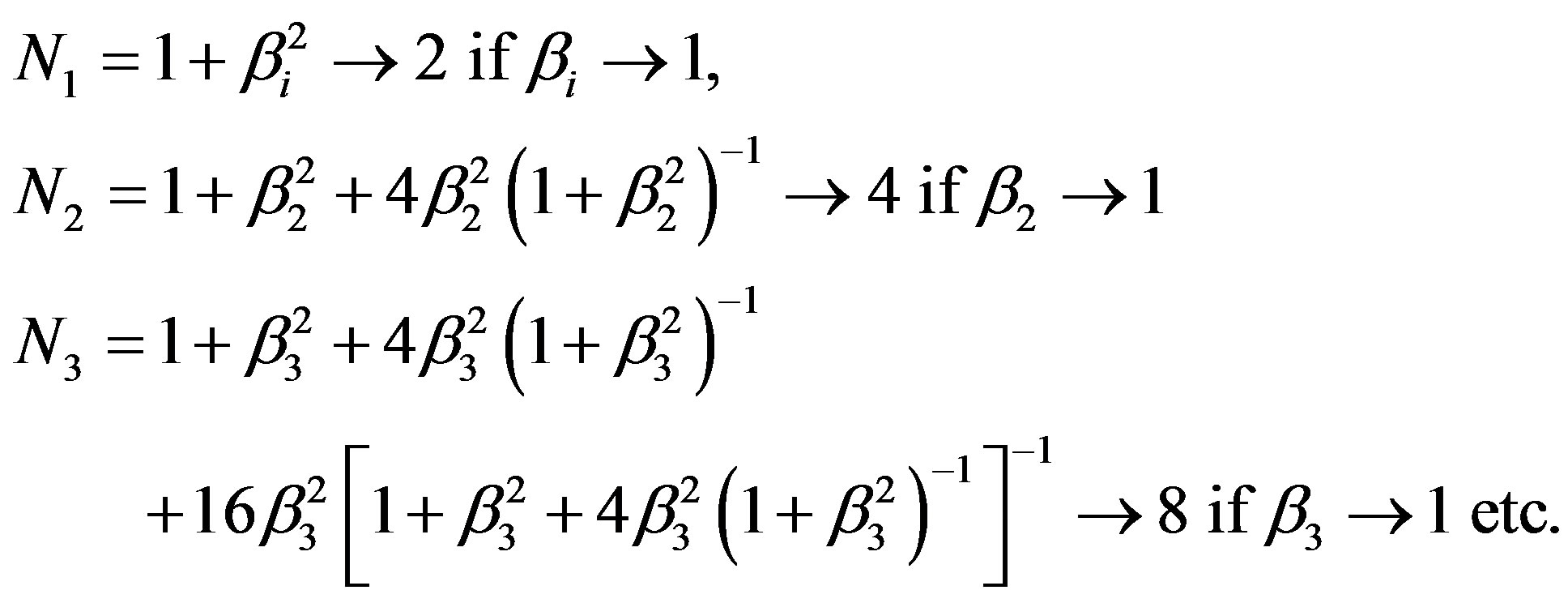 (6a)
(6a)
This implies that Ni always can be approximated. Given the foregoing it is clear that with respect to the preferred frame of reference Σ0, being the kinematic center, the space time of S1 and S2 must be strictly symmetrically equal.
2.2. The Symmetric Lorentz Transformation
Consider the inertial systems S1 and S2 moving uniformly parallelly and oppositely directed referring to the natural frame Σ0 at rest with respect to the former systems. The symmetric transformation equations are derived by assuming the validity of:
1) The Lorentz transformation (principle of relativity);
2) The inherent rest frame of nature Σ0 at rest in every translational movement implying the absolute equality of the inertial systems under consideration with respect to the former (principle of symmetry).
It is understood that the bodies resting in the coordinate sources of S1 and S2 are geometrically identical if they are compared with each other at rest, in compliance with the Einsteinian definition [19]. According to postulate 2) must the transformation be absolutely symmetric with respect to the systems under consideration. Furthermore, according to both postulates observers resting in S1 and S2 must consider themselves at rest and at the same time moving symmetrically relative to Σ0 and the other system. Thus, the observer in S1 will besides the Lorentz transformation according to postulate 1)—first line of (7)—, where he considers himself at rest, deduce a second transformation from the moving frame S2—according to the principle of relativity now considered at rest—back to his own system—now considered moving relative to Σ0 and S2 (see Figures 1 and 2):
 (7)
(7)
with
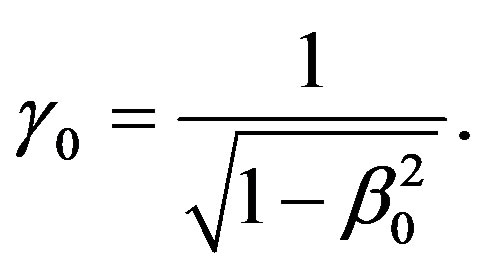
The dashes designate the moving frame  and the open circles the reference rest frame
and the open circles the reference rest frame , now considered moving relative to moving
, now considered moving relative to moving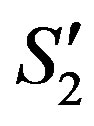 . Likewise the observer resting in S2 considered at rest will deduce:
. Likewise the observer resting in S2 considered at rest will deduce:
 (8)
(8)
According to the above-mentioned presupposition 2) for the observer resting in either system applies:

Figure 1. a: Geometrical proof of relativistic addition of quantized velocity; b: Geometrical derivation of rotated coordinate systems; c: Geometrical derivation of four-vector calculus.
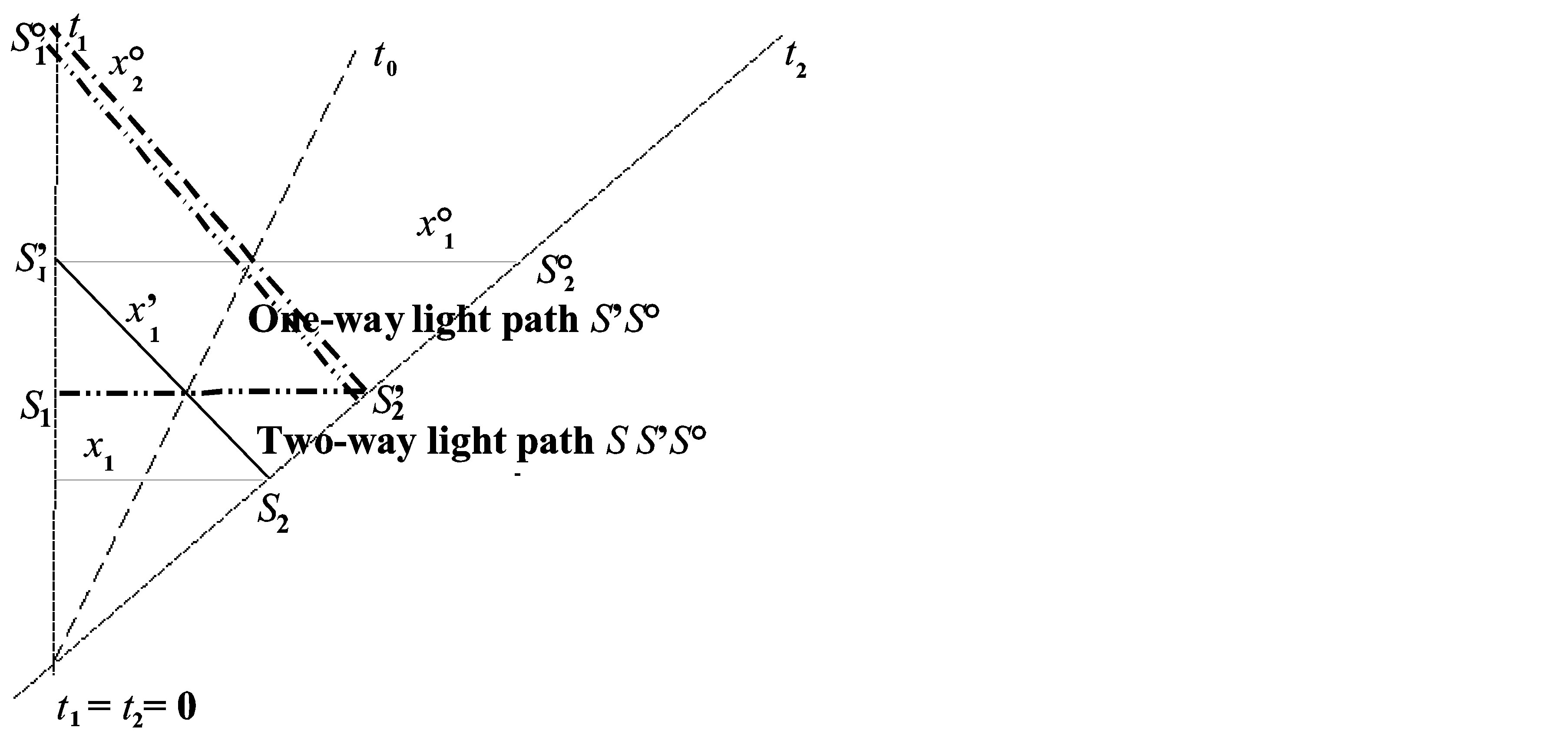
Figure 2. Different lorentzfactors of two-way and one-way signals in SMS.
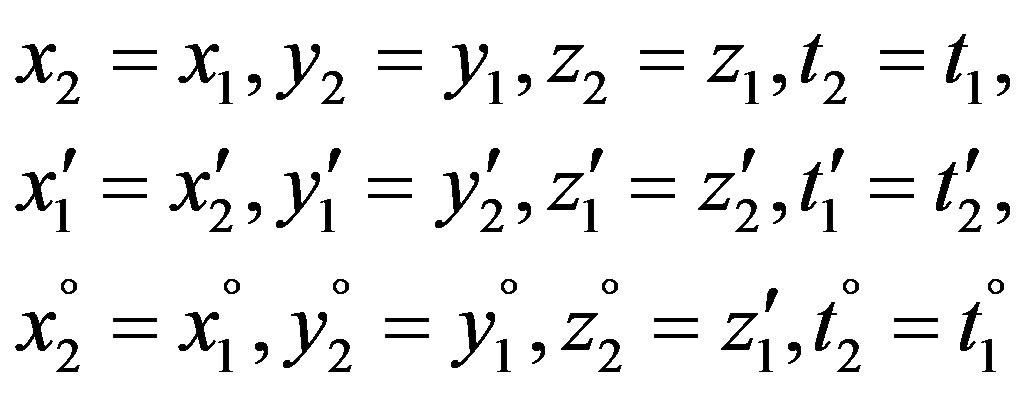 (9)
(9)
and always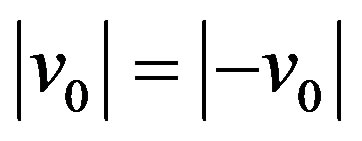 .
.
Eqs.7 to 9 have been deduced by strictly considering transformations from a system considered to be at rest to the one considered to move. The different states of motion have intentionally been made distinguishable by the use of different symbols. The proper inverse Lorentz transformation in (7) and (8) is given by the respective second line, where the former moving system now must be considered to be at rest according to the principle of relativity. The invariance of the scalars
 (10)
(10)
follows from (7) to (9) too. It is clear that according to the principle of symmetry, introduced above, the lower indices 1 and 2 are exchangeable.
2.3. The Symmetric Minkowski-Diagram; Equivalence of Four-Vector and Complex Number Calculus
Now, consider the preferred frame of reference of nature Σ0, relative to which S1 and S2 are moving at oppositely directed velocity v1 and the inertial frame  propagating relative to S1 at velocity v0, and their paths in spacetime (world-lines). Figure 1 shows a diagram of spacetime on the grounds of Eqs.7 to 10. It is evident that due to the absolute symmetry of
propagating relative to S1 at velocity v0, and their paths in spacetime (world-lines). Figure 1 shows a diagram of spacetime on the grounds of Eqs.7 to 10. It is evident that due to the absolute symmetry of 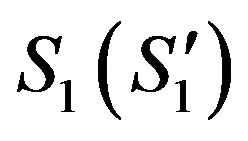 and
and 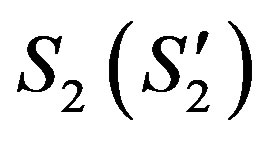 relative to Σ0 the triangles
relative to Σ0 the triangles 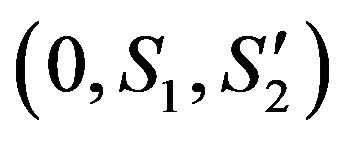 and
and 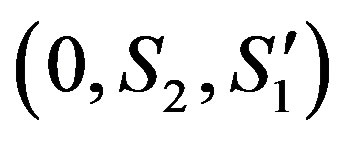 must be Pythagorean ones.
must be Pythagorean ones.
From Figure 1 one directly takes the ratios
 (11)
(11)
according to the addition theorem of trigonometric functions and, therewith,  , being the geometrical proof of Eq.2, whereby 0S1 = 0S2 = 0Σ0 = 1. It is obvious that S1S2 = 2β2 and, thus, on either side of 0Σ0 the geometrical ratios β1/(2β2 ) = 1/(1 +
, being the geometrical proof of Eq.2, whereby 0S1 = 0S2 = 0Σ0 = 1. It is obvious that S1S2 = 2β2 and, thus, on either side of 0Σ0 the geometrical ratios β1/(2β2 ) = 1/(1 +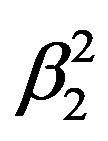 ) from 1/[1 + tan2 (δ/2)] as well as β2/(2β3 ) = 1/(1 +
) from 1/[1 + tan2 (δ/2)] as well as β2/(2β3 ) = 1/(1 +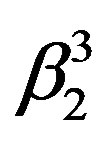 ) from1/[1 + tan2(δ/4)] and so forth follow, resulting in Eq.4, i.e. proving the latter geometrically. Furthermore, one takes from the diagram
) from1/[1 + tan2(δ/4)] and so forth follow, resulting in Eq.4, i.e. proving the latter geometrically. Furthermore, one takes from the diagram
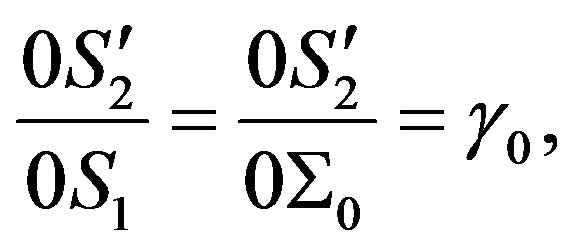 (12)
(12)
implying between Σ0 and 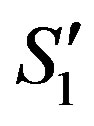 or,
or,  the Minkowskian spacetime relations and, thus, the special relativistic transformation equations
the Minkowskian spacetime relations and, thus, the special relativistic transformation equations
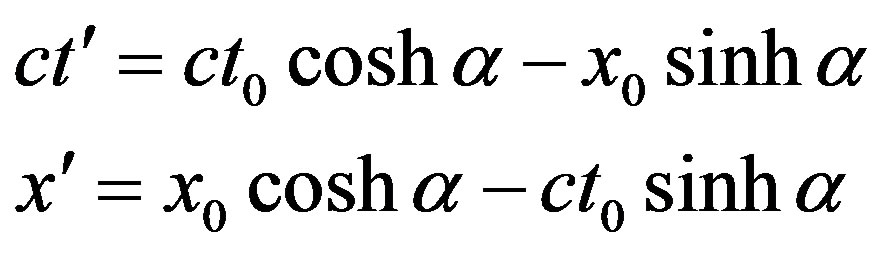
to be valid, where coshα = γ, sinhα = βγ, β = v/c.
As Figure 1(a) shows is the point  of the Pythagorean triangle
of the Pythagorean triangle  the complex number
the complex number  in a complex ct, x-plane of spacetime—we abstract from y and z—, written
in a complex ct, x-plane of spacetime—we abstract from y and z—, written  or in polar notation
or in polar notation
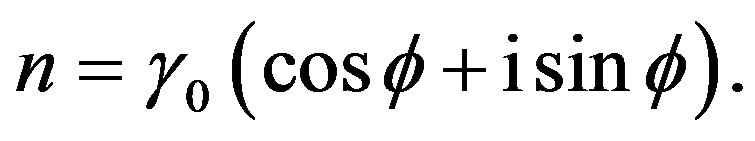
Because  and
and 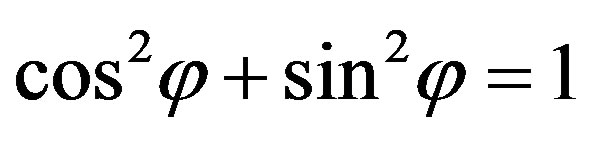 , it follows
, it follows
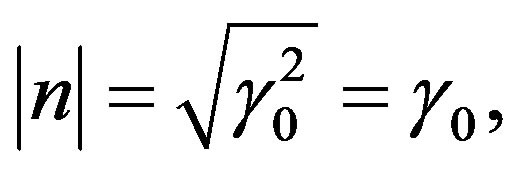
the minimum being .
.
Considering the physical quantities length, time, energy and mass in the transformation steps S, S’ and S° at ratio 1:γ0: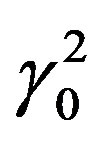 it also must be valid:
it also must be valid:
 (13)
(13)
As Figure 1(b) shows will the special-relativistic space-like world-line S1S through multiplication by the Lorentz factor γ be stretched to the (symmetric) worldline 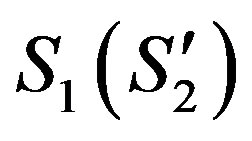 -apart from a factor of
-apart from a factor of 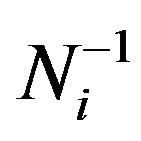 according to (4) and, therewith, the Minkowskian triangle (0, S, S1) be transformed into the Pythagorean one
according to (4) and, therewith, the Minkowskian triangle (0, S, S1) be transformed into the Pythagorean one . In special relativity this is achieved by introduction of
. In special relativity this is achieved by introduction of
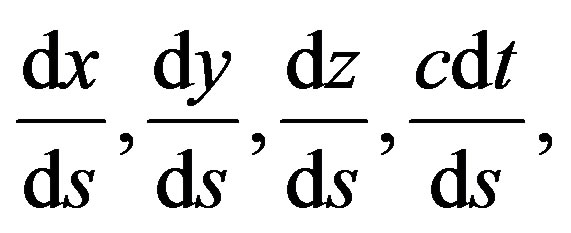 (13a)
(13a)
whereby

and
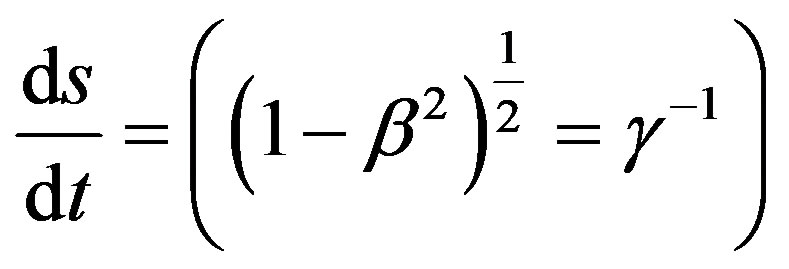
such that the four components (13a) attain the form
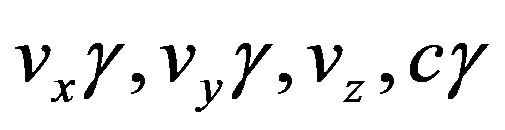
of four-velocity. Thus, the ct, x-plane of the spacetime of special relativity is transformed into a Gaussian plane and the complex number algebra made applicable in the form of the four-vector calculus. Especially result from the complex number algebra directly the innerproduct of two four-vectors q × r = q' × r'=, the square of two fourvectors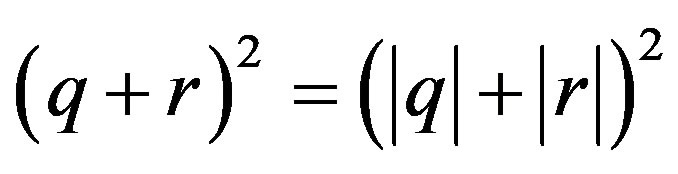 , furthermore, the special relativistic conservation of energy and momentum
, furthermore, the special relativistic conservation of energy and momentum
 (14)
(14)
or the well-known invariant
 (14a)
(14a)
in the usual three-dimensional notation etc. The latter equations do not contradict Eq.13, as will be shown below.
If 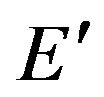 and
and  coincide, evidently E = 0, or, m = 0 follows, i.e. rest energy or mass of the photon. It is clear that
coincide, evidently E = 0, or, m = 0 follows, i.e. rest energy or mass of the photon. It is clear that 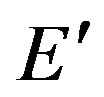 in its lowest approximation
in its lowest approximation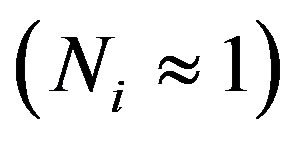 , owing to the absolute symmetry relative to Σ0, denotes twice the center-of-mass energy if material bodies of identical mass are considered and ν0 << c.
, owing to the absolute symmetry relative to Σ0, denotes twice the center-of-mass energy if material bodies of identical mass are considered and ν0 << c.
3. PHYSICS IN SYMMETRIC MINKOWSKI SPACE (SMS)
3.1. Application of the Symmetric Lorentz Transformation on Signals and Volume of Translationally Moving Material Bodies
From the first line of Eq.7 and the second one of Eq.8 in association with (9) the coordinate differences are derivated (see also Figures 1 and 2):
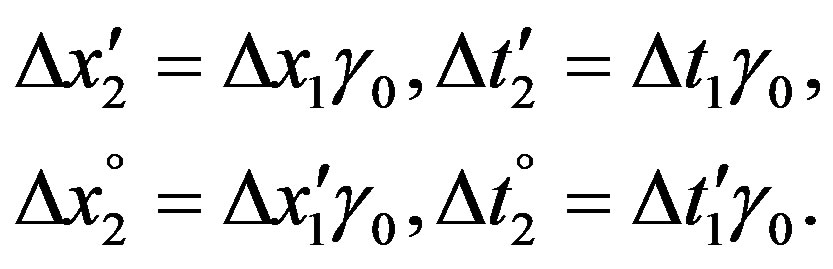 (15)
(15)
Notice that the first line of Eq.8 and the second one of (7) deliver the same result but with mutually exchanged lower indices wherefrom follows
 (15a)
(15a)
Furthermore, from the preceding one straightforwardly infers that any lower indice on either side of the Eqs.7 to 10 can be exchanged without affecting the validity of the latter. Therefore, if feasible henceforth simplified notations of the three transformation steps S, S’ and S˚ and their respective coordinates and coordinate differences of length and time without the lower indices will be used. In accord with the previous behave the transformation steps S’ and S° like the ratios of differences of length and time
 (15b)
(15b)
implying that every observer resting in the coordinate source of any of the former systems considered to be at rest can himself consider resting relative to frame S such that the transformation steps 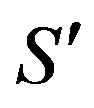 and S˚ at ratio γ0:
and S˚ at ratio γ0: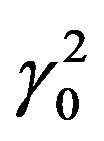 are directly referred to the former frame. But it is clear that the state of rest of frame S as well as the one of the inherent frame of nature Σ0 at rest in every translational movement are relative physical phenomena, too (see below).
are directly referred to the former frame. But it is clear that the state of rest of frame S as well as the one of the inherent frame of nature Σ0 at rest in every translational movement are relative physical phenomena, too (see below).
From the preceding also is evident that the transformation Eqs.7 to 10 are applicable in the case of oppositely directed translational motions.
Consider the kinematical situation according to Eqs.7 and 8 if light signals are transmitted between the involved frames. From the previous it is clear that, first, the light signal emitted from the resting reference frame S1 toward the moving frame  with reflection from the latter back towards the former now designated
with reflection from the latter back towards the former now designated 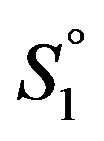 (two-way lightpath) and, second, a light signal emitted from the resting reference frame
(two-way lightpath) and, second, a light signal emitted from the resting reference frame —moving relative to frame S1—and being received at the moving system
—moving relative to frame S1—and being received at the moving system  (one-way lightpath) has to be investigated. The kinematical notion is sketched in Figure 2. From relations (15) and (15a) one receives in the case of the two-way lightpath directly the relation (see also Figure 2)
(one-way lightpath) has to be investigated. The kinematical notion is sketched in Figure 2. From relations (15) and (15a) one receives in the case of the two-way lightpath directly the relation (see also Figure 2)
 (15c)
(15c)
It is clear that any two-way signal travelling at inertial velovity v0 will be observed enhanced by a factor of γ0 as well. Furthermore, in the case of the one-way lightpath follows from the same relations
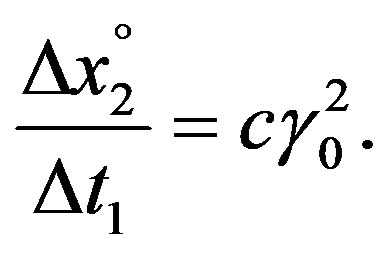 (15d)
(15d)
As in the two-way case this must be valid for inertial velocities as well. The physical significance of this SMS effect will be discussed further below in association with the possible existence of a frame of reference of nature at absolute rest (see below paragraphs 3.3 and 3.4).
It also follows that the left-hand sides of relations (15) and (15a) express the coordinate differences of the respective moving system, excluding the interpretation as a resting one. This clearly implies, the equations above applied on moving bodies, the expansion of the x-dimension, i.e. the dimension parallel to the vector of velocity, namely in the order of magnitude
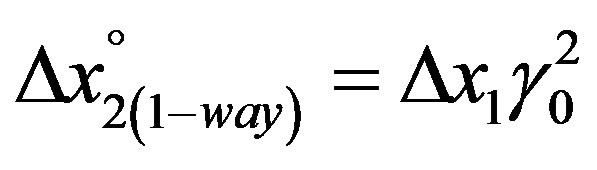 (15e)
(15e)
in the one-way case  and of
and of
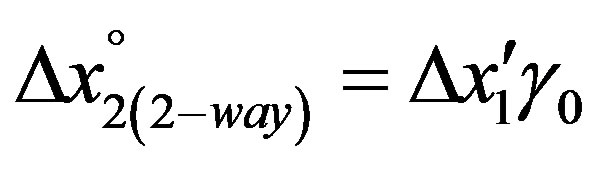 (15f)
(15f)
in the two-way case , e.g. in scattering experiments, so that the respective volumina V are enlarged in the order of
, e.g. in scattering experiments, so that the respective volumina V are enlarged in the order of
 (15g)
(15g)
Further below (paragraph 4.5) it will be proposed that the latter relativistic effects in association with the composite nature of velocity according to Eqs.6 and 6a are the physical cause of the experimentally observed steady increase of cross sections of incident particles in high energy collisions and of the shrinkage of mean free paths of ultra relativistic particels traversing any media.
The previous results are also directly derivable geometrically from Figure 2.
With a view at the latter and in association with relations (9) one straightforwardly derivates for the coordinate differences of either side of SMS the ratios
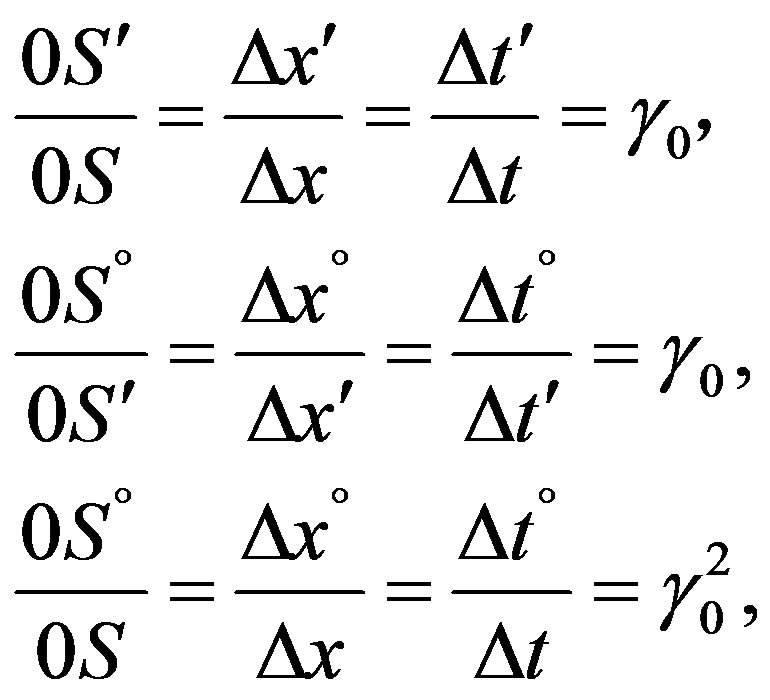 (16)
(16)
where, as in Figure 1, coordinate difference 0S1 = 0S2= 1 and .
.
As already mentioned, the symmetry of the transformation Eqs.7 to 9 implies that the observer resting in his frame of reference at rest at the same time must consider himself moving. This leads necessarily to the above derivations (15) to (16) in the one-way as well as in the two-way case and, thus, excludes the invention of length contraction of the moving system by FitzGerald and Lorentz in the order of γ−1, which Einstein later derived from his transformation equations by reversing state of rest and motion [20].
Besides, one should notice that in the physical application of his theory Einstein himself came to the same hitherto overlooked result, namely, expansion of length according to Eq.15f and, therewith, a respective increase of the volume of a moving body in the order of γ in accord with right-hand Eq.15g as the explanation of the invariance of the electric charge [21].
3.2. Mass and Energy in SMS and Disproof of the Relativity of Simultaneity
That relativistic (dynamic) mass always takes the form mγ0 (and not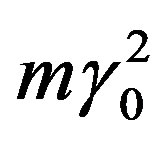 ) results from the fact that inertial mass cannot be derivated physically other than through its momentum e.g. in elastic collisions, i.e. in two-way experiments as already Galilei stated: “Two bodies are of equal mass if one dashes them with oppositely directed, equal velocity against each other and none of both runs down the other.” Thus, the physical notion momentum here appears primary to the one of mass (Weyl, 1923 [22]), which analogously to Eq.15(c) takes the form
) results from the fact that inertial mass cannot be derivated physically other than through its momentum e.g. in elastic collisions, i.e. in two-way experiments as already Galilei stated: “Two bodies are of equal mass if one dashes them with oppositely directed, equal velocity against each other and none of both runs down the other.” Thus, the physical notion momentum here appears primary to the one of mass (Weyl, 1923 [22]), which analogously to Eq.15(c) takes the form
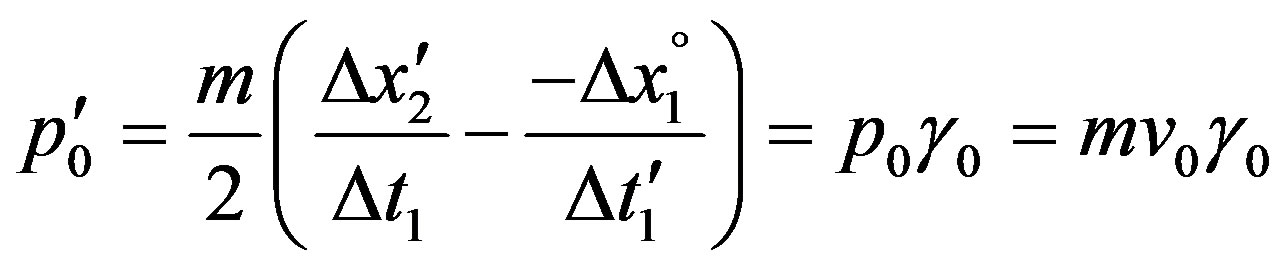 (17)
(17)
if spherically shaped bodies with equal mass m are colliding elastically head on. But note that also weighing in a gravitational field by means of a balance is two-way because through the latter two gravitationally accelerated masses are forced to counteract. It is clear that owing to the special relativistic conservation of energy and momentum (14) and (14a) the physical quantities energy, momentum, mass and time all are transformed in transformation steps 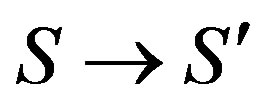 and
and  at ratio 1:γ0 in accord with Eq.13.
at ratio 1:γ0 in accord with Eq.13.
This leads to an interesting derivation. Consider a body of mass m' = , resting in the coordinate source of the frame of reference S’-where
, resting in the coordinate source of the frame of reference S’-where 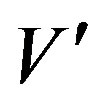 denotes volume as defined by right-hand (15g) and
denotes volume as defined by right-hand (15g) and  density of mass-, moving inertially relative to the frame of reference S, considered to be at rest. From Eq.13 follows m' = mγ0 and, therewith,
density of mass-, moving inertially relative to the frame of reference S, considered to be at rest. From Eq.13 follows m' = mγ0 and, therewith,
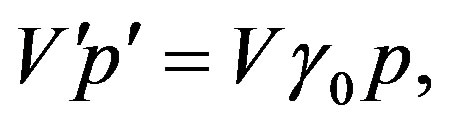 (17a)
(17a)
Replacing 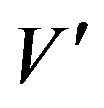 in the left-hand member of (17a) also by Vγ0 yields
in the left-hand member of (17a) also by Vγ0 yields
 (17b)
(17b)
Implying ρ' = ρ = const. Thus, it applies
 (17c)
(17c)
where  = dx'dy'dz' =dx' × dydz. Because ρ' = ρ = const and dydz = const too, the physical cause of the relativistic growing of E'β0 = mγ0 c v0 must be the relativistic expansion of dx' = dx γ0 alone, i.e. the respective relativistic expansion of volume. Therefrom the following propositions are derivated:
= dx'dy'dz' =dx' × dydz. Because ρ' = ρ = const and dydz = const too, the physical cause of the relativistic growing of E'β0 = mγ0 c v0 must be the relativistic expansion of dx' = dx γ0 alone, i.e. the respective relativistic expansion of volume. Therefrom the following propositions are derivated:
1) density of mass of a body is independent of the former’s translational motion at any given velocity, i.e. remains constant for all observers;
2) dynamical (relativistic) mass is solely dependent on the special relativistic expansion spatially of a translationally moving body’s volume by factor of γ0 into the x-direction.
As widely known, Einstein introduced in special relativity the “relativity of simultaneity”. He maintained [18]:
The length l of a translationally and parallely “moving” rod rAB, as measured in the “moving” system, equals “according to the principle of relativity” the length l of a like rod (as compared at rest), resting relative to the former one in a system “at rest”. Hence, the “moving” observer (rAB) would find clocks A and B, positioned at the ends of the rod and synchronized in the system “at rest”, not to be synchronous if a light signal is emitted from A to B, being reflected and received at A, now designated A', so evidently it applies:
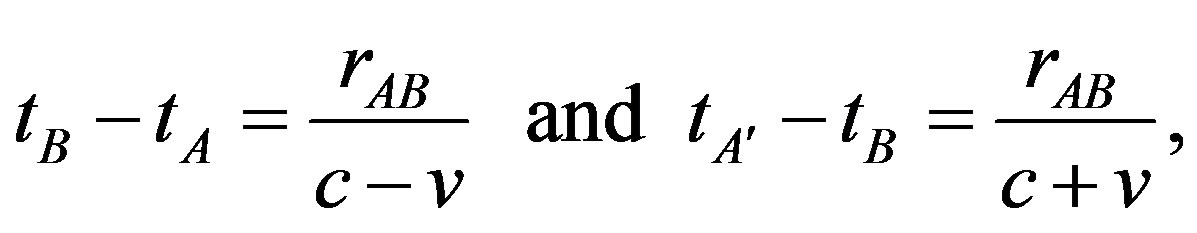 (17d)
(17d)
Already in the framework of Einsteinian special relativity this proposed proceeding is not admissible and violates the very basis of that theory: the principle-ofrelativity hypothesis, including the constancy of the velocity of light for all observers. I.e. if an observer changes from a “resting” system to a “moving” one, becomes the latter according to the principle of relativity the observer’s reference rest frame at rest. According to Eqs.7 and 8 must the former resting system now considered to be moving relative to the new rest frame.
Anyhow, it is clear, now, but has been overlooked ever since that the correct transformation of the spacetime coordinates of a light signal propagating relative to the coordinate source of any moving inertial system into the respective coordinates of another frame, being the rest frame of the observer, in any case requires the application of the Einsteinian addition theorem such that the former Einsteinian equations must take the correct form
 (17e)
(17e)
But anyway, from ratio (15b) straightforwardly follows that the above equs. in either system take the simple form
 (17f)
(17f)
Hence, it is shown that both observers, whether considered resting or moving, will ascertain synchronicity of the above Einsteinian clocks, i.e. invariance of simultaneity.
3.3. Existence of a Preferred Frame of Reference of Nature at Absolute Rest
It is a long-established belief that no physical experiment including the measurement of the light’s velocity can unveil whether an experimenter resting at the zero point of his frame of reference is also resting or translationally moving relative to spacetime, implying the validity of the principle-of-relativity hypothesis. Propagation in spacetime seemingly can be ascertained physically only as a relative one with respect to other frames of reference. The above proposed symmetric extension of special relativity does not change this very basic physical notion, i.e., as already mentioned, the previously introduced preferred frame of reference of nature Σ0 in every translational motion be merely a relative frame with respect to SMS, too. Although the composite nature of motion and velocity implies that a real absolute rest frame of space time should exist, seems the latter not to be derivable theoretically.
On the other hand, from a physical point of view the nearly uniform microwave background radiation (CMB) with a temperature of 2.725 Kelvin seems to constitute an absolute rest frame in SMS for all other frames at least in this part of the Universe, i.e. the latter frames motion relative to the CMB is really recognicable physically including speed and sense. This implies that all systems moving with respect to the CMB at the same velocity and the velocity vectors being congruent with each other must be resting relative to each other. Thus, the conclusion seems unavoidable that the CMB be a really resting preferred reference frame Σ00 of nature in the sense of the preceding, i.e. signifying very rest with respect to the underlying space-fabric of SMS. Tentativily the latter hypothesis will be adopted as the true physical notion of SMS such that relation (15b) would take the form
 (18)
(18)
where Δx00 and Δt00 denote coordinate difference of flight path and travel time, respectively, of signals transmitted from a reference frame Σ00 to another one, both absolutly resting relative to the CMB. Accordingly the propagation of all inertially moving systems or of signals emitted from the latter must be referred to the preferred resting reference frame Σ00 of nature, with important physical consequences, to which we now turn.
Consider a frame of reference Si moving translationally at velocity v0 relative to a frame Σ00 resting with respect to the CMB, implying that the transformation Eqs.7 to 9 are valid. One more frame Sii is introduced resting relative to Si, the space-like coordinates from frame Σ00 to Sii being denoted xii, implying a fixed distance between Si and Sii and, therewith, simultaneous movement of Si and Sii at velocity v0 with respect to Σ00. Obviously, for the latter distance the above demonstrated invariance of simultaneity must be valid. Furthermore, are relations (15) to (17) directly applicable to the kinematical situation between frame Σ00 at absolute rest and the moving frames Si and Sii, respectively, whereby it is clear that according to Eqs.7 and 8 the transformations be also both-way as well. Thus, according to (15c) in the case of two-way transmission of light signals between Σ00 and moving Si it must be valid
 (19)
(19)
Accordingly for the one-way light-signal one receives from (15d):
 (19a)
(19a)
The same results for the frame Sii.
In the following Figure 3, sketching this kinematical notion, the crossing points of the time-like vector too with vectors ti and tii, respectively, in SMS have been made distinguishable by denoting the former t00(ii) at point t00(ii) = tii = 0 and t00(i) at point t00(i) = ti = 0 such that Δtii > Δti. Furthermore, for reasons of simplicity point t00(i) = ti = 0 has been chosen so that it overlaps with zero point of Σ00.
From the sketched SMS situation in Figure 3 one takes the ratios:
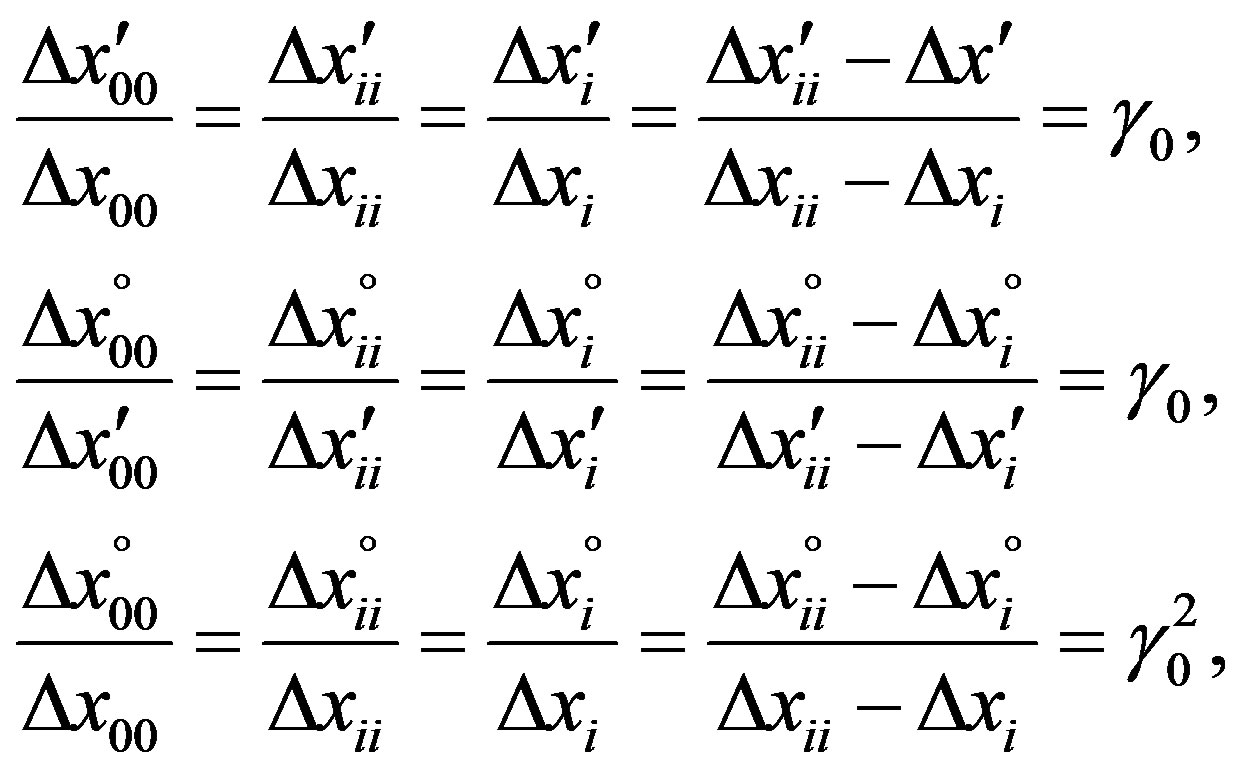 (19b)
(19b)
In accordance with (19) and (19a). The coordinate differences of time behave in the same way. Hence, Figure 3 delivers the geometrical proof of the latter equations. Furthermore, it follows that Eq.19a and the sketched SMS situation are valid for any velocity v0(CMB) of frames of reference travelling relative to the CMB or Σ00, respectively.
The physical notion is simplified if t00(i) = ti = 0 is put at the origin of the x-axis between  and Sii such that
and Sii such that  and Si overlap with the consequence that
and Si overlap with the consequence that 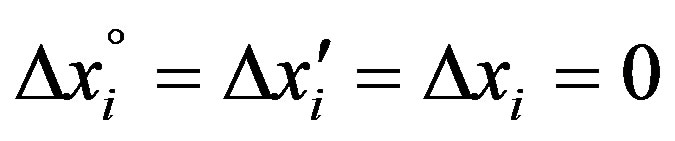 and the fourth column of relations (19a) takes the form of the latter’s second one. This leads to Eq.19, implying the most remarkable result that also light signals between reference frames resting relative to
and the fourth column of relations (19a) takes the form of the latter’s second one. This leads to Eq.19, implying the most remarkable result that also light signals between reference frames resting relative to

Figure 3. Quadratic spacetime structure of one-way signals in SMS.
each other but moving commonly with respect to the CMB will exceed the velocity of light in dependence on the distance between the former and their common velocity relative to the CMB. But, of course, this follows already straightforwardly from the transformation Eqs.7 to 9 in association with their derivations (15) to (15e) and (16), respectively. It is obvious that the latter results for inertial velocity v0, i.e. inertial movement of frames Si and Sii relative to Σ00, are valid too. Furthermore, it follows that the above findings are also valid for any point Σ00(n) between Σ00 and frame Sii.
3.4. Velocities and Distances in SMS in Dependence on One-Way or Two-Way Measurement
The previous results confirm Eq.18, implying that every observer resting in the coordinate source of any of the systems S, S' and S˚, respectively, considered to be at rest, can himself consider resting relative to Σ00 such that the former transformation steps at ratio 1:γ0: can directly referred to the latter frame. Of course, this follows already from the transformation Eqs.7 and 8 if the coordinates of the respective frames S1 and S2 at rest are replaced by those of the absolute rest frame Σ00 such that in accord with (9) be valid x1 = x2 = x00 etc. Thus, it has been shown firstly the up to now hypothetically introduced scalar (10) to follow from theory and secondly that the latter scalar has to be completed to
can directly referred to the latter frame. Of course, this follows already from the transformation Eqs.7 and 8 if the coordinates of the respective frames S1 and S2 at rest are replaced by those of the absolute rest frame Σ00 such that in accord with (9) be valid x1 = x2 = x00 etc. Thus, it has been shown firstly the up to now hypothetically introduced scalar (10) to follow from theory and secondly that the latter scalar has to be completed to
 (20)
(20)
E.g., consider a reference frame S˚ (S) moving (oneway) translationally towards frame S'—which according to Eqs.7 and 8 has to be considered moving synchronously towards resting frame S— at velocity v0 < c, or, a signal emitted from the former with velocity  to be received by the latter. From the ratios (18) follows
to be received by the latter. From the ratios (18) follows  and, therewith, that the respective resting observer will measure the velocity, whether of the moving frame or of the transmitted signal, to be enhanced in the order of
and, therewith, that the respective resting observer will measure the velocity, whether of the moving frame or of the transmitted signal, to be enhanced in the order of
 (21)
(21)
It is clear that an observer resting at the zero point of the moving system S’, now in accord with Eqs.7 and 8 considered as the resting one, must according to (20) also observe the same physical phenomenon. Furthermore, rest time must be variable in dependence on velocity v0(CMB) relative to Σ00 by value of
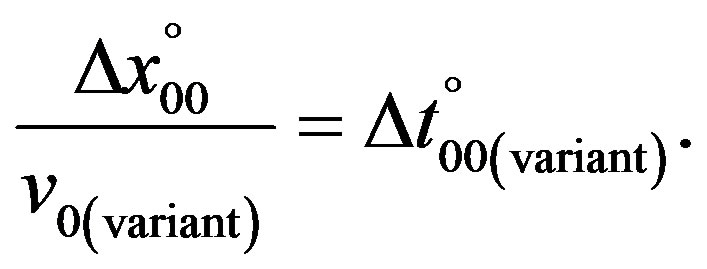 (21a)
(21a)
Hence, neglecting gravitational and rotational effects, referring to the dependence of rest time in the system of the Earth on the latter’s velocity relative to the CMB one generally can write
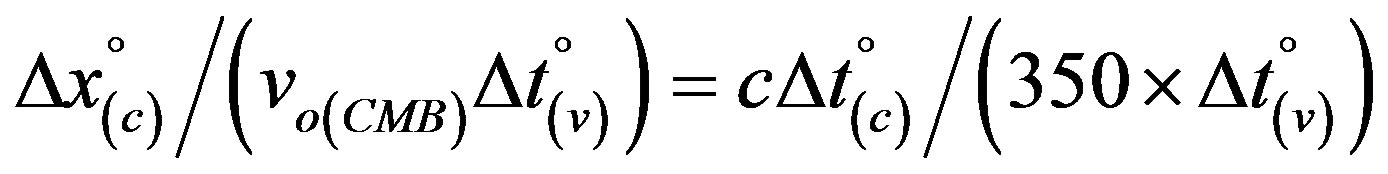 , where v0(CMB)
, where v0(CMB)
= 350 kms−1 being the mean orbital velocity of Earth with respect to the CMB. This implies  and
and 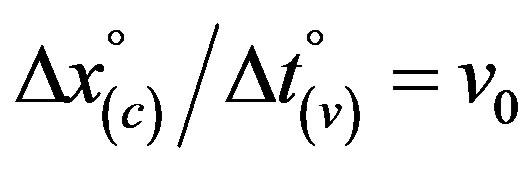 and, therewith, in accord with Eq.21a the ratio:
and, therewith, in accord with Eq.21a the ratio:
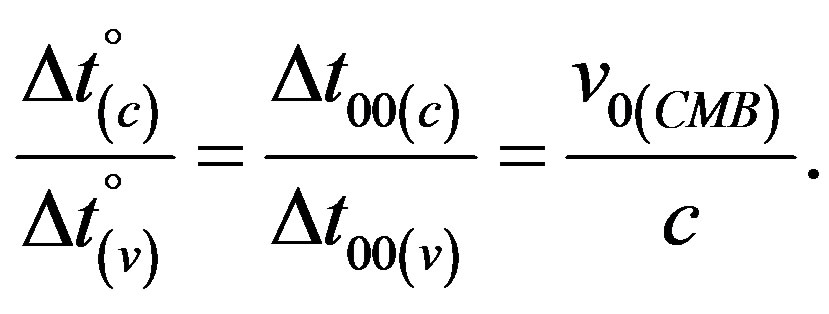 (21b)
(21b)
i.e., because of the constancy of 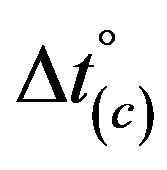 in the numerator of the two left-hand sided ratios will Eq.21b directly indicate changes of rest time, e.g. on Earth owing to the planet’s varying v0(CMB) during one orbit’s time (see Paragraph 4.4 below).
in the numerator of the two left-hand sided ratios will Eq.21b directly indicate changes of rest time, e.g. on Earth owing to the planet’s varying v0(CMB) during one orbit’s time (see Paragraph 4.4 below).
It arises the question, whether the one-way coordinate difference of the space-like vector in SMS is identical with distance d spatially, because in special relativity the latter is defined through the two-way measurement of the time of flight of light over d, whereby it is clear that the time of flight for both ways is expressed in the units of the arbitrary CGS-system. Thus, the Einsteinian definition of the velocity of light in association with Eq.19 takes the form 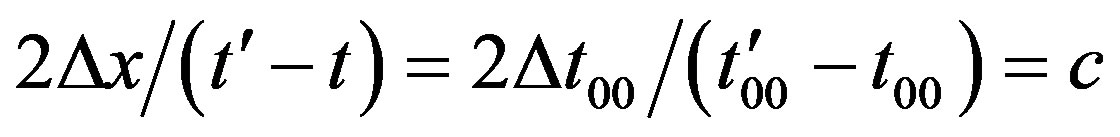 such that for the two-way case follows
such that for the two-way case follows 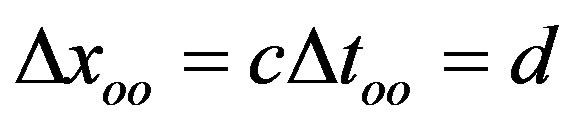 [19]. It is clear that according to the preceding this is only approximately valid near the zero point of the respective frame of reference on moving Earth in the case that
[19]. It is clear that according to the preceding this is only approximately valid near the zero point of the respective frame of reference on moving Earth in the case that 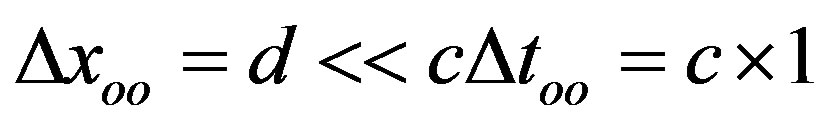 s and, therewith, neglectably small (see also below).
s and, therewith, neglectably small (see also below).
But notice that the above definition of a two-way light signal in association with the quadratic structure of spacetime according to Eq.20 constrains the coordinate difference of the time-like vector of spacetime being expressed in the same arbitrary units of time as the coordinate difference of the space-like vector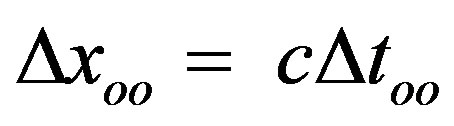 , i.e. in the units of the CGS-system. On the other hand, if the “time dimension” of spacetime really exists by the side of and in union with the spatial dimensions, then, it is not sure from the first that the in two-way experiments (two-fold space-like vector Δxoo) derivated associations of space, time and velocity straightforwardly are transferable to the one-way case. Hence, in the following will the one-way coordinate difference between two reference frames Σ00, i.e. systems resting relative to the CMB and to another, be denoted Δxo1 and Δto1 the respective coordinate difference of time.
, i.e. in the units of the CGS-system. On the other hand, if the “time dimension” of spacetime really exists by the side of and in union with the spatial dimensions, then, it is not sure from the first that the in two-way experiments (two-fold space-like vector Δxoo) derivated associations of space, time and velocity straightforwardly are transferable to the one-way case. Hence, in the following will the one-way coordinate difference between two reference frames Σ00, i.e. systems resting relative to the CMB and to another, be denoted Δxo1 and Δto1 the respective coordinate difference of time.
Figure 3 shows that coordinate difference Δxii and coordinate-difference Δtii shape a quadratic structure Δxii × cΔtii = Δxoo × cΔtoo in SMS. In the absence of any arbitrary unit of time must the parallely running space-like and time-like coordinate-differences, respectively, of the really resting frames Σ00, expressed through natural dimensionless one-way time of flight of light, take the positive form Δto1 = cc−1 = 1 and Δxo1 = c Δto1 = c2c−1 = c, respectively, so that Δxo1 × c Δto1 = (c2c−1)2= c2, i.e. being invariant independent of the magnitude of Δxo1 spatially. Because in the CGS-system the above defined Δxoo is expressed as the product of c and the arbitrary time span (k + l/m) s such that Δxoo = c (k + l/m) = d., where k denotes any non-negative rational number 0,1,...,n, and l/m rational fraction of second s, becomes the square (Δxo1 × cΔto1) to (Δxoo × cΔto1) = c2 (k + l/m) = (c d). The time-like coordinate differences remain really invariant, i.e. cc−1 = 1 independent of c (k + l/m) = d, because the above Einsteinian two-way definition of time and velocity, as already mentioned, is derivated alone from the two-fold space-like vector Δxoo and transfered to the spatially independent time-like vector implying the Phythagorean relation
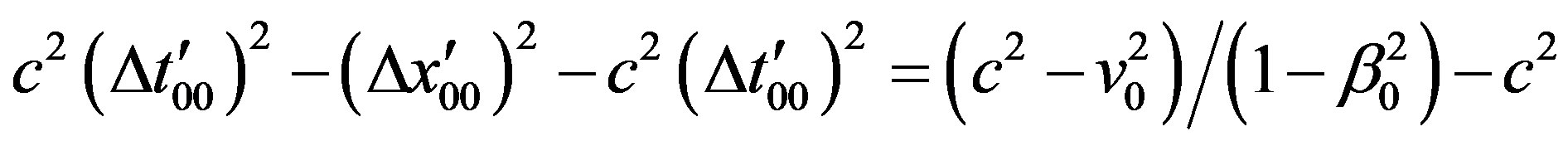 . Now it is obvious that the validity of the latter is restricted to the in two-way experiments in SMS received results only. Only in one-way experiments the real quadratic association of the space-like and the time-like vectors becomes evident, whereby the from the two-fold space-like vector Δxoo in two-way experiments derived association of arbitrary units of time and velocity in the former case cannot be imprinted on natural dimensionless time. Hence, one receives
. Now it is obvious that the validity of the latter is restricted to the in two-way experiments in SMS received results only. Only in one-way experiments the real quadratic association of the space-like and the time-like vectors becomes evident, whereby the from the two-fold space-like vector Δxoo in two-way experiments derived association of arbitrary units of time and velocity in the former case cannot be imprinted on natural dimensionless time. Hence, one receives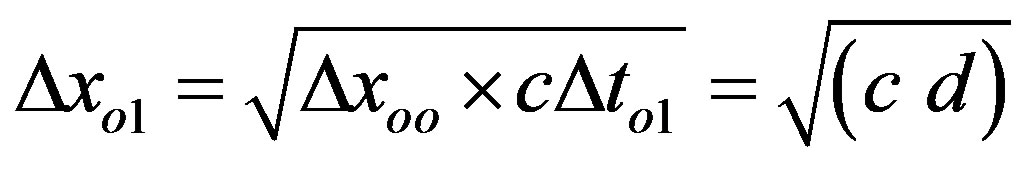 , wherefrom then in association with the preceding for signals travelling at the speed of light is derivated
, wherefrom then in association with the preceding for signals travelling at the speed of light is derivated
 (21c)
(21c)
and for a frame S˚ (S) moving translationally towards frame S’—which according to Eqs.7 and 8 synchronously has to be considered moving towards resting frame S— at any velocity v0 < c
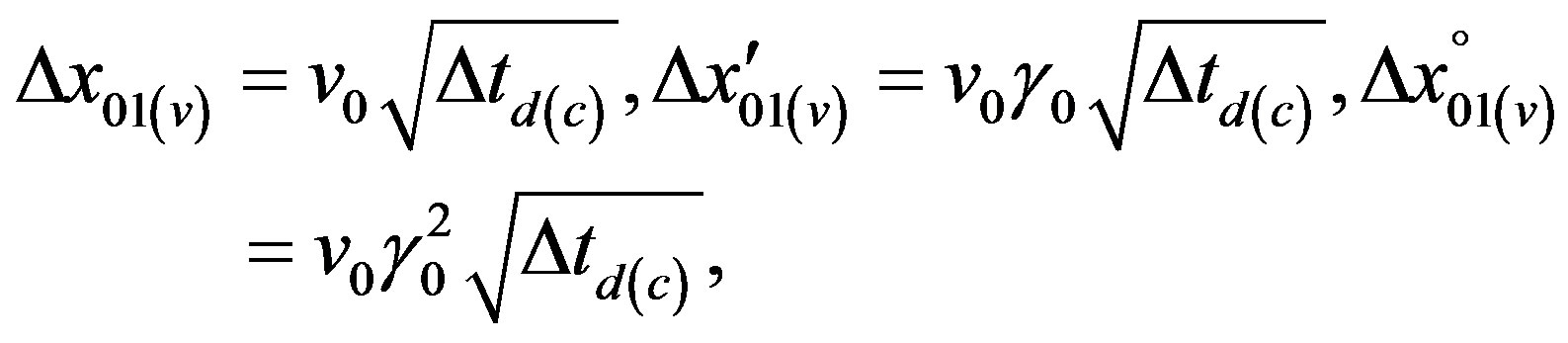 (21d)
(21d)
where Δtd(c) denotes time which light needs to travel distance d in two-way measurements. Eqs.21d follow from (21c) in association with (18).
One aspect of the preceding to be emphasized is that the velocity of bodies travelling one-way towards the respective resting observer, or, of light signals emitted from a source and propagating at or near the velocity of light, always can be measured as the ratio of the distance to the time of flight only, whereas comparison of the time of flight of light to the one of e.g. elementary particles travelling at velocity v0 ≈ c would unveil no measurable difference (see also paragraph 4.2. below). This implies that Eqs.21c and 21d and the following derivations (23) and (23a) basically are applicable in the space of frames of reference only, e.g. in the system of Earth with v0(CMB) = 350 km·s−1.
For two-way light signals simply is given 2 Δxoo/2 = Δxoo = c (k + l/m) = d so that in accord with the above and Eqs.18 and 19 furtheron is valid
 (21e)
(21e)
where Δxoo denotes two-way coordinate difference according to the above Einsteinian definition.
Notice that ratio (21b) straightforwardly follows from the above derivation of natural dimensionless time, too, taking the form
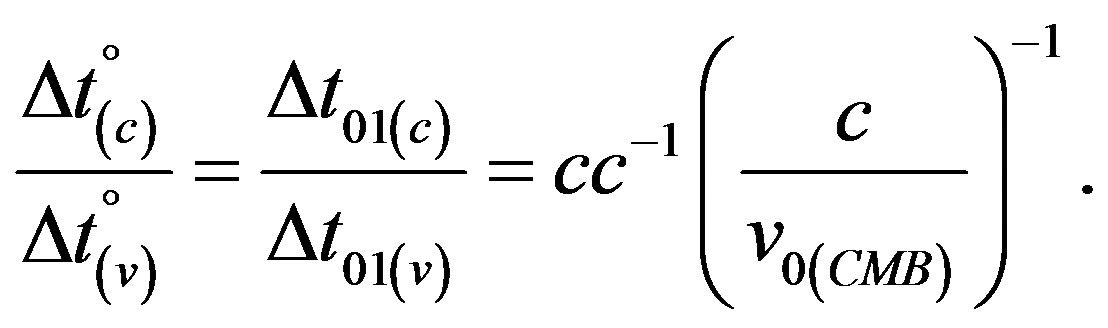 (22)
(22)
From the preceding (also Figures 2 and 3) it is evident that the most right-hand members of Eqs.21c and 21d are the only relevant relativistic derivations which have to be considered for one-way signals in the space of reference frames. Thus, in the latter frames will a light signal emitted towards an observer overshoot the velocity of light in the order of
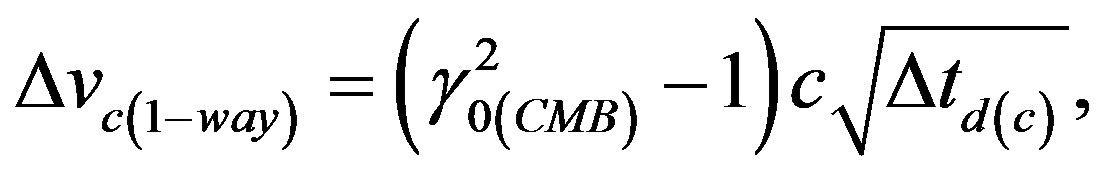 (23)
(23)
whereas the difference of time of flight of one-way signals travelling at or near the canonical velocity of light according to (21c) must be
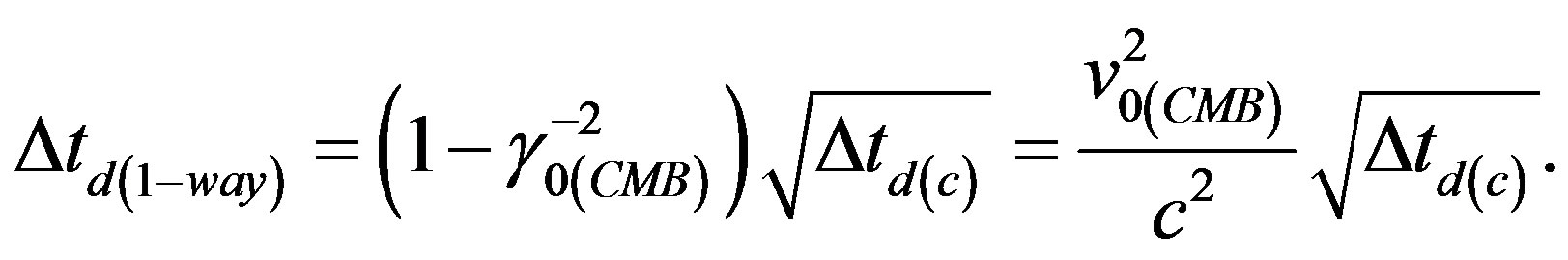 (23a)
(23a)
In the two-way case from Eq.21e in association with (15) e.g. in the system of the Earth simply is given:
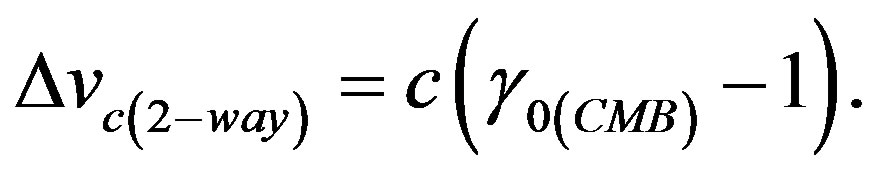 (23b)
(23b)
The above one-way equations consider the light’s time of flight from the emitter to the receiver and translational motions in the space of frames of reference, as sketched in Figure 3. Now, consider a far away cosmic one-way expansion phenomenon or motion on the plane of the sky for reasons of simplicity orthogonal to the line of sight with velocity v0┬ over some distance d. Notice that the motion from the starting point to the latest point of observation—i.e. its evolution according to the right-hand Eq.21d—must be associated with the time-like coordinate difference v0c−1(c Δt01). Hence, because according to the above Δt01 = 1, the far away motion will be observed as the vector product of the diverging coordinate differences of space and time, respectively, in the order of
 (23c)
(23c)
whereby angular dimension π/2 is referred to the angle enclosing the reverse of the vector of the light reaching the observer (first observer) along the line of sight and d and, furthermore, the angle of the vector of the motion along d relative to the line of sight is running backwards from π/2 to zero.
On the other hand, a second observer posted at the end-point of d must observe the scalar product of the converging and in this special case even parallely oriented spatial coordinate differences, namely
 (23d)
(23d)
with angular dimension zero referring to the angle enclosing the spatial coordinate differences along d also running backwards from 0 to π/2.
Obviously, in the one-way case of SMS the above derivations for the speed of light and of translationally moving frames replace the respective two-way-case expressions (19), (21e) and (23b), and, thus, considerably deviate from the common conception of velocity derivated from two-way kinematics. But it is also clear that this does not affect the validity of the Lorentz transformations (7) to (9) and their previous derivations, especially scalar (20), in any way. E.g. remain all relativistic twoway transformations of the physical quantities energy, momentum, mass, time and length at ratio 1:γ0 as well as oneway transformtions of length or volume at ratio 1: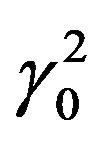 unchanged through the above introduced non-canonical velocities, because the natural dimensionless velocity of Lorentz factors γ0 and
unchanged through the above introduced non-canonical velocities, because the natural dimensionless velocity of Lorentz factors γ0 and  respectively, remains invariant, namely:
respectively, remains invariant, namely:  .
.
4. DISCUSSION OF EXPERIMENTAL RESULTS AND ASTRONOMICAL OBSERVATIONS REFERRING TO TWO-WAY AND ONE-WAY SIGNALS
4.1. Further Disproof of the Length-Contraction Hypothesis
The astronomical and experimental findings which have been mentioned in the beginning can now be investigated in the light of the above results. But beforehand it will be shown that the preceding is in accord with the Michelson-Morley experiment’s of 1887 and similiar one’s outcome, namely the apparent experimental proof that the earthly motion through spacetime does not influence the velocity of light in any spatial direction [23]. As widely known, is the latter result considered as the experimental cornerstone of the Einsteinian principle of relativity and, therewith, as crucial for the special relativity theory. In the said experiment a mirror splitted a beam of yellow light with a wave length of 6 × 10−5 cm into two beams propagating at right angles to another to the ends of 11 m long arms, where they were reflected back to the middle and recombined to one beam which was sent to the receiver at the far side. Michelson-Morley expected that due to the motion of Earth with respect to the Sun an interference pattern should result with a displacement of 0.4 of the yellow light’s wavelength, deduced from an expected time-of arrival difference of
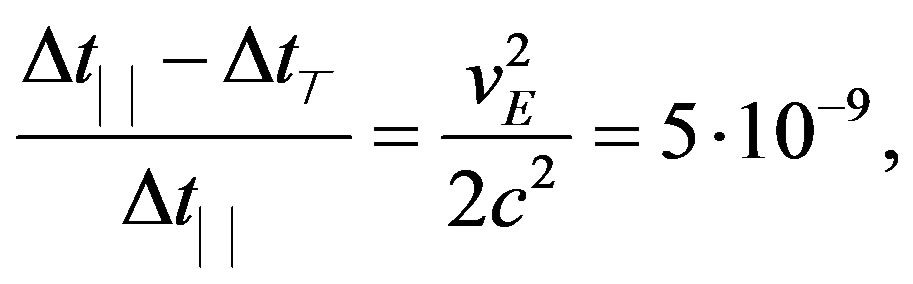 (24)
(24)
where Δt║ denotes travel time of the beam propagating parallely to the velocity of Earth vE 30 kms−1 and Δt┴ travel time rectangular to the former. Instead they observed one-fortieth this, namely 0.02 of the expected displacement, which has been attributed to measurement inaccuracies. Thus, the experiment’s outcome correctly has been considered as an absolute null result. As previously mentioned, has the latter result at that time been explained through the invention of length contraction by FitzGerald and Lorentz in the order of γ−1.
In the light of the previous results it is obvious that the splitted and to the middle reflected beams with assumed time difference Δt║ − Δt┴ in the numerator of the lefthand side are two-way beams, whereas the recombined beam sent to the receiver with assumed running time Δt║ in the denominator of the left-hand side is to consider as an one-way case. Thus, in SMS the above Eq.24 according to Eqs.21e and 23b takes the form
 (24a)
(24a)
Notice that, as announced above, this result disproves the length contraction hypothesis of special relativity, too, i.e. the latter hypothesis is not needed to explain the experiment’s zero outcome. But it is obvious that this result follows already straightforwardly from ratios (18).
4.2. Direct Two-Way and One-Way Measurement of the Velocity of Light in Vacuo and of Particles Propagating at Speeds Near to the One of Light
We turn to # 1) of the introduction, namely the APOLLO facility’s finding that in lunar ranging precision measurements the velocity of light exceeded the tabular value by 200 ± 10 m·s−1. In this clearly two-way case one calculates from Eq.23b right forwardly
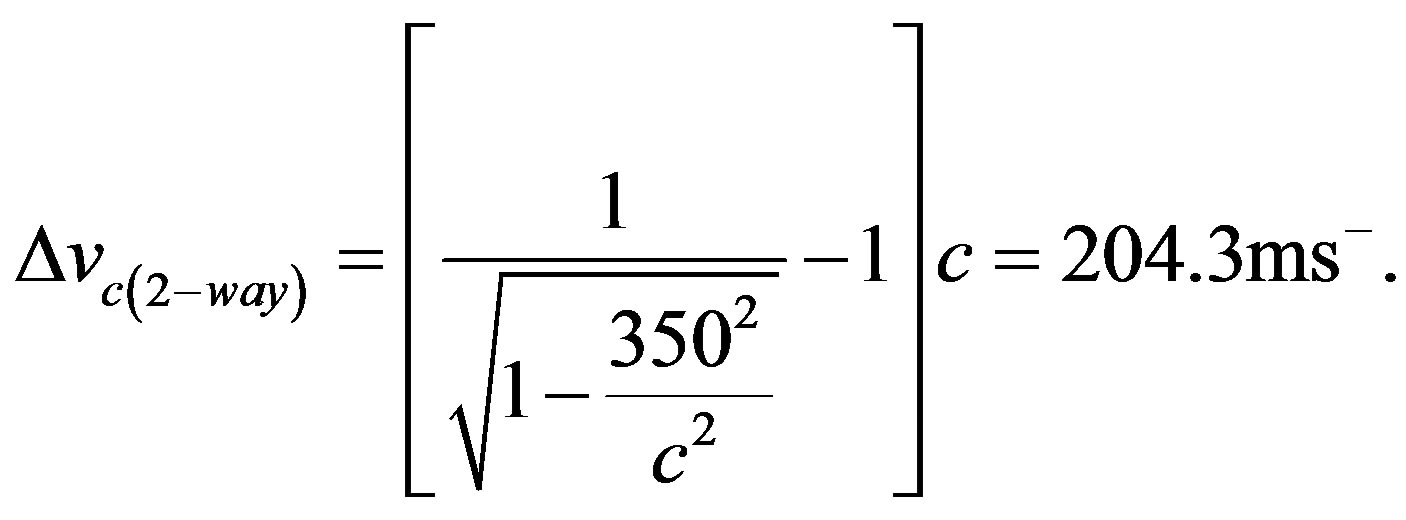 (24b)
(24b)
where the mean value v0(CMB) = 350 km·s−1 of the EarthMoon system has been taken as a reasonable assumption and the true motions of Earth and the Moon been neglected, whereby the tabular velocity of light c = 2.99792 × 105 km. The very good agreement between theory and experiment needs not to be stressed.
The experimental result # 2) of the introduction has been widely and controversially discussed since its arXiv-publication through the OPERA collaboration and is presently thought to be disproved through introductionary #s 3) and 4) (see below). Note that the collaboration’s finding that the neutrinos’= arrival was (60.7 ± 6.9 (stat.) ± 7.4 (sys.)) ns ahead, corresponding to (vv − c)/c ≈18.3 m·s−1 has been infered from the neutrino’s time of flight (TOF) through the Earth’s crust over the precisely measured base line of 731 km from CERN to OPERA with a precision of 0.20 m with the above result [2]. It is obvious that locations on Earth separated by some distance d travel with reference to Σ00 at the same velocity v0(CMB) ≈ 350 km·s−1 and, thus, must be considered as one reference frame in the sense of the above. Other possibly existing relativistic effects due to differences of rotational (accelerational) and gravitational time dilation between CERN and the LNGS are considered neglectably small. Therefore, the neutrino beam constitutes an oneway signal travelling at the velocity of light (or nearly) in the system of the Earth so that Eqs.23 and 23a, respectively, can be applied, wherefrom is calculated
 (24c)
(24c)
The previous mean value v0(CMB) ≈ 350 km·s−1 of Earth has been adopted, but from Eqs.21(b) and 22 it is obvious that in the yearly orbit about the Sun due to the associated rotation of the orbital velocity’s vector with respect to the Sun’s v0(CMB) = 370 km·s−1 slight differences should occur (see below paragraph 4.4). Considering this uncertainty and the ones of the experimental result the agreement between calculations (24c) and experiment seems very good, too.
For the recently proposed Fermilab’s neutrino velocity experiment over a distance of 1300 km predicts Eq.23 a velocity increase of 26.88 m·s−1 with respect to c, coresponding to (vv-c)/c = 2.07 × 10−5, whereby v0(CMB) ≈ 350 km·s−1, under the condition that the neutrino velocity is calculated as the ratio of the precisely measured distance to TOF of neutrinos (see below).
The introductionary # 3) with the experimental result neutrinos from the same source and over the same base line as OPERA ingoing with the speed of light seemingly contradicts OPERA’s finding # 2) and calculation (24c) based on Eqs.23 and 23a.
But other than OPERA, the ICARUS result has been infered from direct comparison of the TOF of neutrinos with the one of light over the said base line: “The absolute UTC timing signal at LNGS is provided every second (PPS) by a GPS system ESAT 2000 disciplined with a Rubidium oscillator operating on the surface Laboratory. A copy of this signal is sent underground every ms (Ppms) and used in ICARUS to provide the absolute time-stamp” [3]. From this and the further description of the experiment clearly follows its outcome to directly result from comparison of the speed of light and neutrinos, respectively (see also below). In this case Eq.23 predicts
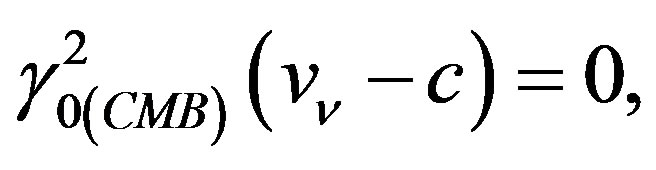 (24d)
(24d)
where vv ≈ c. It follows, ICARUS = result to comply with theory, but the chosen method being unsuitable to uncover the relativistic effect according to Eq.23.
Referring to the introductionarily mentioned announcement of CERN that now all four experiments at Gran Sasso “measure a neutrino TOF consistent with the speed of light” it should be noticed that, compared to the time-consuming OPERA analysis [2] from about 16000 neutrino events of the years 2009, 2010 and 2011, those four experiments were performed in less than one month (May 2012). This leads to the conviction that now in all four experiments principally the much less time-consuming ICARUS-method has been applied, i.e. direct comparison of TOF of neutrinos and light, respectively. This view is corroborated by the recent description of the “GPS-based CERN-LNGS time link for Borexino”, which has been used for the speed measurements in May 2012 by the other experiments, too [24]. According to the latter: “The TOF of neutrinos from CERN to Gran Sasso is measured by making the difference of the readout value of a Cesium clock at CERN and a GPS disciplined Rubidium clock installed in the HPTF at Gran Sasso” .... whereby... “The calibration of the CERN - LNGS GPS link was estimated in (232.6 ± 1.1 ns)”. (the latter value being obviously the difference of TOF of the GPS signal between LNGS and CERN). Of course, in this case the outcome of all four experiments will comply with Eq.24d and the result of ICARUS as well. Besides, it should be remarked that those experiments in principle are equivalent to the measurement of the velocity of relativistic electrons at the linear accelerator of Stanford University in 1974. In the said experiment the velocity of the high energy electrons had been directly compared with the velocity of light over a distance of one km, also with the result that no difference be measurable [25].
Thus, for future one-way experiments on Earth should be obeyed that in accord with the above only OPERA’s original proceeding can unveil this hitherto hidden property of SMS, namely: ...“precision determination of the neutrino velocity defined as the ratio of the precisely measured distance from CERN to OPERA to the TOF of neutrinos”...[2].
The latter requirement has been observed in the # 4) apparent disproof of superluminal neutrinos neither. This time coincidence study of the OPERA and LVD detectors, based on 306 horizontal cosmic muon events, shows a negative time shift in the order of 73 ± 9 ns with respect to a “normal” delayΔt = tLVD − tOPERA = TOF (160 × c−1 × 109 ns) + systematic errors (ns) between both experiments if the period from August 2008 to December 2011 is compared with the time before and after the latter [4] [5]. That systematic shift is about comparable with the above OPERA neutrino velocity excess and, thus, has been ascribed to an apparent malfunction of the original OPERA timing set-up, implying the invalidity of the result # 2), whereby the stability in time of LVD is assumed by the authors. The time shift results from the grouping B = August 2008 to December 2011 and A = time period before and after B such that Δt (A) − Δt (B) = (595 ± 8 ns) − (668 ± 4 ns) = −73 ± 9 ns.
Note that the authors proceed from the presumption their method to be independent of the knowledge of the neutrino base line of 731 km. But one should consider that in order to hit both detectors (which are only some meters apart), the horizontally traversing cosmic muons in principle must follow the neutrino’s flight path, i.e. enter Earth’s crust at CERN pretty exactly. During time period B the GPS-timing system of OPERA was active, i.e. synchronizing time of CERN and the latter and, thus, allowing most exact measuring of TOF of the neutrinos as ratio of distance d = 731 km to speed of neutrinos. Therewith, OPERA was linked timely with CERN such that a signal’s arrival at OPERA has been referred to its start at CERN, whereas LVD was not. This must have been true for all signals starting at CERN during period B, whether neutrinos emitted at CERN or cosmic muons entering Earth’s crust at CERN and following the neutrinos’ track. Their starting time marked the beginning of the reference frame “fixed neutrino base line“ moving relative to the CMB with v0(CMB) ≈ 350 km·s−1, whereas the reception time at OPERA marked the end of the base line, independently of whether the start at CERN had been recorded or not. i.e., CERN has been the point in SMS where the fixed distance d = 731 km has begun and wherefrom the travel time of signals, whether neutrinos or cosmic muons, has to be calculated. Therefore, all signals travelling this base line with v0 ≈ c during time period B from CERN to OPERA arrived the latter’s detector according to Eqs.24c with excess velocity 20.17 m·s−1 and 67.19 ns earlier, implying tOPERA to be 67 ns fast. Thus, because velocity excess of the signal between OPERA and LVD is neglectable (160 m correspond at 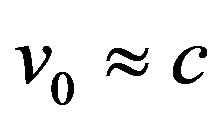 to 9.9 × 10−4 ns earlier arrival) the time difference between both experiments must have been of the order
to 9.9 × 10−4 ns earlier arrival) the time difference between both experiments must have been of the order
 (24e)
(24e)
being equivalent to the authors’ calculation B = 668 ± 4 ns of the synchronized period B, where (160 × c−1 × 109) ns = TOF of the muons from OPERA to LVD [4,5].
It follows that outside the synchronization period B, before August 2008 and after December 2011, denoted A, CERN no more marks the beginning of a fixed distance, but OPERA instead as the starting point of distance d = 160 m between the former and LVD with the probably unmeasurable time difference 9.9 × 10−4 ns such that must be valid
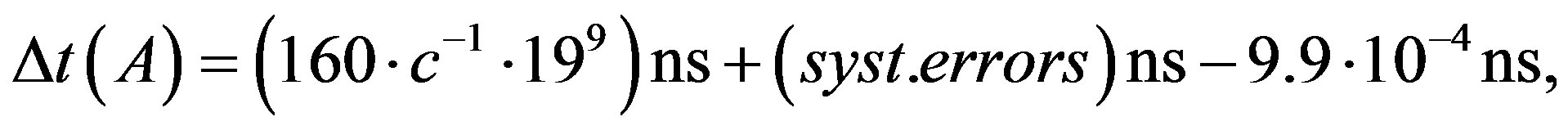 (24f)
(24f)
which, as already remarked above, the authors calculated with A = 595 ± 8 ns so that the theoretical difference Δt (A) − Δt (B) = −67.19 ns is in very good accord with the experimental value −73 ± 9 ns.
Thus, also the result of the above analysis complies with theory and uncovers the relativistic effect (23), but cannot classed correctly with its relativistic orign without knowledge of the SMS background developed above.
In the following some other arguments against the possibility of superluminal neutrinos will be shortly discussed, whereby, considering the previous, the denial of superluminal speed with reference to special relativity will not be dealt with, except the objection that causality may not be preserved. The latter principle cannot be violated, because according to the above signals in SMS travelling at a velocity near that of light ≈ c with respect to the emitter, but exceeding the canonical value of light speed with reference to the receiver with variable maximum c , are inherent to the nature of SMS and, thus, cannot supersede causality. Therefore, this effect of SMS better should be dubbed non-canonical instead of superluminal light speed.
, are inherent to the nature of SMS and, thus, cannot supersede causality. Therefore, this effect of SMS better should be dubbed non-canonical instead of superluminal light speed.
From astrophysical side has been argued that superluminal neutrinos contradict the (anti) neutrino burst from SN 1987A at distance 1.68 × 105 ly away, which arrived 3 hours before the first light from the supernova, in accordance with astrophysical theory [26]. Eq. 23d predicts for photons and neutrinos the same non-canonical velocity and, therewith, the same earlier arrival time such that they arrive with the same time interval as they had been emitted, where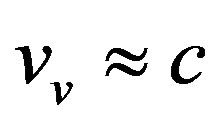 . Note the similiarity with ICARUS’ result Eq.24d.
. Note the similiarity with ICARUS’ result Eq.24d.
It has been argued by theorists and the ICARUS collaboration as well that the superluminal neutrinos should loose energy through Cherenkov-like radiation analogously to charged particles [27,28]. The former collaboration finds energy distribution of the ICARUS events to agree with an unaffected energy distribution of the beam from CERN. From Eqs.18 to 23c one deduces that in SMS the velocity of light be not a rigid barrier as in Einsteinian special relativity theory but dependable on the three transformation steps Σ00 (S), S’ and S˚ instead. Therefore, if reference frames of emitter S’ and receiver S (S), respectively, of one-way signals, whether photons or other particles, are moving jointly relative to Σ00 it is according to the preceding an inherent property of SMS that always the signal carrier’s energy must be the same at emission and reception:
 (24g)
(24g)
where Eν denotes rest mass of neutrino and γ0 Lorentz factor of neutrino speed. The latter result is to expect because according to the previous energy is a clearly two-way parameter physically.
4.3. Velocity and Travel Time of Cosmic Objects on the Plane of the Sky and of Spacecraft in the Solar System
We turn to # 5) of the introduction, where the B 1951 + 32 pulsar’s age of ≈ 64 ± 18 kyr, considerably differs from its astrophysical “characteristic age” of 107 kyr.
It is clear that the observation of the pulsar’s flight path from its birth-place to the present position and the derived speed have been leading to the conclusion that for the former path only ≈ 65 kyr instead of 107 kyr on the grounds of current astrophysical theory should be required. In this case the movement of the far-away emitter travelling on the plane of the sky (one-way case) shall be investigated. i.e. the pulsar’s earlier arrival due to velocity according to Eq.23c at the point of last observation on the sky will be calculated, considering its “characteristic age” of 107 kyr from the starting point to the point of last observation.
Owing to the pulsar’s transverse velocity of 240 ± 40 km·s−1 a velocity v0(CMB) ≈ 500 km·s−1 has been assumed implying that according to current theory the former would travel distance d ≈ 107 ky × 500/c = 178.33 lyr on the plane of the sky in 107 kyr. Therefore, an observer on Earth would according to (23c) on the plane of the sky observe the pulsar’s flight be about
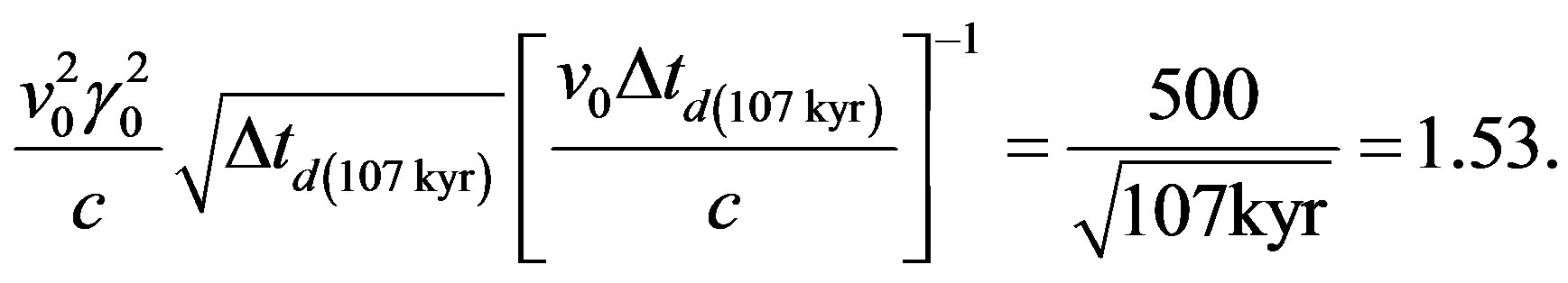 (24h)
(24h)
times fast, whereby 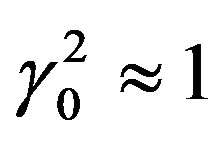 and, therewith, be of apparent age:
and, therewith, be of apparent age:
 (24i)
(24i)
The latter result is in good accord with the empirical value 64 ± 18 kyr. Note that with increasing “characteristic age” the pulsar would appear ever younger in comparison to the respective nowadays characteristic age (see also next paragraphs).
According to the introduction’s # 6) indicate the motions of optical filaments of the Crab nebula projected backward the mean date of the supernova event as A. D. 1130 ± 16 yr (in comparison to the authentic historical date A. D. 1054 from Chinese astronomical records), being consistent with other authors. The investigations have been performed over a time span of about 50 years. For the following calculation the latter observation period has been assumed and A.D. 2010 taken as the last year of observation such that the time span from the supernova’s first appearance till the beginning and the end of 50 years observation time being 906 and 956 years, respectively. By virtue of the 50 years observation of the nebula’s expansion velocity, and starting according to Eq.23c from the ansatz
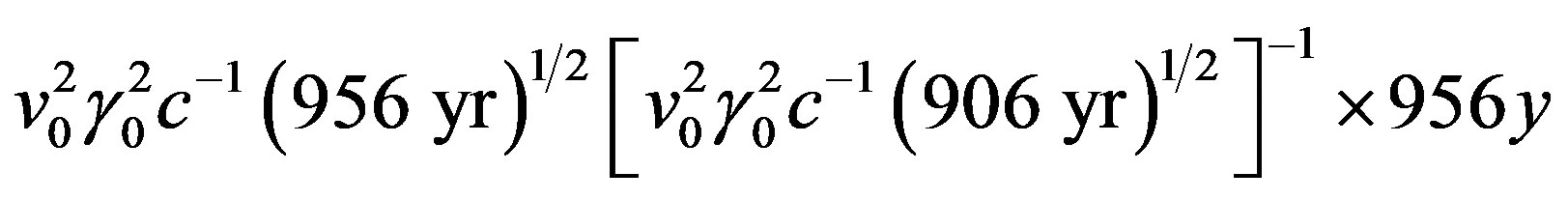 one calculates a reduction of the year of first observation A.D. 1054 in the order of
one calculates a reduction of the year of first observation A.D. 1054 in the order of
 (24j)
(24j)
i.e. about in that year the crab nova would have been observed on the strength of the observed accelerated velocity of filaments in the time from about 1960 to 2010. Considering the uncertainties, the latter result is in very good accord with the astronomical findings, too. Furthermore, explains the growing of (24j) in dependence on the square root out of elapsed observation time the observed accelerative expansion of the crab nebula and similar cosmic objects in a fully way. e.g. predicts (24j) for A. D. 2060, i.e. after then 100 years observation time, a further reduced time of the pulsar’s first observation in A. D. 1208.
The astronomical results #s 7) and 8) of the introduction have been controversially discussed, too, because with supernovae showing cosmological time dilation and quasars not, but both in about the same cosmological distance, they apparently seem to exclude one another. In the following will be shown that the astronomical findings only seemingly are contradictionable, because according to the previous the cosmological time dilation totally can be cancelled through the relativistic velocity acceleration proportional to the square root out of elapsed time according to Eq.23c if only time is long enough. This takes the reciprocal ratio
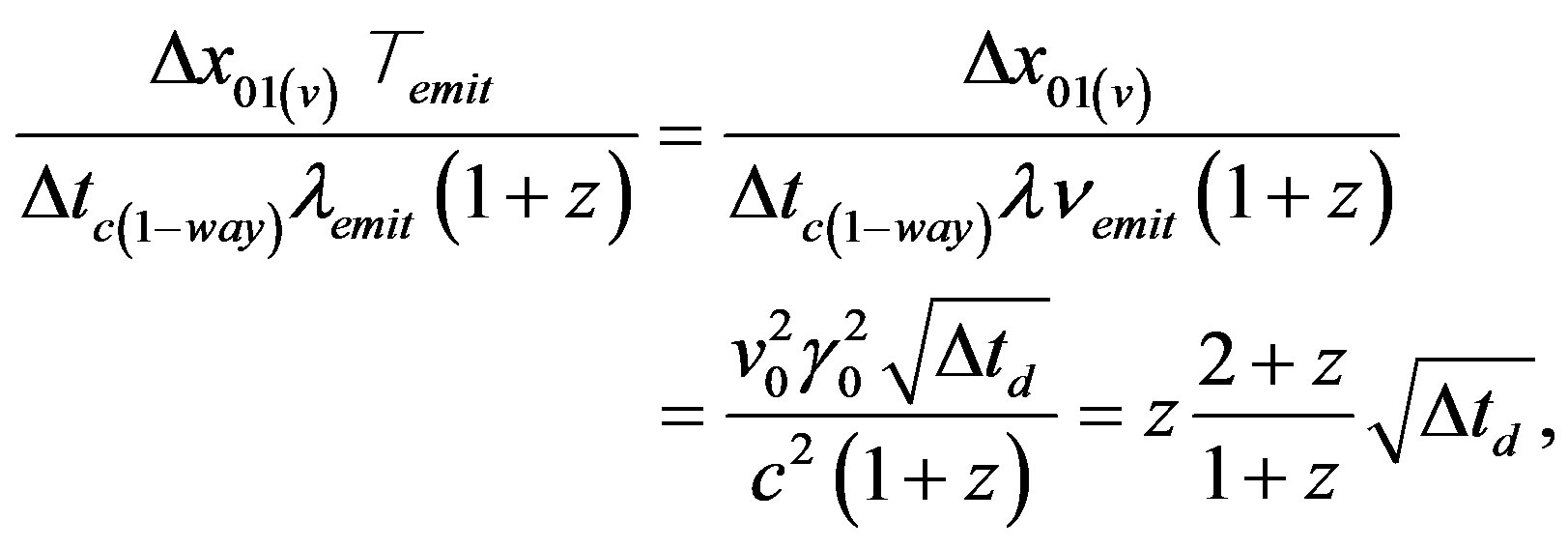 (25)
(25)
because according to (23c) “velocity” referring to coordinate difference Δxo1 must be 
 , whereas “velocity” in association with 1 + z is derivated in the form λemit (Τemit)−1 = λemit vemit = c and
, whereas “velocity” in association with 1 + z is derivated in the form λemit (Τemit)−1 = λemit vemit = c and 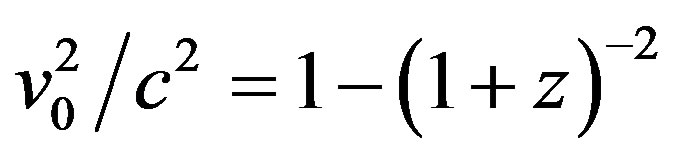 , Τ denotes time, λ wavelength, v frequency and γo Lorentz factor based on cosmic expansion velocity v0 at distance d such that must be valid γo = 1 + z and, furthermore, Δtd travel time in years. Thus, at the # 7) quasar samples’ distances of 6 × 109 lyr (z ≈ 0.7) and 10 × 109 lyr (z ≈ 1.6), furthermore, a mean
, Τ denotes time, λ wavelength, v frequency and γo Lorentz factor based on cosmic expansion velocity v0 at distance d such that must be valid γo = 1 + z and, furthermore, Δtd travel time in years. Thus, at the # 7) quasar samples’ distances of 6 × 109 lyr (z ≈ 0.7) and 10 × 109 lyr (z ≈ 1.6), furthermore, a mean  taken from 50 days and 28 years, the acceleration effect exceeds the reciprocal of the cosmological redshift in the order of magnitude
taken from 50 days and 28 years, the acceleration effect exceeds the reciprocal of the cosmological redshift in the order of magnitude
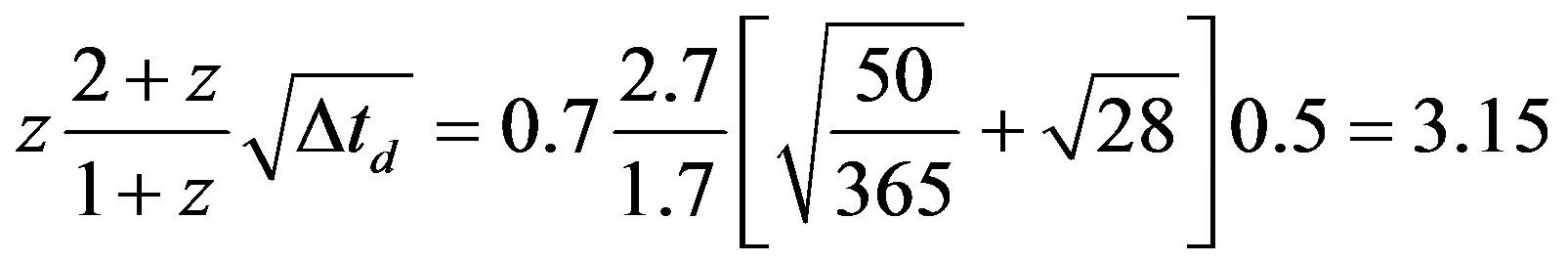 (25a)
(25a)
and
 (25b)
(25b)
It is clear that with growing Δtd and expansion velocity those ratios will increase as well, i.e. much farer away quasars will show enhanced acceleration effect.
On the other hand delivers ratio (25) in the case # 8) of the supernovae at z = 0.35 and 0.46, respectively, with a mean observation time of 275 days (time of ≈ 250 - 300 days within which the evolution of SN lightcurves essentially is completed; e.g. see Figure 1 of [9]) the results
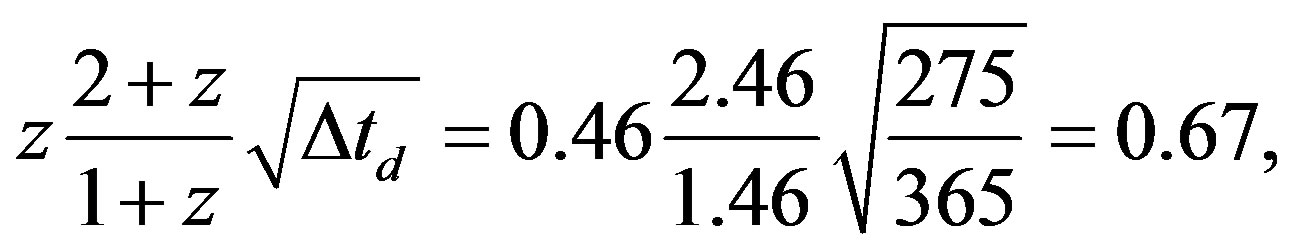 (25c)
(25c)
and
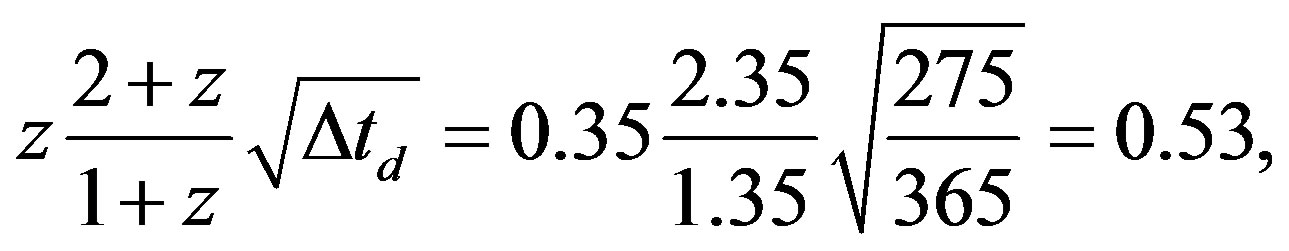 (25d)
(25d)
i.e. about the astronomical findings in the reciprocal form (1 + z)−1. In the case of the sample of more than 800 supernovae with redshifts between z = 0.3 to 0.7 the authors constructed a mean lightcurve which fits more or less the curve expected from the impact of cosmological time dilation. In the case of the Type Ia SN 1997ex with redshift z = 0.361 one straightforwardly calculates
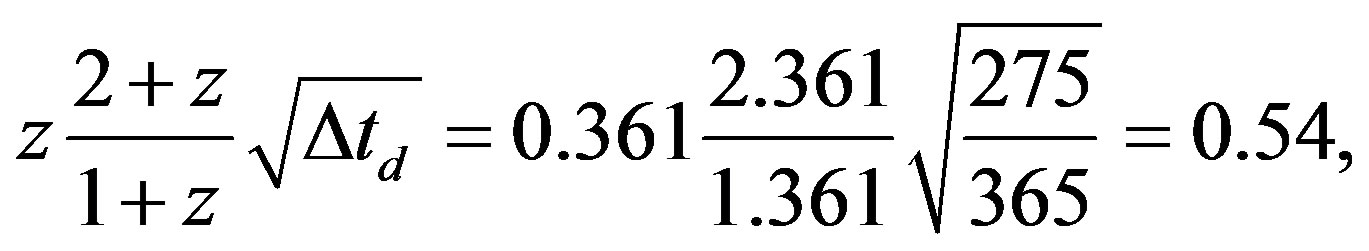 (25e)
(25e)
Eventually an application of Eq.23d to spacecraft cruising the solar system, not mentioned in the introductionary part, shall be discussed.
Obviously predicts the latter formula for direct flights of spacecraft from Earth to other planets of the solar system with no swing-by an earlier arrival than current relativistic theory basically. E.g., travelled Pioneer 10 after launch on 2 March 1972 as the first craft on a slightly hyperbolic course directly, with no swing-by, to Jupiter with closest approach on 3 December 1973, about 60 seconds ahead of the planned time, as well as Pioneer 11, which was launched on 6 April 1973 and achieved after 607 days travel time its closest approach to Jupiter on 3 December 1974 (e.g. see http://history.nasa.gov/SP 349/ch1.htm, p. 5).
According to Eq.23d Pioneer 10 would after then 642 days flight time to Jupiter have arrived about
 (25f)
(25f)
ahead, in comparison to calculations on the grounds of current theory. The median velocity ≈ 14.4 km·s−1 of the craft in comparison to v0(CMB) ≈ 350 km·s−1 of the Earth could be neglected. For Pioneer 11 one accordingly calculates the time of arrival to be 58.29 s ahead.
These slight deviations of both Pioneers from the calculated time of closest approach to Jupiter remained unnoticed yet, because NASA right forwardly sought explanation of the earlier arrival of the former craft by assuming a slightly higher mass of the planet in the order of magnitude of the moon’s mass (at the same place as above).
4.4. Variability of Rest Time on Earth in Dependence on the Latter’s Variable Natural Dimensionless Orbital Velocity Relative to the CMB
According to the preceding, the experimental results # 9) are to expect, although not as a consequence of Earth’s varying distance to the Sun but rather as a result of her varying dimensionless velocity v0(CMB)/c relative to Σ00 during one orbit and the associated small changes in rest time according to Eqs.21(b) and 22, respectively. Owing to the constant decay rates of nuclides can the latter be considered as natural clocks fixed to Earth, showing the respective variant rest time Δt˚(variant) = Δx˚/(v0(CMB) = variant).
According to astronomical findings travels the Sun presently into direction l = 58.87˚ (galactic longitude), b = 17.72˚ (galactic latitude) on her way around the galactic center (apex), whereas her current movement relative to Σ00 is counter directed roughly with l = 276 ± 3˚, b = 30 ± 3˚ of the radio-astrophysical dipole at velocity v0(CMB) ≈ 370 km·s−1 Therefore, rounding off the latter longitudenal values to l = 280˚ and l = 60˚, respectively, and neglecting galactic latitude, one receives l = 240˚ for the counter direction of the Sun’s apex and δ = 40˚ for the angular deviation of l = 240˚ from the direction of the Sun’s dipole vector l = 280˚. It is clear that Earth’s orbit annually shortly must be aligned with Sun’s velocity vector l = 60˚ and counter directed to l = 240˚ on the opposite side, whereas at the by a quarter orbit displaced points of Earth’s orbit and vector l = 60˚ must cross perpendicularly and that for the addition of the respective velocities the Einsteinian addition theorem must be valid.
As a consequence of Earth’s counterclockwise revolution with respect to the north pole of the ecliptic, oppositely to the Galaxy’s clockwise one, travels the former annually around beginning of June into direction l = 240˚, and, angle δ = 40˚ farther away, or, 12 × 40˚ / 360° = 1.33 months later, into direction l = 280˚, i.e. parallely to vector of v0(CMB) = 370 km·s−1. Thus, addition of the latter velocity and Earth’s orbital velocity of 30 km·s−1 results in v0(CMB)≈ 400 km·s−1 at around middle of July. Thereby, and also in the following the addition theorem is negligible because of the smallnes of the effect. In the early days of December Earth moves parallely to the apex direction l = 60˚ and, again 1.33 months later, in January antiparallely to vector of v0(CMB) = 370 km·s−1, pointing to l = 280˚ such that at this time Earth’s velocity relative to the CMB must be the difference v0(CMB) ≈ 370 − 30 = 340 km·s−1. Hence, owing to the revolution of Earth around the Sun will the dimensionless velocity v0(CMB)/c of the former relative to the CMB or Σ00, respectively, according to Eqs.21(b) and 22 annually be modulated with the implication that the ratios of resttimes must exhibit a slight semiannual pattern with a highest value in July in the order of about
 (26)
(26)
and a lowest value in January—below the median being unity—with ratio
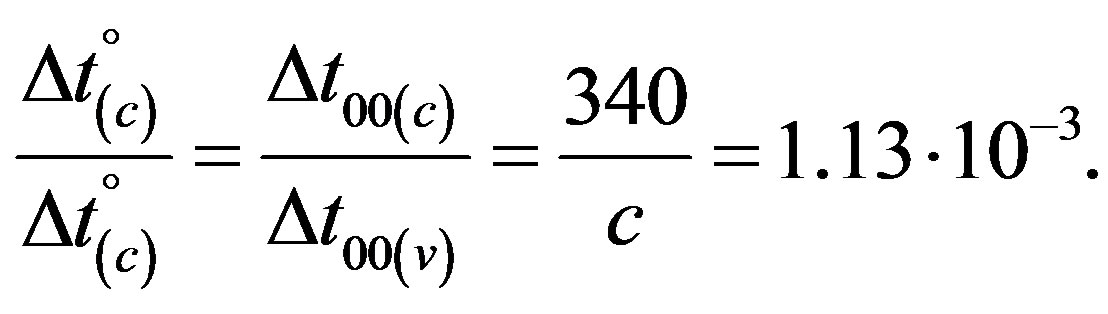 (26a)
(26a)
Both deviations from unity add to 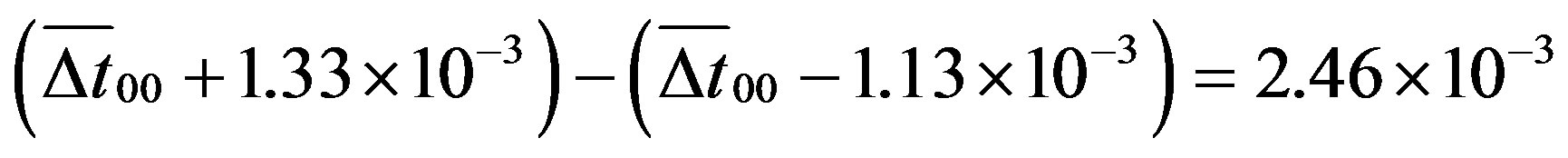 in the order of which the above decay constant should oscillate during one orbit’s time, being in good accord with the experimental finding ≈ 3 × 10−3 [12,13].
in the order of which the above decay constant should oscillate during one orbit’s time, being in good accord with the experimental finding ≈ 3 × 10−3 [12,13].
It is evident that the Earth’s small changes of natural dimensionless orbital velocity v0(CMB)/c relative to Σ00, being equivalent to the reciprocal of dimensionless time 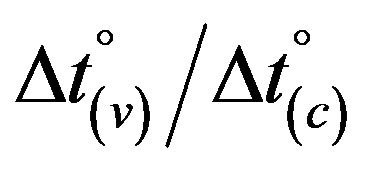 according to ratios (26) and (26a), should also be perceptible as slight variations of the muon flux of the introduction’s # 10). But other than in preceding # 9), where the intrinsic variations of counting rates as ticks of a natural clock in dependence on dimensionless orbital velocity v0(CMB)/c of Earth have been considered, constitute the cosmic muons a constant flux from all directions in relation to a variable dimensionless time
according to ratios (26) and (26a), should also be perceptible as slight variations of the muon flux of the introduction’s # 10). But other than in preceding # 9), where the intrinsic variations of counting rates as ticks of a natural clock in dependence on dimensionless orbital velocity v0(CMB)/c of Earth have been considered, constitute the cosmic muons a constant flux from all directions in relation to a variable dimensionless time 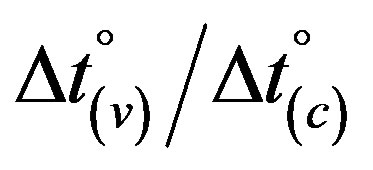 during one orbit’s time. Because according to (26) during the latter orbit the detector’s time is most dilated in July with the muon flux remaining constant, implies this an increase of counts, whereas in December according to (26a) time now is less dilated than the median with an unchanged muon flux, implying a lowest count rate. Both theoretical derivations exactly comply with experimental results [14].
during one orbit’s time. Because according to (26) during the latter orbit the detector’s time is most dilated in July with the muon flux remaining constant, implies this an increase of counts, whereas in December according to (26a) time now is less dilated than the median with an unchanged muon flux, implying a lowest count rate. Both theoretical derivations exactly comply with experimental results [14].
Due to the muon’s high energy up to 1.3 TeV are solar magnetic fields and the solar wind at the solar maximum as a cause of the above annular modulations excluded, as the authors underline. Furthermore, “no evidence for such long-term modulation in the effective stratosperic temperature close to from Gran Sasso has been found, and, in addition, it seems rather unlikely the former to be sinusoidal” [14].
4.5. Two-Way Expansion of Volume in the Order of  as the Cause of Increasing Interaction Radii and Total Cross Sections, Respectively, and One-Way Expansion by Value
as the Cause of Increasing Interaction Radii and Total Cross Sections, Respectively, and One-Way Expansion by Value  as of the Shrinkage of Interaction Mean-Free-Paths
as of the Shrinkage of Interaction Mean-Free-Paths
Referring to # 11) of the introduction it is obvious that according to Eq.17 scattering events in high energy physics with elastic or inelastic collisions of the incident particles and the resulting particles dedected in receivers have to be considered as two-way cases in the sense of the above. Likewise, it is evident that the relativistic elongation of length or expansion of volume into the x-direction according to relations (11b) to (11d) should be noticable in high relativistic collisions of material particles. i.e. there must exist a simple relationship between interaction-radii or scattering cross sections and the above predicted relativistically enlarged physical size of the particles at high velocities, i.e. energies, where the electric force and the de Broglie wavelength are negligible. However, according to Eqs.6 and 6(a) it is clear that prior calculating the former volume expansions, the conventional energy values of accelerators and colliders first of all must be adapted to the composite concept of velocity (see below).
To begin with the relationship between interactionradii or scattering cross sections and the predicted relativistically enlarged physical size of the particles at high velocities: Because nearly all high energy collisions more or less occur grazingly, must the mean geometrical dimensions of the colliding particles be averages over all three spatial axes Δx, Δy, and Δz of the according to Eqs.16 and 17 relativistically enlarged volumina V. Especially the average of the x-dimension must be
 (27)
(27)
Consider two real material bodies (m ≠ 0) being spherically symmetrical and identical in all aspects, their centers resting in the coordinate sources of S1 and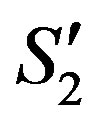 , to collide at Σ0 at time
, to collide at Σ0 at time 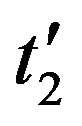 = t1 = t0 = 0. At that moment Eqs.7 and 16 are fully valid with the consequence that the x-dimension of the body in
= t1 = t0 = 0. At that moment Eqs.7 and 16 are fully valid with the consequence that the x-dimension of the body in  appears still altered relativistically—as observed from S1—so that its median effective scattering volume at the time of collision must be
appears still altered relativistically—as observed from S1—so that its median effective scattering volume at the time of collision must be
 (27a)
(27a)
and in the inverse case:
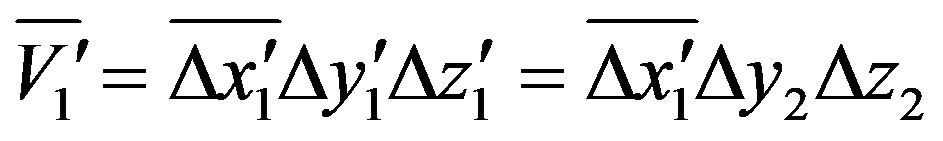 (27b)
(27b)
In association with Eq.15g we receive
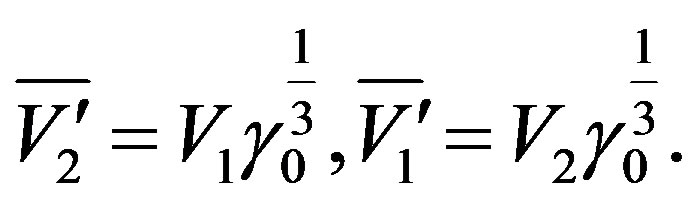 (27c)
(27c)
Thus, as deduced from either system considered to be at rest, in ultra relativistic collision events the body resting in the system considered moving must in the average seem enlarged by a factor of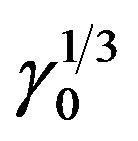 . Hence, its median relative geometrical interaction-radius averaged over the three spatial dimensions must be
. Hence, its median relative geometrical interaction-radius averaged over the three spatial dimensions must be
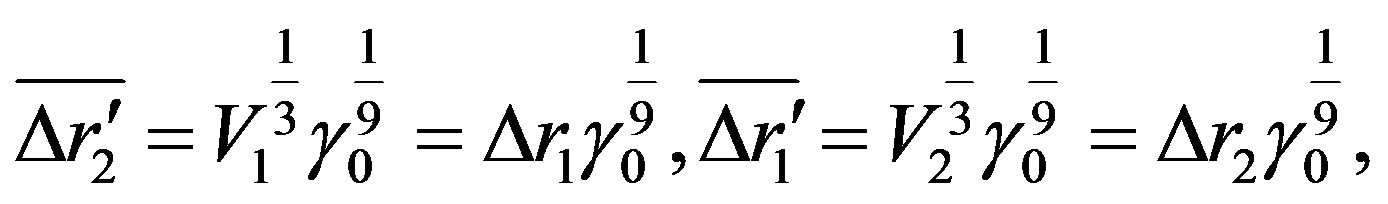 (28)
(28)
where from the mean geometrical cross sections follow:
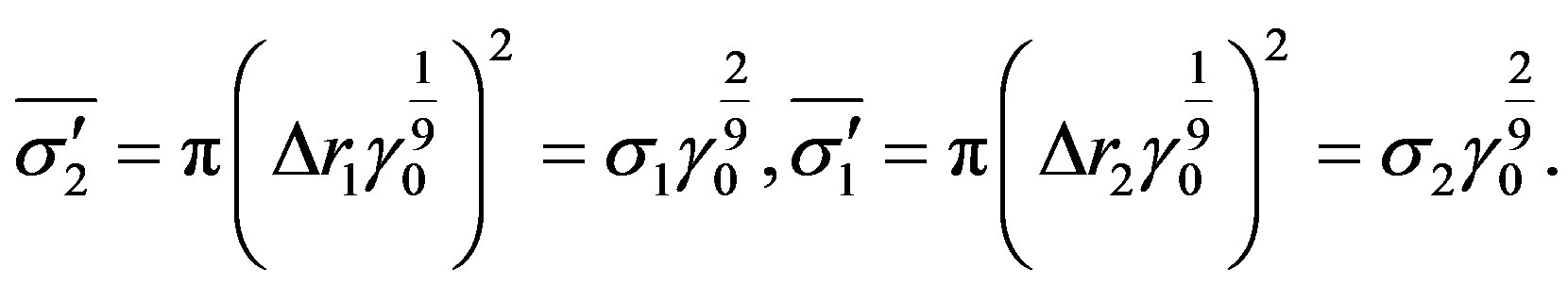 (28a)
(28a)
In either system the colliding bodies are resting, the same enhancement of the interaction-radius (24) or of the geometrical cross section (25) with growing velocity will be noticed. Therefore, relative to the kinematic center Σ0, which at the time 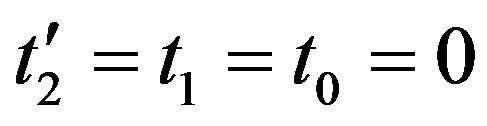 coincides with S1 and S2, the median total geometrical cross section must be
coincides with S1 and S2, the median total geometrical cross section must be
 (28b)
(28b)
whereby from the foregoing it is clear that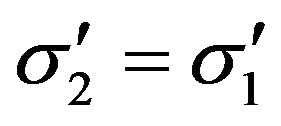 . As shown below are Eqs.28 and 28b directly related to the interaction radii as derived from high energetic collisions on the strength of the optical theorem and the total cross sections σtot = σel + σinel of hadrons at hard and elastic high relativistic collisions, respectively. We restrict to protrons and antiprotrons, which are considered to be alike geometrically (only).
. As shown below are Eqs.28 and 28b directly related to the interaction radii as derived from high energetic collisions on the strength of the optical theorem and the total cross sections σtot = σel + σinel of hadrons at hard and elastic high relativistic collisions, respectively. We restrict to protrons and antiprotrons, which are considered to be alike geometrically (only).
The geometrical cross section of the resting or “slowly moved” protron (antiprotron) is measured with ≈1(fm)2 = 10−26 cm2 = 10 mb (millibarn). Consequently, according to Eq.28 the mean interaction-radius of the protron (antiprotron) amounts to (in Fermis)
 (29)
(29)
and the median total geometrical cross section according to Eq.28b rises to (in millibarn)
 (30)
(30)
irrespectively of quantum-mechanical effects. Effects of spin are considered to average out over a wide range of collision events.
Now, we can turn to the conversion of energy values of accelerators and colliders into the previously introduced composite concept of velocity.
Because in high energy collisions the incident particle’s velocity tends to approach the one of light, the former’s composite nature should according to Eqs.6 and 6(a) make itself ever more felt pronouncedly with steadily rising energy. Therefore, to calculate mean interaction-radii and geometrical cross sections according to Eqs.29 and 30 from composite βn = vn/c according to Eq.6a, one first has to conceive fair approximations of Ni yet and, therewith, of γ0 as a function of the center-ofmass energy to render those computations. According to Eq.14 the composite relativistic momentum is given from
 (31)
(31)
if E0 >> E and the latter be neglectable, where E0 denotes total composite center-of-mass energy and E rest energy. Thus, if β0 → 1 then in a first-order approximation and in association with Eq.6 is deduced
 (31a)
(31a)
where E* denotes conventional total center-of-mass energy  and γ the conventional Lorentz factor. In association with Eqs.26 to 28(a) there from is given
and γ the conventional Lorentz factor. In association with Eqs.26 to 28(a) there from is given
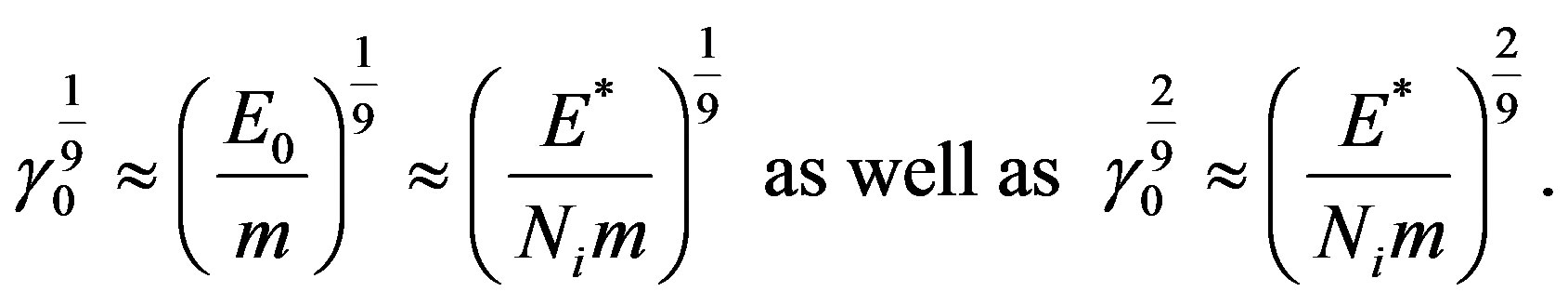 (31b)
(31b)
From the relativistic addition theorem follows
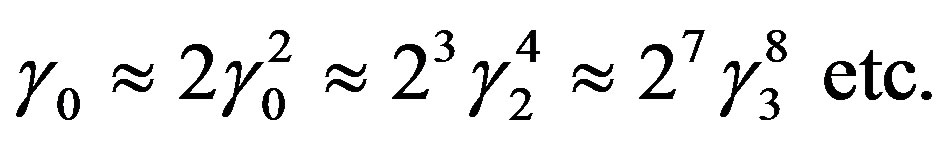 (31c)
(31c)
if . According to Eq.6a in the case of N1 - N3 is valid:
. According to Eq.6a in the case of N1 - N3 is valid: . Therefore, to compute
. Therefore, to compute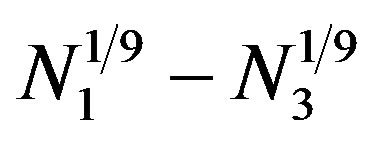 , or
, or , respectively, it will be only a neglectable error to deduce β1 - β3 from the approximations
, respectively, it will be only a neglectable error to deduce β1 - β3 from the approximations
 (31d)
(31d)
if the respective total center-of-mass energy E* successively is reached, where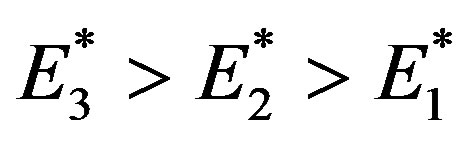 . There from is given:
. There from is given:
 (31e)
(31e)
At higher velocities (energies), i.e. if β3→1, a further approximation is necessary because  and, thus,
and, thus,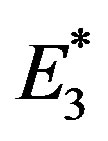 in the denominator of the right-hand side of Eq.31d and in the numerator of (31e) be halve this, implying a correction factor of 2 throughout. Inserting the respective results of Eq.31e into Eq.6a yields N1 - N3. If E* is given in GeV for protrons (antiprotrons), then in the case of colliders from (31b) follows
in the denominator of the right-hand side of Eq.31d and in the numerator of (31e) be halve this, implying a correction factor of 2 throughout. Inserting the respective results of Eq.31e into Eq.6a yields N1 - N3. If E* is given in GeV for protrons (antiprotrons), then in the case of colliders from (31b) follows
 (32)
(32)
and in the case of accelerators
 (33)
(33)
where mp denotes protron (antiprotron) mass = 0.938 GeV and 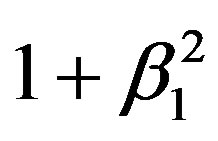 in the denominator of the right-hand side of Eq.33 is due to the relativistic addition of 2E*, implying Ni to start with
in the denominator of the right-hand side of Eq.33 is due to the relativistic addition of 2E*, implying Ni to start with . Inserting Ni—computed from (6a)—into Eq.32, or, Eq.33 yields γ0 as a function of E* and, therewith, the interaction-radius in Fermis according to Eq.29 or the total geometrical cross section in millibarn according to Eq.30. In the following some exemplary calculations are compared with experiment, whereby in Table 1 experimental results as well as theoretical predictions are given as interaction-radii in Fermis and the respective values in Table 2 as cross sections in millibarn.
. Inserting Ni—computed from (6a)—into Eq.32, or, Eq.33 yields γ0 as a function of E* and, therewith, the interaction-radius in Fermis according to Eq.29 or the total geometrical cross section in millibarn according to Eq.30. In the following some exemplary calculations are compared with experiment, whereby in Table 1 experimental results as well as theoretical predictions are given as interaction-radii in Fermis and the respective values in Table 2 as cross sections in millibarn.
Table 2 includes predictions for CERN’s Large Hadron Collider (E* = 7 TeV, 8 TeV, 10 TeV and 14 TeV) and for the cancelled Superconducting Super Collider, which could have reached 40 TeV. Especially should be noticed that the predictions for E* = 7 and 8 TeV very well fit the recent measurements of σtot = σel + σinel of protron-protron collisions from the TOTEM Collaboration at the LHC ([16,33]) and, thus, all experimental results practically exactly comply with the theoretical predictions ranging from E* ≡ = 5 GeV up to 8 Tev on the grounds of only three parameters: The geometrical size of the resting particle, its composite velocity according to Eq.4 and associated relativistic expansion of volume according to the right-hand Eq.15g.
= 5 GeV up to 8 Tev on the grounds of only three parameters: The geometrical size of the resting particle, its composite velocity according to Eq.4 and associated relativistic expansion of volume according to the right-hand Eq.15g.
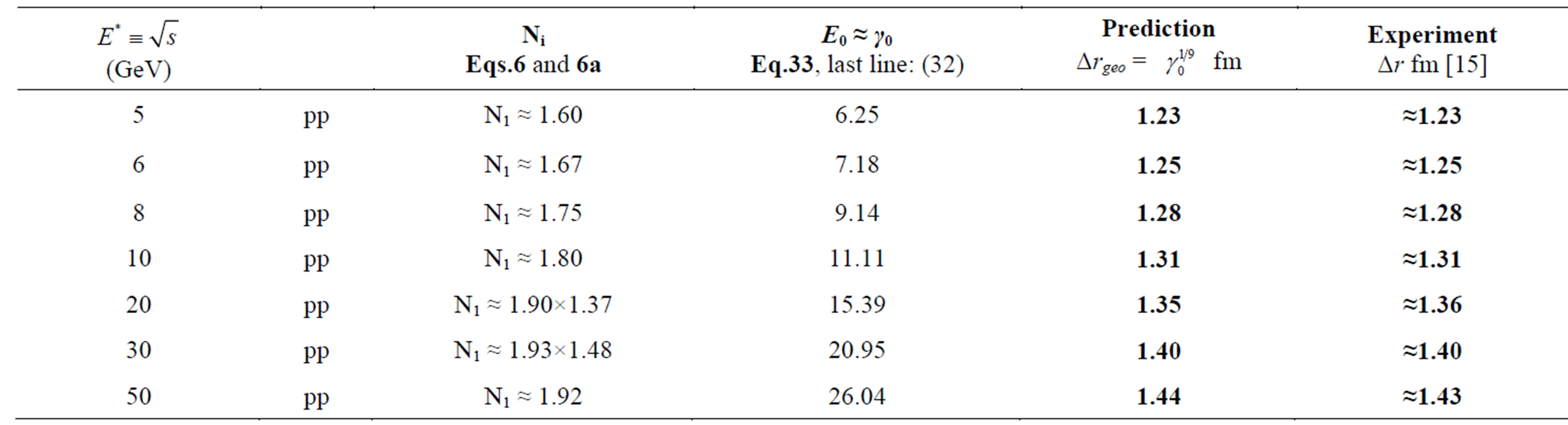
Table 1. Interaction-radii (accelerators; last line: collider).

Table 2. Cross sections (colliders).
Predictions for E* = 10 and 14 TeV have been included with respect to CERN’s recent upgrading decision and, hence, can be compared with experiment very soon. One also should note that, beginning at the kinematical region E* ≈ 60 GeV, the total cross sections of protrons and antiprotrons seem to coincide, to furtheron solely depend on their mean geometrical cross sections according to Eq.30, i.e. they seem to be alike geometrically.
Also very recently a protron-air cross section of 505 ± 22 (stat)  (sys) mb at E* = 57 TeV per nucleon has been reported by the Pierre Auger Collaboration (2012, [34]). A rough calculation results in 490 mb, being in very good accord with the latter measurement. Thereby the median air cross section has been estimated to be roughly the sixfold of the resting protron’s one from the approximate ratio of 3:1 of N2 and S2 nuclei in the atmosphere, such that σgeo (N2) ≈ 142/3 = 5.81 × σgeo and σgeo (S2) ≈162/3 = 6.35 × σgeo with a mean of 5.95 (≈ 6), where the rounded mass of the N2 nucleus ≈ 14 mp and the one of the S2 nucleus ≈ 16 mp has been taken. Finally, it is predicted that 1) the total cross sections of hadrons furtheron will increase with rising velocity (energy) and the associated relativistic elongation of the spatial x-dimension in accord with the above (see Table 2);
(sys) mb at E* = 57 TeV per nucleon has been reported by the Pierre Auger Collaboration (2012, [34]). A rough calculation results in 490 mb, being in very good accord with the latter measurement. Thereby the median air cross section has been estimated to be roughly the sixfold of the resting protron’s one from the approximate ratio of 3:1 of N2 and S2 nuclei in the atmosphere, such that σgeo (N2) ≈ 142/3 = 5.81 × σgeo and σgeo (S2) ≈162/3 = 6.35 × σgeo with a mean of 5.95 (≈ 6), where the rounded mass of the N2 nucleus ≈ 14 mp and the one of the S2 nucleus ≈ 16 mp has been taken. Finally, it is predicted that 1) the total cross sections of hadrons furtheron will increase with rising velocity (energy) and the associated relativistic elongation of the spatial x-dimension in accord with the above (see Table 2);
2) this relativistic effect be valid for all material particles of whatever kind as well;
3) the relativistic two-way enhancement of the geometrical cross section or interaction-radius, respectively, delivers the physical explanation of the so-called EMC-effect;
4) the strong relativistic elongation of colliding particles in the beam direction leads to the experimentally observed growing transversal deviations of secondary particles out of collisions with ever growing velocity (energy), including energetic collisions of all kinds of nuclei.
We turn to # 12) of the introduction, the announced rarer and less spectacular but nevertheless already wellknown one-way cases in particle physics.
Consider a particle, based at a system , moving through a dense material medium at high relativistic velocity and coming to a halt within the medium. With respect to
, moving through a dense material medium at high relativistic velocity and coming to a halt within the medium. With respect to  the atoms, constituting the medium and resting relative to another, obviously represent the “real resting” system S1 according to Eq.7. According to Eqs.18 and 19 a moving particle
the atoms, constituting the medium and resting relative to another, obviously represent the “real resting” system S1 according to Eq.7. According to Eqs.18 and 19 a moving particle  would relative to the resting atoms seem enhanced by a factor of
would relative to the resting atoms seem enhanced by a factor of 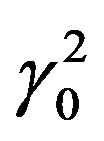 in the x-direction. Analogous application of Eqs.28b and 30 in association with Eqs.31b to 33 leads to the geometrical cross section
in the x-direction. Analogous application of Eqs.28b and 30 in association with Eqs.31b to 33 leads to the geometrical cross section
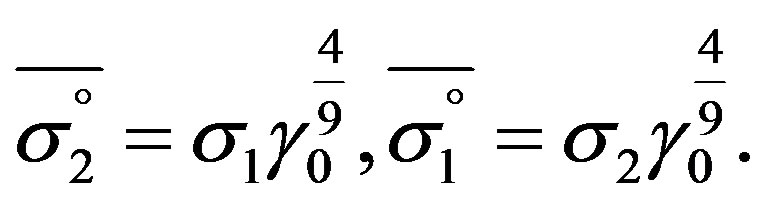 (34)
(34)
This result predicts a shrinkage of the interaction mean-free-paths of particles plunging through some material before coming to a halt in the order of
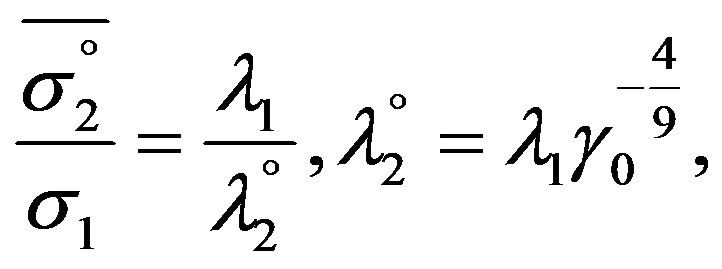 (35)
(35)
where λ1 denotes mean-free-path of a slowly moving particle within any material and σ1 the mean geometrical cross section if . According to Eq.35 the interaction mean-free-paths of nucleii or particles coming to a stop within some material (e.g. nuclear track emulsion), after traversing it at high relativistic velocity (energy), must shrink proportionally to a factor of
. According to Eq.35 the interaction mean-free-paths of nucleii or particles coming to a stop within some material (e.g. nuclear track emulsion), after traversing it at high relativistic velocity (energy), must shrink proportionally to a factor of .
.
E.g. studied the EMU 08 experiment at CERN the interactions of oxygen beams at E* = 200 and 60 GeV/ nucleon in nuclear emulsion and found for inelastic events the interaction mean-free-paths for higher and lower energy beams to be 10.89 cm and 12.84 cm, respectively [35]. Prediction by extrapolating from E* = 60 GeV with a mean-free-path of 12.84 cm to E* = 200 GeV results according to Eq.35 in 10.89 cm, too, being in exellent agreement with experiment.
For secondary particles the latter relativistic effect is also experimentally well-known and has since its discovery been controversially discussed under the term “anomalons” (secondary nuclei with abnormal short meanfree-paths after collision of primaries within some material (see e.g. [36])).
5. CONCLUDING REMARKS
The proposed extension of the spacetime of special relativity to the symmetric Minkowski spacetime (SMS) with quantized velocity according to Eq.4 implies a temporarily existing preferred but relative frame of reference of nature Σo between any two inertially moving frames of reference and of an absolute rest frame of nature Σ00 in the form of the space-fabric of SMS, indicated through the CMB. The latter relativistic notion seems to model physical reality very well and especially allows quantitative solutions of various physical phenomena on and near Earth, but on microscopic, galactic and cosmic scale as well with sufficient accuracy. Furthermore, it has been revealed, the existence of an absolute rest frame of nature Σ00 in SMS to imply a duality of the speed of light as well as of inertial velocity in dependence on one-way or two-way measurement, respectively.
As a further result of the proposed symmetry of SMS follows the velocity of light and translationally moving frames of reference to be invariant with respect to the spacetime fabric and the latter frames as well, independently of their respective state of motion. Through its movement relative to the CMB, the associated time dilation and expansion of length of the x-dimension of the geometrical basis of the respective rest frame by a factor of γ0 will according to Eq.18 be transformed to a state of apparent rest, i.e. such that Δxoo/Δtoo = Δx/Δt = Δx’/Δt’ = Δx˚/Δt˚ ≤ c, respectively. If true, this is the very foundation physically of the up-to-now hypothetical principle of relativity (Copernicus, Galilei, Poincaré, Einstein), as already stated above. But from Eqs.18 to 22a it is clear, now that this principle is strictly valid at the zero point x = y = z = t = 0 of the respective frame of reference in SMS only, implying the variance of Lorentz frames on larger scales spatially. Furthermore, it has been shown the strictly relativistic notion of SMS to imply the invariance of simultaneity for all observers.
Last but not least, it has been shown non-canonical (superluminal) speed of light as well as of frames of reference moving inertially at velocity v0 → c relative to nature’s absolute rest frame of SMS to be possible basically. This result is only in apparent contradiction to the experimental evidence e.g. concerning the observed dilated decay time of unstable particles circling in storage rings (colliders) with respect to Earth as the reference frame. The latter circular motion clearly is not a constant rectilinear but rather an accelerated one, which for not special relativity but general relativity in the form of the weak equivalence principle is the proper theory. The same is valid for satellites orbiting Earth as well as for all experiments where the dilated time of clocks aboard flying aircraft is compared to synchronized clocks resting on Earth. The powered flight of aircraft through and against the frictional resistance of the atmosphere is also a steadily accelerated one and on no accounts inertial motion, whereas in the preceding considerations translational motion in SMS with no acceleration is involved only. It is evident that relativistic effects due to acceleration are not Lorentz-invariant, i.e. the state of rest to the one of motion being identical to its inverse in accord with Eq.20. This explains the one-sidedness of the above time dilations and the association of the underlying velocities with Earth as the rest frame in a full way. But it is also obvious that in the case of measuring the velocity of one-way or two-way signals e.g. between orbiting satellites and Earth in accord with the above the receiver’s rest frame has to be considered resting relative to the CMB.
In memoriam Käthe and Ernst Kunst, Minna and Karl Hagenstein.