Extra dimensions in addition to the usual 4 dimensions of space-time are a common ingredient of the theoretical attempts aiming at combining gravitation with the other interactions [1-5]. Historically, the Kaluza-Klein approach in the 1920’s assumes a 5th dimension, which is enough to account for the tensor field of gravitation and for the vector field of electromagnetism. In addition, it predicts an extra scalar field and it is a common feature of unification theories to predict the existence of additional fields and particles. However, the later evidence of weak and strong interactions has shown that the original KaluzaKlein model was not sufficient for a comprehensive description of the fundamental interactions. The idea of introducing additional dimensions in order to account for all the known fundamental interactions including gravitation has flourished from the 1980’s, e.g. with the string theories which require at least 10 dimensions to be consistent [6].
According to certain models, the size of those extra dimensions is very small, of the order of Planck’s length (10−35 m). The common image is that of a plain seen from the top of a hill: if the hill is high enough, the height of the grass is not perceived by the eye and the plain seems to be a 2-dimension domain. The extra dimensions are supposed to be compactified and wrapped so that they are hidden to us. According to other works, they could be much larger, up to 0.1 mm [7]. However, it is not sure that the question of the size of those dimensions is really meaningful. We experience space and time with our senses or through our instruments but the way we perceive space and time is quite different. For instance, the smallest distance we can perceive with our eyes is of the order of 0.1 mm, and the smallest time interval we can feel is about 0.04 s (the interval between two images in a movie). If we convert those 0.04 s into length (x = ct) we get 12,000 km, 11 orders of magnitude larger than 0.1 mm. In the same manner as space and time are differently perceived and cannot be compared via that this type of conversion, the 6 extra dimensions might be of another nature than usual space or time; nevertheless we actually feel those extra dimensions in as much as “the fundamental interactions of particle physics” can be interpreted as the manifestations in our usual world of the geometry of the extra dimensions. If this is correct, we suggest that the connection between those 6 extra dimensions and the 3 usual dimensions of space involves a new physical constant, like the speed of light connecting space and time, which may be different from the gravitation constant which appears in Planck’s length.
The goal of this paper, essentially a phenomenological approach, is to show the possibility, through a relatively simple mathematical apparatus, that a few basic assumptions on the geometrical properties of a 10-dimension space-time allow deriving the main features of the fundamental interactions: types and symmetries of the particles (hadrons and leptons), types and symmetries of the gauge fields. Moreover, this description, combined with gravitation and with the postulate of a minimal Lagrangian, predicts the existence of additional fields resulting from the coupling of gravitation with the other force fields; those hypothetical extra fields do not act the same way upon hadrons and leptons, thus inducing a violation of the equivalence principle.
2. THE 10-DIMENSION SPACE-TIME
The experimental confirmations of General Relativity lead us to acknowledge that, at least at a macroscopic scale, the geometry of space-time is that of a 4-dimension curved surface 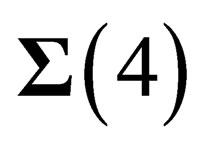 locally invariant under the Lorentz group
locally invariant under the Lorentz group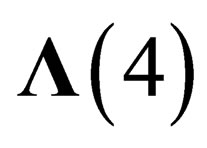 . On another hand a curved surface of dimension d can be embedded inside a flat space with
. On another hand a curved surface of dimension d can be embedded inside a flat space with 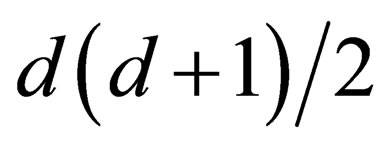 dimensions; hence
dimensions; hence 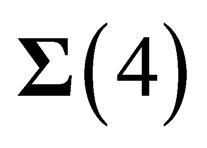 can be embedded inside a flat space with 10 dimensions. We will hereafter make the basic assumption that our physical universe is a flat (pseudo) Euclidian space with 10 dimensions
can be embedded inside a flat space with 10 dimensions. We will hereafter make the basic assumption that our physical universe is a flat (pseudo) Euclidian space with 10 dimensions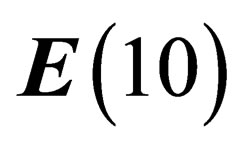 , invariant under some symmetry group
, invariant under some symmetry group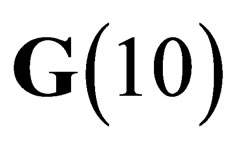 .
.
Let 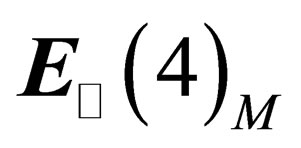 be the tangent space to
be the tangent space to 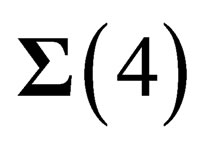 in any point M of
in any point M of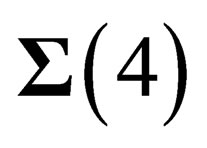 , and
, and 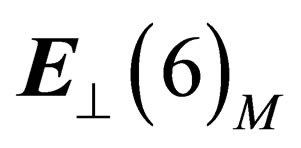 be the orthogonal space to
be the orthogonal space to 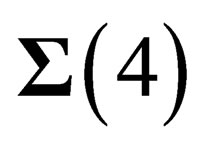 in M.
in M. 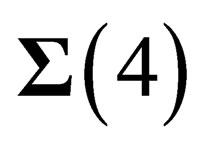 is locally invariant under
is locally invariant under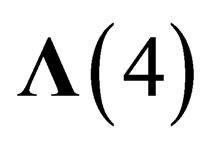 , i.e.
, i.e. 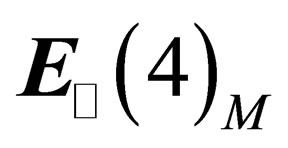 is invariant under
is invariant under .
. 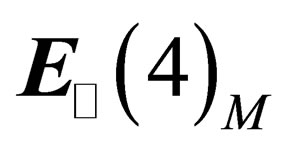 is a 4- dimension flat space in which one can define a system of 4 (pseudo) orthonormal coordinates
is a 4- dimension flat space in which one can define a system of 4 (pseudo) orthonormal coordinates 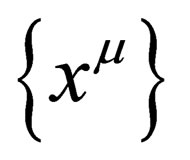 with µ ranging from 0 to 3, i.e. one time coordinate
with µ ranging from 0 to 3, i.e. one time coordinate 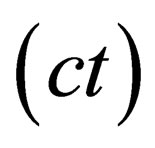 and 3 space coordinates
and 3 space coordinates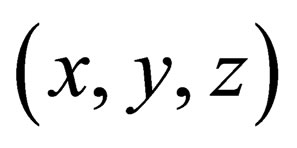 . Given such a local reference frame for
. Given such a local reference frame for , one can find an infinity of other equivalent reference frames by applying to
, one can find an infinity of other equivalent reference frames by applying to  any combination of rotations and Lorentz transformations while conserving the invariance of the pseudo Euclidian norm
any combination of rotations and Lorentz transformations while conserving the invariance of the pseudo Euclidian norm 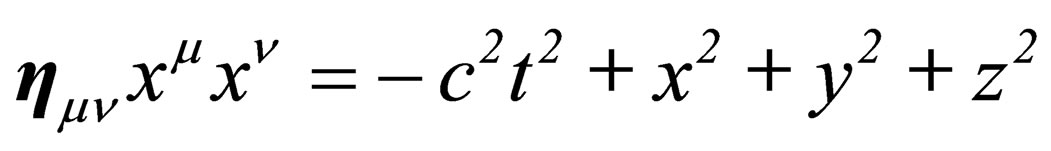 [8]. The effect of the local curvature of the surface can be interpreted on
[8]. The effect of the local curvature of the surface can be interpreted on 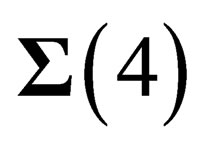 as resulting from a force field which is identified with gravitation.
as resulting from a force field which is identified with gravitation.
 is a 6-dimension space. A priori we do not know anything about the metrics of this space but we will hereafter assume that
is a 6-dimension space. A priori we do not know anything about the metrics of this space but we will hereafter assume that  is a flat space invariant under a symmetry group which conserves the true Euclidian norm
is a flat space invariant under a symmetry group which conserves the true Euclidian norm 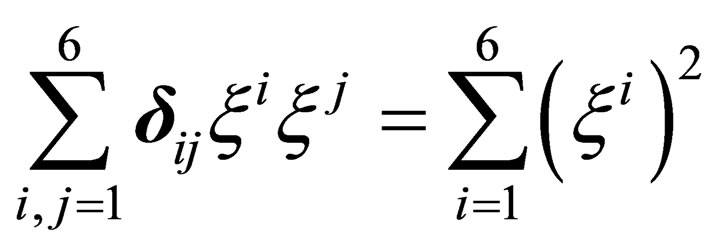 where
where  denotes a set of 6 orthonormal coordinates, i.e. it is the orthogonal group
denotes a set of 6 orthonormal coordinates, i.e. it is the orthogonal group  or one of its subgroups. We restrict ourselves to the special orthogonal group
or one of its subgroups. We restrict ourselves to the special orthogonal group 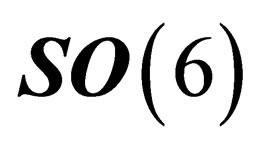 as we will see later on that the transformation
as we will see later on that the transformation 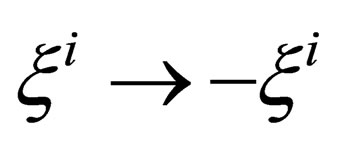 with i ranging from 1 to 6, equivalent in the “internal” space
with i ranging from 1 to 6, equivalent in the “internal” space  to what parity and time reversal represent in the “orbital space”
to what parity and time reversal represent in the “orbital space”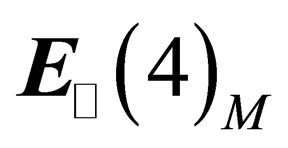 , expresses the charge conjugation.
, expresses the charge conjugation.
The uncertainty principle implies that the physical states are not restricted to 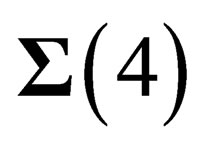 but they have an extension in the other dimensions. Thus in any point M of
but they have an extension in the other dimensions. Thus in any point M of 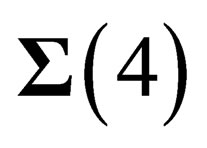 there are 4 “orbital” degrees of freedom along
there are 4 “orbital” degrees of freedom along 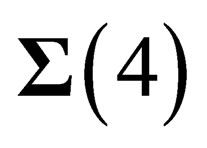 and 6 “internal” degrees of freedom in the transverse directions.
and 6 “internal” degrees of freedom in the transverse directions.
In the following section, gravitation will be assumed to be decoupled from the other interactions; it will be introduced in a later section.
3. HADRONS AND LEPTONS
3.1. Fundamental Assumption
We will henceforth consider the subgroups of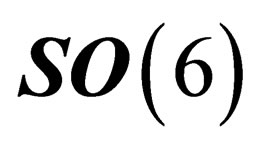 . In the base
. In the base any infinitesimal transformation of
any infinitesimal transformation of 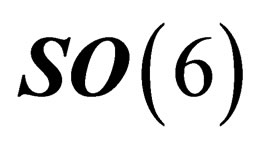 can be written as [9]
can be written as [9]
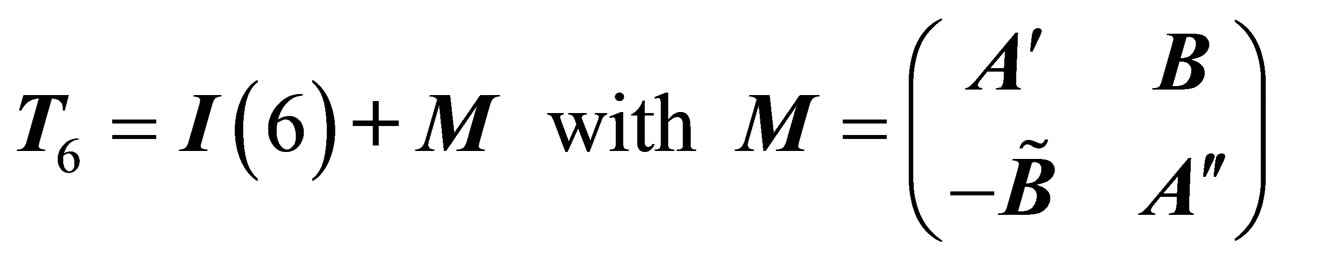 (1)
(1)
 is a fully antisymmetric real 6 × 6 matrix,
is a fully antisymmetric real 6 × 6 matrix, 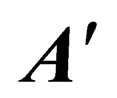 and
and  are two antisymmetric 3 × 3 matrices,
are two antisymmetric 3 × 3 matrices,  is a 3 × 3 matrix and
is a 3 × 3 matrix and  denotes the transposed matrix of
denotes the transposed matrix of ;
; 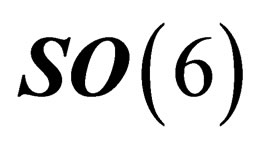 has got 15 infinitesimal generators.
has got 15 infinitesimal generators.
 can be written as
can be written as , where
, where 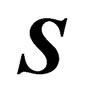 is a scalar times the 3-dimension identity
is a scalar times the 3-dimension identity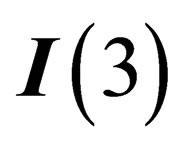 ,
,  is a 3 × 3 antisymmetric matrix and
is a 3 × 3 antisymmetric matrix and  a null-trace 3 × 3 symmetric matrix.
a null-trace 3 × 3 symmetric matrix.  can then be expressed as the sum of 3 matrices
can then be expressed as the sum of 3 matrices
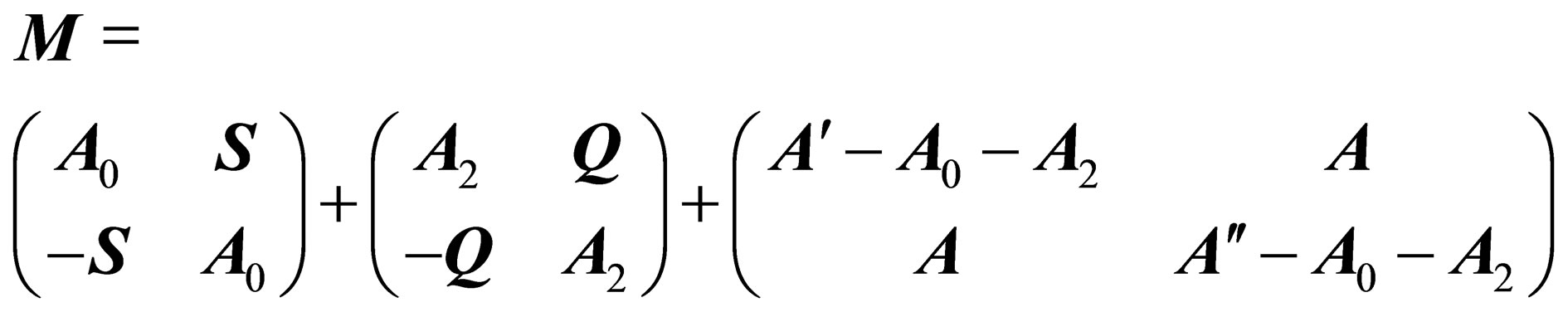 (2)
(2)
It can be checked from their commutation relations that the matrices 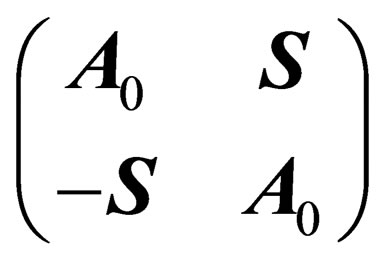 and
and 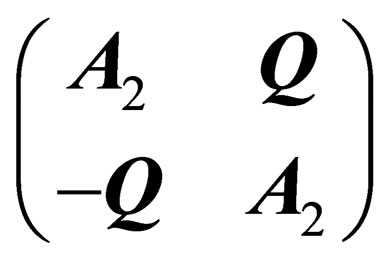 generate 2 subgroups of
generate 2 subgroups of 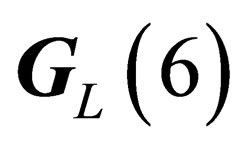
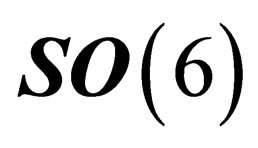 and
and 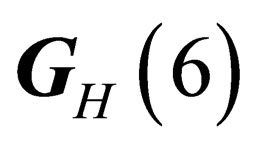 with respectively 4 and 8 infinitesimal generators. Those 2 subgroups have rather similar structures since
with respectively 4 and 8 infinitesimal generators. Those 2 subgroups have rather similar structures since
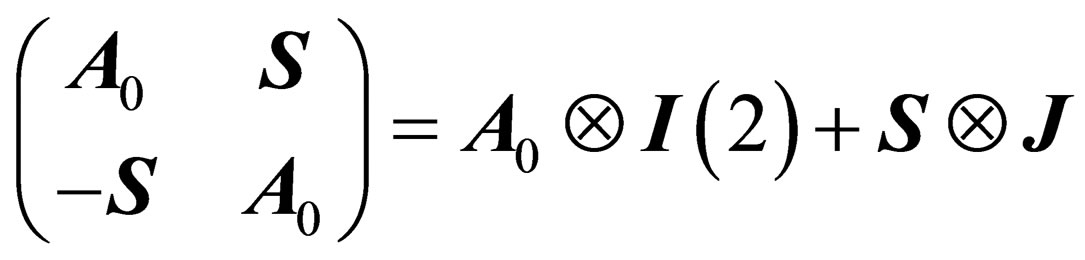 (3)
(3)
and
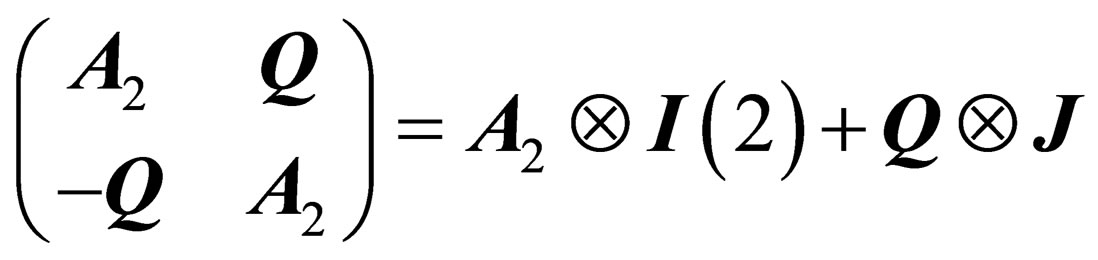 (4)
(4)
where 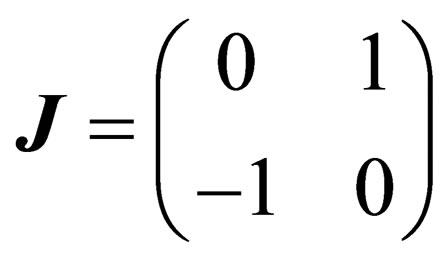 is the single generator of the special orthogonal group
is the single generator of the special orthogonal group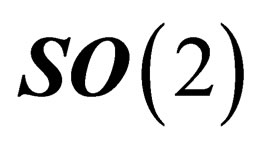 .
.
From the commutation relations of their infinitesimal generatorsit can be checked that  is isomorphous to
is isomorphous to 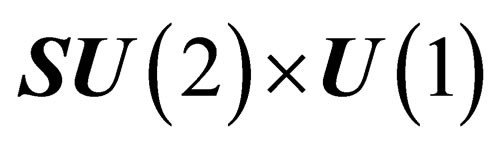 and that
and that  is isomorphous to
is isomorphous to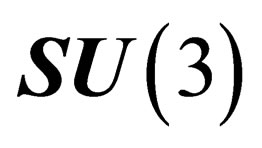 .We also note that
.We also note that 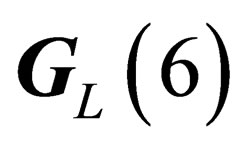 and
and 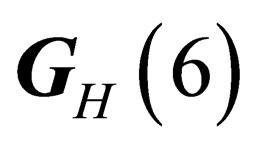 are 2 invariant, or distinguished, subgroups of
are 2 invariant, or distinguished, subgroups of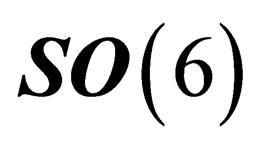 . Those 2 groups have in common
. Those 2 groups have in common 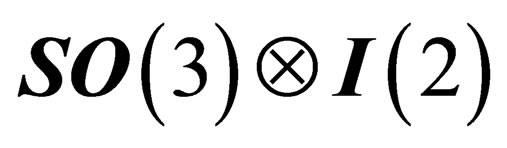 as a maximal subgroup, where
as a maximal subgroup, where 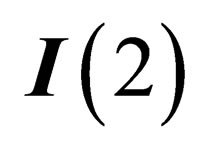 denotes the 2-dimension identity.
denotes the 2-dimension identity.
The matrices 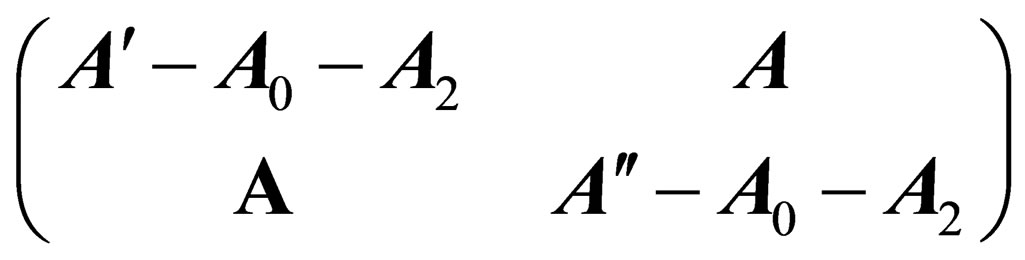 do not generate an invariant subgroup of
do not generate an invariant subgroup of 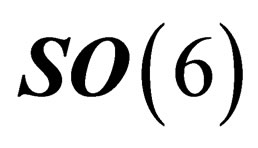 since
since
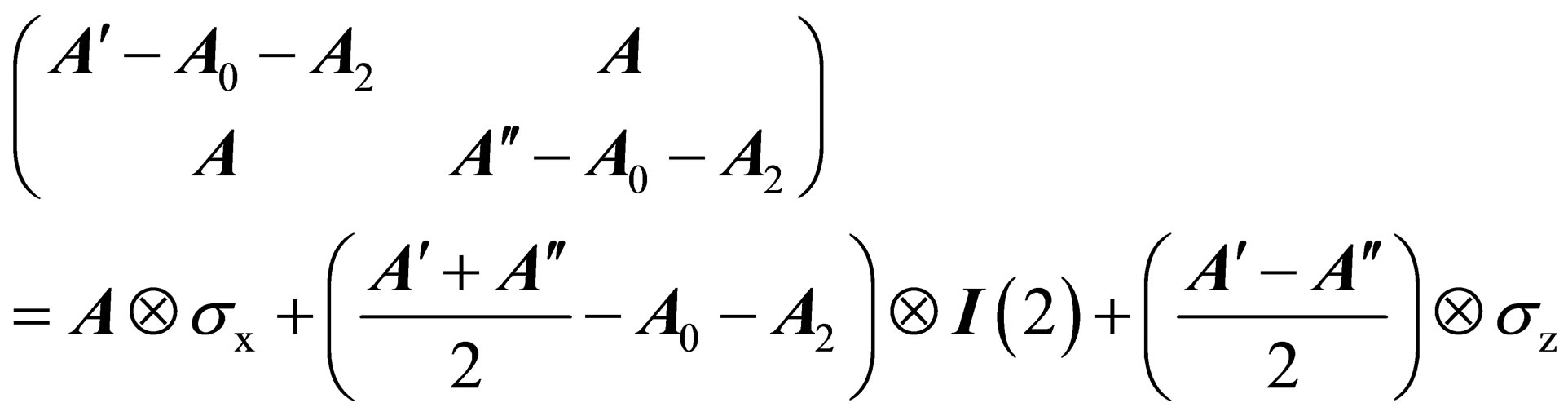 (5)
(5)
where the 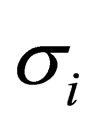 are the Pauli matrices (the pair
are the Pauli matrices (the pair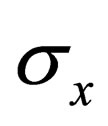 ,
, 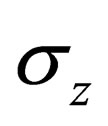 does not generate a group).
does not generate a group).
We here make the following fundamental assumption: only the invariant subgroups of 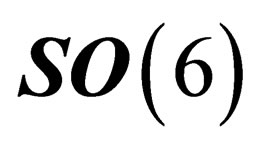 can be symmetry groups for the extension of the physical states in
can be symmetry groups for the extension of the physical states in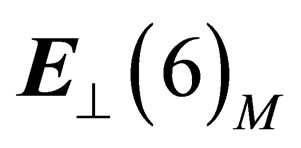 . In other words,
. In other words,  shall be of the form
shall be of the form
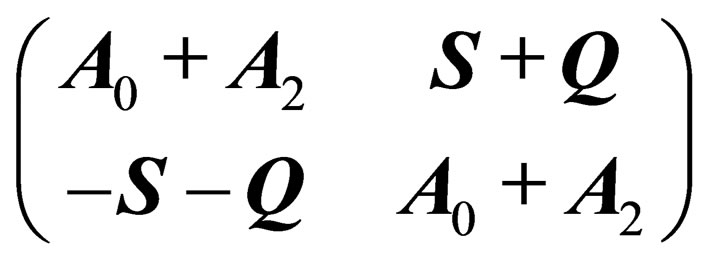 (6)
(6)
As a consequence only the pair of subgoups 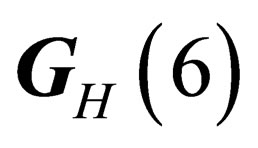 and
and 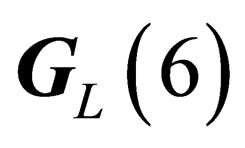 is relevant to characterize the physical states, which accordingly can be classified after the irreducible representations of
is relevant to characterize the physical states, which accordingly can be classified after the irreducible representations of 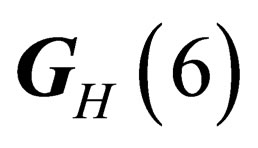 and
and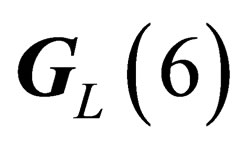 , the same as those of
, the same as those of 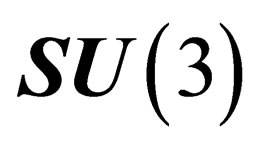 and
and 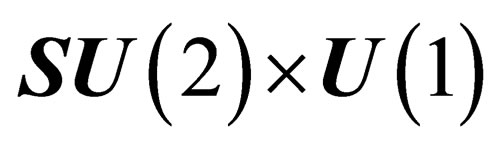 respectively. We can thus evidence two types of “internal” physical states, each type being characterized by a symmetry group: the “hadronic states” experiencing a
respectively. We can thus evidence two types of “internal” physical states, each type being characterized by a symmetry group: the “hadronic states” experiencing a 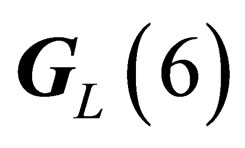 - symmetry, and the “leptonic states” experiencing a
- symmetry, and the “leptonic states” experiencing a 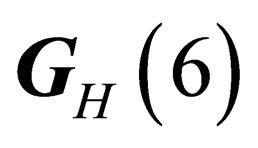 -symmetry. Those two local symmetries can be interpreted through the existence of two gauge fields respectively acting upon the hadrons for
-symmetry. Those two local symmetries can be interpreted through the existence of two gauge fields respectively acting upon the hadrons for 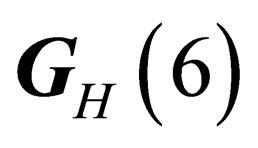 and upon the leptons for
and upon the leptons for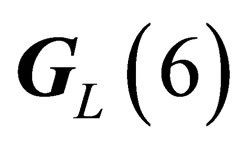 .
.
3.2. Hadrons
Agauge field identified with the strong interaction can be associated to the symmetry group .
. 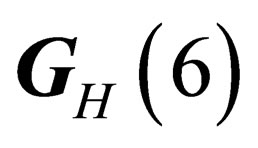 like
like 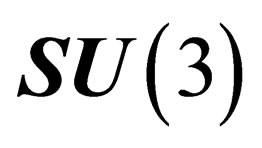 has 8 infinitesimal generators which subtend a 8-dimension representation of
has 8 infinitesimal generators which subtend a 8-dimension representation of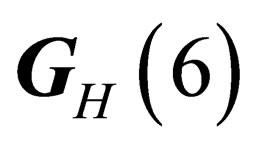 . Any given irreducible representation of
. Any given irreducible representation of 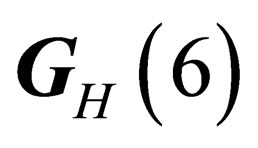 is characterized by the two numbers Y (hypercharge) and I (isospin), each base vectors of the irreducible representation
is characterized by the two numbers Y (hypercharge) and I (isospin), each base vectors of the irreducible representation 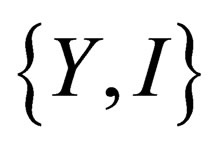 is characterized by the 3 numbers Y, I and mI. The strong interaction is mediated through a set of 8 neutral massless vector fields, the so-called “gluons”.
is characterized by the 3 numbers Y, I and mI. The strong interaction is mediated through a set of 8 neutral massless vector fields, the so-called “gluons”.
Let  and
and  be the two fundamental conjugated 3-dimensionals representations of
be the two fundamental conjugated 3-dimensionals representations of 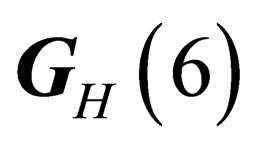 or
or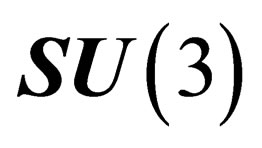 from which all the others representations can be built [10]. The isospin doublet
from which all the others representations can be built [10]. The isospin doublet 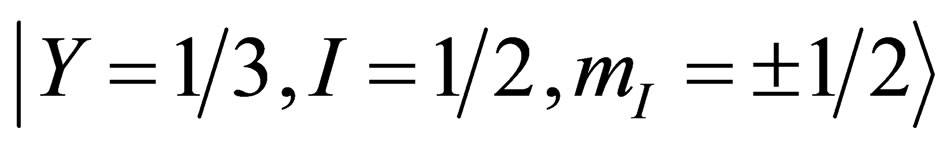 and the isospin singlet
and the isospin singlet 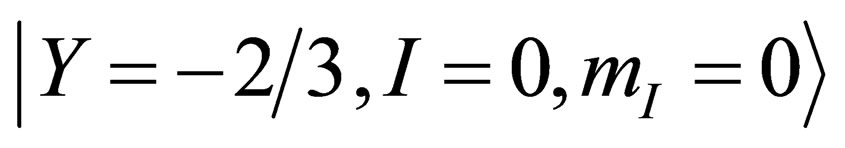 are a set of base states for
are a set of base states for , the doublet
, the doublet 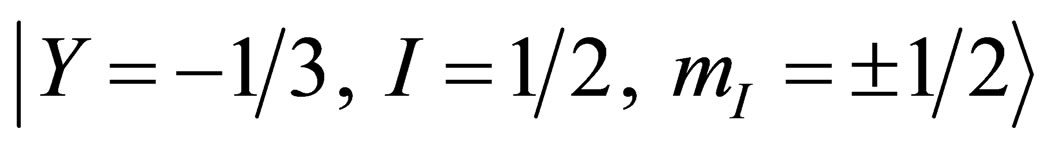 and the singlet
and the singlet 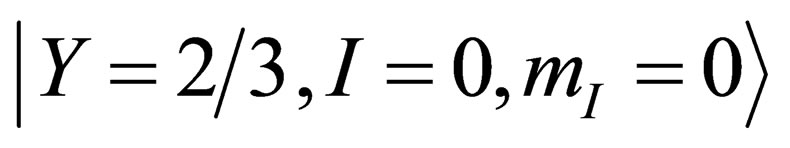 are a set of base states for
are a set of base states for . As
. As 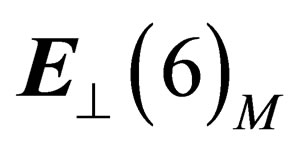 has 6 dimensions, there are two such distinct triplets, the so-called quarks, plus their images by charge conjugation.
has 6 dimensions, there are two such distinct triplets, the so-called quarks, plus their images by charge conjugation.
3.3. Leptons
Agauge field, which we call “pseudo electro-weak interaction”, can be associated to the symmetry group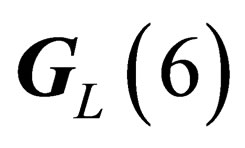 . It has the same symmetry as but it is intrinsically different from the usual electro-weak interaction.
. It has the same symmetry as but it is intrinsically different from the usual electro-weak interaction. 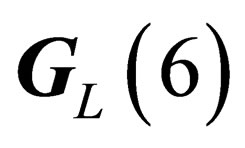 like
like 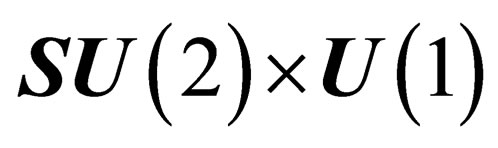 has 4 infinitesimal generators which subtend a 4-dimension representation of
has 4 infinitesimal generators which subtend a 4-dimension representation of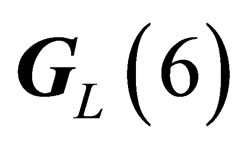 . Any given irreducible representation of
. Any given irreducible representation of 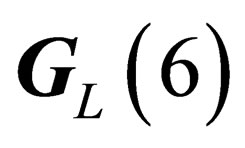 is characterized by the two numbers Z (pseudo electro-weak hypercharge) and J (pseudo electro-weak isospin), the representations
is characterized by the two numbers Z (pseudo electro-weak hypercharge) and J (pseudo electro-weak isospin), the representations 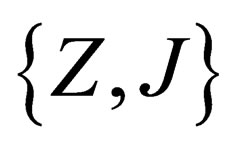 and
and 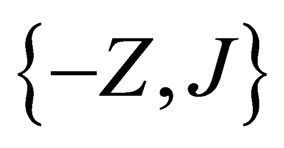 are conjugated, the dimension of the representation is 2J + 1. Each of the base vectors of the irreducible representation
are conjugated, the dimension of the representation is 2J + 1. Each of the base vectors of the irreducible representation 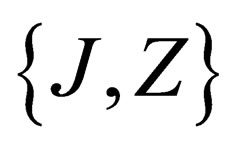 is characterized by the 3 numbers Z, J, mJ. The “pseudo electro-weak interaction” is mediated through a set of 4 neutral massless vector fields, that we call “gluinos”. Those gluinos, which are bosons, shall not be confused with the so-called gluinos of the super symmetric theories, where they are the fermion partners of the gluons. The existence of this pseudo electro-weak interaction mediated by 4 extra bosons is a major difference with the Standard Model (see 4.3 hereunder).
is characterized by the 3 numbers Z, J, mJ. The “pseudo electro-weak interaction” is mediated through a set of 4 neutral massless vector fields, that we call “gluinos”. Those gluinos, which are bosons, shall not be confused with the so-called gluinos of the super symmetric theories, where they are the fermion partners of the gluons. The existence of this pseudo electro-weak interaction mediated by 4 extra bosons is a major difference with the Standard Model (see 4.3 hereunder).
Let  and
and  be the two fundamental conjugated 2-dimension representations of
be the two fundamental conjugated 2-dimension representations of 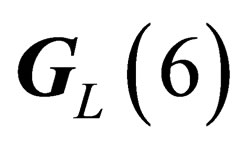 or
or 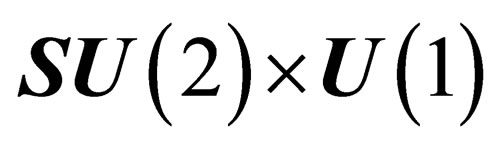 from which all the others representations can be built. The two states
from which all the others representations can be built. The two states  constitute a set of base states for
constitute a set of base states for , the 2 states
, the 2 states 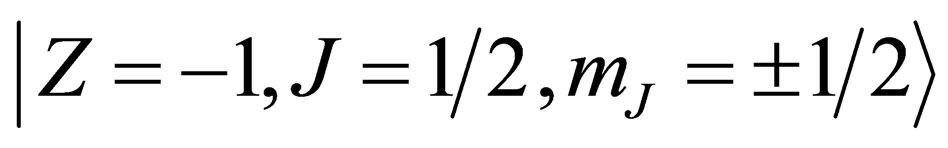 constitute a set of base states for
constitute a set of base states for . As
. As 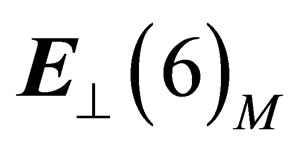 has 6 dimensions, there are actually 3 distinct pairs of such doublets, plus their images by charge conjugation.
has 6 dimensions, there are actually 3 distinct pairs of such doublets, plus their images by charge conjugation.
4. ONE STEP BEYOND
4.1. Weak Interaction
Since a 3-dimension hyper surface can be embedded within a 6-dimension flat space, let us consider inside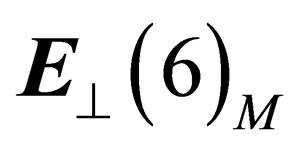 a 3-dimension hyper surface
a 3-dimension hyper surface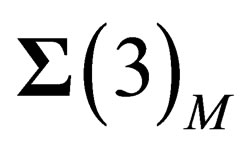 . Let
. Let 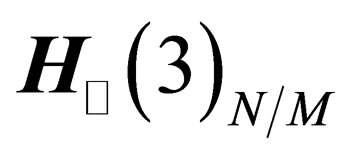 and
and  respectively be the tangent space and the orthogonal space to
respectively be the tangent space and the orthogonal space to  in some point N of
in some point N of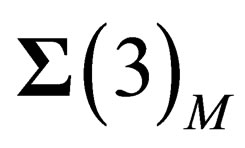 . In
. In  the particles have 6 degrees of freedom, 3 of them in the tangent space
the particles have 6 degrees of freedom, 3 of them in the tangent space 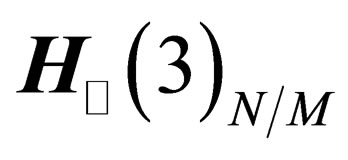 and the 3 others in the orthogonal space
and the 3 others in the orthogonal space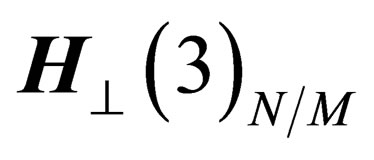 . Both
. Both 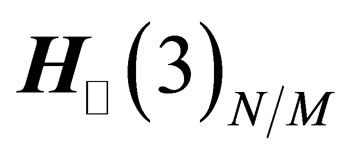 and
and  are 3-dimension flat spaces, invariant under the 3d special orthogonal group
are 3-dimension flat spaces, invariant under the 3d special orthogonal group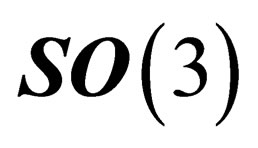 . Actually, the choice of N has no effect on what follows as all the points on
. Actually, the choice of N has no effect on what follows as all the points on 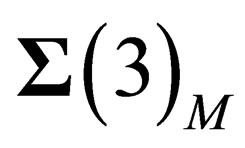 are equivalent. The symmetry properties above only depend upon the coordinates of M on
are equivalent. The symmetry properties above only depend upon the coordinates of M on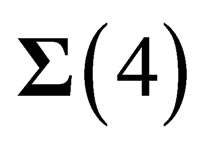 , which is consistent with the existence of a gauge field experienced by both hadrons and leptons since we have already noticed that
, which is consistent with the existence of a gauge field experienced by both hadrons and leptons since we have already noticed that 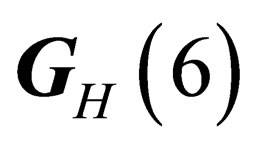 and
and 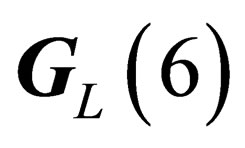 have in common
have in common 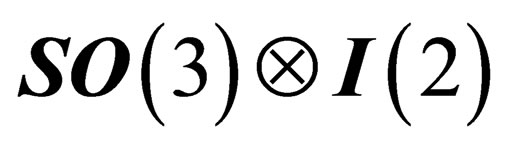 as a maximal subgroup. This gauge field is associated to the symmetry group
as a maximal subgroup. This gauge field is associated to the symmetry group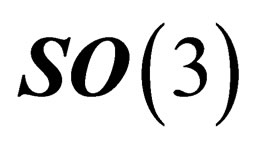 , isomorphous to the special unitary symmetry
, isomorphous to the special unitary symmetry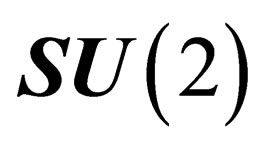 , and it is identified with the weak interaction [11]. It may lift the degeneracy of the multiplets associated to the irreducible representations of
, and it is identified with the weak interaction [11]. It may lift the degeneracy of the multiplets associated to the irreducible representations of 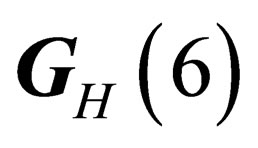 and
and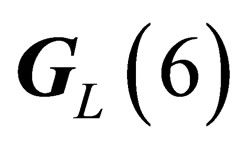 . Since
. Since 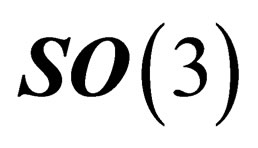 has three infinitesimal generators which subtend a 3-dimensional representation
has three infinitesimal generators which subtend a 3-dimensional representation 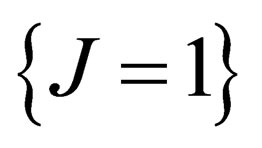 of
of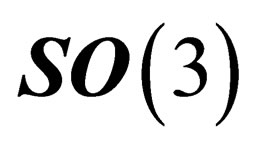 , the weak interaction is mediated through a triplet of neutral massless vector fields.
, the weak interaction is mediated through a triplet of neutral massless vector fields.
4.2. Electromagnetic and BEH Interaction
The orthogonal space 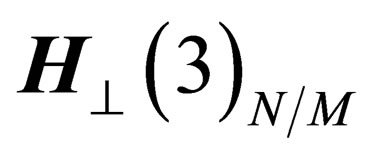 to
to 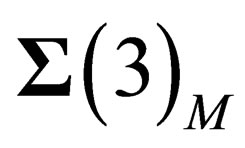 in any point N is also a 3-dimension space invariant under
in any point N is also a 3-dimension space invariant under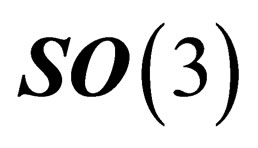 . Since a 2-dimension surface can be embedded within a 3-dimension flat space, let us consider within
. Since a 2-dimension surface can be embedded within a 3-dimension flat space, let us consider within  a 2-dimension hyper surface
a 2-dimension hyper surface 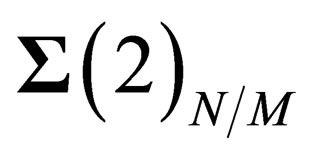 invariant under
invariant under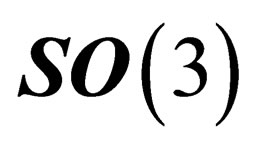 , i.e.
, i.e. 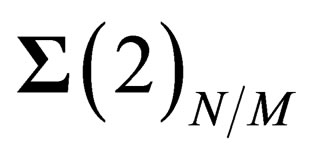 is a sphere. Let
is a sphere. Let 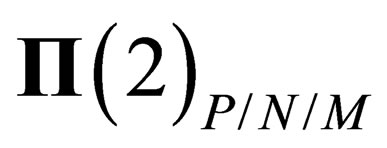 be the tangent plane to
be the tangent plane to 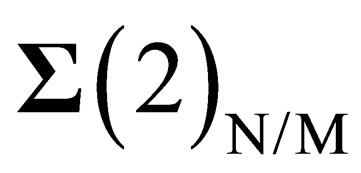 in any point P of
in any point P of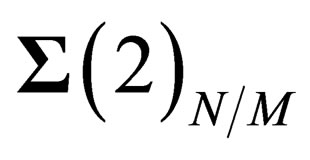 .
. 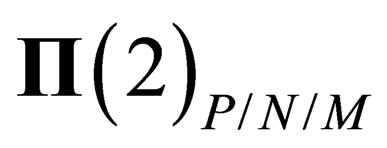 is invariant under the 2d special orthogonal group
is invariant under the 2d special orthogonal group 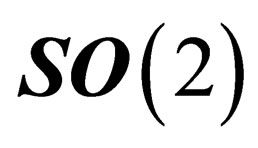 in any point P of
in any point P of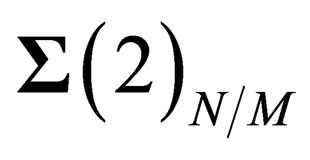 . Actually, the choice of P has no effect on what follows as all the points on
. Actually, the choice of P has no effect on what follows as all the points on 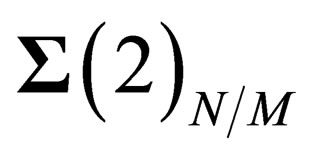 are equivalent. The symmetry properties above only depend upon the coordinates of M on
are equivalent. The symmetry properties above only depend upon the coordinates of M on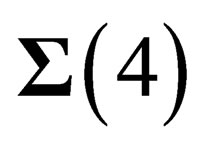 , which is consistent with the existence of agauge field experienced by both hadrons and leptons and associated to the special unitary symmetry group
, which is consistent with the existence of agauge field experienced by both hadrons and leptons and associated to the special unitary symmetry group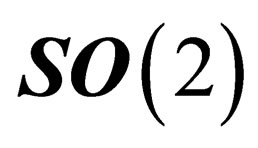 , isomorphous to the unitary symmetry group
, isomorphous to the unitary symmetry group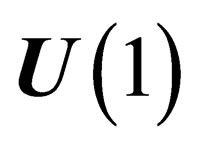 . This interaction is identified with the electromagnetic interaction. It eventually lifts the residual degeneracy of the multiplets associated to the irreducible representations of
. This interaction is identified with the electromagnetic interaction. It eventually lifts the residual degeneracy of the multiplets associated to the irreducible representations of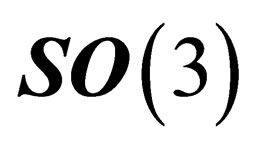 .
.
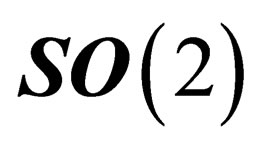 has only one infinitesimal generator and its irreducible representations are of dimension 1, each of them being characterized by a relative integer number Q, which is identified with the electric charge. The representations
has only one infinitesimal generator and its irreducible representations are of dimension 1, each of them being characterized by a relative integer number Q, which is identified with the electric charge. The representations  and
and 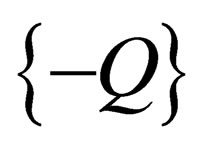 are conjugated, the totally symmetric representation
are conjugated, the totally symmetric representation  being self-conjugated. The interaction is mediated through a single massless vector field which is identified with the photon.
being self-conjugated. The interaction is mediated through a single massless vector field which is identified with the photon.
The orthogonal space to 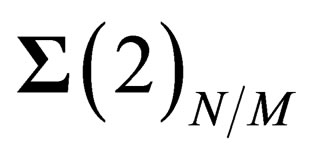 in P is a line
in P is a line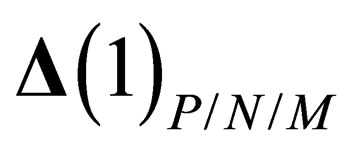 ; in the space
; in the space 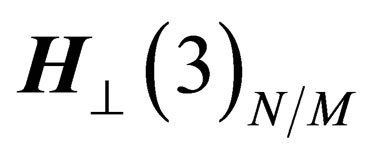 the particles have 3 degrees of freedom, 2 of them in the plane
the particles have 3 degrees of freedom, 2 of them in the plane , and the third one along
, and the third one along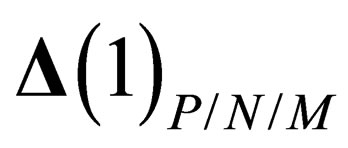 .
. 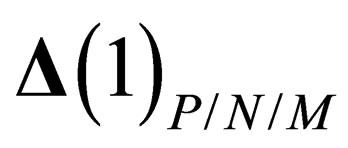 is a 1-dimension space whose only symmetry is
is a 1-dimension space whose only symmetry is 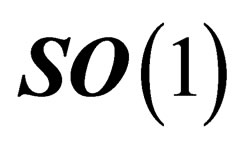 i.e. the trivial identity
i.e. the trivial identity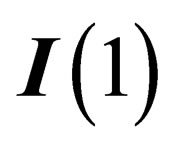 ; that can be interpreted as featuring an additional scalar field. As a consequence, both hadrons and leptons can experience a same scalar interaction mediated through a particle which can be identified with the BEH boson.
; that can be interpreted as featuring an additional scalar field. As a consequence, both hadrons and leptons can experience a same scalar interaction mediated through a particle which can be identified with the BEH boson.
4.3. Consequences
To summarize, in every point M of the 4d-space-time 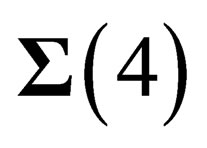 there is a local extra 6d Euclidian space
there is a local extra 6d Euclidian space 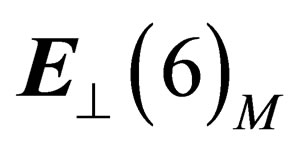 in which is inscribed a 3d hypersphere. In any point of that hypersphere there is a 3d Euclidian subspace in which is inscribed a sphere. That unfolding, coming with a group-to-subgroup declination, reveals the interactions embedded as Russian dolls. The hadronic states are classified according to the symmetry
in which is inscribed a 3d hypersphere. In any point of that hypersphere there is a 3d Euclidian subspace in which is inscribed a sphere. That unfolding, coming with a group-to-subgroup declination, reveals the interactions embedded as Russian dolls. The hadronic states are classified according to the symmetry 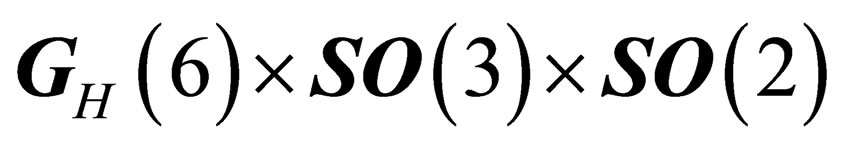 isomorphous to
isomorphous to  , and the leptonic states are classified according to the symmetry
, and the leptonic states are classified according to the symmetry 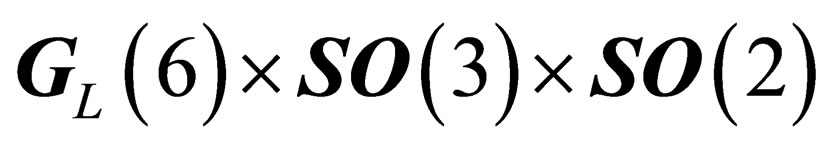 isomorphous to
isomorphous to 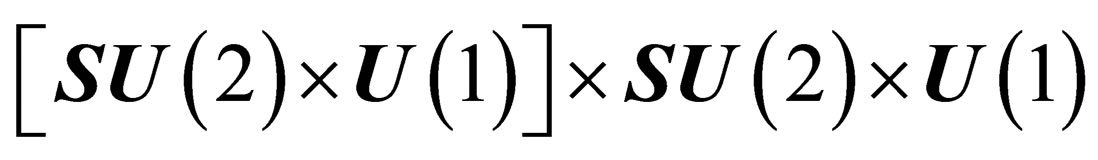 .
.
As 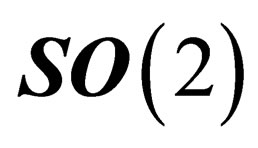 and
and 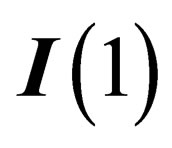 are orthogonal subgroups of
are orthogonal subgroups of , the BEH boson has no electric charge and the photon has no mass. Due to the effect of the electromagnetic field on the one hand, and of the BEH field on the other hand, the fundamental representation
, the BEH boson has no electric charge and the photon has no mass. Due to the effect of the electromagnetic field on the one hand, and of the BEH field on the other hand, the fundamental representation 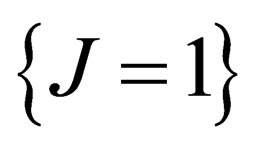 of
of 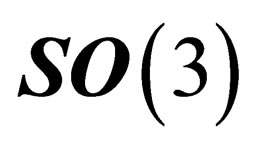 is splitted into a singlet (charge
is splitted into a singlet (charge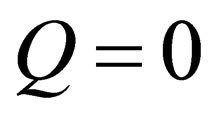 , mass
, mass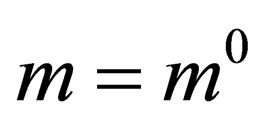 ) and a doublet (charge
) and a doublet (charge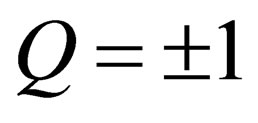 , masse
, masse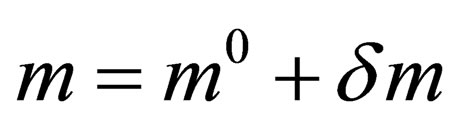 ) so that the 3 mediators of the weak interaction above gain an electric charge and a mass; they are respectively identified with the
) so that the 3 mediators of the weak interaction above gain an electric charge and a mass; they are respectively identified with the 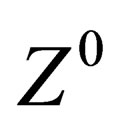 and
and 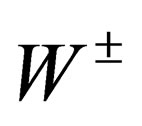 particles. The same mechanism confers an electric charge and a mass to hadrons and leptons.
particles. The same mechanism confers an electric charge and a mass to hadrons and leptons.
We have thus evidenced 3 interactions common to both hadrons and leptons and which can be identified with the weak, elecromagnetic and BEH interactions. Finally we have one scalar coupling and a set of fields respectively mediated through 8 gluons, 4 gluinos, 3 bosons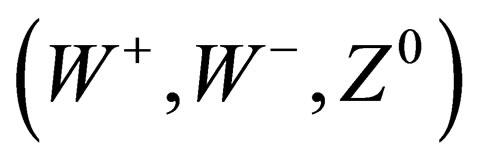 , 1 photon. The vector character of the gluons, gluinos,
, 1 photon. The vector character of the gluons, gluinos, 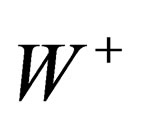 ,
,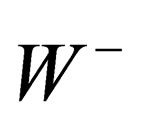 ,
,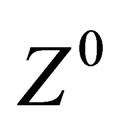 and photon is verified in the Annex [12].
and photon is verified in the Annex [12].
The hypothetical existence of a pseudo electro-weak interaction mediated by the 4gluinos is a major difference with the Standard Model based upon the 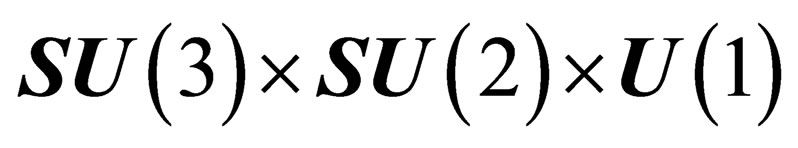 gauge symmetry. It has been shown [13] that a Kaluza-Klein-type theory consistent with the Standard Model requires 11 dimensions, with 7 additional compactified dimensions. Now, that pseudo electro-weak interaction superposed to the usual electro-weak interaction which has the same symmetry is presumably very weak.
gauge symmetry. It has been shown [13] that a Kaluza-Klein-type theory consistent with the Standard Model requires 11 dimensions, with 7 additional compactified dimensions. Now, that pseudo electro-weak interaction superposed to the usual electro-weak interaction which has the same symmetry is presumably very weak.
If the “orbital” degrees of freedom are taken into account, the resulting states of fields and particles will be classified according to the irreducible representations of 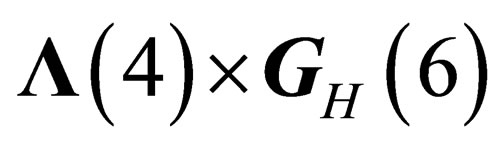 for hadrons and
for hadrons and 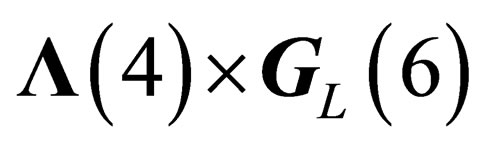 for leptons, built from the irreducible representations of
for leptons, built from the irreducible representations of 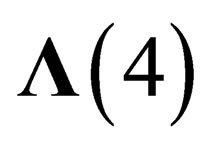 and
and 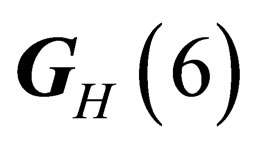 or
or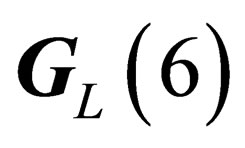 .
.
We notice that inside the “internal space” 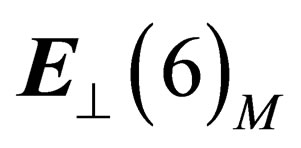 the charge conjugation simply appears as the equivalent of what are parity and time reversal in the “orbital space”
the charge conjugation simply appears as the equivalent of what are parity and time reversal in the “orbital space”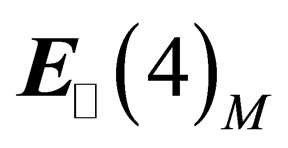 , i.e. the transformation
, i.e. the transformation 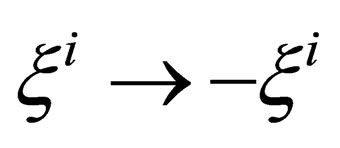 within ranging from 1 to 6 is analogous to
within ranging from 1 to 6 is analogous to 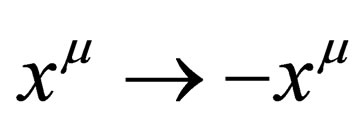 with
with 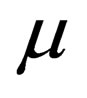 ranging from 0 to 3.
ranging from 0 to 3.
5. THE GRAVITATION FIELD
We now consider again the original 10-dimensional space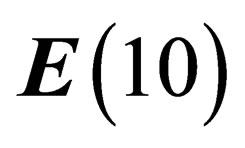 , which has been assumed to be globally invariant under a symmetry group
, which has been assumed to be globally invariant under a symmetry group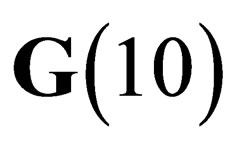 . In any point M of the 4-dimension surface
. In any point M of the 4-dimension surface 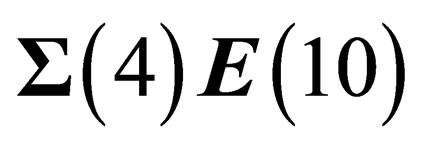 is the tensor product of a 4-dimensional “orbital” space invariant under the Lorentz group
is the tensor product of a 4-dimensional “orbital” space invariant under the Lorentz group 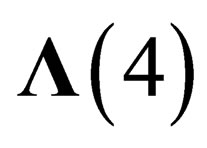 and of a 6-dimension “internal” space
and of a 6-dimension “internal” space 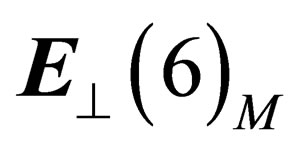 invariant under
invariant under .
. 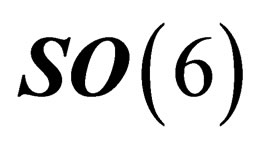 and
and 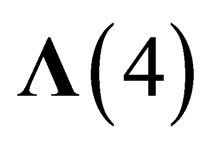 are both invariant, or distinguished, subgroups of
are both invariant, or distinguished, subgroups of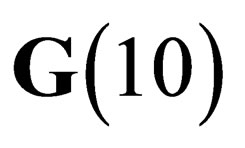 .
.
In the previous sections, we have considered several gauge fields associated to symmetries of the “internal” space. Now gravitation can also be considered as a gauge field by which the global Lorentz invariance of special relativity is changed into a local invariance at any point M of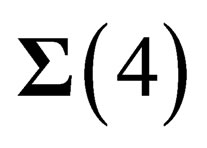 .
.
With 4 dimensions, if the global Lorentz invariance of special relativity is changed into a local symmetry on the 4-dimension hyper surface, then 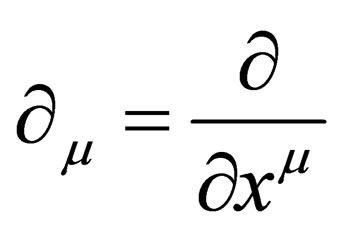 is changed into
is changed into
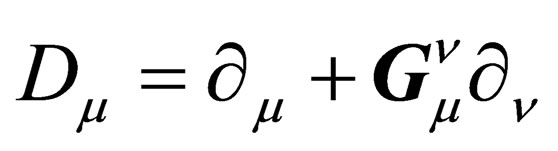 . (7)
. (7)
with µ ranging from 0 to 3, where 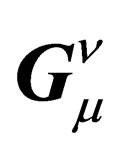 is a tensor quantity featuring the local geometry of
is a tensor quantity featuring the local geometry of . The impulsion
. The impulsion
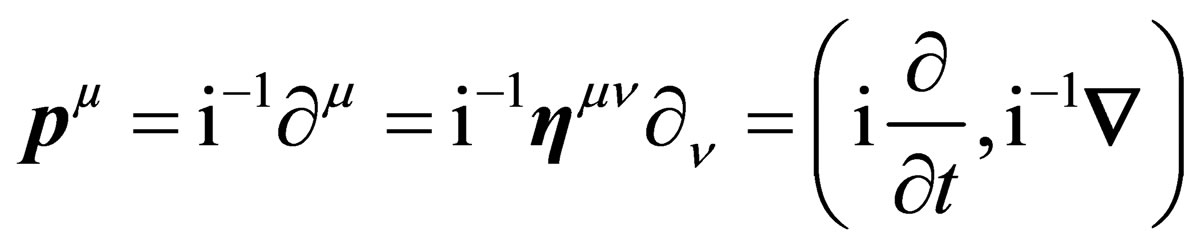 (8)
(8)
is thus changed into
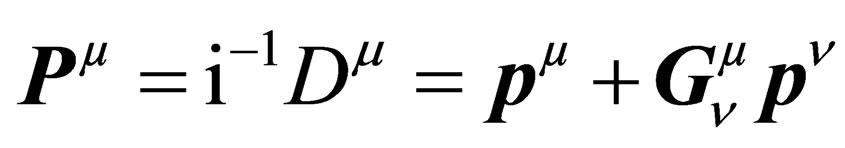 . (9)
. (9)
There is some flexibility in the determination of the 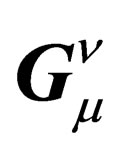 ‘s which allows to impose the 4 conditions
‘s which allows to impose the 4 conditions
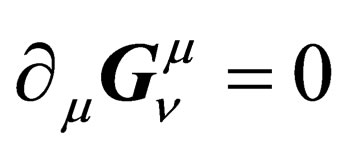 . (10)
. (10)
We will now see how this can be extended if the 4- dimension surface is supposed to be embedded in the full 10-dimension flat space-time. In the previous sections, we had separately assumed the conservation of the pseudo Euclidian norm 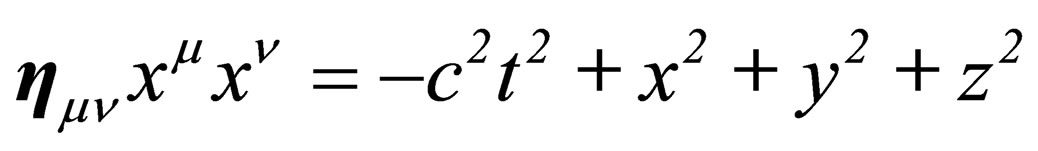 within
within  and the conservation of a true Euclidian norm
and the conservation of a true Euclidian norm 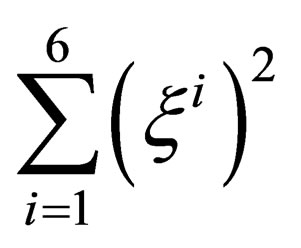 within
within . We now further postulate the conservation of the full pseudo Euclidian norm
. We now further postulate the conservation of the full pseudo Euclidian norm
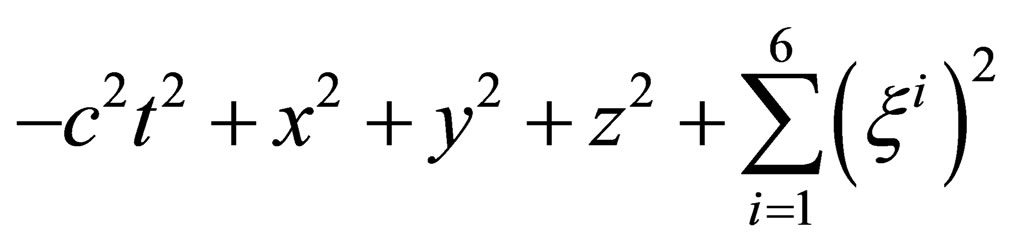 within
within . The full 10-dimension space
. The full 10-dimension space 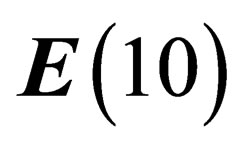 is thus assumed to be a pseudo Euclidian space which preserves a pseudo norm
is thus assumed to be a pseudo Euclidian space which preserves a pseudo norm 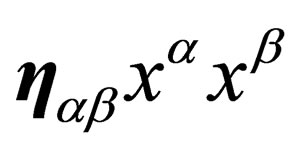 with
with 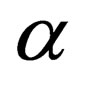 and
and 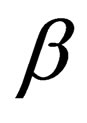 ranging from 0 to 9, i.e.
ranging from 0 to 9, i.e. 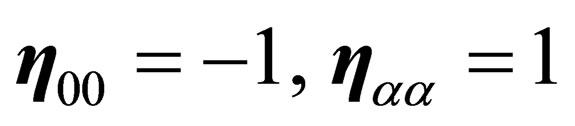 if
if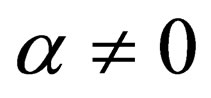 ,
, 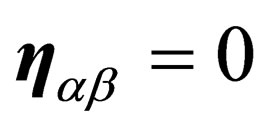 otherwise.
otherwise.
Let us postulate that in a 10-dimension reference frame of , the Lagrangian
, the Lagrangian 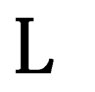 attached to a field
attached to a field 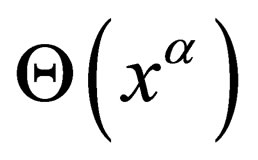 simply is
simply is
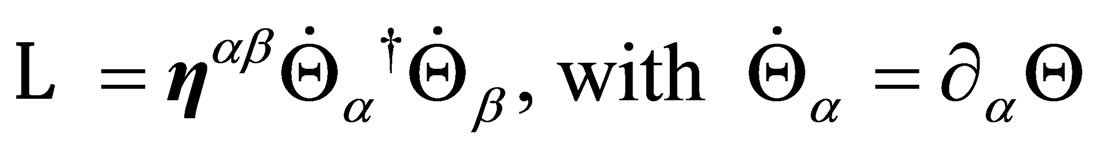 (11)
(11)
Now taking into account the local character of the symmetries with respect to the reference frame  attached to the point M of
attached to the point M of , we extend to
, we extend to  what has been done above with the Lorentz invariance in the case of a 4-dimension space-time. The transformation Equation (7) readily becomes
what has been done above with the Lorentz invariance in the case of a 4-dimension space-time. The transformation Equation (7) readily becomes
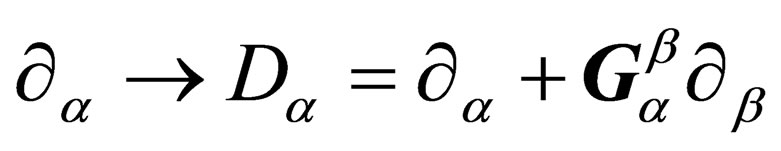 (12)
(12)
And the Lagrangian Equation (11) is changed into
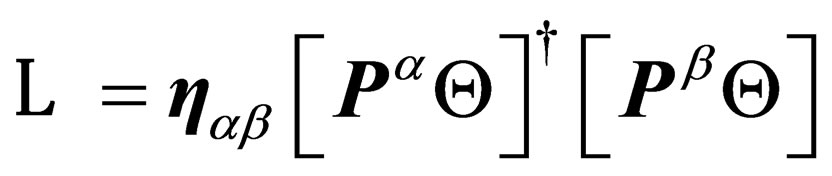 (13)
(13)
or
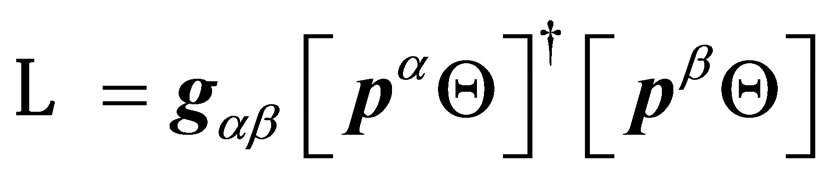 (14)
(14)
where we have introduced the effective 10 × 10 metric tensor
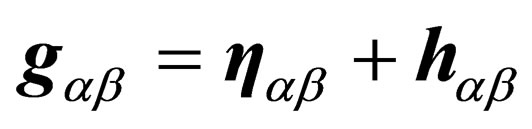 (15)
(15)
with
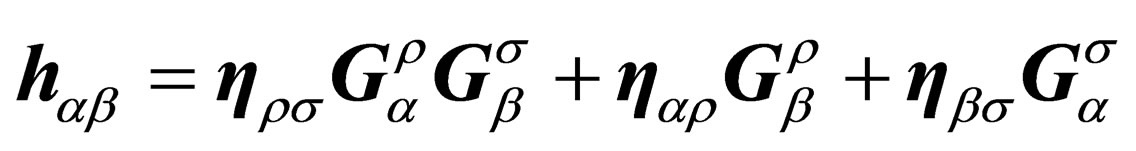 (16)
(16)
From the expression of  as a function of the
as a function of the 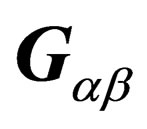 s it is obvious that
s it is obvious that . Applying the Lagrange equations to the
. Applying the Lagrange equations to the  field, i.e.
field, i.e.
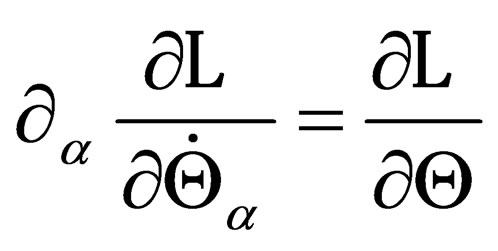 , (17)
, (17)
gives
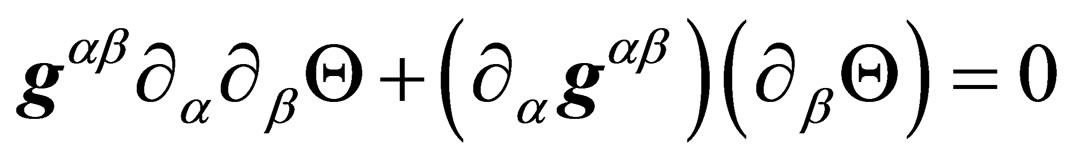 (18)
(18)
The gauge properties give some flexibility in the determination of the  ‘s so that we can impose the 10 conditions
‘s so that we can impose the 10 conditions
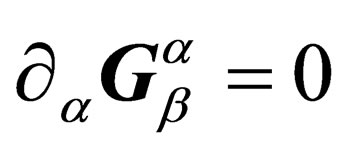 (19)
(19)
from which we derive
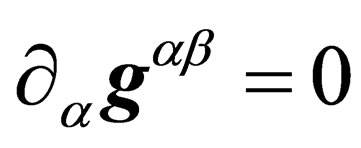 (20)
(20)
The equation of evolution Equation (18) thus becomes
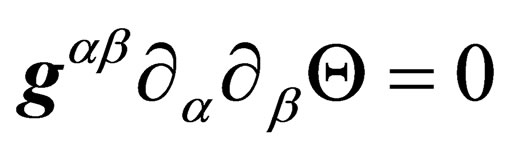 (21)
(21)
That expression means that the only accessible physical states are those whose measure is null in . With the correspondence
. With the correspondence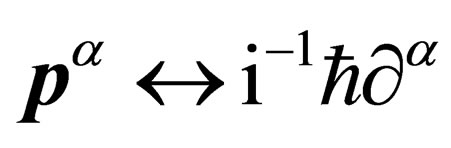 , one equivalently gets
, one equivalently gets
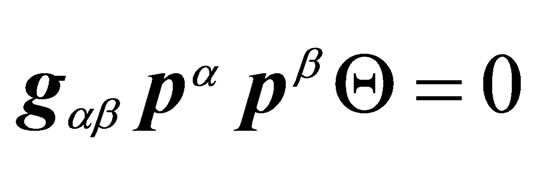 . (22)
. (22)
 has the following form
has the following form
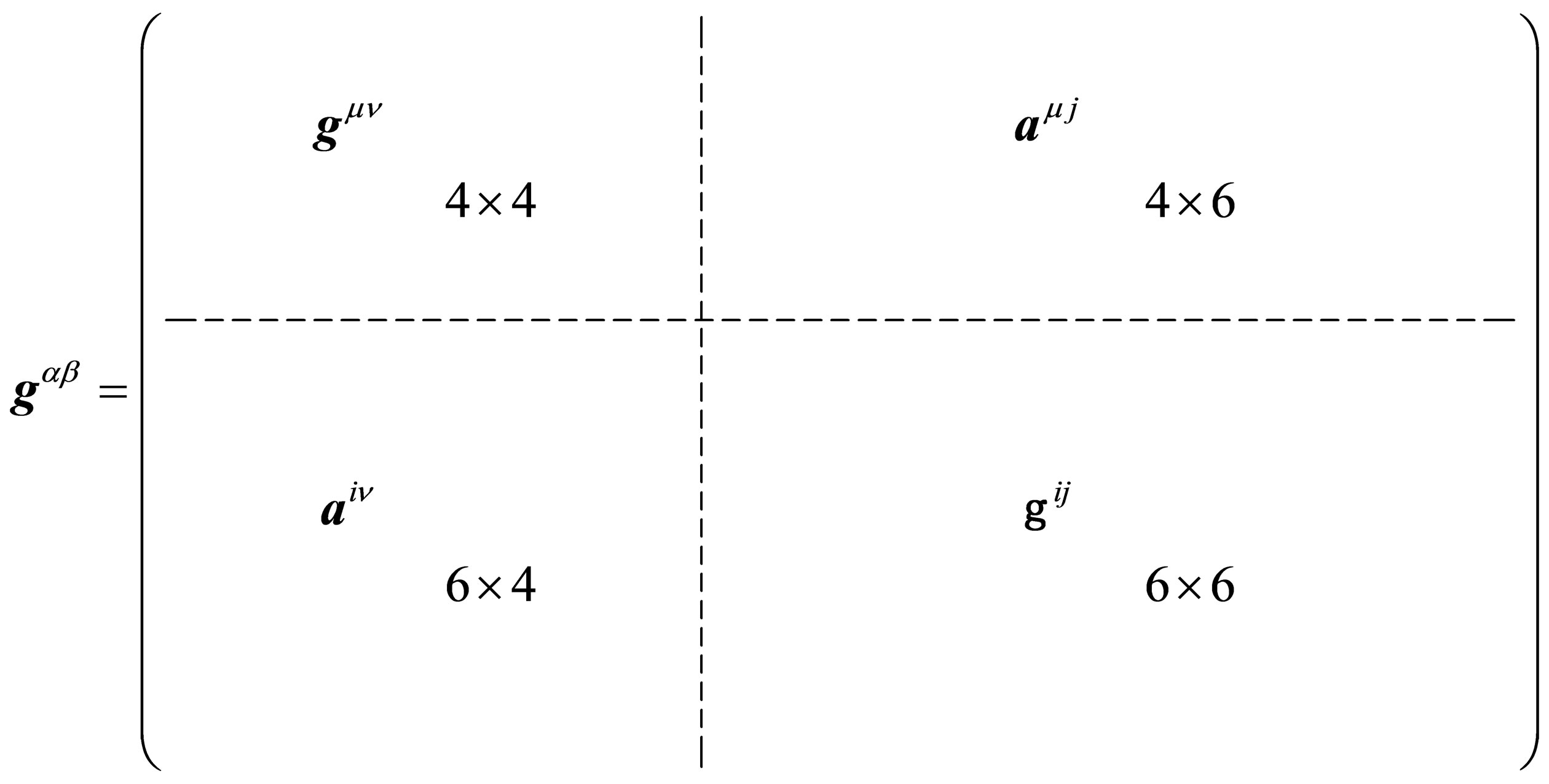 (23)
(23)
Since 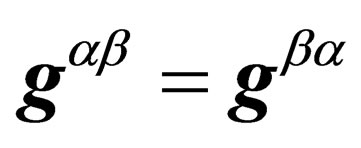 and
and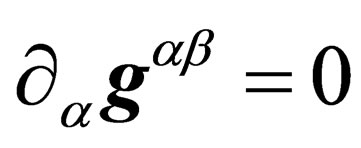 ,
,  has 55 distinct components, of which 45 are independent.We can also choose
has 55 distinct components, of which 45 are independent.We can also choose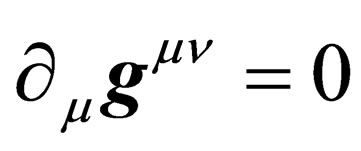 , with
, with 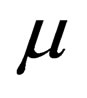 and
and 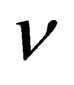 ranging from 0 to 3, and
ranging from 0 to 3, and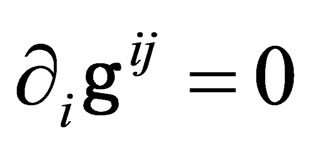 , with
, with 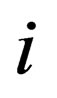 and
and 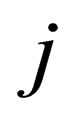 ranging from 4 to 9, so that
ranging from 4 to 9, so that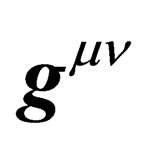 ,
, 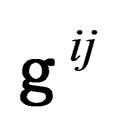 and
and 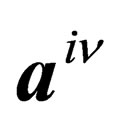 respectively have 10, 21 and 24 distinct components, of which 6, 15 and 24 are independent.
respectively have 10, 21 and 24 distinct components, of which 6, 15 and 24 are independent.
Now, we look for  special solutions which can be expressed as a product
special solutions which can be expressed as a product
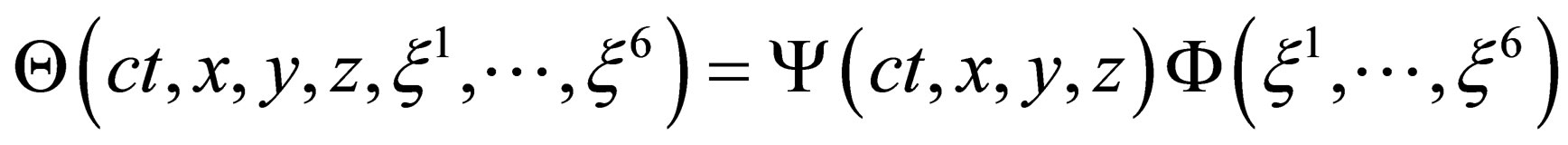 ,(24)
,(24)
With the expressions Equation (23) for  and Equation (24) for
and Equation (24) for , the equation of evolution becomes
, the equation of evolution becomes
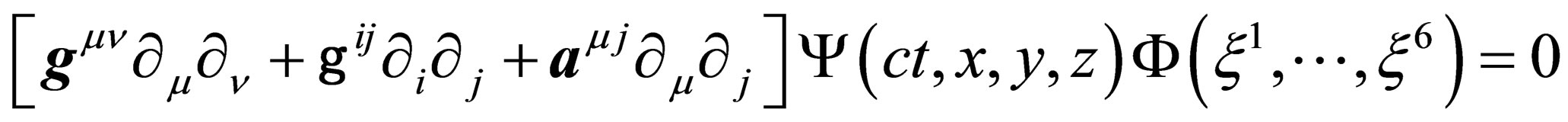 (25)
(25)
Multiplying Equation (25) by  and integrating over the 6 degrees of freedom of
and integrating over the 6 degrees of freedom of  yields
yields
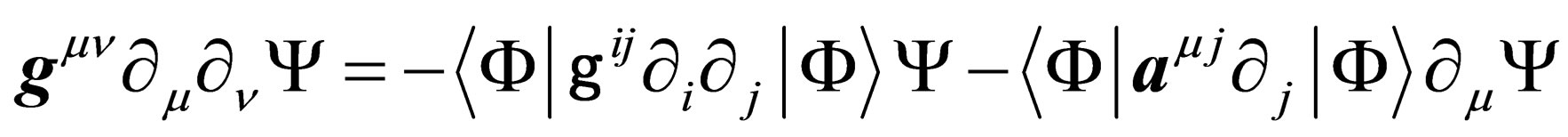 (26)
(26)
with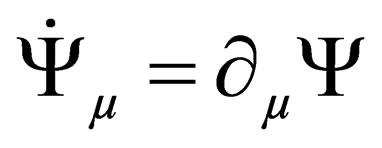 , or
, or
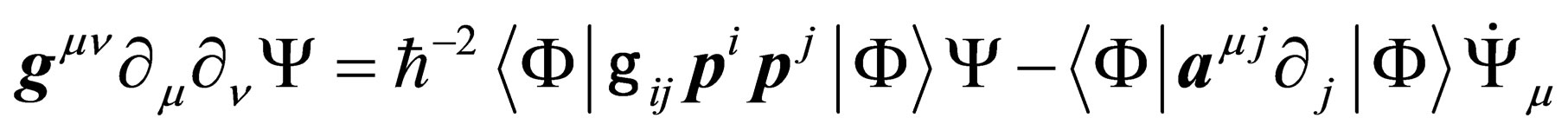 (27)
(27)
i.e.
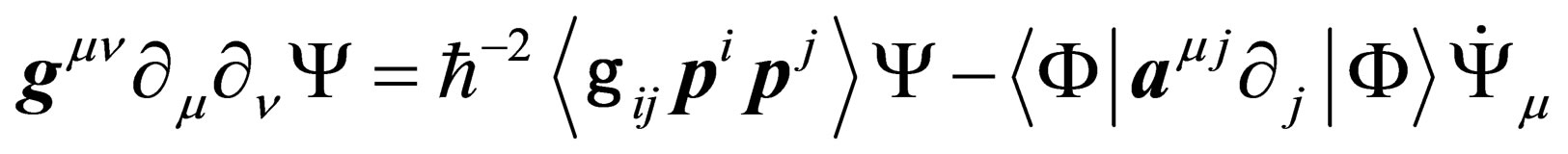 . (28)
. (28)
Let us consider the first term on the right hand side of the above equation and in first approximation let us neglect the second term. We get
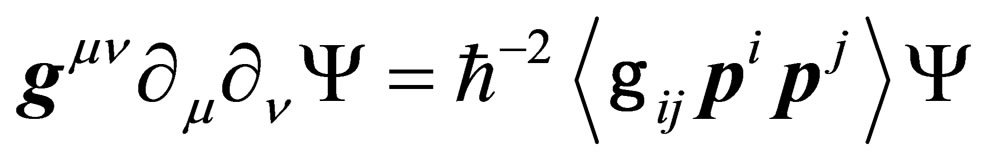 (29)
(29)
It can be compared with the Klein-Gordon equation in the presence of a gravitation field
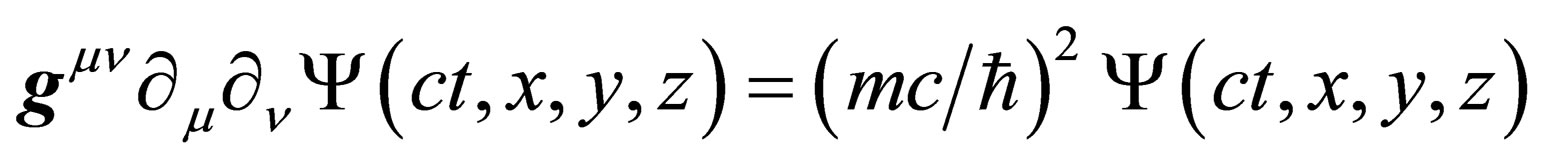 (30)
(30)
where m is the particle mass. Identifying m with the self energy term in Equation (29), i.e.
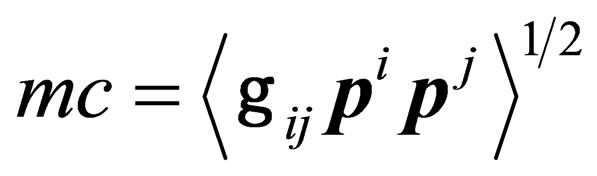 , (31)
, (31)
means that the particle mass originates from the 6 extra dimensions of space-time, i.e. from the symmetries of the local orthogonal space .
.
Now let us focus on the second term on the right hand side of Equation (28). It can be interpreted as the coupling between  and a set of 6 additional massless vector fields
and a set of 6 additional massless vector fields
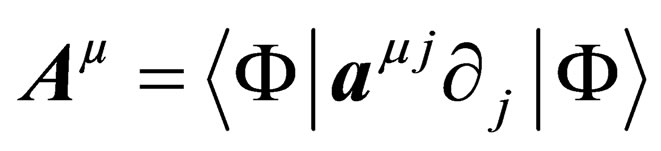 (32)
(32)
so that the field equation for  can be written as
can be written as
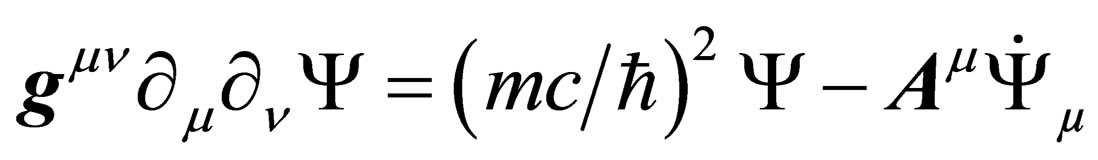 . (33)
. (33)
Those extra fields express the connection between gravitation in the “orbital” 4-dimension space-time and the other interactions which have their origin in the symmetry properties of the “internal” space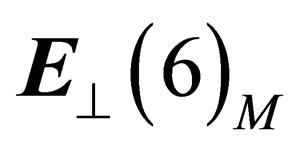 .
.
A priori those fields are massless and thus they have an infinite range; they are superposed to gravitation, but should be much weaker so as to be in accordance with the experimental data. Now if they get a mass through some mechanism, e.g. via an additional scalar field, they then may have a finite range and consequently the laws of gravitation should be modified below some scale. That could account for the dark matter/dark energy problem.
The hypothetical existence of those vector companions of gravity implies a violation of the equivalence principle. The way the gravitation field has been here above introduced in the 4-dimension space-time naturally implies the equivalence between gravitational mass and inertial mass. However if we consider the full 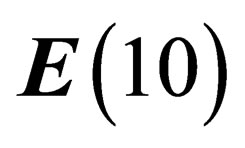 space we have seen that the hadrons experience a symmetry
space we have seen that the hadrons experience a symmetry 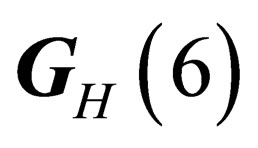 isomorphous to
isomorphous to 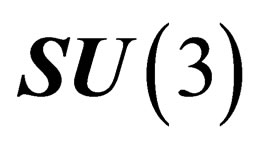 whereas the leptons experience a symmetry
whereas the leptons experience a symmetry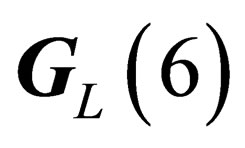 isomorphous to
isomorphous to 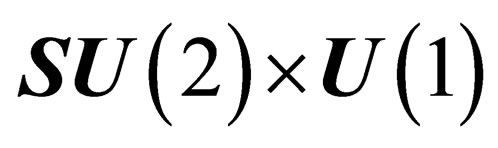 . As a consequence, the interactions
. As a consequence, the interactions 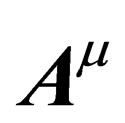 should be different for hadrons and leptons and thus bodies with different composition would not behave the same way under
should be different for hadrons and leptons and thus bodies with different composition would not behave the same way under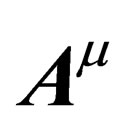 . Experimentally that would result in a violation of the equivalence principle [14].
. Experimentally that would result in a violation of the equivalence principle [14].
6. CONCLUSION
We have given a coherent presentation of the fundamental interactions of physics including gravitation by considering the symmetry properties of a 10-dimension real space-time. The usual space-time is a 4-dimensional surface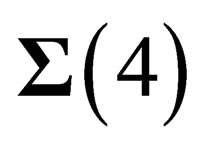 , whose local symmetry is the Lorentz group
, whose local symmetry is the Lorentz group , embedded in a flat 10-dimensional space
, embedded in a flat 10-dimensional space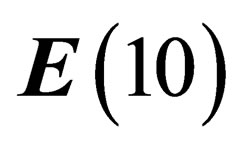 . In every point of that “orbital” space
. In every point of that “orbital” space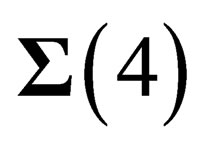 , there is a 6-dimension “internal” space
, there is a 6-dimension “internal” space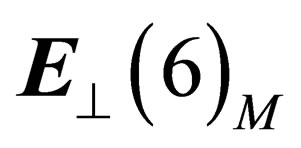 , orthogonal to the surface
, orthogonal to the surface . Simple assumptions about the geometry of
. Simple assumptions about the geometry of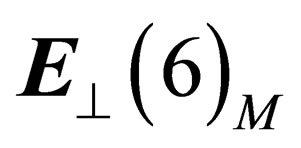 : allow deriving the following: hadrons and leptons, 8 gluons for the strong interaction, 4 gluinos for a pseudo electro-weak interaction, 3 intermediate bosons for the weak interaction, 1 photon, plus an additional scalar field identified with the BEH field.
: allow deriving the following: hadrons and leptons, 8 gluons for the strong interaction, 4 gluinos for a pseudo electro-weak interaction, 3 intermediate bosons for the weak interaction, 1 photon, plus an additional scalar field identified with the BEH field.
When gravitation is introduced, the connection between the “orbital” and the “internal” degrees of freedom shows that mass has its origin in the “internal” space and that there exists additional couplings, mediated by a set of 6 extra vector fields. Those hypothetical companions of gravity do not act the same way with hadrons and leptons and should be revealed through a violation of the equivalence principle.
ANNEX
In the main section, w e have evidenced one scalar interaction (identified with the BEH field) and a set of fields respectively mediated through 8 gluons, 4 gluinos, 3 bosons identified with the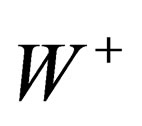 ,
,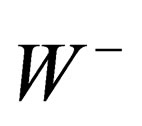 ,
,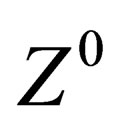 and 1 photon, each of them being associated to a symmetry group
and 1 photon, each of them being associated to a symmetry group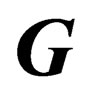 . The elementary operations associated to any of them have the form
. The elementary operations associated to any of them have the form
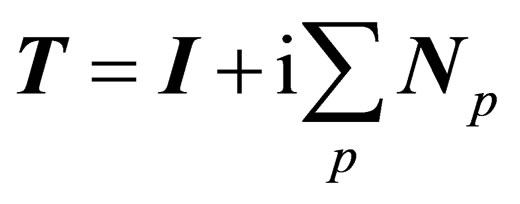 (A1.1)
(A1.1)
where Np is an infinitesimal generator of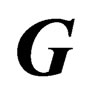 . More generally, any operation of
. More generally, any operation of 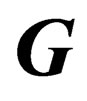 can be written as
can be written as
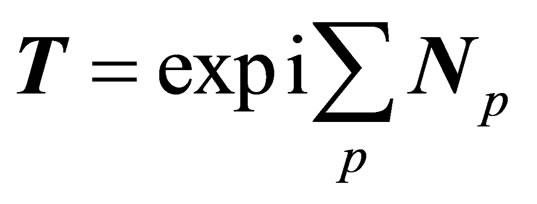 (A1.2)
(A1.2)
We now consider a scalar particle of mass m (but the procedure can be generalized to any spin) associated to the field 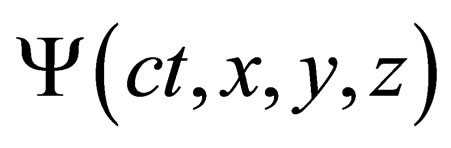 in the 4-dimension space-time. Its Lagrangian density is
in the 4-dimension space-time. Its Lagrangian density is
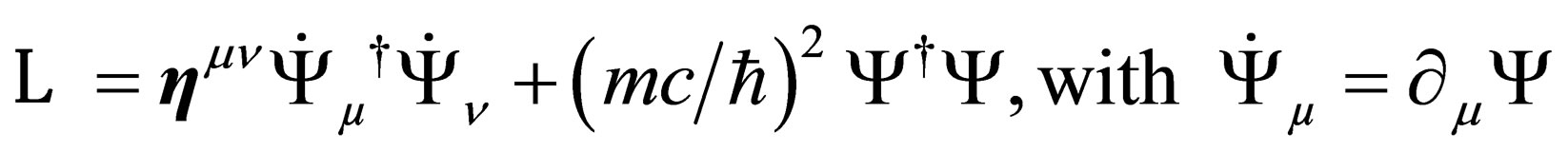 (A1.3)
(A1.3)
or

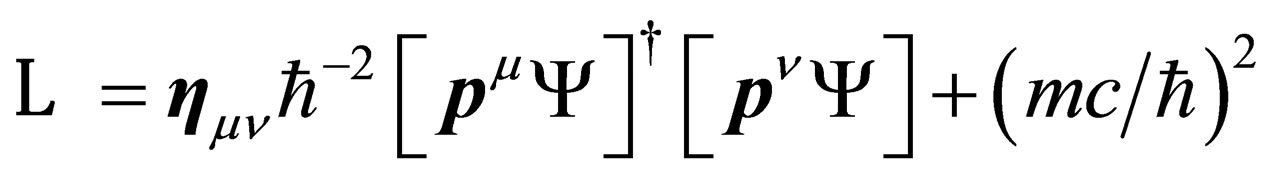 (A1.4)
(A1.4)
with 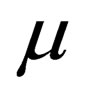 and
and 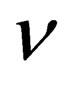 ranging from 0 to 3.
ranging from 0 to 3.
If a global symmetry 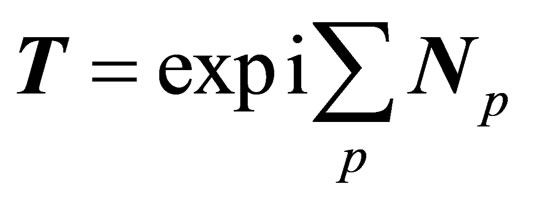 is assumed to be a local one, i.e.
is assumed to be a local one, i.e.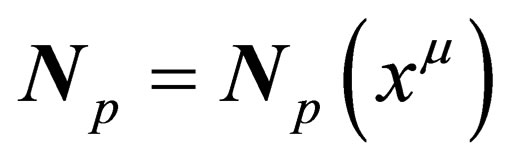 , then
, then
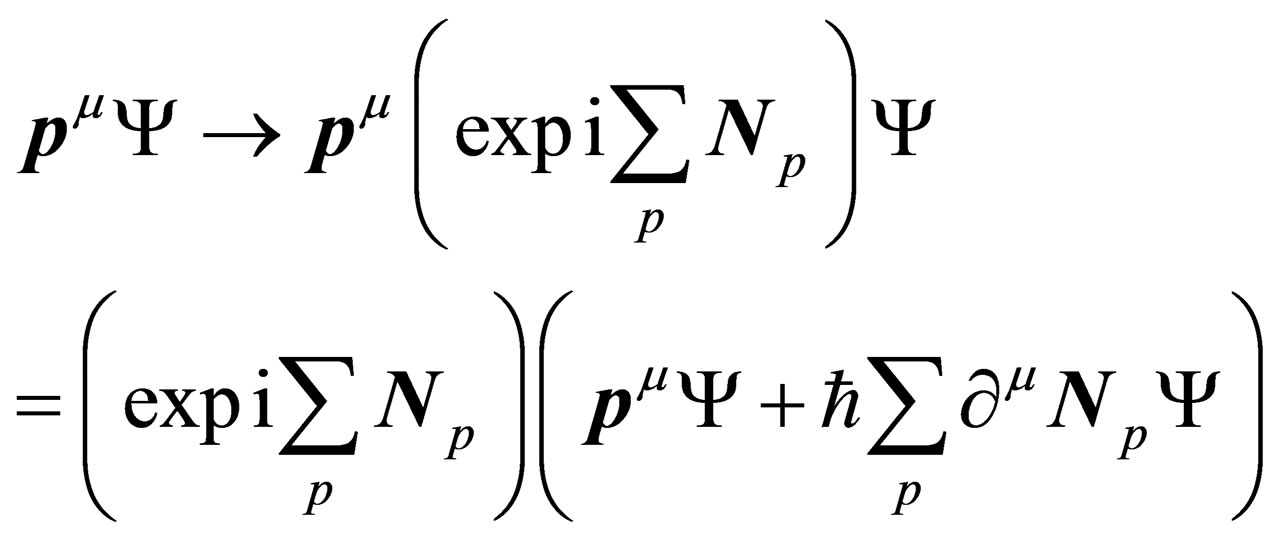 (A1.5)
(A1.5)
Writing the full state of the particle as a product of the “orbital” state 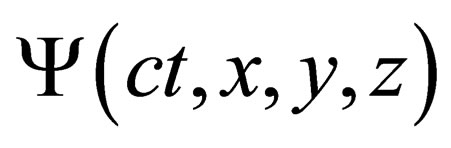 times an “internal” state
times an “internal” state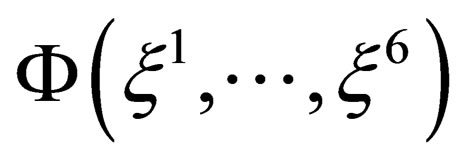 , the conservation of the Lagrangian imposes inside
, the conservation of the Lagrangian imposes inside 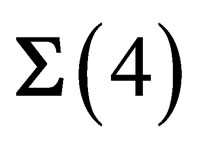 the existence of a vector-type gauge field
the existence of a vector-type gauge field
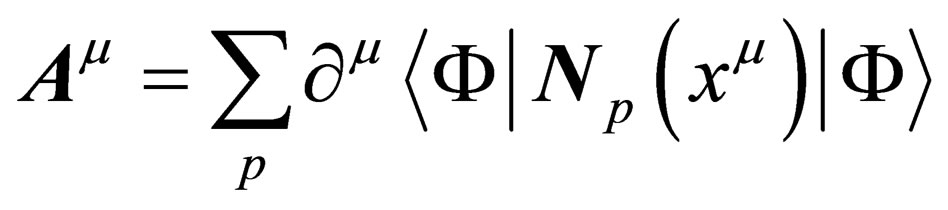 (A1.6)
(A1.6)
after averaging over the 6 degrees of freedom  since
since 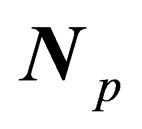 exclusively acts upon the variables
exclusively acts upon the variables .
.
It implies the vector character of the above fields: gluons, gluinos, 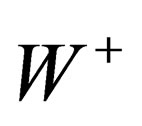 ,
,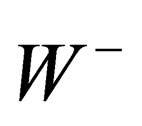 ,
,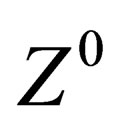 and photon.
and photon.