Symmetry and relativity: From classical mechanics to modern particle physics ()
Quoting H. Weyl’s sentence summarized by: “Symmetry is one idea by which man through the ages has tried to comprehend and create order, beauty, and perfection...” ([2]), one can add that symmetry represents a methodology followed by Modern Physics in order to build coherent and successful models whose aim is to understand the fundamental physical laws at all scales, from the microscopic world to the macroscopic Universe.
Let us come to Relativity Theory and how it is related to Symmetry in Physics. Firstly, one has to remind that Relativity is born from the unsufficiencies of Classical Physics, both Newton Mechanics and Maxwell Electromagnetism, in which the absolute character of time and the existence of a hypothetic medium—the aeter, are postulated, which fills the vacuum and serves as a support for the propagation of electromagnetic waves, among them the visible light.
After the publication of A. Einstein’s historical paper [3], time like space components becomes an ordinary component of a four-dimensional structure, the Minkowski space-time manifold. Thus, a complete symmetry arises between space and time, and this new feature leads to important physical consequences as it will be shown in the next sections.
This review is organized around three main topics:
• Contribution of Relativity Theory to the different symmetries in Classical Physics (Section 2).
• Relativistic Symmetries in Quantum Mechanics (Section 3).
• Role of the Relativity Theory in the discovery of new symmetries (and asymmetries) in Elementary Particle Physics (Section 4).
The conclusion will be devoted to some open issues in the common field of Relativity and Symmetry.
It is worth noticing that the different parts of the review are related to each other by two motivations: 1) the first one is the evolution of the physical concepts initiated by Relativity Theory, and 2) the second one is the breakthrough that some discoveries brought to the Physical Sciences, notably in our understanding of the Symmetry concept.
2. RELATIVITY AND SYMMETRIES IN CLASSICAL PHYSICS
2.1. Classical Mechanics
One of the main difficulties which appeared in Classical Mechanics was its unconsistency with the electromagnetic phenomena, notably the problem of magnetic induction in a moving circuit. This unconsistency has been amplified by the negative result of the MichelsonMorley experiment whose aim was measuring the translation velocity of the Earth in the aether. In order to cure these problems, A. Einstein succeeded in establishing new basis for Mechanics by setting three new postulates:
• Time is a relative notion and each observer possesses its own time.
• The speed of light is isotropic and does not depend on the state of motion of the observer.
•  being an inertial frame moving with a constant velocity
being an inertial frame moving with a constant velocity  according to another frame
according to another frame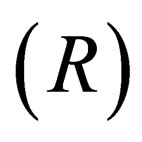 , the coordinate transformation between these two inertial frames is given by the Lorentz formula [4].
, the coordinate transformation between these two inertial frames is given by the Lorentz formula [4].
A straightforward consequence of these new principles was the fusion of space and time in one entity called “Space-Time”, which was performed by H. Minkowski ([5]). In this new 4-space, time and space components are completely symmetric, as it is shown by the following series of equalities relating space-time components of the same event between the two frames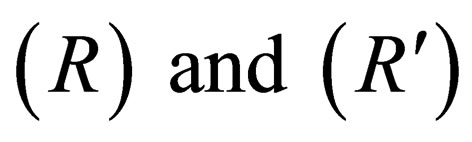 :
:
 (1)
(1)
and
 (2)
(2)
where  is the Lorentz factor, and the sign
is the Lorentz factor, and the sign  appears in Equation (2) because the velocity of
appears in Equation (2) because the velocity of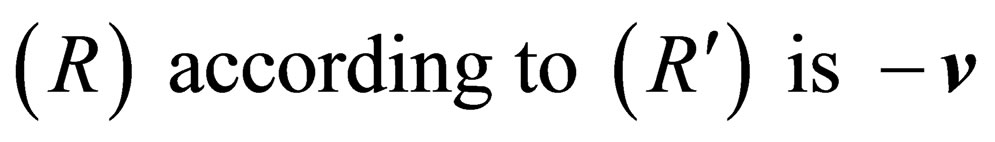 .
.
Physical interpretation of these relations becomes more obvious by adopting the point of view of Special Relativity: Analysis of physical phenomena does not depend on the motion of the observer(s). Observer O in frame  and observer O’ in frame
and observer O’ in frame  have completely a symmetric role. It is worth stressing that Einstein’s postulates and Minkowski’s 4-space lead to a new physical concept, the Relativistic Invariance one, which have important consequences in the foundations of Modern Physics.
have completely a symmetric role. It is worth stressing that Einstein’s postulates and Minkowski’s 4-space lead to a new physical concept, the Relativistic Invariance one, which have important consequences in the foundations of Modern Physics.
Thanks to a new mathematical entity, the 4-vector introduced by Minkowski, one can set many fundamental invariants, among them:
• The square of the space-time interval, 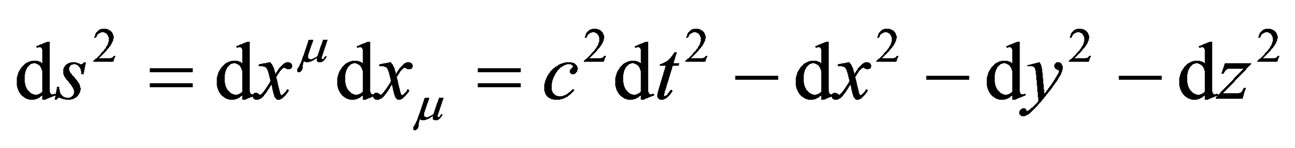 , from which one can deduce automatically the relation of clock retardation [6].
, from which one can deduce automatically the relation of clock retardation [6].
• The square of the energy-momentum 4-vector,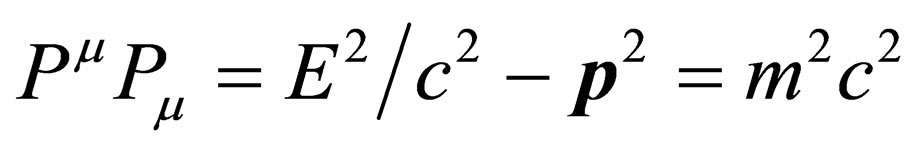 .
.
Applying this last relation to a massive particle at rest , the Einstein breakthrough formula emerges,
, the Einstein breakthrough formula emerges, 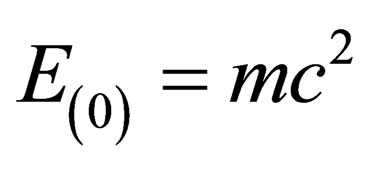 , which represents a new symmetry, the equivalence between Energy and Mass [7]; symmetry which does not exist in Newton Mechanics.
, which represents a new symmetry, the equivalence between Energy and Mass [7]; symmetry which does not exist in Newton Mechanics.
2.2. Classical Electrodynamics
In his seminal paper, A.Einstein was motivated by showing that the two standard views of the induction phenomenon (Lenz-Faraday law) were really the same one. Departing from the Relativity principles, he achieved merging the two different processes and he found again the standard results of the Maxwell’s equations: any variable electric field  generates a magnetic field
generates a magnetic field , and reciprocally. So, a complete symmetry is established between the electric and magnetic fields, despite the absence (temporary?) of magnetic charges. This physical property is clearly reflected in the relativistic formalism with the introduction of a new entity, the electromagnetic tensor
, and reciprocally. So, a complete symmetry is established between the electric and magnetic fields, despite the absence (temporary?) of magnetic charges. This physical property is clearly reflected in the relativistic formalism with the introduction of a new entity, the electromagnetic tensor 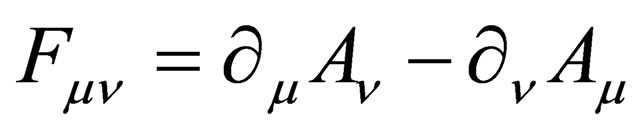 1, which is an antisymmetric tensor whose six components are respectively those of the electric
1, which is an antisymmetric tensor whose six components are respectively those of the electric  and magnetic
and magnetic  fields. Doing some calculations with this new tensor like the following,
fields. Doing some calculations with this new tensor like the following,
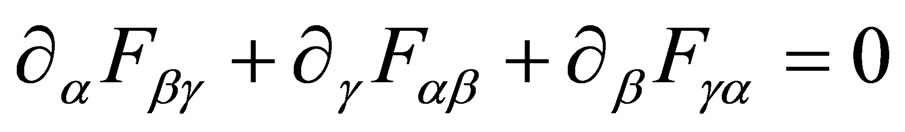
(indices  are varying from 0 to 3), allows to find again the standard Maxwell-Faraday equations:
are varying from 0 to 3), allows to find again the standard Maxwell-Faraday equations:  .
.
2.3. Summary
At the classical level, the Relativity Theory introduces new aspects of symmetry in fields where symmetry was not conjectured: Space and Time, Electric and Magnetic fields and the Mass-Energy equivalence. Furthermore, its mathematical formulation includes, in a simple and direct way, the symmetry properties of the physical processes [8].
3. RELATIVITY AND THE SYMMETRY PROPERTIES OF QUANTUM MECHANICS
We will deal successively with non-relativistic Quantum Mechanics (NRQM), relativistic Wave Mechanics of De Broglie and the relativistic approach to Quantum Mechanics initiated by P. Dirac. By following the historical steps, emphasis is put on the basic physical ideas and the main experimental discoveries in each field. Technical calculations will be avoided.
3.1. Symmetry in Non-Relativistic Quantum Mechanics
The importance of Symmetry in NRQM leads to a wide use of Group Theory methods when describing quantum systems, from the simple hydrogen atom to complicated molecular structure [9]. This feature is related to the mathematical structure of Quantum Mechanics itself: any physical quantity which can be measured, or observable, is represented by a hermitean operator  acting on a Hilbert space built from state vectors or kets; the last ones represent the physical states of the system and form an algebraic vector space [10]. How ordinary QM has been made relativistic? Before answering this question, it is fair to recall how Special Relativity has been firstly introduced in Quantum Physics.
acting on a Hilbert space built from state vectors or kets; the last ones represent the physical states of the system and form an algebraic vector space [10]. How ordinary QM has been made relativistic? Before answering this question, it is fair to recall how Special Relativity has been firstly introduced in Quantum Physics.
3.2. De Broglie Relativistic Wave Mechanics
In his doctoral thesis (Paris, 1924), the french physicist L. de Broglie generalized the important notion of wave-particle duality (first introduced by A. Einstein for the Photon in 1905 [11]) by extending it to massive relativistic particles [12]. Departing from the hypothesis that each material corpuscle has an internal vibration whose frequency is given by the Planck-Einstein relation, 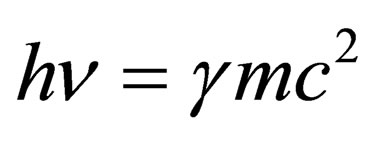 , and supposing that this vibration is in phase with a “phase wave” propagating at the speed
, and supposing that this vibration is in phase with a “phase wave” propagating at the speed 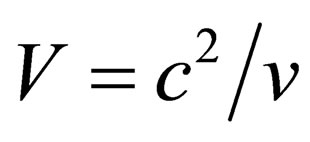 (2), De Broglie inferred the expression of the particle wave-length:
(2), De Broglie inferred the expression of the particle wave-length:
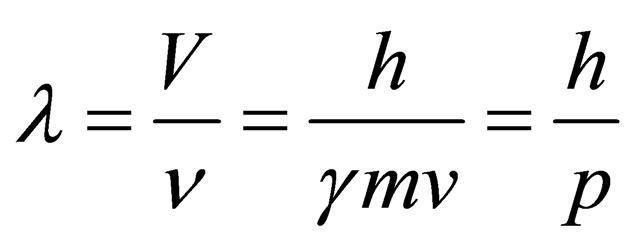
which is identical to the photon wave-length given by the Planck-Einstein relation,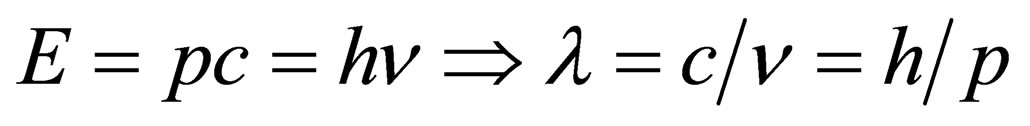 . This famous relation, which has been confirmed by the experimental discovery of the electron diffraction (Davisson and Germer, 1927), links together the two main aspects of matter, wave and/or particle. Thus, a new symmetry at the level of the elementary particles has been revealed, as a consequence of the Einstein-De Broglie relations. Then, the wave nature of any quantum system has been exploited very deeply to set fundamental equations: the non-relativistic Schrodinger equation [13], and the relativistic Klein-Gordon one [14].
. This famous relation, which has been confirmed by the experimental discovery of the electron diffraction (Davisson and Germer, 1927), links together the two main aspects of matter, wave and/or particle. Thus, a new symmetry at the level of the elementary particles has been revealed, as a consequence of the Einstein-De Broglie relations. Then, the wave nature of any quantum system has been exploited very deeply to set fundamental equations: the non-relativistic Schrodinger equation [13], and the relativistic Klein-Gordon one [14].
3.3. Dirac Equation and Its Consequences
In the years 1927-1928, the British physicist P. Dirac succeeded in formulating a relativistic wave equation for the electron characterized both by its simplicity and its ingenuity [15].

where  is the 4-momentum of the particle and
is the 4-momentum of the particle and  are the Dirac matrices with
are the Dirac matrices with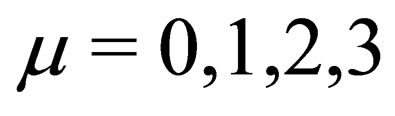 .
.
The Dirac equation has a linear evolution according to time, like the Schrodinger equation and, furthermore, it reveals a perfect similarity among space and time components. Thus, it has the great advantage to be relativistic invariant. Applied to the known massive particles (at this epoch there were only electrons and protons), Dirac equation leads to fascinating results:
• The value of the spin,  , is deduced automatically with a gyromagnetic factor of the electron,
, is deduced automatically with a gyromagnetic factor of the electron,  , which agrees with the experimental measurements.
, which agrees with the experimental measurements.
• There appear negative-energy states for the electron• 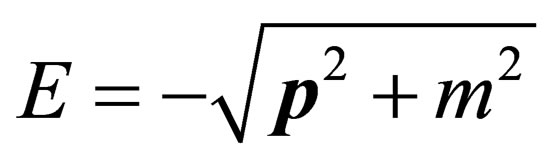 , as with the Klein-Gordon equation. But, according to the fermionic nature of the electron, these states are interpreted as an electron with positive electric charge, or an anti-electron called also a positron [16]. This particle has been discovered by Anderson in 1933 [17], which marks the beginning of the Antimatter Era.
, as with the Klein-Gordon equation. But, according to the fermionic nature of the electron, these states are interpreted as an electron with positive electric charge, or an anti-electron called also a positron [16]. This particle has been discovered by Anderson in 1933 [17], which marks the beginning of the Antimatter Era.
• Thanks to the relativistic Dirac equation a new symmetry is born:
Matter  Antimatter
Antimatter
and it confirmed the prediction of Dirac that “every particle has its own antiparticle, whatever its spin is”. Then, there were the discoveries of the antiproton, the antimuon, the antineutron and the other ones [18].
• What is really fundamental in this new kind of symmetry is that it firstly appeared in the world of elementary particles, a field governed by the rules of Quantum Mechanics, and not in the macroscopic world where Classical Physics dominates.
It is worth saying too that taking account of the importance of the Relativity principles in both the two approaches to Quantum Physics, De Broglie’s Wave Mechanics or Standard (Dirac) Quantum Mechanics, have paved the way to the development of a new field of research, the physics of Elementary Particles.
4. MODERN PARTICLE PHYSICS
At the same period than the Dirac equation, Quantum Field Theory (QFT) was developed on relativistic principles [19]. It was essentially devoted to the interactions between quantized electromagnetic fields and charged particles, which is called Quantum Electrodynamics (QED). The formal language of QFT uses intensively Relativity Theory; its exposition lies outside the scope of this review. However, QFT is the best framework for describing interactions among elementary particles; this research field being characterized by new symmetry properties and, sometimes, by asymmetry ones.
4.1. Elementary Particles and Fundamental Symmetries
As shown in the preceding sections, Relativity Theory introduces fundamental tools for apprehending new physical processes. These are essentially:
• Relativistic Conservation Laws, like the conservations of the total energy-momentum (including the mass) and of the total angular momentum (including the spin of the particles).
• Relativistic Covariance. It is a new principle which stipulates that the description of any quantum process must have the same analytical form, independently of the reference frame in which the process is observed; the best example being the computation of the transition probabilities between different quantum states.
• According to these new principles, E. Wigner wrote a paper devoted to the representations of the Lorentz Group [20] which constitutes a new breakthrough in Relativistic Quantum Physics (including QFT). He applied techniques of Group Theory to the Hilbert space describing a quantum system obeying Relativity principles; and he succeeded to derive two Relativistic Invariants (RI), independently of the internal dynamics of the physical system. The two RI are respectively the mass of the quantum system (already found since the introduction of the Minkowski 4- space) and its intrinsic angular momentum or its quantized spin.
An immediate consequence of these RI is related to the massless particles which move at the speed of light c like photons, gravitons and even neutrinos if their masses are neglected: the projection of the spin of a massless particle along its momentum or helicity,  , has only two values,
, has only two values, . It could be seen that the massless quantum state with
. It could be seen that the massless quantum state with  is the mirror image of the other state with
is the mirror image of the other state with  and vice-versa. This intuitive symmetry will be tested experimentally and important features will be deduced.
and vice-versa. This intuitive symmetry will be tested experimentally and important features will be deduced.
• It is quite remarkable that Wigner’s achievement completes the seminal work of Dirac: by means of the relativistic formulation of the quantum principles, the intrinsic angular momentum of a particle, or its spin, emerges directly. Spin is an essential ingredient for describing atoms, nuclei and particles; and it is worth noticing that, thanks to the existence of the spin, Pauli formulated his famous Exclusion Principle which explains the stability of atoms and molecules.
• Other important symmetries in Subatomic Physics are the Discrete Symmetries whose experimental tests are still a challenge for Nuclear and Particle Physics. These are:
1) Charge Conjugation, C, which transforms any particle with charge q into its antiparticle with charge  by keeping its mass and its spin unchanged (it is a consequence of the relavistic Dirac equation).
by keeping its mass and its spin unchanged (it is a consequence of the relavistic Dirac equation).
2) Parity, P, (or mirror symmetry) which transforms the vectors  into
into .
.
3) Time Reversal, T, which transforms  and spin
and spin , and exchanges both initial and final states.
, and exchanges both initial and final states.
It is usually argued that a quantum system is invariant by one of these three symmetries, 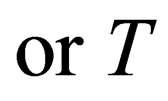
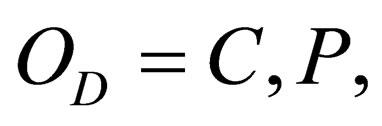 , if its hamiltonian H, which governs its evolution in time, keeps the same form after applying
, if its hamiltonian H, which governs its evolution in time, keeps the same form after applying  on the physical system. Mathematically, it leads to
on the physical system. Mathematically, it leads to 
The two symmetries, P and T, are already used in NRQM, especially for establishing selection rules [21]; but their relativistic aspect becomes more crucial in Particle Physics which deals with energetic particles like electrons or neutrinos whose velocities are often very close to the speed of light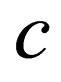 .
.
• In this context, sophisticated experiments have been performed in order to test the validity of these symmetries, as suggested by theorists T. D. Lee and C. N. Yang in 1956 in order to solve the “ puzzle” [22]. An historical experiment analyzing electron angular distributions from nuclear
puzzle” [22]. An historical experiment analyzing electron angular distributions from nuclear  decay [23], followed by another one studying weak decay of the muon,
decay [23], followed by another one studying weak decay of the muon,  [24], proved in an undoubtful way that both Parity and Charge Conjugation are violated in weak interactions: whatever the initial decaying particle is, the neutrino is a left-handed particle, while the anti-neutrino is a right-handed one (3 ). But the combined operation, CP or PC, is still a good symmetry [25]. This hypothesis was true until the experimental discovery of Cronin et al. (1964) which shown the breakdown of CP symmetry in the neutral meson system,
[24], proved in an undoubtful way that both Parity and Charge Conjugation are violated in weak interactions: whatever the initial decaying particle is, the neutrino is a left-handed particle, while the anti-neutrino is a right-handed one (3 ). But the combined operation, CP or PC, is still a good symmetry [25]. This hypothesis was true until the experimental discovery of Cronin et al. (1964) which shown the breakdown of CP symmetry in the neutral meson system, 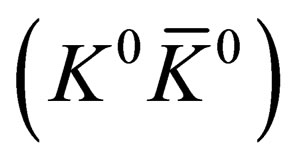 , made out by a pair of particle-antiparticle evolving differently with time [26].
, made out by a pair of particle-antiparticle evolving differently with time [26].
• After the failure of the Discrete Symmetries, a main question arose [27]:
Discrete symmetries being only approximate, is there any fundamental law which could relate a particle or a system of particles to their corresponding antiparticles?
The answer to this crucial question comes again from Relativistic QFT, thanks to the CPT theorem [28] which states the following: “Assuming Lorentz Invariance of the interactions among particles, physical laws are invariant by the product of the three discrete symmetries C, P and T taken in any order: CPT, TPC, TCP, ...”.
This theorem concerns any local interaction described in the Minkowski 4-space, like Strong, Electromagnetic and Weak interactions, and does not depend on the fact that any discrete symmetry is conserved or violated. It leads to important physical consequences which are still valid on the experimental side:
• The equality of mass of any particle (X) with its antiparticles  [29].
[29].
• The total lifetimes of  are identical.
are identical.
• The intrinsic magnetic moments of  are opposite in sign but they have the same absolute value.
are opposite in sign but they have the same absolute value.
• Inverse reaction with antiparticles:
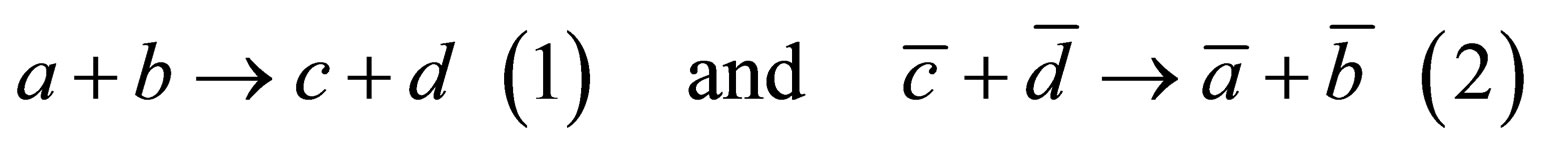
Reaction (2) has the same probability of occurrence than reaction (1), even if symmetry CP or T is violated.
4.2. Quarks, Leptons and Gauge Fields
Gauge field theories and their applications to Particle Physics represent today the heart of Modern Physics and of all the activities turning around them, both theoretical and experimental. It requires a huge literature to describe them and, in this paragraph, emphasis will be put on the basic principles and the original ideas which guided their development.
• According to their physical properties (mass, charge, spin) and to their mutual interactions, particles are classified into specific families called multiplets. An evident example is the proton-neutron system which forms a doublet with regard to the strong interaction. Thus, it is said that the relativistic proton-neutron interaction is invariant by the symmetry group .
.
After the discovery of many particle families, new quantum numbers arose like strangeness, charm, beauty..., and their classification become an urgent problem for Theoretical Physics. Despite their differences, particles present several common aspects and notably symmetry properties which lead to the use of Group Theory techniques.
Finally, two important families emerged: quarks and leptons, and their interactions are described by gauge fields.
4.2.1. Gauge Field
A gauge field is any field (classical or quantized) which remains invariant by a gauge transformation, like Classical Electrodynamics or QED. Let us consider the electromagnetic 4-potential  If each component
If each component  is transformed like:
is transformed like:  ,
, 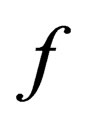 being any continuous function of
being any continuous function of , the electromagnetic tensor
, the electromagnetic tensor 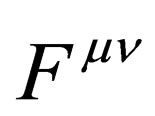 (defined in sect.2) will remain unchanged.
(defined in sect.2) will remain unchanged.
This simple transformation (Abelian in the language of Group Theory) can be generalized to other fields, like nuclear field or quark field, by taking account of the “internal symmetry” which characterizes particles belonging to the same multiplet [30]. In this last case, the gauge transformation is called a non-Abelian one.
4.2.2. Quarks
Quarks [31] are the fundamental constituents of the Hadrons, heavy particles like Mesons and Baryons which are produced by strong interactions. When interacting among themselves, quarks exchange gluons (massless partcles like the photon) and this kind of interaction requires a new quantum number called color. The color is described by a relativistic gauge field theory which is similar to QED (describing electron and photon interactions). It is called Quantum Chromodynamics (QCD) [32].
All the quark properties are deduced from symmetry principles underlying the physical properties of the hadrons [33]. Their charges are fractions of the elementary electric charge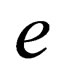 , and they can be classified into two groups, light quarks and heavy ones. They are respectively:
, and they can be classified into two groups, light quarks and heavy ones. They are respectively:
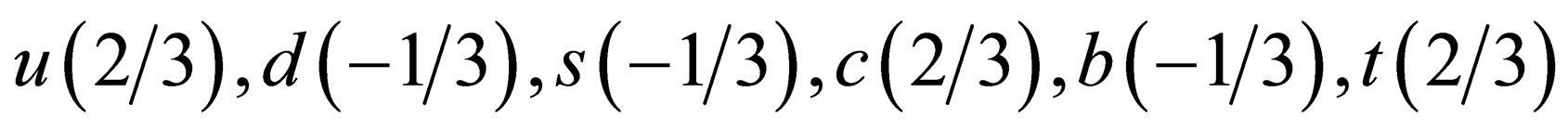 .
.
Number inside parenthesis indicates the charge of the quark in unit of ; the three first quarks, u, d and s, are the light ones while the three last ones are the heavy quarks.
; the three first quarks, u, d and s, are the light ones while the three last ones are the heavy quarks.
Quarks have another physical property: they undergo electromagnetic and weak interactions like the hadrons in which they are confined. Thus, in the Electroweak Model of Glashow-Weinberg-Salam [34-36], quarks are classified into doublets, each doublet having an Up quark with charge 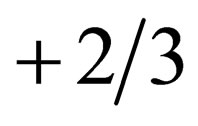 and a Down quark with charge
and a Down quark with charge .
.
4.2.3. Leptons
The word Lepton means initially a light particle, like the electron whose mass is approximately 1856 smaller than the proton mass. The neutrino, which is simultaneously produced with the electron in  decay, is a lepton too. Then, after the discovery of the muon,
decay, is a lepton too. Then, after the discovery of the muon, 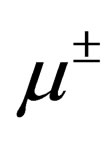 , which has the same properties than the electron except its mass (the muon is 210 heavier than the electron), “lepton” usually indicates particles which are not sensitive to the strong interaction. Leptons are sensitive only to electromagnetic and weak interactions; and each lepton has its own quantum number called the “leptonic number”.
, which has the same properties than the electron except its mass (the muon is 210 heavier than the electron), “lepton” usually indicates particles which are not sensitive to the strong interaction. Leptons are sensitive only to electromagnetic and weak interactions; and each lepton has its own quantum number called the “leptonic number”.
At this level, particle physicists noticed a stringent similarity between Leptons and Quarks in the electroweak domain; it was the birth of the Standard Model which classifies all the fundamental particles into doublets according to their electroweak interactions [37].
The discovery of the third charged (and heavy!) lepton, the , with its associated neutrino the
, with its associated neutrino the 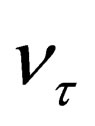 [38,39], followed by those of the quarks b (beauty) and t (top), confirmed in a brilliant manner the exactness and the accuracy of the Standard Model (SM).
[38,39], followed by those of the quarks b (beauty) and t (top), confirmed in a brilliant manner the exactness and the accuracy of the Standard Model (SM).
Needless to say that the SM is now a true theory. All its predictions have been verified experimentally: aside heavy quarks cited above, there were the discovery of the massive intermediate vector bosons, 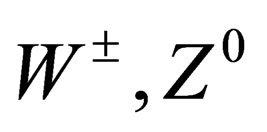 (CERN 1983) and the one, more spectacular, of the Higgs boson (CERN, 2012-2013) whose field generates the mass for the fundamental constituents of matter.
(CERN 1983) and the one, more spectacular, of the Higgs boson (CERN, 2012-2013) whose field generates the mass for the fundamental constituents of matter.
5. CONCLUSIONS
Attempt has been made to give a large survey on the importance and intrication of Relativity Theory with Symmetry in the physical processes. From Classical to Modern Physics especially Particle Physics, numerous aspects of symmetry would not be understood even discovered without the principles of (Special) Relativity. Thanks to the wedding of Relativity and Quantum Mechanics and the inclusion of new symmetry principles, the resulting quantum fields get a predictive power like the Standard Model one. However, several fundamental problems remain unsolved:
Do magnetic monopoles exist in Nature? Their absence still indicates a dissymmetry between Electricity and Magnetism. Could modern Theoretical Physics realize a complete synthesis between General Relativity and Quantum Mechanics, as Dirac achieved eighty years ago? At a deep level of Quantum Mechanics, is there a real symmetry, or super symmetry, between Bosons and Fermions?
All these open problems require a large use of symmetry principles including sophisticated methods from Group Theory, which is nowadays visible with the impressive development of Mathematical Physics. On another side, experimental physics could answer and eventually solve all these passionate problems.
ACKNOWLEDGMENTS
The author would like to thank many colleagues and friends for stimulating discussions about symmetries in Physics. He is particularly very grateful to V. Morenas whose comments and remarks helped him in clarifying difficult problems.
NOTES
1 is the four-vector potential given by
is the four-vector potential given by  is the partial derivation according to the component
is the partial derivation according to the component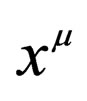 .
.
2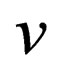 is the velocity of the massive particle which is identified with the group velocity of the wave, while V is the phase velocity which could be greater than
is the velocity of the massive particle which is identified with the group velocity of the wave, while V is the phase velocity which could be greater than , h is the Planck constant and
, h is the Planck constant and .
.
3Recalling that helicity is given by , only neutrinos with
, only neutrinos with 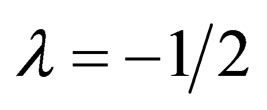 called left neutrino
called left neutrino  exists, while only anti-neutrinos with
exists, while only anti-neutrinos with  called right anti-neutrino
called right anti-neutrino  exists in Nature. The transformation allowing the transition from
exists in Nature. The transformation allowing the transition from 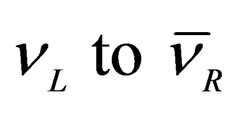 is the product of C and P, or CP Symmetry.
is the product of C and P, or CP Symmetry.