An Approach for Personalized Social Matching Systems by Using Ant Colony ()
Many of them are designed to group your users (or create a recommendation list) according to their preferences and goals: sites for dating, language learning, exchanges of experiences in travel, research development, etc. For the last ones, strategy of grouping should take into consideration the goal of each member (or compatibility between a pair of them) and also all the desirable characteristics of the group members (as diversity of knowledge, experience and skills).
The performance of these sites depends on the users satisfaction, which is directly related to the quality of the recommendations and the number of attempts made by the user, until achieve success.
In this work a new formulation for the problem of recommending one or more people for each individual of a network is proposed, in order to reduce the number of tries made by users. This approach can be used in any situation that is necessary to create a recommendation list, not only for dating.
The main idea is to create groups of 2 or more components, taking into account compatibility between 2 people (discrepancy between personal characteristics and the desirable ones from the other person) and the heterogeneity of the group (discrepancy between the personal characteristics among group individuals) [1].
These are two components of objective function in the optimization problem proposed, which is solved using an algorithm based on Ant Colony heuristic (ACO) [2].
This paper is organized as follows. Section 2 describes the formulation that combines homogeneity and heterogeneity of the groups. Section 3 shows the proposed algorithm. Section 4 contains the results of numerical experiments. Finally, Section 5 presents some conclusions.
2. Recommendation Lists
Customized social grouping systems can be seen as recommender systems, which point to a specific person other members of a social network instead of recommending products [3].
The people recommendation is much more complicated than the products recommendation [4], since two people have the same characteristics not always be recommended to each other. That is, personal characteristics may not be the person’s preference, and the immediate consequence is that most of the techniques of recommendation may not be appropriate [5].
Moreover, the number of members of such social networking has grown rapidly in recent years, which has generated a considerable growth of computational complexity. As an example, one of the largest social networking sites in Brazil has over 30 million registered users1 and an average of 1000 new members every day.
In general, a function that measures the similarity between the desirable characteristics of an individual in question and those submitted by other members of the network is used to generate the recommendation list. Then, this same individual receives the recommendation following the order of similarity: people with greater similarity have priority in the recommendation [6].
However, even considering people classified in the first places of similarity (in relation to same person), they may be similar to each other. The consequence is a possible successive recommendation of people with the same characteristics; the user can feel unmotivated after several attempts without dating successfully [3].
One way to increase the chances of success during the recommendation process is to consider the recommendation of several network members at once (a group), taking into account the similarity between the relevant characteristics of a person and desirable another one, and the discrepancy between the relevant characteristics of two people from the group.
Thus, if the social network is related to a dating site, the chance of finding a suitable person to start a relationship increases. If the site intents create discussion groups, these groups are more likely to generate a high level debate, with different points of view.
Formulation
A social network can be represented as a complete graph with N nodes (individuals). Each node i has three sets of CN informations/features: the individual’s ones (vector ui), the desirable in the partner (vector vi), and the importance of these features (vector wi, with values2 in the range [0, 1]).
The components ui and vi in this work represent attributes such as height, weight, age, education, gender, etc., with normalized values.
Without loss of generality, consider that the recommendation will be made to the person 1. A recommendation list with NR individuals can be represented by a closed path3 that passes by at node 1 and has NR + 1 nodes. Therefore, at each edge (i, j) we can associate a variable xij with value 1 if the edge belongs to the path X, and 0 otherwise.
Using these vectors is possible to build a function that will dock compatibility and heterogeneity of a group, taking into account the result of the interaction between each pair of individuals in this group.
The compatibility between node 1 and node j is inversely proportional to the weighted discrepancy (C(X)) between the desirable characteristics of 1 and features of j (and vice versa).

Thus, a suitable list of recommendation will be build when function C(X) is minimized.
The heterogeneity of a recommendation group can be measured as the discrepancy between the characteristics ui and uj of all group’s members, and can be estimated as −H(X), where

Accordingly, to generate the recommendation group, the following minimization problem must be solved.
 (1)
(1)
where θ is a weighting factor, which reflects the importance of each portion of the function.
The constraints ensure that: the group has NR people (besides the node 1); node 1 belongs to group; generated path is connected and passes through each node at most once (respectively).
The proposed model suits different types of recommendation. For example, by adopting ui = vi and α = 1, the solution will bring together nodes with the same characteristics. If the social network is aimed to connect people with common interests to discuss about a specific subject, the discussion group will have greater propensity to present diversity of ideas (α = 0), generating more interesting debates.
Such formulation ensures that the group produces a highly attractive list recommendation, not only to contemplate the desirable characteristics of member 1, but also being formed by people with heterogeneous characteristics.
However, it should be noted that a same set of nodes can be connected in many different ways. Hence, the proposed formulation has several global minimizers. Furthermore, problem (1) is a constrained min-max problem, non differentiable, which has many local minimizers [7].
Because of these characteristics and the combinatorial nature of the problem (NP-complete [8]), it is necessary to use heuristics for its resolution.
3. Proposed Algorithm
3.1. Ant Colony Optimization
The proposed algorithm for solving the problem (1) is based on the search for the optimal using an adapted Ant Colony heuristic (Ant Colony Optimization, ACO) [9,10].
Ant colony optimization algorithm (ACO) meta-heuristic (which is inspired by the behavior of real ants) is one of the best-known examples of swarm intelligence systems, that can be used to find approximate solutions and near-solutions to intractable discrete optimization problems [2,9]; this probabilistic technique can be reduced to finding good paths through graphs.
The artificial ants incrementally build solutions by moving on the graph. The solution construction process is stochastic and is biased by a pheromone model (a set of parameters associated with graph components, whose values as modified at runtime by the ants).
3.2. Adapted Heuristic
A social network can be represented as a complete graph.
To solve the problem (1), each artificial ant k walks the graph, from node i to node j according to a probabilistic rule. The artificial ant moves successively, culminating in a closed path that corresponds to the connections among members of the same group. Thus, each path (with node 1) corresponding to a potential solution to the problem (1).
Ants deposit pheromone on the path in a quantity proportional to the quality of the solution represented by that path. This indirect form of communication (stigmergy) focuses de search around the most promising parts of the search space.
There is also a degree of pheromone evaporation, which allows some past history to be forgotten, to diversity the search. Therefore, when all the ants have completed a solution, the trails are updated by
 (2)
(2)
where 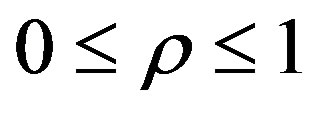 is the amount of pheromone deposited on a state transition (i,j),
is the amount of pheromone deposited on a state transition (i,j), 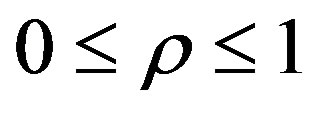 is user-defined pheromone evaporation coefficient. The amount of pheromone deposited is obtained by
is user-defined pheromone evaporation coefficient. The amount of pheromone deposited is obtained by
 (3)
(3)
where Lk is the cost of the k-th ants tour, and Q is constant.
Besides the pheromone, the probability of linking node i to node j depends on the attractiveness ηij on edge (i,j). The probability is obtained deterministically or randomly according to a pre-fixed parameter 0 ≤ γ1 ≤ 1.
 (4)
(4)
where Ri is the set of nodes that can be connected to i (complement of a tabu set Ik); the parameters α and β control the influence of pheromone (trail) and attractiveness, respectively; γ2 e γ3 are random numbers in [0,1]. The construction of the tabu set Ik takes account the maximum total tour length of an ant.
The attractiveness is the factor responsible for the grouping nodes taking into account the goal; it has high value when the pair of nodes promotes an decrease in objective function, and low otherwise.
In order to solve this problem, the attractiveness depends on the current path of the ant. In this way, the same edge (i, j) has different values of attractiveness for different ants
 (5)
(5)
if j belongs to Ik (the set formed by the nodes already chosen by ant k), and 0 otherwise. The second term is inspired by heterogeneity and the first one is inspired bu compatibility (with an adjustment to result in positive values, since the smaller value for the attractiveness is 0).
The ant system performs an outer iteration where m ants construct in parallel their solutions, thereafter updating the trail levels. The performance of the algorithm depends on the correct tuning of all parameters, including the initial trail level τij. The algorithm is the following.
Algorithm 3.1 1. (Initialization)
Initialize τij, for all i,j.
2. (Construction)
For each ant k (state 1 initial) do repeat compute 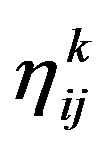 for all j (by means of (5)).
for all j (by means of (5)).
choose in probability the state to move into (by means of (4)).
append the chosen move to the k-th ant’s set tabu Ik.
until ant k has complete its solution.
end for 3. (Trail update)
Compute fk = θC(Xk) + (1-θα)H(Xk) for all k = 1,···,m, where Xk is the path described by ant k.
Set p the ant which has the lowest image (current best solution).
For each ant p move (i,j) do compute Δτij (by means of (3)).
update the trail matrix.
end for 4. (Terminating condition)
If not(end test) go to step 2.
The stop criterion is given by a pre-fixed number of outer iterations without find a new best solution.
4. Numerical Results
Tests were performed for N = 20, 50, and 100 users; preferences and their relevance (as well as personal data) to 5 features were generated randomly:
Feature 1: height (145 to 220 cm);
Feature 2: weight (45 to 150 kg);
Feature 3: age (18 to 90 years);
Feature 4: gender (0—female; 1—male);
Feature 5: education level (0—elementary school, 1— high-school, 2—undergraduate, 3—graduate, 4—postgraduate).
For each data set, tests were performed by using 11 values of θ (0, 0.1, 0.2, ···, 1), which is a weighting factor in the objective function. This factor is responsible for balance the compatibility with node 1 and the heterogeneity of the list generated.
The parameters used during implementation were γ1 = 0.05 (rate-deterministic probability), α = 1 (exponent of pheromone—function probability), β = 2 (attractiveness exponent—function probability), and ρ = 0.1 (evaporation rate of the pheromone). Maximum number of outer iterations was 10000, and the stopping criterion was a maximum number of outer iterations (100) without changing current optimal solution. Number of ants per inner iteration was 100.
In all tests, the solution is a recommendation to user 1 of 5 others users.
In Tables 1-3, as the value of θ increases, the value of H(X) increases (heterogeneity decreases), while the C(X) decreases (compatibility increases).
The solutions θ = 0 and θ = 1 correspond to users with greater heterogeneity among themselves and greater compatibility with user 1, respectively.
The proposed algorithm had a good performance, in the robustness and efficiency sense: the algorithm converged in all proposed scenarios, always finding a global minimize with a low execution time.
The algorithm has good performance even considering a larger number of users. In this case, one can use a parallel implementation of the Ant Colony adapted to reach fast execution time [11].
5. Conclusions
In this work a new formulation was proposed for the problem in order to provide a recommendation list to a user, in a social network. An Ant Colony algorithm was adapted to solve the problem; this algorithm was robust and it had a good behavior in all performed simulations, finding global minimizers.

Table 1. Numerical results—N = 20.

Table 2. Numerical results—N = 50.
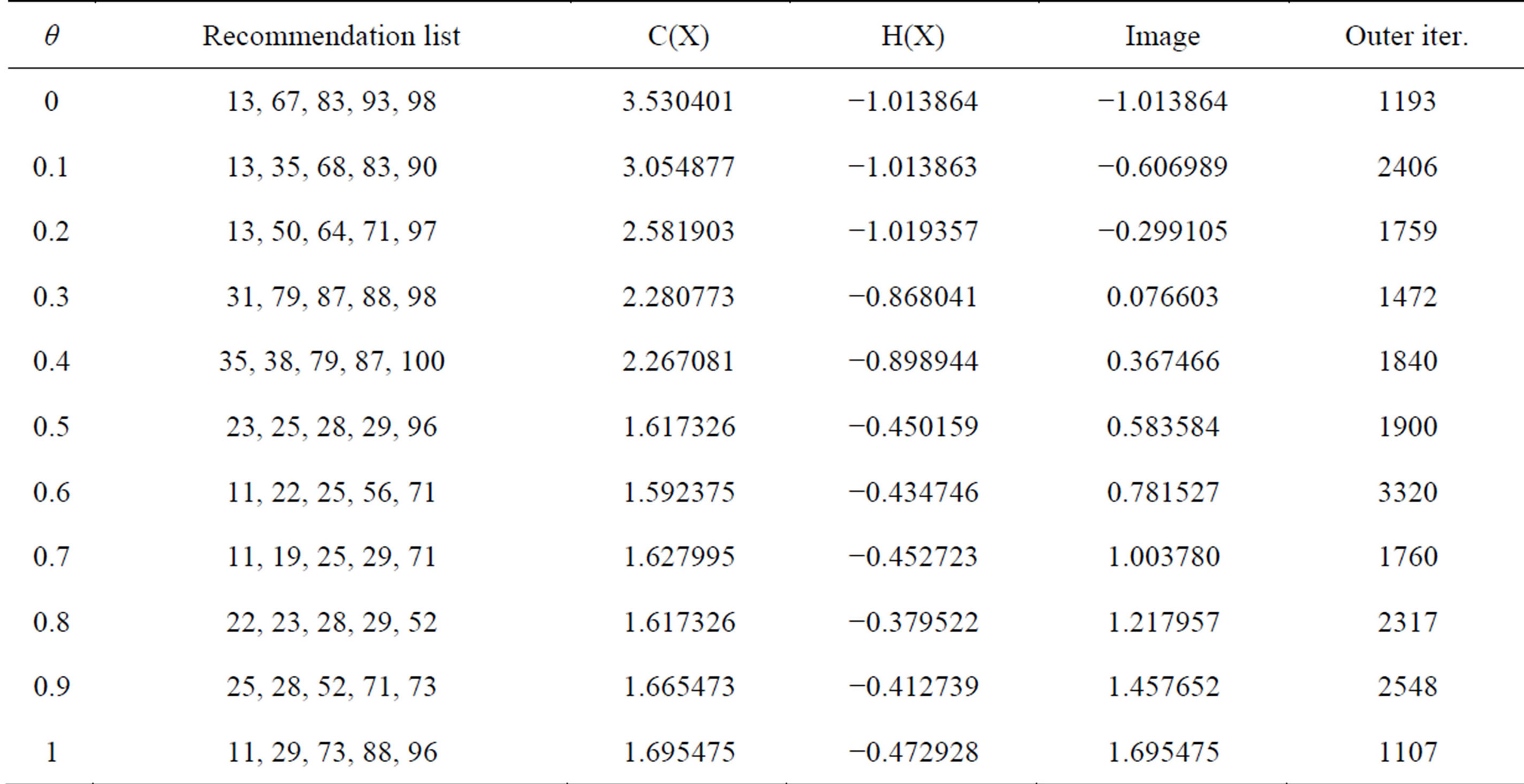
Table 3. Numerical results—N = 100.
In this formulation, the objective function is a weighted average of compatibility and heterogeneity between two users belonging to the list (both interactions, node i to j and vice versa, are checked). This approach increases de user’s chance to find a partner quickly, improving the success of social network.
Future tests will be performed with several homogeneity, heterogeneity and attractiveness functions in order to evaluate and improve the quality of the generated clustering.
NOTES
2Values close to 1 indicate high relevance of the feature.
3An immediate consequence is that there are several different representations for the same group.