A New Delay-Constrained Multicast Routing Algorithm Based on Shared Edges ()
From global point of view, optimize network resources can be seen as optimize a multicast routing tree’s total cost, finding a minimum cost multicast routing tree can be formalized as Steiner tree problem. As Steiner tree problem is NP-hard problem [2], so that many scholars have proposed heuristic algorithm to compute standardSteiner tree, the most typical is the MPH algorithm [3]. Besides, the KPP algorithm in literature [4] and BSMA algorithm in literature [5] are able to produce a high performance multicast tree, however, due to the excessive calculation, it is difficult to be applied in practice. Although the calculation of CDKS algorithm proposed by literature [6] is much lower than the previous two algorithms, the cost of the spanning tree is too high. So the literature [7] proposed a algorithm named ESAMPH, this algorithm is based on the basic idea of MPH algorithm to construct a multicast tree, compared with other similar algorithms, it takes full advantage of the shared edges to reduce the cost of the spanning tree, it can get a better balance among consideration, delay and computational complexity, it has a better comprehensive performance. However, the algorithm may chose those who do not satisfy the limit but less costly path add to the spanning tree when selects the next destination node which to be added. So, this paper combines the advantages of MPH multicast in generate multicast tree and the performance of CDKS algorithm on compute time, based on the algorithm of ESAMPH, proposed an improved multicast routing algorithm, named ESAMPH_D.
2. Questions and Modeling
Generally, we formalized the network as an empowerment undirected graph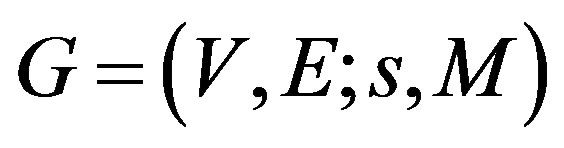 , in which
, in which 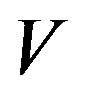 is the set of nodes of the graph
is the set of nodes of the graph , each node represents a host or a router.
, each node represents a host or a router. 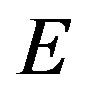 is the set of edges in graph
is the set of edges in graph  and
and  represents the number of edges (or links) of the set
represents the number of edges (or links) of the set .
. 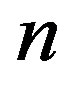 represents the number of nodes in graph
represents the number of nodes in graph  and
and .
. 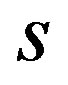 is the source node,
is the source node, 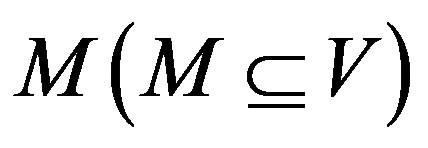 represents the set of destination nodes. Suppose that
represents the set of destination nodes. Suppose that 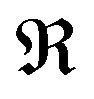 is the set of trees that rooted with s and ended with
is the set of trees that rooted with s and ended with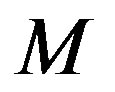 ,
,  represents the path that from the source node
represents the path that from the source node 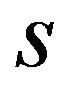 to node
to node 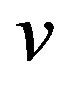 in tree
in tree .
.
We defines two functions on each edge , cost function
, cost function  and delay function
and delay function 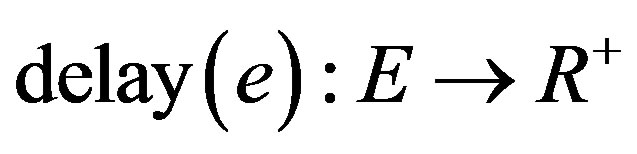 (
(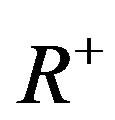 represents a positive real number set in these functions). Here, the cost can be seen as the price of use the link or the measure of some resources on network, the delay is the total delay when a packet get through the link, including queuing delay, sending delay and transmission delay.
represents a positive real number set in these functions). Here, the cost can be seen as the price of use the link or the measure of some resources on network, the delay is the total delay when a packet get through the link, including queuing delay, sending delay and transmission delay.
In the real transmission problems, it often demand to minimum the cost while meet the certain requirements of the delay constraint at the same time. So, we can get the model of the problem like this:
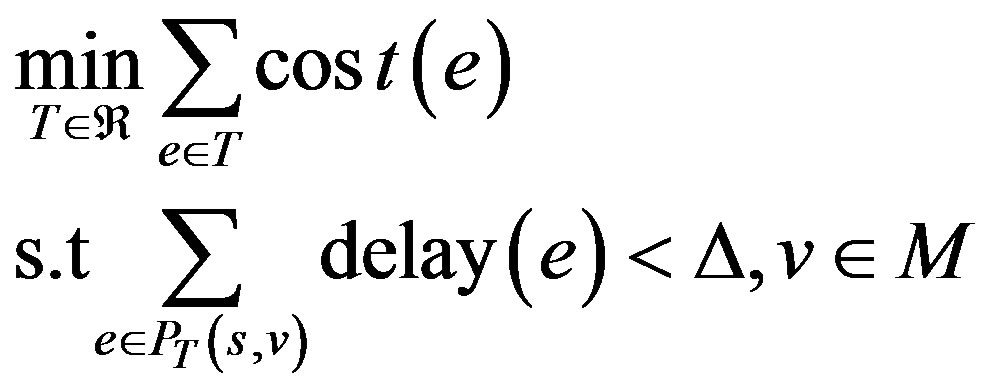
Here,  is a positive real number, it presents the end to end delay constraint.
is a positive real number, it presents the end to end delay constraint.
3. Problem Solving Methods
3.1. The Analysis and Improvement on ESAMPH Algorithm
The basic idea of the algorithm of ESAMPH is mainly based on the MPH algorithm that can generated a low cost tree, it choose the node that has more shortest path pass through to reduce the multicast tree cost further. The algorithm calculated the minimum cost path among all multicast nodes at first, for , if the minimum cost path which satisfies the delay constraint pass through the node (except the head and the tail node), then adjustment the metric factor (increase the metric value), find the maximum metric factor and save it. Second, we treat the source node S as the multicast tree
, if the minimum cost path which satisfies the delay constraint pass through the node (except the head and the tail node), then adjustment the metric factor (increase the metric value), find the maximum metric factor and save it. Second, we treat the source node S as the multicast tree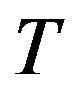 . Third, calculate the minimum cost path from the other nodes
. Third, calculate the minimum cost path from the other nodes  to multicast tree
to multicast tree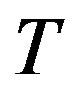 . If the minimum cost path include the maximum metric value node, then we let it divided by an integer (the integer is bigger than one) and then compare, we choose the minimum cost path connect to the tree
. If the minimum cost path include the maximum metric value node, then we let it divided by an integer (the integer is bigger than one) and then compare, we choose the minimum cost path connect to the tree 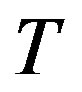 after compare. Repeat the steps above, until all of the destination nodes are connected to the tree.
after compare. Repeat the steps above, until all of the destination nodes are connected to the tree.
As we can see from the process above, the algorithm calculate the minimum cost path among all multicast nodes by using the Dijkstra algorithm at first, so that the path that not satisfy with the delay constraint may also be included, it adds extra space cost. At the same time, it may also leads to that the path is not satisfy with the delay constraint when choose the minimum cost path to join in the multicast tree.
According to the insufficient of ESAMPH algorithm, this paper proposed the algorithm named ESAMPH_D, this algorithm can be described briefly as below.
Here we use three sets ,
, 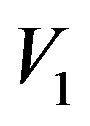 and
and .
. 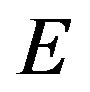 represents the set of minimum cost path that satisfy the delay constraint from each destination node to the other nodes.
represents the set of minimum cost path that satisfy the delay constraint from each destination node to the other nodes. 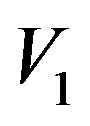 represents the set of nodes which are included by the path in
represents the set of nodes which are included by the path in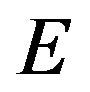 .
. 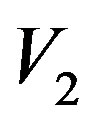 represents the set of nodes that have more shortest path get through.
represents the set of nodes that have more shortest path get through.
Step 1. Use the improved Dijkstra algorithm seeking the minimum cost path that satisfy the delay constraint from the destination nodes to the other nodes, add the path into 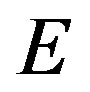 and add the nodes which are in these paths into
and add the nodes which are in these paths into .
.
Step 2. For , if the minimum cost path get through the node, adjustment the metric factor (increase the metric value), then find the node that has the maximum metric value, to join in the set of
, if the minimum cost path get through the node, adjustment the metric factor (increase the metric value), then find the node that has the maximum metric value, to join in the set of .
.
Step 3. Rooted with the source node  and initial multicast tree
and initial multicast tree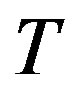 .
.
Step 4. Choose a destination node from set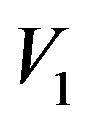 , then find all paths from set
, then find all paths from set 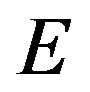 which associated with the node that have not joined into the tree but satisfy the delay constraint. If none of the paths contains the nodes included in
which associated with the node that have not joined into the tree but satisfy the delay constraint. If none of the paths contains the nodes included in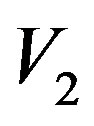 , choose the minimum cost path to join into
, choose the minimum cost path to join into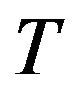 . Or, we let the cost on this path multiplied by a coefficient
. Or, we let the cost on this path multiplied by a coefficient , then make a comparison, and choose the minimum cost path link to
, then make a comparison, and choose the minimum cost path link to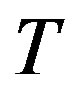 .
.
Step 5. Repeat the Step 4 until all of the destination nodes are all joined into the spanning tree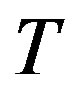 .
.
The ESAMPH_D algorithm does not calculate all the minimum cost path between every two nodes, but just calculate the minimum cost path that satisfy the delay constraint, so, this algorithm has a low spatial complexity compared with ESAMPH algorithm. On the other hand, the fourth step of this algorithm is to choose the minimum cost path from the minimum set of path that satisfy the delay constraint, and the set of nodes that have more shortest path pass through may be more likely to be selected. Thereby, the algorithm can reduce the cost of the whole tree by achieving more link sharing, and improve the performance of the whole tree, it can overcome the shortcoming of the ESAMPH algorithm when choose the next destination node to join into the tree while the cost is the minimum but the delay is not satisfy the delay constraint.
Here are the pseudo codes for the algorithm ESAMPH_D:

3.2. The Time and Space Complexity Analysis
Theorem 1. The time complexity of ESAMPH_D is O(mn2).
Proof: Consider n represents the network nodes, s represents the source node, and m represents the destination nodes. The first step of the algorithm is use the improved Dijkstra algorithm to find the minimum cost path that satisfy delay constraint from destination nodes to the other nodes, it’s time complexity is . The second step is to calculate the weights for the nodes on each paththe complexity is
. The second step is to calculate the weights for the nodes on each paththe complexity is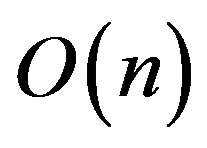 , and the path like this has
, and the path like this has  in total, so the complexity is
in total, so the complexity is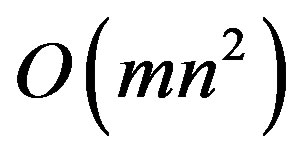 . The time complexity of the third step is a constant number
. The time complexity of the third step is a constant number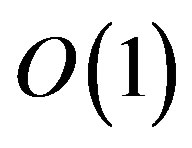 . The fourth step choose the minimum cost path that satisfy the delay constraint to the tree
. The fourth step choose the minimum cost path that satisfy the delay constraint to the tree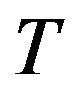 , we consider the times of comparisons: suppose the number of nodes that have added to the tree are
, we consider the times of comparisons: suppose the number of nodes that have added to the tree are , then we need to decide how to add the number
, then we need to decide how to add the number 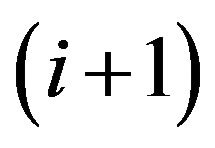 node to the tree. The worst cast is that it has
node to the tree. The worst cast is that it has  nodes added to the tree, there still have
nodes added to the tree, there still have 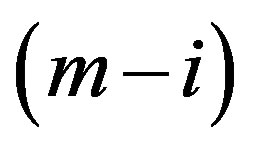 destination nodes are not added, in the selection process, if the relative path contains the node in
destination nodes are not added, in the selection process, if the relative path contains the node in , then we must compare
, then we must compare 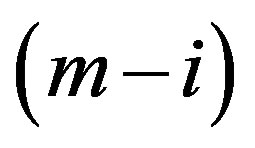 times, Therefore we need to compare
times, Therefore we need to compare  times before we find the best path, so, the complexity of Step 4 and Step 5 is:
times before we find the best path, so, the complexity of Step 4 and Step 5 is:
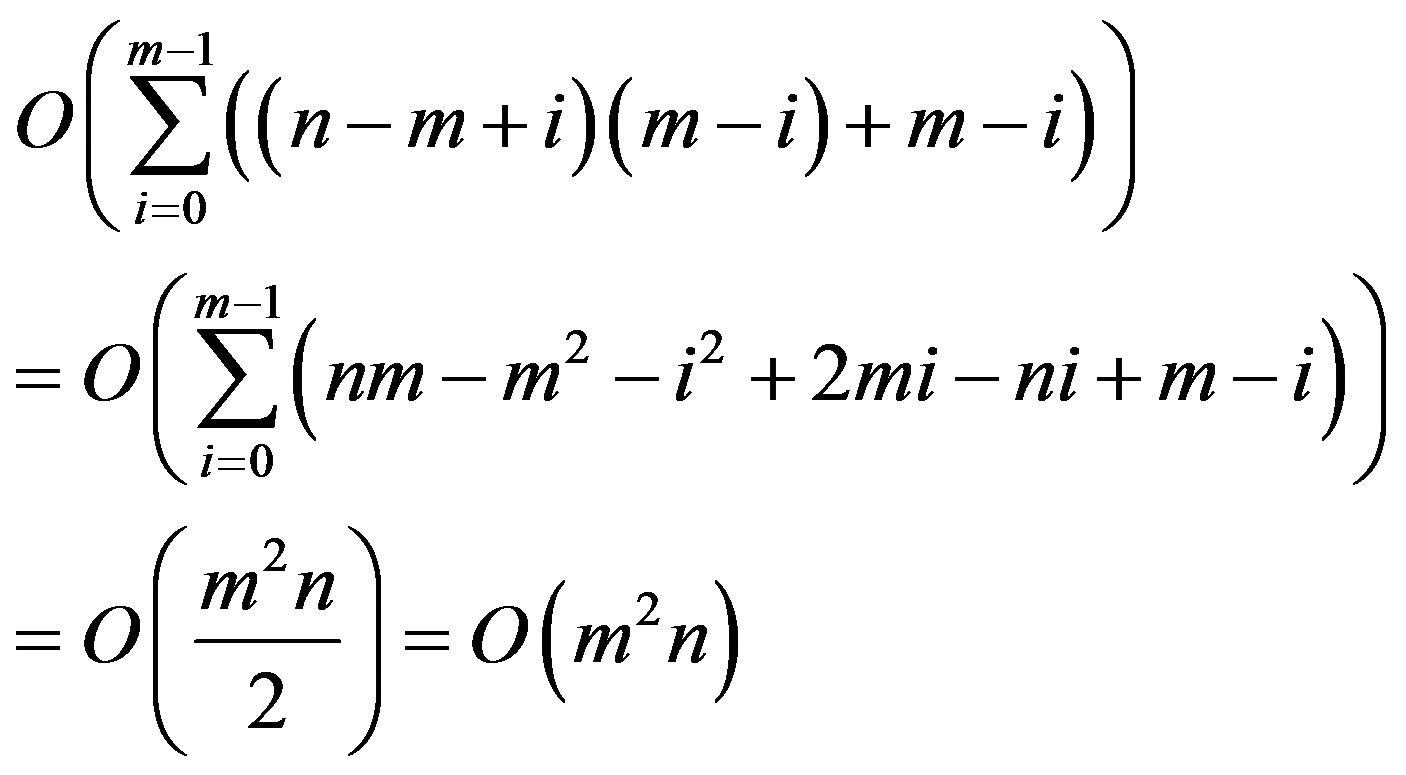
Because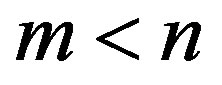 , so the total time complexity of the algorithm is:
, so the total time complexity of the algorithm is:

The time complexity of ESAMPH algorithm is O(mn2), so ESAMPH_D is equivalent to ESAMPH in the time complexity.
Theorem 2. The space complexity of ESAMPH_D is lower than (or equal to in worst) the algorithm ESAMPH.
Proof: By analysis of ESAMPH and ESAMPH_D, we can find that the space cost of the algorithm is mainly lies on Step 1 and Step 2, the ESAMPH has to store the paths with 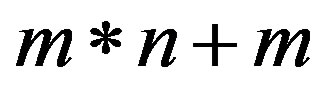 storage locations, while ESAMPH_D just needs
storage locations, while ESAMPH_D just needs  storage locations, and
storage locations, and 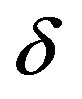 represents the maximum number of paths that satisfy the delay constraint from one destination node to the other nodes, so,
represents the maximum number of paths that satisfy the delay constraint from one destination node to the other nodes, so, . Above all, the space complexity of ESAMPH_D equals to ESAMPH in worst.
. Above all, the space complexity of ESAMPH_D equals to ESAMPH in worst.
4. Simulation and Performance Analysis
In this simulation experiment part, we use the random graphs to verification the effectiveness and correctness of the improved algorithm, and the random graphs used in the simulation are constructed using the method proposed by Waxman [8,9]. The  nodes of a graph are randomly placed on a Cartesian coordinate grid with unit spacing, considering all possible pairs of node, edges are placed with probability like:
nodes of a graph are randomly placed on a Cartesian coordinate grid with unit spacing, considering all possible pairs of node, edges are placed with probability like:

where 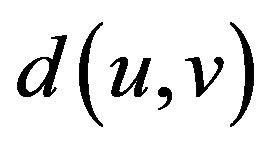 is the Manhattan distance between nodes
is the Manhattan distance between nodes 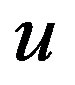 and
and , L is the maximum possible distance between two nodes,
, L is the maximum possible distance between two nodes, 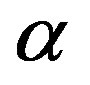 and
and 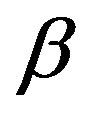 are in the range
are in the range 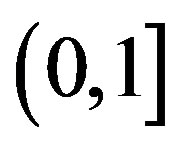 and can be selected to obtain desired characteristics in the graph. Here, we choose
and can be selected to obtain desired characteristics in the graph. Here, we choose 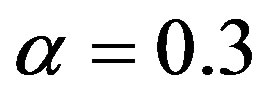 and
and .
.
Figure 1 shows the relationship between the multicast tree cost and the number of network nodes: make the number of the destination nodes maintaining 20, then change the number of network nodes from 40 to 100, the increments is 10 each time. We can see that the cost of the multicast tree is lower when using the ESAMPH_D algorithm.
Figure 2 shows the relationship between the multicast tree cost and the number of destination nodes: make the number of the network nodes maintaining 160, then change the number of destination nodes from 20 to 80, the increments is 10 each time. We can see that using ESAMPH_D is better than ESAMPH algorithm in generating the multicast tree.
Figure 3 shows the relationship between the multicast

Figure 1. The relationship between the multicast tree cost and the number of network nodes.
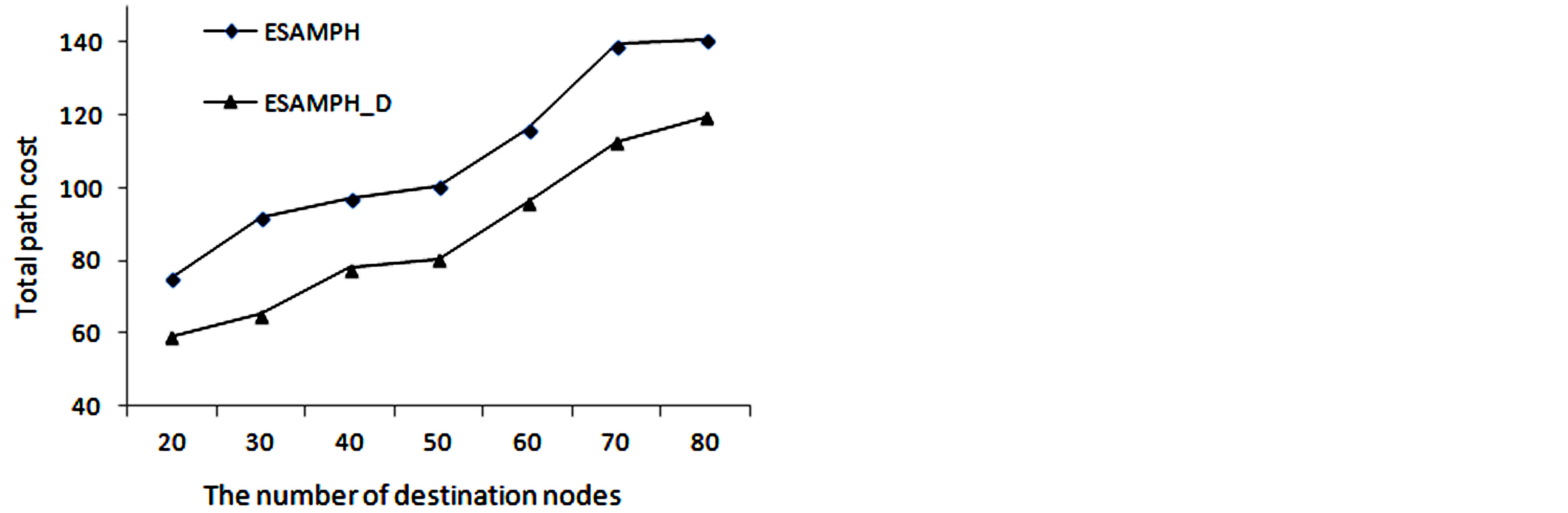
Figure 2. The relationship between the multicast tree cost and the number of destination nodes.

Figure 3. The relationship between the multicast tree cost and the delay constraint.
tree cost and the delay constraint: make the other conditions remaining, change the delay constraint from 5 to 30, the increments is 5 each time. We can see that the cost of the multicast tree is lower when using the ESAMPH_D algorithm at the same delay constraint condition.
5. Conclusion
This paper proposed the ESAMPH_D algorithm based on the weak point of ESAMPH algorithm, the improved algorithm did not add any extra cost in space or time when generating the low-cost multicast tree, so it ensuring the availability of the algorithm in practical application.