Construction and Application of Subdivision Surface Scheme Using Lagrange Interpolation Polynomial ()
1. Introduction
There are two general classes of subdivision schemes, namely, approximating and interpolating schemes. The limit curve of an approximating scheme usually does not pass through the control points of control polygon. As the level of refinement increases, the polygon usually shrinks towards the final limit curve. The interpolating schemes are more attractive than approximating schemes because of their interpolation property. All vertices in the control polygon are located on the limit curve of the interpolation scheme, which facilitates and simplifies the graphics algorithms and engineering designs.
Lian generalized the classical binary 4-point and 6-point interpolatory subdivision schemes to a-ary setting for any integer a ≥ 3. After that, the a-ary 3-point and 5-point interpolatory subdivision schemes for curve design for arbitrary odd integer a ≥ 3 [3,4] were introduced. After that, Lian [5] investigated both the 2m-point, a-ary for any a ≥ 2 and (2m + 1)-point, a-ary for any odd a ≥ 3 interpolatory subdivision schemes for curve design. Ko [6] presented explicitly a new formula for the mask of (2N + 4)-point binary interpolating and approximating subdivision schemes with two parameters. The proposed work presents a new observation about the curve case given by Najma [7]. In this work, we avoid finding the mask of subdivision schemes separately, as a result, its approach is simple and avoids complex computation when deriving subdivision rules.
The rest of the paper is organized as follows. Section 2 gives some preliminaries results and a new relation for (2N + 4)-point n-ary interpolating curve scheme for closed and open polygon to access main result. Section 3 presents the construction for general formula of the surface case using Lagrange interpolating polynomial, and some characteristics are also discussed. In Section 4, we also give some numerical examples for the visual performance of the proposed work. This work also provides some special cases of the classical subdivision schemes.
2. Preliminary Results
Let  be the set of integers and
be the set of integers and 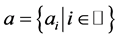 a set of constants. The general form of univariaten-ary subdivision scheme which maps a polygon
a set of constants. The general form of univariaten-ary subdivision scheme which maps a polygon  is defined by
is defined by
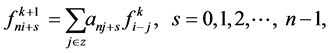 (2.1)
(2.1)
where the set 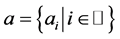 of coefficients is called mask of the subdivision scheme. A necessary condition for the uniform convergence of the subdivision scheme is
of coefficients is called mask of the subdivision scheme. A necessary condition for the uniform convergence of the subdivision scheme is
 (2.2)
(2.2)
Let  be the space of all polynomials of degree
be the space of all polynomials of degree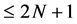 . Where,
. Where, 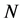 is a non-negative integer. If
is a non-negative integer. If
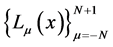 is fundamental Lagrange polynomial corresponding to the nodes
is fundamental Lagrange polynomial corresponding to the nodes  defined by
defined by
 (2.3)
(2.3)
for which
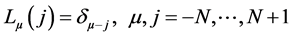
and

where, 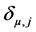 is the Kronecker delta, defined as
is the Kronecker delta, defined as
 (2.4)
(2.4)
Using all the above mentioned identities Ko [6] presented the general formula for the mask of 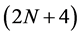 -point binary interpolating symmetric subdivision schemes. After that Najma [7] generalized the result for
-point binary interpolating symmetric subdivision schemes. After that Najma [7] generalized the result for 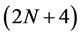 -point n-ary interpolating symmetric subdivision scheme and gave the following formula for the mask of n-ary interpolating schemes.
-point n-ary interpolating symmetric subdivision scheme and gave the following formula for the mask of n-ary interpolating schemes.
 (2.5)
(2.5)
where

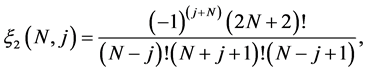
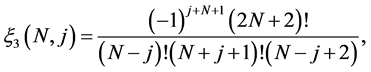
and
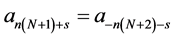 (2.6)
(2.6)
The free parameters 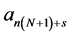 can be explicitly defined as
can be explicitly defined as
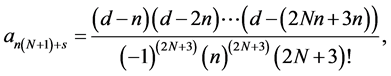
where .
.
Here, n stands for n-ary subdivision scheme (i.e. n = 2(binary), 3(Ternary), 4(quaternary)···),
 . Considering the symmetry of the scheme and construction of the mask formula described above,
. Considering the symmetry of the scheme and construction of the mask formula described above, 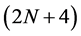 -point interpolating subdivision schemes are presented in the following form
-point interpolating subdivision schemes are presented in the following form
 (2.7)
(2.7)
Here,  with the symmetry condition is
with the symmetry condition is
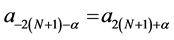
Setting 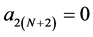 and
and , the mask
, the mask 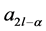 of the schemes comes from the generalized formula for the mask of
of the schemes comes from the generalized formula for the mask of 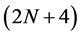 -point interpolating schemes (2.5). Following the procedure of binary case, we have derived the following form of
-point interpolating schemes (2.5). Following the procedure of binary case, we have derived the following form of 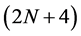 -point ternary interpolating subdivision schemes are presented in the following form
-point ternary interpolating subdivision schemes are presented in the following form
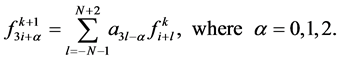 (2.8)
(2.8)
Here, 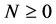 and for the symmetry condition,
and for the symmetry condition, 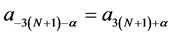
Setting 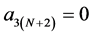 and
and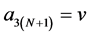 , the mask
, the mask  is calculated from the same mask formula (2.5). In the same way,
is calculated from the same mask formula (2.5). In the same way, 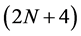 -point quaternary interpolating subdivision scheme has the form
-point quaternary interpolating subdivision scheme has the form
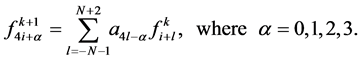 (2.9)
(2.9)
where,  and for the symmetry of the scheme,
and for the symmetry of the scheme,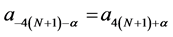 .
.
Setting 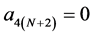 and
and . Finally, from (2.7)-(2.9),
. Finally, from (2.7)-(2.9), 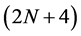 -point n-ary interpolating schemes has the following form
-point n-ary interpolating schemes has the following form
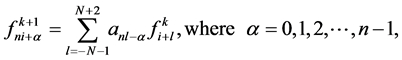 (2.10)
(2.10)
With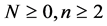 , and for the following symmetry condition
, and for the following symmetry condition
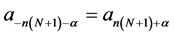 (2.11)
(2.11)
where 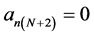 and
and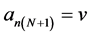 .
.
Construction of the Schemes for Open Polygon
When dealing with open initial polygon 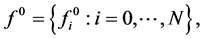 it is not possible to refine the first and last edges by rules (2.10) for interpolating subdivision schemes. However the extension of this strategy to deal with open polygon requires a well-define neighborhood of end points. Since the first and last edges can be treated analogously, it will be sufficient to derive the rules only for one side of the polygon. To this aim define the auxiliary point
it is not possible to refine the first and last edges by rules (2.10) for interpolating subdivision schemes. However the extension of this strategy to deal with open polygon requires a well-define neighborhood of end points. Since the first and last edges can be treated analogously, it will be sufficient to derive the rules only for one side of the polygon. To this aim define the auxiliary point 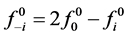 as extrapolatory rule in the initial polygon
as extrapolatory rule in the initial polygon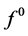 . Then the nonrefined open polygon
. Then the nonrefined open polygon
 can be refined by the rules defined below. The formula described in (2.10) for interpolating scheme is not helpful to refine first and last edges of open polygon. Then to refine the open polygon by
can be refined by the rules defined below. The formula described in (2.10) for interpolating scheme is not helpful to refine first and last edges of open polygon. Then to refine the open polygon by
 -point interpolating scheme using auxiliary points is defined as following
-point interpolating scheme using auxiliary points is defined as following
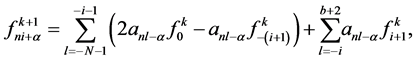 (2.12)
(2.12)
where ,
, 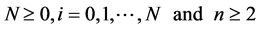 , where, the weights satisfies the same condition (2.11).
, where, the weights satisfies the same condition (2.11).
Example: If an open polygon is refined by using the 6-point ternary interpolating subdivision scheme using (2.10), then two auxiliary points  and
and 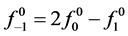 has to be defined in the coarsest polygon
has to be defined in the coarsest polygon
 . The first two edges
. The first two edges  and
and 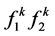 of the nonrefined polygon
of the nonrefined polygon  can be refined by the rules that can be calculated directly by (2.12). Substituting
can be refined by the rules that can be calculated directly by (2.12). Substituting 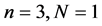 in (2.12),
in (2.12),
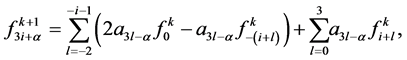
where 
Then, for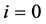 ,
,
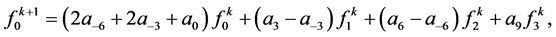
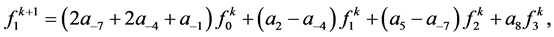

For, 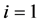

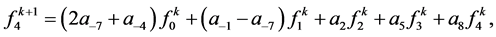

3. Tensor Product of (2N + 4)-Point Interpolating Subdivision Scheme
Given a set of control points 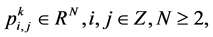 where k is a non-negative integer indicates the subdivision level. n-ary subdivision surface is tensor product of n-ary subdivision curve defined by
where k is a non-negative integer indicates the subdivision level. n-ary subdivision surface is tensor product of n-ary subdivision curve defined by
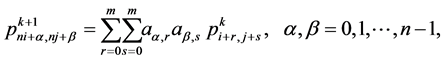 (3.1)
(3.1)
where, 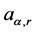 satisfies
satisfies
 (3.2)
(3.2)
Given initial values 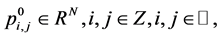 then in the limit
then in the limit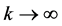 , the process (3.1) defines an infinite set of points in
, the process (3.1) defines an infinite set of points in . The sequence of values
. The sequence of values 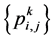 is related, in a natural way, with a diadic mesh points
is related, in a natural way, with a diadic mesh points
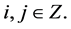
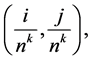 The process then defines a scheme whereby
The process then defines a scheme whereby  replaces the value
replaces the value  at the mesh point
at the mesh point 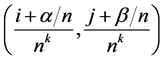 for
for , while the values
, while the values 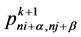 are inserted at the new mesh points
are inserted at the new mesh points 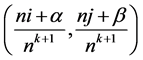 for
for 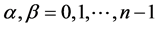 (where α and β are not zero at the same time). Labeling of old and new points is shown in Figure 1, which illustrates subdivision schemes (3.1).
(where α and β are not zero at the same time). Labeling of old and new points is shown in Figure 1, which illustrates subdivision schemes (3.1).
 (a)
(a) (b)
(b) (c)
(c)
Figure 1. Solid lines show one face of coarse polygons whereas dotted lines are refined polygons. (a)-(c) can be obtained by subdividing one face into four, nine and sixteen new faces by using (3.1) for n = 2,3,4 respectively.
Construction
Let 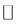 be the set of integers and the space of all polynomials of degrees
be the set of integers and the space of all polynomials of degrees  and
and 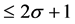 is denoted by
is denoted by 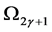 and
and 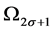 respectively. If
respectively. If 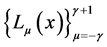 are fundamental Lagrange interpolating polynomials corresponding to the nodes
are fundamental Lagrange interpolating polynomials corresponding to the nodes 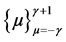 and
and . The Lagrange interpolation polynomial for tensor product case is defined as [1],
. The Lagrange interpolation polynomial for tensor product case is defined as [1],
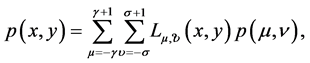
where
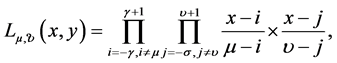 (3.3)
(3.3)

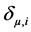 and
and 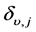 are Kroneker delta symbols defined as,
are Kroneker delta symbols defined as,

and

Here, some important results for the formulation of required form of tensor product scheme can be verified using (2.3). That is for each 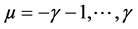 and
and  (Using the result [1]),
(Using the result [1]),

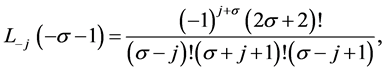

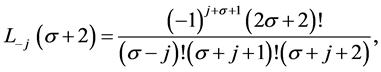
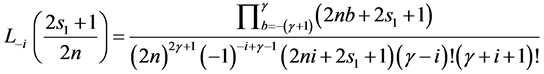
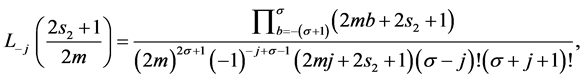
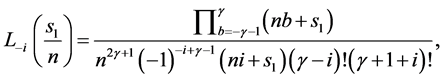

The mask of a subdivision scheme shows the contribution of a single original vertex to each new, subdivided vertex. To find the mask of a scheme, we need to find all ways to get from the origin to each point in the grid. For the tensor product scheme, this is simply the tensor product of the univariate case.
Lemma 3.1. [8] Given initial control polygon ,
,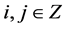 ,let the values
,let the values 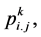
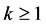 be defined recursively by subdivision process (3.1) together with (3.2) then the scheme derived by tensor product naturally get four-sided support region.
be defined recursively by subdivision process (3.1) together with (3.2) then the scheme derived by tensor product naturally get four-sided support region.
It can be loosely say that the support is the tensor product of the supports of the two regions, just as one can loosely say that Doo-Sabin is the generalization of the tensor product of two Chaikin constructions.
Lemma 3.2. [9] Given initial control polygon 
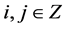 , let the values
, let the values  be defined recursively by subdivision process (3.1) together with (3.2), then if a scheme is derived from a tensor product, then the level of continuity can be determined between pieces by reference to the underlying basis functions, i.e. all the tensor product schemes have the same continuity as their counterparts.
be defined recursively by subdivision process (3.1) together with (3.2), then if a scheme is derived from a tensor product, then the level of continuity can be determined between pieces by reference to the underlying basis functions, i.e. all the tensor product schemes have the same continuity as their counterparts.
The general formula which generates the mask  and
and 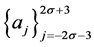 of n-ary approximating schemes presented by [7] is
of n-ary approximating schemes presented by [7] is
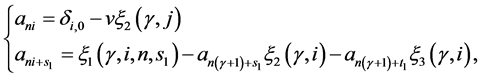 (3.4)
(3.4)
and
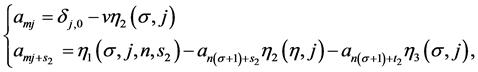 (3.5)
(3.5)
where
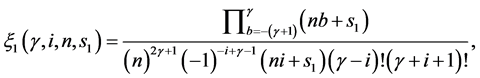
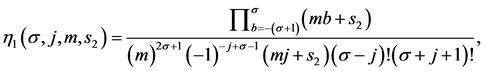
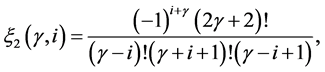
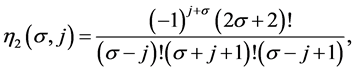
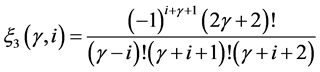

Here, n, m stands for n-ary, m-ary subdivision schemes respectively (i.e n, m = 2(binary), 3(ternary), 4(quaternary)···), 

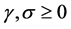 ,
,  ,
,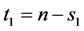 , and
, and 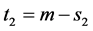
The free parameter 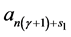 and
and 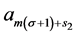 are defined as
are defined as
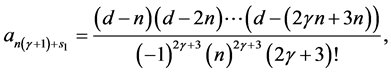 (3.6)
(3.6)
where 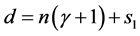 and
and
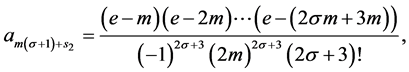 (3.7)
(3.7)
where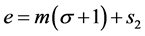 .
.
As each mask 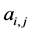 of the refinement rule satisfies
of the refinement rule satisfies , where
, where 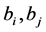 are the mask of univariate subdivision schemes, then
are the mask of univariate subdivision schemes, then
 .
.
The tensor product of 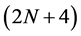 -point interpolating subdivision scheme is presented as,
-point interpolating subdivision scheme is presented as,
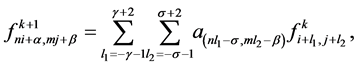 (3.8)
(3.8)
where,  ,
, 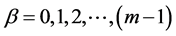 ,
, 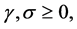 and
and 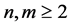 and symmetry conditions are,
and symmetry conditions are,
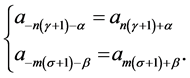 (3.9)
(3.9)
Taking , and the constants
, and the constants 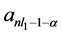 and
and 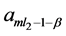 could be evaluated by using the results (3.4) and (3.5).
could be evaluated by using the results (3.4) and (3.5).
Example: Consider the tensor product of the 4-point DD interpolating subdivision scheme, while DD scheme can be calculated using the result (2.5) mentioned in Section 2. The Laurent polynomial of the scheme is given as

This implies
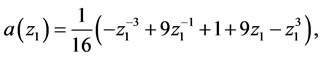

Since,  then, we can obtain the Laurent polynomial of the 4-point tensor product binary interpolating scheme
then, we can obtain the Laurent polynomial of the 4-point tensor product binary interpolating scheme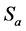 . So that the suggested 4-point tensor product binary interpulating scheme is
. So that the suggested 4-point tensor product binary interpulating scheme is
 (3.10)
(3.10)
Using the result obtained above for the tensor product of interpolatory scheme (3.8), tensor product of 4-point DD scheme can be calculated directly. Since the DD scheme has  continuity, then by lemma (3.2) its tensor product has the same continuity. Substituting
continuity, then by lemma (3.2) its tensor product has the same continuity. Substituting 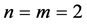 in (3.8) and (3.9),
in (3.8) and (3.9), 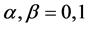 and
and , the symmetry conditions becomes
, the symmetry conditions becomes
 (3.11)
(3.11)
then formula (3.8) attains the form,
 (3.12)
(3.12)
As each mask  of the refinement rule satisfies
of the refinement rule satisfies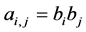 , then
, then

As 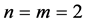 so
so  for both n and m, when
for both n and m, when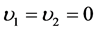 ,
, 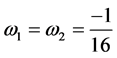 ,
, 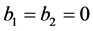 and
and  is substituted in (3.8) and (3.9) our requirement is fulfilled, that is the rules (3.10) are obtained.
is substituted in (3.8) and (3.9) our requirement is fulfilled, that is the rules (3.10) are obtained.
Example: A simple interpolatory subdivision scheme for quadrilateral nets with arbitrary topology is presented by L. Kobbelt [2] which generates  surfaces in the limit. In the first step they present the refinement rules derived by the modification of the well-known Dyn et al. [10] 4-point interpolatory subdivision scheme for curve design. The natural way to define refinement operators for quadrilateral nets is therefore to modify a tensor product scheme such that special rules for the vicinity of non regular vertices are found.
surfaces in the limit. In the first step they present the refinement rules derived by the modification of the well-known Dyn et al. [10] 4-point interpolatory subdivision scheme for curve design. The natural way to define refinement operators for quadrilateral nets is therefore to modify a tensor product scheme such that special rules for the vicinity of non regular vertices are found.
The modified form of Dyn scheme can be evaluated by setting the value of n = 2, N = υ  = 0,
= 0,  and
and 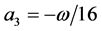 (where
(where ) in (2.10) and (2.11), the following refinement rules are obtained
) in (2.10) and (2.11), the following refinement rules are obtained
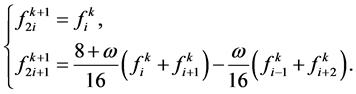 (3.13)
(3.13)
They used the simple tensor product as the basis for the modification of refinement rules of irregular quadrilateral nets. Since it is interpolating scheme, so 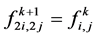 and the edge points
and the edge points  and
and 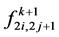 are given as,
are given as,

Finally, the face point 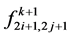 is,
is,
 (3.15)
(3.15)
Instead of taking the tensor product the above rules can be directly obtained by substituting 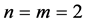 in (3.8) and (3.9), then
in (3.8) and (3.9), then 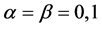 and
and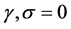 , the symmetry conditions are then written as,
, the symmetry conditions are then written as,
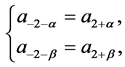 (3.16)
(3.16)
then the formula (3.8) acquires the form,
 (3.17)
(3.17)
At each mask  of the refinement rule satisfies
of the refinement rule satisfies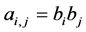 , then
, then
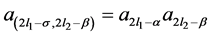
Using the result (3.4) and (3.5) the constants 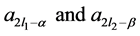 are evaluated by substituting
are evaluated by substituting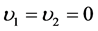 ,
, 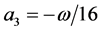 ,
, 
 and
and 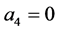 for both n and m. After substituting the weights in (3.17) we get the same rules (3.14) and (3.15).
for both n and m. After substituting the weights in (3.17) we get the same rules (3.14) and (3.15).
Example: Using the results for the interpolating curve subdivision schemes (2.10) the 4-point interpolatory scheme [3] is obtained. Further here the tensor product of the scheme is evaluated by using the result (3.8).
Put 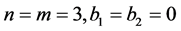 in (3.8),
in (3.8),
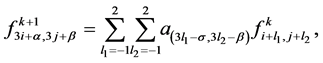 (3.18)
(3.18)
Also, from (3.9)

Taking ,
, 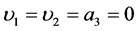 ,
, ,
,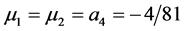 . Also for interpolatory scheme
. Also for interpolatory scheme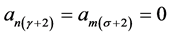 , as
, as 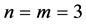 gives
gives 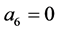 for both n and m.
for both n and m.
After calculating the mask from (3.4) and (3.5) and substituting all the results in equation (3.18) following 4-point ternary interpolating tensor product scheme is obtained
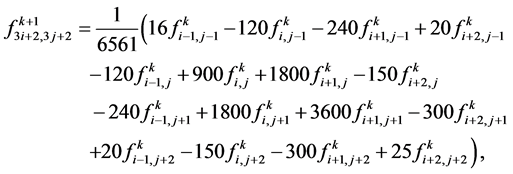 (3.19)
(3.19)
4. Numerical Examples
Here, the performances of some of the schemes which are deduced from the proposed formula are shown. Figure 2 shows the tensor product of 4-point ternary interpolating scheme (3.19), and Figure 3 gives the performance of the proposed 4-point binary scheme (3.10).
NOTES
*Corresponding author.