Fast Fading Channel Neural Equalization Using Levenberg-Marquardt Training Algorithm and Pulse Shaping Filters ()
1. Introduction
It is well known that the mobile communication system performance is degraded by thermal noise, Intersymbolic Interference (ISI) and fading. Assuming that the thermal noise is Additive White Gaussian Noise (AWGN channel), its effects can be minimized using matched filter at the receiver and equalizers can be employed to combat ISI effects and fading. Most papers in the scientific literature deal with time-invariant channels, but nowadays the majority of channels are time-variant, which diminish system performance and their effects are difficult to mitigate. Recent works [1-3] analyse systems involving slow fading channels but do not propose robust solutions to fast fading.
Artificial Neural Network (ANN) has been largely used in equalization problems where equalizers based on perceptrons are applied to improve performance of some nonlinear channels [4,5]. In the present paper, two independent recurrent perceptrons are applied, separating the processing of real and imaginary parts of the signal, providing a more accurate solution by avoiding the approximation  present in previous works [6,7] and analysed by [8].
present in previous works [6,7] and analysed by [8].
The Recurrent Neural Network (RNN) proposed in [1] and [2] cannot cope with fast fading channels. The first one presents a slow convergence rate due to complexity of its structure, which leads to high computational cost, whereas the second one has a training algorithm capable of producing convergence instability. It is well known that Gauss-Newton (GN) algorithm, proposed in [2] for training ANN, is a quasi-Newton optimization method that does not guarantee convergence. This may raise some concerns when it is applied to severe time-variant channels.
To reduce the unstable behavior of the GN algorithm, in this work we propose to use the Levenberg-Marquardt (LM) approach, a well-known modification of the GN algorithm, which includes the convergence guarantee of Gradient techniques. However, the replacement of algorithm is not enough to solve the fast fading equalization problem, and other subsystems must be added to the transmitter and receiver front-ends in order to improve signal quality, before being processed by the equalizer (Figure 1). In practical mobile communication systems, a matched filter is usually employed to accomplish this task, but here we decide to include a pulse shaping filter, which behaves like a matched filter in base band. The results presented here show that this filter helps reduce the ISI and AWGN distortion effects on the signal before being treated by the equalizer. Using both approaches, it is possible to better equalize fast fading channels and outperform systems such as those presented in [1,2], usually applied to slow fading channels.
2. System Modeling
In practical communications systems, it is necessary to implement a scheme capable of mitigate signal distortions caused by ISI and AWGN in fading channels. In this work the proposed scheme is composed by an equalizer and a pulse shaping filter that together can deal better with distortions in 4-QAM signals. The equalizer is a RNN with two perceptrons, each one as proposed in [2], and a pulse shaping filter is added to limit the transmitted/received signal and noise bandwidth. In our understanding, the equalizer alone is not sufficient to accomplish a better equalization of fast fading channels.
The proposed RNN equalizer is equivalent to a Decision Feedback Equalizer (DFE) based on perceptrons and implemented with parameters m = 3, n = 2 and d = 2 [1]. The DFE is a kind of nonlinear equalizer that uses a feedback filter with n inputs together with a forward filter with m inputs. It means that the previous symbols decisions are taken into account in the current symbol estimation, with a time delay d between the current and the last estimated symbol. A DFE is generally applied for channel with severe ISI.
The activation function chosen for the DFE-LM training is the hyperbolic tangent function, whereas the hard decision sign function is implemented during testing. The present work does not use the well-known approximation  which leads to errors in the synaptic weight updating. To improve the accuracy, the tanh function was implemented separating
which leads to errors in the synaptic weight updating. To improve the accuracy, the tanh function was implemented separating
the real and imaginary parts of 4-QAM symbols.
3. Pulse Shaping
At the transmitter, it changes the signal shape by using a raised cosine filter which limits the pulse spectral components. The roll-off factor defines the transmitted signal bandwidth. Roll-off factor of 0.2, which was chosen by trial and error, provided the best system perform.
On the order hand, the Pulse Shaping filter limits the amount of the noise spectrum that is passed on to next stages at the receiver and correlates the transmitted and received signals. In this paper were consider two samples per symbol, the minimum amount to allow the pulse shaping filter to work properly and make possible to reach higher transmission rates.
4. Learning Algorithm
A GN algorithm modification, proposed by LevenbergMarquardt, is implemented in this work to update the synaptic weights during the DFE-LM training. In the LM algorithm the synaptic weights are updated according to Equation (1).
 (1)
(1)
The LM differs from GN algorithm by the λI term.
The new term improves the convergence stability of the GN algorithm. The λ factor must increase in Equation (1) as the error e(k) increases, making the algorithm behaves like a Gradient algorithm. If the error decreases for each update step, then the λ factor must decrease in Equation (1) as well, leading to a GN type solution. There is a trade-off between convergence assurance of the Gradient algorithm and fast convergence rate of the GN algorithm.
The error is a function of several local minima. Sometimes, after the training phase, the algorithm converges to a set of weights that does not satisfy an acceptable Bit Error Rate (BER). To avoid this possibility, we decided to introduce, in the algorithm, a BER evaluation before start the test phase. If the BER is greater than a threshold, then the algorithm initial value is changed and the training phase is run again. This approach enables the algorithm to escape from local minimum solutions and allow it to carry on searching for a better minimum, capable of satisfying the best BER requirement.
5. Channel Model
The system performance was evaluated over different time-variant channels, modeled by the transfer function in Equation (2).
 (2)
(2)
When 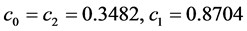 and
and  the transfer function H(z) becomes a typical fixed channel recommended by ITU for simulations. This type of channel has been largely used in literature [9,10] and it is considered as a nonminimum-phase linear channel that causes severe distortions to communication signals. The time-variant coefficients have been proposed in [1,2] to make the fixed channel behaves like time-variant one. These time-variant coefficients are generated in such way to be statistically independents, as proposed in [11].
the transfer function H(z) becomes a typical fixed channel recommended by ITU for simulations. This type of channel has been largely used in literature [9,10] and it is considered as a nonminimum-phase linear channel that causes severe distortions to communication signals. The time-variant coefficients have been proposed in [1,2] to make the fixed channel behaves like time-variant one. These time-variant coefficients are generated in such way to be statistically independents, as proposed in [11].
The time-variant coefficients are independently generated by passing white noise signal through a low pass second-order Butterworth filter, with normalized cut-off frequency at 0.1 [11].
6. Performance Evaluation
Figure 2 shows the BER versus Signal-to-Noise Ratio (SNR) performance for the proposed DFE-LM and other equalizers. All of them have been evaluated over the channel model (Equation (2)) with standard deviation coefficient (σ) of 0.1, using 400 symbols for training and 400,000 for testing. Each BER waterfall curve is the result of an average over 10 statistically independent trials, keeping frozen the weights during test phase. The DFE-LM presented the best performance for lower SNR, whereas the DFE-GN and DFE-UKF outperformed it at higher SNR, which may suggest a failure of the DFE-LM algorithm to cope with this situation. However, this behavior may be explained by the presence of pulse shaping filters at receiver and transmitter ends, which lead to larger noise power reduction in low signal-to-noise ratios.
It may seem unfair compare systems with different structures. The pulse shaping filters could improve the DFE-EKF and DFE-UKF results, but due to its high computational cost, they do not seem to be suitable for mitigation of fast fading channel ISI in practical applications. Furthermore, the GN algorithm convergence issues cannot be solved by adding the pulse shaping filter.
Finally, Figure 3 shows the performance of the DFE-

Figure 2. Performance comparison for different DFE equalizers.

Figure 3. DFE-LM behavior for different channel conditions.
LM over the channel model (Equation (2)) with coefficient standard deviation 0.1, 0.3 and 0.5, keeping the same simulations conditions described before. The BER performances are acceptable even for channels with standard deviation of 0.5 (fastest fading) and SNR of 6dB. This last result shows that the proposed equalization system is a promising alternative to deal with a severe fast fading channel ISI.
Both of Figures 2 and 3 show the recurrent neural structures performance applied to the equalization problem. From the literature [12], it is known that recurrent neural architectures are suitable to deal with channels with deep spectral nulls. The results suggest that smaller neural structures outperform the complex ones in fast fading channels equalization problem. These results may be explained by the overfitting problem in bigger structures [13,14], which present a greater number of parameters than the necessary. The fit of the parameters to track the signal, which vary rapidly, is a hard work in bigger structures, like the DFE-EKF or DFE-UKF.
7. Conclusion
A RNN based on the DFE structure was proposed to mitigate 4-QAM signal distortions over fading channels. A pulse shaping filter was added to overcome the equalizer limitations in this task. The synaptic weights were updated during the training phase by the LM algorithm. The approach was evaluated in traditional time-varying channels mentioned in the literature, and the signal was submitted to different levels of fading. The proposed structure has been able to deal with severe time-varying conditions and outperform previous works [1,2] in low SNR.