Influence of initial molecular substance on the diffusion flux across cell membranes ()
1. INTRODUCTION
A diffusion process has been one of the most interesting processes in physical sciences since the diffusion provides physical insights into the flux variation in various scientific areas, such as biology, chemistry, mathematics, and physics. In biological fields, the diffusion process is used in animal dispersal, bacteria motion, cell movement, chemical diffusion such as drug release in membrane and tissues, and plant electrophysiology [1-8]. Especially, the theory of transport into or out of a cell by the intra-cellular diffusion has received considerable attention since this process has wide applications in biological sciences. It has been shown that the diffusion in the human body is noteworthy over small distance scales on the order of  and the diffusion plays an important role in the metabolic activity [9]. It has been also shown that the diffusion phenomena in cells would be strongly biased by the influence of environments. Hence, it is expected that the diffusion in a cell membrane involving double lipid layers would be significantly influenced by the location of the initial location of a molecular solute. Thus, in this paper we investigate the influence of initial placement of molecular substance on the diffusion fluxes at outer walls of the cell membrane by using the theoretical analysis with the boundary conditions since the diffusion processes are significant for the characterization of cellular and physiological processes and for the operation of biomedical machines [10], such as the heart-lung bypass device, kidney dialysis device, and membrane oxygenator. The diffusion fluxes and recovery curves in the cell membrane are obtained by considering the single-spot and double-spot concentrations, respectively, inside the cell membrane. The influence of initial location of the concentration inside the cell membrane on the net diffusion fluxes at the outer walls of the cell membrane is also discussed.
and the diffusion plays an important role in the metabolic activity [9]. It has been also shown that the diffusion phenomena in cells would be strongly biased by the influence of environments. Hence, it is expected that the diffusion in a cell membrane involving double lipid layers would be significantly influenced by the location of the initial location of a molecular solute. Thus, in this paper we investigate the influence of initial placement of molecular substance on the diffusion fluxes at outer walls of the cell membrane by using the theoretical analysis with the boundary conditions since the diffusion processes are significant for the characterization of cellular and physiological processes and for the operation of biomedical machines [10], such as the heart-lung bypass device, kidney dialysis device, and membrane oxygenator. The diffusion fluxes and recovery curves in the cell membrane are obtained by considering the single-spot and double-spot concentrations, respectively, inside the cell membrane. The influence of initial location of the concentration inside the cell membrane on the net diffusion fluxes at the outer walls of the cell membrane is also discussed.
This paper is composed as follows. In Section 2, the diffusion equation in the cell membrane with the detailed initial and boundary conditions and the Danckwert’s method for the diffusion-reaction equation are discussed. In Section 3, we obtain the solutions of the diffusion equation for the single-spot and double-spot concentrations inside the cell membrane and the recovery curves for both single-spot and double-spot concentrations. In Section 4, we obtain the net flues at the wall boundary for the single-spot and double-spot concentrations inside the cell membrane. In Section 5, the influence of initial placement of molecular substance on the diffusion fluxes at outer walls of the cell membrane is discussed. In addition, we discuss the variations of the concentrations and recovery curves inside the cell membrane. Finally, the conclusions are given in Section 6.
2. DIFFUSION IN THE CELL MEMBRANE
From Fick’s first and second equations for the flux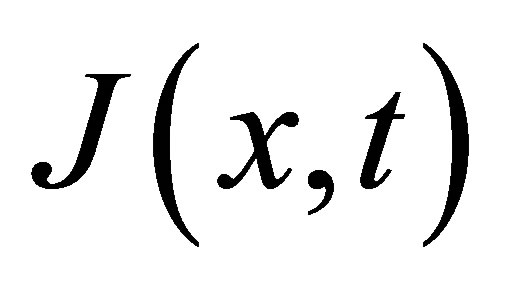 , the diffusion equation [5] for the concentration
, the diffusion equation [5] for the concentration 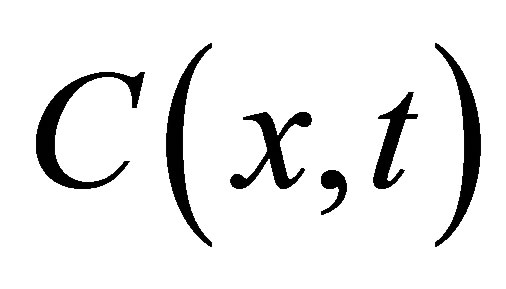 in the cell membrane is represented by
in the cell membrane is represented by
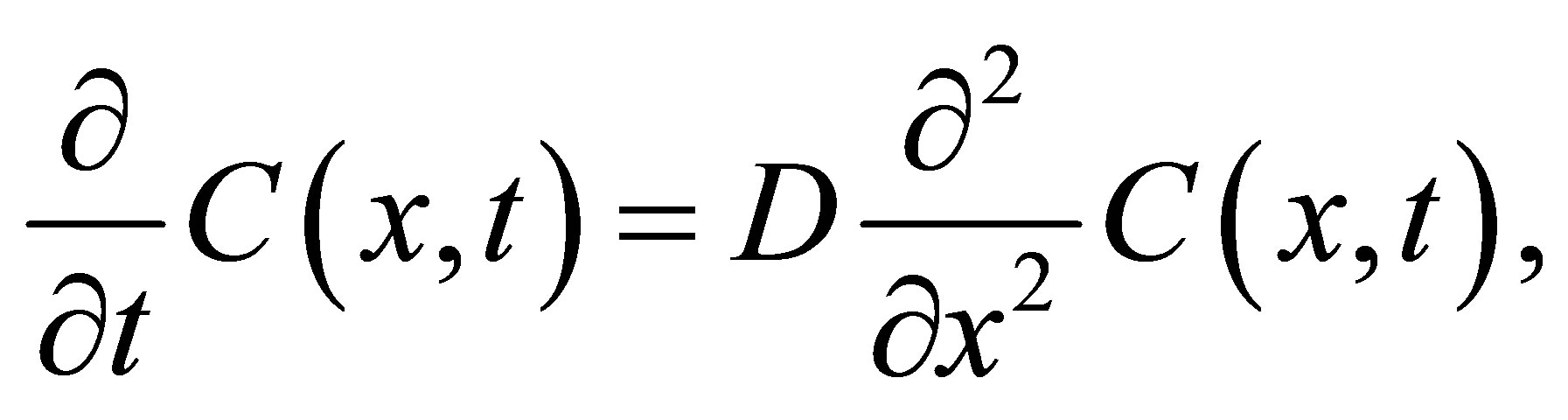 (1)
(1)
where x is the position in one-dimension, t is the time, and D is the diffusion coefficient. It is known that a typical value of the diffusion coefficient for ions such as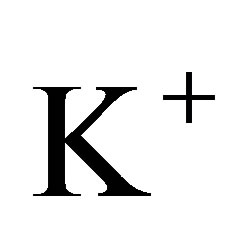 ,
,  , and
, and 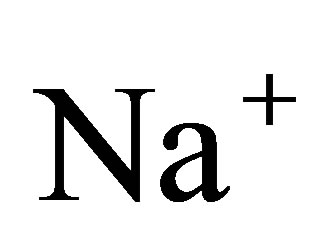 is about
is about 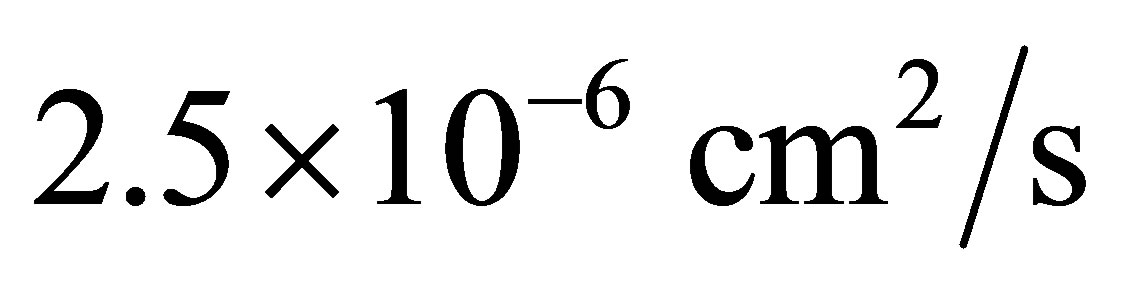 [11]. For the sake of the simplicity, we consider the one-dimensional diffusion problem for the investigation of the diffusion fluxes across cell membranes. In Equation (1), we retain only the diffusive flux term, but neglect the electrical drift effect since the influence of initial placement of molecular or ion substance on the diffusion fluxes at outer walls of the cell membrane is the main purpose of this work. Hence, we assume that the cell membrane has been localized in the domain of
[11]. For the sake of the simplicity, we consider the one-dimensional diffusion problem for the investigation of the diffusion fluxes across cell membranes. In Equation (1), we retain only the diffusive flux term, but neglect the electrical drift effect since the influence of initial placement of molecular or ion substance on the diffusion fluxes at outer walls of the cell membrane is the main purpose of this work. Hence, we assume that the cell membrane has been localized in the domain of 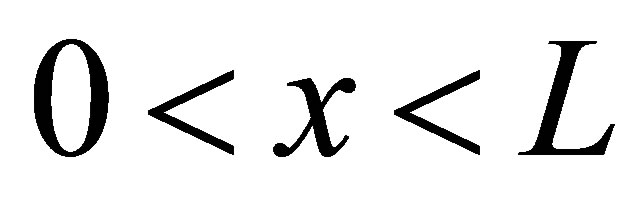 and the molecular concentrations at the domain boundaries as the boundary conditions are
and the molecular concentrations at the domain boundaries as the boundary conditions are 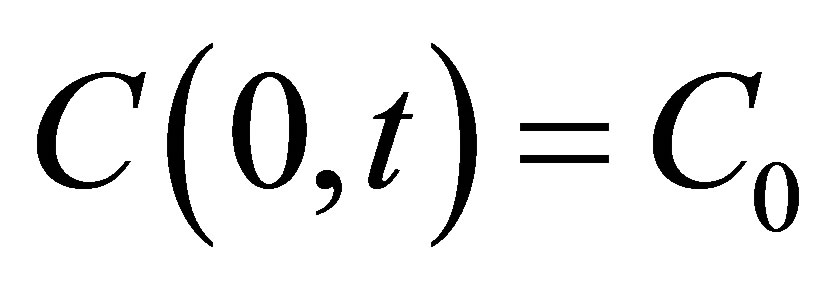 and
and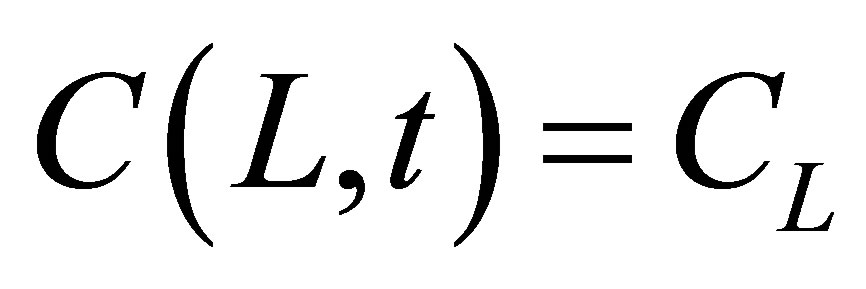 . Two cases for the initial intracellular concentration as the initial conditions shall be considered:
. Two cases for the initial intracellular concentration as the initial conditions shall be considered: 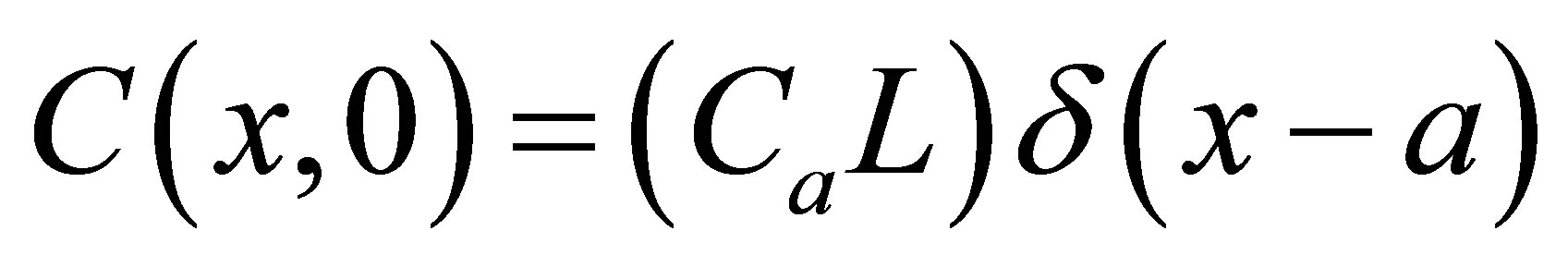 for the single-spot concentration case and
for the single-spot concentration case and 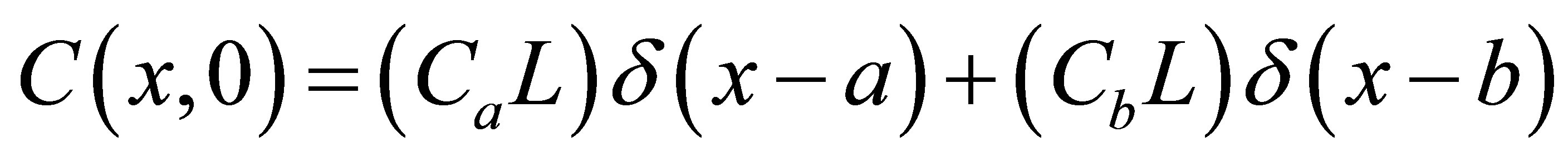 for the double-spot concentration case, where
for the double-spot concentration case, where 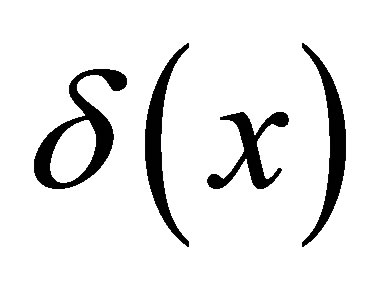 is the Dirac delta function and a and b are initial locations of the molecular concentrations. If the reaction phenomenon is involved in the diffusion process, the righthand side of Equation (1) would have an extra term proportional to the concentration:
is the Dirac delta function and a and b are initial locations of the molecular concentrations. If the reaction phenomenon is involved in the diffusion process, the righthand side of Equation (1) would have an extra term proportional to the concentration: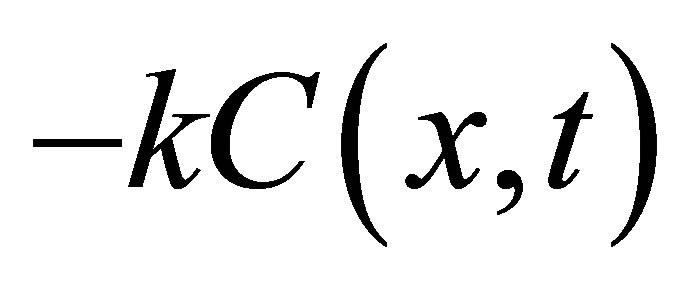 , where k is a constant. In this case, the diffusion-reaction equation in the cell membrane is given by
, where k is a constant. In this case, the diffusion-reaction equation in the cell membrane is given by
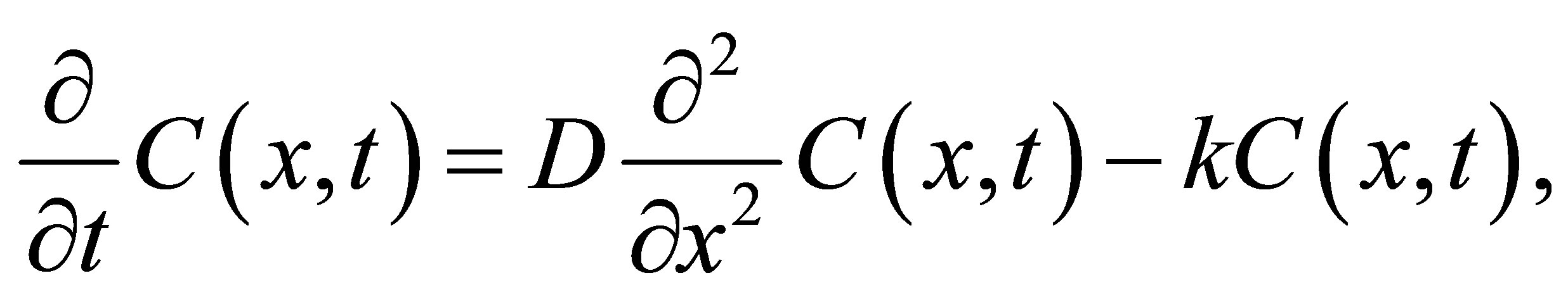 (2)
(2)
where 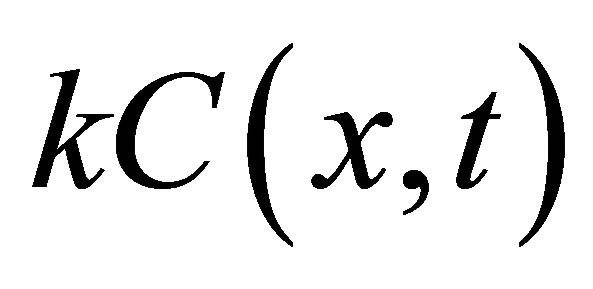 represents the rate of removal of diffusing substance. It has been also shown that the diffusion-reaction equation is useful for the mathematical modeling of glioma growth and also for the investigation on the spreading of brain tumors [12] and
represents the rate of removal of diffusing substance. It has been also shown that the diffusion-reaction equation is useful for the mathematical modeling of glioma growth and also for the investigation on the spreading of brain tumors [12] and 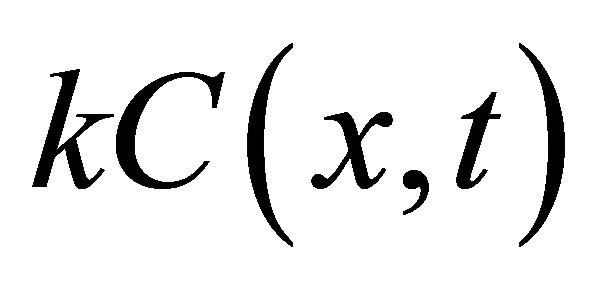 term corresponds to the death of cells in the tumor growth model. It has been well known that the general solution of Equation (2) can also be obtained the following transformation based on Danckwert’s method [13, 14]:
term corresponds to the death of cells in the tumor growth model. It has been well known that the general solution of Equation (2) can also be obtained the following transformation based on Danckwert’s method [13, 14]:
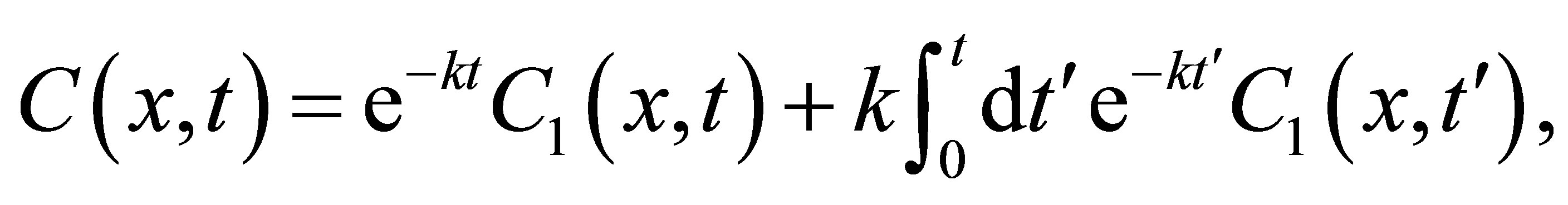 (3)
(3)
where 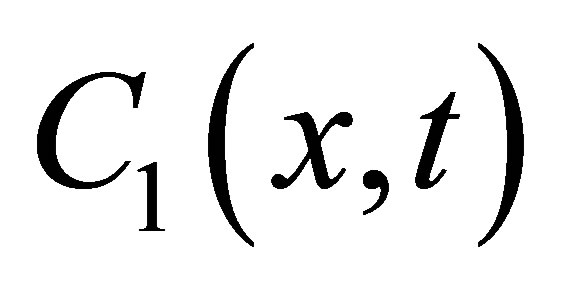 is the solution of Equation (1) with the same boundaries. As a result, the standard diffusion equation, Equation (1), is used to examine the change in diffusion fluxes at outer walls of the cell membrane depended the initial molecular substance. In the following Section III, the solutions,
is the solution of Equation (1) with the same boundaries. As a result, the standard diffusion equation, Equation (1), is used to examine the change in diffusion fluxes at outer walls of the cell membrane depended the initial molecular substance. In the following Section III, the solutions, 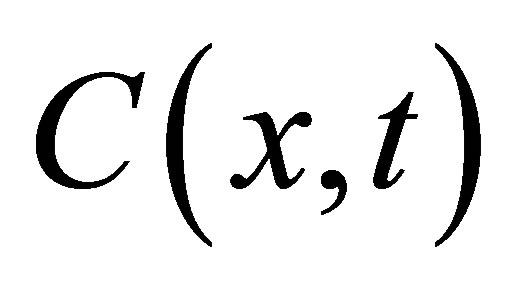 for the single-spot and for the double-spot concentrations inside the cell membrane are discussed.
for the single-spot and for the double-spot concentrations inside the cell membrane are discussed.
3. SINGLE-AND DOUBLE-SPOT CONCENTRATIONS
Using the separation of variables method, the solution of the diffusion equation for the domain 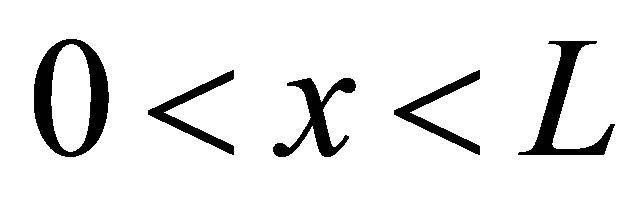 would be represented by
would be represented by
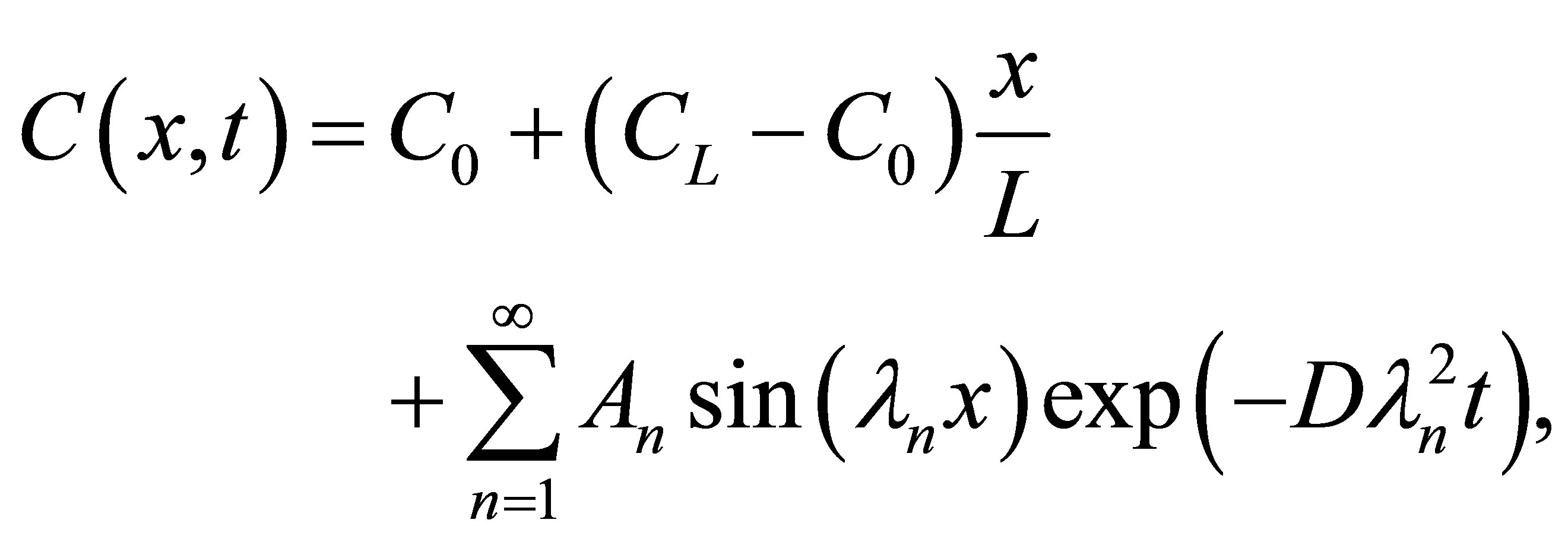 (4)
(4)
where 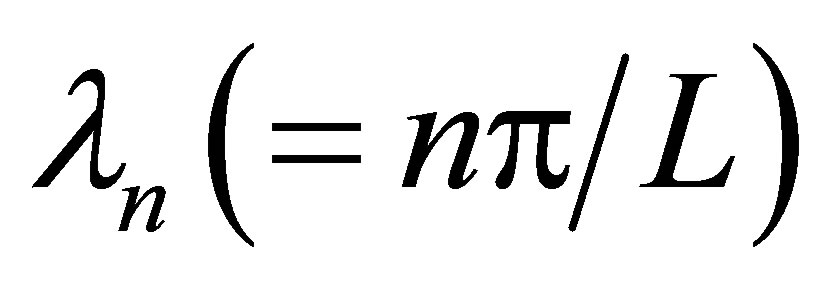 is the separation constant determined by the boundary condition at
is the separation constant determined by the boundary condition at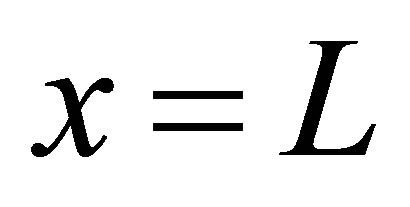 ,
, 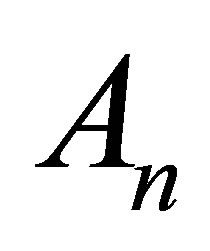 are coefficients to be determined by the initial condition at
are coefficients to be determined by the initial condition at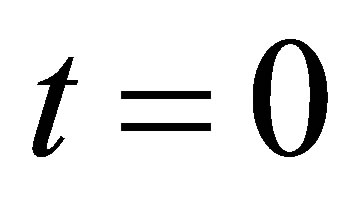 , and the first two terms
, and the first two terms 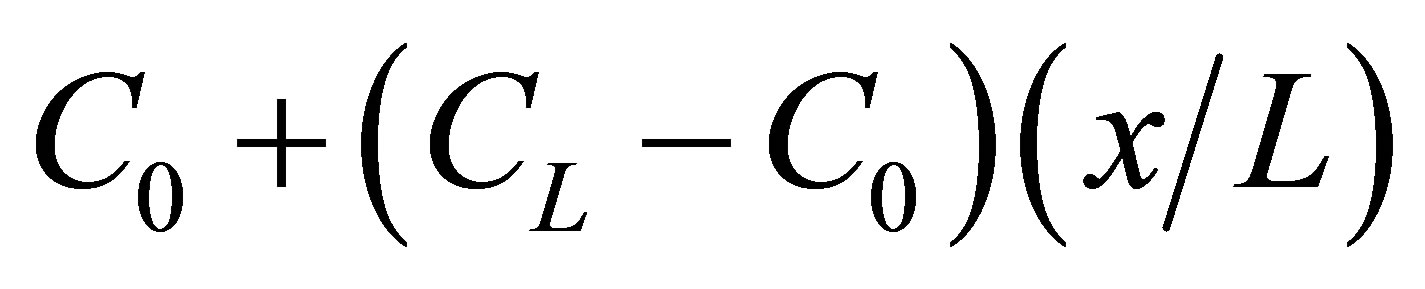 represents the solution when the separation constant is zero. Since we are interested in the effect of the initial molecular concentration
represents the solution when the separation constant is zero. Since we are interested in the effect of the initial molecular concentration 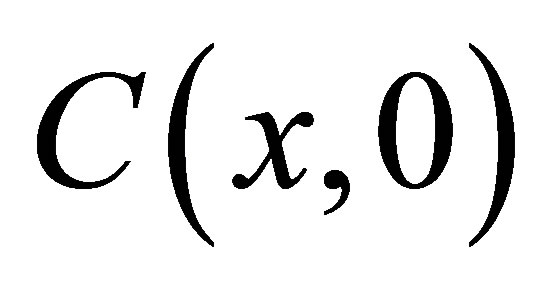 inside the cell membrane, the coefficients
inside the cell membrane, the coefficients 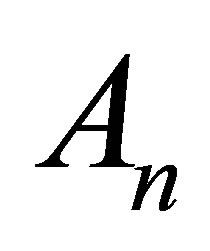 are determined by
are determined by
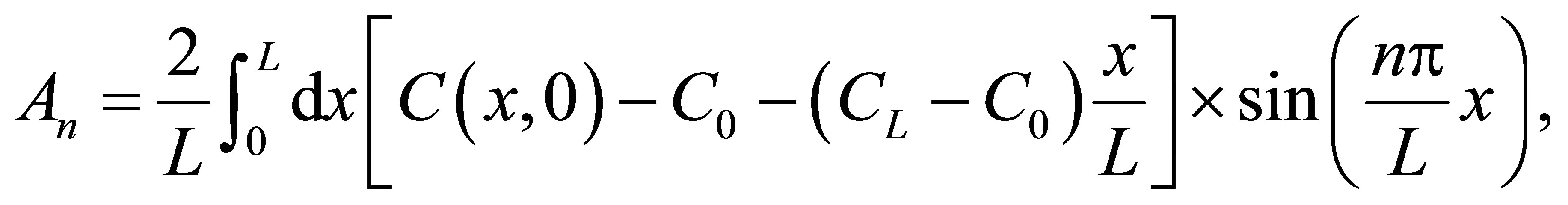 (5)
(5)
where  would be, respectively,
would be, respectively, 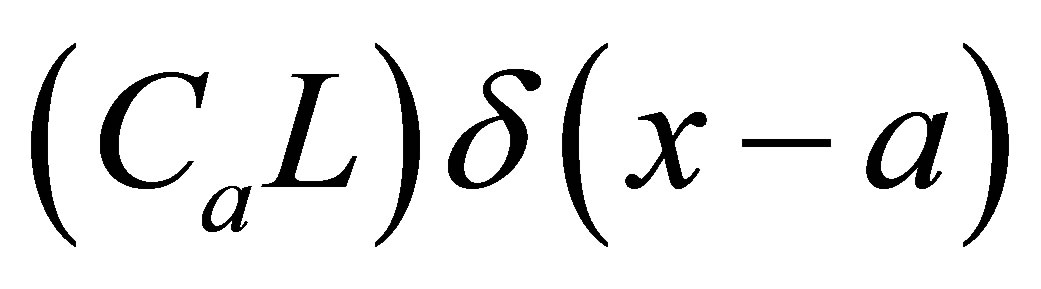 for the single-spot concentration and
for the single-spot concentration and
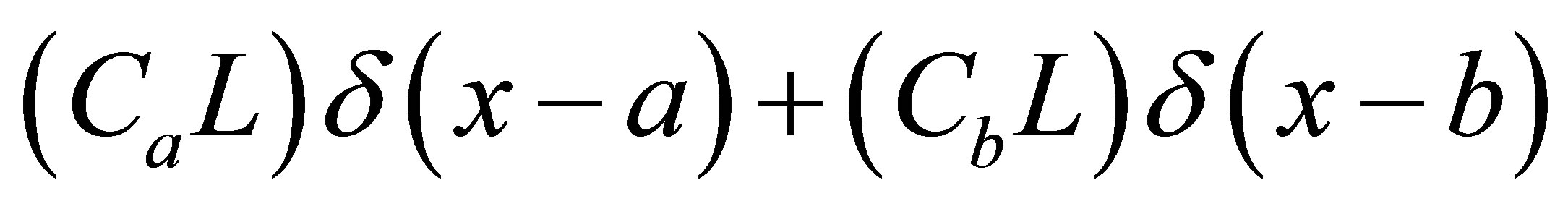 for the double-spot concentrations with
for the double-spot concentrations with  and
and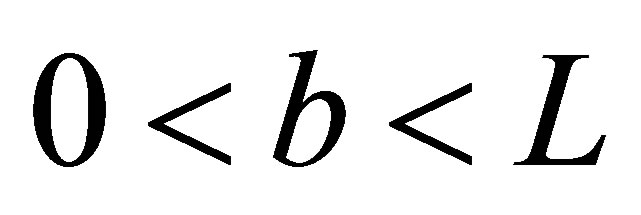 . The consideration of the initial concentration inside the cell membrane would be also quite useful to understand the behavior of the tumor growth since it has been known that the spatial arrangement effect is crucial for the spatial spread of the cancerous cells and also for the appearance of the tumor in the human body [12]. Hence, the general solutions for the diffusion equations with the singleand double-spot concentrations are, respectively, found to be the following forms:
. The consideration of the initial concentration inside the cell membrane would be also quite useful to understand the behavior of the tumor growth since it has been known that the spatial arrangement effect is crucial for the spatial spread of the cancerous cells and also for the appearance of the tumor in the human body [12]. Hence, the general solutions for the diffusion equations with the singleand double-spot concentrations are, respectively, found to be the following forms:
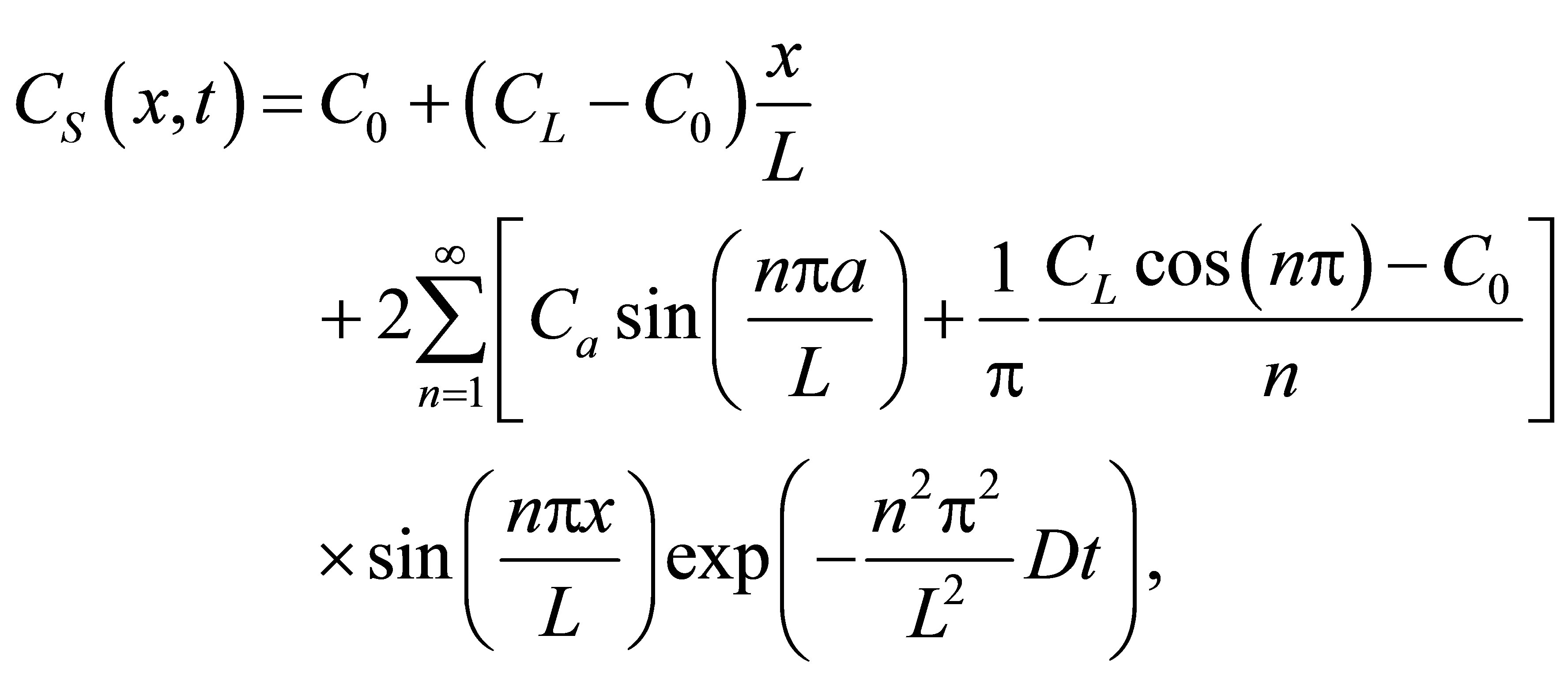 (6)
(6)
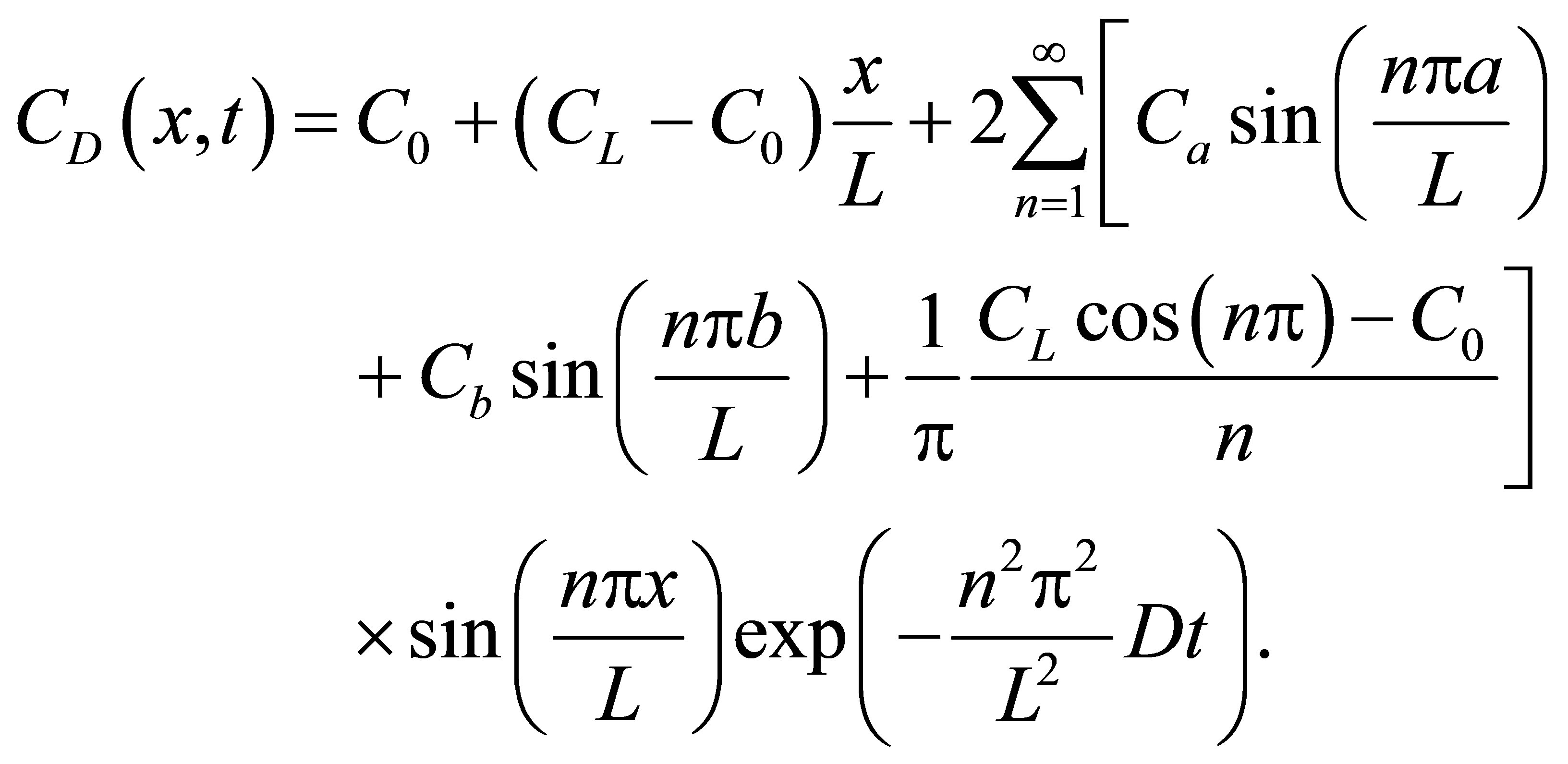 (7)
(7)
Once the concentration function 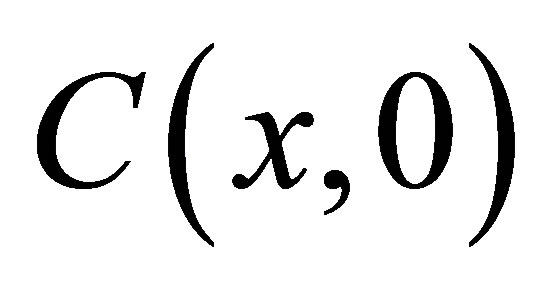 is obtained, the measurement of the concentration fluctuations would be determined by the signal correlation function
is obtained, the measurement of the concentration fluctuations would be determined by the signal correlation function 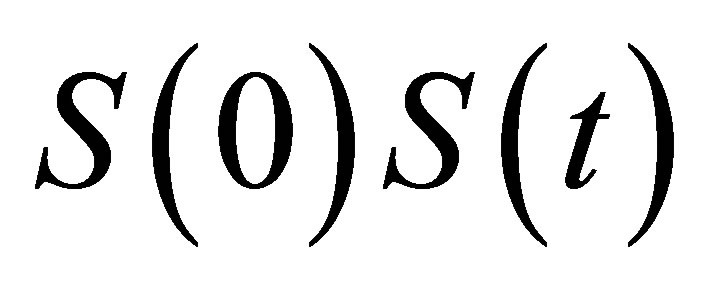 between the time at
between the time at 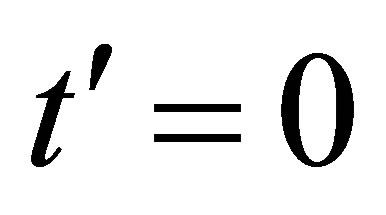 and
and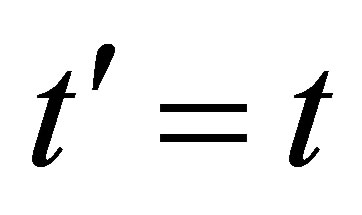 , where
, where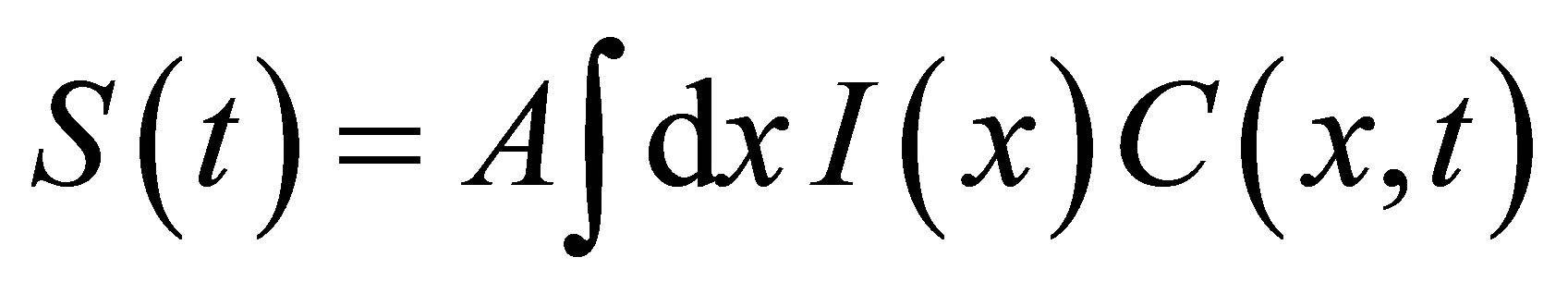 , A is a factor related to the experimental detection, and
, A is a factor related to the experimental detection, and 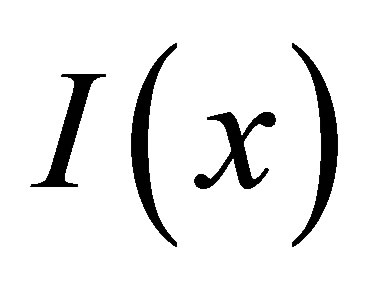 is the intensity of the laser beam [15]. A detailed investigation on the correlation spectroscopy for the influence of initial placement of molecular or ion substance on the concentration fluctuations will be treated elsewhere. The recovery curves for the single-spot
is the intensity of the laser beam [15]. A detailed investigation on the correlation spectroscopy for the influence of initial placement of molecular or ion substance on the concentration fluctuations will be treated elsewhere. The recovery curves for the single-spot  and two-spot
and two-spot 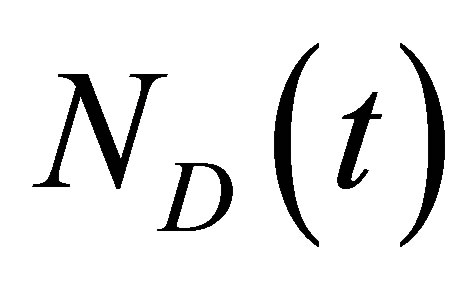 concentrations are then, respectively, obtained as follows:
concentrations are then, respectively, obtained as follows:
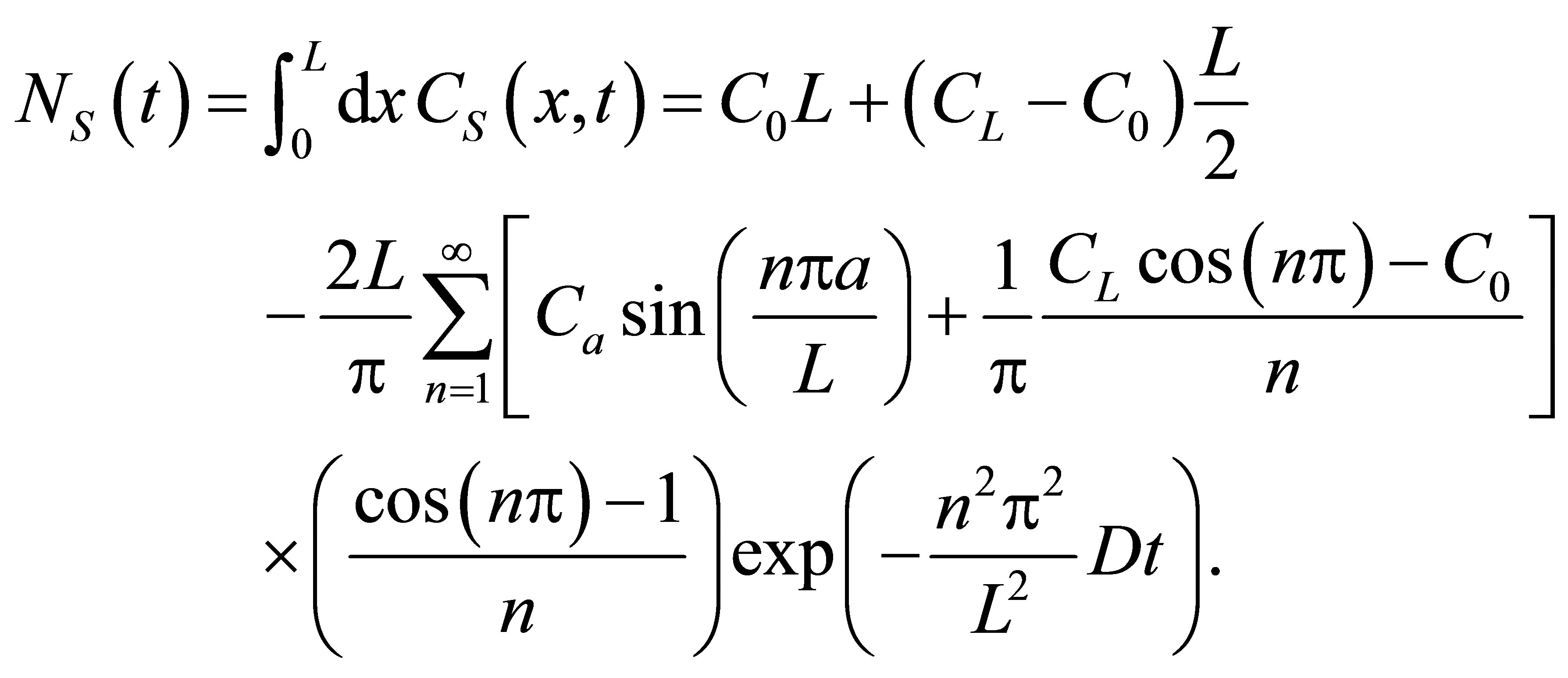 (8)
(8)
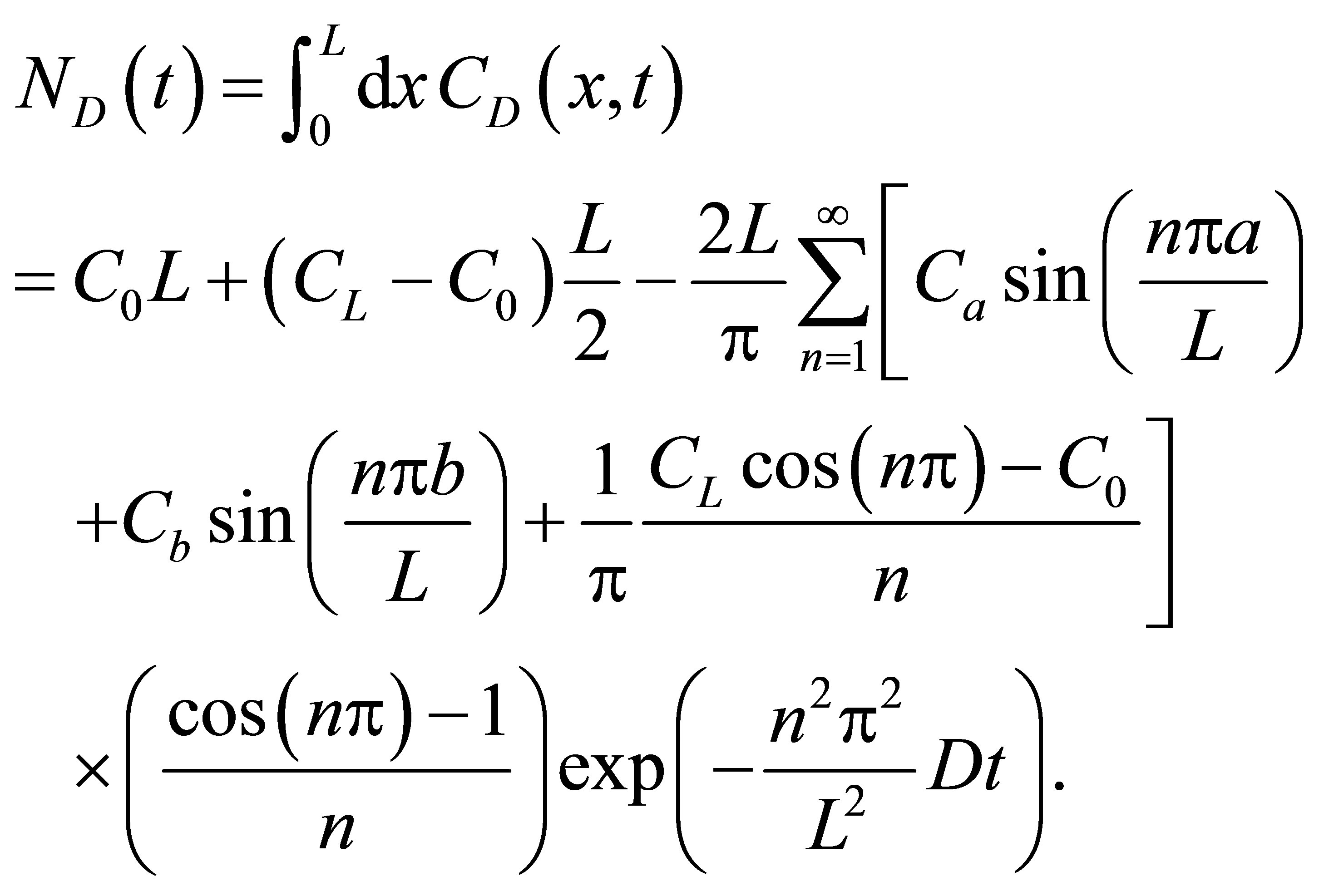 (9)
(9)
4. NET DIFFUSION FLUX IN THE CELL MEMBRANE
The diffusion fluxes at the wall boundaries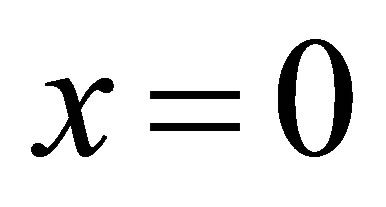 , i.e.,
, i.e., 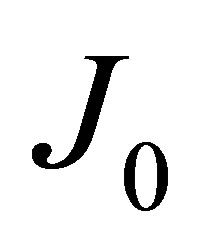 , and
, and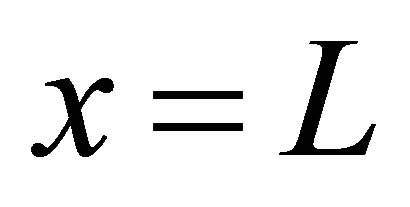 , i.e.,
, i.e., 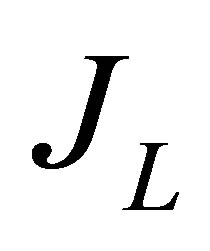 , for the case of the single-spot concentration are, respectively, given by
, for the case of the single-spot concentration are, respectively, given by
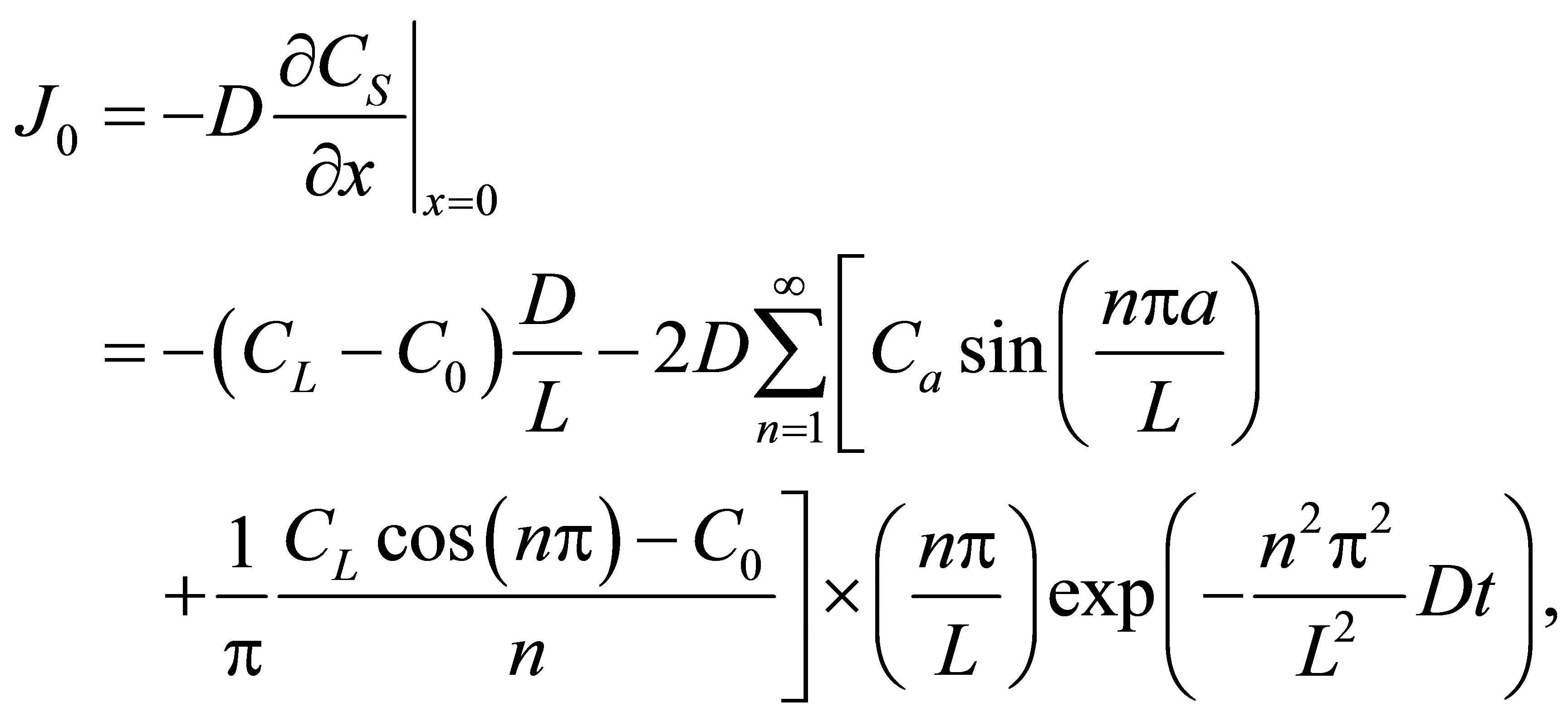 (10)
(10)
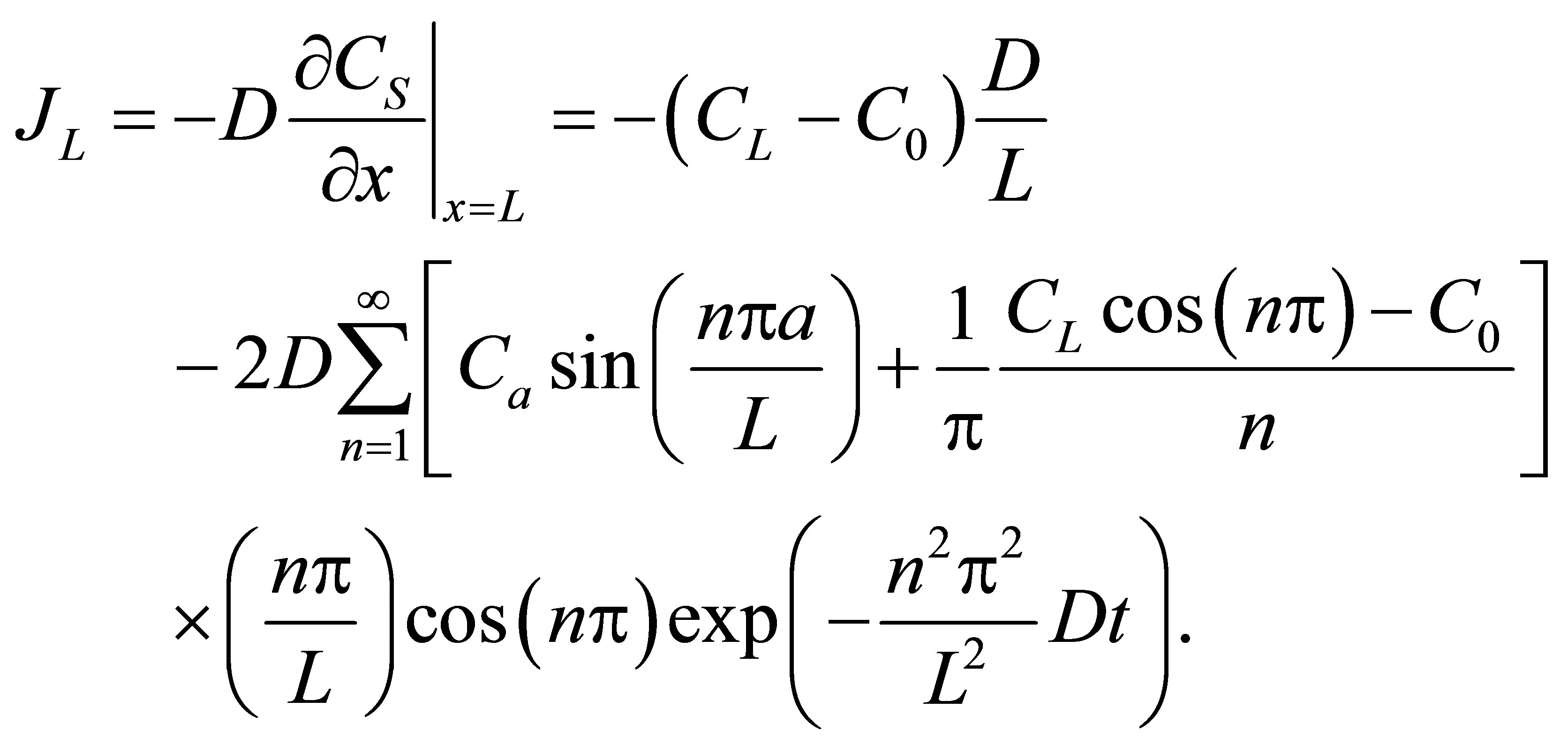 (11)
(11)
If we retain on the first term in the series, the net flux 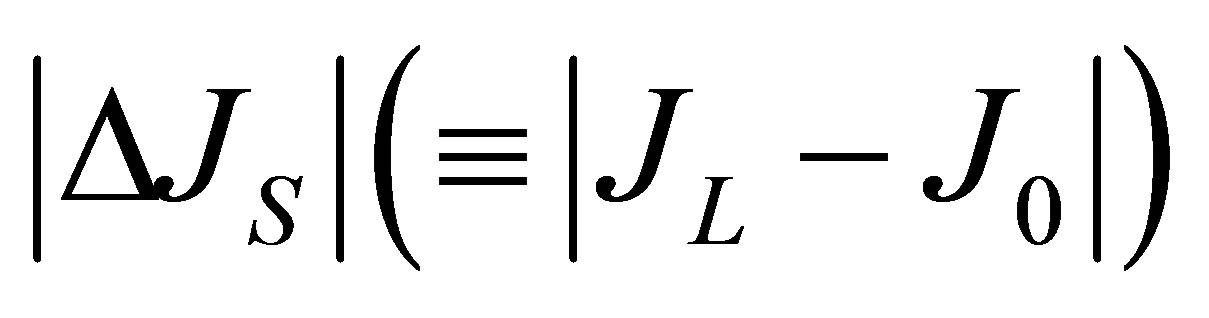 for the single-spot concentration is then found to be
for the single-spot concentration is then found to be
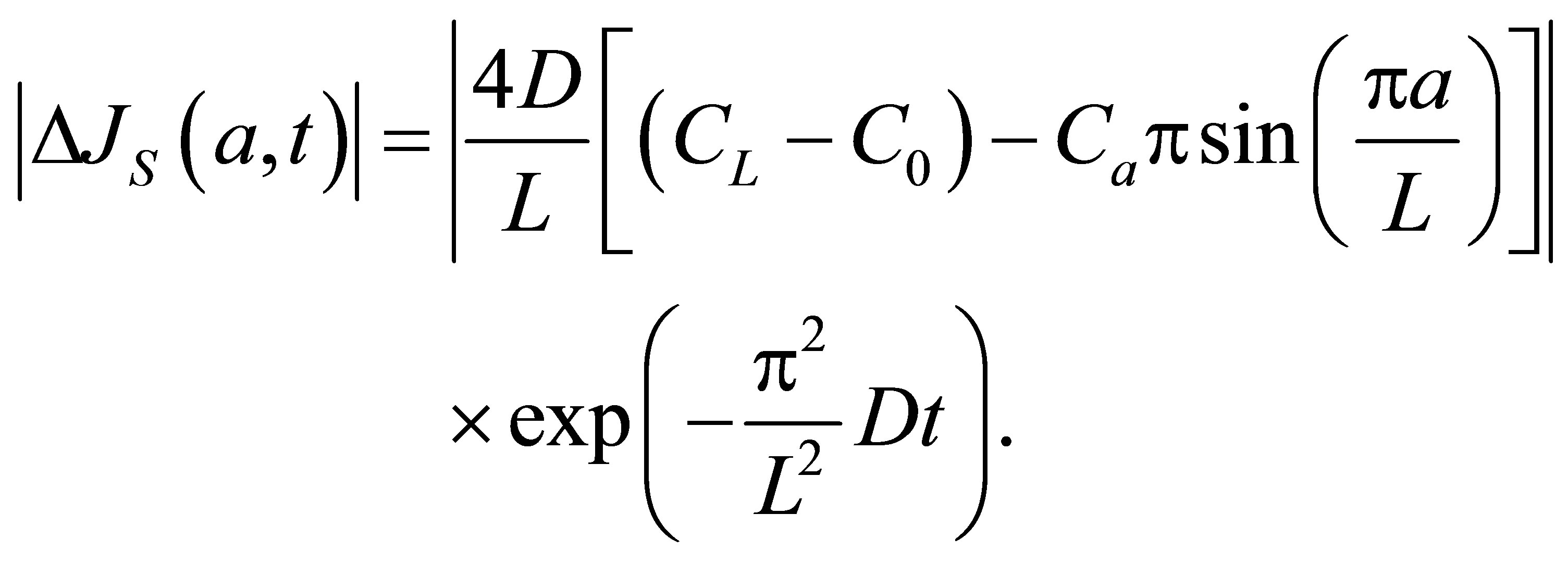 (12)
(12)
As it is seen in Equation (12), the net flux in the cell membrane is completely determined by the location  and amount
and amount 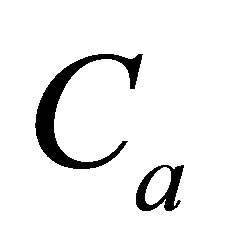 of the initial molecular concentration inside the cell membrane. Likewise, the diffusion fluxes at the wall boundaries
of the initial molecular concentration inside the cell membrane. Likewise, the diffusion fluxes at the wall boundaries  and
and 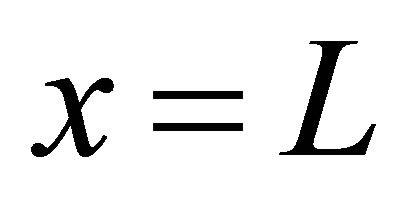 for the case of the double-spot concentrations are, respectively, obtained by
for the case of the double-spot concentrations are, respectively, obtained by
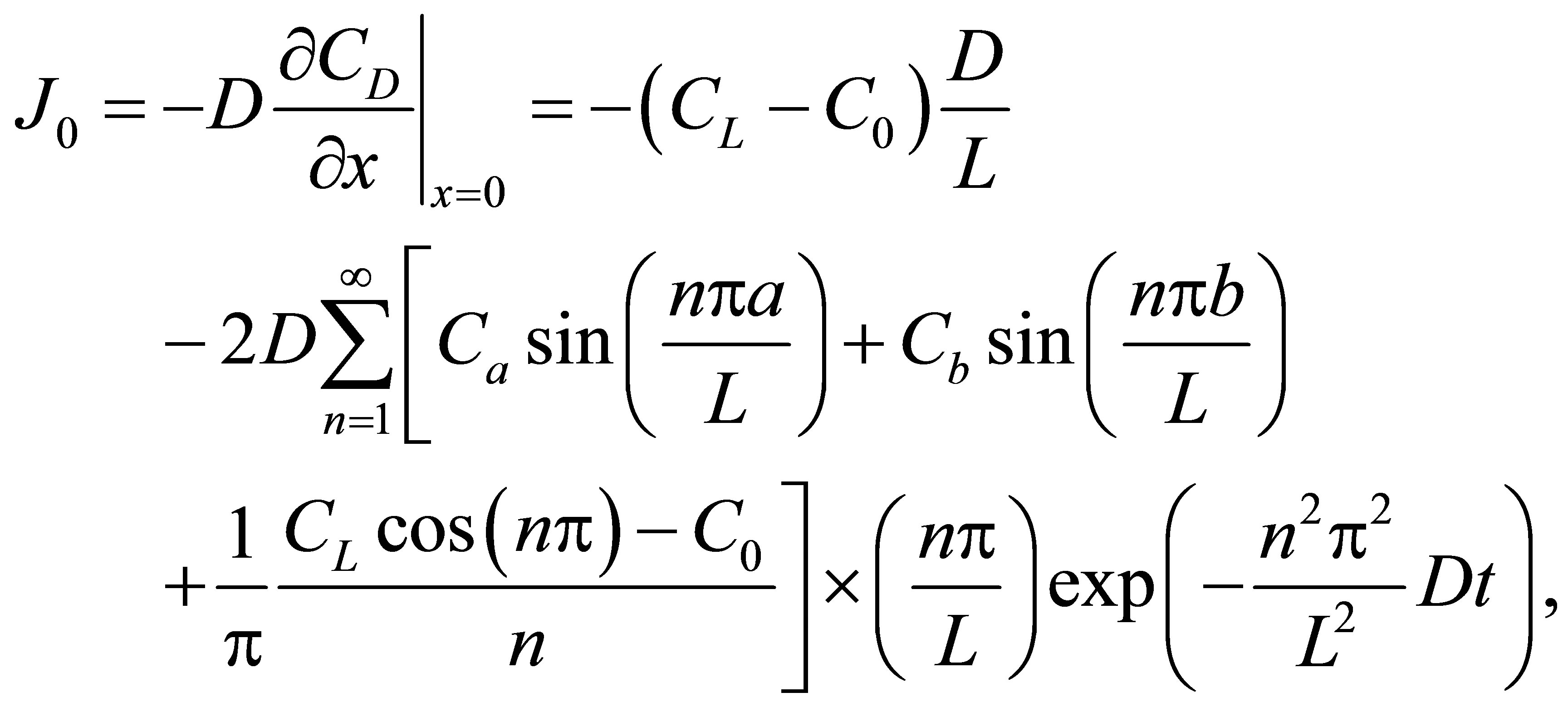 (13)
(13)
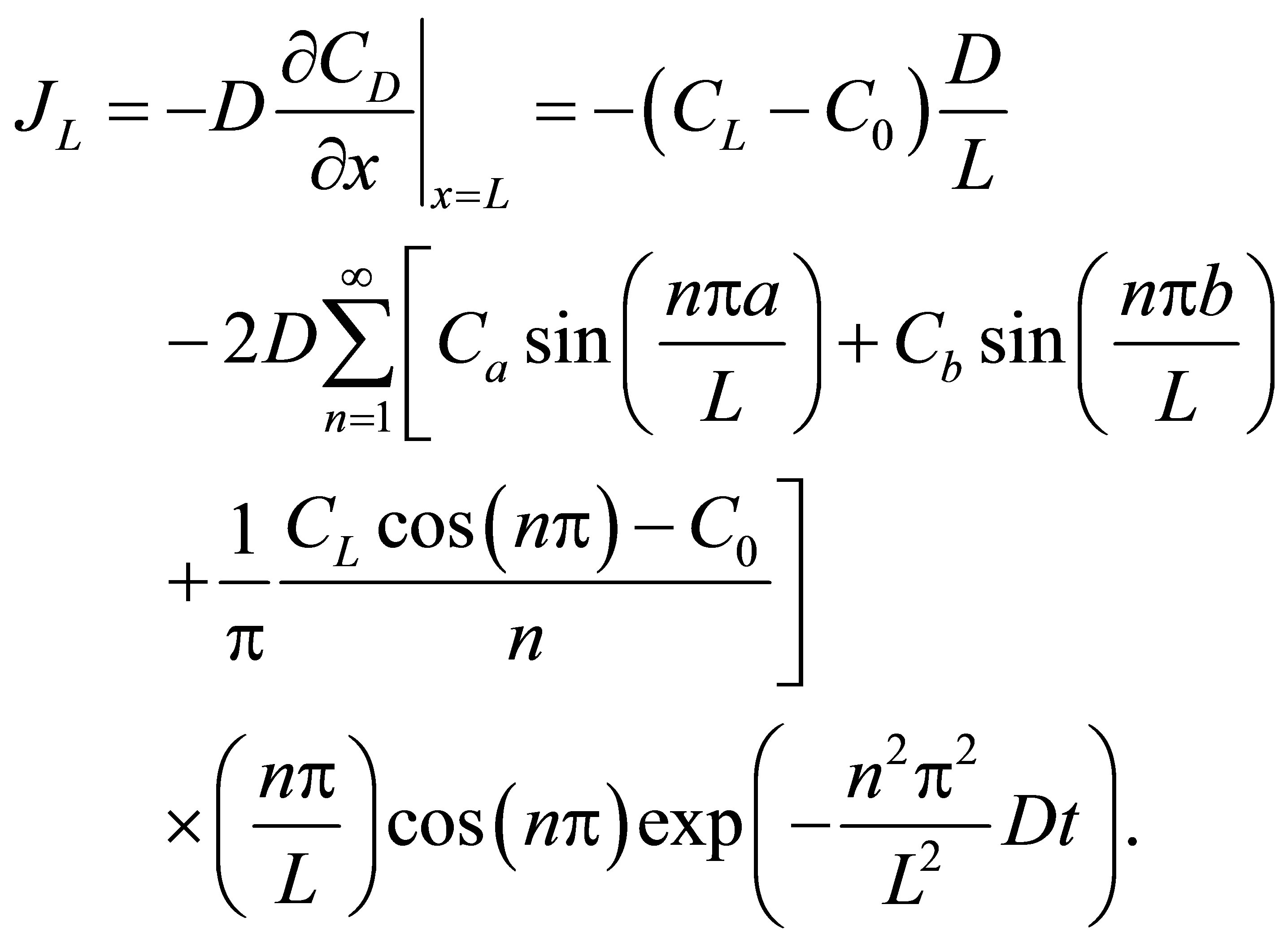 (14)
(14)
If we also retain on the first term as we did in Equation (12), the net flux 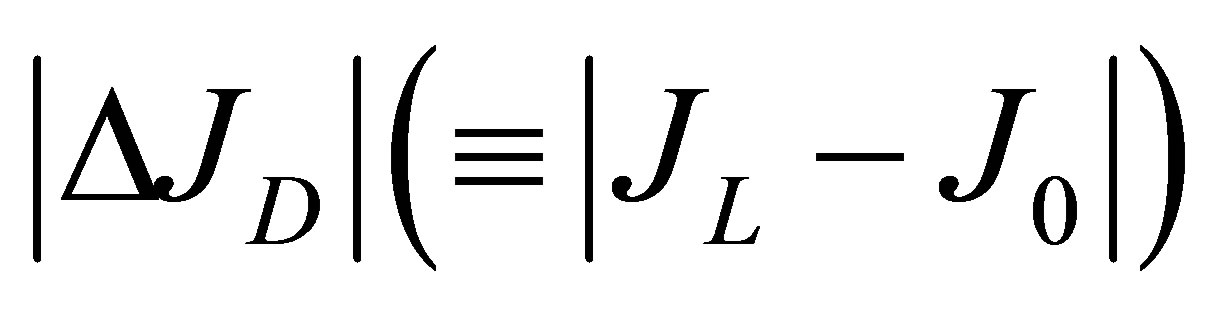 for the twospot concentrations is then obtained as
for the twospot concentrations is then obtained as
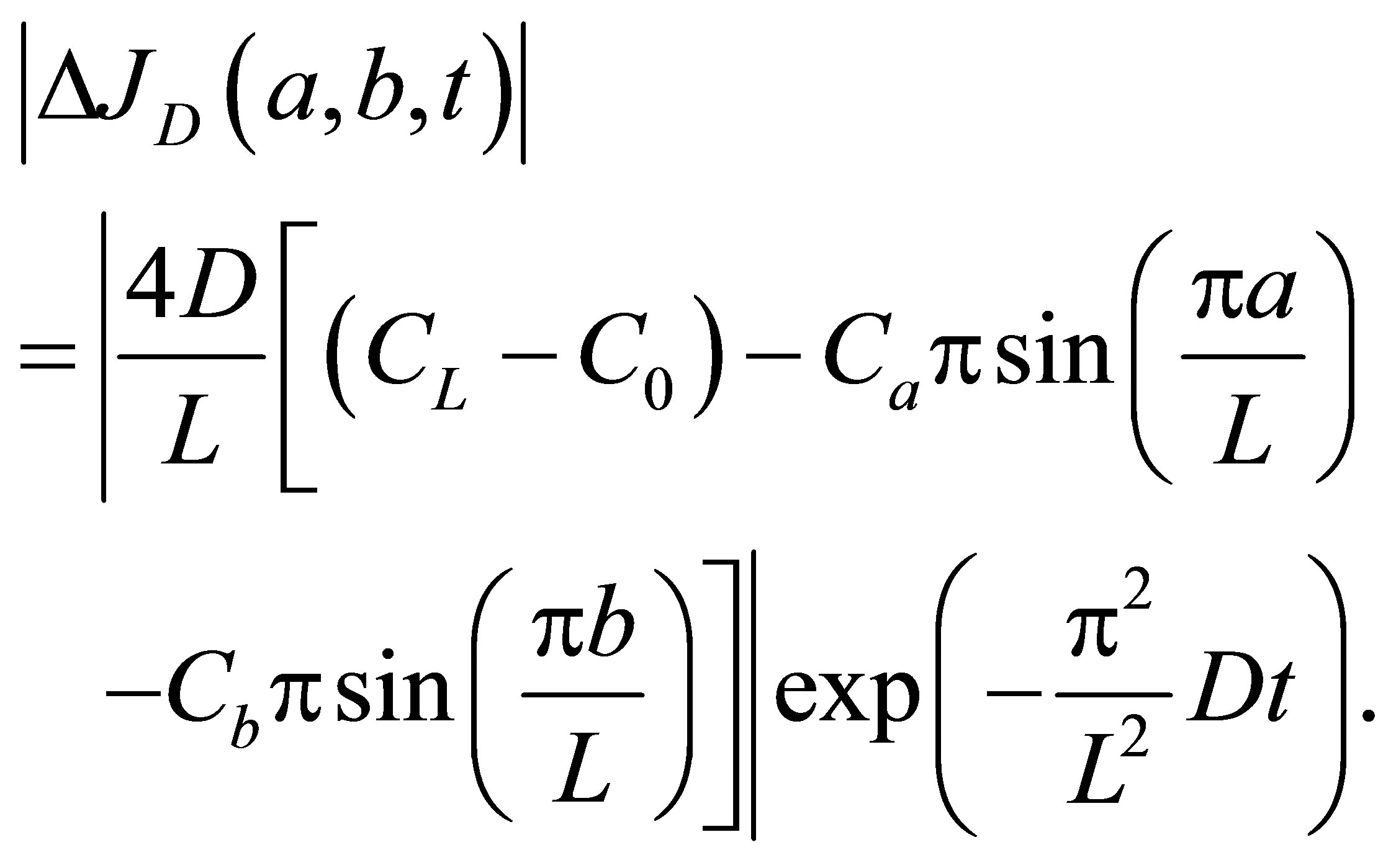 (15)
(15)
As shown in Equation (15), the net flux in the cell membrane is also completely controlled by the locations 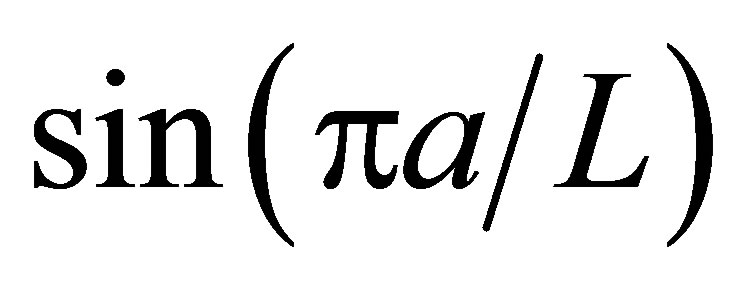 and
and 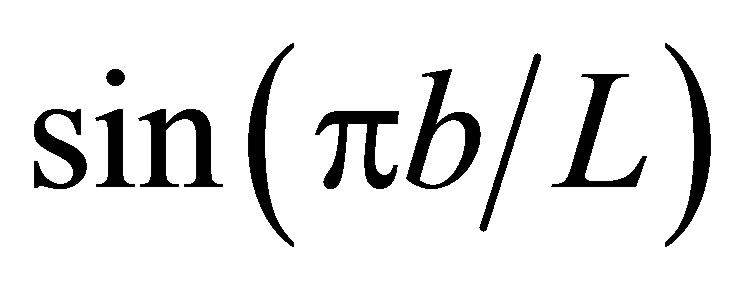 and amounts
and amounts 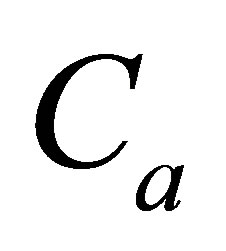 and
and 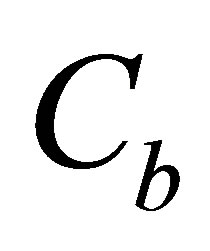 of the initial molecular concentrations inside the cell membrane.
of the initial molecular concentrations inside the cell membrane.
Since the ion diffusion in biological membranes is one of the main transport processes [16], the results of 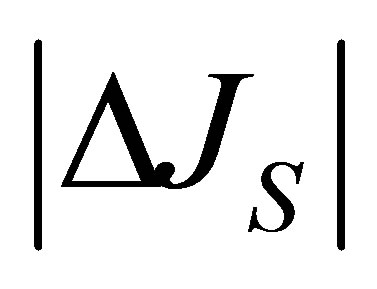 and
and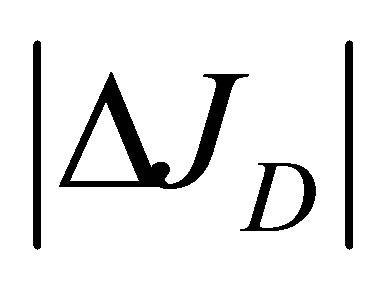 , Equations (12) and (15), in this model analysis would provide useful information on the electric current and the membrane potential. Recently, the diffusional anisotropy has been investigated in avascular collagenous tissues since the diffusion in articular cartilage is the main molecular transport process [17]. Hence, the effects of the initial placement of molecular substance on the two-dimensional anisotropic diffusion process will be treated elsewhere.
, Equations (12) and (15), in this model analysis would provide useful information on the electric current and the membrane potential. Recently, the diffusional anisotropy has been investigated in avascular collagenous tissues since the diffusion in articular cartilage is the main molecular transport process [17]. Hence, the effects of the initial placement of molecular substance on the two-dimensional anisotropic diffusion process will be treated elsewhere.
5. INFLUENCE OF INITIAL ION PLACEMENT
In this section, the graph plotting for the 2D and 3D plots are obtained by the technical computing software Mathematica. Figure 1 represents the net flux 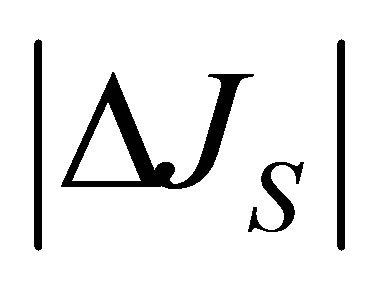 for the initial single-spot concentration case as a function of the scaled position
for the initial single-spot concentration case as a function of the scaled position 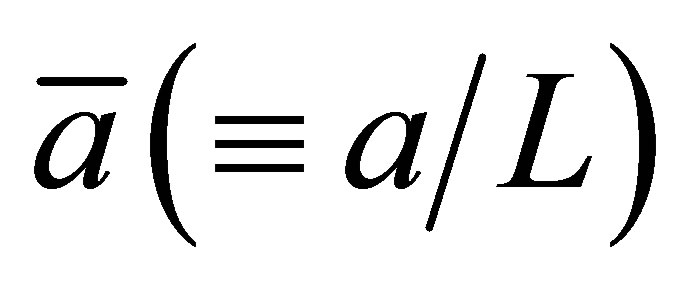 for various values of the diffusion time t when
for various values of the diffusion time t when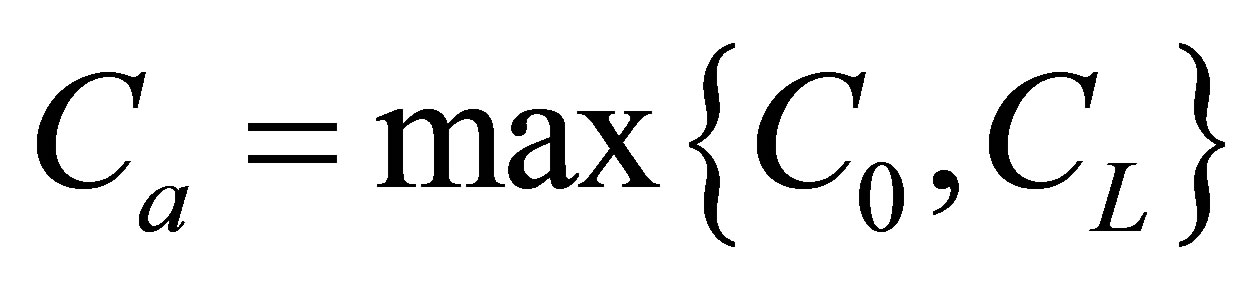 . As it is seen, it is found that two non-flux positions for
. As it is seen, it is found that two non-flux positions for 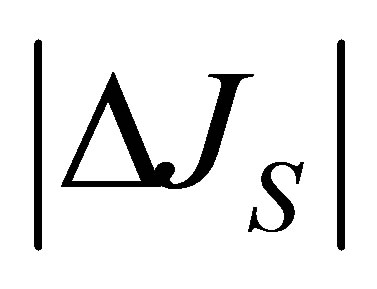 can be existed when the initial molecular concentration inside the cell membrane is equal to the larger one between two molecular concentrations at the domain boundaries. We have also found that that two non-flux positions are placed near the wall boundaries. In addition, it is found that the net flux
can be existed when the initial molecular concentration inside the cell membrane is equal to the larger one between two molecular concentrations at the domain boundaries. We have also found that that two non-flux positions are placed near the wall boundaries. In addition, it is found that the net flux  decreases with an increase of the diffusion time t.
decreases with an increase of the diffusion time t.
Figure 2 shows the net flux 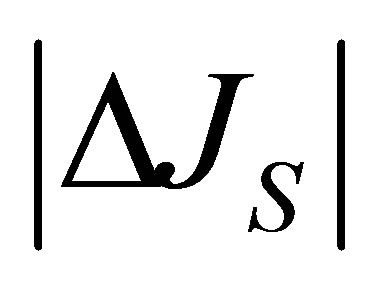 for the initial single-spot concentration case as a function of the scaled position
for the initial single-spot concentration case as a function of the scaled position 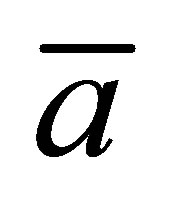 for various values of the diffusion time t when
for various values of the diffusion time t when 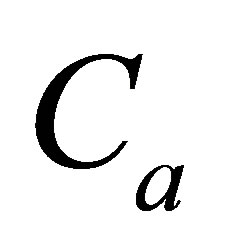 is smaller than
is smaller than  and
and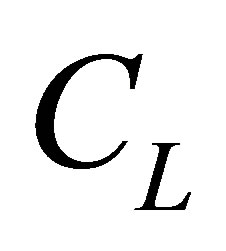 . As shown in this figure, it is interesting to note that the non-flux positions for
. As shown in this figure, it is interesting to note that the non-flux positions for 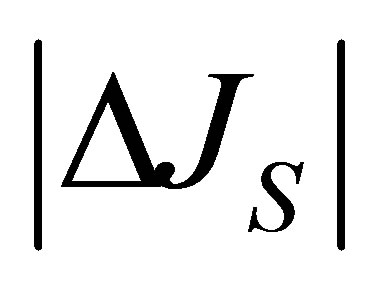 are disappeared inside the cell membrane when the initial molecular concentration inside the cell membrane is smaller than two molecular concentrations at the wall boundaries. In addition, the net flux
are disappeared inside the cell membrane when the initial molecular concentration inside the cell membrane is smaller than two molecular concentrations at the wall boundaries. In addition, the net flux 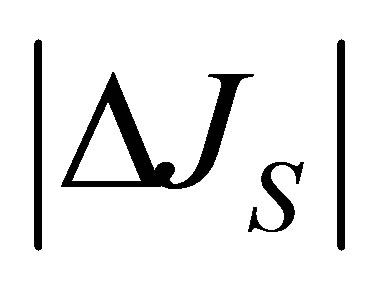 is found to be quite small at the center of the cell membrane.
is found to be quite small at the center of the cell membrane.
Figure 3 represents the scaled recovery curve
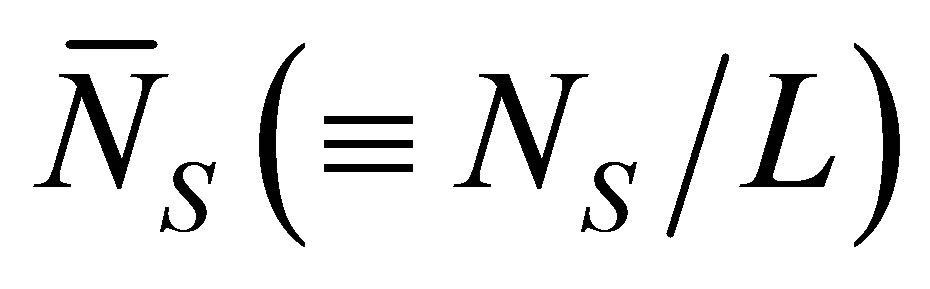 for the initial single-spot concentration
for the initial single-spot concentration
case as a function of the scaled diffusion time 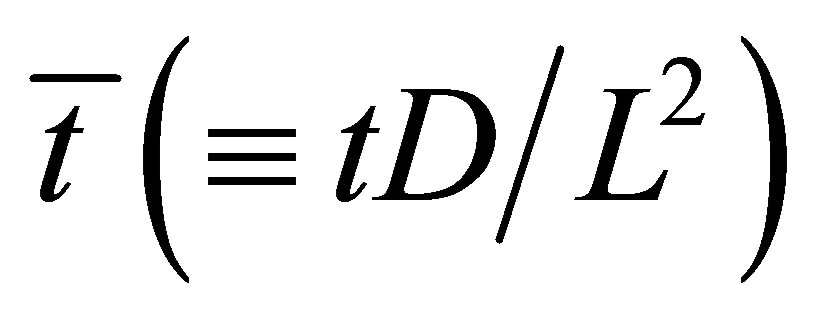 for various values of the initial location
for various values of the initial location 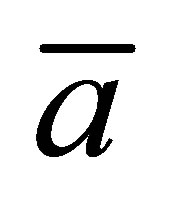 when
when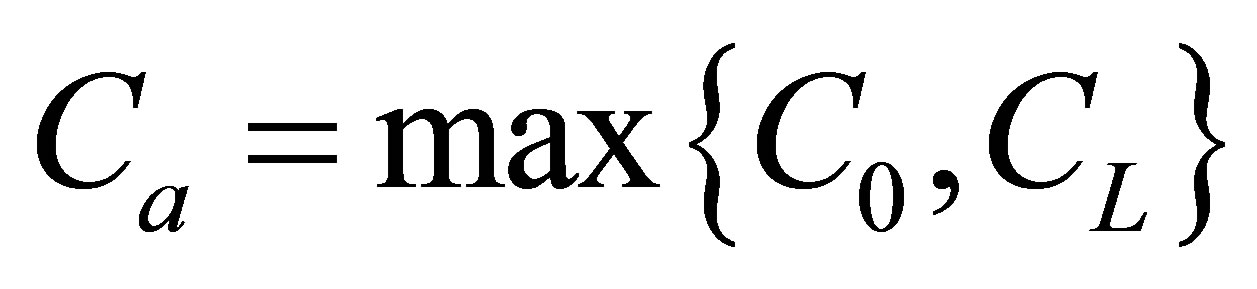 . From this figure, it is found that the recovery curve
. From this figure, it is found that the recovery curve 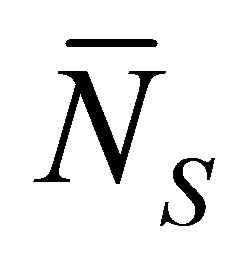 would have the maximum value when the initial single-spot concentration is placed near the right wall boundary and decreases with an increase of the diffusion time
would have the maximum value when the initial single-spot concentration is placed near the right wall boundary and decreases with an increase of the diffusion time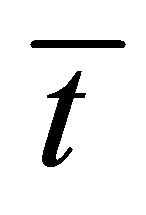 . However, we have found that the recovery curve
. However, we have found that the recovery curve 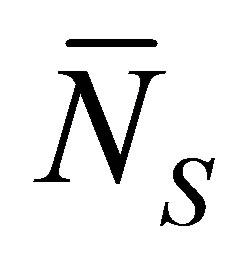 would have the minimum value when the initial single-spot concentration is placed near the left wall boundary and increases with an increase of the diffusion time
would have the minimum value when the initial single-spot concentration is placed near the left wall boundary and increases with an increase of the diffusion time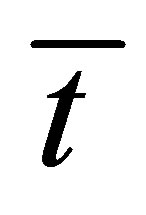 . It is also found that that the recovery curve
. It is also found that that the recovery curve  decreases monotonically with an increase of the diffusion time when the initial single-spot concentration is placed at the center of the cell membrane.
decreases monotonically with an increase of the diffusion time when the initial single-spot concentration is placed at the center of the cell membrane.
Figure 4 shows the scaled recovery curve 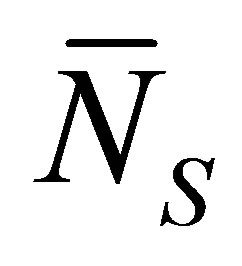 for the initial single-spot concentration case as a function of the scaled diffusion time
for the initial single-spot concentration case as a function of the scaled diffusion time 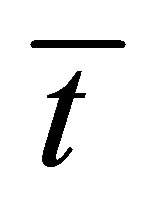 for various values of the initial location
for various values of the initial location 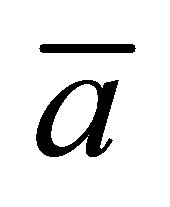 when
when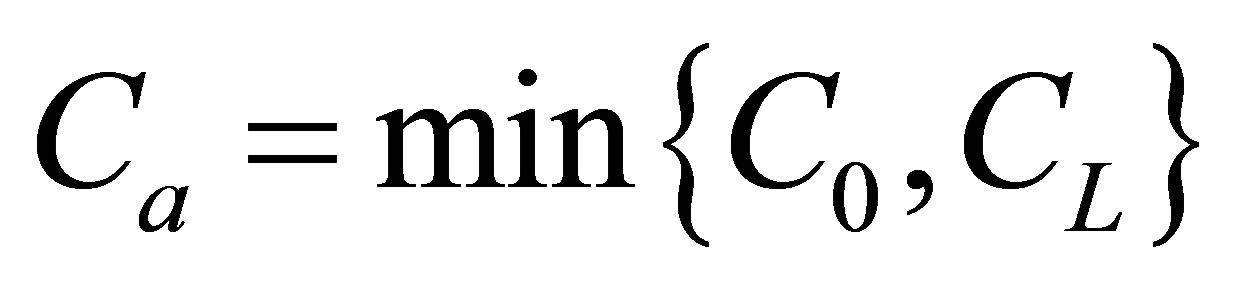 . As shown in this figure, it is found that the recovery curve
. As shown in this figure, it is found that the recovery curve 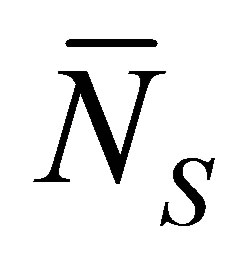 would have the minimum value when the initial single-spot concentration is placed near the left wall boundary at the center of the membrane and increases with an increase of the diffusion time
would have the minimum value when the initial single-spot concentration is placed near the left wall boundary at the center of the membrane and increases with an increase of the diffusion time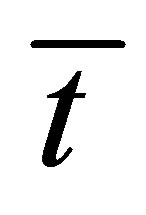 . However, we have found that the recovery curve
. However, we have found that the recovery curve 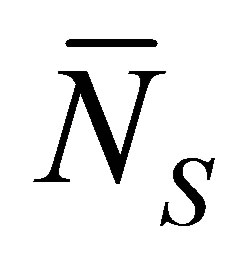 has the maximum value when the initial single-spot concentration is placed near the right wall boundary and decreases with an increase of the diffusion time
has the maximum value when the initial single-spot concentration is placed near the right wall boundary and decreases with an increase of the diffusion time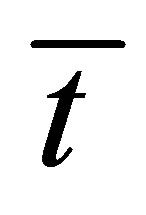 .
.
Figure 5 represents the surface plot of the net flux 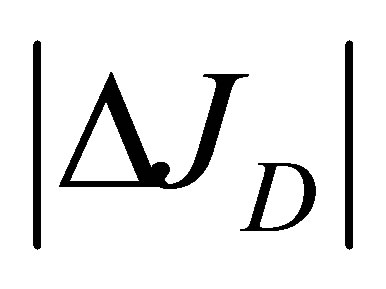 for the initial double-spot concentration case as a function of the scaled positions
for the initial double-spot concentration case as a function of the scaled positions  and
and 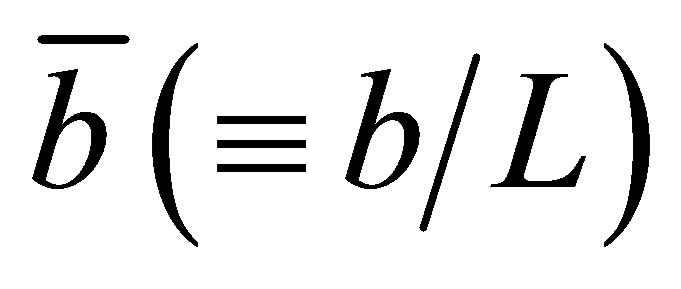 when
when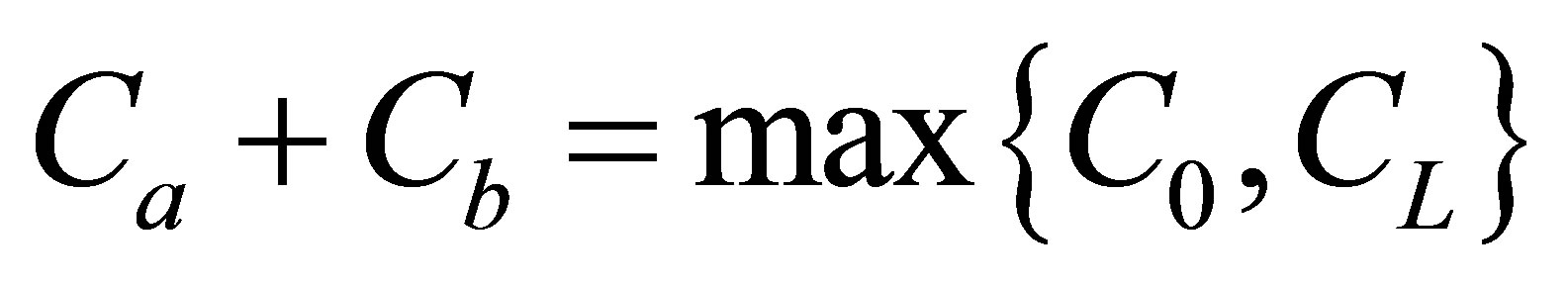 . As we can see from this figure, it is found that two non-flux posi-
. As we can see from this figure, it is found that two non-flux posi-
tions for 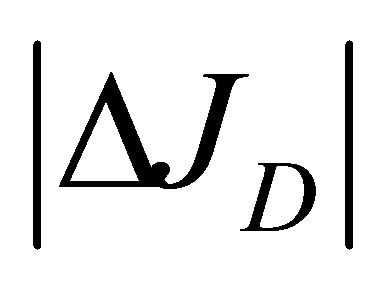 can be existed for the scaled position
can be existed for the scaled position 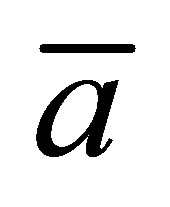 for a given
for a given  and also for the scaled position
and also for the scaled position 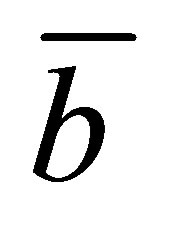 for a given
for a given . It is also found that the two non-flux positions are located near the wall boundaries. In addition, the net flux
. It is also found that the two non-flux positions are located near the wall boundaries. In addition, the net flux 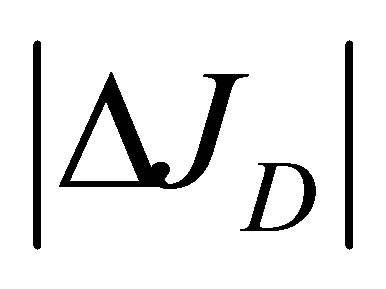 has the maximum value at the center of the cell membrane.
has the maximum value at the center of the cell membrane.
Figure 6 represents the surface plot of the net flux  for the initial double-spot concentration case as a function of the scaled positions
for the initial double-spot concentration case as a function of the scaled positions 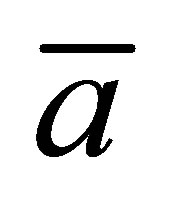 and
and  when the summation of concentrations
when the summation of concentrations 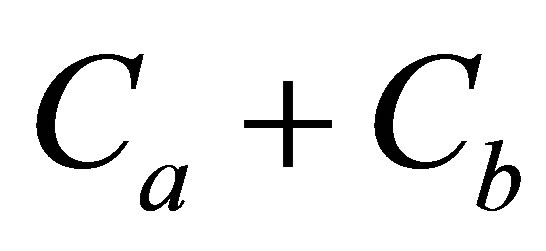 is smaller than
is smaller than  and
and . As it is seen in this figure, it is found that the non-flux positions for
. As it is seen in this figure, it is found that the non-flux positions for 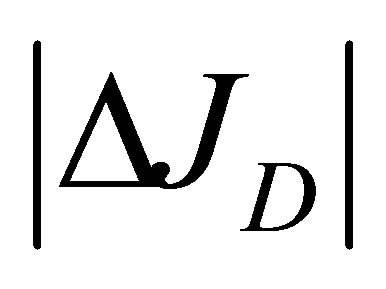 are disappeared inside the cell membrane when the initial total molecular con-
are disappeared inside the cell membrane when the initial total molecular con-
centration  inside the cell membrane is smaller than two molecular concentrations
inside the cell membrane is smaller than two molecular concentrations 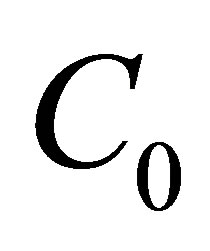 and
and 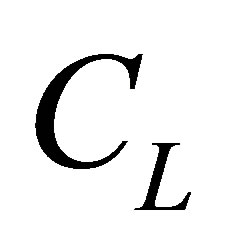 at the wall boundaries. The net flux
at the wall boundaries. The net flux 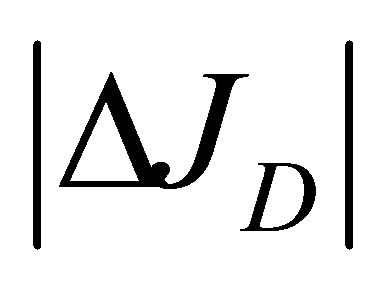 for the initial double-spot concentration case is found to be also quite small at the center of the cell membrane.
for the initial double-spot concentration case is found to be also quite small at the center of the cell membrane.
Figure 7 shows the scaled recovery curve 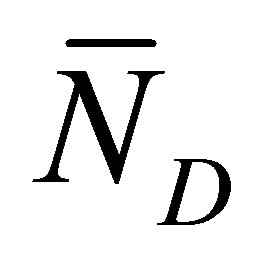 for the initial double-spot concentration case as a function of the scaled diffusion time
for the initial double-spot concentration case as a function of the scaled diffusion time 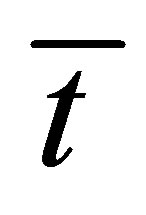 for various values of the scaled positions
for various values of the scaled positions 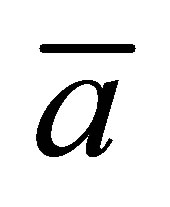 and
and 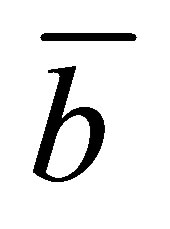 when
when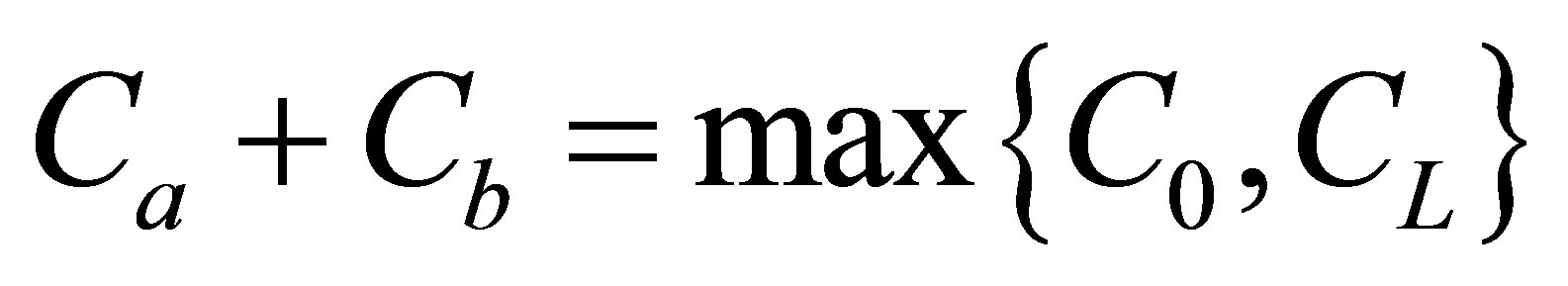 . As it is seen in this figure, the recovery curves
. As it is seen in this figure, the recovery curves 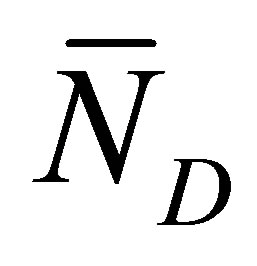 have maximum values at very short diffusion times
have maximum values at very short diffusion times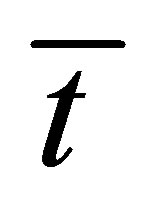 . It is also found that the maximum time of the recovery curve
. It is also found that the maximum time of the recovery curve  has been increased as the two positions are getting close to the center of the cell membrane.
has been increased as the two positions are getting close to the center of the cell membrane.
Figure 8 represents the scaled recovery curve 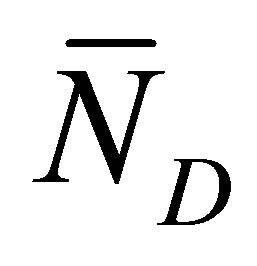 for the initial double-spot concentration case as a function of the scaled diffusion time
for the initial double-spot concentration case as a function of the scaled diffusion time 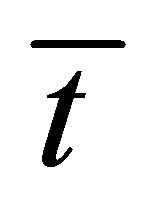 for various values of the scaled positions
for various values of the scaled positions 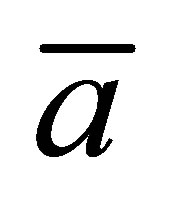 and
and 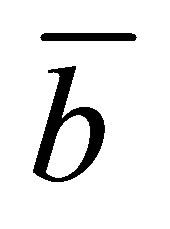 when
when
 . From this figure, we have found that the recovery curve
. From this figure, we have found that the recovery curve 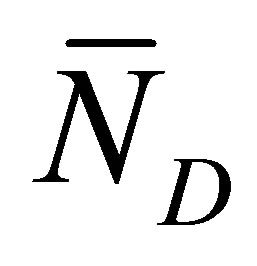 has no maximum and increases and finally saturates with increasing diffusion time
has no maximum and increases and finally saturates with increasing diffusion time 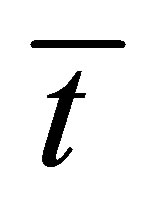 when the two locations
when the two locations 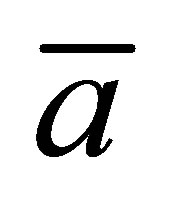 and
and  are away from the center of the membrane. However, it is found that the recovery curve
are away from the center of the membrane. However, it is found that the recovery curve 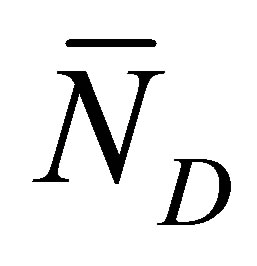 has the maximum value at the small diffusion time and saturates with an increase of the diffusion time
has the maximum value at the small diffusion time and saturates with an increase of the diffusion time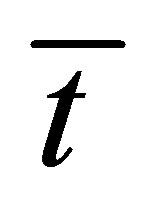 .
.
6. CONCLUSIONS
In this work, we inspected the influence of initial placement of molecular or ion substance on the diffusion fluxes at outer walls of the cell membrane. The recovery curves in the cell membrane were obtained for the single-
spot and double-spot concentrations, respectively. The net diffusion fluxes were obtained by considering both single-spot and double-spot concentrations across the cell membrane. For the initial single-spot concentration case, it was found that two non-flux positions would exist near the wall boundaries if the initial molecular concentration inside the cell membrane were equal to the larger one between the two molecular concentrations at the domain boundaries. It is also found that the two non-flux positions were placed near the center of the cell membrane when the initial molecular concentration inside the cell membrane was equal to the smaller one between the two molecular concentrations at the wall boundaries. In addition, we have found that the non-flux positions disappeared inside the cell membrane when the initial molecular concentration was smaller than two molecular concentrations at the wall boundaries. The molecular concentration 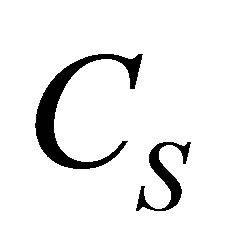 could be increased more than
could be increased more than 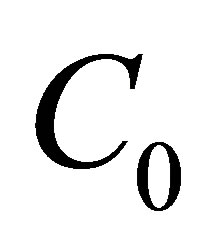 when the initial single-spot concentration was placed near the left wall boundary and
when the initial single-spot concentration was placed near the left wall boundary and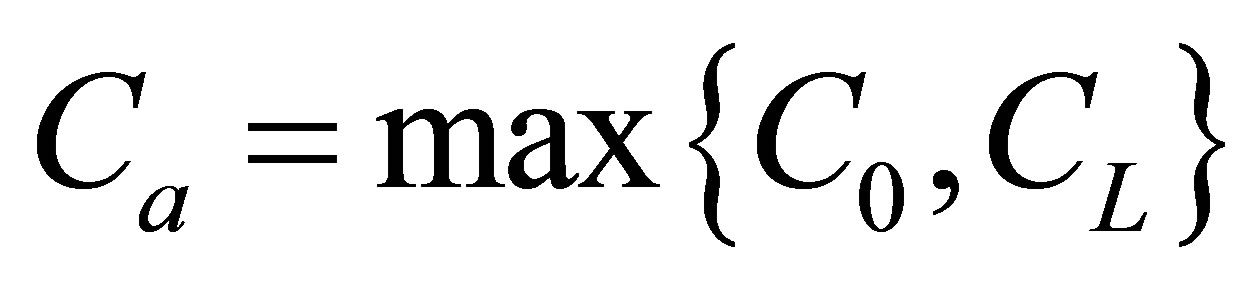 . However, we have found that the molecular concentration monotonically decreases with an increase of the position when the initial single-spot concentration is placed at the center or near the right wall boundary. Moreover, we have found that the molecular concentration can be smaller than
. However, we have found that the molecular concentration monotonically decreases with an increase of the position when the initial single-spot concentration is placed at the center or near the right wall boundary. Moreover, we have found that the molecular concentration can be smaller than 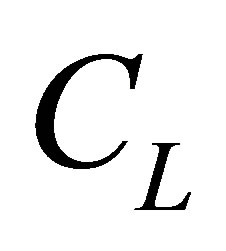 when the initial single-spot concentration was placed near the left wall boundary. Thus, the recovery curve would have the maximum vale when
when the initial single-spot concentration was placed near the left wall boundary. Thus, the recovery curve would have the maximum vale when 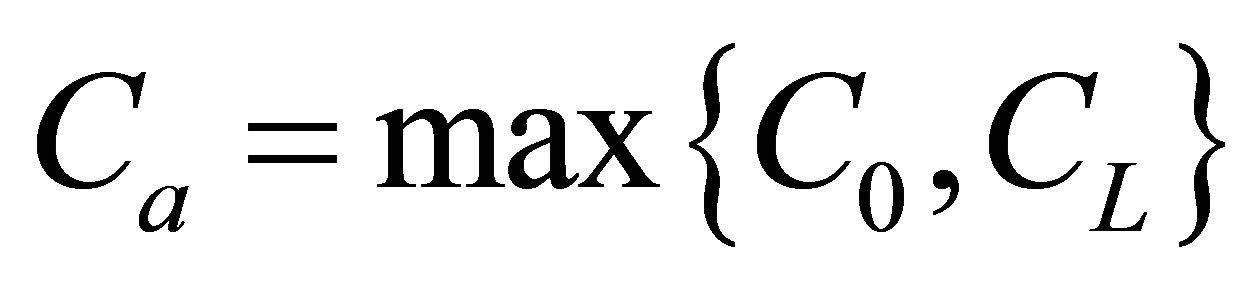 and the initial single-spot concentration was placed near the right wall boundary and the recovery curve decreases with an increase of the diffusion time. The minimum value would be when
and the initial single-spot concentration was placed near the right wall boundary and the recovery curve decreases with an increase of the diffusion time. The minimum value would be when 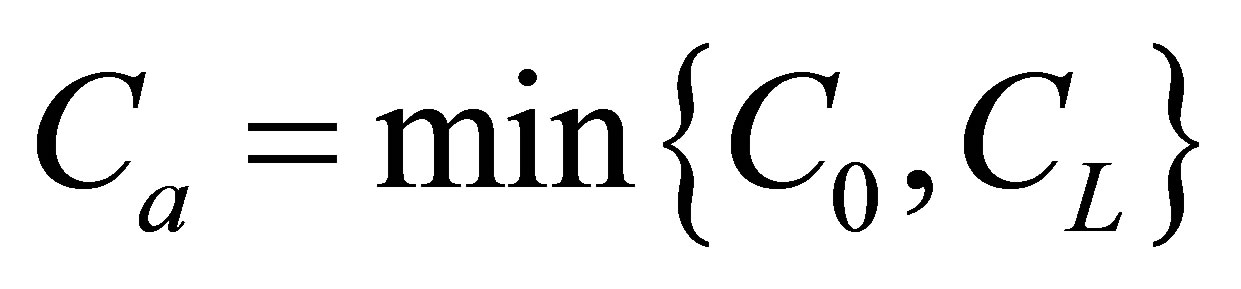 and the initial single-spot concentration was placed near the left wall boundary at the center of the membrane and increases with an increase of the diffusion time. For the initial double-spot concentration case, it was found that two non-flux positions were located near the wall boundaries when
and the initial single-spot concentration was placed near the left wall boundary at the center of the membrane and increases with an increase of the diffusion time. For the initial double-spot concentration case, it was found that two non-flux positions were located near the wall boundaries when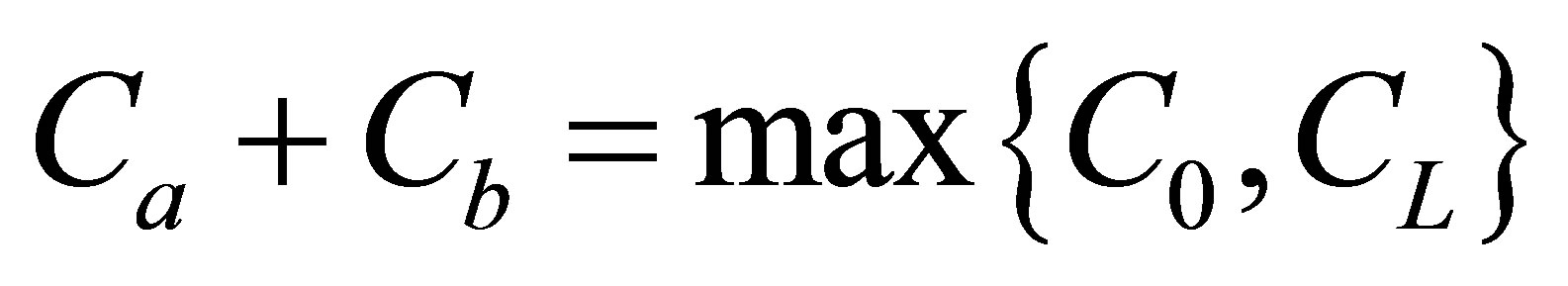 . It is also found that the net flux had the maximum value at the center of the cell membrane. We found two non-flux positions could also be existed near the center of the cell membrane when
. It is also found that the net flux had the maximum value at the center of the cell membrane. We found two non-flux positions could also be existed near the center of the cell membrane when 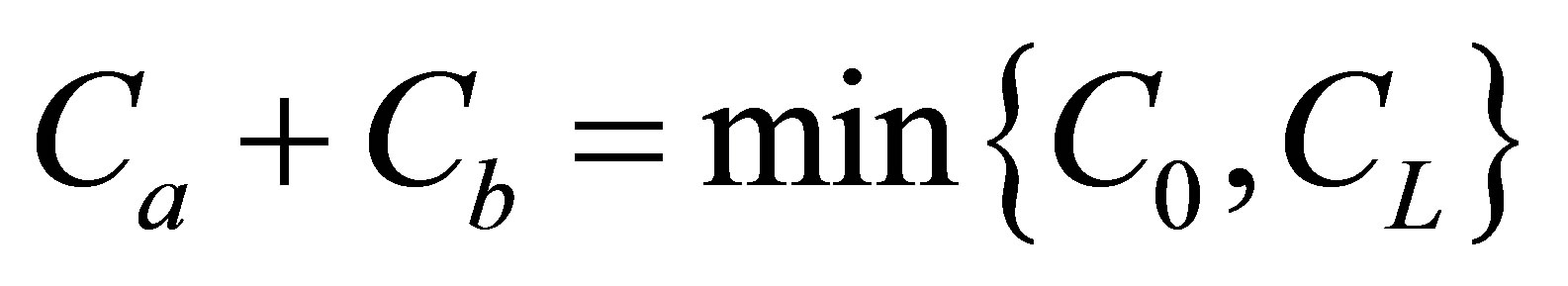 and the net flux was still quite small at the center of the cell membrane. However, we have found that the non-flux positions were disappeared inside the cell membrane when
and the net flux was still quite small at the center of the cell membrane. However, we have found that the non-flux positions were disappeared inside the cell membrane when 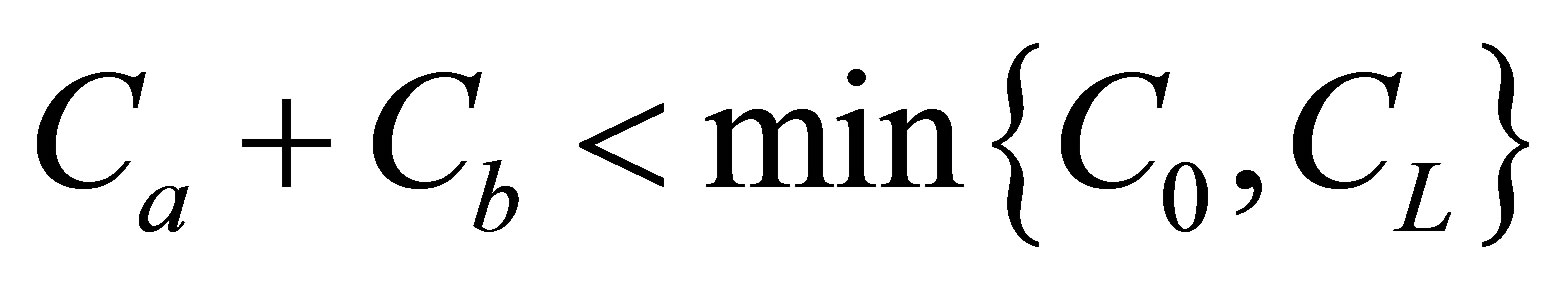 and the net flux for the initial double-spot concentration case was found to be also quite small at the center of the cell membrane. We have found that the molecular concentration
and the net flux for the initial double-spot concentration case was found to be also quite small at the center of the cell membrane. We have found that the molecular concentration 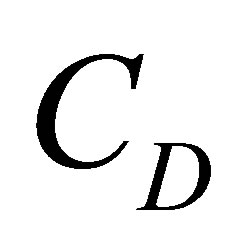 had the maximum value when two positions were near the center of the cell membrane when
had the maximum value when two positions were near the center of the cell membrane when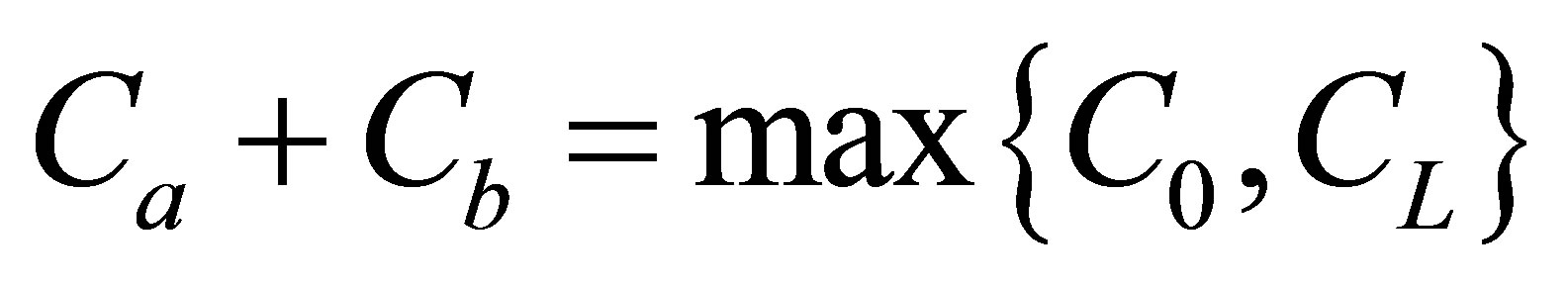 . However, we have found that the molecular concentration decreased with an increase of the distance
. However, we have found that the molecular concentration decreased with an increase of the distance 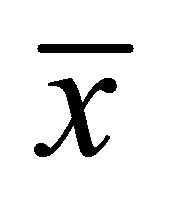 regardless of the locations of the initial double-spot concentrations when
regardless of the locations of the initial double-spot concentrations when
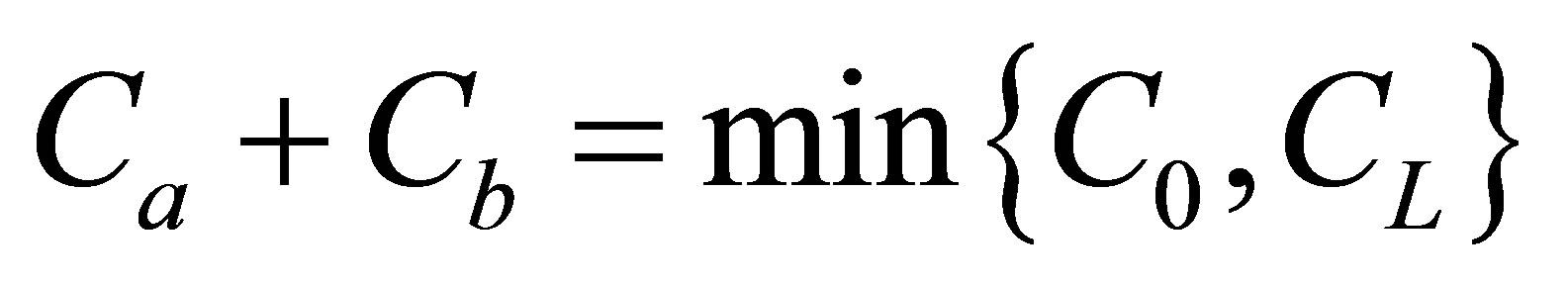 . It is found that the recovery curves had maximum values at very short diffusion times and the recovery curve increased as the two positions were getting close to the center of the cell membrane when
. It is found that the recovery curves had maximum values at very short diffusion times and the recovery curve increased as the two positions were getting close to the center of the cell membrane when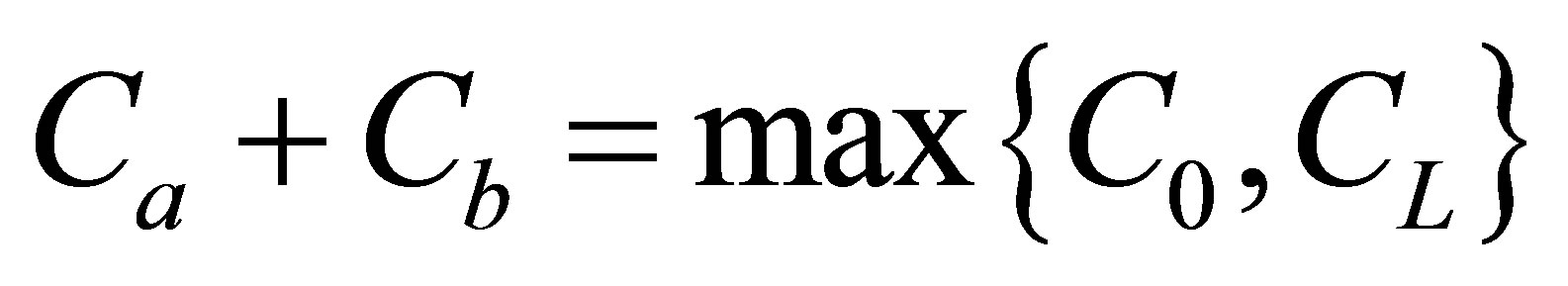 . It is found that the recovery curve at first had no maximum, but increased and finally saturated with increasing diffusion time when the two initial locations were away from the center of the membrane. It had the maximum value at the small diffusion time and saturated with an increase of the diffusion time when
. It is found that the recovery curve at first had no maximum, but increased and finally saturated with increasing diffusion time when the two initial locations were away from the center of the membrane. It had the maximum value at the small diffusion time and saturated with an increase of the diffusion time when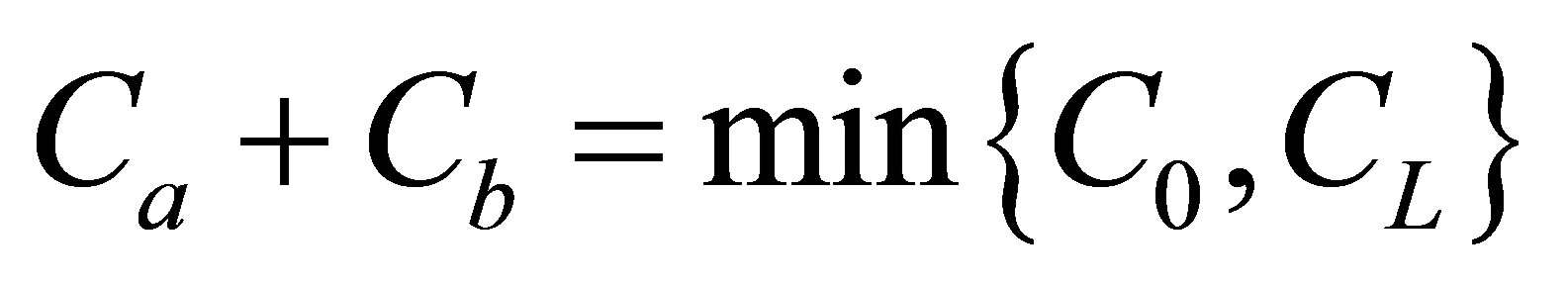 . From this work, we have found that the influence of initial locations and amounts of the molecular substance plays a significant role on the diffusion fluxes across the cell membrane. Since the results are obtained in the analytic expressions with the appropriate physical conditions, the equations in this work would be quite reliable for understanding the diffusion process in biological systems. Hence, the results of this work would be useful for understanding the characteristics and properties of the intracellular diffusion process as well as the spread of the cancerous cell and appearance of the tumor. The results in this work can also be applied to the enhancement of the diffusion process in articular cartilage. Moreover, these results would be applied to the biomedical machines related to the biological diffusion processes including the initial ion concentrations inside the wall boundaries.
. From this work, we have found that the influence of initial locations and amounts of the molecular substance plays a significant role on the diffusion fluxes across the cell membrane. Since the results are obtained in the analytic expressions with the appropriate physical conditions, the equations in this work would be quite reliable for understanding the diffusion process in biological systems. Hence, the results of this work would be useful for understanding the characteristics and properties of the intracellular diffusion process as well as the spread of the cancerous cell and appearance of the tumor. The results in this work can also be applied to the enhancement of the diffusion process in articular cartilage. Moreover, these results would be applied to the biomedical machines related to the biological diffusion processes including the initial ion concentrations inside the wall boundaries.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge Prof. Y.-K. Lim for useful discussions and encouragements while visiting the Proton Therapy Center at National Cancer Center of South Korea. This research was initiated while one of the authors (B. J. Jung) from Rensselaer Polytechnic Institute, USA was affiliated with the Proton Therapy Center at National Cancer Center as a Summer Intern Scholar.