Influence of Chemical Reaction and Thermal Radiation on MHD Boundary Layer Flow and Heat Transfer of a Nanofluid over an Exponentially Stretching Sheet ()
Keywords:Nanofluid; Exponentially Stretching Sheet; Chemical Reaction; Thermal Radiation; Boundary Layer Flow; Heat and Mass Transfer
1. Introduction
The study of flow and heat transfer over a stretching surface has gained considerable attention due to its vast applications in industry and important bearings on several technological and natural processes. Such processes are hot rolling, wire drawing, spinning of filaments, metal extrusion, crystal growing, continuous casting, glass fiber production, paper production, cooling of a large metallic plate in a bath, which may be an electrolyte, etc. In all these cases, a study of the flow field and heat transfer can be of significant importance since the quality of the final product depends to a large extent on the surface heat transfer rate and the skin friction coefficient.
The problem of heat transfer enhancement was first sorted out by Choi [1] upon inventing “nanofluid” indicating engineered colloids composed of nanoparticles dispersed in a base fluid. The characteristic feature of nanofluids is thermal conductivity enhancement, a phenomenon observed by Masuda et al. [2]. These fluids are engineered colloidal suspensions of nanoparticles in a base fluid. The nanoparticles used in nanofluids are typically made of metals (Al, Cu), oxides (Al2O3, TiO2 and CuO), carbides (SiC), nitrides (AlN, SiN), or nonmetals (Graphite, carbon nanotubes) and the base fluid is usually a conductive fluid, such as water or ethylene glycol. Other base fluids are oil and other lubricants, bio-fluids and polymer solutions. Nanofluids commonly contain up to a 5% volume fraction of nanoparticles to ensure effective heat transfer enhancements. Nanofluids have novel properties that make them potentially useful in many applications in heat transfer. They exhibit enhanced thermal conductivity and the convective heat transfer coefficient compared to the base fluid. Typical thermal conductivity enhancements are in the range 15% - 40% over the base fluid and heat transfer coefficient enhancements have been found up to 40% [3]. Increases in thermal conductivity of this magnitude cannot be solely attributed to the higher thermal conductivity of the added nanoparticles, and there must be other mechanisms attributed to the increase in performance. A comprehensive survey of convective transport in nanofluids was made by Buongiorno [4], who has considered seven slip mechanisms that can produce a relative velocity between the nanoparticles and the base fluid. Buongiorno’s analysis [4] consisted of a two-component equilibrium model for mass, momentum, and heat transport in nanofluids and found that a non-dimensional analysis of the equations implied that energy transfer by nanoparticle dispersion is negligible, and cannot explain the abnormal heat transfer coefficient increases. It was further suggested that the boundary layer has different properties due to the effect of temperature and thermophoresis. The viscosity may be decreasing in the boundary layer, which would lead to heat transfer enhancement. An excellent assessment of nanofluid physics and developments has been provided by Das et al. [5] and Eastman et al. [6]. Buongiorno and Hu [7] observed that although convective heat transfer enhancement has been suggested to be due to the dispersion of the suspended nanoparticles, this effect is too small to explain the observed enhancement.
Many literatures are also available on boundary layer flow over a stretching surface where the velocity of the stretching surface is assumed to be linearly proportional to the distance from the fixed origin. However, it is often argued that [8] realistically stretching of plastic sheet may not necessarily be linear. Magyari and Keller [9] investigated the heat and mass transfer in the boundary layers on an exponentially stretching surface. Suction and heat transfer characteristics in the flow over an exponentially stretching sheet have been addressed by Elbashbeshy [10]. Approximate analytic similarity solution for viscoelastic boundary layer flow over an exponentially stretching surface has been presented by Khan and Sanjayanand [11]. Sajid and Hayat [12] examined the effects of thermal radiation on the flow due to an exponentially stretching surface. MHD boundary layer flow due to an exponentially stretching sheet having the effect of radiation was studied by Anuar Ishak [13]. An analysis on the effect of magnetic field on boundary layer flow and heat transfer of a dusty fluid over an exponentially stretching surface with an exponential temperature distribution was made by Gireesha et al. [14] by considering the Saffman model for flow problem.
The situation of boundary layer flow and heat transfer over an exponential stretching sheet was beautifully explained for the case of nanofluid by Sohail Nadeem and Changhoon Lee [15] in their work on boundary layer fluid flow of nanofluid over an exponentially stretching surface. Recently, various aspects of such problems have been investigated by many authors. Mustafa et al. [16] have conducted the studies on boundary layer flow of a nanofluid over an exponentially stretching sheet with convective boundary conditions.
The objective of this paper is to solve the problem of flow and heat transfer of a nanofluid over an exponentially stretching sheet by considering the effect of chemical reaction and thermal radiation parameters along with the suction parameter numerically by adopting the well known Runge-Kutta-Fehlberg method of fourth-fifth order. Present analysis on nanofluid has taken the effect of Brownian motion and thermophoresis parameters. Validation of the analysis has been performed by comparing the present results with those available in the open literature [16] and [13] and a very good agreement has been established.
2. Formulation of the Problem
Consider a steady, laminar, two-dimensional boundary layer flow of an incompressible nanofluid over an exponentially stretching sheet coinciding with the plane 
and the flow being confined to
. The flow is generated due to the linear stretching of the sheet, caused by the simultaneous application of two equal and opposite forces along the x-axis. Keeping the origin fixed, the sheet is then stretched with a velocity 
varying linearly with the distance from the slit. It is assumed that at the stretching surface, the temperature 
and the nanoparticle fraction 
take constant values 
and 
respectively. The ambient values are attained as 
tends to infinity, of 
and 
are denoted by 
and 
respectively. Under the usual boundary layer approximations, the flow and heat transfer of nanofluid is governed by the following equations on mass, momentum, energy and concentration in Cartesian coordinates 
and 
as,
(1)
(2)
(3)
(4)
The boundary conditions considered for the present flow analysis are
(5)
To examine the flow, the following transformations are used:
(6)
To determine the velocity, temperature distribution and rate of heat and mass transfer in the above boundary layer (5), we solve the equations related to the stretching sheet problem to obtain the following similarity equations using (6). In deriving these equations, the external electric field is assumed to be zero and the electric field due to polarization of charges is negligible.
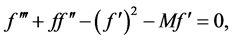(7)
(8)
(9)
The transformed boundary conditions take the following forms
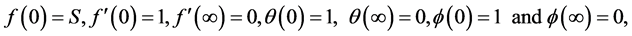(10)
3. Numerical Solution
The equations (7)-(9) together with the boundary condition (10) forms highly non-linear ordinary differential equations. In order to solve these equations numerically we adopt symbolic software Maple which is very efficient in using the well known Runge-Kutta-Fehlberg fourth-fifth order method. In accordance with the boundary layer analysis, the boundary condition (10) at 
is replaced by 
Obtained coupled ordinary non-linear equations (7)-(9) are solved by RKF-45 method for the boundary condition (10). Accuracy of this numerical method shown in Table 1 is being validated by direct comparison with the numerical results reported by Meraj Mustafa et al. [16], and Anuar Ishak [13] when 
The numerical computations of 
and 
for the values of 
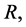
and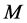 
are shown in Table2
4. Results and Discussion
To provide a physical insight into the flow problem, comprehensive numerical computations are conducted for various values of the parameters that describe the flow characteristics and results are illustrated graphically.
Figure 1 portrays the behavior of Prandtl number 
on the temperature profile. An increase in 
Pr rapidly shifts the profiles towards the boundary causing a diminution in the thickness of thermal boundary layer. A bigger Prandtl number has a relatively lower thermal diffusivity. Thus an increase in 
reduces conduction and thereby increases the variation in the thermal characteristics. As expected, the variation in the temperature is more pronounced for smaller values of 
than its larger values.
From the figure 2 it is observed that velocity field near the boundary layer decreases with the increasing values of suction parameter 
and the velocity profile tends asymptotically to the horizontal axis, the non-dimensional velocities absorbs maximum at the wall. Moreover, the suction causes the reduction of the boundary layer, which in turn stabilizes the boundary layer growth.
Table 1. Comparison of results for 
with previous published works.
Figure 1. Effect of Prandtl number Pr on temperature profile.
Figure 3 depict the variation of temperature and concentration with coordinate for various values of Lewis numbers
. The thickness of the boundary layer concentration is found to be smaller than the thermal boundary layer thickness for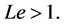 
Both the temperature and concentration profiles decrease with an increase in 
But, the concentration profile is affected more with Le as compared to temperature profile.
The influence of thermophoresis parameter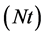 
on the temperature and concentration boundary layer is noticed in figure 4. An abnormal increase in the concentration 
is found for a weaker Brownian motion
. In fact an over shoot in the concentration function occurs as we gradually increase 
the same effect is seen in the case of temperature profile but an appreciable increase in temperature profile is found for the increasing values of 
Figure 5 plots the temperature and concentration functions versus 
for different values of the Brownian motion parameter
. Here unlike the temperature 
concentration boundary layer reduces as 
increases which thereby enhances the nanoparticles concentration at the sheet. Further it is noticed that concentration 
is only affected for the values of 
in the range 
Figure 6 shows the velocity and temperature profiles for various values of the magnetic parameter
. It is noted that the velocity along the surface decreases the momentum boundary layer thickness and increases the thermal boundary layer thickness. Physically, temperature increases in the nanofluid because of its high thermal conductivity.
Influence of chemical reaction parameter 
on nanoparticle volume fraction profile is as shown in figure 7. It is observed that the nanoparicle volume fraction decreases with the increase of chemical reaction parameter, while the profiles for velocity and temperature are not significant with the chemical reaction parameter.
Figure 8 shows the variation of thermal radiation parameter 
over the energy field. It is noticed that an increase in R yields a decrease in the nanofluid’s temperature, which leads to an increase in the heat transfer rates. Thus the radiation should be at its minimum in order to facilitate the cooling process. All these physical behavior are due to the combined effects of the strength of the Brownian motion and thermophoresis particle deposition.
Figure 2. Effect of suction parameter S on velocity profile.
Figure 3. Effect of Lewis number Le on temperature and concentration profiles.
Figure 4. Effect of thermophoresis parameter Nt on temperature and concentration profiles.
Figure 5. Effect of Brownian motion parameter Nb on temperature and concentration profiles.
Figure 6. Effect of magnetic parameter 
on temperature and velocity profiles.
Figure 7. Effect of chemical reaction parameter 
on concentration profile.
Figure 8. Effect of thermal radiation parameter R on temperature profile.
5. Conclusions
A numerical study corresponding to the flow and heat transfer in a steady flow region of nanofluid over an exponential stretching surface and the effect of chemical reaction, thermal radiation, magnetic and suction parameters are examined and discussed in detail. The outcomes of present flow analysis are listed below:
• The increase in Prandtl number is to decrease the temperature of nanofluids.
• Heat transfer rate has simple dependency on almost all parameters except for higher values of 
Increasing the values of thermophoresis 
Brownian motion 
and Lewis number 
results in a reduction in heat transfer rate.
• An increase in 
appreciably enhances the mass flux due to temperature gradient which in turn raises the nanoparticles concentration.
• The impact of chemical reaction and thermal radiation in the presence of uniform thermophoresis and Brownian diffusion motion has a substantial effect on flow field.
• Thermophoresis serves to warm the boundary layer for low values of 
and Lewis number 
Acknowledgements
We express our thanks to reviewers for their constructive suggestions.
Nomenclature:
: velocity components along the 
and 
axes,
: density of the nanofluid,
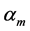: thermal diffusivity,
: kinematic viscosity,
: Brownian diffusion coefficient,
: thermophoresis diffusion coefficient,
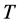: nanofluid temperature,
: is heat capacity of the fluid,
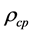: is the effective heat capacity of the nanoparticle,
: induced magnetic field,
: ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid,
: is the chemical reaction coefficient,
: volumetric volume expansion coefficient,
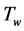: temperature of the nanofluid near wall,
: free stream temperature of the nanofluid,
: thermal conductivity,
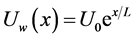: is the stretching sheet velocity,
: suction velocity,
: stretching rate being a positive constant,
: magnetic parameter called Hartmann Number,
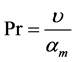: Prandtl number,
: thermophoresis parameter,
: Brownian motion parameter,
: Lewis number,
thermal radiation parameter,
: chemical reaction parameter,
: suction parameter.
NOTES
*Corresponding author.