Anti-Windup Digital Control Design for Time-Delayed Analog Nonlinear Systems Using Approximated Scalar Sign Function ()
1. Introduction
Various types of hardware limitations always exist in practical control systems with potential effects on the final control performance. A typical one encountered in practice is actuator saturation. For instance, as common actuation devices, motors have limited speed and torque range, power sources have output bounds, control valves cannot be more than fully open or fully closed, etc. As the control command is saturated at the top or bottom limit during actuator saturation, the control loop is broken and the controller loses the ability to regulate plant’s behavior for the time being. This phenomenon, called controller windup, may lead to significant degradation in control performance, such as long settling time, high overshoot or even instability [1].
In order to circumvent the windup effect, there exist many anti-windup approaches in the literature in the past decades. Most of them are proposed for linear systems, like the extensively-studied two-phase approach [1-4] (a nominal linear controller is first designed with the saturation constraints ignored and then a conditioning scheme is developed for reducing the windup effects of saturation) and Linear Matrix Inequalities (LMI)-based methods [5-7]. To the authors’ knowledge, however, few anti-windup approaches have been developed for nonlinear systems. The very limited efforts include the work of converting the physical constraint problem to a statedependent constraint problem through a coordinate transformation method [8,9], and those based on input-output linearization or feedback linearization [8-11].
This paper proposes an approximated-scalar-signfunction-based anti-windup technique for analog nonlinear systems with input constraints. As a non-differentiable function, sign function or absolute-value function has the inherent capability to describe the instantaneous jumps where the system model loses smoothness, so they commonly appear in many analytical models of nonsmooth nonlinearities, such as Bouc-Wen hysteresis model [12,13] and Stribeck friction model [14]. In this paper, sign function is used to represent the constrained input functions, capturing the instantaneous behavior as saturation occurs. In order to solve the non-differentiability due to sign function, approximated scalar sign function in [15] is utilized. Arising from the matrix sign function and the matrix sector function [15,16], the approximated scalar sign function is able to approximate the sign function in a smooth rational form with adjustable accuracy. Compared with other approximation techniques, like Hyperbolic tangent function, the approximated scalar sign function is stable in numerical evaluation. The constrained input functions represented with the approximated scalar sign function are differentiable, then optimal linearization in [17] is applied for the local linear model at any operating point and a state-feedback controller is developed via Linear Quadratic Regulator (LQR) for each point. As saturation occurs, an iterative procedure is developed to systematically adjust control gains by tuning the LQR weighting matrices until the saturation limits are not violated.
In addition to input constraints, time-delayed systems are another practical concern in the proposed design. This concern arises from the fact that in a sampled-data control system which is a popular control scheme nowadays due to the advance of computer technology, some fundamental operations like controller computation, A/D and D/A conversions, sensing and actuation etc, could cause time delays in the control loop. Another example is networked control systems where components communicate with each other through a real-time network, which inevitably causes transmission delays. Ignoring the delays in a control loop may lead to the failure of designed control so it is of practical interest to extend the developed anti-windup methodology to time-delayed systems. In this paper, the authors propose an input-delay-compensating digital redesign approach: an analog state-feedback controller is first designed in the delayfree case for the desired control performance; then a digital controller is obtained from the analog one through global digital redesign with the delay compensation considered. The resulting digital controller is able to maintain the essential control performance of the analog counterpart even in a time-delayed environment.
The rest of this paper is organized as follows. Section 2 introduces preliminary techniques used in the proposed anti-windup design, including approximated scalar sign function, optimal linearization and LQR. In Section 3, a global digital redesign method is developed for input delay compensation. The proposed anti-windup methodology is described in Section 4. Section 5 gives simulation results of proposed method on the swing up and stability control of single rotary inverted pendulum. Finally, the paper is concluded in Section 6.
2. Preliminaries
A) Approximated Scalar Sign Function
The scalar sign function is defined in [18] as
 (1)
(1)
where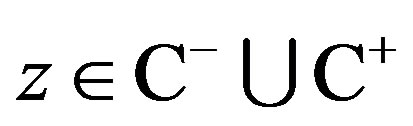 ,
, 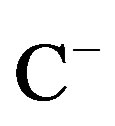 and
and 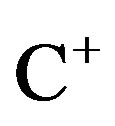 denotes the open lefthalf complex plane and the open right-half complex plane, respectively. It is noted that the imaginary axis
denotes the open lefthalf complex plane and the open right-half complex plane, respectively. It is noted that the imaginary axis 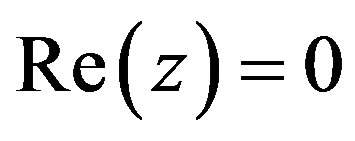 is undefined in
is undefined in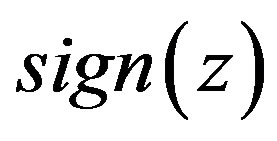 .
.
The scalar sign function has an alternative form in [15] as
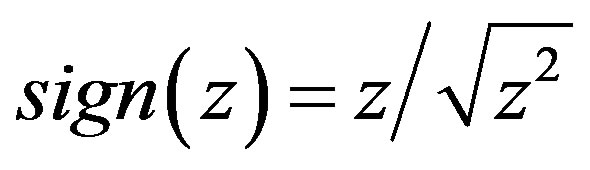 (2)
(2)
where 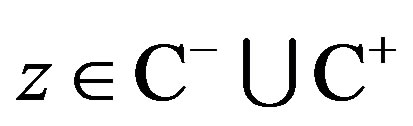 and
and
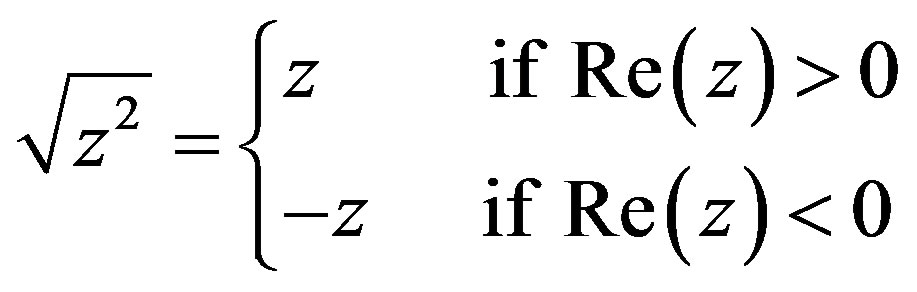 (3)
(3)
It is also reported in [15] that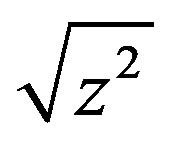 , called the principal square-root of
, called the principal square-root of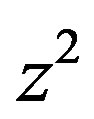 , can be expanded into a continued fraction form as
, can be expanded into a continued fraction form as
 (4)
(4)
and its j-th truncation can be written as
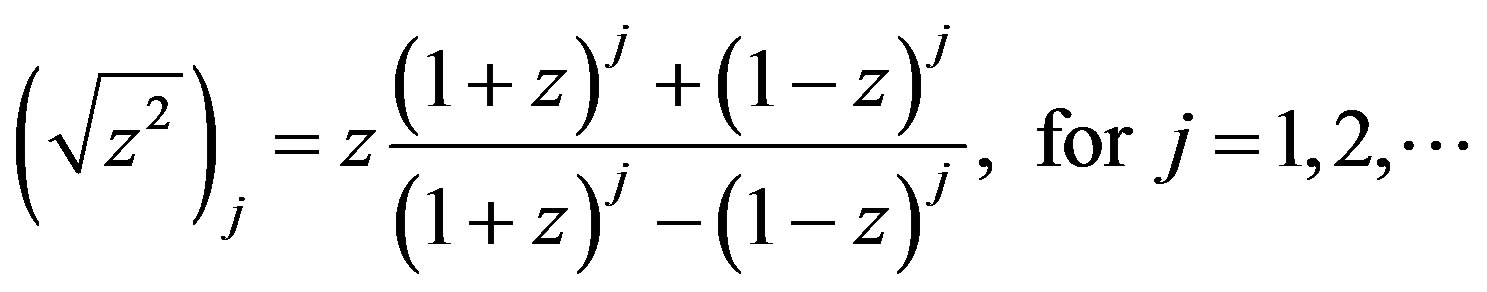 (5)
(5)
It can be shown that the j-th truncation (5) gives the better approximation of (3) as the value of j approaches the infinity, i.e.
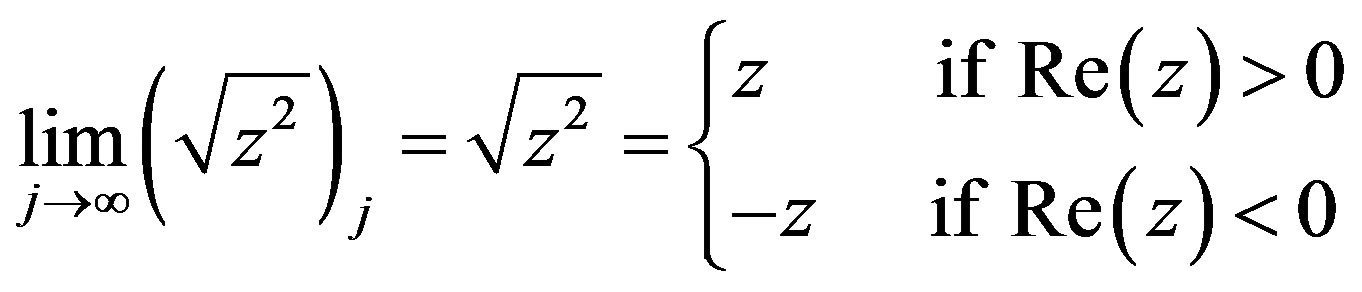 (6)
(6)
Replacing 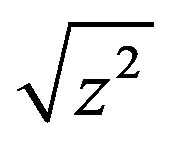 in (2) with the j-th truncation (5) yields the approximated scalar sign function for a complex number
in (2) with the j-th truncation (5) yields the approximated scalar sign function for a complex number 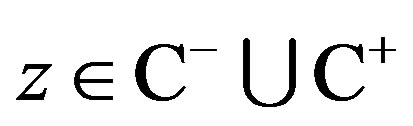 as
as
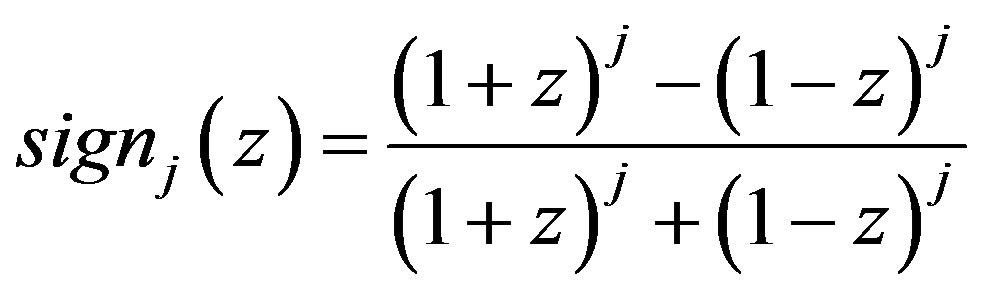 (7)
(7)
where  which denotes the positive integer set. It can be inferred from (6) that (7) has the limit
which denotes the positive integer set. It can be inferred from (6) that (7) has the limit
 (8)
(8)
Particularly, the approximated scalar sign function for a real number 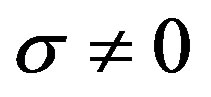 is
is
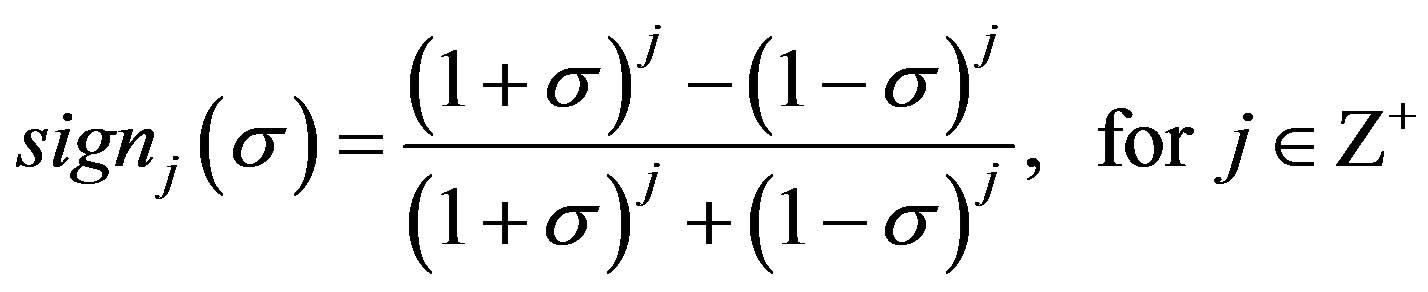 (9)
(9)
which has the limit
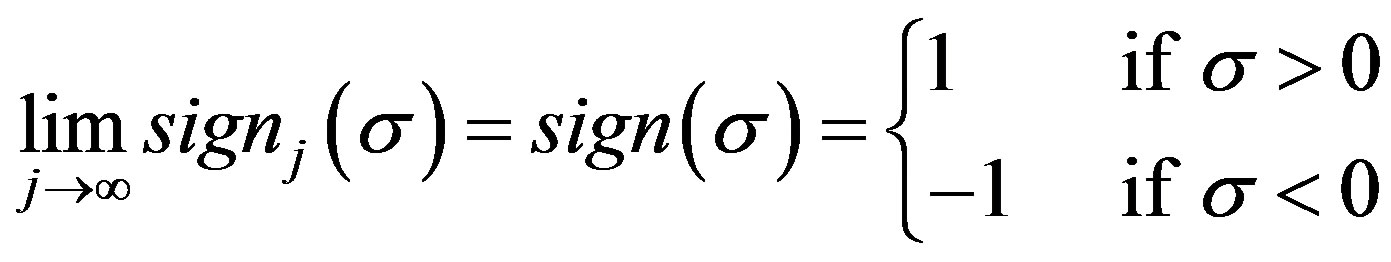 (10)
(10)
If the definition of scalar sign function for real numbers is extended to include zero, i.e.
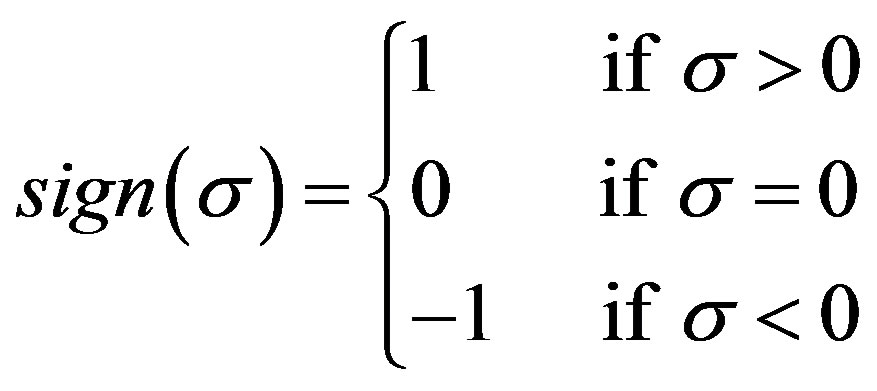 (11)
(11)
then
 , (12)
, (12)
as .
.
The concern of this paper is limited to the real number case (9) and the definition (11) is considered. Differentiating the approximated scalar sign function (9) with respect to the real number σ yields
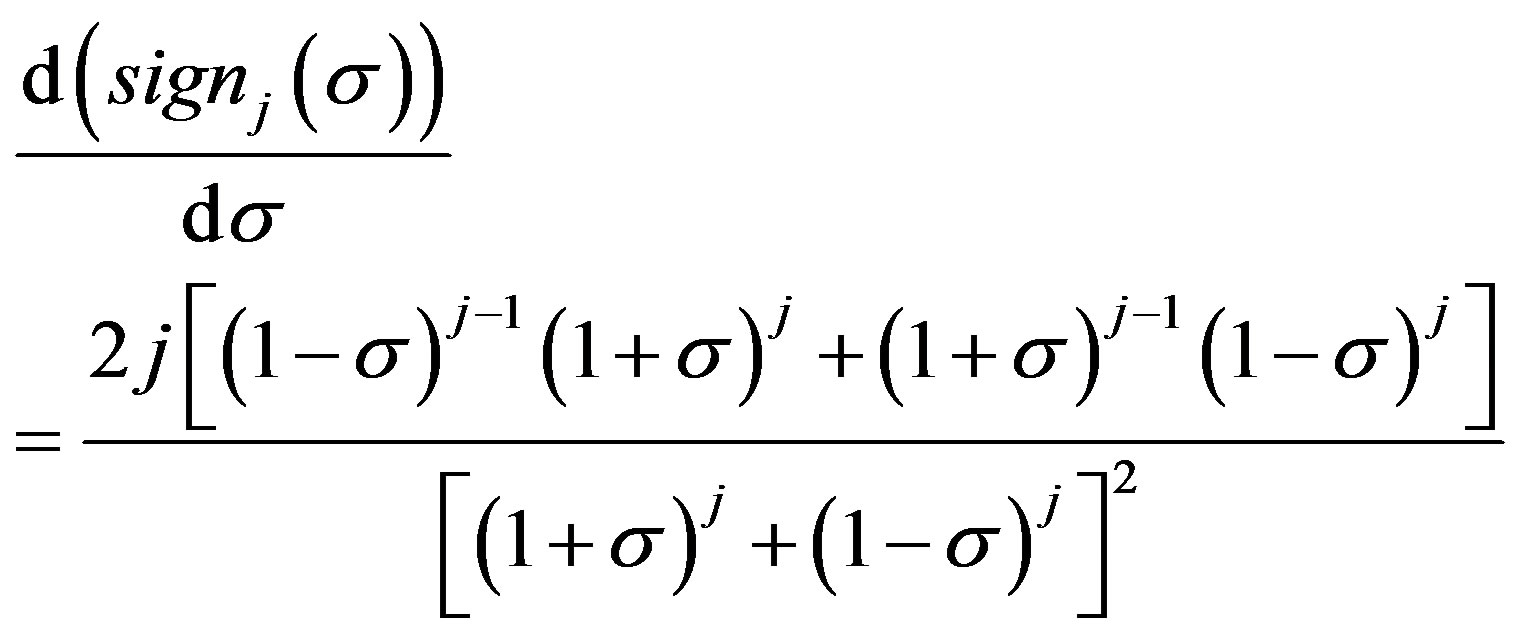 (13)
(13)
for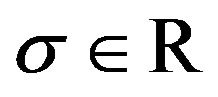 . It is easy to find that (13) is continuous everywhere, which proves the approximated scalar sign function (9) is differentiable everywhere.
. It is easy to find that (13) is continuous everywhere, which proves the approximated scalar sign function (9) is differentiable everywhere.
Figure 1(a) gives a big scope of the evaluated approximated scalar sign function (9) for different values of j, and Figure 1(b) shows the figure detail near zero. The corresponding derivative (13) is shown in Figure 2(a) and the figure detail near zero in Figure 2(b). It can be found from Figure 1 that the larger the value of j is, the closer the curve of the approximated scalar sign function (9) approaches the one of the scalar sign function (11), so j is also called the approximation order in the following context. Figure 2 shows that the approximated scalar sign function (9) is differentiable everywhere because its derivative value is always finite with the largest one located at σ = 0, equal to the approximation order j.
By utilizing the approximated scalar sign function, an approximate model can be obtained for a non-smooth
 (a)
(a) (b)
(b)
Figure 1. Approximated scalar sign function.
dynamical system with sign function constraints, whose approximation accuracy can be adjusted with the approximation order j. Due to the smoothness and nonlinearity of the approximated scalar sign function, the resulting approximate model is still nonlinear, but differentiable everywhere, which makes possible the further local linearization.
Remark 1: As shown in Figure 1,  for j is even. This property will be exploited in the proposed anti-windup method in Section IV.
for j is even. This property will be exploited in the proposed anti-windup method in Section IV.
B) Optimal Linearization
Local linearization is a typical way of handling nonlinear systems and the most popular technique is Jacobian linearization [19]. However, as pointed out in [17,20], Jacobian Linearization usually produces an affine rather than linear model even at the equilibrium operating point. The only exception case is that the operating point is an equilibrium at the origin, which cannot be ensured throughout a nonlinear control process.
In order to circumvent the limitation of Jacobian linearization, Teixeira and Zak formulated linearization prob-
 (a)
(a) (b)
(b)
Figure 2. Derivative of approximated scalar sign function.
lem as a convex constrained optimization problem and proposed an optimal linearization approach in [17]. According to this approach, an optimal local linear model can be achieved at any operating point, which possesses the exact dynamics of the original nonlinear system at the operating point and minimum approximation error (in the least square sense) in the neighborhood of that point. Due to the space limit, only the final conclusions are briefed below.
Consider a general class of nonlinear system in the form
 (14)
(14)
where  is the state vector,
is the state vector, 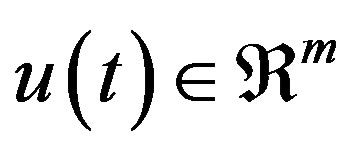 is the input vector,
is the input vector, 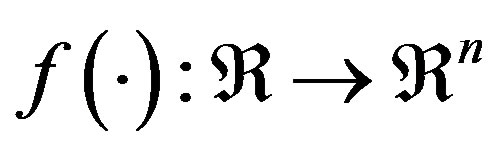 with
with  is a differentiable nonlinear function vector and
is a differentiable nonlinear function vector and 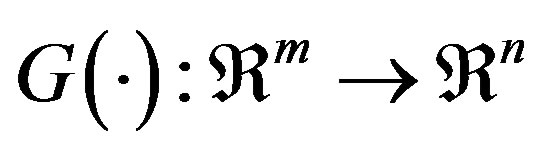 is a function matrix. Its optimal local linear model at an arbitrary operating point
is a function matrix. Its optimal local linear model at an arbitrary operating point 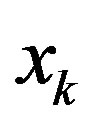 is in the state-space form
is in the state-space form
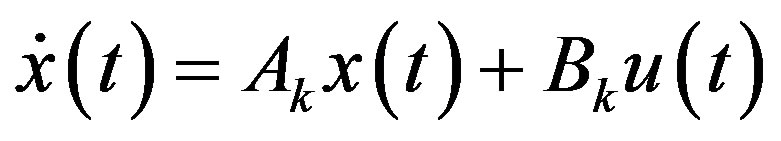 (15)
(15)
where
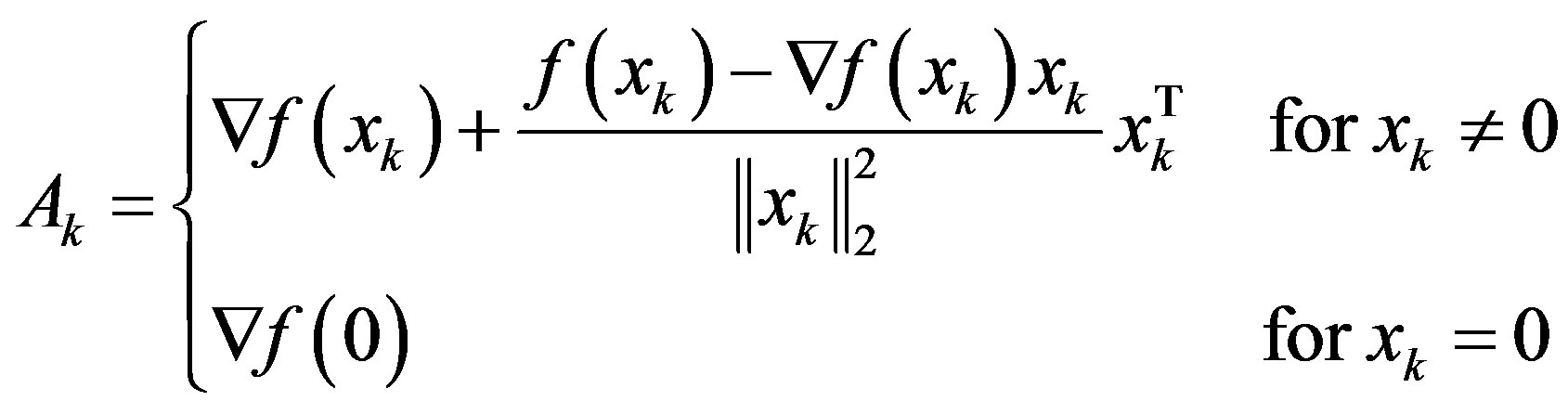 (16)
(16)
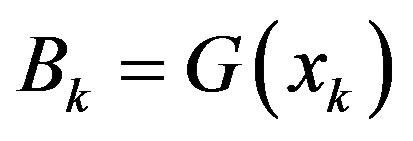 (17)
(17)
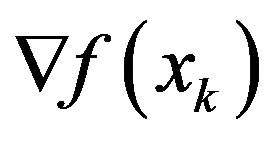 is the Jacobian matrix of
is the Jacobian matrix of 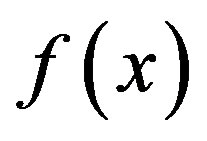 evaluated at the operating point xk. It is noted that the case for xk = 0 in (16) agrees with the aforementioned exception case of the operating point being an equilibrium at the origin.
evaluated at the operating point xk. It is noted that the case for xk = 0 in (16) agrees with the aforementioned exception case of the operating point being an equilibrium at the origin.
Remark 2: When f(x) in (14) is a scalar nonlinear function, (16) is reduced to a scalar number as
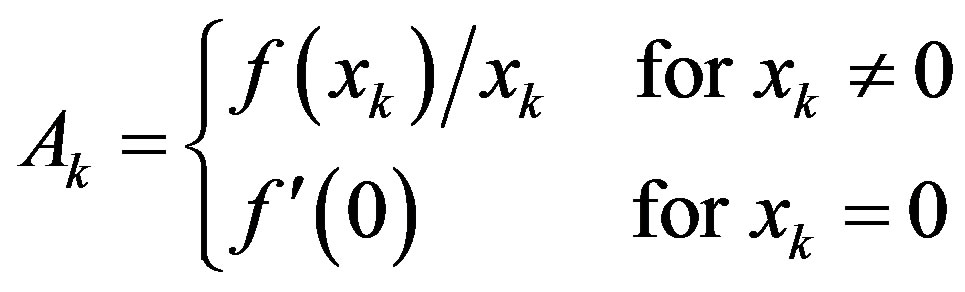 .
.
C) Analog Linear Quadratic Regulator
Together with a linear output equation, the linearized state Equation (15) constitutes a complete local linear model as
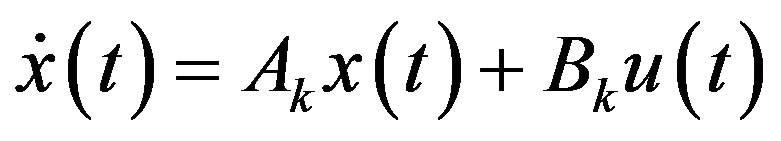 (18a)
(18a)
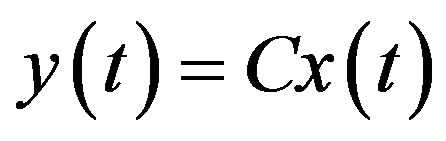 (18b)
(18b)
where  is the controlled output vector and
is the controlled output vector and 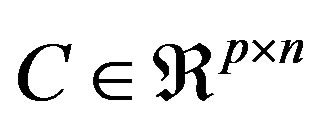 is a constant matrix. According to LQR [21], if the linear system (18) is both controllable and observable, the optimal control law to minimize the performance index
is a constant matrix. According to LQR [21], if the linear system (18) is both controllable and observable, the optimal control law to minimize the performance index
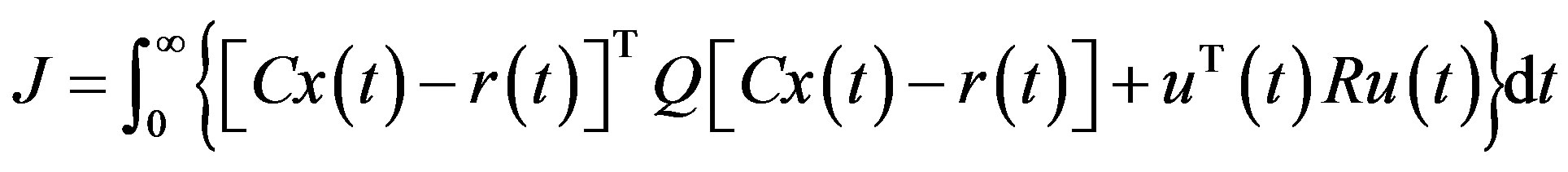 (19)
(19)
with  and
and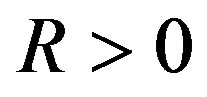 , is then given by
, is then given by
 (20)
(20)
where
 (21)
(21)
 (22)
(22)
r(t) is the reference for the controlled output y(t) to track, and Pk is the positive definite and symmetric solution of the Ricatti equation
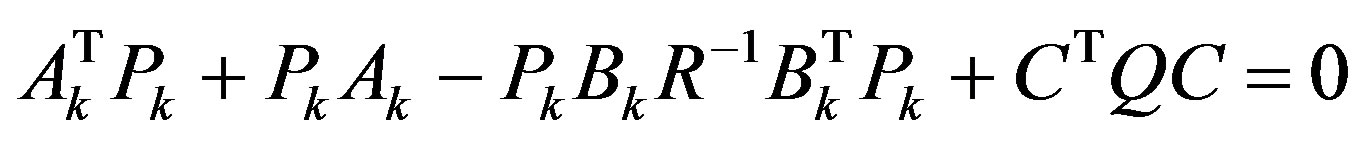 (23)
(23)
The weighting matrices Q and R should be tuned to make the resulting analog controller (20) give a desired control performance in the delay-free case.
3. Digital Redesign with Delay Compensation
For time-delayed systems where delays can be caused by network transmission, controller computation, A/D and D/A conversions etc, a delay compensating technique is proposed next based on global digital redesign. Compared with the conventional digital redesign methods that the conversion is limited in the scope of the controller, like the bilinear transformation  [22], closed-loop global digital redesign techniques take into account the closed-loop nature of the whole control system, so the resulting digital controller is able to maintain the essential performance of the analog counterpart even with a low sampling frequency [20,23-25].
[22], closed-loop global digital redesign techniques take into account the closed-loop nature of the whole control system, so the resulting digital controller is able to maintain the essential performance of the analog counterpart even with a low sampling frequency [20,23-25].
For a Single-Input-Single-Output (SISO) plant, the time delays in a control loop from network transmission, controller computation, A/D and D/A conversions, sensing and actuation etc, can be combined and then allocated to either the input or the output side of the plant for control design purpose [26]. The input side is used in this paper, so the local linear model (15) is modified to include the time delays as
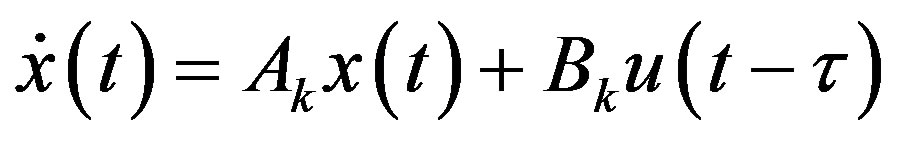 (24)
(24)
where τ is the combined input delay. Among global digital redesign methods, the prediction-based digital redesign in [20] reduces the conversion errors by shifting the digital control signal to defined inter-sampling instant, which is readily extendable for input delay compensation. This method is briefly introduced as follows and then extended to develop the proposed digital controller featuring the input delay compensation.
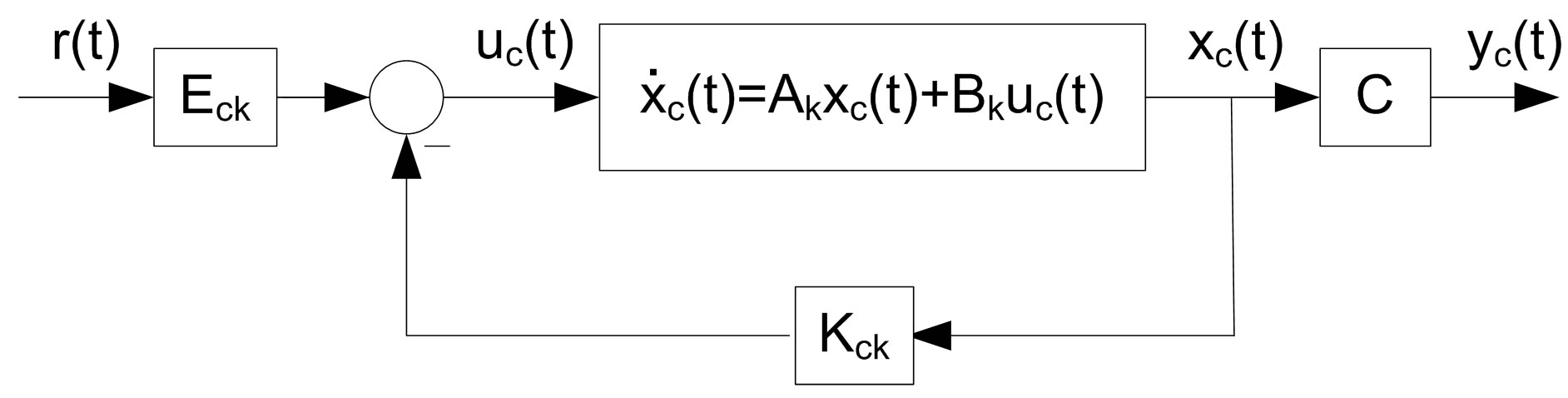
The analog linear plant (18) and the analog control law (20) constitute a complete analog control system as depicted in Figure 3(a) where the subscript c is intended to differ from the following equivalent hybrid system which is subscripted with d. Suppose the equivalent hybrid system as depicted in Figure 3(b) and formulated by
 (25a)
(25a)
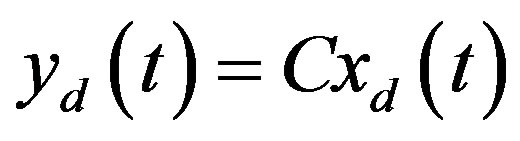 (25b)
(25b)
 (25c)
(25c)
where the analog control input  is a piecewiseconstant signal generated from the digital control input
is a piecewiseconstant signal generated from the digital control input  through Zero Order Hold (ZOH) as
through Zero Order Hold (ZOH) as 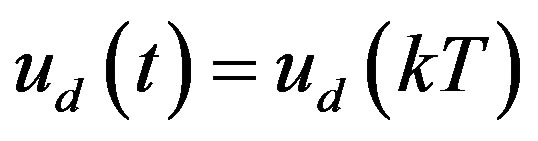 for
for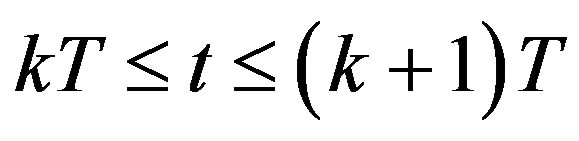 , and the digital state xd(kT) is the sample of the analog state xd(t) at the sampling instant t = kT; T is the sampling/control period. Equation (25c) is the digital control law to be designed so that the closed-loop state
, and the digital state xd(kT) is the sample of the analog state xd(t) at the sampling instant t = kT; T is the sampling/control period. Equation (25c) is the digital control law to be designed so that the closed-loop state 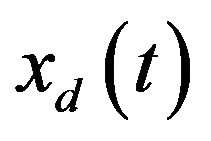 in the hybrid system can closely match the closed-loop state
in the hybrid system can closely match the closed-loop state 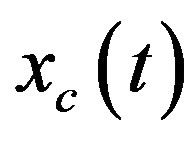 in the analog system at defined inter-sampling instant.
in the analog system at defined inter-sampling instant.
The solution 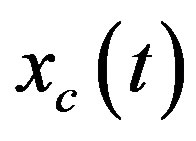 of (18a) at
of (18a) at  for
for 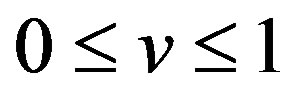 is
is
 (a)
(a) (b)
(b)
Figure 3. Analog control system and its equivelent hybrid cotnrol system.
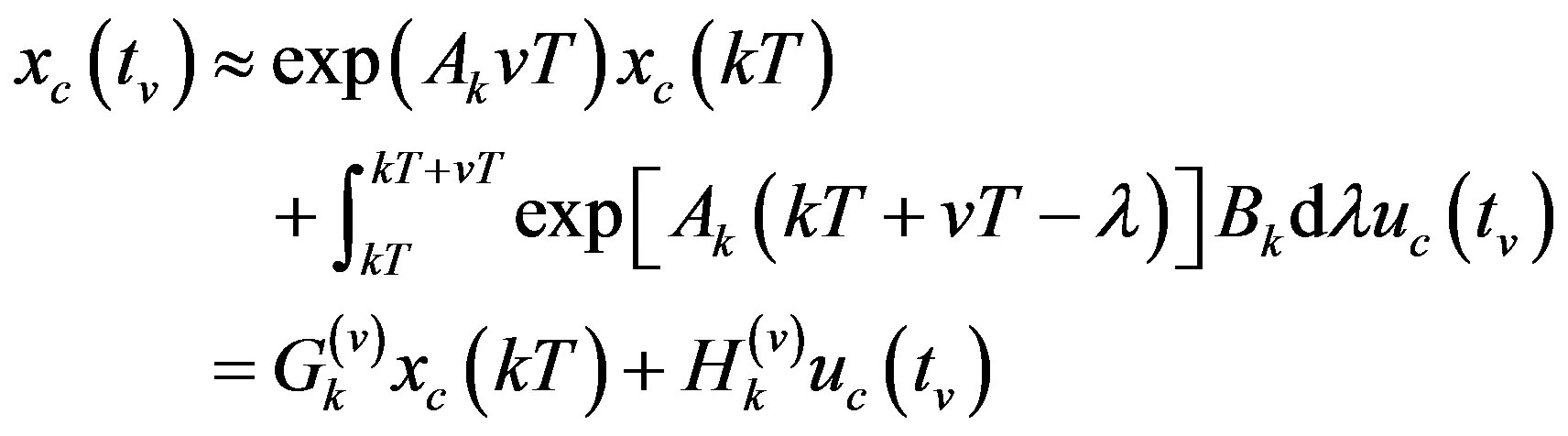 (26)
(26)
where 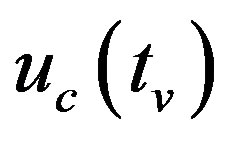 is a piecewise-constant input,
is a piecewise-constant input,
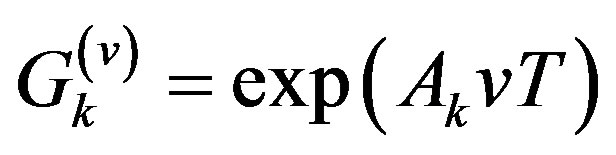
and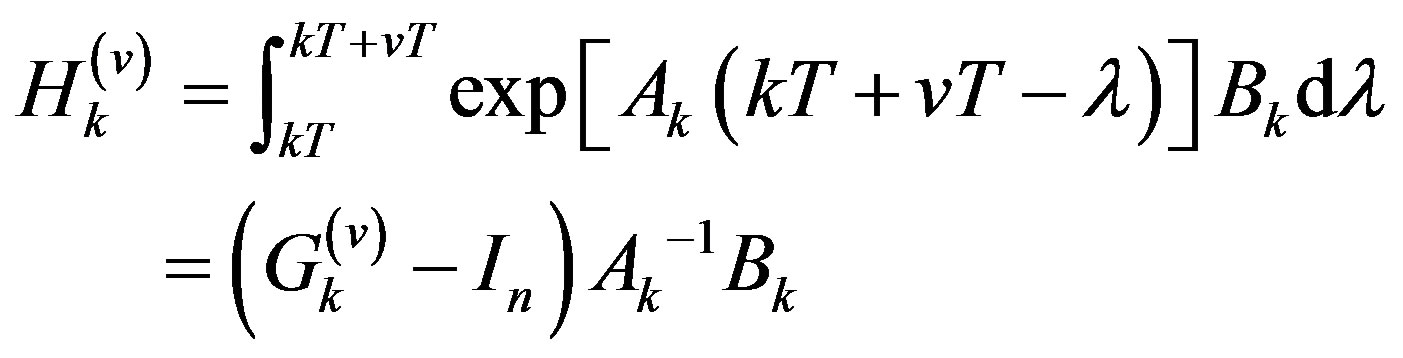 in which
in which 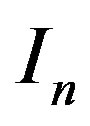 is an identity matrix of appropriate dimension. The solution
is an identity matrix of appropriate dimension. The solution 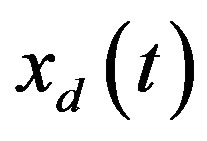 of (25a) at
of (25a) at 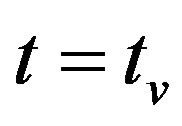 is
is
 (27)
(27)
Comparing (27) with (26) yields that with the assumption of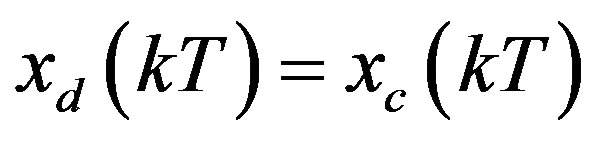 , the condition of
, the condition of 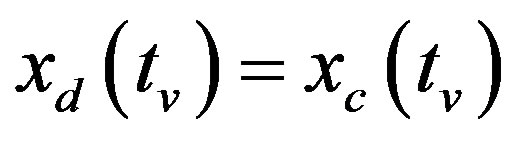 is
is , which leads to the prediction-based digital controller
, which leads to the prediction-based digital controller
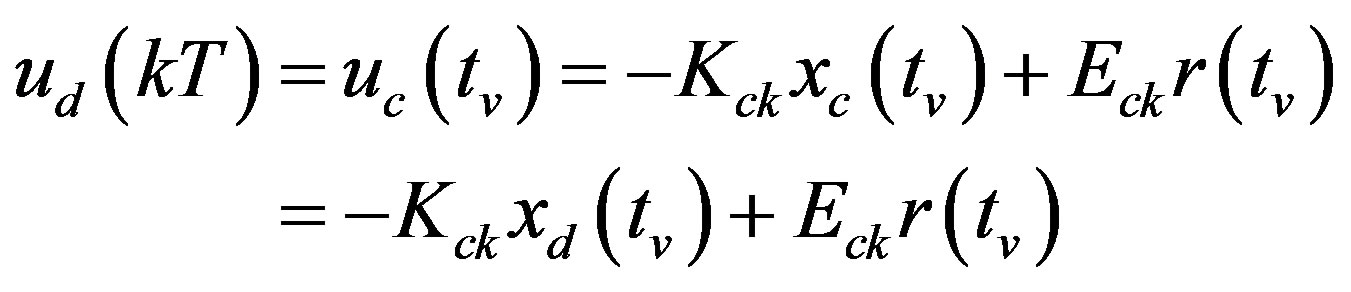 (28)
(28)
By substituting (27) into (28), 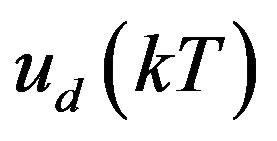 is solved as
is solved as

(29)
where  is an identity matrix of appropriate dimension. As a result, the desired digital control law (25c) is found from (29) having digital control gains
is an identity matrix of appropriate dimension. As a result, the desired digital control law (25c) is found from (29) having digital control gains
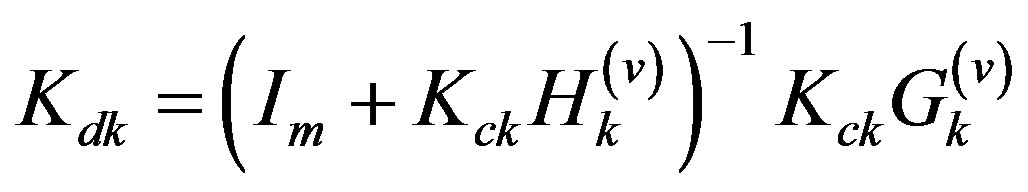 (30a)
(30a)
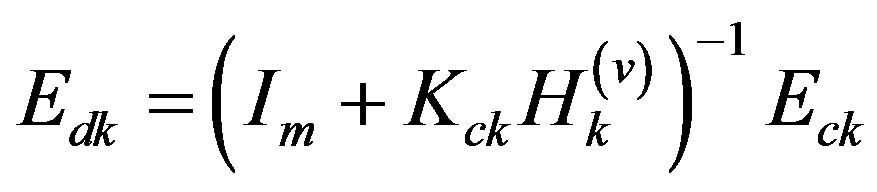 (30b)
(30b)
and the digital reference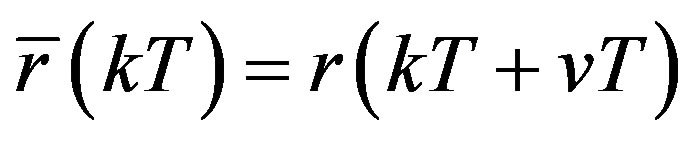 . The parameter v can be tuned to adjust the control performance.
. The parameter v can be tuned to adjust the control performance.
Next, the conclusion in (28) will be extended for the input delay compensation. Considering the combined input delay τ, the state equation (25a) in the hybrid system is changed to
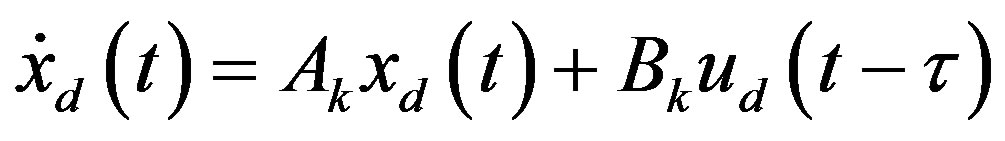 (31)
(31)
In order to compensate the input delay, the digital control input 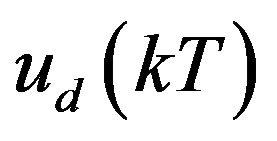 in (28) should be further predicted for the delay duration τ as
in (28) should be further predicted for the delay duration τ as
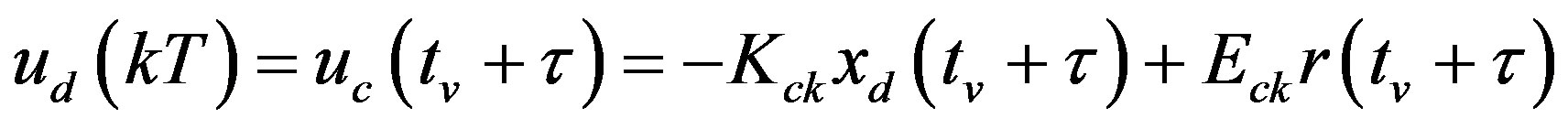 (32)
(32)
where the future state 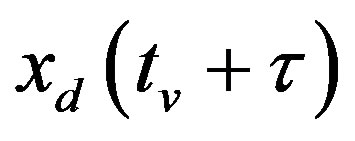 needs to be predicted based on the available signals
needs to be predicted based on the available signals 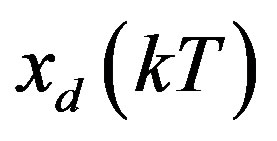 and
and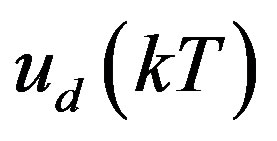 .
.
Compared with the sampling/control period, the time delays from controller computation, A/D and D/A conversions etc, are relatively small, so a reasonable assumption is made in the following reasoning for simplicity purpose that the total duration of time delays in the control loop should not be larger than a sampling period, i.e. the combined input delay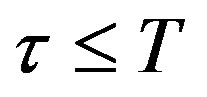 . As for the case that
. As for the case that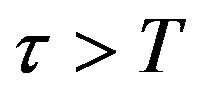 , the proposed method can still handle but will produce a more complicated controller structure.
, the proposed method can still handle but will produce a more complicated controller structure.
Let , so
, so 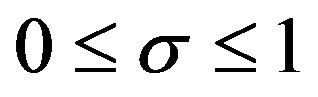 and
and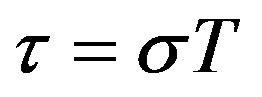 . The solution
. The solution 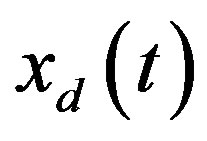 of (31) at
of (31) at  is
is
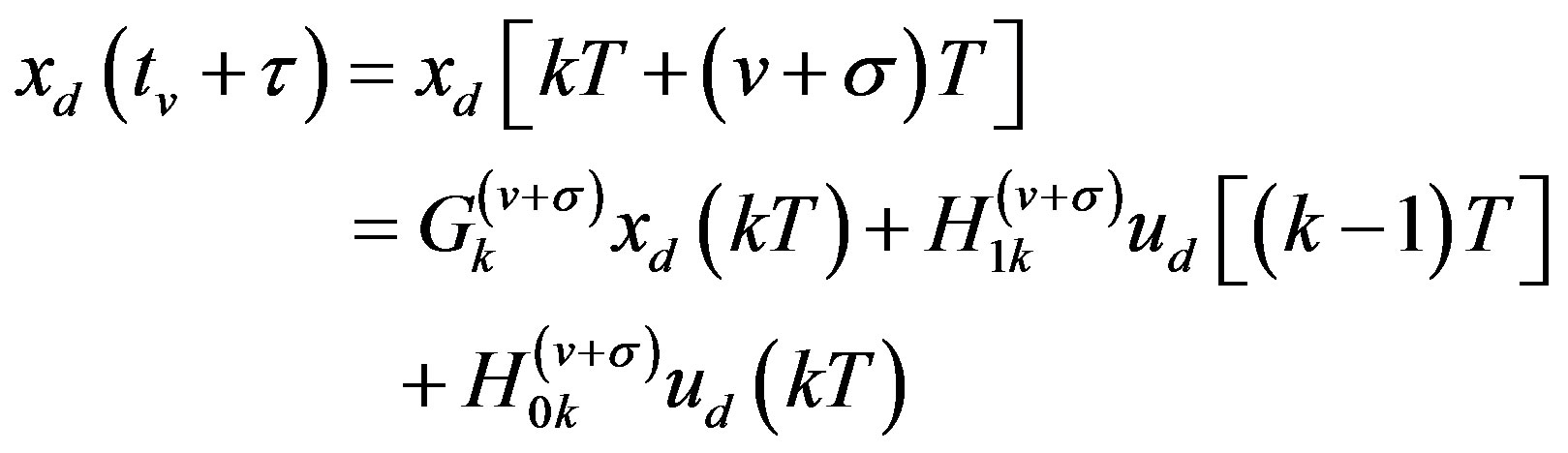 (33)
(33)
where 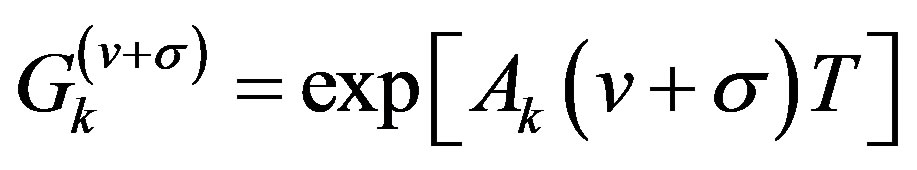 ,
, 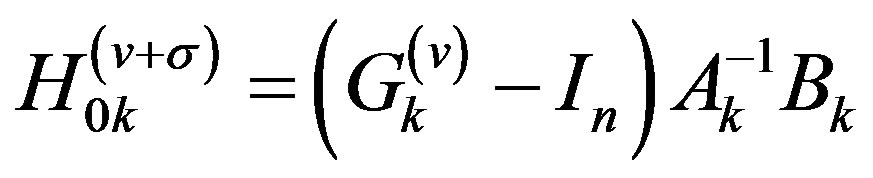 and
and .
.
By substituting (33) into (32), 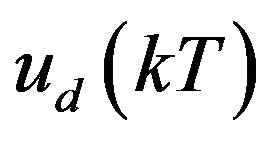 is solved as
is solved as
 (34)
(34)
As a result, the desired digital controller for input delay compensation is derived from (34) as
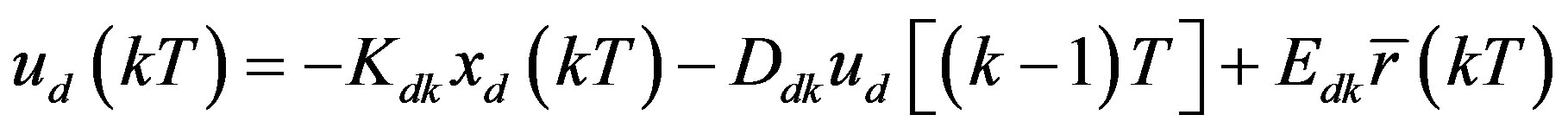
(35)
where
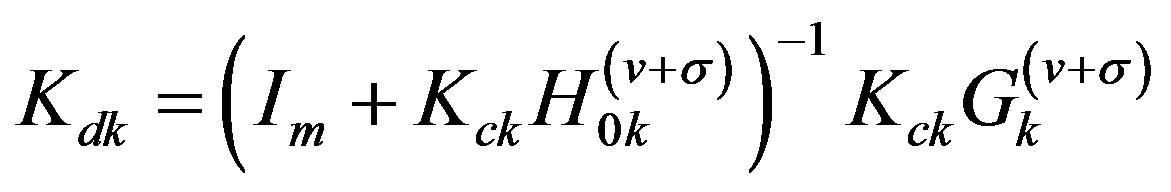 (36a)
(36a)
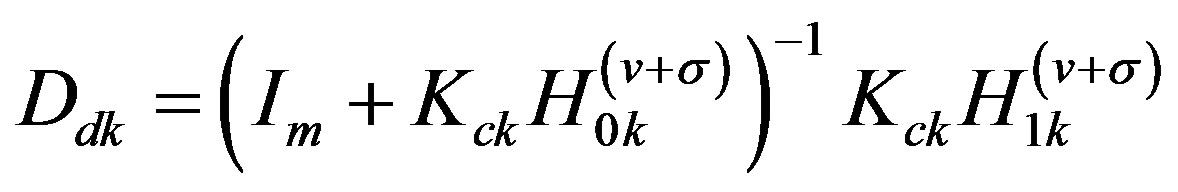 (36b)
(36b)
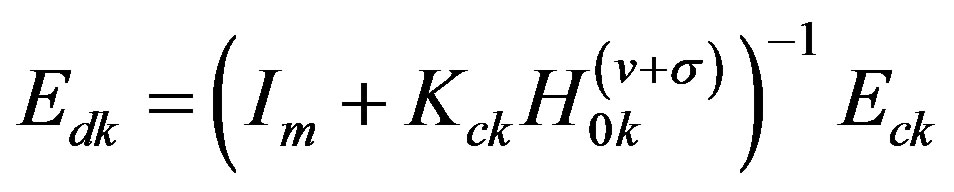 (36c)
(36c)
and . The resulting hybrid control system has the configuration as shown in Figure 4. It is noted that for τ = 0, i.e. in the delay-free case, (35) agrees with the prediction-based digital control law (25c) as
. The resulting hybrid control system has the configuration as shown in Figure 4. It is noted that for τ = 0, i.e. in the delay-free case, (35) agrees with the prediction-based digital control law (25c) as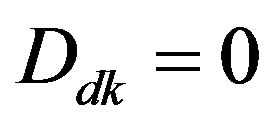 . Therefore, the prediction-based digital redesign can be taken as a special case of proposed delay-compensating digital redesign.
. Therefore, the prediction-based digital redesign can be taken as a special case of proposed delay-compensating digital redesign.
4. Iterative Procedure for Anti-windup Control
Consider a general nonlinear plant
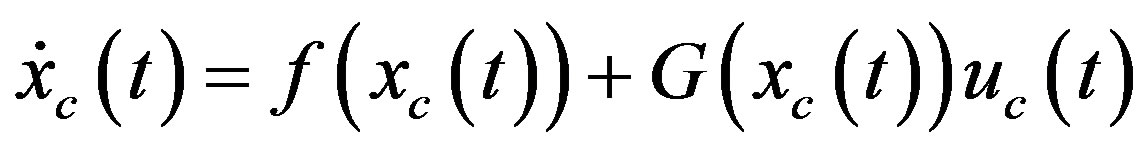 (37a)
(37a)
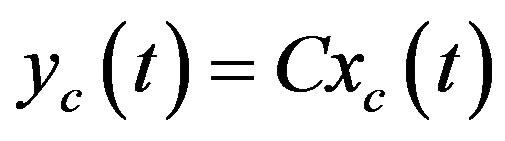 (37b)
(37b)
where the symbols are defined as in (14) and (18b), 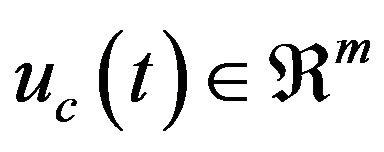 is the true input vector whose i-th entry has the constraints
is the true input vector whose i-th entry has the constraints
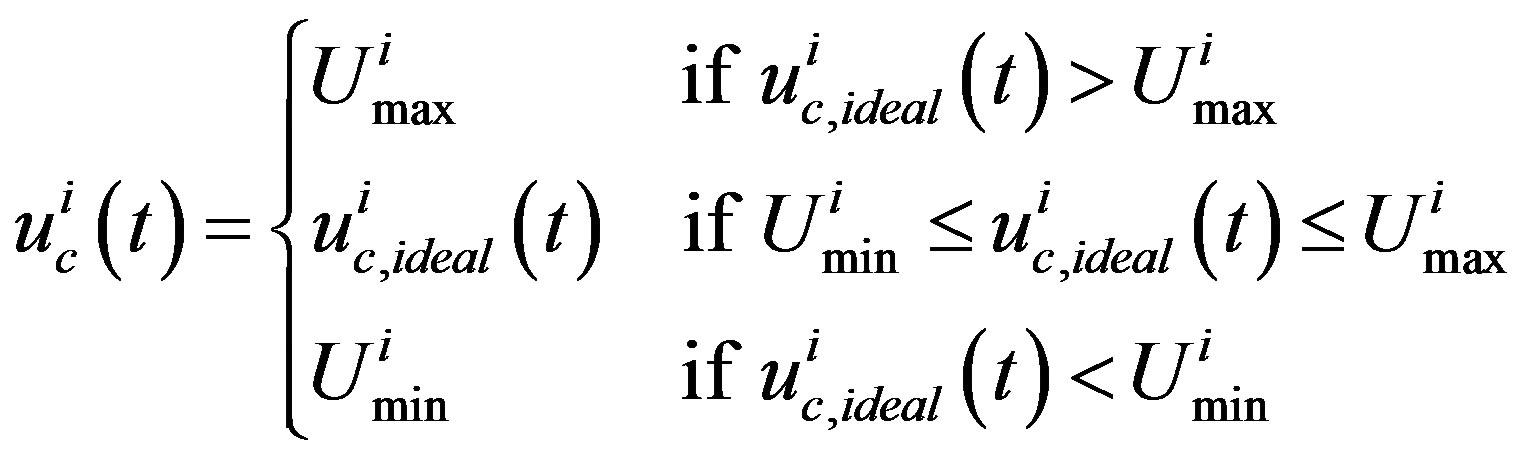 (38)
(38)
for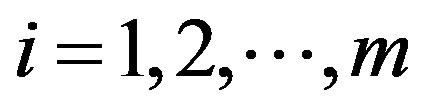 , in which
, in which 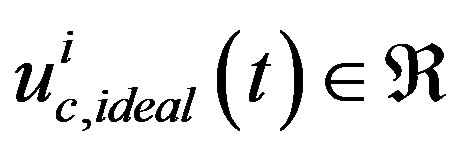 is the ideal i-th input and
is the ideal i-th input and 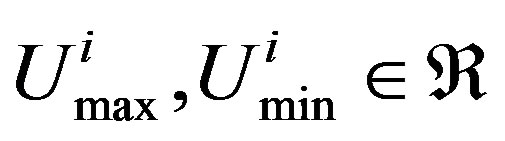 are the top and bottom limits for the i-th input, respectively. For the purpose of simplicity, let
are the top and bottom limits for the i-th input, respectively. For the purpose of simplicity, let 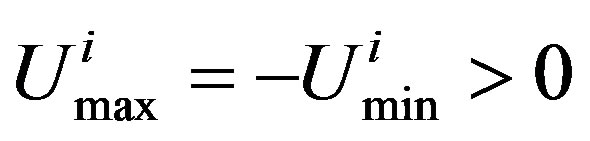 in the following reasoning. Through the optimal linearization in Section 2, the optimal local linear model of the nonlinear plant (37) at the k-th sampling instant is obtained as
in the following reasoning. Through the optimal linearization in Section 2, the optimal local linear model of the nonlinear plant (37) at the k-th sampling instant is obtained as
 (39a)
(39a)
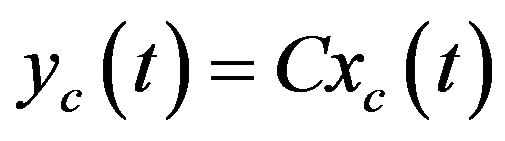 (39b)
(39b)
where 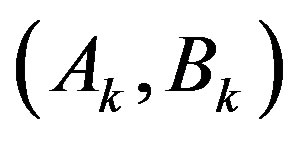 are given by (16) and (17), respectively. Should no input saturation occur, i.e.
are given by (16) and (17), respectively. Should no input saturation occur, i.e. 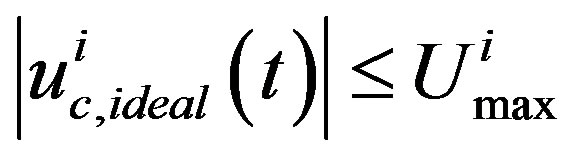 for
for , the state equation (39a) becomes
, the state equation (39a) becomes 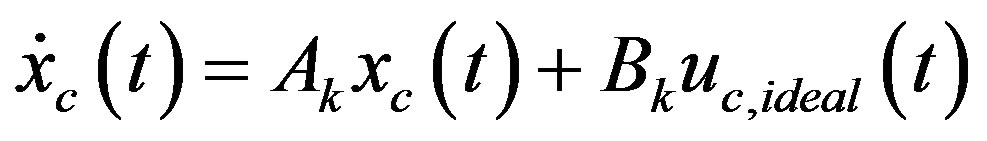 as
as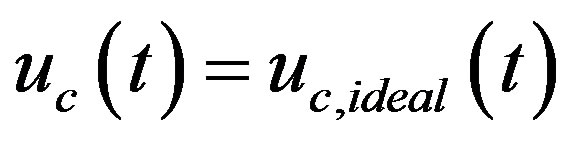 .
.
Whenever input saturation happens, say, the i-th ideal input  is out of limits, the state Equation (39a) becomes
is out of limits, the state Equation (39a) becomes

Figure 4. Proposed control scheme for input delay compensation.
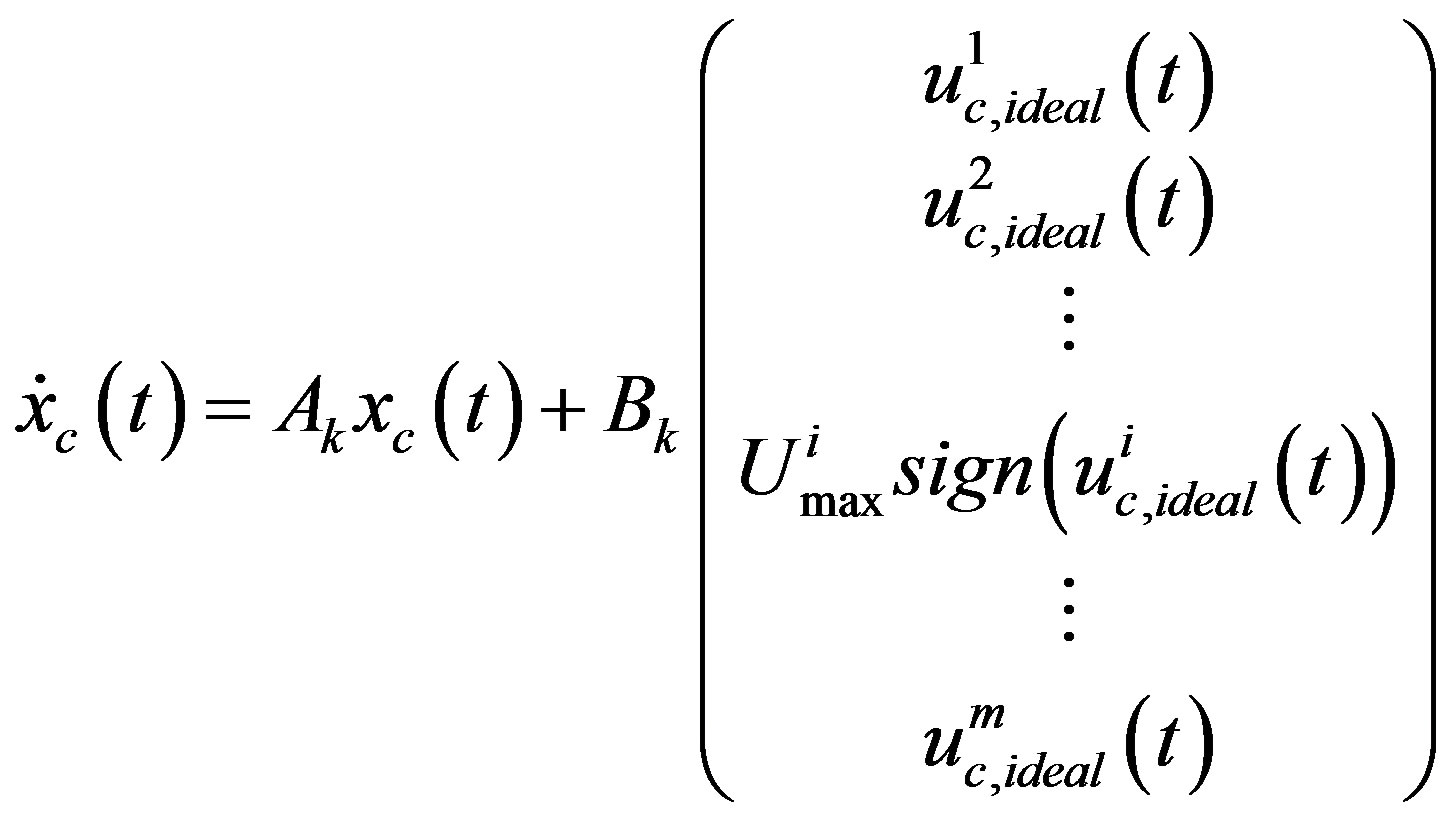 (40)
(40)
which is apparently non-smooth due to the scalar sign function. Substituting approximated scalar sign function (9) for  yields an approximated equation as
yields an approximated equation as
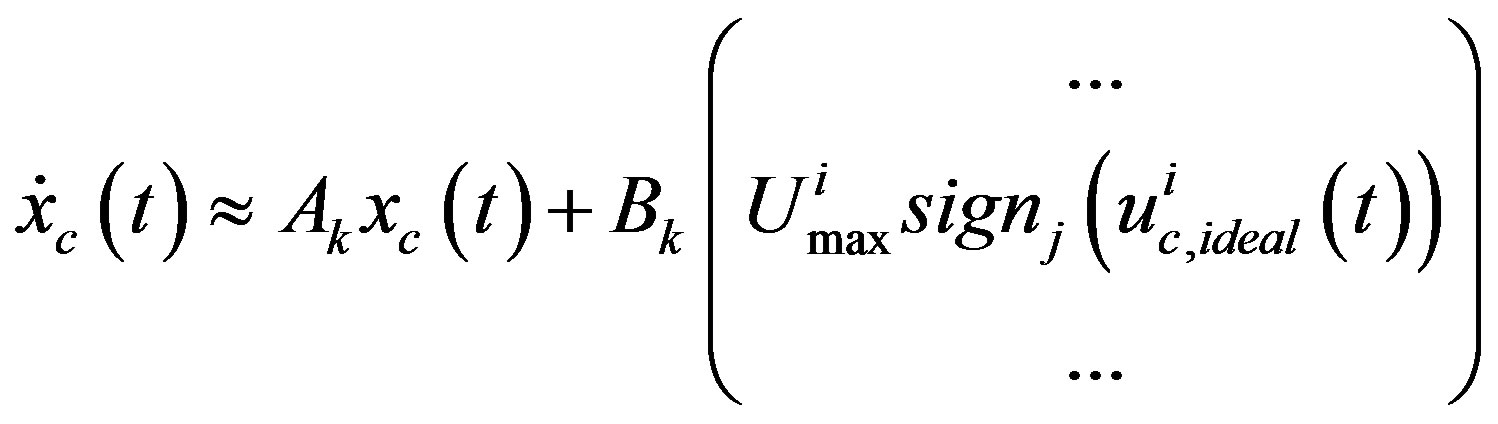 (41)
(41)
Equation (41) is still nonlinear due to  which can be further linearized by Remark 2 as
which can be further linearized by Remark 2 as
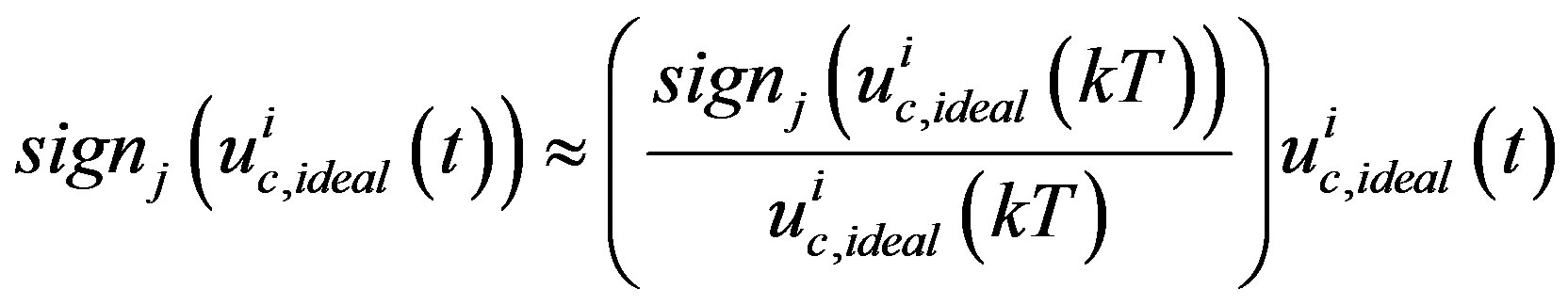
where  is the k-th operating point of
is the k-th operating point of 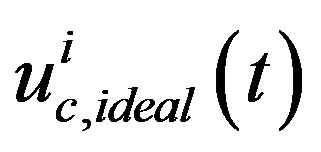 . In this way, the non-smooth saturation Equation (41) is fully linearized as
. In this way, the non-smooth saturation Equation (41) is fully linearized as
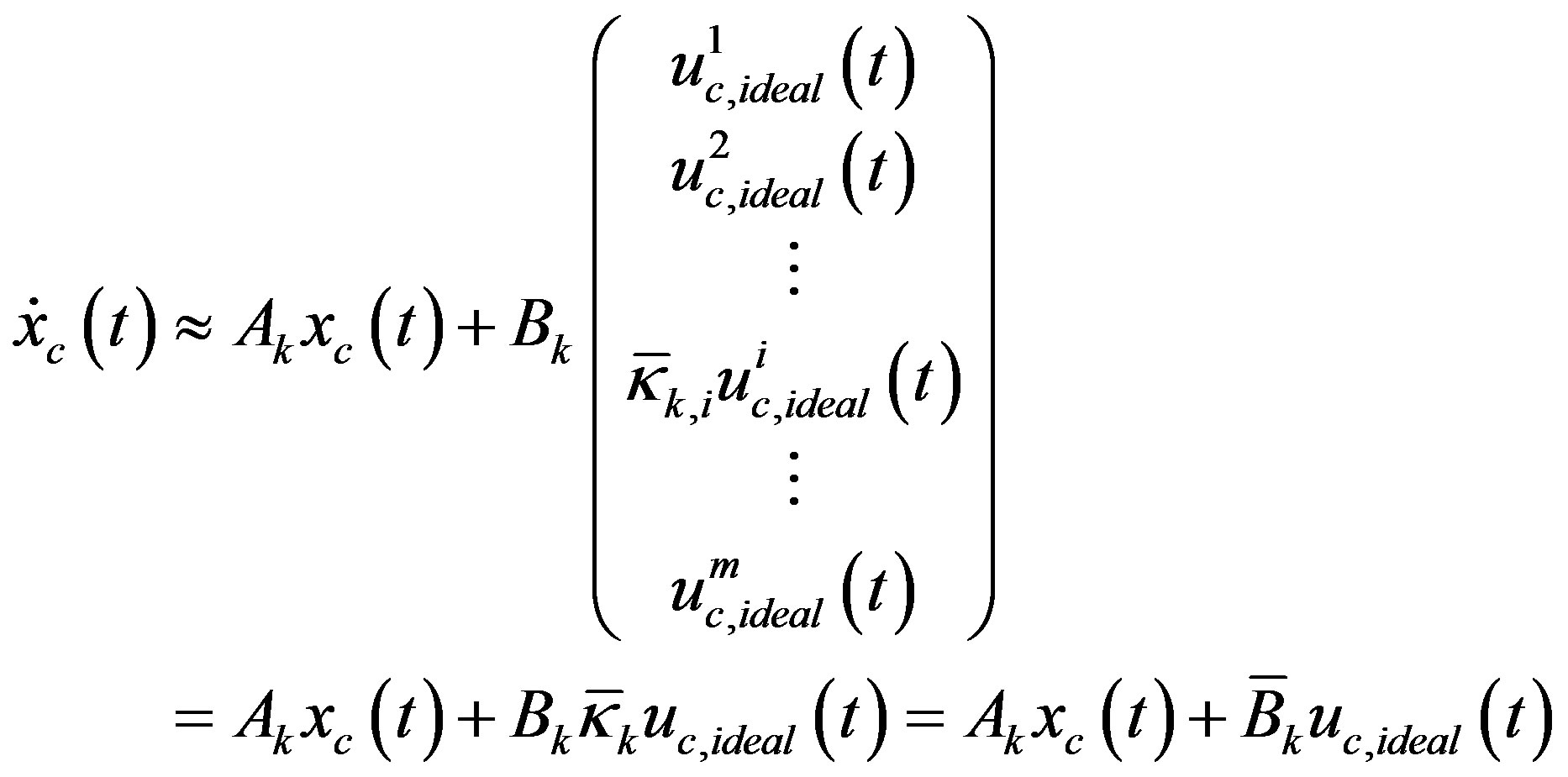 (42)
(42)
where
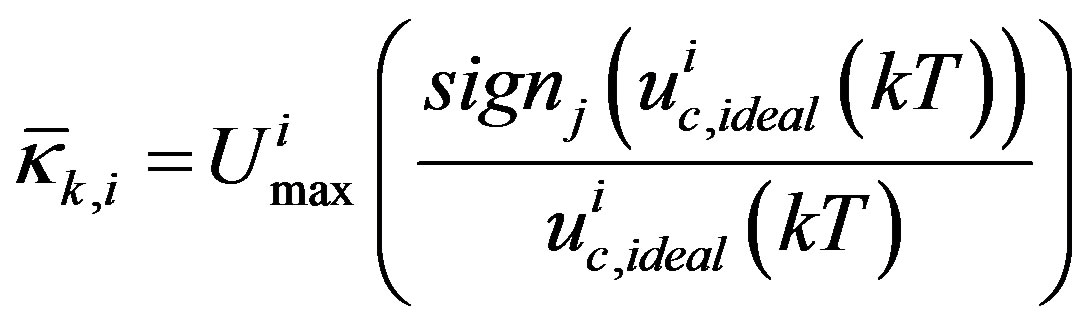 ,
,
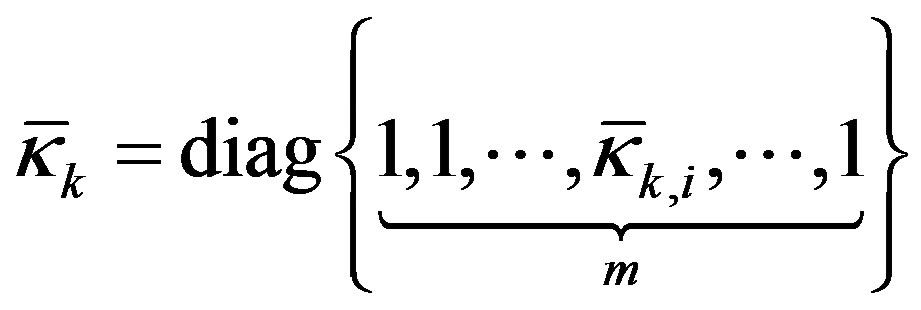
and .
.  is called input scaling factor.
is called input scaling factor.
To prevent the i-th input from saturation at t = kT, the input scaling factor  should be tuned such that
should be tuned such that
 , that is
, that is
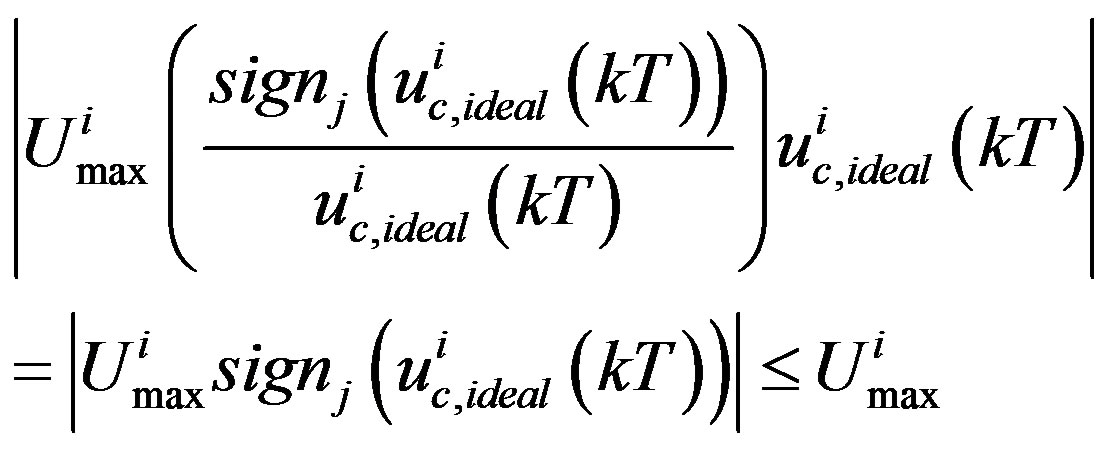 .
.
As mentioned in Remark 1, 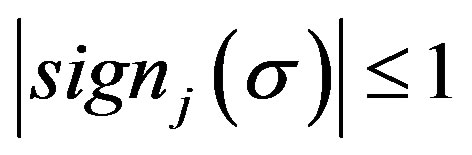 for j is even, so the approximation order j is always an even number in the proposed anti-windup design.
for j is even, so the approximation order j is always an even number in the proposed anti-windup design.
From the linear state Equation (42), the input matrix 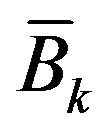 is required for designing the ideal control input
is required for designing the ideal control input , while the input scaling factor
, while the input scaling factor , which determines
, which determines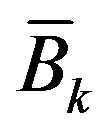 , involves the ideal control input
, involves the ideal control input  at t=kT which has not been designed yet. To break this deadlock, a pre-designed control input is used to estimate
at t=kT which has not been designed yet. To break this deadlock, a pre-designed control input is used to estimate 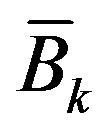 which is then utilized to design the true control input. For a sampled-data control system, a pre-designed digital control input can be used for this purpose. As a result, the linear state Equation (42) is modified to
which is then utilized to design the true control input. For a sampled-data control system, a pre-designed digital control input can be used for this purpose. As a result, the linear state Equation (42) is modified to
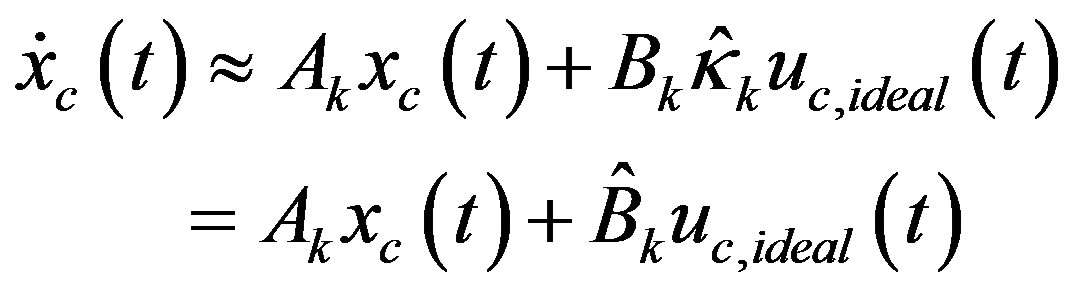 (43)
(43)
where the estimated input matrix 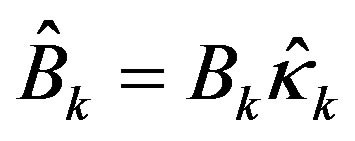 , the estimated input scaling factor
, the estimated input scaling factor  with
with
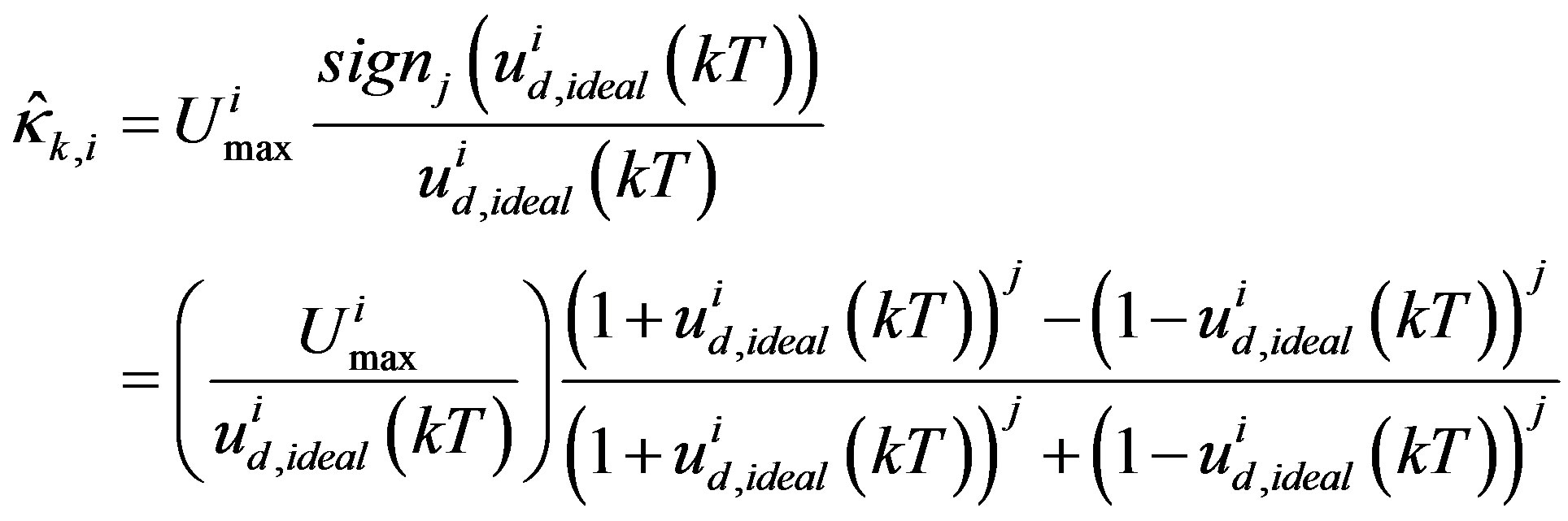 (44)
(44)
for j is even. 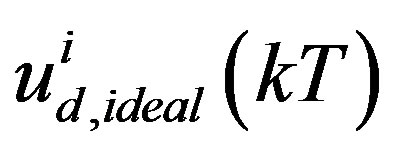 is the pre-designed digital control input which can be the digitally redesigned control input for the i-th component of
is the pre-designed digital control input which can be the digitally redesigned control input for the i-th component of  at t = kT from the prediction-based digital redesign (25c) or the proposed delay-compensating digital redesign (35). With arbitrary input elements saturated, the state Equation (43) is generalized as
at t = kT from the prediction-based digital redesign (25c) or the proposed delay-compensating digital redesign (35). With arbitrary input elements saturated, the state Equation (43) is generalized as
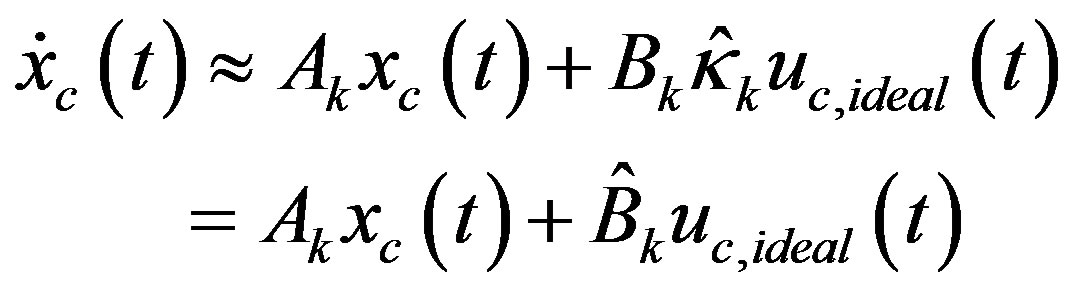 (45)
(45)
with 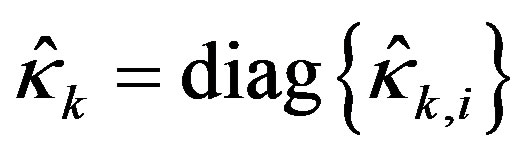 for
for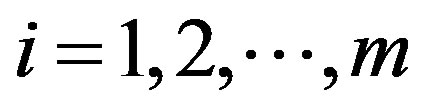 , where
, where 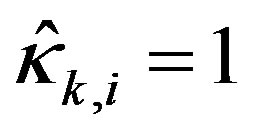 or is given by (44) depending on whether the corresponding ideal input violates the constraints or not.
or is given by (44) depending on whether the corresponding ideal input violates the constraints or not.
The general saturated state Equation (45) and the output Equation (39b) form a saturated system with modified system matrices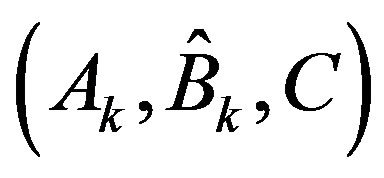 . Applying LQR (21-23) to it yields that with weighting matrices (Q, R), the optimal control law is determined by solving the Riccati equation
. Applying LQR (21-23) to it yields that with weighting matrices (Q, R), the optimal control law is determined by solving the Riccati equation
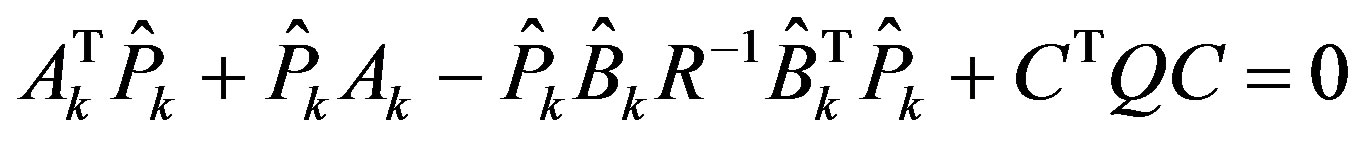 (46)
(46)
which can be rewritten as
 (47)
(47)
where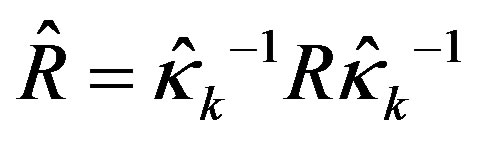 . The resulting optimal control law is
. The resulting optimal control law is
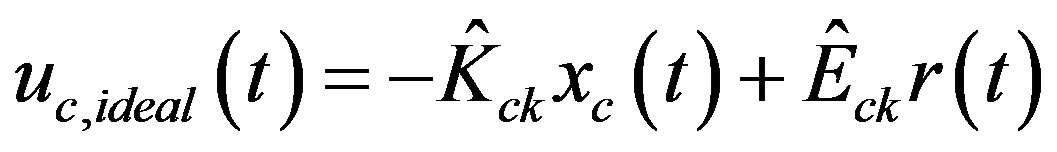 (48)
(48)
where the feedback gain 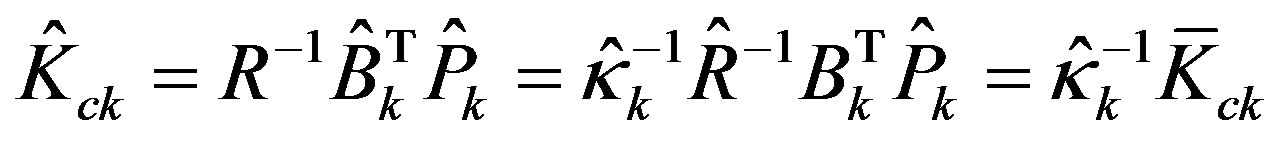 with
with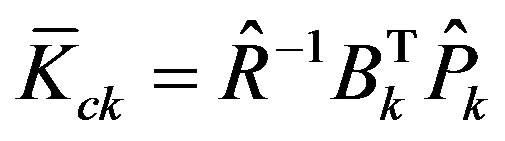 , and the forward gain
, and the forward gain
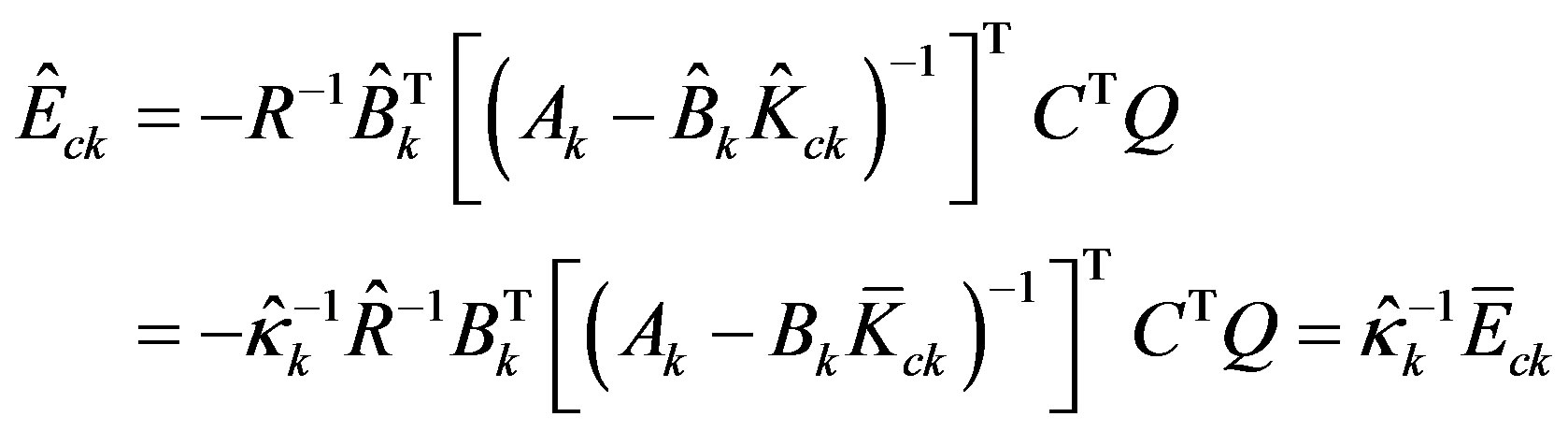
with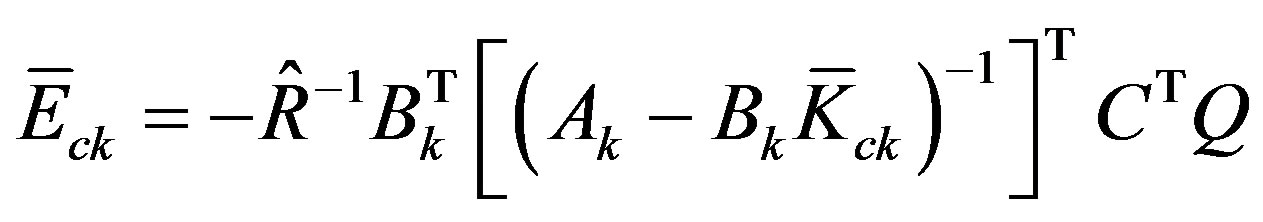 .
.
On the other hand, applying LQR to the original system 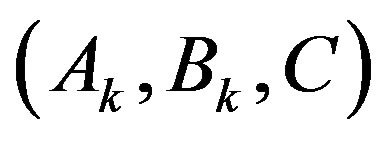 in (39) with the modified weighting pair
in (39) with the modified weighting pair  yields the optimal control law
yields the optimal control law
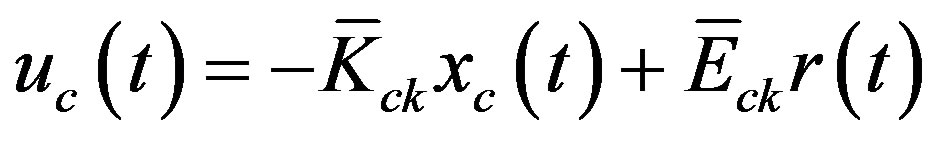 (49)
(49)
where the feedback gain 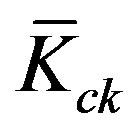 and the forward gain
and the forward gain 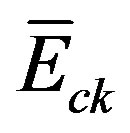 are shown above. The corresponding Riccati equation is the same as (47).
are shown above. The corresponding Riccati equation is the same as (47).
It can be observed by comparing the above two LQR designs that the problem of finding the optimal control law for the saturated system (45) with the weighting matrices (Q, R) can be reformulated as the same problem for the original system (39) using the same performance index (19), but with the new weighting matrices where
where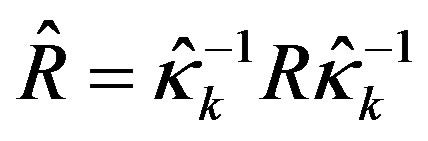 . Generally, both weighting matrices are selected to be positive definite diagonal matrices. So when the input scaling factor’s i-th diagonal element
. Generally, both weighting matrices are selected to be positive definite diagonal matrices. So when the input scaling factor’s i-th diagonal element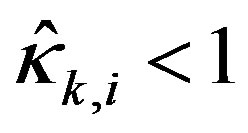 , the corresponding i-th diagonal elements of R and
, the corresponding i-th diagonal elements of R and 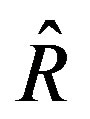 have the relationship of
have the relationship of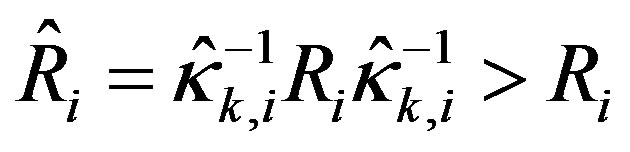 . As the matrix Q is kept the same in the performance index, the resulting control law
. As the matrix Q is kept the same in the performance index, the resulting control law  with
with  will have a smaller i-th element than the counterpart with (Q, R). Accordingly, the corresponding i-th element of digitally redesigned control input
will have a smaller i-th element than the counterpart with (Q, R). Accordingly, the corresponding i-th element of digitally redesigned control input  would be smaller as well, thus possibly avoiding input saturation. It is noted that although
would be smaller as well, thus possibly avoiding input saturation. It is noted that although 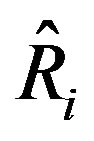 is
is 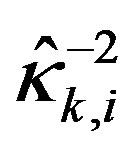 times greater than Ri, the newly resulting digital input
times greater than Ri, the newly resulting digital input 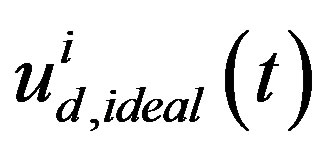 is not necessarily
is not necessarily 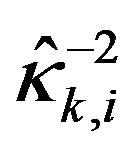 times smaller than the original one and may be still out of input limits after a single update. Therefore, it might be necessary to recursively update on
times smaller than the original one and may be still out of input limits after a single update. Therefore, it might be necessary to recursively update on 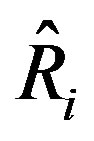 until the input lies within the saturation limits. Figure 5 summarizes the general steps of proposed antiwindup digital controller design for analog nonlinear system with input constraints. The digital redesign adopted is the proposed delay-compensating technique, so besides the anti-windup functionality, the proposed digital controller can also survive in a time-delayed environment.
until the input lies within the saturation limits. Figure 5 summarizes the general steps of proposed antiwindup digital controller design for analog nonlinear system with input constraints. The digital redesign adopted is the proposed delay-compensating technique, so besides the anti-windup functionality, the proposed digital controller can also survive in a time-delayed environment.
Remark 3: The approximation order j in the approximated scalar sign function can be tuned to achieve certain tradeoff between the control performance and the recursion efficiency. As shown in Figure 1, a smaller
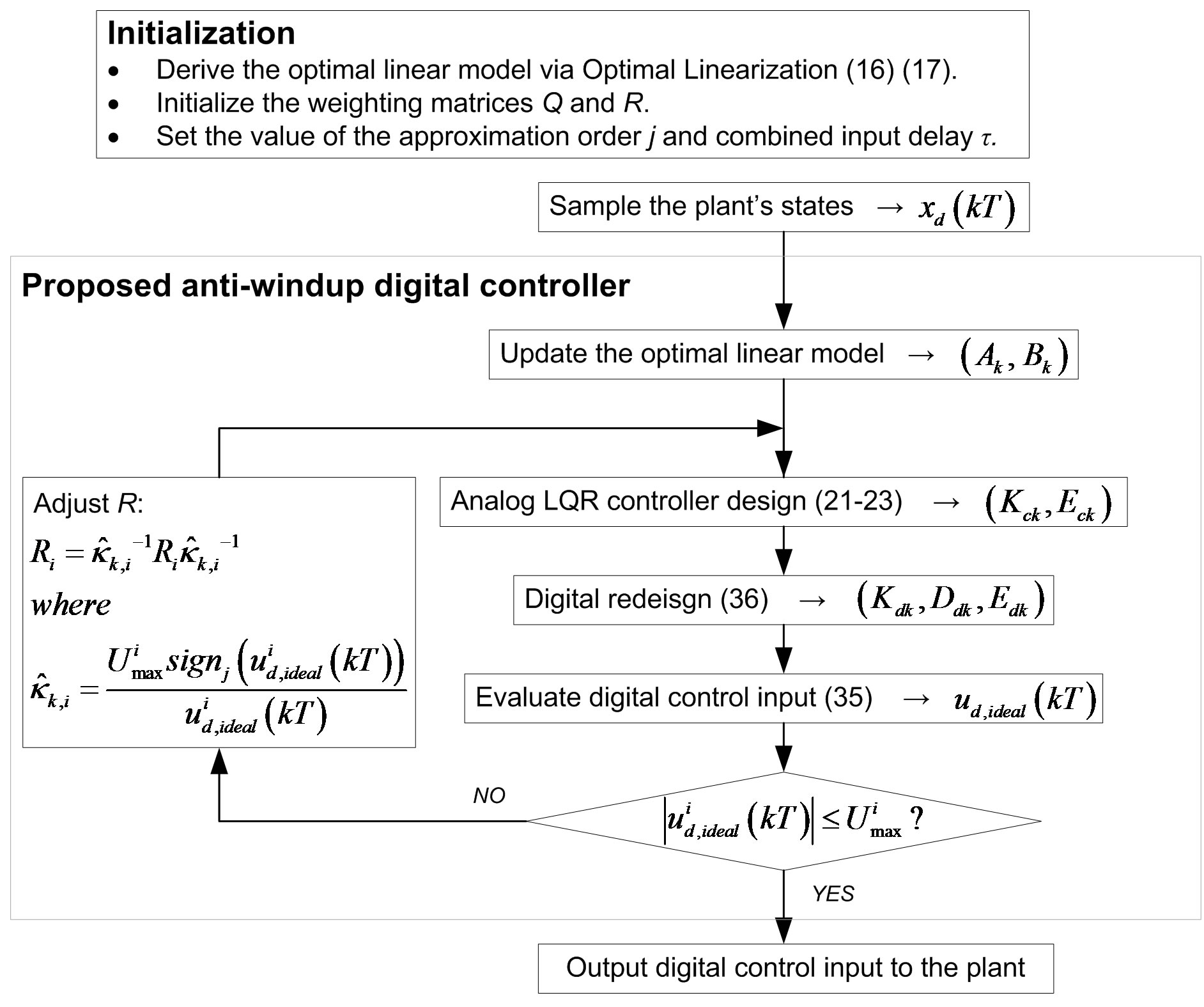
Figure 5. Anti-windup plus delay-compensating digital controller.
approximation order j leads to a faster decaying approximated scalar sign function, which results in a smaller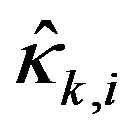 . This can be regarded as an ‘aggressive’ update scheme with the advantage that a smaller number of iterations are needed for suppressing the input to within the limits. But the disadvantage is that the input could be suppressed too much below the limit, which may bring a fairly slow system response.
. This can be regarded as an ‘aggressive’ update scheme with the advantage that a smaller number of iterations are needed for suppressing the input to within the limits. But the disadvantage is that the input could be suppressed too much below the limit, which may bring a fairly slow system response.
5. Simulation Results
As a typical nonlinear system, the rotary inverted pendulum system depicted in Figure 6 presents many challenging topics for investigation, like coupling, underactuation, instability, multivariable, time-sensitivity etc. The pendulum control can be simply categorized into swing-up (the motor drives the L-shaped arm to swing the pendulum up to around the upright position) and stabilization (the motor drives the arm to stabilize the pendulum at the upright position). Nonlinear control methods are usually proposed for swing-up control while LQR is commonly used for stabilization control. The failure to apply LQR on swing-up control results from the deficiency of traditional linearization method which only works around the equilibrium points while the pendulum is running in off-equilibrium region in swing-up process. In the proposed anti-windup design, the optimal linearization approach is utilized to obtain the local linear model at any operating point, and then LQR is applied to produce a state-feedback controller optimal for each operating point. Therefore, the proposed design can be applied throughout both swing-up and stabilization processes, avoiding the trouble of switching controllers in conventional methods.
The dynamics between the arm angle θ, the pendulum angle α and the motor voltage Vm is derived using Lagrangian equations as
 (50a)
(50a)
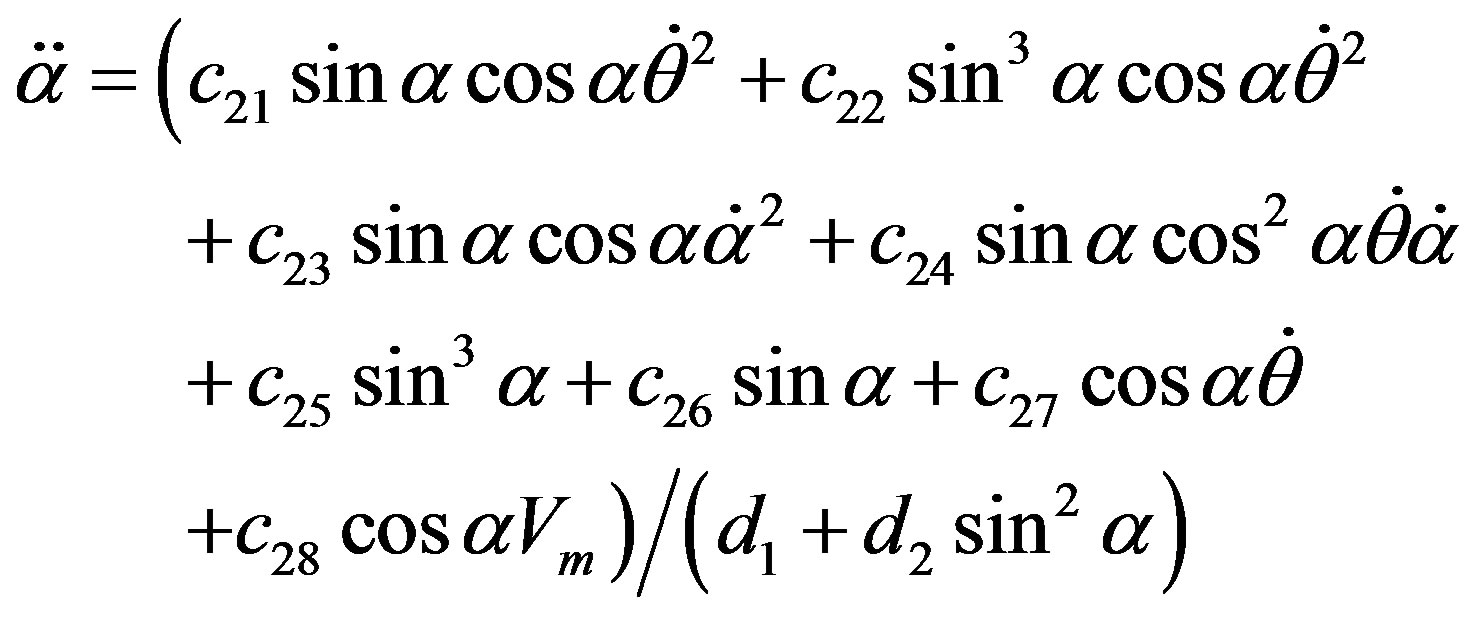 (50b)
(50b)
where
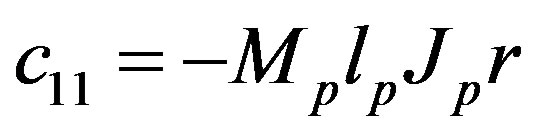 ,
,  ,
, 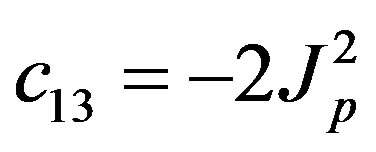 ,
,
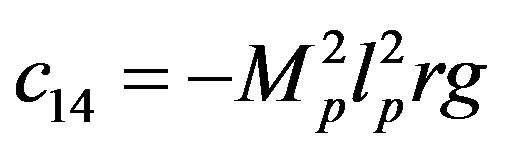 ,
, 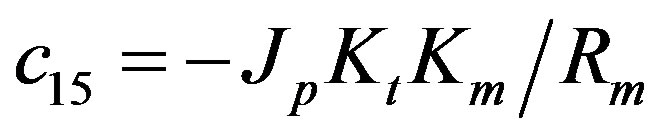 ,
, 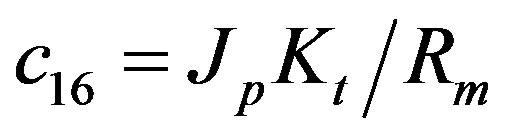 ,
,
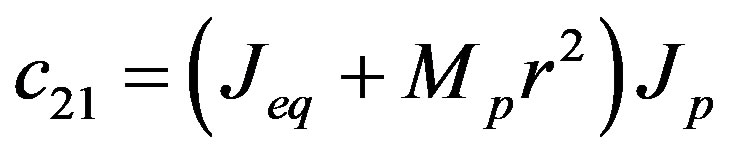 ,
, 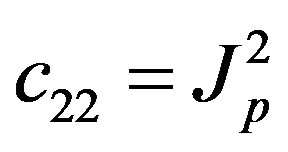 ,
, 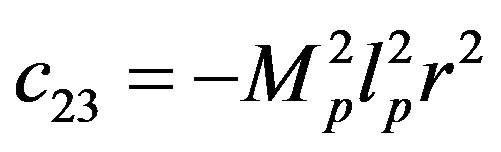 ,
,
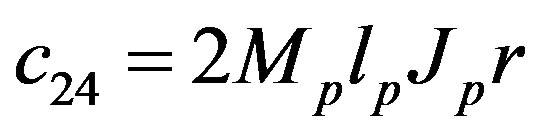 ,
, 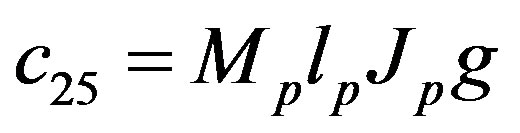 ,
,
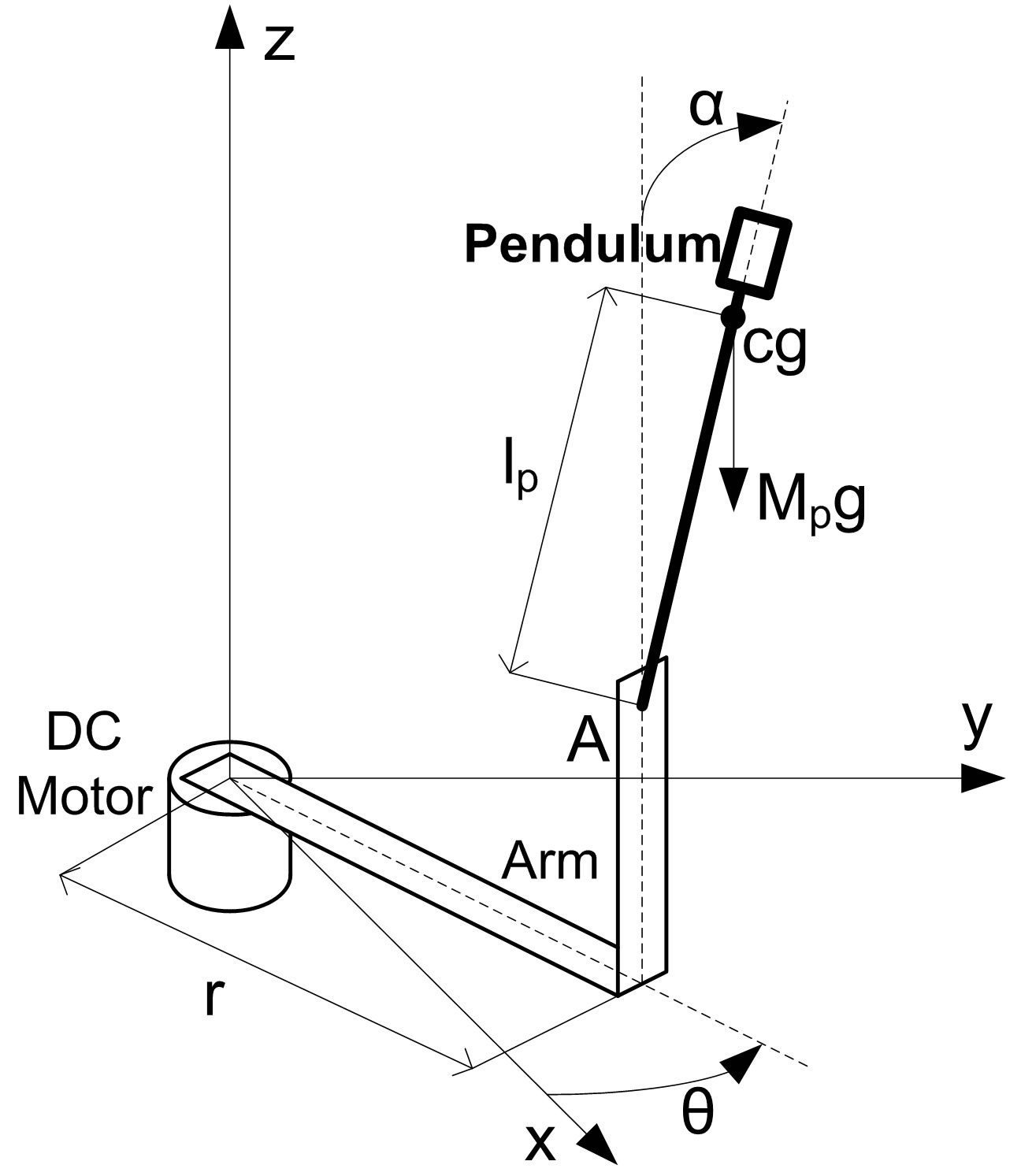
Figure 6. Single rotary inverted pendulum.
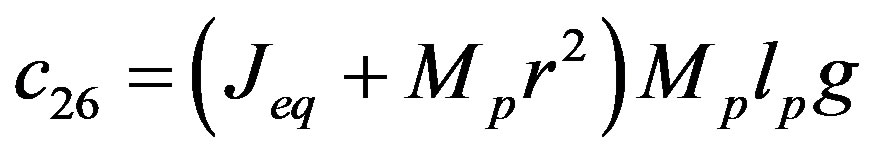 ,
, 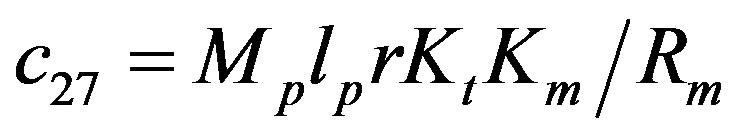 ,
,
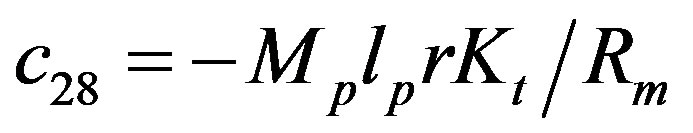 ,
, 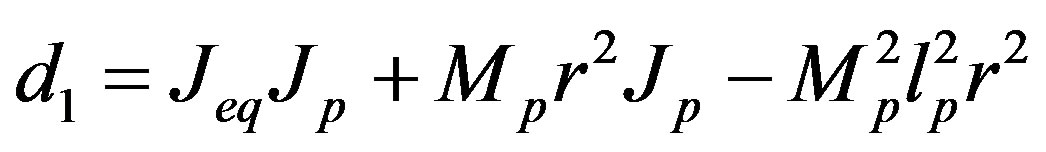 ,
,
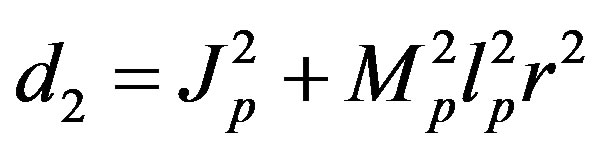 .
.
The parameters have physical meanings defined in Table 1 as well as their values used in the following simulations. Apparently, (50) is highly nonlinear and coupled expressions.
For space-saving purpose, the derivation of optimal local linear model of (50) is skipped, and only salient simulation results and necessary explanations are presented here. The proposed anti-windup methodology in Figure 5 was implemented in simulations with the initial pendulum angle of 179˚ (almost the downward position), the initial weighting matrices Q = diag{50, 0, 1, 0} and R = 1, and the digital control period T = 0.01 s. Figure 7 compares the simulated control performances of proposed method under no input limit and the limits ±30 V with different approximation order j. The corresponding control inputs are shown in Figure 8. Obviously, the freely redesigned digital control voltage in Figure 8 is out of the limits ±30 V over multiple control periods; using the proposed anti-windup method, whatever the value of j is, the control voltage is successfully suppressed to within the specified limits ±30 V. Another apparent fact is that over the first few control periods, the control voltage for j = 16 is suppressed more than the one for j = 26, which results in a little slower control performance in Figure 7. This echoes the claims by Remark 3. No time delay is introduced in the control loop in this case, so the proposed delay-compensating digital control law (35) converges to the prediction-based digital control law (25c) and the parameter v is set to 1.
Next, an input time delay is introduced between the pendulum’s motor and the digital controller to represent

Table 1. Single rotary inverted pendulum nomenclature.
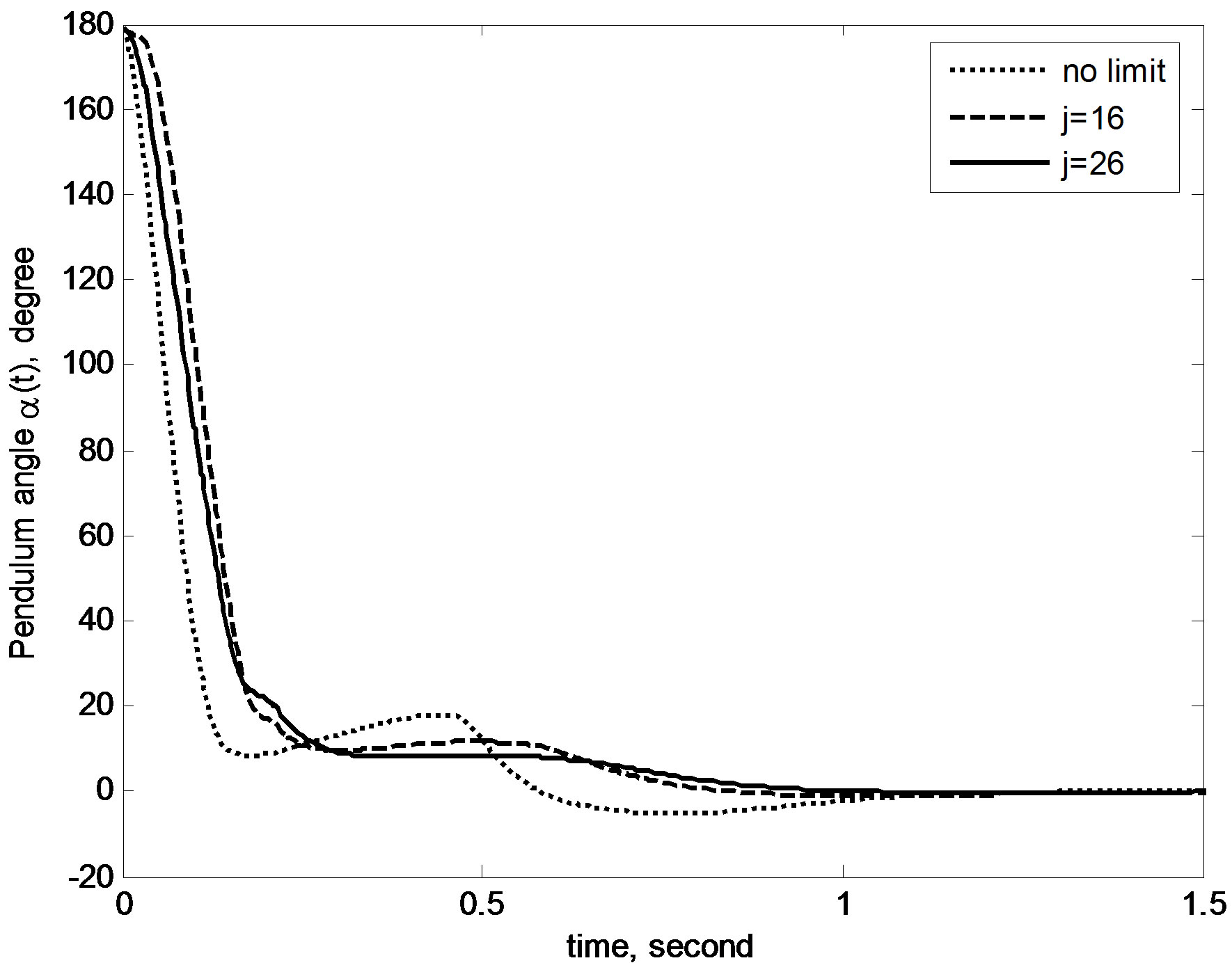
Figure 7. Control performance of proposed design in the delay-free case.
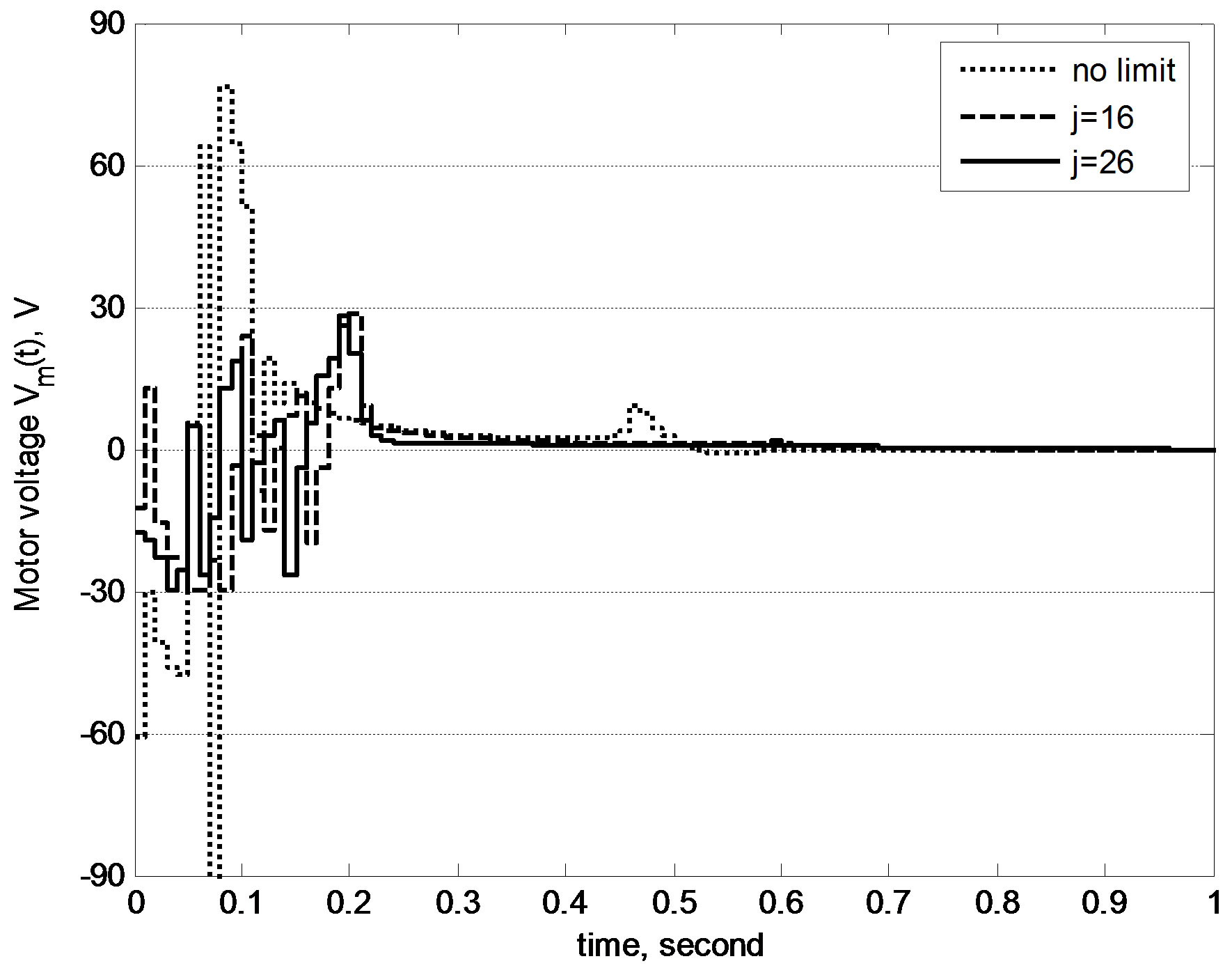
Figure 8. Control inputs of proposed design in the delayfree case.
the potential time delays in the real-world control loop. In order to demonstrate the delay-compensating capability, a reasonably long time delay τ = 0.02 s is used. The control period T is accordingly extended to 0.02 s as the proposed design assumes a control period no shorter than the delay duration. Other parameters and initial conditions are the same as the delay-free case. Simulation results showed that the controller from the prediction-based digital redesign cannot succeed any more, exhibiting an unstable behavior. In contrast, the proposed anti-windup plus delay-compensating controller can still survive with performances shown in Figure 9. Figure 10 depicts the evolutions of control inputs: the motor voltages in constrained cases are successfully suppressed to within the desired range. Hence, the efficacy of proposed design is well demonstrated.
6. Conclusions
This paper describes the design and application of an
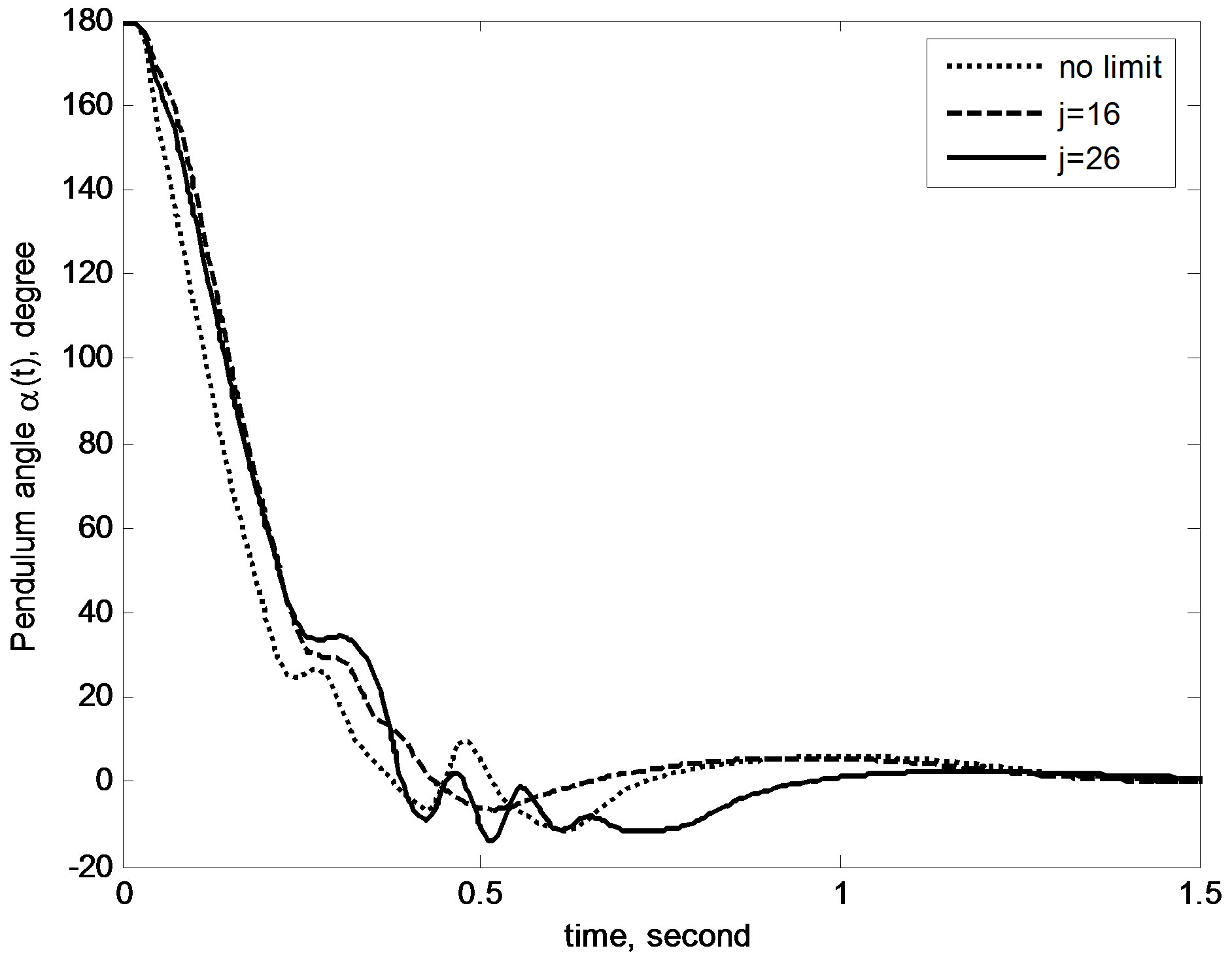
Figure 9. Control performance of proposed design in the delayed case.
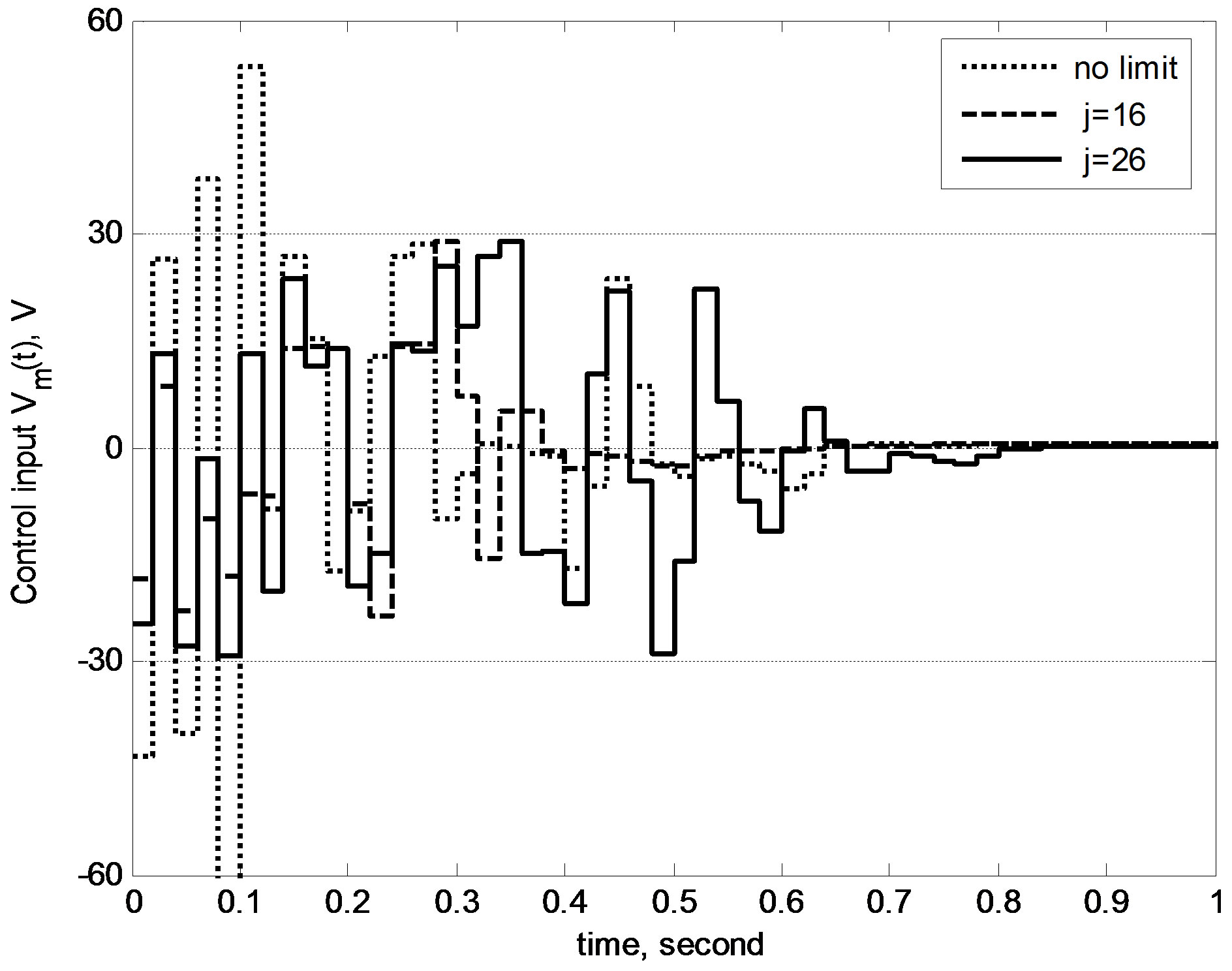
Figure 10. Control inputs of proposed design in the delayed case.
optimal anti-windup digital controller for analog nonlinear plants subject to input constraints. As a new antiwindup technique for sampled-data control systems, the proposed method has the following contributions: 1) the approximated scalar sign function is utilized to model non-smooth input saturations, which presents a new effective solution to sign-function constrained non-smooth problems; 2) through the optimal linearization, a general approach is developed for handling nonlinear systems with linear control theories in a broader region instead of conventionally being limited to around equilibriums; 3) aside from the anti-windup functionality, the proposed digital controller is capable of compensating time delays in the control loop, which would help guarantee its designed performance in real world implementations.
Funding
Research supported by NSF award #1238859, and Department of Education, HBGI Grant.
NOTES