Pricing Credit Default Swap under Fractional Vasicek Interest Rate Model ()
Keywords:Credit Default Swap; Bond; Contagious Risk; Fractional Vasicek Interest Rate Model; Looping Default
1. Introduction
Credit risk is one of the main risks in the financial industry. It is very important for the financial industry to manage credit risk effectively. Since credit default swap (CDS) appeared, it soon became one of the most important derivatives to manage credit risk because of its great advantages. However, as the rapid expansion of credit default swap market, some concealed contradictions exposed gradually, such as the United States subprime crisis and the European sovereign debt crisis. They make people realize that credit derivatives bring convenience and contain huge risk at the same time, especially contagious risk. Therefore, the valuation and pricing of credit derivatives have called for more effective models according to the real market.
Until now, there have been mainly two basic models: the structural model and the reduced-form model. In the first model, the firm’s default is governed by the value of its assets and debts, while the default in the reduced-form model is governed by the exogenous factor. However, the information of the firm’s assets is usually unknown and the problem of the valuation of credit derivatives involving the jump-diffusion process is still difficult to get explicit results in the event of defaulting before the maturity date in the structural model. Therefore, comparing with the structural approach, the reduced-form approach is more flexible and tractable in the real market. In this paper, we will price the bonds and CDS in the reduced-form models.
The reduced-form model was pioneered by [1,2]. They introduced exogenous mechanism to describe the firm’s default. Their models considered the default as a random event which was controlled by an exogenous intensity process. Later, [3] extended their models and considered the default intensity which satisfied the Cox process. [4] further discussed the jump affine intensity, and so on.
In the reduced-form model, suppose that  is a filtered probability space satisfying the usual conditions, where
is a filtered probability space satisfying the usual conditions, where  (
( is large enough but finite), and
is large enough but finite), and  is an equivalent martingale measure under which discounted securities’ prices are martingales. On
is an equivalent martingale measure under which discounted securities’ prices are martingales. On , there is a
, there is a 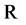 -valued process
-valued process  where
where  represents the economy-wide state variable. Denote
represents the economy-wide state variable. Denote  and
and , where
, where  represents the default process of company
represents the default process of company . When
. When 
first jumps from 0 to 1, we call the company  defaults and denote
defaults and denote  be the default time of company
be the default time of company .
.
Thus,  where
where  is the indicator function. This paper consider that the interest rate is the only state variable and that the default intensity
is the indicator function. This paper consider that the interest rate is the only state variable and that the default intensity  is stochastic. The default times of company
is stochastic. The default times of company  can be defined as
can be defined as
 (1)
(1)
where  is the unit exponential random variable. The distributions of conditional default probability of company
is the unit exponential random variable. The distributions of conditional default probability of company  are given by
are given by
 (2)
(2)
The fractional Brownian motion was firstly defined and studied by Kolmogorov in Hilbert space, and was named to the Wiener spiral. Because the fractional Brownian motion has the properties of self-similarity and long-range dependence and many phenomena in financial market show these properties in some certain, the fractional Brownian motion becomes a very suitable tool in different applications such as mathematical finance.
However, for the Hurst index , the fractional Brownian motion is neither a Markov process, nor a semimartingale, and we can not use the usual stochastic calculus to analyze it. Worse still after a pathwise integration theory for fractional Brownian motion was developed by [5,6], it was proved that their market mathematical models driven by the fractional Brownian motion could have arbitrage ([7]). Later, after the development of a new kind of integral based on the Wick product (see [8,9]) called fractional Ito integral, it was proved ([9]) that the corresponding Ito type fractional Black-Scholes market has no arbitrage. In the same paper, a formula for the price of a European option at
, the fractional Brownian motion is neither a Markov process, nor a semimartingale, and we can not use the usual stochastic calculus to analyze it. Worse still after a pathwise integration theory for fractional Brownian motion was developed by [5,6], it was proved that their market mathematical models driven by the fractional Brownian motion could have arbitrage ([7]). Later, after the development of a new kind of integral based on the Wick product (see [8,9]) called fractional Ito integral, it was proved ([9]) that the corresponding Ito type fractional Black-Scholes market has no arbitrage. In the same paper, a formula for the price of a European option at  was derived. Based on these conclusions, [10] proved some results regarding the quasi-conditional expectation and obtained a risk-neutral valuation formula of the European option for every
was derived. Based on these conclusions, [10] proved some results regarding the quasi-conditional expectation and obtained a risk-neutral valuation formula of the European option for every 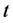 before the maturity date. All the conclusions build a solid theoretical foundation for its application in the financial field.
before the maturity date. All the conclusions build a solid theoretical foundation for its application in the financial field.
This paper also consider the Hurst index . We will give the following definitions and theorems without the proofs. The details can be found in [10].
. We will give the following definitions and theorems without the proofs. The details can be found in [10].
Definition 1 Let  be measurable. Then
be measurable. Then  if
if

where ,
, .
.
Definition 2 (Fractional Brownian motion) Let  be the filtered probability space satisfying the usual conditions.
be the filtered probability space satisfying the usual conditions.  is a constant. The fractional Brownian motion with Hurst index
is a constant. The fractional Brownian motion with Hurst index 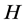 is a continuous Gauss process
is a continuous Gauss process , which satisfies 1)
, which satisfies 1) ;
;
2) .
.
Definition 3 (Quasi-conditional expectation) Let ,
,  be the random distribution space with inductive topology, then the quasi-conditional expectation of
be the random distribution space with inductive topology, then the quasi-conditional expectation of  with respect to
with respect to
 is defined by
is defined by
 (3)
(3)
where . For simplicity, we denote it as
. For simplicity, we denote it as .
.
Definition 4 (Quasi-martingale) Suppose that  is an adapted stochastic process with respect to
is an adapted stochastic process with respect to
 . If
. If ,
,  then we say that
then we say that  is a quasi-martingale.
is a quasi-martingale.
From the above definitions, it is easy to prove the following theorems:
Theorem 1 ([10])
1)  is a quasi-martingale;
is a quasi-martingale;
2) Let , then
, then  is a quasi-martingale;
is a quasi-martingale;
3) Let , then
, then  is a quasi-martingale.
is a quasi-martingale.
The interest rate has an important influence on pricing credit derivatives, especially after the fixed interest rate is replaced by the floating interest rate, and the impact will be more important. From the point of time, the interest rate also has the characteristics of the fractional Brownian motion. Therefore, [11] used the fractional Brownian motion to describe the interest rate process which was the fractional Vasicek interest rate model and priced the European option. In this paper, we also consider the Vasicek interest rate model:
 (4)
(4)
where  is the fractional Brownian motion which describes the market risk,
is the fractional Brownian motion which describes the market risk, 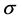 is the standard deviation which represents the stochastic volatility, parameter
is the standard deviation which represents the stochastic volatility, parameter  is the long-term average of interest rate, and
is the long-term average of interest rate, and  represents the speed of recovery that
represents the speed of recovery that  returns to
returns to  from the deviation value of the long-term average. The interest rate has the following explicit solution:
from the deviation value of the long-term average. The interest rate has the following explicit solution:
 (5)
(5)
where  is the interest rate value at time 0.
is the interest rate value at time 0.  follows the normal probability distribution with mean
follows the normal probability distribution with mean  and the variance
and the variance . Thus,
. Thus,  is the normal stochastic variable with mean
is the normal stochastic variable with mean  and the variance
and the variance .
.
To make the formula simple, we suppose that the face value of bond is 1 dollar. The default-free bond’s price was obtained in [11] as following:
Theorem 2 ([11]) Let  be the time-t value of the default-free bond with the maturity date
be the time-t value of the default-free bond with the maturity date . The interest rate is derived by the fractional Brownian motion as above. The price of market risk is
. The interest rate is derived by the fractional Brownian motion as above. The price of market risk is , then
, then
 (6)
(6)
where


2. Bonds’ Pricing under the Looping Default Model
[12] firstly proposed the model of credit contagion to account for concentration risk in large portfolios of defaultable securities (DL Model). Later, [13] thought the traditionally structural and reduced-form models were full of problems because they all ignored the firm’s specific source of credit risk. They made use of the Davis’s contagious model and introduced the concept of counterparty risk which was from the default of firm’s counterparties. In their models, they paid more attention to the primary-secondary framework in which the intensity of default was influenced by the economy-wide state variables and the default state of the counterparty. Beside these, there are also other similar applications such as [14,]">15] and so on. In recent years, [16,]">17] further allowed the stochastic interest rate to follow an jump-diffusion process and studied the pricing problem of bonds and CDS in details. Based on the obtained conclusions, we will price the bonds and CDS with the fractional Vasicek interest rate in the looping default framework.
In the following, we only consider the case with two firms: firm  and firm
and firm . Their defaults are mutually influenced and both correlated with the market interest rate. We assume their intensity processes respectively satisfy some linear relations below:
. Their defaults are mutually influenced and both correlated with the market interest rate. We assume their intensity processes respectively satisfy some linear relations below:
 (7)
(7)
 (8)
(8)
where ,
,  ,
,  ,
,  are positive constants,
are positive constants,  ,
,  are the real numbers which satisfy
are the real numbers which satisfy ,
, We will give the defaultable bond’s price without the proof (see [13]). Let
We will give the defaultable bond’s price without the proof (see [13]). Let .
.
Lemma 1 ([13]) Suppose that the bond issued by firm  has the maturity date
has the maturity date  and the recovery rate
and the recovery rate . Let the default time be
. Let the default time be , the default intensity be
, the default intensity be  and the interest rate be
and the interest rate be , then
, then
 (9)
(9)
Now, we calculate the conditionally marginal distributions of default time  and
and  in [0, T] before deriving the prices of bonds. To avoid the looping influences, we firstly apply the change of measure to get the joint conditional distributions of
in [0, T] before deriving the prices of bonds. To avoid the looping influences, we firstly apply the change of measure to get the joint conditional distributions of  and
and . We define two firm-specific probability measures
. We define two firm-specific probability measures  by
by
 (10)
(10)
Under the new measure , the intensity
, the intensity 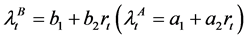 for
for 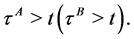
Thus, the default model can be simplified and the calculation of the default probabilities and bonds’ prices will be relatively easy.
Theorem 3 Let  and
and 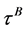 be the default times of firm
be the default times of firm  and
and . Assume the interest rate
. Assume the interest rate  and the default intensities
and the default intensities ,
,  satisfy (4), (7) and (8). If no defaults occur up to time
satisfy (4), (7) and (8). If no defaults occur up to time , then the joint conditional distribution of
, then the joint conditional distribution of  and
and  on
on  is given by the following:
is given by the following:

when  and
and

when 
Proof. Let  When
When , from the properties of quasi-conditional expectation ([10])we have
, from the properties of quasi-conditional expectation ([10])we have

where 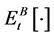 denotes the quasi-conditional expectation
denotes the quasi-conditional expectation  under probability measure
under probability measure 
When , the intensity of
, the intensity of  becomes
becomes  under
under , so we have
, so we have
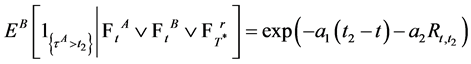
Denote 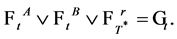 Hence, we proceed to calculate the quasi-conditional expectation in the first term of the above joint conditional distribution as follows.
Hence, we proceed to calculate the quasi-conditional expectation in the first term of the above joint conditional distribution as follows.

Then, substituting the obtained two quasi-conditional expectation into the joint conditional distribution, we can deduce the conclusion of the theorem when  When
When , the calculating process is similar to above. We omit it.
, the calculating process is similar to above. We omit it.
Corollary 1 Let  and
and 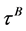 be the default times of firm
be the default times of firm  and
and . Suppose that the default intensities
. Suppose that the default intensities 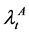 and
and  satisfy (7) and (8). If no defaults occur up to time
satisfy (7) and (8). If no defaults occur up to time , then the conditionally marginal distributions of
, then the conditionally marginal distributions of  and
and  on
on  are given by
are given by
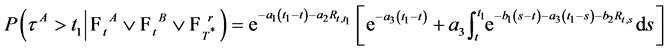 (11)
(11)
 (12)
(12)
Proof. We can obtain the corollary from Theorem 3, so omit the process.
Now, we apply the above results to price the bonds issued by firm  and
and  in the looping default framework. We firstly give the other form of pricing formula for the bond. Later, we will price the bonds based on this formula.
in the looping default framework. We firstly give the other form of pricing formula for the bond. Later, we will price the bonds based on this formula.
Lemma 2 ([13]) The defaultable bond price can also be expressed as
 (13)
(13)
In this paper, we will not consider the risk from the recovery rate. Therefore, without loss of generality, we suppose that the recovery rates  and the face value of bond
and the face value of bond  is 1 dollar.
is 1 dollar.
Theorem 4 Assume the interest rate follows the fractional Vasicek model and the default intensities  and
and  satisfy (7) and (8). If no defaults occur up to time
satisfy (7) and (8). If no defaults occur up to time , then the time-
, then the time- prices of bonds issued by firm
prices of bonds issued by firm ,
,  with the same maturity date
with the same maturity date  are respectively given by
are respectively given by
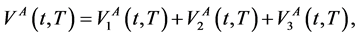 (14)
(14)
 (15)
(15)
where


where

Proof. Firstly, according to the pricing formula on fractional quasi-martingale in Hu and  Ksendal (2003) and Lemma 2, we can obtain the price of bond issued by firm
Ksendal (2003) and Lemma 2, we can obtain the price of bond issued by firm  at time
at time  on
on  is
is

where

By Corollary 1, we have

From the equation of , we find that the key step is to calculate the three quasi-conditional expectation
, we find that the key step is to calculate the three quasi-conditional expectation ,
,  and
and
 . By (5), we show
. By (5), we show

Further, substituting it into  and by the definition of quasi-martingale and (2) in Theorem 1, we show that
and by the definition of quasi-martingale and (2) in Theorem 1, we show that

In the above equality,

Similarly,

then
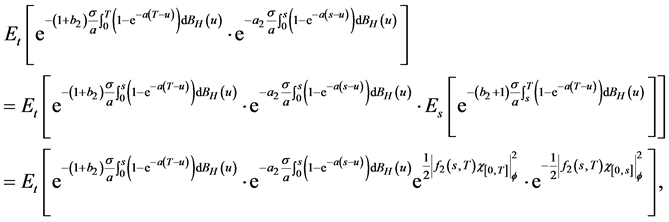 where
where

Therefore,

When , we apply the properties of quasi-conditional expectation and obtain
, we apply the properties of quasi-conditional expectation and obtain

Finally, we substituting the above quasi-conditional expectations into . We show that (15) holds. The pricing formula (14) of bond issued by firm
. We show that (15) holds. The pricing formula (14) of bond issued by firm  can be derived though the similar proving process of
can be derived though the similar proving process of . Hence, we omit it. The proof is complete.
. Hence, we omit it. The proof is complete.
3. CDS’s Pricing
In this section, we apply the results in section 2 to price CDS related to the zero coupon bond issued by firm . Firm
. Firm  holds a bond issued by the reference firm
holds a bond issued by the reference firm  with the maturity date
with the maturity date . To seek protection against the possible loss, firm
. To seek protection against the possible loss, firm  buys a default swap with the maturity date
buys a default swap with the maturity date  from firm
from firm  on condition that firm
on condition that firm  gives the payments to seller
gives the payments to seller  at a fixed swap rate in time while seller
at a fixed swap rate in time while seller  promises to compensate buyer
promises to compensate buyer  for the loss caused by the default of firm
for the loss caused by the default of firm  at a certain rate. Each party has the obligation to make payments until its own default. The source of credit risk may be from three parties: the issuer of bond, the buyer of CDS and the seller of CDS.
at a certain rate. Each party has the obligation to make payments until its own default. The source of credit risk may be from three parties: the issuer of bond, the buyer of CDS and the seller of CDS.
In the following, we discuss a simple situation which only contains the default risk from reference firm 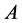 and the CDS’s seller
and the CDS’s seller . At the same time, to make the calculation convenient, we suppose the recovery rate of the bond issued by firm
. At the same time, to make the calculation convenient, we suppose the recovery rate of the bond issued by firm 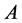 is zero and the notional is 1 dollar. In the event of firm
is zero and the notional is 1 dollar. In the event of firm ’s default, firm
’s default, firm  compensates firm
compensates firm  for 1 dollar if he doesn’t default, otherwise 0 dollar.
for 1 dollar if he doesn’t default, otherwise 0 dollar.
Now, we give some notations. Denoted the swap rate by a constant  and interest rate by
and interest rate by . Let the default times of firm
. Let the default times of firm  and
and  be
be  with the intensity
with the intensity  and
and  with the intensity
with the intensity  respectively. We analyze the values of two legs: contingent leg and premium leg. The time-0 market value of buyer
respectively. We analyze the values of two legs: contingent leg and premium leg. The time-0 market value of buyer ’s payments to seller
’s payments to seller  is
is

the time-0 market value of firm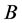 ’s promised payoff in case of firm
’s promised payoff in case of firm ’s default is
’s default is

Then, in accordance with the arbitrage-free principle, we obtain
 (16)
(16)
Theorem 5 Suppose the interest rate  satisfies fractional vasicek interest rate model and the intensities
satisfies fractional vasicek interest rate model and the intensities  and
and 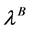 satisfy
satisfy

Then, if no defaults occur up to time , the swap rate
, the swap rate  has the following expression
has the following expression
 (17)
(17)
where  are the simple forms of (6) and (14) in Theorem 2 and Theorem 4, and
are the simple forms of (6) and (14) in Theorem 2 and Theorem 4, and

Proof.
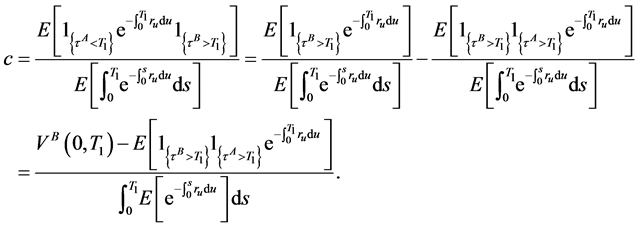
To derive the swap rate of CDS in the looping default framework, we define a firm-specific probability measure  by
by

then
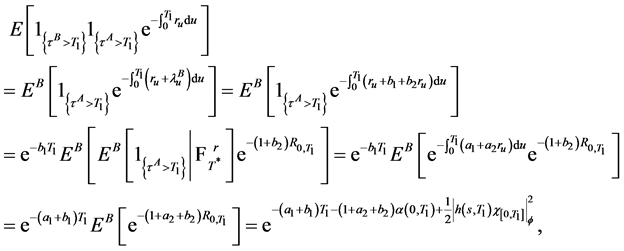
Substituting the quasi-conditional expectation into the above formula of the swap rate , we deduce (17).
, we deduce (17).
4. Conclusions
This paper discusses the pricing problem of defaultable bonds and CDS in the fractional Brownian motion environment. In our model, we consider the case that the defaults of the firms are mutually influenced. The default intensity is correlated with the counterparty’s default and the interest rate following fractional Vasicek model, which is more realistic.
In fact, we consider that the source of credit risk may be from the issuer of bond and the seller of CDS. In this case, there are also four cases for the defaults of firm  and firm
and firm :
:
Case 1. The defaults of firm  and firm
and firm  are mutually independent conditional on the interest rate;
are mutually independent conditional on the interest rate;
Case 2. Firm  is the primary party whose default only depends on the risk-free interest rate (the only economy state variable) and the firm
is the primary party whose default only depends on the risk-free interest rate (the only economy state variable) and the firm  is the secondary party whose default depends on the interest rate and the default state of firm
is the secondary party whose default depends on the interest rate and the default state of firm ;
;
Case 3. Firm  is the primary party and the firm
is the primary party and the firm  is the secondary party;
is the secondary party;
Case 4. The defaults of firm  and firm
and firm  are mutually contagious (looping default).
are mutually contagious (looping default).
In this paper, we only discuss the complex case 4 but the other cases are relatively simple which can be considered as the special situations of case 4. The pricing problem in case 2 has been studied in the other paper. In addition, we can try to discuss the more general situations. For example, we can consider the case that the impact of one firm’s default to the other firm’s default is attenuated over time or the relevant recovery rate is stochastic. In a word, the contagious model of credit security is very necessary to be further discussed in the future.
5. Funds
It is supported by the National Natural Science Foundation of China (No:11271259); the TianYuan Special Funds of the National Natural Science Foundation of China (No:11326170); Innovation Program of Shanghai Municipal Education Commission (No:13YZ125); Funding scheme for training young teachers in Shanghai Colleges (ZZshjr12010).