Measurement of the Nucleon Nucleon Scattering Length with the ESC04 Interaction ()
Keywords:Nucleon-Induced Reactions; S-Matrix Theory; Scattering Theory
1. Introduction
In nuclear physics, important information can be obtained from the scattering length associated with lowenergy nucleon-nucleon scattering. At these energies, the nucleon-nucleon interaction can be treated non-relativistically and the scattering was studied by means of a single particle Schrödinger equation which involves a nonlocal effective potential, derived from [1-]">4] using an extended soft-core model (ESC interaction). In the present manuscript, we consider a potential that involves a central part, a spin-spin interaction, a spin-orbital interaction and a tensor part and perform a numerical study of the associated Schrödinger equation. Also, we determine a numerical value for proton-proton and neutron-proton scattering lengths.
The present work is realized by considering energies in the range of 0 £ Tlab £ 350 MeV. For nucleon-nucleon scattering, it has been demonstrated that the interaction from the ESC model gives a description that is in good agreement with the nucleon-nucleon data. The extended soft-core model, also known as ESC, is used for nucleonnucleon (NN), hyperon-nucleon (YN), and hyperonhyperon (YY) scatterings. The particular version of the model ESC, called ESC04 [T. A. Rijken, Phys. Rev. C 73, 04007 (2006)], describes NN and YN interaction in an unified way using broken SU (3) symmetry.
A good fit with the experimental data is obtained by using the ESC04 model. The manuscript is organized as follows: in Section II, we give a theoretical review of the model; in Section III, we present our numerical results and in Section IV, we draw our conclusions.
2. Theory
2.1. The Schroedinger Equation with Non-Local Potential
The model we are going to study numerically involves a radial Schrödinger equation with ESC04 potential; namely
 , (1)
, (1)
where  is the reduced mass of the nucleons whose individual masses are m1 and m2, and have spins
is the reduced mass of the nucleons whose individual masses are m1 and m2, and have spins  and
and ; r is the distance between the nucleons. The potential is parameterized as
; r is the distance between the nucleons. The potential is parameterized as

where  is a second rank tensor operator.
is a second rank tensor operator.
For an S-state we introduce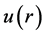 , where
, where
 .
.
For a given value of the quantum number J,
 , (2)
, (2)
where we introduce
 , (3)
, (3)
where the symbol  denotes a ClebschGordan coefficient, and YLML are the spherical harmonics, and
denotes a ClebschGordan coefficient, and YLML are the spherical harmonics, and
 ;
;
 ;
;
 .
.
The subscript on c refers to the magnetic projection quantum number MS of the spin-1 state, while a and b represent spin up and spin down for the particular spin-½ nucleon indicated by the subscript.
The Equation (2) forms an orthonormal set spanning the space of spin-1 functions and functions of the direction r. The normalization of  requires that the radial functions satisfy,
requires that the radial functions satisfy,
 . (4)
. (4)
The Schrödinger equation [Equation (1)] is processed by the method of separation of variables, we obtain as its radial component,
 . (5)
. (5)
We use the parametrized potential

and

for an S-state to obtain,
 , (6)
, (6)
where  [5], and S12 may be written as an operator of the form
[5], and S12 may be written as an operator of the form

with l = 2 and j1 = j2 = 1. Here  is the Clebsch-Gordan coefficient.
is the Clebsch-Gordan coefficient.
Using Racha algebra (see appendix A of [6]) we can show that
 . (7)
. (7)
2.2. Numerical Solution of the Schrödinger Equation
Considering the single state for the 1S0 wave, Equation (6) for the neutron-neutron system has the form (S = J = L = 0, L’ = −1, 0, 1),
 (8)
(8)
where S00-1 = S001 = 0, S000 = 2 are calculated from Equation (7).
For the proton-proton system we add the Coulomb effect to Equation (8), .
.
The numerical techniques necessary to solve equation (8) with this ESC04 potential are explained in chapter 3, Equation (3.28) of [7]. The solutions of u0 from Equation (8) are introduced in the S matrix (Equation (10.58) of [7], which is,
 , (9)
, (9)
where the S matrix is evaluated in the last two points on a mesh of size e (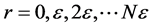 ). Ul are the solutions to Equation (8) with the ESC04 potential previously calculated and hl are the spherical Hankel functions defined in Equation (10.52) of [7].
). Ul are the solutions to Equation (8) with the ESC04 potential previously calculated and hl are the spherical Hankel functions defined in Equation (10.52) of [7].
We insert the numerical solution of the S matrix in the solution of the S matrix for a real potential
 , (10)
, (10)
where dl is real and is known as the phase shift.
Once the d0 phase shift is found the ann scattering length and the effective range rnn are calculated. For l = 0 the expression for  can be parameterized in the following form,
can be parameterized in the following form,
 . (11)
. (11)
The quantity a is called the scattering length and r0 is known as the effective range.
In the limit of low energies the scattering length is given in terms of the s-wave phase shift (see appendix B of [8]),
 , (12)
, (12)
where  is the center-of-mass momentum (the wave number) and  indicates the real part.
is the center-of-mass momentum (the wave number) and  indicates the real part.
2.3. Extended Soft-Core Potential (ESC04)
An Extended Soft-core potential is calculated consisting of a central, spin-spin, spin-orbital, and a tensor part. The potential of the ESC04 model is generated by one-bosonexchange (OBE), two-meson-exchange (TME) and meson-pair-exchange (MPE); this potential is calculated and explained in [1-4]. In Figure 1 the total ESC04 potential is plotted as a function of the r distance. In Figure 2 we show the central, spin-spin, spin-orbital, and tensor part of this total potential.
The algoritms for the YN potential are found in [9].
3. Results
The ann Scattering Length The ann scattering length is calculated obtaining a numerical value ann = −18.62497 fm and an effective range of rnn = 2.746615 fm. We use an ESC04 potential below 350 MeV. In Figures 3 and 4 the phase shift  is plotted for the proton-proton and neutron-proton case.
is plotted for the proton-proton and neutron-proton case.
Table 1 shows the results for the low-energy parameters from the scattering lengths and the effective ranges for neutron-proton, proton-proton and neutron-neutron system using the ESC04 interaction.
4. Conclusions
In the present work, we have numerically solved the Schrödinger equation with an ESC04 potential and obtained the nucleon-nucleon scattering lengths. Summarizing our main conclusions:
1) Recent calculations using the ESC04 interaction for nucleon-nucleon dispersion have been realized [4], and reproduced with the Schrödinger equation.
2) The numerical solution of the radial Schrödinger equation has been realized and has been demonstrated to give a good fit to the nucleon-nucleon data.
3) The scattering lengths app, anp and ann have been calculated and are consistent with the experimental re-

Figure 1. Total potential in the partial wave 1S0, for I = ½.

Table 1. ESC04 low-energy parameters: S-wave scattering lengths and effective ranges.

Figure 2. Central (a), spin-spin (b), spin-orbital (c), and tensor (d) part of the YN potential.

Figure 3. Solid curve, proton-proton I = 1 phase shifts (degrees), as a function of Tlab (MeV), numerical solution for the ESC04 model. Dots, phases of the Rijken analysis [4]. Circles, s.e. phases of the Nijmegen93 PW analysis. Triangles, the m.e. phases of the Nijmegen93 PW analysis [10].

Figure 4. Solid curve, neutron-proton I = 0 phase shifts (degrees), as a function of Tlab (MeV), numerical solution for the ESC04 model. Dots, phases of the Rijken analysis [4]. Circles, s.e. phases of the Nijmegen93 PW analysis. Triangles, the m.e. phases of the Nijmegen93 PW analysis [10]. Diamonds, Bugg s.e. [11].
sults. The final value for ann from this study is ann = −18.625 fm. Results from previous studies are
 [12],
[12],
 [13]and
[13]and
 [14]The presented ESC model is thus successful in describing the NN data.
[14]The presented ESC model is thus successful in describing the NN data.
Acknowledgements
This work was partially supported by PIEIC-UNACH 2012 and SIINV UNACH 2012.
NOTES