Impacts of waveforms on the fluid flow, wall shear stress, and flow distribution in cerebral aneurysms and the development of a universal reduced pressure ()
1. INTRODUCTION
An aneurysm, which is a weakening in the wall of an artery that leads to extensive deformation of the flow passage, can be a significant health risk if it ruptures. A major challenge in dealing with aneurysms is that the factors which predict rupture are not well understood. In fact, despite extensive efforts to predict aneurysm rupture, there are no accepted techniques that are available to practicing physicians [1]. There are some flow characteristics that have been linked to aneurysms, in particular the local fluid pressure, the wall shear stress, and the oscillatory shear stress, but a comprehensive diagnostic ability remains to be found [2-9].
Past studies of aneurysm blood flow include experimental [10] and many numerical studies [11-14] as examples of the wealth of literature. Among the computational studies, some have evaluated very specific computational issues such as the treatment of outflow boundary conditions [15,16], the treatment of the wall motion [17,18], issues of non-Newtonian blood properties [19- 21] and mesh convergence [22]. The literature listed here is just a small sample of the overwhelming breadth of research performed on blood flows. Over the past few years, the focus has moved toward patient-specific modeling with a goal of identifying those features of the flow that are predictive of aneurysm growth and rupture. In addition to the evolution of aneurysms, flow dynamics are important for predicting transport processes which occur within the artery wall [23-27].
To the best knowledge of the authors, there have been no generic studies of the impact of various categories of flow on the hemodynamics. In particular, patient waveforms may differ in flow rate or the frequency of pulsation. For instance, patients may have rapid or slow heartbeats or they may have high or low flowrates. It is the intent of this study to evaluate the impact of these parameters. To carry out the study, a numerical simulation has been developed based on an aneurysm geometry that was obtained by medical imaging. The simulation used inputs from seven different waveform types. Descriptions of the seven waveforms are listed in Table 1. The descriptor “baseline” refers to a 60 Hz waveform obtained from medical imaging. The geometry was available from the Mayo Clinic Aneurysm Database, and detailed information from the patient is protected by privacy laws. The “fast” and “slow” baseline cases have similar magnitudes of flow compared to the baseline, however, the period is either shortened or lengthened. Finally, the highflow and lowflow cases have flow magnitudes that are 75% or 125% that of the baseline case. Simulations were performed and results presented for each of the cases in later portions of this report.
2. MATHEMATICAL AND GEOMETRIC MODELS
2.1. Boundary Conditions
Flow measurements using the methodology of [28] as reported in [29] were used as inlet conditions on the geometry. The inlet flow was actually applied at an upstream extension of the arterial geometry so that natural flow development could occur at the aneurysm entrance. The baseline waveform is shown for four cycles in Figure 1.
Figure 2 has been prepared to show the differences between the seven cases listed in Table 1. From the figure, it is seen that the magnitude of the flow and the duration of the cycle are varied to represent various cardiac cycles. The durations were increased (decreased) by 25% to create slow (fast) cycles. Similarly, the flowrate throughout the cycle was increased or decreased to create the high and low flows.
At all walls, a no-slip condition was enforced. At the multiple outlets, an area-averaged pressure of 0 was applied and weak conditions were enforced on all transported variables (second derivative = 0).
2.2. Geometry
Figure 3 shows the geometry of an ophthalmic aneurysm

Table 1. Summary of different waveforms.

Figure 1. Four cardiac cycles of the baseline waveform.

Figure 2. Seven waveforms used to simulate various cardiac cycles.

Figure 3. The fluid region in the vicinity of the aneurysm.
under study. The geometry was extracted from medical imaging technology and was converted to a solid model geometry. From the figure, it can be seen that there is an inlet (not shown) and three individual outlets. At the inlet, a long extension (~10 diameters) has been made upstream. The flows from Figures 1 and 2 are actually applied to this extension so that there is an opportunity for the blood to naturally develop prior to entry into the aneurysm geometry. This approach was deemed more appropriate than enforcement of a velocity profile at the inlet proper. It is recognized that any changes to the shape or direction of the artery upstream of the aneurysm will have significant impacts on the flow patterns that enter the solution domain. However, without information on the upstream geometry, a natural development was determined to be most appropriate. On the other hand, the actual shape of the inlet profile is not likely to significantly impact the flow patterns at the aneurysm because of the tortuous path that the fluid encounters.
As can be seen in Figure 3, there is one inlet plane with a total area of 2.36e-5 m2 and three outlets with areas of 4.84e-6, 6.05e-6, and 3.87e-6 m2, respectively.
2.3. Mathematical Model
The simulations were carried out through the use of commercially available CFD software (CFX 14.0). This software requires the subdivision of the solution domain into a multitude of elements. Equations of conservation of mass and momentum are solved at each computational element. Further details of the geometry and the computational mesh will be provided later in this section.
The simulated flow was laminar because of the very low values of the Reynolds number, even at peak systole (all Reynolds numbers less than 2300). All calculations were unsteady and the simulations spanned four cardiac cycles. From past experience, flow patterns become quasi-steady by this time [30,31]. The results which are to be presented are taken from the last cardiac cycle. The relevant conservation equations are:
 (1)
(1)
for conservation of mass and
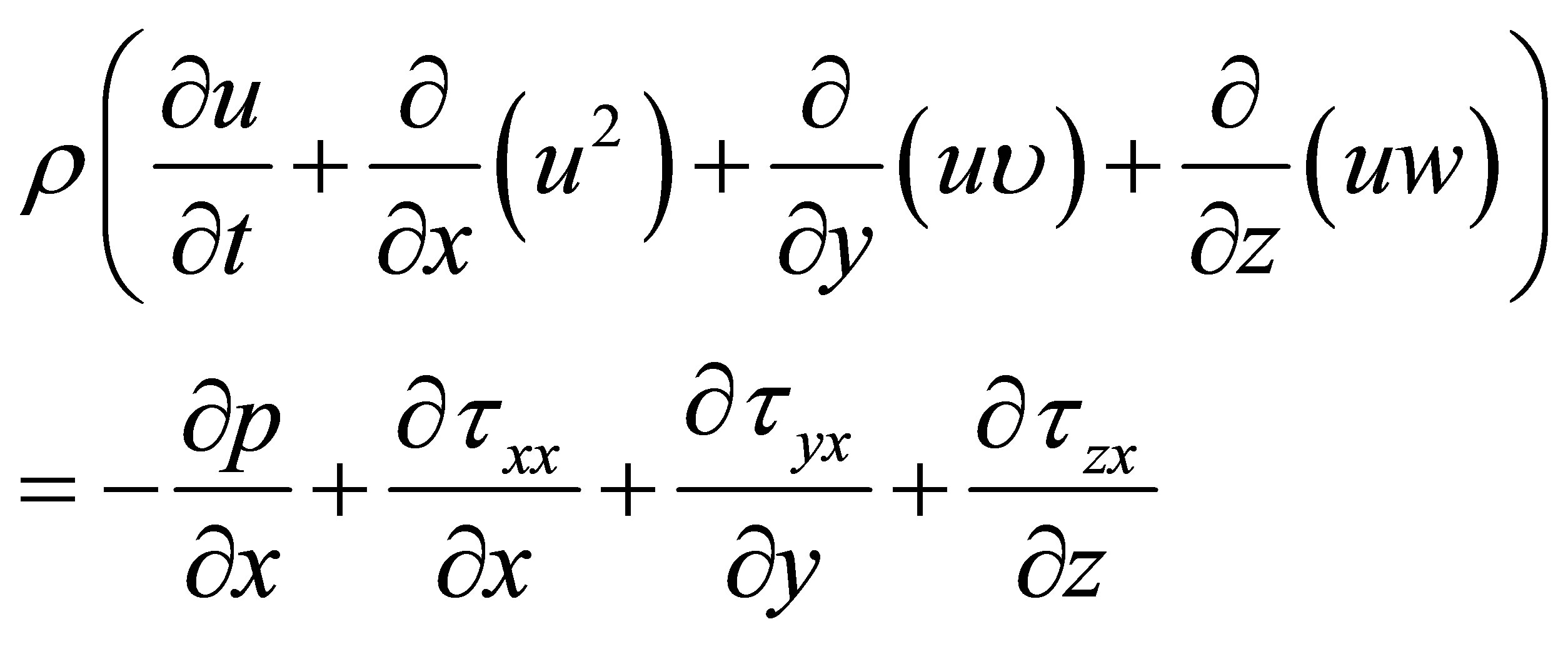 (2)
(2)
 (3)
(3)
 (4)
(4)
for momentum in the three coordinate directions. In these equations, u,  , and w are velocities in the x, y, and z directions, respectfully. The symbol
, and w are velocities in the x, y, and z directions, respectfully. The symbol  represents the stress tensor in the fluid. In addition, blood was treated with an Ostwald-de Waele non-Newtonian model as described in [31]. The constitutive equation for shear stress is:
represents the stress tensor in the fluid. In addition, blood was treated with an Ostwald-de Waele non-Newtonian model as described in [31]. The constitutive equation for shear stress is:
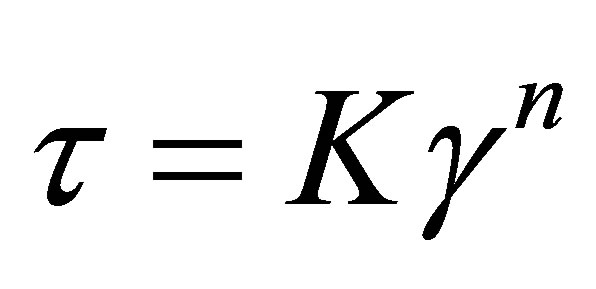 (5)
(5)
with K = 0.0147 (kg/m-s1.22),  is the strain rate, and n = 0.78 [32]. Blood density was set to be 1050 kg/m3.
is the strain rate, and n = 0.78 [32]. Blood density was set to be 1050 kg/m3.
Insofar as the simulations are unsteady, it is necessary to calculate the results at a series of timesteps. A detailed timestep study was undertaken to ensure that the results are independent of time step. During this timestep study, the cardiac cycle was subdivided into 100, 200, 400, 1000, and 4000 time steps. A comparison of the results showed that 4000 time steps were sufficiently small (cycle-average pressure drop through the geometry differed by ~2%).
Similarly, calculations were performed with element counts of 2.6 million, 4.3 million, 7.8 million, 13 million, and 20 million. It was discovered that a mesh entailing 2.6 million elements provided results (inlet pressure, flow distribution, wall shear) that were indistinguishable from the more refined cases. Consequently, the results which will be displayed were taken from the 2.6 million element case. Figure 4 has been prepared to show the deployment of elements along the flow geometry. It is seen that the elements are refined in areas of particular interest, including the aneurysm neck.
3. RESULTS AND DISCUSSION
There are a number of results that are of particular interest. Some of those results are global in nature, such as the inlet pressure and the flow subdivision to each of the three outlets. Comparisons will be made for each of the relevant global quantities and the impact of the waveform will be highlighted. In addition to global quantities, local flow patterns are of interest. Among the most important local features of the flow are the wall shear stress values in the aneurysm and the velocity patterns.
3.1. Comparison of Wall Shear and Flow Patterns
The first comparison to be made is of the flow patterns
within the artery region. To facilitate the discussion, Figure 5 was prepared to show a semitransparent view of the artery with an opaque plane. The plane is positioned to provide contour plots of fluid velocities. The location of the plane was selected to capture some of the key flow features within the system.
Next, velocity patterns are shown for a subset of the cases listed in Table 1 (Figure 6). The images are extracted at peak systole. The selected cases were chosen to maximize the differences between the results (slow, low, high, and fast). Despite this attempt, the patterns of flow are remarkably similar to each other. The similarity is in the gross scale as well as in fine detail. In particular, at the exit of the aneurysm, there is a jet of high-speed fluid (red colored) and secondary flows (eddies). These flow structures appear in all four cases. While the results shown in Figure 6 are extracted at peak systole, it was found that similar results would be obtained if flow patterns at other times were to be evaluated.
In addition to the velocity patterns, values of the wall shear stress are helpful in determining whether an aneurysm grows or ruptures. Figure 7 has been created to illuminate the values of the wall shear stress, with a focus on areas of particular interest (the aneurysm neck). It is seen that for all the cases shown in Figure 7, the wall stress is very high at the neck compared to elsewhere in the artery. High local shear stress is expected here because of the flow acceleration that occurs at the neck contraction. Also, the higher flowrate cases express higher values of shear stress. In fact, the maximum wall stress values vary nearly linearly with the peak flowrate. There is a local maximum in the wall shear stress which occurs at the location where a jet of high speed fluid exits the aneurysm. All results are extracted at peak systole.
The similarity in the size and position of the maximum shear stresses is remarkable. If shear stress patterns were

Figure 5. Viewing plane used to extract velocity contours.

Figure 6. Comparison of flow patterns on the plane of Figure 5 for four different cases.
extracted at other times during the cardiac cycles, the similarities between the cases would persist.
To complete the exposition of shear stress results, a summary listing of the maximum wall shear stress values is provided in Table 2. As noted earlier, the maximum shear stress is closely correlated with the peak flows so that faster pulses and higher flowrates give rise to larger

Figure 7. Wall shear stress near the aneurysm neck for low, base, and highflow cases.

Table 2. Maximum wall shear values.
stresses. Alternatively, slower pulses and lower flows cause lower stresses. While this behavior would have been expected based on basic fluid mechanics, the quantification of the results is useful.
3.2. Pressure Drop and Flow Distribution
A quantity of particular interest from both a fluid dynamic and clinical standpoint is the overall pressure drop through the system. There are two main sources of pressure losses which are additive. The first is pressure loss associated with friction between the fluid and the wall. The common expression for frictional pressure losses in a straight tube is [33]
 (6)
(6)
The symbols f, L, and D are the friction factor, length, and diameter, respectively.
This expression, which was developed for flows in straight tubes and ducts, cannot be applied directly to the present case because of the changes in cross section that occur in the flow direction. However, it is still illuminating because the friction factor f varies inversely with the cross sectional average velocity for laminar flows. Consequently, for laminar flow, the friction pressure loss contribution varies as ~velocity.
The second source of pressure loss is from flow separation as the fluid passes through obstructions and direction changes in the passageway. The separation pressure loss (commonly called minor loss in fluid mechanic texts [31]), is typically calculated by Equation (7), where KLOSS is the loss coefficient.
 (7)
(7)
For flow in pipes and ducts, catalogs of loss coefficients are available in handbooks and fluid textbooks. For more unique shapes, such as those of the aneurysm, the loss terms must be determined on a case-by-case basis. However, regardless of the value of KLOSS, the relationship between the separation pressure losses and cross sectional average velocity is ~velocity2.
When the two pressure loss components of Equations (6) and (7) are considered together, Equation (8) is obtained
 (8)
(8)
where the two terms should give rise to a dependence on velocity that is 1 < n < 2. While the relative strengths of the friction and separation terms are not known a priori, and depend on patient-specific flow and geometry, it is reasonable to attempt to normalize the pressure loss through the system according to Equation (9).
 (9)
(9)
So that a reduced pressure term is defined for the seven cases of Table 1 that is
 (10)
(10)
The area-average reduced pressure at the aneurysm inlet is shown in Figure 8. It is immediately seen that the choice of division has nearly collapsed the set of curves. No attempt is made to annotate the separate lines of Figure 8 because of their close proximity to each other, although a color legend associates the curves with a particular flow case.
In order to explore the connection between the pressure and the flowrate, Figure 9 has been prepared. That figure has two curves, each with its own vertical axis. The velocity, which is taken at the inlet, is linked to the axis on the left. The pressure at the inlet is quantified on the right. The data for Figure 9 is one of the cases in Table 1 (Case 5), however, if another case were shown, a similar graph would result. It is seen that the pressure rise occurs prior to the increase in velocity ( ) where T is the pulsation period. In fact, the increase in inlet pressure causes the acceleration of flow. Similarly, it is seen that the pressure decreases prior to the slowdown of flow (
) where T is the pulsation period. In fact, the increase in inlet pressure causes the acceleration of flow. Similarly, it is seen that the pressure decreases prior to the slowdown of flow ( ). The lag ehavior displayed in Figure 9 is expected from basic fluid mechanics, however, the results of the simulation allow a quantification of the lag, which is approximately 0.1 times the cardiac period.
). The lag ehavior displayed in Figure 9 is expected from basic fluid mechanics, however, the results of the simulation allow a quantification of the lag, which is approximately 0.1 times the cardiac period.
Another major item of interest is the impact of inlet waveform on flow distribution. To investigate this, the cycle-averaged flow through each outlet was calculated for the seven cases of Table 3. All values are rounded to the nearest decimal so that the rounded values may exceed 100%. An overview of the results suggests that the details of the waveform at the inlet have a very minor impact on the downstream distribution of flow through the respective outlets.
4. CONCLUDING REMARKS
A detailed numerical study has been performed on the impact of waveform on the flow patterns, wall shear stress, overall pressure drop through an aneurysm, and flow distribution. Seven waveforms were considered to be

Figure 8. Values of reduced pressure, Pʹ, at the neck of the aneurysm.

Figure 9. Superposition of pressure and average velocity (equivalency of flowrate) at the aneurysm inlet.

Table 3. Summary of flow distribution through outlets.
varied in duration and flowrate. It was found that despite the significant differences between the inputs, a remarkable agreement was achieved in the results. For instance, it was found that the flow patterns were remarkably similar, even when small flow features were investigated. It was also found that the patterns of wall shear stress were remarkably consistent from one case to another. It was seen that the magnitude of the maximum shear stress scaled nearly linearly with the peak systolic flowrate. Another major similarity was with regard to the flow distribution to the multiple outlets. Among the seven cases, the flow distributions were similar within two percent.
In addition to the aforementioned, it was found that there is a reduced pressure, scaled by the velocity, that allows the inlet pressures to nearly collapse onto a single curve. To the best knowledge of the authors, this universal curve has not appeared in the literature. It is expected that while the universal curve is patient-specific, it is not dependent on the pulse rate or overall flowrate.
Finally, it was found that the pressure variations at the inlet preceded changes to the velocity by about 10% of the cardiac period.