1. Introduction
The thermal physics [1] of noble gases attracts a large attention of both researchers and practitioners.
• For researchers it puts a challenging goal to build precise models of atomic interactions basing on relatively simple structures of atomic systems as opposed to much more complex molecular systems.
• For practitioners it is important to operate with advanced mathematical models of noble gases to improve the controllability and repeatability of precise technological processes, such as production of semiconductor crystals and devices in controllable inert atmosphere [2] or utilization of noble gases in the precise metrology [3].
Widely used theoretical models of atomic interactions in real gases, such as the famous Lennard-Jones approach [4], consider the atoms of noble gases as round spheres and do not take into consideration the angular dependence of their interaction potential [5]. It will be shown here that this assumption meets a contradiction with experimental results.
One of aims of this work is to apply the recently developed thermal analysis method [6] to noble gases for estimation of their pair interaction parameters with a due precision. This thermal analysis of precise experimental thermophysical data for pure gases shows that even in noble gases the pair atomic interaction cannot be reduced to the round sphere model [6]. The discovered here growth of the dimers’ bond energy in noble gases at low temperatures tells about the mutual orientation of atoms in gaseous dimers due to the lack of rotational symmetry of their outer electronic shells.
The next problem in the equilibrium thermal physics of real gases is connected with the interpretation of experimental data via virial expansions [7,8] of thermophysical data utilizing the total densities or pressures of real gases as arguments for series expansions. The virial expansions are very useful in practice: they help to generalize experimental data and to provide the mathematical models for the technology control. But their physical interpretation should be performed with a due care. In the virial approach it was silently supposed that the i-th virial coefficient is determined by interactions inside the iparticle cluster [7]. It is important to admit that the high order virial coefficients also depend on the interactions between smaller clusters and even monomers because the total values of density and pressure are combinations of partial values for different cluster fractions. For this reason neither density nor pressure used as arguments in virial expansions may lead to precise physical models of real gases.
The second aim of this paper is to show that only the series expansion of thermophysical data by the monomer fraction density [9] permits to provide the extraction of molecular and atomic interaction mechanisms and parameters from precise thermophysical data for pure real gases. For this task the most informative thermophysical property of real gases has proven to be the potential energy density that is composed of the partial potential energy densities of different cluster fractions [10].
Our approach is phenomenological and is opposite to the microscopic simulations of the many particle systems with model interaction potentials [5,11]. It is directed towards the clarification of the atomic and molecular interaction details and utilizes only one assumption that the available databases with regularized thermophysical data are precise enough to provide the estimation of the atomic and molecular interaction parameters with an acceptable precision. In this respect we follow the statement of J. Willard Gibbs: “The first problem of molecular science is to derive from the observed properties of bodies as accurate a notion as possible of their molecular constitution. The knowledge that we may gain of their molecular constitution may then be utilized in the search for formulas to represent their observable properties [12].” To the contrary, as it is seen from the work [5], the precision of assumptions about the interaction potential and its parameters, even for atomic gases, is crucial for the simulation methods: the smallest deviations in the model potential result in a large spread of the found atomic interaction parameters.
The task of any parameters extraction from experimental data belongs to the class of inverse mathematical problems [13], the resulting errors of which greatly overcome the errors in initial data. Therefore, to come to the interaction parameters with an acceptable precision, we should use only those initial thermophysical data that have the smallest errors. In this respect a significant role belongs to the regularization of raw experimental data in modern databases, such as the NIST (USA National Institute of Standards and Technology) thermophysical database [14]. The regularization of data consists of the critical evaluation and generalization of experimental data from different sources and of their interpolation by high order polynomials with an account for the thermodynamics correlations of different thermophysical properties [15]. This process permits to suppress the main errors in the raw experimental data, leaving small residual errors that may be reduced further in the future experimental and analytical works. The author’s experience in the computer aided analysis of the NIST data [14] shows that for many investigated pure real gases the results are stable enough and permit to make conclusions about mechanisms of interactions and the cluster structure of gases.
Some decades ago, the attempts to apply the inverse mathematics for extraction of the interaction parameters from thermophysical properties of real gases failed and stopped, mainly because of a large level of errors in experimental data. But now the greater purity of substances, the significantly improved precision of the computerized measuring equipment, the world-wide cooperation of researchers and computer processing of raw experimental data drastically changed the situation: the regularized in the available databases thermophysical data became precise enough to permit the extraction from them the atomic and molecular interaction parameters. Now this method is ready to repeat the successful development of the computer tomography that makes the contrast sensitivity high enough for imaging of soft tissues instead of the traditional X-ray identification of bones.
The thermal physics of real gases will surely benefit from an inevitable growth with time of the experimental data precision. The results of the thermophysical data analysis [6] will be progressively improved without changing its basic principles, only due to the growing precision of experimental data.
2. The New Approach to Thermal Physics of Real Gases
2.1. The Chemical Thermodynamics Based Variable for Series Expansions of Thermophysical Values
The new method of the computer aided analysis of thermophysical data for pure gases [6] is based on the monomer fraction density [9] as the main variable for series expansions of the equilibrium thermophysical values. The monomer fraction density Dm is the molar density of those basic particles that are temporarily not bound and participate only in elastic collisions with other particles. Instead of this rather vague definition, the monomer fraction density Dm, like fugacity, can have a phenomenological definition via the molar Gibbs energy G, named as chemical potential, and can be found from the Equation (1) [9]:
 (1)
(1)
At small pressures the monomer fraction density, Dm, is close to the total density, D, but at near critical pressures there is a great difference between Dm and D (Figure 1).
Therefore, the results of series expansions of thermophysical values by powers of Dm and virial expansions by D may differ significantly.

Figure 1. The monomer fraction density Dm (thin line) as compared to the total density D (thick line) and the ideal gas density Dp = P/RaT (dashed line) for Xenon at the near critical temperature T = 300 K.
2.2. The Potential Energy Density as a Source of Information about Clusters
To estimate the molecular interaction parameters we use the positive density W = −UD of the potential energy U. U can be defined as the difference between the molar internal energies E at the existing pressure P and zero pressure: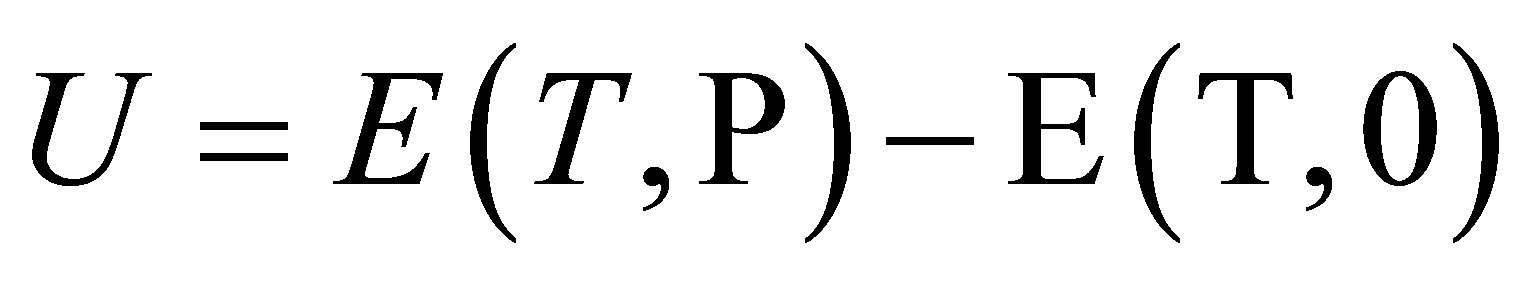 .
.
The monomer fraction density is the analogue of the molar densities for elementary components in the equilibrium chemical reaction media and the n-particle cluster is the analogue of the n-component chemical compound. It permits to apply the chemical equilibrium principles and the Mass action law to cluster fractions in pure gases. On this basis, the n-th term of the potential energy density Wn series expansion by the monomer fraction density Dm reflects the contribution of the n-particle cluster fraction in the potential energy density and is equal to Wn = Kun , where Kun is the series expansion coefficient depending only on T.
, where Kun is the series expansion coefficient depending only on T.
The potential energy density W in pure real gases may be given by the formula:
 (2)
(2)
Here Dn = Cun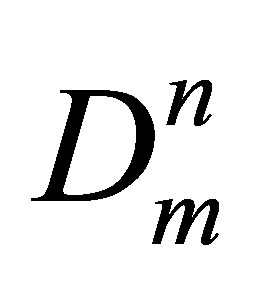 are the molar densities of n-particle cluster fractions, En—the bond energies of the n-particle clusters and Cun—potential energy based equilibrium constants for n-particle clusters. Wr is the repulsion part of the potential energy density that is small at low temperatures. The series expansion of W by Dm and summation in the Equation (2) start from the terms with n = 2. In this work a special procedure is developed to exclude from W the repulsions between monomers at their elastic collisions just to come to attractive potential energy density of dimers in noble gases.
are the molar densities of n-particle cluster fractions, En—the bond energies of the n-particle clusters and Cun—potential energy based equilibrium constants for n-particle clusters. Wr is the repulsion part of the potential energy density that is small at low temperatures. The series expansion of W by Dm and summation in the Equation (2) start from the terms with n = 2. In this work a special procedure is developed to exclude from W the repulsions between monomers at their elastic collisions just to come to attractive potential energy density of dimers in noble gases.
For pair interactions we should estimate Ku2(T), as the zero density limit of the  dependence on Dm. For noble gases to find the Ku2(T) correctly we should estimate at least two higher coefficients, Ku3(T) and Ku4(T), just to exclude from the
dependence on Dm. For noble gases to find the Ku2(T) correctly we should estimate at least two higher coefficients, Ku3(T) and Ku4(T), just to exclude from the  function the linear and quadratic dependences on Dm. These higher coefficients correspond to trimers and tetramers.
function the linear and quadratic dependences on Dm. These higher coefficients correspond to trimers and tetramers.
2.3. The Thermal Analysis of Isochoric Thermophysical Data for Noble Gases
It should be noted that the databases in some way reflect the history of science. The data for different gases in the databases utilize the experimental data received at different times and thus correspond to different historic values for the so called Universal gas constant R. Therefore, for the data to be analyzed instead of the contemporary nominal value of R we should first determine the specific apparent value Ra = lim(P/TD) at zero pressure.
To find the Kun(T) dependences in the desired range of temperatures we usually analyze the isothermal data for a discrete row of temperatures in this range. This process requires a lot of computations to come to smooth temperature dependence Kun(T). But for noble gases it is enough to use the isochoric data for several specially selected density values. These values cannot exceed the saturation density for the lowest temperature in the range. The row of selected densities D(i) (i = 2, 3,∙∙∙) includes at least three density values with equal spacings between them to exclude the quadratic part of the 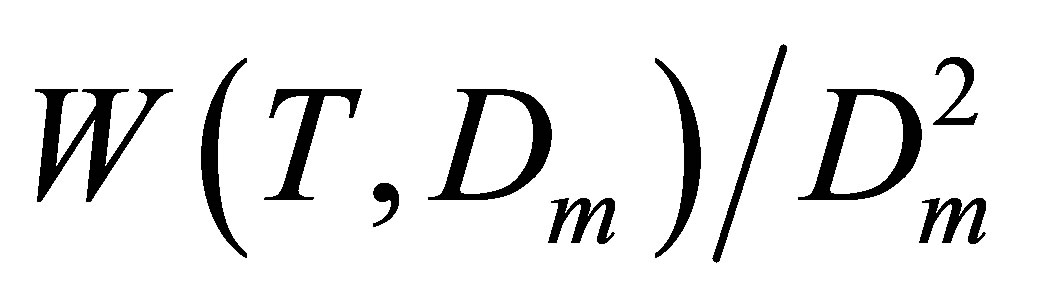 function. And the initial density D(1) that is by an order of magnitude smaller than the other densities D(i) provides the initial value for
function. And the initial density D(1) that is by an order of magnitude smaller than the other densities D(i) provides the initial value for .
.
The values Dm(i) for i = 2, 3,∙∙∙ are found for any T from the Equation (1) by the original numerical integration expression:
 (3)
(3)
Here  are the steps of pressure, corresponding to steps in density ∆D(i). The formula (3) has proven to provide a precise numerical integration of Equation (1) even at large steps ∆P(i) that is important to diminish the volume of data to be processed. The remarkable feature of the expression (3) is that the step ∆P(i) for numerical integration of the Equation (1) enters both the numerator and denominator of the expression. It improves the precision of the numerical integration and reduces the sensitivity of results to occasional deviations of initial data from regular dependencies.
are the steps of pressure, corresponding to steps in density ∆D(i). The formula (3) has proven to provide a precise numerical integration of Equation (1) even at large steps ∆P(i) that is important to diminish the volume of data to be processed. The remarkable feature of the expression (3) is that the step ∆P(i) for numerical integration of the Equation (1) enters both the numerator and denominator of the expression. It improves the precision of the numerical integration and reduces the sensitivity of results to occasional deviations of initial data from regular dependencies.
Then, by extrapolation of values E(i) for internal energy at a fixed T to zero density we find the internal energy E(0) for ideal gas. The difference E(i) − E(0) gives us the molar potential energy U(i). The potential energy density W(i) = −U(i)D(i). After its division by 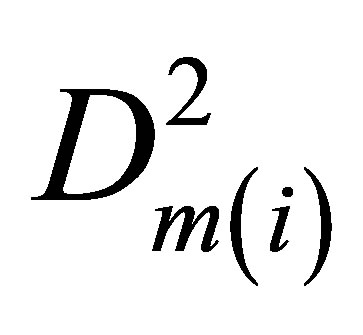 we come to the function Ku2(i), quadratic extrapolation of which to zero density provides the needed pair interaction coefficient Ku2(T).
we come to the function Ku2(i), quadratic extrapolation of which to zero density provides the needed pair interaction coefficient Ku2(T).
2.4. Determination of the Pair Interaction Bond Energies
The bond energies En of clusters in real gases are the averaged energies of the clusters decomposition to monomers. Unlike the widely used approach to the cluster bond energy as the maximal depth of the potential curve, our definition is thermodynamically correct and opens a clear way to determine the cluster bond energies from experimental thermophysical data. To find the En values we plot the logarithm of the Kun(T) versus the reverse temperature. For pair interactions we plot ln(Ku2) versus β = 1000/T (Figure 2). In the zones of temperature, where the graph is linear, the tangent of slope of the line gives the dimer bond energy in kK.
It is seen that at T over 250 K the graph becomes nonlinear that leads to apparent growth of the pair bond energy E2(T) at high temperatures. The nonlinearity can be explained by a large contribution K2r of the monomers’ mutual repulsion in Ku2. The K2r versus T dependence for noble gases has proven to be linear:
 (4)
(4)
Here Ra is the apparent gas constant. For Argon the data from the NIST database [14] correspond to Ra = 8.31451 J/mol∙K. Vr is the effective volume of the repulsion mechanism. Its value may be properly selected just to provide the maximal linearity of the ln(Ku2 − K2r) versus β at high temperatures.
If we subtract the K2r(T) from Ku2(T), we receive the corrected value Ku2corr(T) that corresponds purely to bound states of the dimer fraction, with no influence of mutual repulsions of monomers at their elastic collisions. It is seen (Figure 3) that the graph for ln(Ku2corr) versus β at specially selected value Vr for Argon is much more linear than the graph for ln(Ku2) even for temperatures as high as 700 K.
The differentiation of the ln(Ku2corr) by β returns the apparent pair interaction bond energy E2 in kK:
 (5)
(5)

Figure 2. The second series expansion coefficient Ku2 in a logarithmic scale versus the reverse temperature for Argon at T between 100 and 500 K.

Figure 3. The ln(Ku2) (solid line) and its corrected version (dashed line) at Vr = 0.0056 mol/l versus β for Argon in the temperature range 84 - 700 K.
At temperatures lower 200 K on the Figure 3 there is seen a slight growth of the tangent of slope for the ln(Ku2corr) graph versus β. This growth corresponds to the growth of the pair bond energy E2(T) at low temperatures (Figure 4).
As it is seen, after correction of the Ku2(T) dependence for the elastic monomer-monomer interactions the found E2(T) values for the Argon gas in a large temperature range 400 - 700 K are constant and equal to 73.3 K. The growth of the pair bond energy in noble gases at low temperatures may be explained by the lack of rotational symmetry of the outer electronic shells. In the Argon gas the pair bond energy grows from its stable value E2hT = 73.3 K to E2lT = 93.5 K at the triple point. This growth is very significant and should be taken into account in computations of thermophysical properties for noble gases. A similar growth is typical for all noble gases and for many molecular gases, except the hydrocarbons [10]. In molecular gases a growth of the pair bond energy at low temperatures may be explained by the angular dependence of their interaction potential due to structural features of molecules [16].
We thus see that the method of the clusters’ bond parameters estimation from the potential energy operates not only by potential energies of clusters’ binding, but also by the potential energy of monomers’ repulsions. It is an inevitable shortcoming of any method of the clusters’ characterization via series expansions of the thermophysical properties. This problem is met in the series expansions of pressure and density by the monomer fraction density. The found deviations of the apparent equilibrium constant for PDT relations from the real equilibrium constant for dimers have been explained by the virtual dimers appearing in the result of the monomermonomer elastic interactions [6,9,10].
2.5. The Effective Volume of the Repulsion Mechanism
The linearity with temperature of the repulsion part of the second interaction coefficient had been noticed both for

Figure 4. Pair bond energy E2(T) for dimers in Argon at T between 84 and 700 K after corrections for the monomers’ repulsion potential energy.
noble gases and for no polar molecular gases. For gases with a high value of the maximal temperature in the database to the triple point temperature ratio, such as Nitrogen, the linearity of the repulsion potential energy holds till temperatures approximately ten times larger than the triple point temperature. And for Argon the linearity region covers all temperature range displayed in the database [14].
The discovered linearity of the repulsion potential energy versus temperature is a generous present of Nature permitting to clear the dimer characteristics from the monomer-monomer elastic interactions. In the range of high temperatures, where the atoms in dimers rotate freely, the pair bond energy should not depend on temperature. So, it is possible to select the value for the repulsion zone volume Vr basing on the criterion of constant pair bond energy E2 at high temperatures.
2.6. Determination of the Equilibrium Constants for Dimers in Noble Gases
In the zones of temperature with constant bond energy the based on the potential energy of gas equilibrium constant Cu2(T) should be equal to the equilibrium constant Cs2(T) found by spectroscopy methods. But for gases with small pair bond energy E2 as compared to the temperature values the bound states are densely spaced and widely scattered by the thermal movement that prevents from the utilization of spectroscopic methods for the dimers’ bond energies and equilibrium constants precise determination. So, for noble gases there is the only method for determination of the dimers’ equilibrium constants via their potential energy.
The corrected function Ku2corr(T) reflects properties of dimers, cleared from the monomer-monomer repulsions. According to the Equation (2), . Dividing Ku2corr(T) by E2(T) we can find the dimers’ equilibrium constant Cu2(T) (Figure 5).
. Dividing Ku2corr(T) by E2(T) we can find the dimers’ equilibrium constant Cu2(T) (Figure 5).
The Figure 5 displays also the apparent pair equilibrium constant Cd2 responsible for PDT relations via the

Figure 5. The equilibrium constants for dimers in the Argon gas: Cu2 (thick line) found from the potential energy and Cd2 (thin line) found from the PDT relations.
system of equations [6,9,10]:
 (6)
(6)
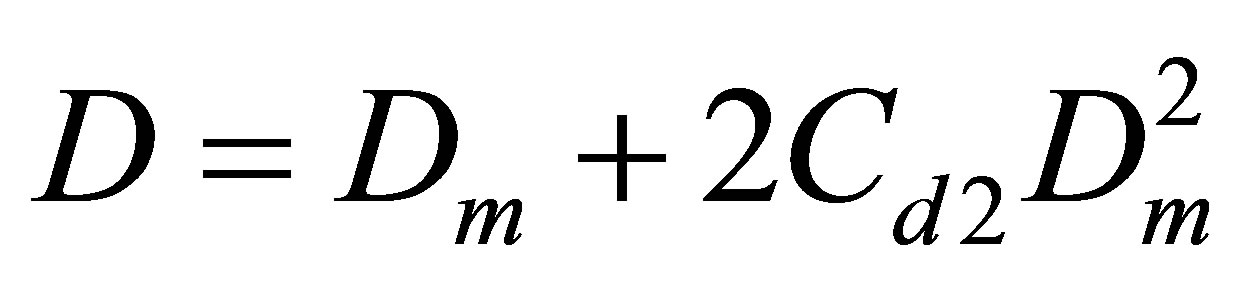 (7)
(7)
The Cd2(T) temperature dependence is similar to the Cu2(T) dependence with a shift due to the action of virtual clusters [9] reflecting the influence of the monomermonomer elastic interactions on the pressure P and density D.
2.7. Determination of the Attraction Zone Volume V2
Dividing the found dimers’ equilibrium constants by the Boltzmann factor we come to the pair attraction zone volume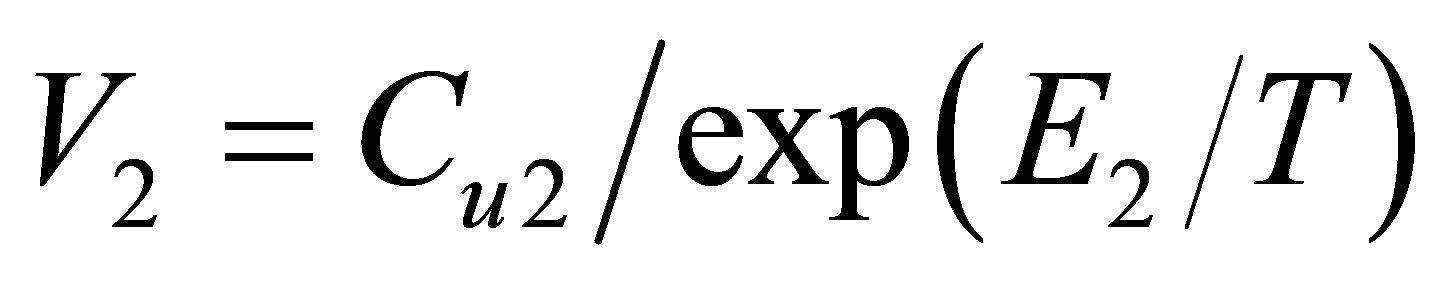 , Figure 6.
, Figure 6.
It is seen that the attraction zone volume V2 is constant at temperatures, where the pair bond energy is constant too. But at small temperatures, near the triple point, the V2 values become smaller because of limited mutual angular positions of interacting atoms in dimers. For Argon this difference does not exceed 5%, but it can be clearly seen due to the high precision of used data from the NIST database [14].
3. The Results and Their Discussion
3.1. Bond Parameters for He, Ne, Ar, Kr and Xe
When the value for Vr is found, Table 1, it becomes possible to estimate the corrected value for the high temperature pair bond energy E2hT. This correction slightly influences also the low temperature values for the pair bond energy E2lT. The effective volumes Vr of the repulsion zones are specific for every gas and characterize their types of repulsion part of the interaction potential.
For Helium there is seen an anomalous negative value for apparent high temperature bond energy E2hT. This anomaly can be seen also from the pressure dependence of the constant volume heat capacity of the Helium real gas at temperatures between 7 and 11 K, Figure 7.

Figure 6. The pair attraction zone volume V2 for the Argon gas.

Table 1. The low and high T pair bond energies, E2lT, E2hT, and repulsion volumes Vr for some noble gases.

Figure 7. An anomalous constant volume heat capacity Cv in Helium at temperatures: 6 K—thin dashed line, 8 K—thin solid line, 10 K—thick solid line, 12 K—thick dashed line.
The Figure 7 shows that at temperatures equal to 8 and 10 K the Cv values become smaller than the ideal gas heat capacity. It means that the absolute value of the clusters’ potential energy in Helium at T over 7 K grows with temperature. This phenomenon separates Helium from other real gases as far as the pair interaction mechanism is concerned. This fact signals about more complex pair interaction mechanism in the Helium real gas as compared to other noble gases. For Helium the method of the pair bond energy estimation described in the Section 2.4 needs to be corrected taking into account the specific thermophysical properties of the Helium gas.
3.2. The Pair Bond Energies for Kr and Xe
The pair bond energies for larger atoms of Kr and Xe, Figures 8 and 9, show much larger temperature dependences than for Ar, Figure 4.
The shown at these figures, large differences between E2lT and E2hT for Kr and Xe signal about the strong orien-
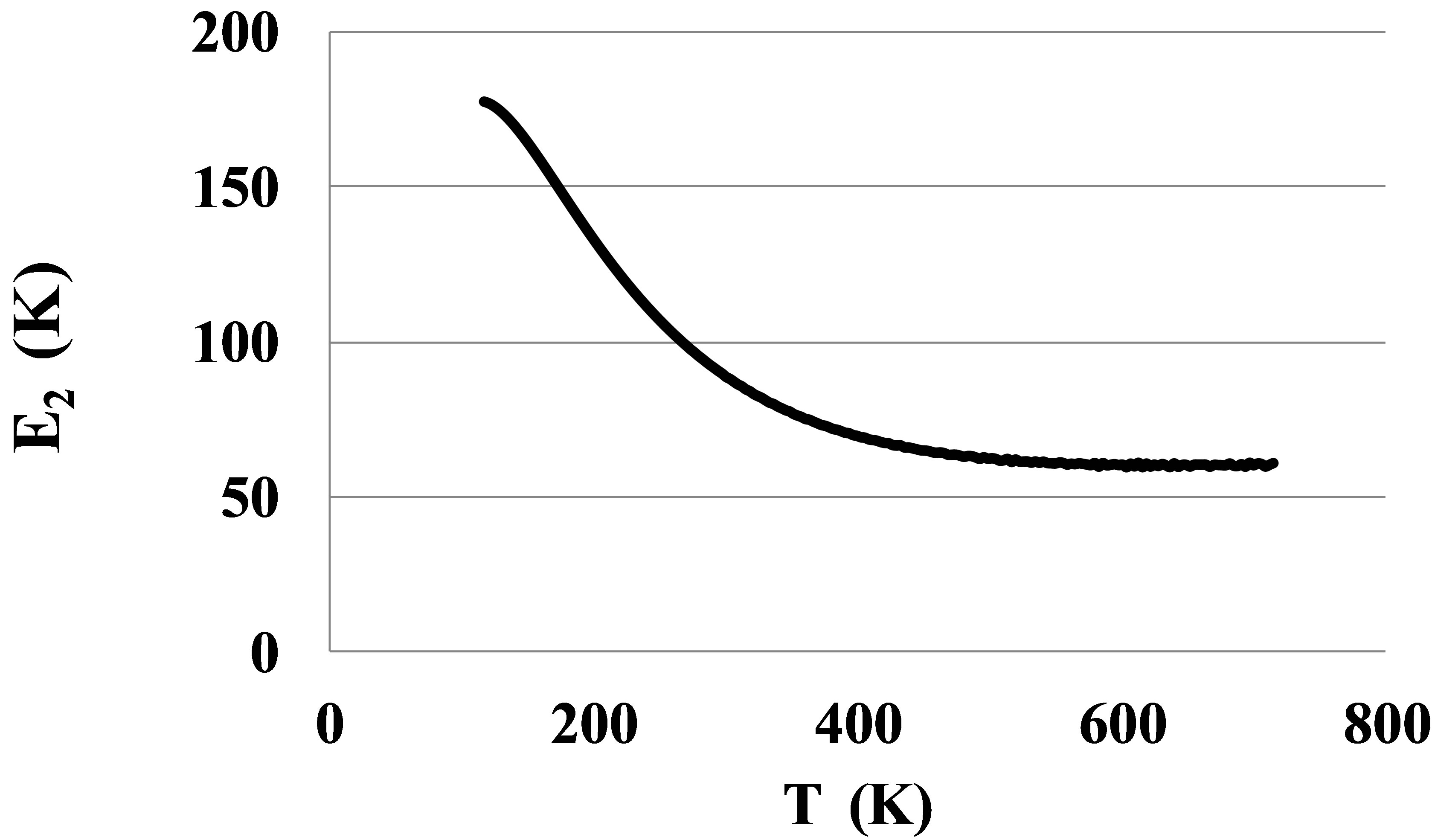
Figure 8. The bond energy for dimers in Kr.

Figure 9. The bond energy for dimers in Xe.
tation of the dimer bonds by outer electronic shells of atoms near the triple points. This orientation disappears only at temperatures exceeding 500 - 600 K. Only at these temperatures the atoms of Kr and Xe can be considered as round spheres.
• 4. Conclusions
• The monomer fraction density based analysis of precise thermophysical data for pure noble gases provides the physically clear picture of pair atomic interactions.
• The potential energy density, expanded in series by powers of the monomer fraction density, provides information about the dimers’ equilibrium constants in noble gases and the bond parameters: bond energy and attraction zone volume.
• A linear dependence of the monomer-monomer repulsion potential energy on the temperature in an extended range of temperatures permits to clear the second order series expansion coefficients for potential energy from the monomer-monomer interactions and to find the dimers’ interaction parameters in noble gases.
• The high precision of data from the NIST database [14] permits to notice the changes in the pair bond energy and attraction zone volume for dimers in the noble gases near triple point, signaling about the limited mutual angular positioning of noble gases’ atoms at low temperatures.