Design and Digital Implementation of Controller for PMSM Using Extended Kalman Filter ()
1. Introduction
Permanent Magnet synchronous Motor (PMSM) has a high torque/inertia ratio, high speed, high efficiency as well as high reliability and is of compact size. These qualities render PMSM as one of the most applicable AC machines for servo control applications and PMSM is therefore gaining extensive research attention in recent years [1-3]. PMSM weighs less and is of low maintenance; it offers many advantages in the high performance application areas such as in robotics, aerospace, navigation and many more. The modeling and control of the PMSM is complex because of two main reasons: 1) the multi-input nature of the motor, 2) the coupling between the stator current and rotor speed are non-linear. For high performance of PMSM that drives the vector control theory is applied, in which 3-ф stationary frame transforms into 2-ф synchronously rotating rotor reference frame; thus the flux and torque can be controlled independently, similar to the DC motor [4-6]. Though, the vector control is a complex control technique, the progress in the development of fast semiconductors switches and cost efficiency micro-controller has made the vector control feasible. PMSM uses known rotor shaft position as well as the inverter to control the armature currents, and is usually employed in direct drive system. The direct drive systems are more prone to load variations and these variations directly impact the motor shaft; this deteriorates the performance of the system. In order to mitigate these defects, the disturbance rejection control technique is used.
In this paper a vector control method is developed and implemented by means of a conventional observer combined with Extended Kalman Filter algorithm to provide the speed control and disturbance rejection. In the vector control method, to achieve better control performance, it is important to know the information of the rotor speed and position. Here, state space representation of the model and observer is obtained. Utilizing the state space model, a PID controller is designed using Linear Quadratic Regulator (LQR) approach [7]. Commonly, the aim of the observer design is to reduce the observation error, but it is used to serve as feed forward compensation for the load disturbance in the proposed method [8].
Many research works have been done in speed and position estimation of PMSM using sliding mode, high frequency signal injection method, adaptive control theory, fuzzy control, state observer, EKF [9-16]. In all, EKF is more attractive as well as popular and is continuously being used in research and applications because it delivers rapid, precise, and accurate estimation. In many applications EKF is implemented because of its low-pass filter characteristics [17,18]. The feedback gain used in EKF achieves quick convergence and provides stability for the observer.
In this article, the conventional observer combined with the Extended Kalman Filter is presented. The accurate estimation of states is very essential to achieve better control and performance of the PMSM drives. Here the EKF is utilized for the precise estimation of the rotor speed and stator q-axis current. Since the drive speed and drive current are measured directly from the machine terminals contain noise, they are not precise for speed control. In the proposed approach, the speed and q-axis current are estimated accurately by introducing EKF algorithm theory. The estimated current acts as an input to the state observer while the estimated speed is compared with the reference speed. The proposed method yields a smooth and quick speed tracking, reduction in the disturbance applied to the system, and better control of the control signal variation. The overall system performance is greatly enhanced with the proposed method.
2. Model of PMSM
The stator voltage and stator flux linkages equations in the rotor references frame are [4]:
 , (1)
, (1)
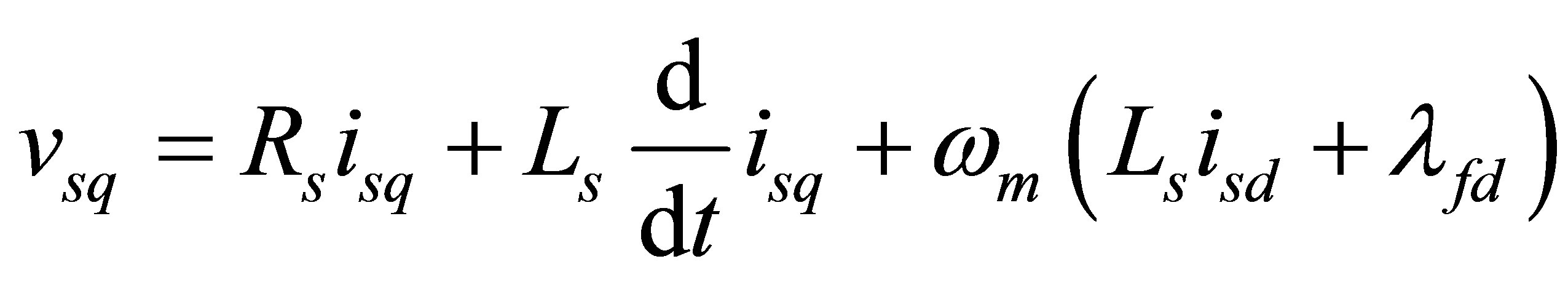 , (2)
, (2)
 , (3)
, (3)
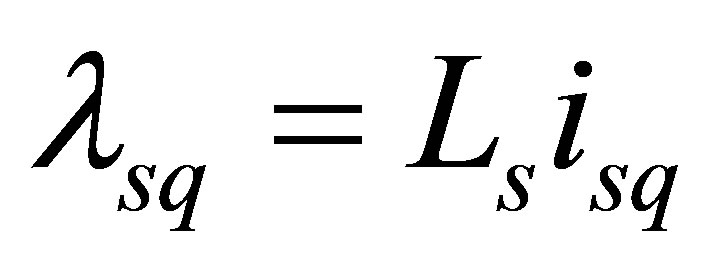 (4)
(4)
where ,
,  ,
,  ,
,  ,
, 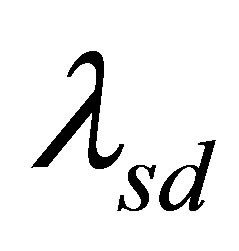 ,
, 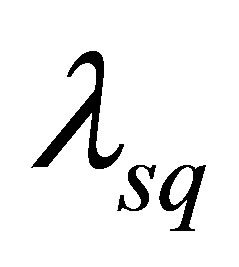 are d-axis and qaxis voltages, currents and flux linkages respectively.
are d-axis and qaxis voltages, currents and flux linkages respectively. ,
, 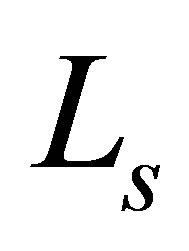 are the stator winding resistance and inductance.
are the stator winding resistance and inductance.
The electromagnetic torque generated and the acceleration is given by:
 , (5)
, (5)
 , (6)
, (6)
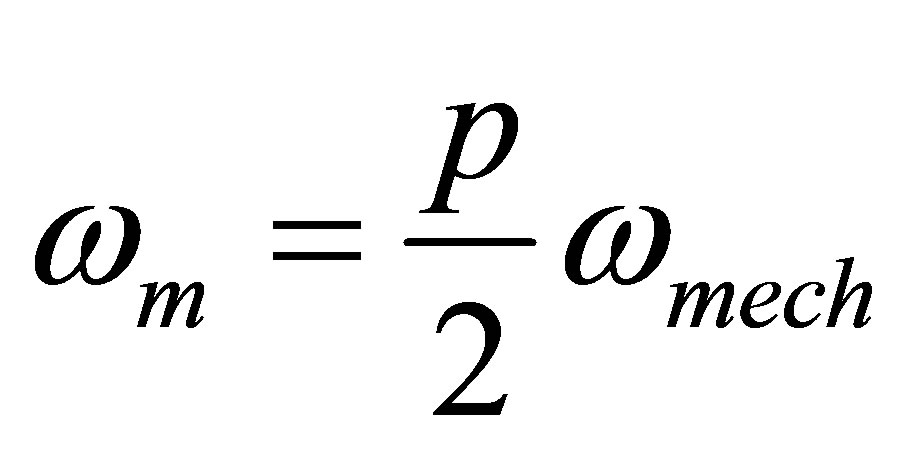 (7)
(7)
where 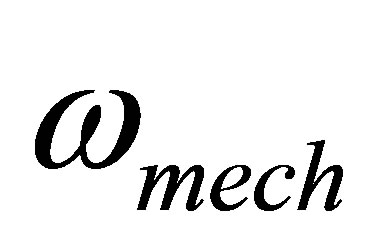 is the speed of the motor and p is the number of poles.
is the speed of the motor and p is the number of poles.
Since the torque developed by the motor is directly proportional to the motor drive current, it is difficult to control the drive current directly. Therefore the drive current is indirectly controlled through the input voltage. The simplified model of the PMSM q-axis subsystem is shown in Figure 1.
In vector control, assuming ids = 0, the state-space model of the PMSM q-axis subsystem is derived as [8]:
 (8)
(8)
For the speed controller design, the system output is
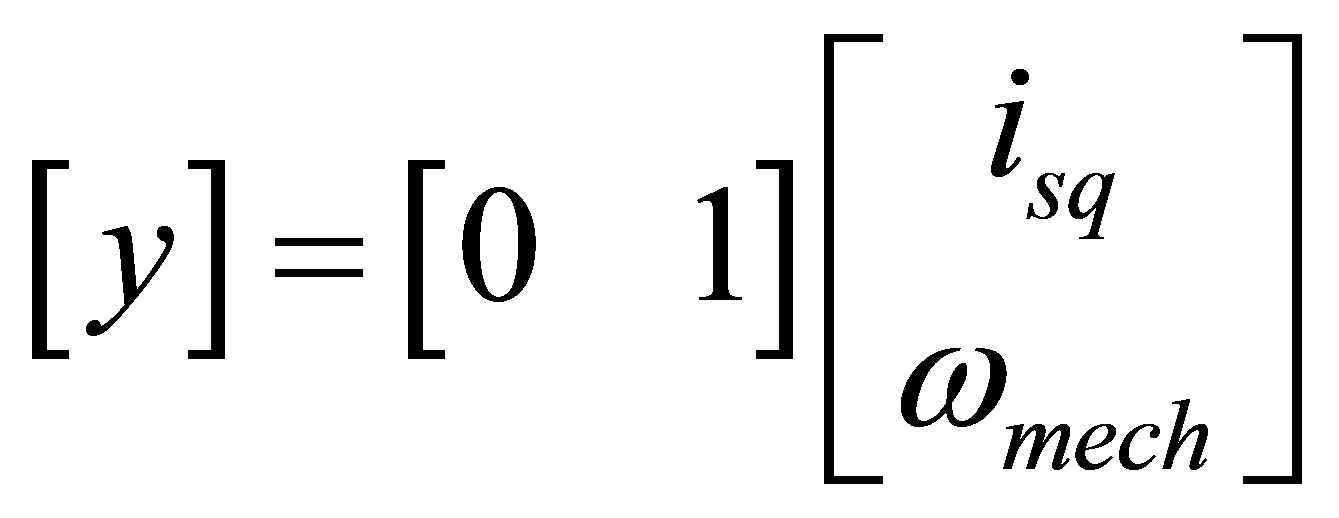 (9)
(9)
If the motor output is considered as the drive current, then the motor output is given by:
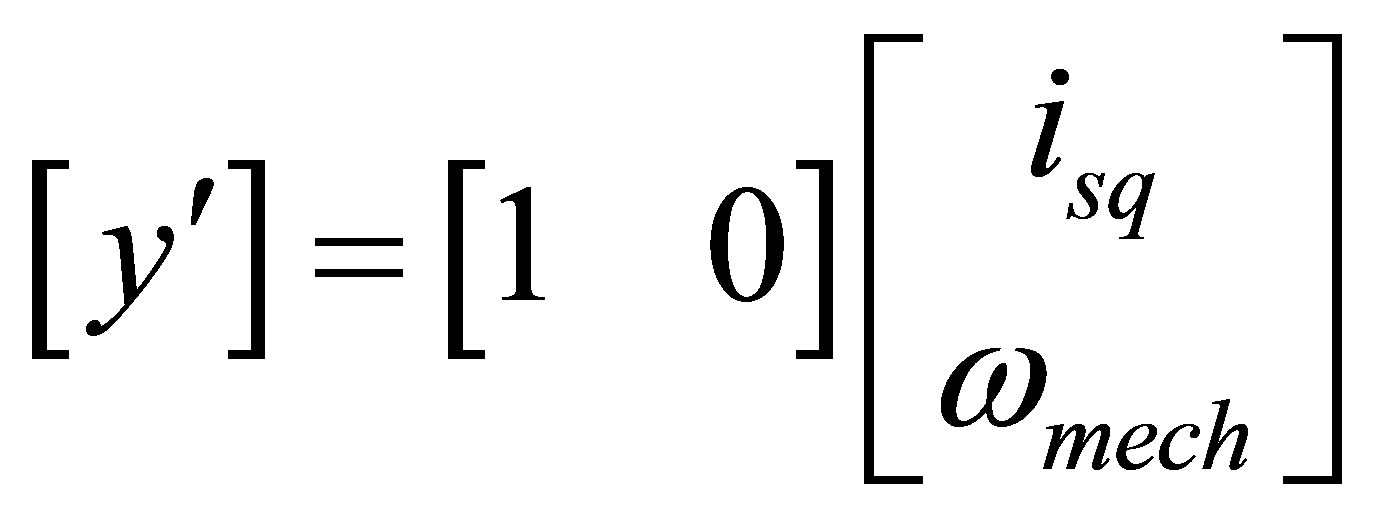 (10)
(10)
3. PID Parameters Tuning with State-Feedback and State-Feed forward LQR
The controller is designed as a single-input—single-output (SISO) system. The following discussion is based on the

Figure 1. Q-axis subsystem of a simplified PMSM.
q-axis controller/observer design [8].
The state space model of the simplified PMSM,  , with reference to the q-axis is:
, with reference to the q-axis is:
 (11a)
(11a)
 (11b)
(11b)
where,  ,
, 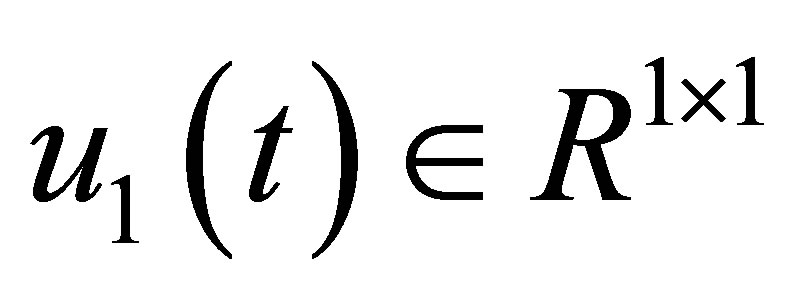 ,
, 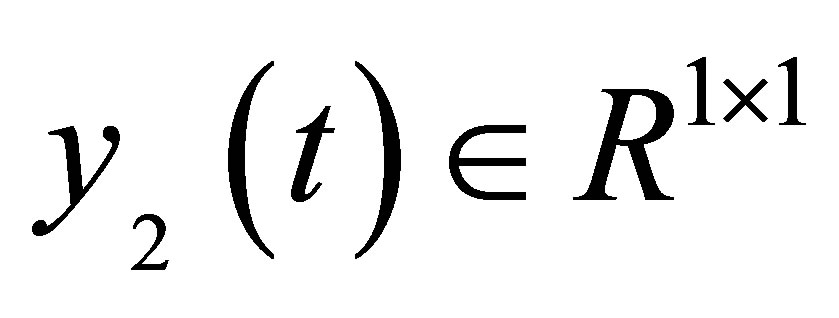 , and A1, B1 and C1 are constant matrices.
, and A1, B1 and C1 are constant matrices.
The entire system output is the sum of the motor output and load disturbance and is given by:
 (12)
(12)
where ,
, 
The state space model of the speed controller, 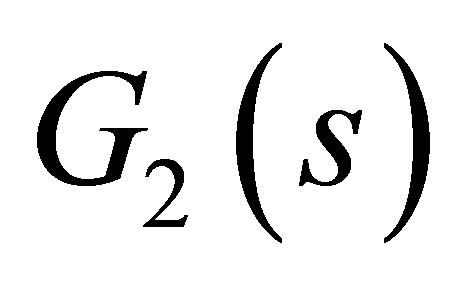 , can be written as:
, can be written as:
 , (13a)
, (13a)
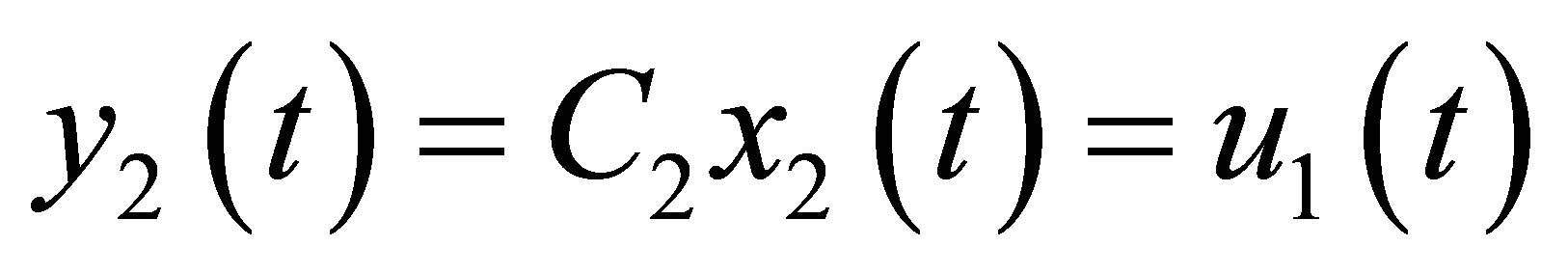 , (13b)
, (13b)
 (13c)
(13c)
where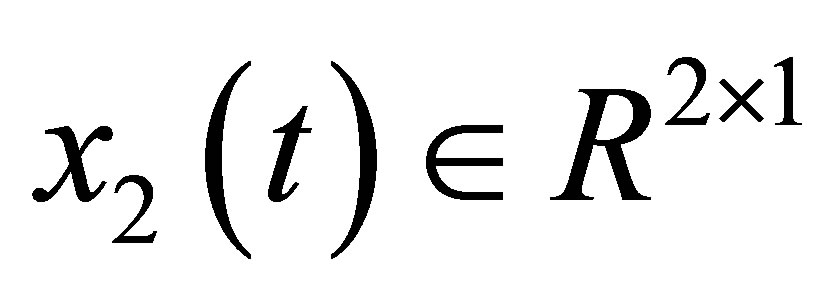 ,
, 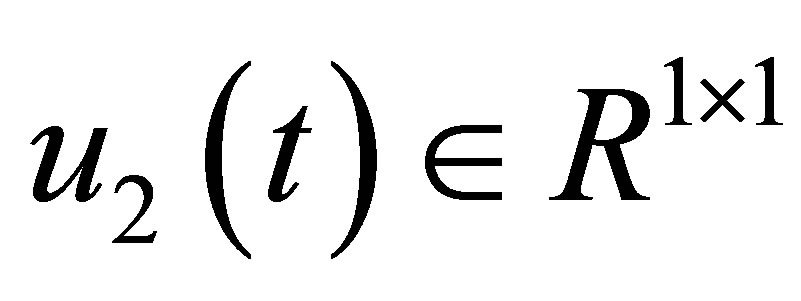 ,
,  ,
,  , and
, and 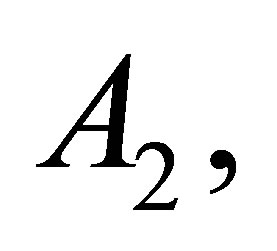
 ,
,  ,
,  are constant matrices.
are constant matrices.
In order to convert the PID tuning problem to an optimal design, we modify the closed loop cascade system into an augmented system with . The result is the following equation:
. The result is the following equation:
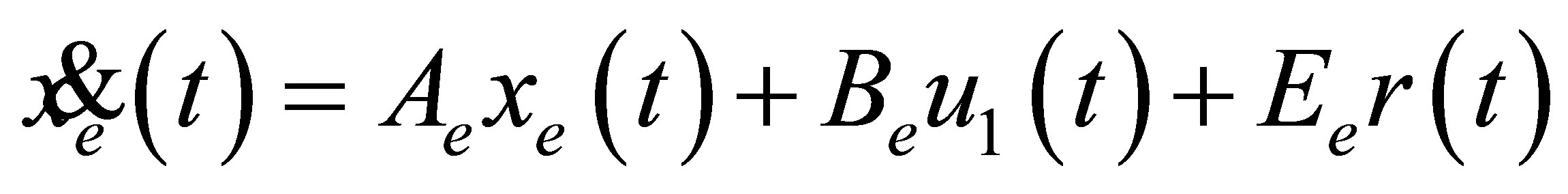 (14a)
(14a)
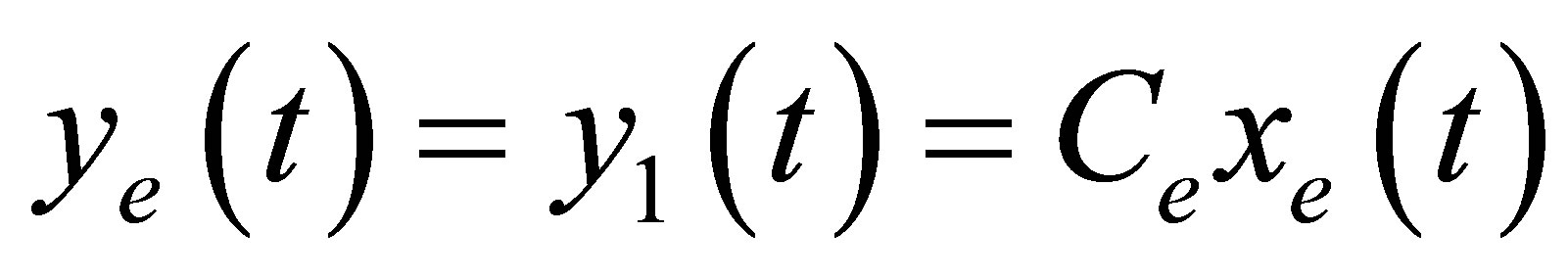 (14b)
(14b)
where
 .
.
The resulting state-feedback LQR for the augmented system is:
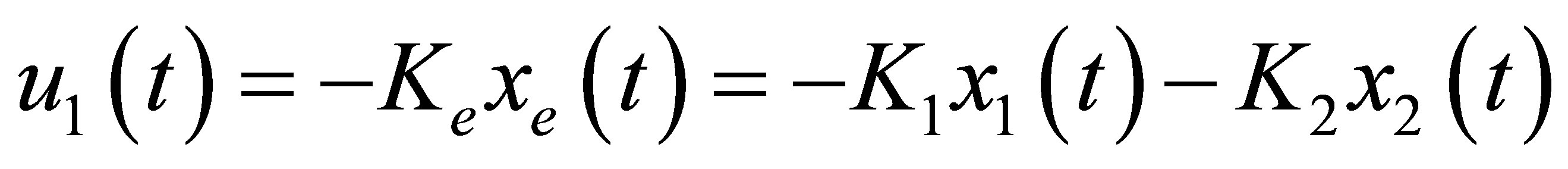 (15)
(15)
where ,
,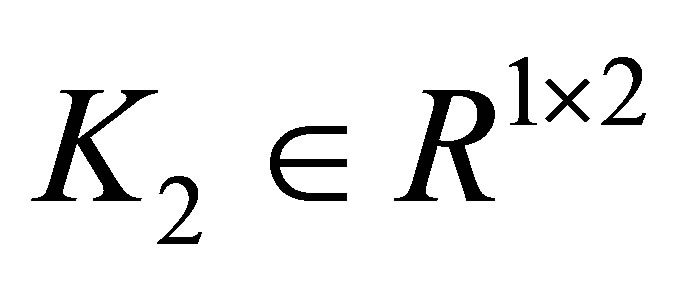 .
.
The quadratic cost function for the system J, is given as:
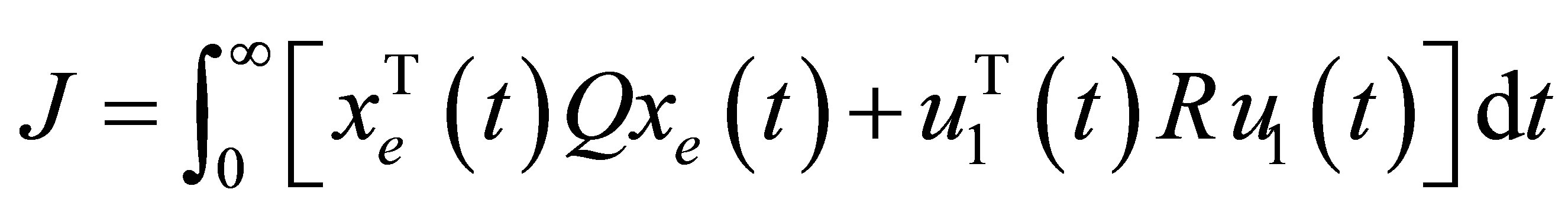 (16)
(16)
where ,
,  , which represent the states variation and control energy consumption, respectively.
, which represent the states variation and control energy consumption, respectively.
The optimal state-feedback control gain which minimizes the performance index is given by:
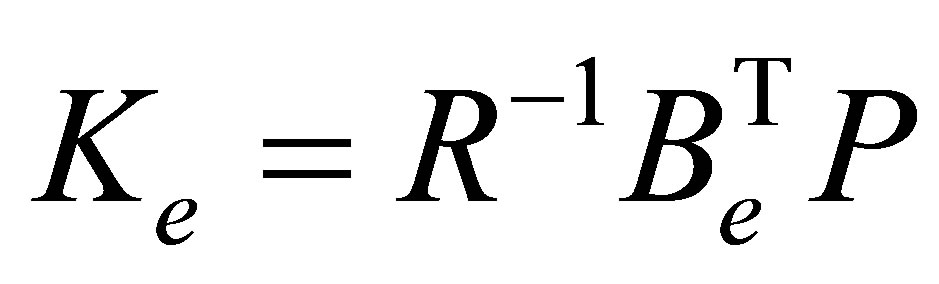 . (17)
. (17)
The solution of the revised Riccati equation is given by:
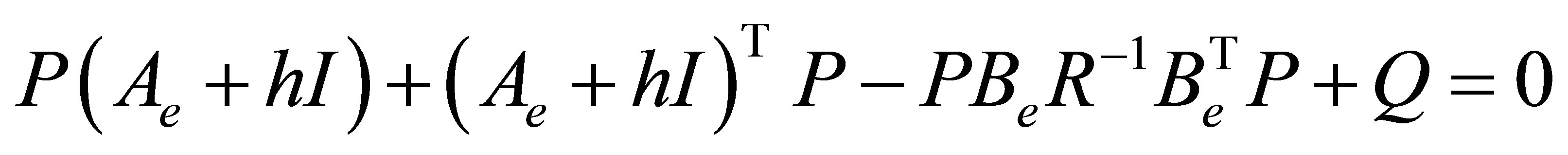 (18)
(18)
where ,
,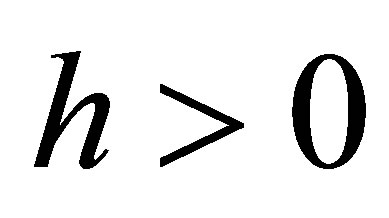 .
.
The motor states feedback actually act as the proportional and derivative controller 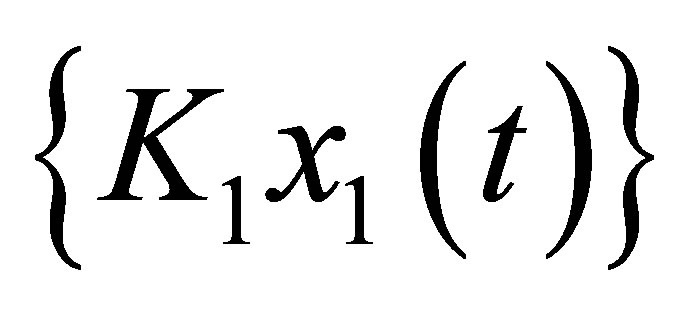 respectively and the controller act as an integral only. Then
respectively and the controller act as an integral only. Then  is a gain for the integral controller. Hence, the total control law is equivalent to a PID controller. By choosing the desired values of h and the weighting matrices Q and R, the control gain can be determined. The block diagram of the designed augmented system including the controller is shown in the Figure 2.
is a gain for the integral controller. Hence, the total control law is equivalent to a PID controller. By choosing the desired values of h and the weighting matrices Q and R, the control gain can be determined. The block diagram of the designed augmented system including the controller is shown in the Figure 2.
The calculated control gains are given by:
 , (19a)
, (19a)
 . (19b)
. (19b)
4. Design of Observer
A state observer is constructed mainly to achieve the speed control and disturbance rejection. The observation error and properly adjusted observer gain can provide feed-forward compensation for the output disturbance.
Suppose the state space model of the PMSM 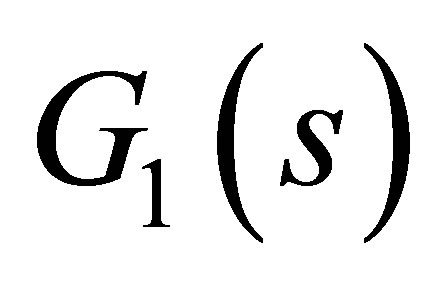 is:
is:
 , (20a)
, (20a)
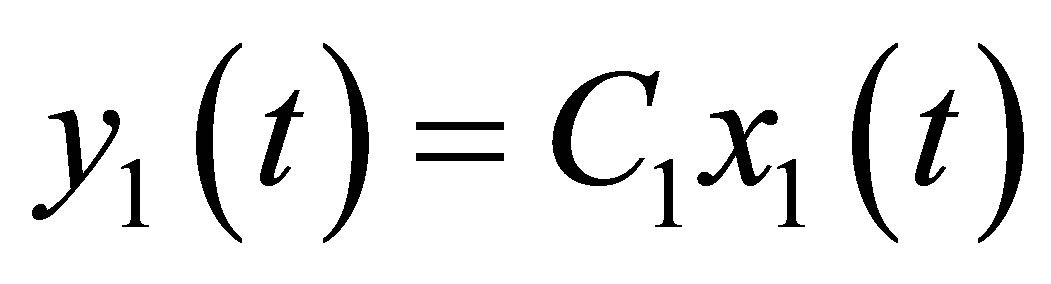 (20b)
(20b)
with the entire system output being the sum of the motor output and load disturbance as :
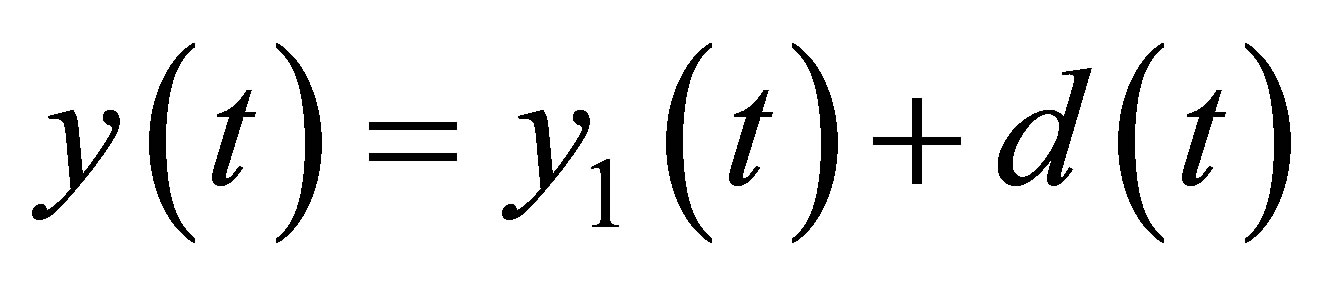 . (21)
. (21)
The design of an observer, whose dynamic function is the same as that of the motor is as follows (see Equation (22)):
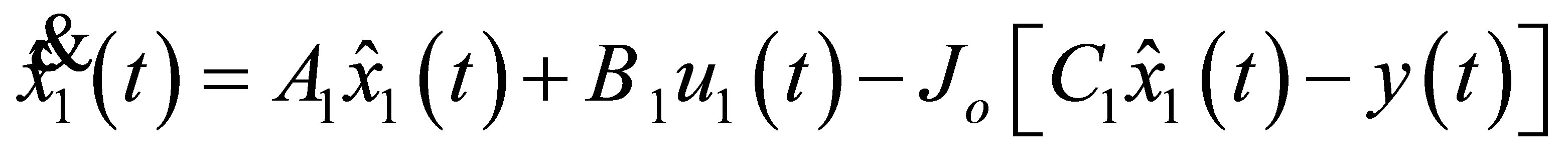 (22)
(22)
where 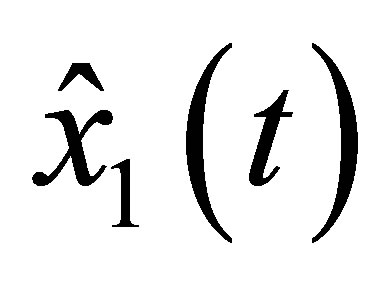 is an observed state and
is an observed state and 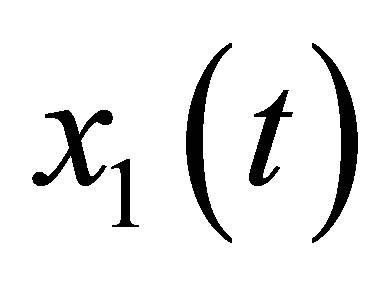 is the real state.
is the real state.
Then
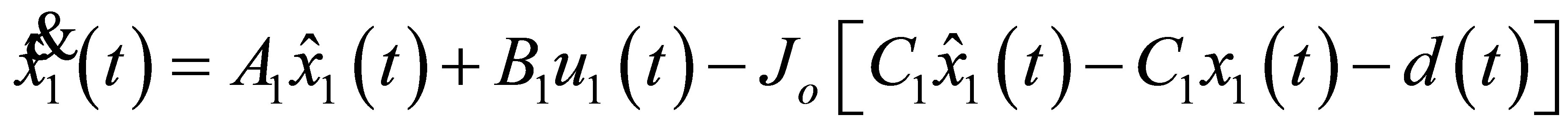 (23)
(23)
The observation error is expressed as:
 . (24)
. (24)
The observation error dynamic function is then given by:
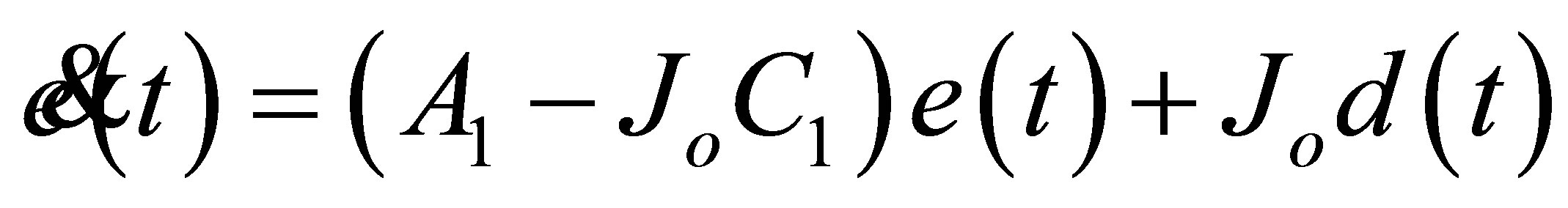 (25)
(25)
Applying the Laplace transform, we get
 . (26)
. (26)
From the above equation it is clear that the observation error will inevitably exist due to the load disturbance, and then the observed-state feedback can be regarded as:
 (27)
(27)
where, the term  is the exact motor state feedback, while the term
is the exact motor state feedback, while the term 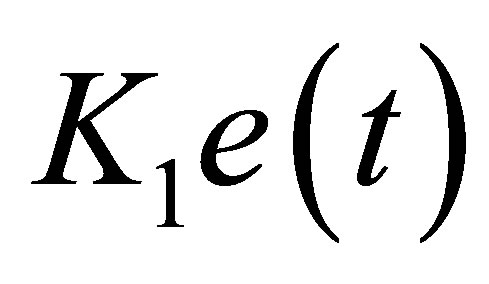 comes from the observation error. The PID controller system including the observer structure is shown in the Figure 3.
comes from the observation error. The PID controller system including the observer structure is shown in the Figure 3.
The feedback of the observation error actually acts as feed forward compensation for the load disturbance. Also the proper adjustment of the observer gain makes sure that the system is less affected by the load disturbance and provides additional feed forward compensation.
The speed signal differentiated through the position output of the encoder is very noisy. Thus 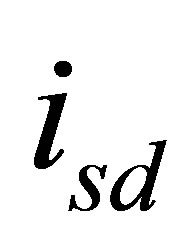 instead of
instead of  can be regarded as the system output in the following observer design. Selecting appropriate values for h, Q and R, the revised Riccati equation is solved as follows [8]:
can be regarded as the system output in the following observer design. Selecting appropriate values for h, Q and R, the revised Riccati equation is solved as follows [8]:
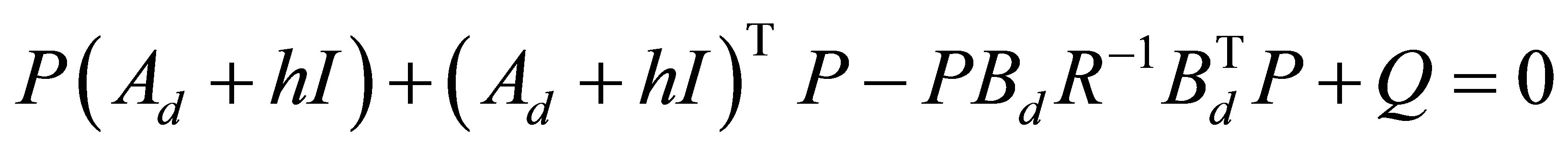 (28)
(28)
yields the desired optimal observer gain given as:
 (29)
(29)
where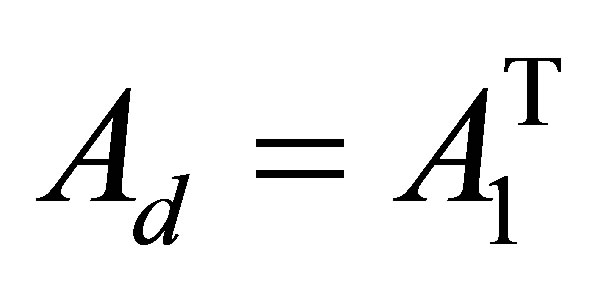 ,
,  ,
, .
.
5. State Observer Based Extended Kalman Filter
The Extended Kalman Filter is a set of mathematical equations which produces the optimal estimation of the state system based on least square method. The EKF estimates the process by using a feedback control. The EKF provides considerable good tolerance for the mathematical model error and noises in the measurement inaccuracy [19].
The state space model of the simplified PMSM given by “(11a)” and “(11b)” is the non-linear system. To apply the EKF algorithm, the system needs be discretized and linearized [20].
The discrete approximated equation is given by:
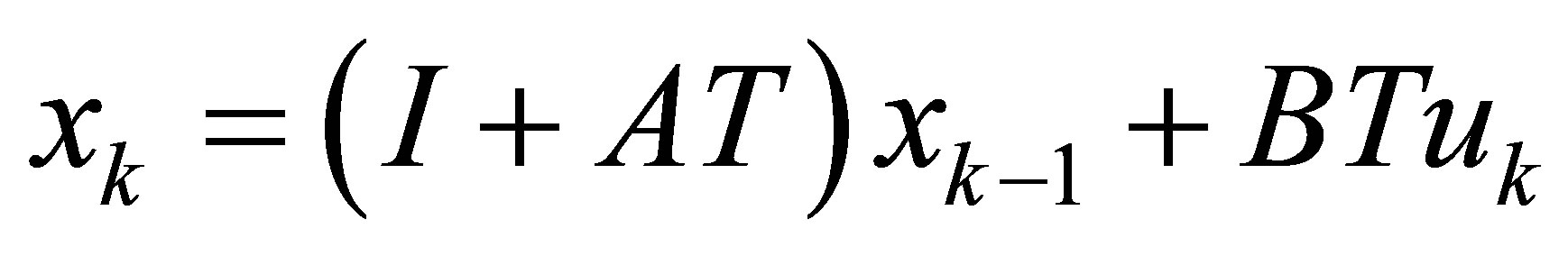 , (30a)
, (30a)
 . (30b)
. (30b)
The nonlinear stochastic equation is:
 (31)
(31)
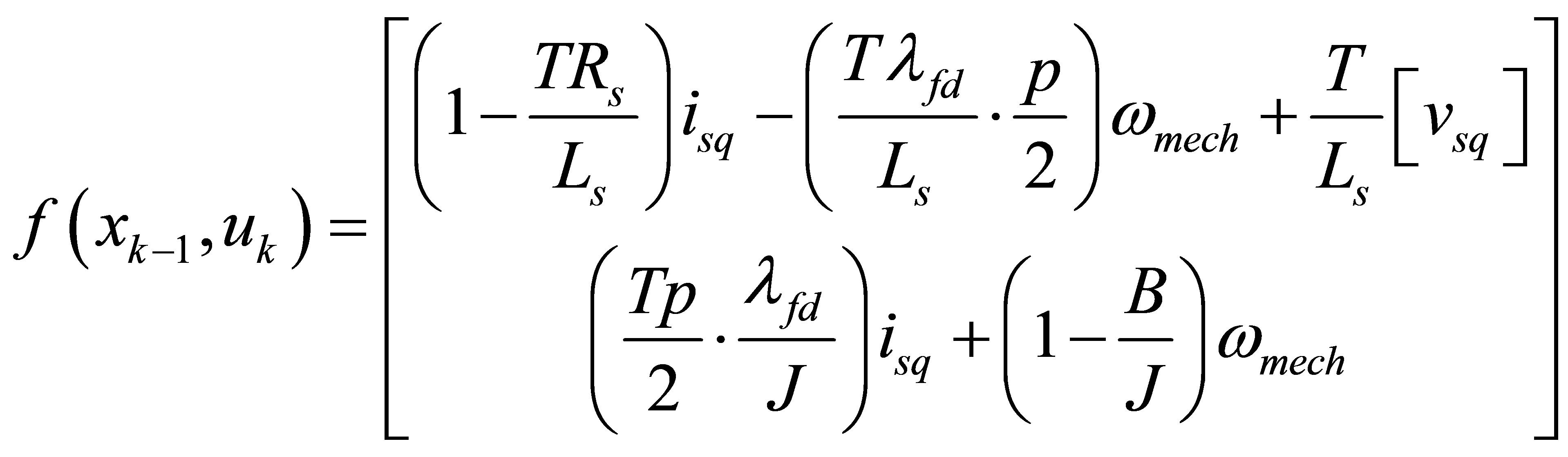 (32)
(32)
The Jacobian matrices of the partial derivative of f and h with respect to x are:
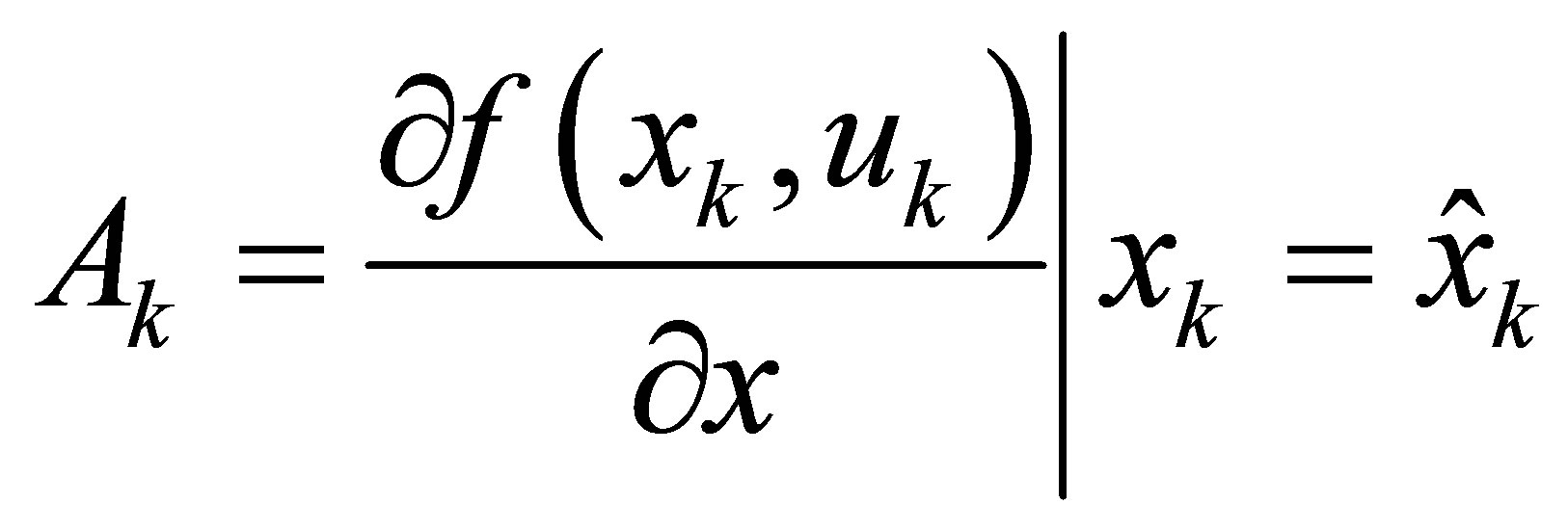 , (33a)
, (33a)
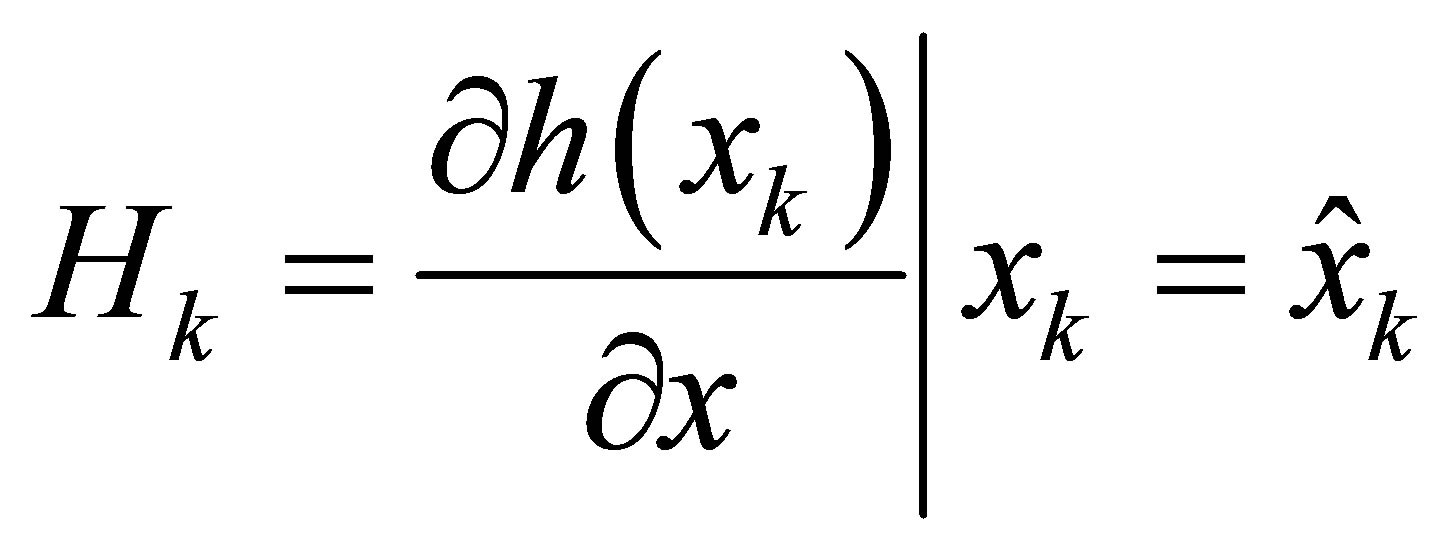 (33b)
(33b)
The motor nonlinear state equations given in the discretized form is as follows:
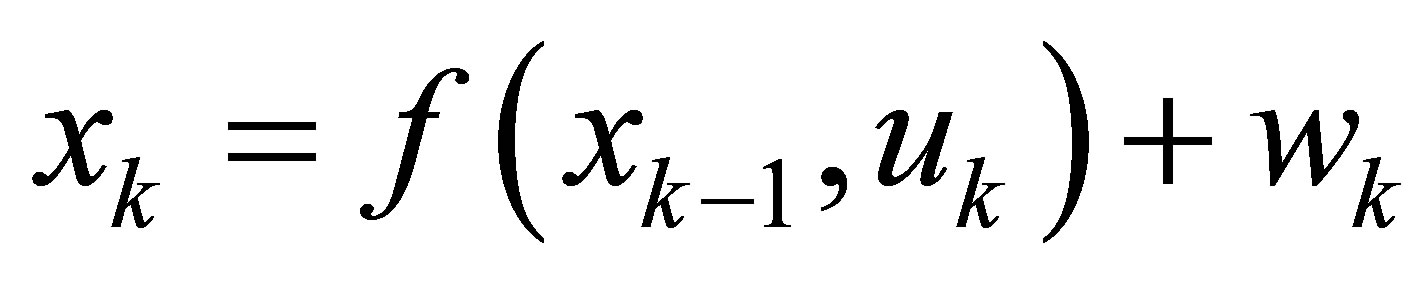 , (34a)
, (34a)
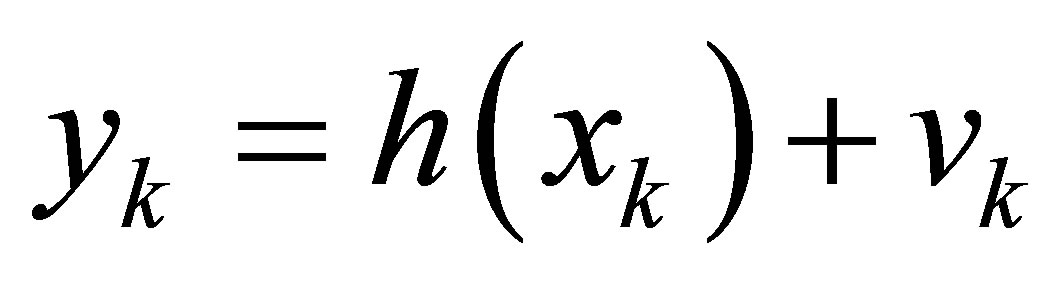 (34b)
(34b)
where  and
and  are zero-mean White Gaussian noise process and measurement noise with covariance Q and R. Mainly, there are two states in the Extended Kalman Filter, namely the prediction state and the correction state.
are zero-mean White Gaussian noise process and measurement noise with covariance Q and R. Mainly, there are two states in the Extended Kalman Filter, namely the prediction state and the correction state.
In the prediction state also called the time update, the optimal state estimate  and state covariance P are predicted.
and state covariance P are predicted.
 (35)
(35)
In the correction state also called the measurement update, the predicted state estimate  and covariance matrix P are corrected as follows:
and covariance matrix P are corrected as follows:
 (36)
(36)
The important and difficult part in the design of the EKF is choosing the proper values for the covariance matrices Q and R [21,22]. The change of values of covariance matrices affects both the dynamic and steadystate. By using trial and error method, a suitable set of values of Q and R are selected to insure better stability and convergence time.
The chosen values of Q, R and P are:
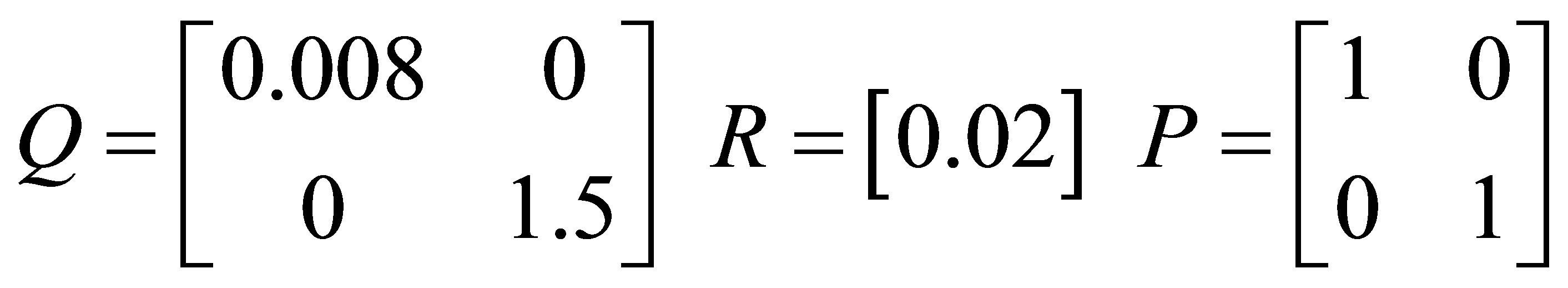 (37)
(37)
6. Simulation Results
The PMSM model is constructed to verify the speed control and load disturbance rejection using the conventional observer combined with EKF. The simulation is implemented using MAT Lab/Simulink. The parameter of the motor model is given in Table 1. Based on optimal control theory, the desired control gain K1 and K2 and optimal observer gain (Jo) are determined and the filter gain is obtained using EKF algorithm. The output drive current and speed are estimated through the observer theory and EKF algorithm is implemented using S-Function block. The input to the S-Function block is taken directly from the machine terminals. The noise-free, accurately estimated output current is fed to the observer as input while the estimated speed is compared with reference speed. At the output, the motor response is checked and the disturbance rejection is observed. The block diagram used in the simulation is as shown in the below Figure 4 and the simulation results are shown in Figures 5-10.
With the reference speed of 200 rad/s, the simulation
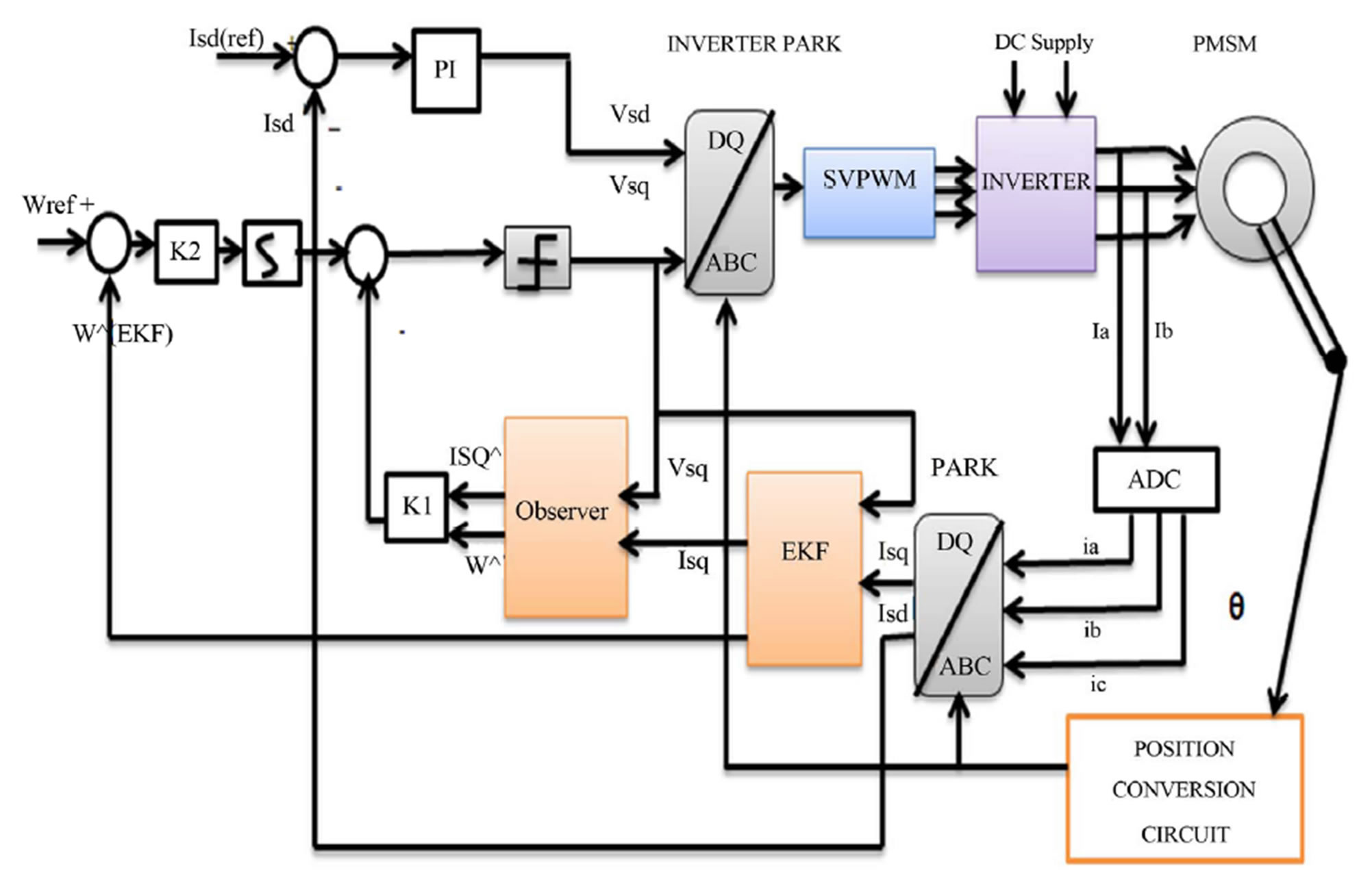
Figure 4. Block diagram of PMSM drive with observer combined with EKF.
 (a)
(a) 
 (b)
(b)
Figure 5. (a) Speed response; (b) control signal response for observer acting alone (no load).
 (a)
(a)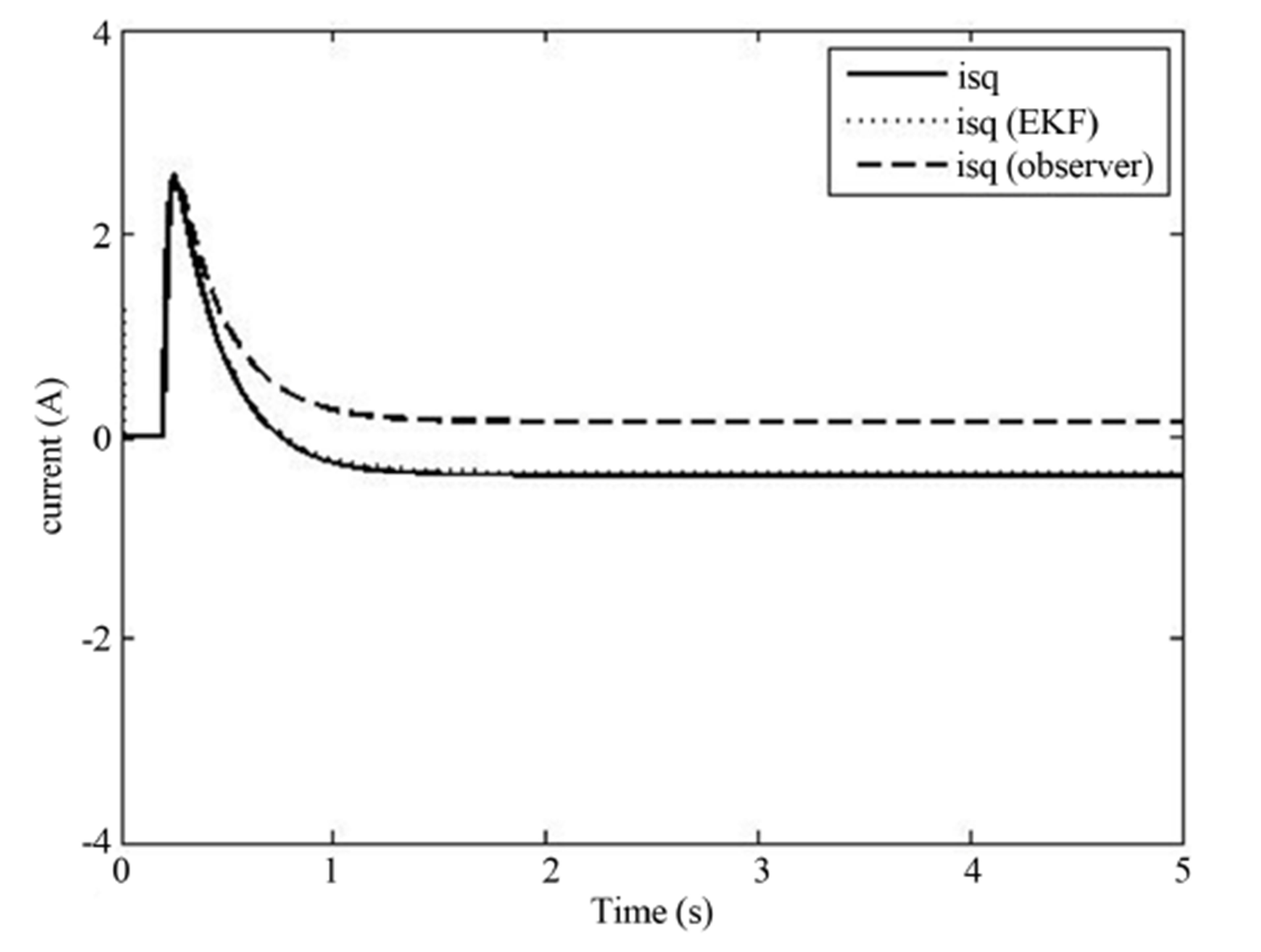
 (b)
(b)
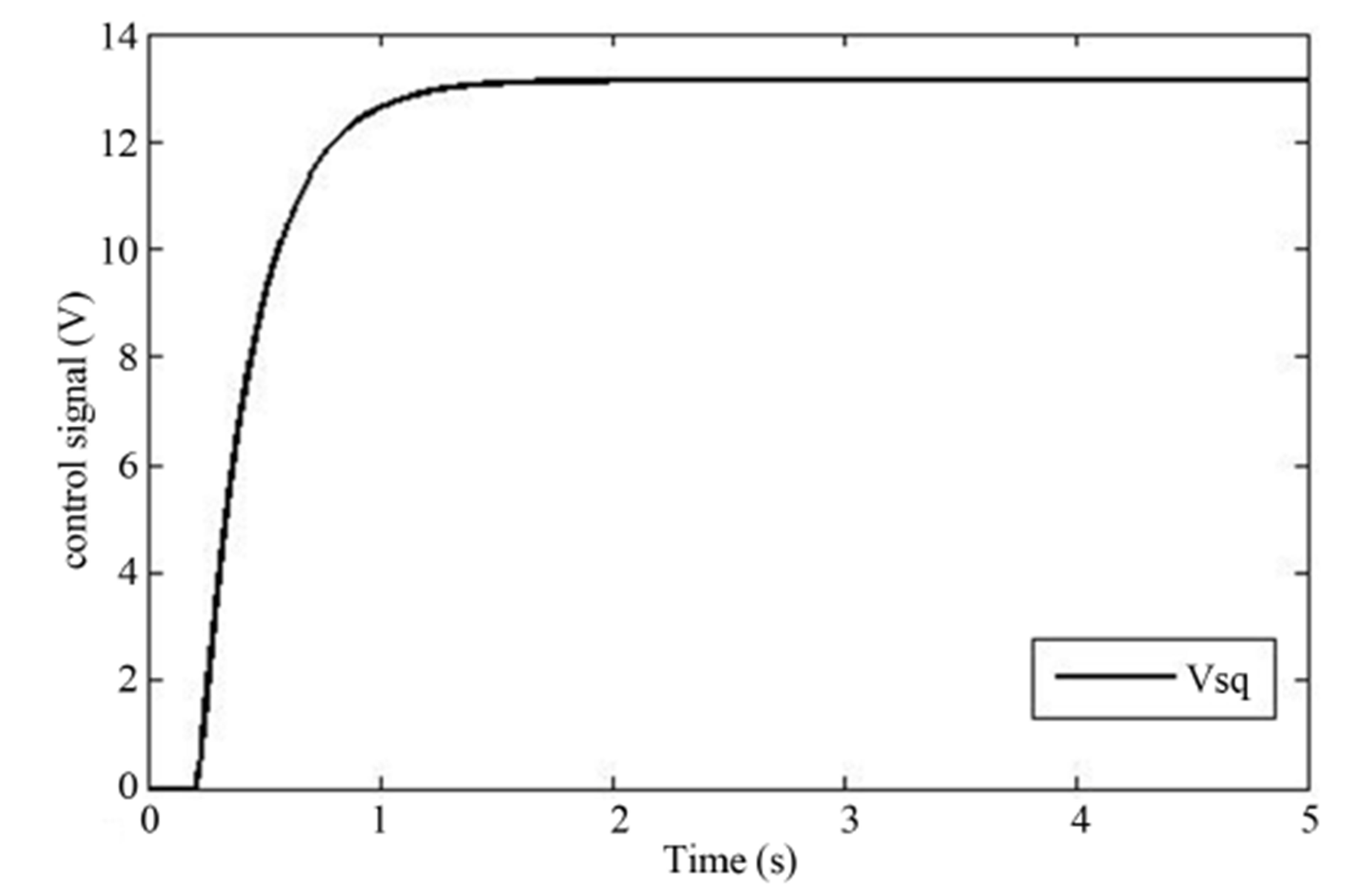
Figure 6. (a) Speed response; (b) control signal response for observer combined with EKF (no load).
results with observer acting alone and observer combined with EKF are shown in Figures 5 and 6, under no load condition. It is observed that the motor speed tracks the reference speed quickly and smoothly.
To account for the speed estimation performance of the observer acting alone and observer combined with EKF for a step change in steady state operation of PMSM,
 (a)
(a)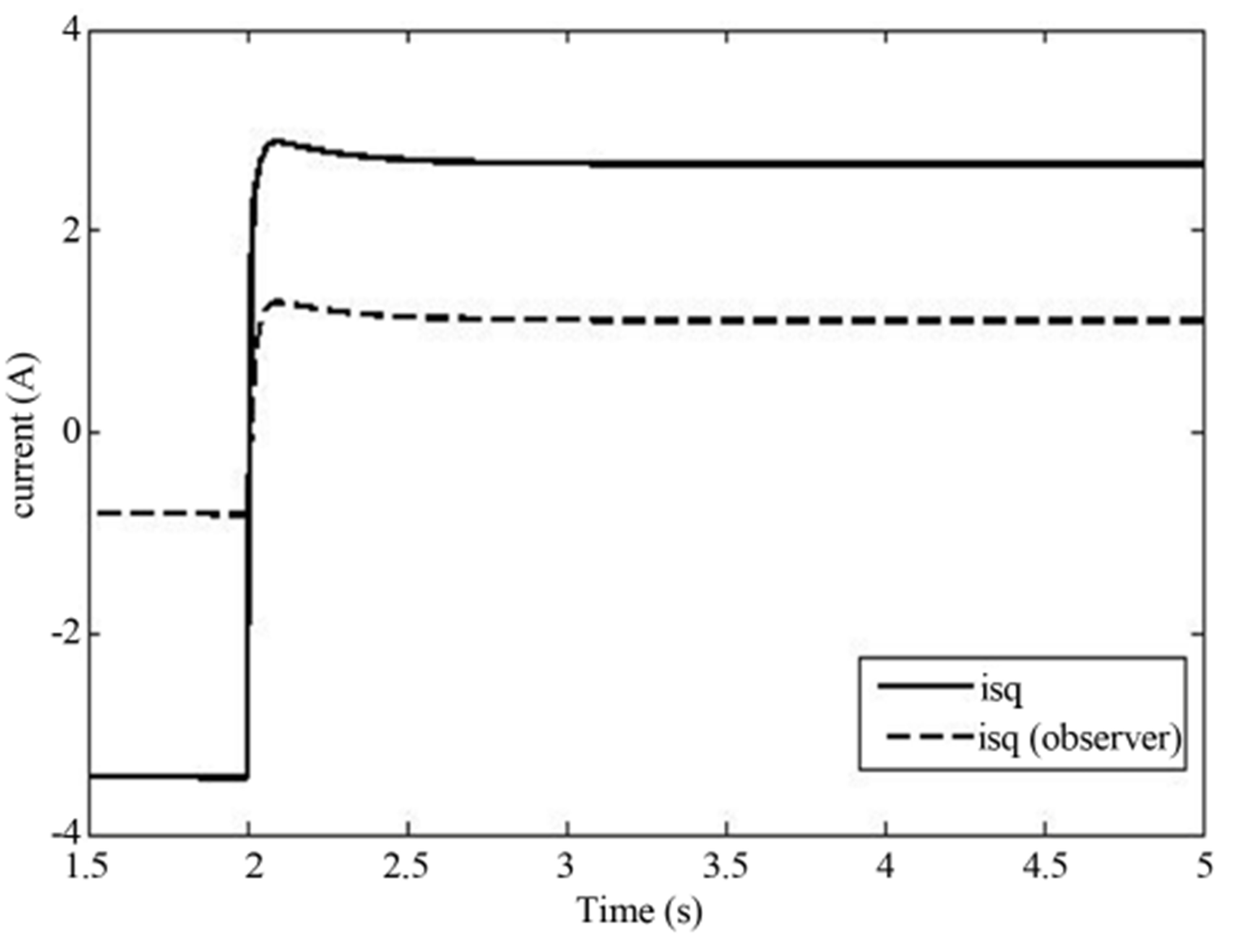
 (b)
(b)
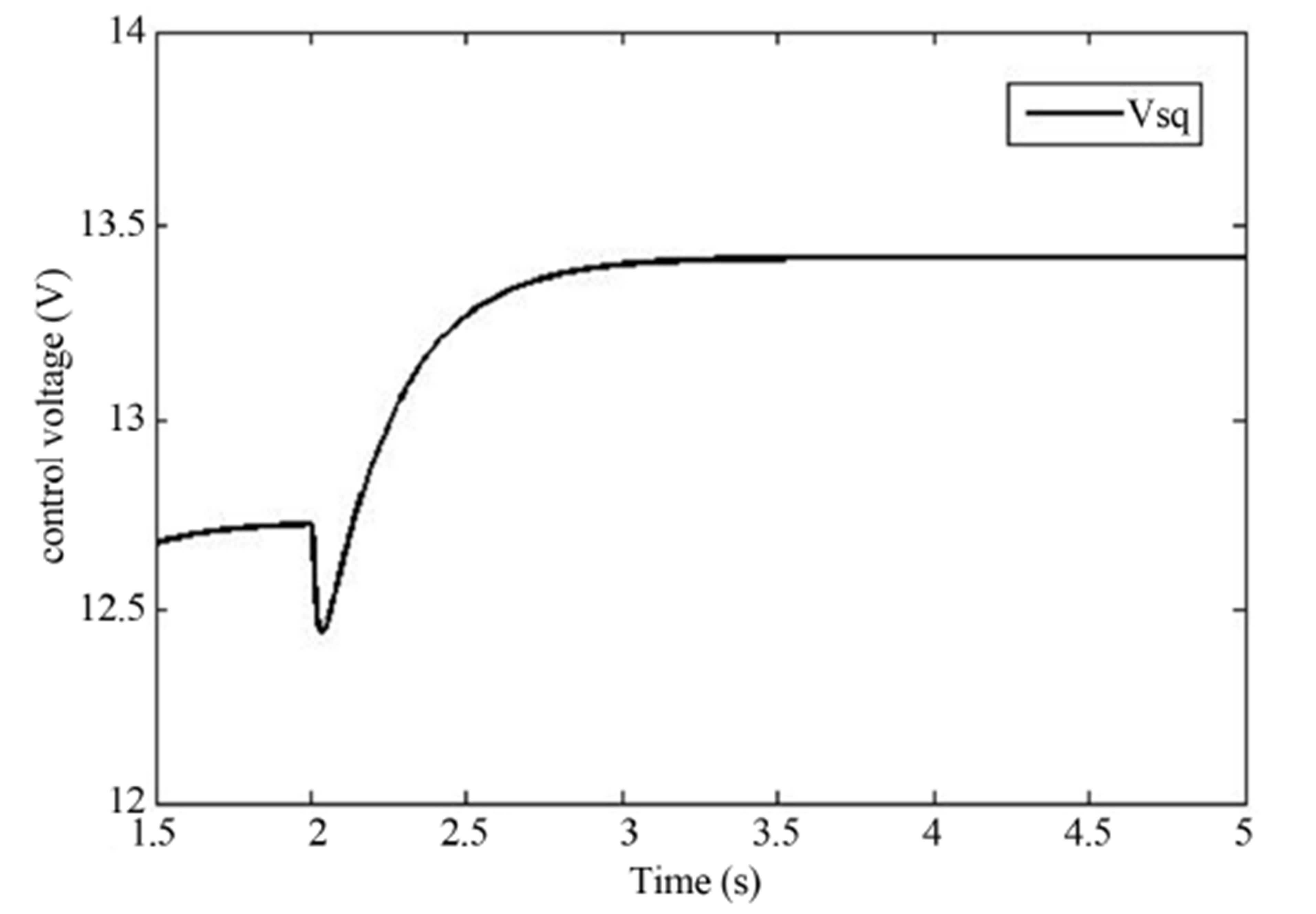
Figure 7. (a) Speed response; (b) Control signal response for observer acting alone (increase load).
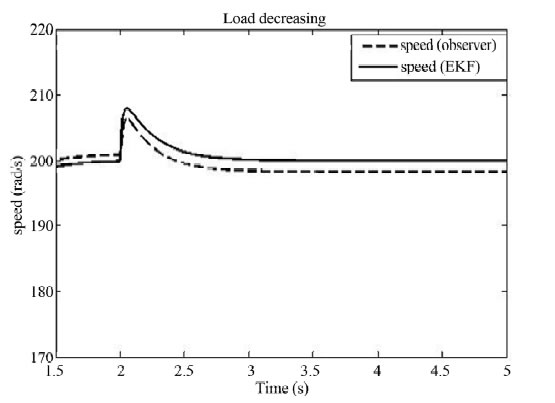
the load disturbance is applied at t = 2 s. The simulation results are shown in Figures 7 and 8 for the increasing load. Figures 9 and 10 shows the situation for the decreasing load.
From the obtained result, it is evident that the speed
 (a)
(a)
 (b)
(b)
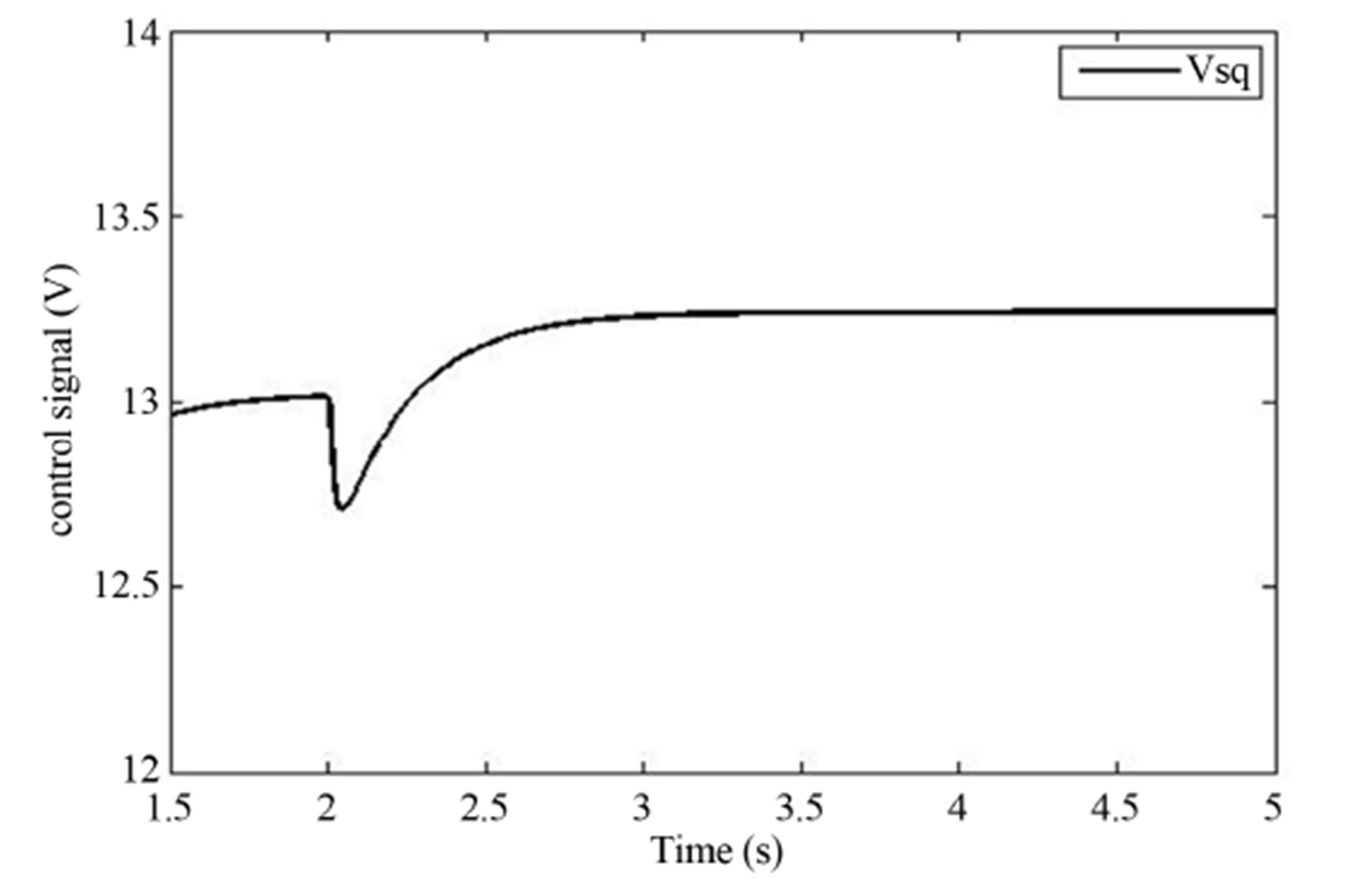
Figure 8. (a) Speed response; (b) Control signal response for observer combined with EKF (increase load).
variation caused by the load disturbance is significantly reduced in the case where the observer is combined with the EKF as compared with the case where the observer is acting alone. Also, as the simulations show, the input signal variation is reduced. The proposed approach mitigates speed deviation caused by the load disturbance variations. Reduction in the transient input signal variation, reduces the risk of potential input signal saturation,
 (a)
(a)
 (b)
(b)
Figure 9. (a) Speed response; (b) Control signal response for observer acting alone (decrease load).
and prevents the deterioration of the system performance. The simulation results are confirms the effectiveness of the proposed method.
7. Conclusion
A novel digital implementation of speed controller for a
 (a)
(a) 
 (b)
(b)
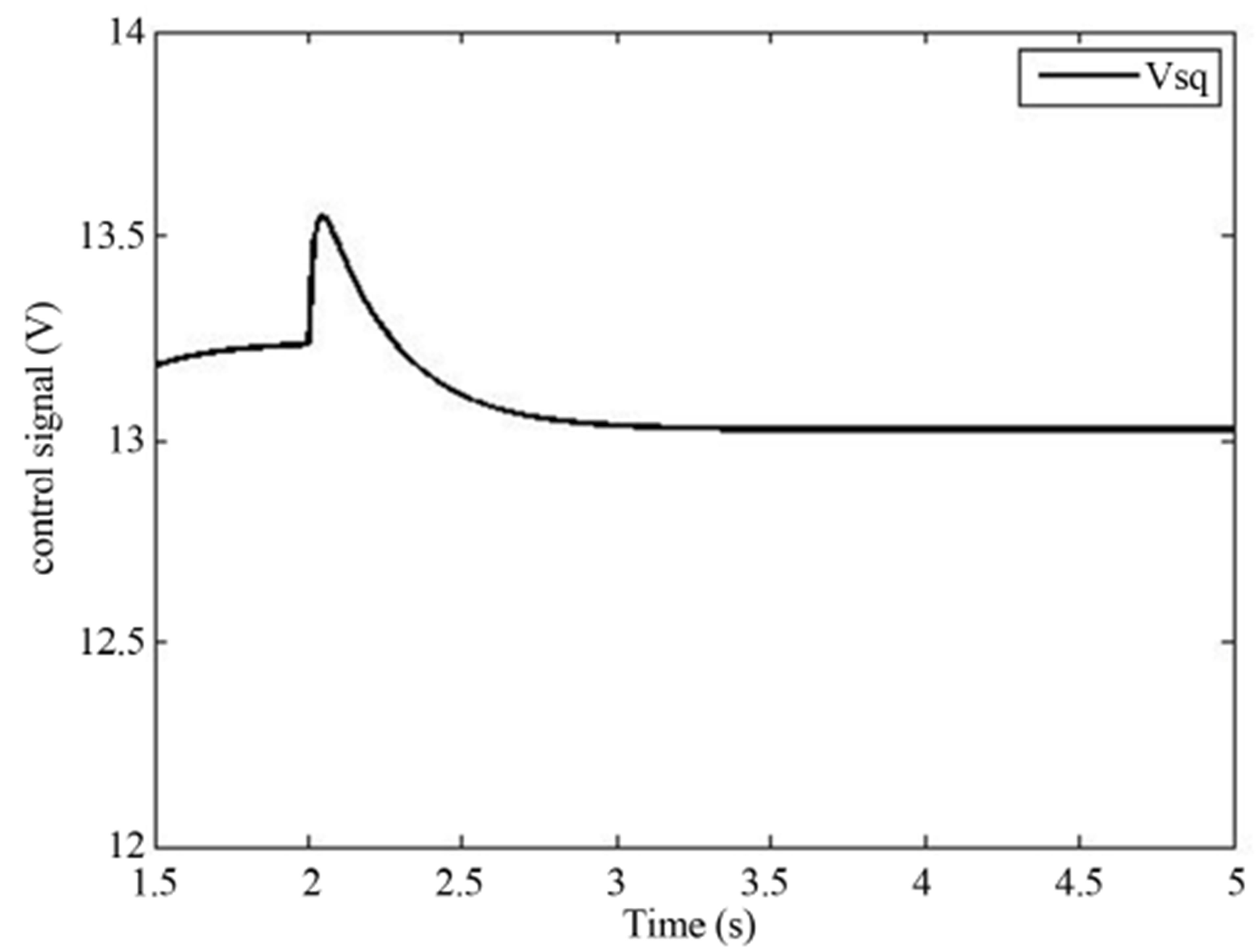
Figure 10. (a) Speed response; (b) Control signal response for observer combined with EKF(decrease load).
Permanent Magnet Synchronous Motor (PMSM) with disturbance rejection using conventional observer combined with Extended Kalman Filter (EKF) is proposed. The observer combined with EKF algorithm method attenuates the speed deviation caused by the load disturbance. In addition, the magnitude of the variation in the control signal is much less compared to the situation with an observer alone. The saturation of input and state is reduced effectively and the system performance is enhanced significantly.