A Possibility of Application of Wave Flow Method for Visualization of Shor States ()
The present work provides a brief analysis of experimental investigations related to quantum computer creation. The first step to the real quantum creation could be visualization of Shor states. Such visualization is based on the use of the phenomenon of the secondary wave generated by incident electromagnetic irradiation on the object which undergoes screening. This electromagnetic irradiation under certain conditions can be transformed into waves of other type, for example, surface plazmons. The massif from n quantum objects generating secondary irradiation, in principle, can be considered as a route to materialization on Shor cells. In such a way, a system of q-bites of quantum computer can be realized.
1. Introduction
Just after R. Feynman’s pioneer works [1,2] concerning the need and possibility of the quantum computer creation as well as after Yu. P. Manin’s monograph, in which the problem of noncomuptable functions and the related algorithmically insoluble tasks are discussed in detail [3], a number of theoretical studies on the specified topic have been performed. They resulted in numerous publications including reviews and monographs (see, for example, reviews [4-7] and the literature cited therein). Theoretical successes in the solution of the quantum computers problem were based on the ideas of application of physical processes which would ensure the realization of the logical operations similar to those occurring in classical computers. It was supposed that employment of quantum objects specifics will allow improving the computation procedure, but will not change essentially its essence. It seemed that the necessary conditions, which should provide soon successful experimental realization of R. Feynman’s ideas, were eventually found. Moreover, the landmark Shor’s work [8] has specified the scope of real tasks, which can be solved only with usage of quantum computers. Conviction in fast creation of quantum computers was strengthened in 1998 when it was reported on realization of elementary quantum algorithm based on two q-bits using nuclear magnetic resonance (NMR) phenomenon. In one work it dealt with nuclear spins of hydrogen atoms (protons), and in other paper hydrogen and carbon nuclear spins were studied [9,10]. Later on, the number of q-bits in the NMR processor increased to seven and Shor algorithm was implemented in elementary variant [11]. In the above mentioned processor, logic operations were performed with participation of nuclear spins of two carbon atoms (13C) and five fluorine atoms (19F). The role of elementary processor was carried out by a molecule of perfluorobutadienyl iron complex.
Here it is pertinent to note that the application of nuclei spins as possible candidates and the NMR phenomenon for creation of the quantum computer were not casual. Exclusive informational content of these methods and ever-increasing universality of NMR spectrometers make their predominant in wide aspect of scientific research. Essentially, the main advantage of the NMR method is the possibility of designing the nuclear spinhamiltonian practically without any limitation that allows formulating and solving the most various problems including those of special research [12]. In the NMR arsenal there is a wide set of pulse radio-frequency sequences which can ensure the performance of unitary transformations over the system of q-bits with selective impact on each of them. In particular, it gave occasion to modeling Toffoli gate, an important element of computation procedure, by the system of spins ABC characterized by parameters δА, δВ, δС; JАВ ¹ 0; JАС ≠ 0; JСВ ¹ 0; JАВ > JАС и JСВ; ,
, 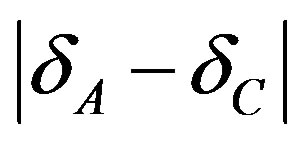 ,
,  , JАС и JСВ. Here d is chemical shift of the corresponding nuclei signal, J is a constant of spin-spin interaction between these nuclei [13].
, JАС и JСВ. Here d is chemical shift of the corresponding nuclei signal, J is a constant of spin-spin interaction between these nuclei [13].
2. The Problem of Real Computer
Despite the first experimental achievements in the realization of R. Feynman idea, the possibility of practical implementation of real quantum computations (using NMR or other physical methods) has to be proved. In accordance with the current representations, one should develop the system containing quite large number of quantum particles (at least, about hundred, and even better—more than hundred), playing a role of q-bits and obeying to the laws of quantum physics which account for, first of all, the collective behavior of q-bits which is reflected entanglement of states. Probably, in this situation the above-designated problem should be solved via modeling of the scheme which will be realized in real quantum computer [14]. Paramagnetic molecules, in which strong interelectron correlations are realized, can be employed for this purpose. These interactions can lead to the intramolecular rearrangements causing finally a entanglements of quantum states in natural way, i.e., without external influence on the system of q-bits [15].
Coming back to the difficulties encountering in creating the quantum computers, capable of solving the real problems, one can make the following remarks. There is the impression that in all currently realized schemes a kind of “hybrid” is used instead of real quantum processor. These schemes describe the computation procedure in macroworld by parameters characteristic for macroobjects. However, as it was already mentioned above, the computation procedure in such devices should be based on the application of microobjects located in specific quantum states. This fact can be illustrated by the example of the NMR processor. The NMR phenomenon is a response of spin system to the resonance conditions using macro-devices such as spectrometers and relaxometers. Such response induces EMF, which can be analyzed on the basis of the Faraday’s law of electromagnetic induction. The induced EMF generates electric current in a macrosample. This current represents an object for manipulation in the NMR spectrometers at the level of a macroworld. Another basic condition, which one should take into account, is as follows. It is difficult to imagine a molecule containing, for example, hundred nuclei of heteroatoms (atoms of one series a priory give significantly inappropriate spectrum for quantum calculations), a molecule which will have the NMR spectrum obeying the rules of first order with preservation of the necessary ratios between values of spin-spin interaction constants. Thus, one needs somehow to connect separate molecules to perform real computing operations.
All the aforementioned gives a reason, at least, to discuss two interrelated questions. First, is it possible to create a processor, which could perform the computations from start to finish within the quantum world? Second, what should be such quantum computer, capable of solving the real problems? To try to answer these questions, it is justifiable to address to the well-known scheme of operation of the classical computer which can be represented as sequence of three operations: 1) input of basic data into the computer register; 2) performance of computations; 3) output of the results. It is also assumed that operation of the quantum computer should be performed according to this scheme. Actually there is a trend to force quantum objects to work as processors following the rules of classical computers functioning. But the question is whether such trend fits the realities which should take place in the quantum computer?
The first stage of the classical computer operation can compare with the stage of initial state preparation of the quantum computer. This means creation of a devise (similar to the register of the classical computer) containing quite large number of quantum objects which are in the entangled states [4,6]. To understand whether this stage of the quantum computer operation correlates with the input of the date into classical computer register, one should make here the following explanation. According to laws of quantum physics, if the system consists of n two-level q-bits, its state generally represents a superposition of 2n basic states 
 , i.e. (the standard designations are used here) [6]:
, i.e. (the standard designations are used here) [6]:
 . (1)
. (1)
If to use rather small number
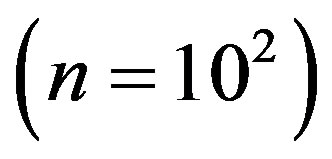
of q-bits, it is possible to receive rather large
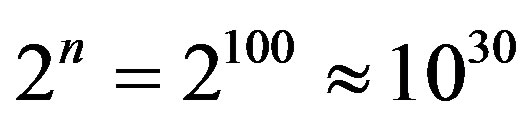 (2)
(2)
mathematical information resource of the quantum computer. From here follow the main advantages of the quantum computer. Really, during the record of a number containing n figures, the amount of cells occupied from the total number equaling 1030, will be just n figures. Other (not occupied) cells can be used for performing the parallel computations.
Here it is necessary to emphasize that these cells are not specific elements of schemes or magnetic sites (domains), on which one can record the necessary information. They are referred to own values of the operator of the physical characteristic describing the system of q-bits which, according to the laws of quantum mechanics, can be determined with a probability. In certain sense it is a question of a big set of virtual (in terms of availability) cells, the application of which is far from to be obvious. This is one of fundamental problems. Further, after the information (for example, digital) will be put into these cells, they need to be operated somehow to perform the computation operations. And, at last, it is necessary to find a way to output the result after finishing the computations. From this follow difficulties of basic character which should be overcome in the course of quantum computer creation.
3. Application of Wave Flow Phenomenon for Materialization of Virtual Quantum States
All the above-stated indicate the most important issue in the problem of quantum computer creation. This is visualization or materialization of the aforementioned states which are not subjected to decoherence. Only after this problem will be solved, one can speak about correspondence of the first stage of quantum computer operation to the stage of input (record) of digital information in the classical computer register. Moreover, one must bear in mind that visualization should not change reality, i.e. ensure quantum character of q-bits states. Apparently, to reach this goal, it will be sufficient to use states corresponding to specific spatial and electron states of molecular (atomic) systems, one can say, to their architecture. If to draw an analogy with the classical computer, these states, determined by molecular structure of q-bits, correspond to elements of the register, into which Boolean variables (0 and 1) have not been entered yet. These states should have content similar to this of Boolean variables. Such states have to be concrete and exist as long as possible, as it is realized in classical computer.
One of possible ways of such visualization can be based on the use of the phenomenon of the secondary wave generated by incident electromagnetic irradiation on the object which undergoes screening. According to the theory of wave flow, the incident primary electromagnetic irradiation under certain conditions can be transformed into waves of other type, for example, surface plasmons. In particular, the application of secondary waves for screening of the nano-sized microobjects in optical range of frequencies turned out to be effective [16,17]. It is a common knowledge that the description of collective behavior of a system with many quantum particles is often associated with the quasiparticle concept. Surface plasmons belong to such type of microobjects (quantum in essence). Therefore, the massif from n quantum objects generating secondary irradiation, in principle, can be considered as a route to materialization of Shor cells. In other words, in such a way, a system of q-bits, can be realized. The irradiation thus generated will ensure visualization of states characterizing this system in accordance with the expression. Essentially that the luminescence of such cells has the secondary nature. It allows controlling their states from macroworld. In the simplest case the luminescence can correspond 1, no is 0.
As noted above, the entanglement of states is a necessary stage of the formation of a system containing n interacting q-bits because this ensures creation of mathematical information resource of the quantum computer, which can provide its advantages. But the the entanglement of states is not end in itself. In other words, the main thing here is a possibility to create the mentioned massif as a source of a large number of the cells ready for their involvement in the computation process. Fluorescent quantum objects, due to the fact that their irradiation can be controlled by primary electromagnetic radiation, allow using them for the specified purposes. Indeed, the realization, for example, of state , if
, if 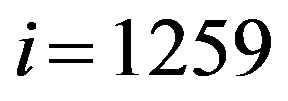 means that the corresponding quantum dot gives secondary irradiation. The current advances in physics of lowsize heterostructures and technology of their development make it possible to create nanoobjects with sizes of about ten nanometers at the basis and height of some nanometers located from each other at distance of ~ 50 nanometers (see, for example, [18] and the references cited therein). Analyzing these findings, one can easily estimate that one square centimeter can contain up to 1010 islands. Naturally, the key question is about structure and properties of such nanoobjects. This problem requires separate study. Partially this study has been performed in [15].
means that the corresponding quantum dot gives secondary irradiation. The current advances in physics of lowsize heterostructures and technology of their development make it possible to create nanoobjects with sizes of about ten nanometers at the basis and height of some nanometers located from each other at distance of ~ 50 nanometers (see, for example, [18] and the references cited therein). Analyzing these findings, one can easily estimate that one square centimeter can contain up to 1010 islands. Naturally, the key question is about structure and properties of such nanoobjects. This problem requires separate study. Partially this study has been performed in [15].
Strictly speaking, simple selection of i values allows preparing the cells corresponding to own values of the operator 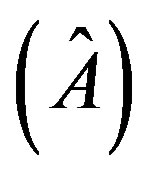 of a physical characteristic which describes the process in the quantum computer, for example, current or wave process
of a physical characteristic which describes the process in the quantum computer, for example, current or wave process . But the mathematical resource of the quantum computer relates also to the application of non-diagonal matrix elements, i.e.
. But the mathematical resource of the quantum computer relates also to the application of non-diagonal matrix elements, i.e. 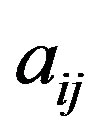 This purpose, obviously, requires the usage of additional methods, for example, the tunneling phenomena.
This purpose, obviously, requires the usage of additional methods, for example, the tunneling phenomena.
4. Conclusion
The analysis of the current experimental data related to creation of the quantum computer allows one to make the following conclusions. In all the realized cases, instead of real quantum processor, a kind of “hybrid” has been developed. In such a hybrid, the computation process is described by parameters, characteristic for macroobjects. Meanwhile, the computation procedure in such devices should be based on application of the microobjects which are located in certain quantum states. Probably, the most important prerequisite to solve the problem of real quantum computer creation is visualization of Shor virtual states. One of possible ways of such visualization can be based on the use of the phenomenon of the secondary wave generated by incident electromagnetic irradiation on the object which undergoes screening. In such a way, a system of q-bits can be realized. The irradiation thus generated will ensure visualization of states which can be controlled.