Investigation of Infrasound Radiated from Highway Bridge Owing to Moving Truck ()
1. Introduction
The movement of vehicles over a bridge produces vibrations in the bridge. Furthermore, infrasound—which is low-frequency noise in the 0 - 20 Hz range—radiates from the bridge. Infrasound radiation, which can produce a rattling sound, can cause mental and physical discomfort to people.
In general, the dynamic response of a bridge is influenced by the running speed [1], vehicle load [2], and suspension system [3] of the truck; truck’s lane position on the bridge [1]; road surface roughness [4]; and bridge dynamics by the matching of the bridge’s and the truck’s natural frequencies [5]. In particular, the infrasound radiated from the bridge is related to the frequencies of the bridge vibration, truck suspension spring vibration, and tire spring vibration [6].
Conventional trucks with a rear leaf suspension [6,7] have frequencies of about 3.0 Hz; furthermore, their tire spring vibration frequencies are 10 - 20 Hz. When the frequency of the truck’s vibration (suspension spring vibration or tire spring vibration) and that of the bridge’s vibration are similar, there is likely to be a rise in complaints from nearby residents about rattling sounds— owing to the truck’s suspension spring vibration, which has a frequency of about 3.0 Hz—and/or mental and physical discomfort—owing to the truck’s tire spring vibration, which has a frequency of 10 - 20 Hz [6].
If infrasound is produced, effective and inexpensive countermeasures are required to prevent this problem. Previously, complaints about mental and physical discomfort owing to infrasound produced by bridge vibrations upon resonance with the truck’s tire spring vibration at a frequency of 10 Hz have been reported [8,9]. The use of the extended deck method as a countermeasure led to a reduction in these complaints.
Because countermeasures are expensive, the relation between their cost and their reduction effect on infrasound should be investigated based on the results of an analytical simulation of a running vehicle when identifying an ideal countermeasures.
Therefore, this study dealt with complaints about rattling sounds near a highway bridge. First, the cause of the sound was investigated using a test truck and conventional trucks. The cause was determined based on the experimental results. Moreover, various preventive measures for the infrasound produced by the highway bridge owing to running trucks were considered. The effectiveness of each preventive measure was investigated by simulating the dynamic response using the running truck model. The differences among the various measures’ effectiveness were determined through a comparison of their simulation results to obtain a clear picture of infrasound reduction methods. In this study, above mentioned estimation method applicable to bridges was proposed.
2. Object Bridges
This study considers two object bridges consisting of two lanes: one bridge has two eastbound lanes, and the other, parallel, bridge has two westbound lanes. The eastbound bridge, constructed in 1967, has a simple steel composite girder with 25.2 m span and three spans of continuous steel composite girders each with a 49.0 m span, as shown in Figure 1(a). On the other hand, the westbound bridge, constructed in 1972, has a simple steel composite girder with a 36.47 m span and three spans of continuous steel composite girders with 48.59 m, 49.09 m, and 49.09 m spans, respectively, as shown in Figure 1(b). The westbound and eastbound bridges have four and three girders, respectively. The simple composite girders of the westbound and eastbound bridges are jointed with continuous bridges by a joint-less system. The daily traffic over these bridges is 30,000 - 35,000 vehicles, of which about 30% are trucks. Complaints about rattling sounds caused by the infrasound radiated from the bridge arose from Houses A and B near the girder (P1 - P2) of the westbound bridge, as shown in Figure 1(c).
3. Characteristics of Infrasound
To investigate the causes of the complaints about rattling
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 1. Object highway bridge and observation points. (a) Side view (Eastbound bridge); (b) Side view (Westbound bridge); (c) Plane view.
sounds, infrasound produced by conventional trucks was measured for 10 min per hour from 9:00 PM to 8:00 AM. For this purpose, low-frequency microphones were installed as shown in Figure 1.
Figure 2 shows every 1/3 octave band frequency of the infrasound at each measurement point; these are the averages of the peak levels for each 10 min per hour period. Figures 2(a) and (b) show the 1/3 octave band frequencies of the infrasound at the abutment (A1) and mid span (P1 - P2) of the eastbound and westbound bridges, respectively. Both bridges have frequencies with similar characteristics. The different peak level frequencies of the abutment (A1) and mid span (P1 - P2) appear at frequencies of 4.0 and 2.5 - 3.15 Hz, respectively. Furthermore, the abutments (A1) of both the eastbound and the westbound bridges share the same band level at frequencies of 12.5 and 16.0 Hz. Similarly, the mid spans (P1 - P2) of both the eastbound and the westbound bridges share the same band level at a frequency of 12.5 Hz.
Figure 2(c) shows the 1/3 octave band frequencies of the outside and the 2nd floor of House A. The 2nd floor of House A has frequencies (2.5 - 4.0 and 12.5 Hz) with the same characteristics as those (2.5 - 4.0 and 12.5 Hz) at the mid span (P1 - P2). House A is affected by frequencies of 2.5 - 4.0 and 12.5 Hz. Similarly, Figure 2(d) shows the 1/3 octave band frequencies of the outside and the 1st floor of House B. The 1st floor of House B has frequencies (4.0 and 12.5 Hz) with the same characteristics as those (4.0 and 12.5 Hz) at the abutment (A1). Both Houses A and B are affected by frequencies of 2.5 - 4.0 and 12.5 Hz. Therefore, both houses are affected by both bridges’ vibration modes at 2.5 - 4.0 Hz.
A comparison of the 1/3 octave band frequencies with the reference values for complaints about rattling sounds and complaints of mental and physical discomfort by the Japanese Ministry of Environment [6] is shown in the same figures. Although this rattling sound curve is only defined beginning from 5 Hz, the levels measured in Houses A and B appear to be larger than the rattling sound curve defined by the Japanese Ministry of Environment for frequencies of 2.5 - 4.0 Hz. Therefore, Houses A and B are affected to a greater extent by infrasound with frequencies of 2.5 - 4.0 Hz radiated from both bridges.
4. Examinations
To investigate the causes of the above frequencies, a running test was conducted using a test truck with 196 kN weight. Figure 1 shows the observation points. This test mainly measured (a) the acceleration of the superstructure’s vibration and (b) the infrasound measured using the low-frequency microphone. The running speed of the test truck was 80 km/h.
5. Analytical Bridge Models
Analytical bridge models of both bridges were developed to understand the vibration mode at a frequency of 2.5 - 4 Hz, which predominantly affected Houses A and B. Figure 3 shows the details of the analytical model of the eastbound bridge. The decks and webs of the steel girders and the central crossbeams were modeled using shell elements. Other members such as upper and lower flanges and lateral and sway bracings were modeled using beam elements. The steel girders were joined with the decks using rigid elements. The stiffness and mass of the wheel guards were considered in the analysis. The pavement was considered only as a mass without stiffness. The shoes were modeled as spring elements.
6. Vibration Characteristics
Figures 4 and 5 show the vibration modes obtained by the eigenvalue analysis of the eastbound and westbound bridges, respectively. These vibration modes were validated through a comparison with measured frequencies and mode shapes.
These bridges show many similar vibration modes at frequencies of 2 - 5 Hz. The bending vibration modes with the same phase at each span in the westbound bridge at a frequency of 2.5 - 4.0 Hz (Anal.: 2.43, 3.24, and 3.90 Hz, Exp.: 2.49, 3.29, and 3.94 Hz) clearly affect Houses A and B. Because each span vibrates with the same phase, the most powerful sound pressure appears to be caused by the infrasound transmitted to Houses A and B. The bending vibration modes with the same phase in the eastbound bridge appear at 2.5 - 3.0 Hz (Anal.: 2.35 and 3.11 Hz, Exp.: 2.36 and 3.00 Hz); a comparison of the measured 1/3 octave band frequencies of the infrasound suggests that these vibration modes also affect Houses A and B.
7. Dynamic Response Analyses by Running Truck Model
To compare the characteristics of the dynamic response

Figure 3. Details of analytical bridge model.
 Bending 1st (Anal.: 1.86 Hz, Exp.: 1.85 Hz)
Bending 1st (Anal.: 1.86 Hz, Exp.: 1.85 Hz)
 Bending 2nd (Anal.: 2.35 Hz, Exp.: 2.36 Hz)
Bending 2nd (Anal.: 2.35 Hz, Exp.: 2.36 Hz)
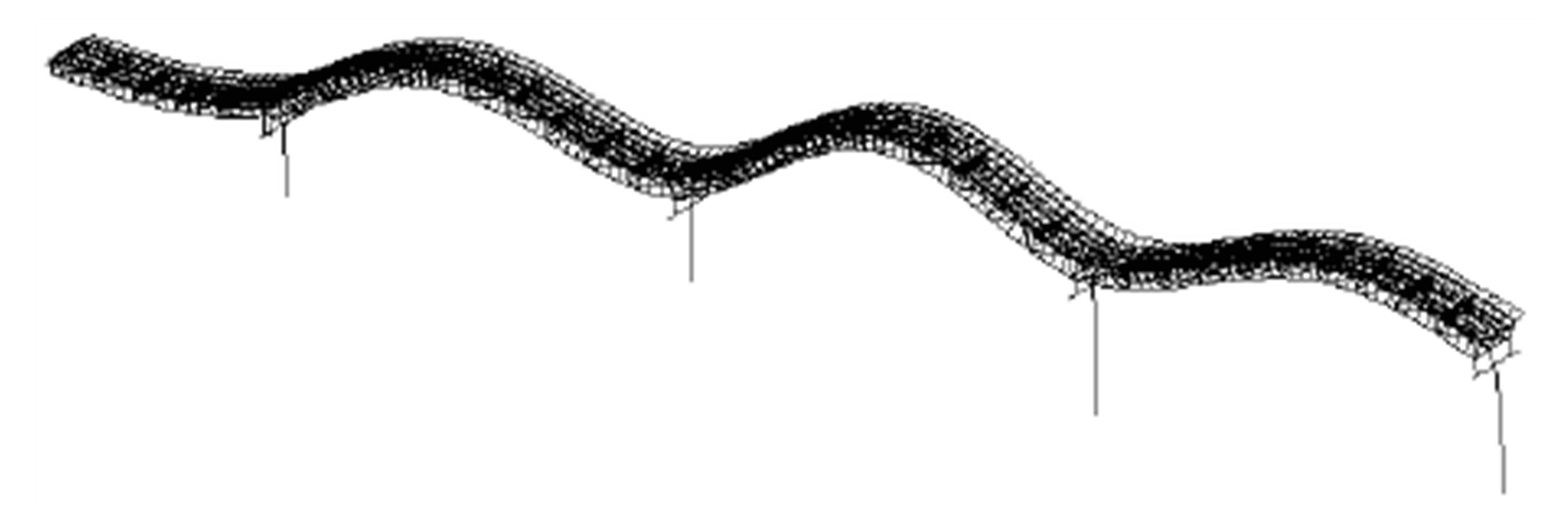 Bending 3rd (Anal.: 3.11 Hz, Exp.: 3.00 Hz)
Bending 3rd (Anal.: 3.11 Hz, Exp.: 3.00 Hz)
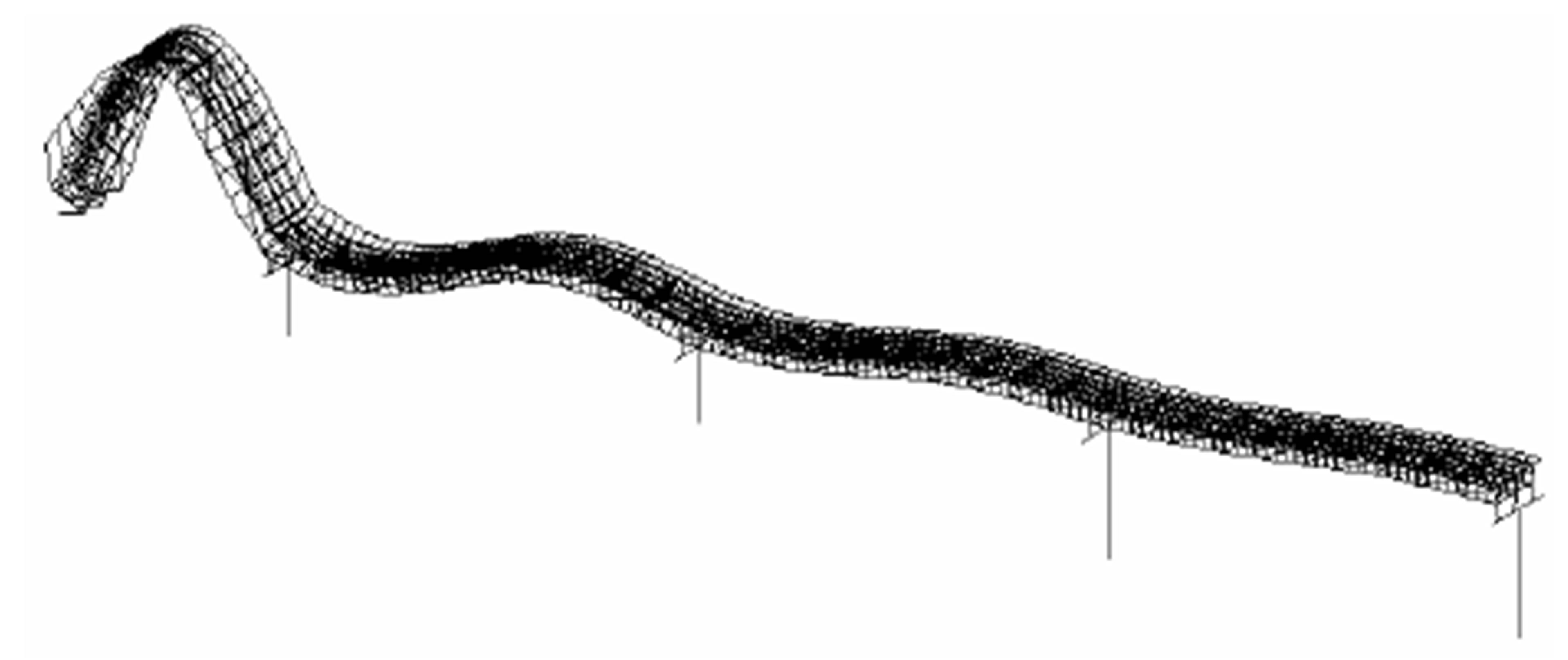 Bending 4th (Anal.: 5.53 Hz, Exp.: 5.42 Hz)
Bending 4th (Anal.: 5.53 Hz, Exp.: 5.42 Hz)
Figure 4. Vibration modes (Eastbound bridge).
 Bending 1st (Anal.: 1.84 Hz, Exp.: 1.93 Hz)
Bending 1st (Anal.: 1.84 Hz, Exp.: 1.93 Hz)
 Bending 2nd (Anal.: 2.43 Hz, Exp.: 2.49 Hz)
Bending 2nd (Anal.: 2.43 Hz, Exp.: 2.49 Hz)
 Bending 3rd (Anal.: 3.24 Hz, Exp.: 3.29 Hz)
Bending 3rd (Anal.: 3.24 Hz, Exp.: 3.29 Hz)
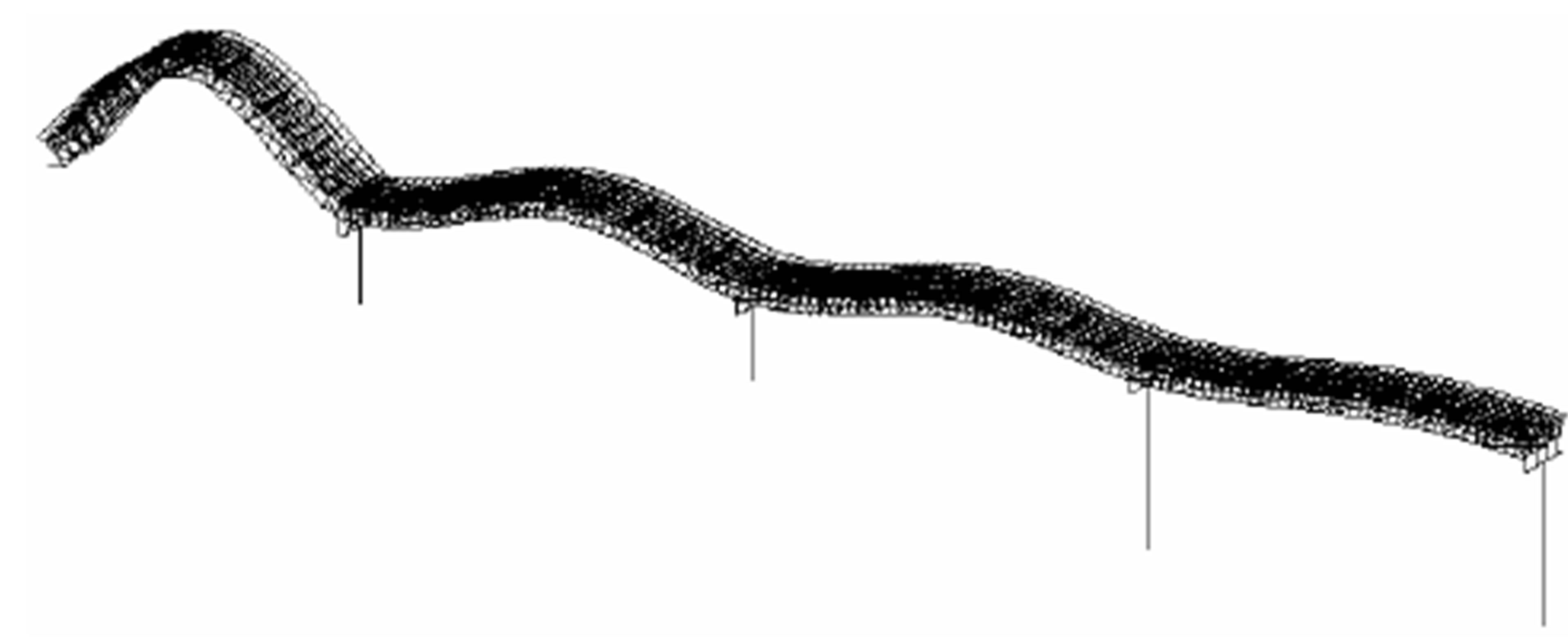 Bending 4th (Anal.: 3.90 Hz, Exp.: 3.94 Hz)
Bending 4th (Anal.: 3.90 Hz, Exp.: 3.94 Hz)
Figure 5. Vibration modes (Westbound bridge).
between analysis and experiment by running the truck, dynamic response analysis under the conditions of the truck model running on the bridge model are carried out using the direct integration method, specifically, the Newmark β method (β = 1/4, t = 0.01 s) by considering the measured road roughness [10,11].
7.1. Damping
The proportional damping of the strain energy is calculated using the ratio of the strain energy and equivalent (material) damping constants, as shown in Equation (1).
 (1)
(1)
where hi is the damping constant of the ith mode; {φij}, the mode vector of the material elements j in the ith mode; Dj, the material element j of the equivalent (material) damping constant; [Kj], the stiffness matrix of the material element j; {φi}, the global mode vector in the ith mode; [K], the stiffness matrix of the global structure; and n, the number of elements.
The equivalent damping constants of each material are used as follows: concrete and steel of the superstructure are 1.0%; concrete of the substructure is 2.0%; and shoe is 2.0%. Rayleigh damping is assumed using two sets of each damping and frequency.
The experimental frequencies and the damping constants were computed by using Eigensystem Realization Algorithm (ERA) [12]. The results obtained by the ERA are shown in Table 1. The experimental damping constants for each mode scatter by 1.0% - 2.0%.
7.2. Truck Model
The truck is modeled in 3D [13] as shown in Figure 6. The parameters of the test truck model are listed in Table 2. An axle of the truck model comprises a two-degreeof-freedom spring-dashpot system that consists of a suspension spring and a tire spring. The truck model is assembled from the spring-dashpot system in each axle.
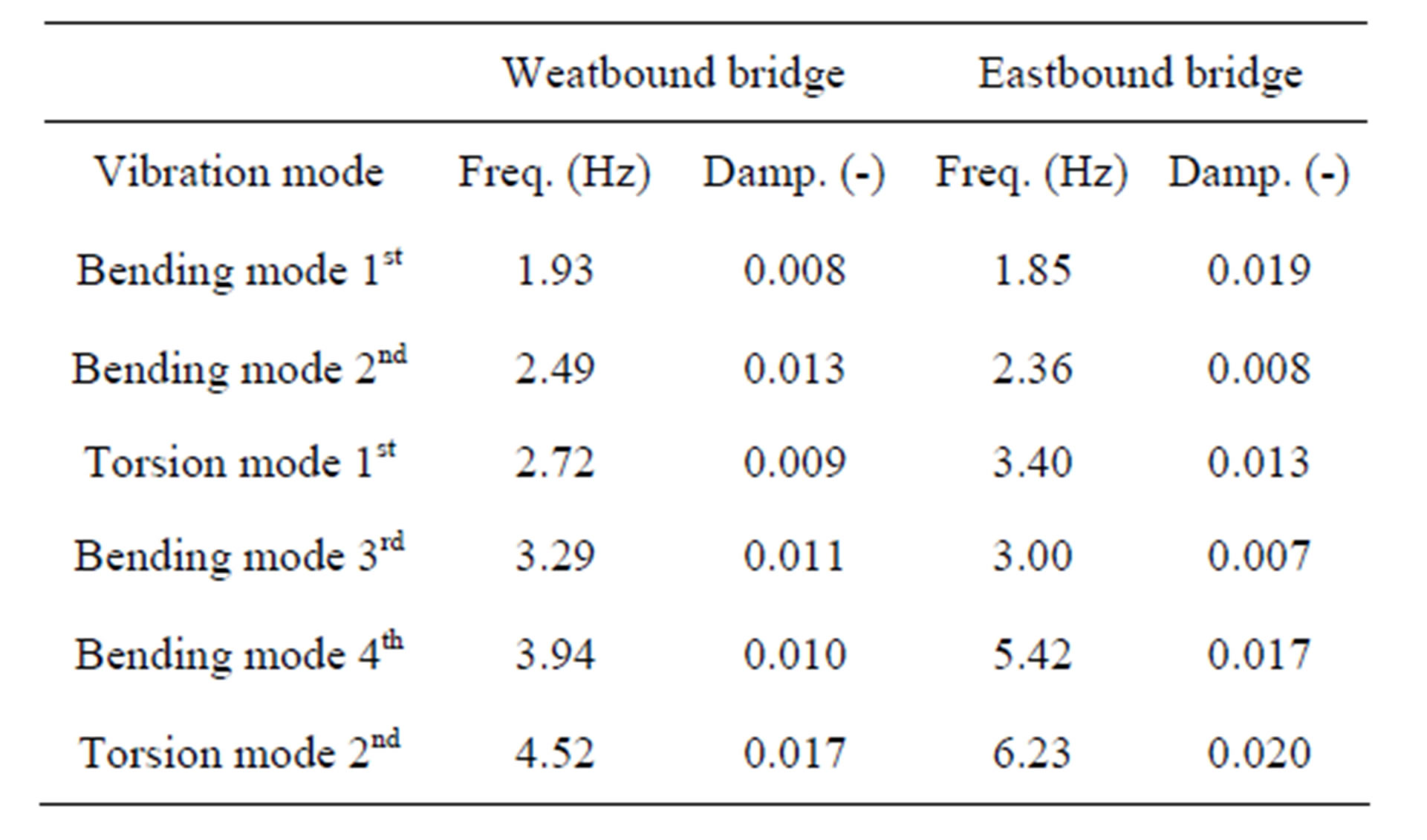
Table 1. Frequencies and damping constants.

Table 2. Parameters of test truck model.
7.3. Road Roughness
The profiling data of the road roughness used for the dynamic response analysis were measured using a 8 m profile meter. Figure 7 shows the road roughness of both bridges at the left axle position of the slow or the fast lane. The road roughness of the slow and the fast lane in the same bridge is almost the same. In particular, the road roughness of the slow and the fast lane in the eastbound bridge are much greater than those in the westbound bridge. The road roughness of these bridges has a large amplitude on each pier and mid span. Figure 8 shows the power spectral density as simulated by the maximum entropy method using this measured road roughness. An estimation of the road roughness based on ISO 8608 [14] is also shown in this figure. ISO 8608 classifies the road roughness into eight categories (A-H)
 (a)
(a)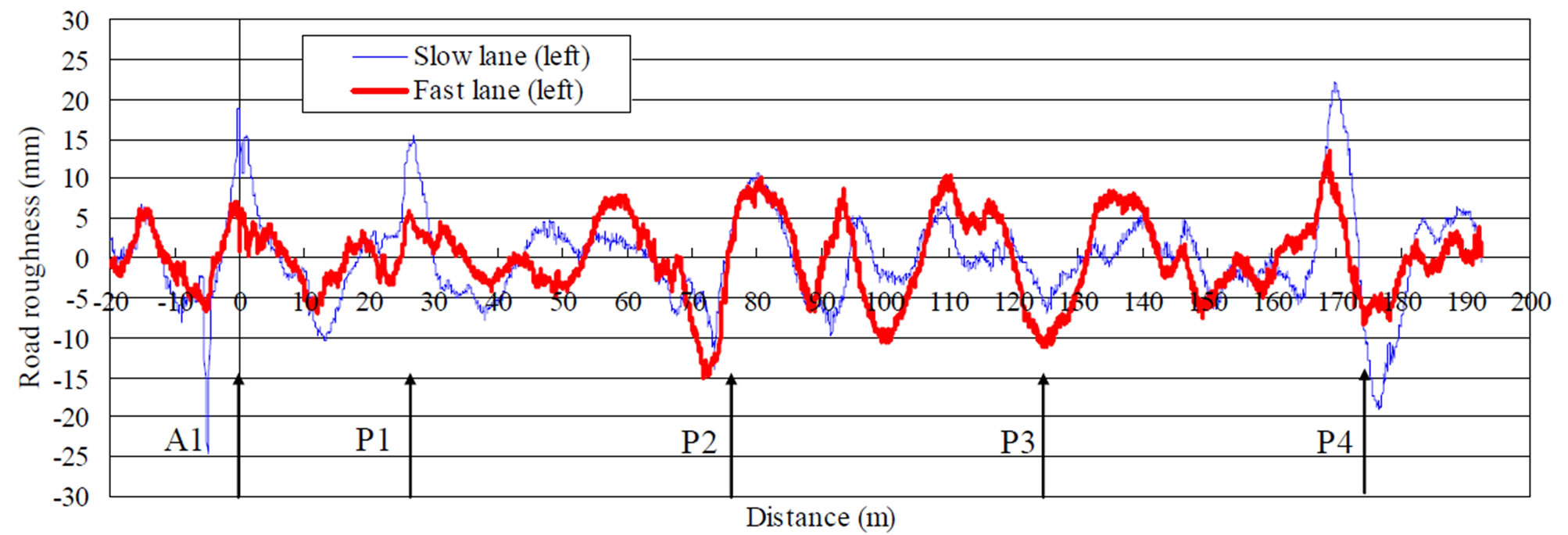 (b)
(b)
Figure 7. Road roughness. (a) Westbound bridge; (b) Eastbound bridge.
 (a)
(a)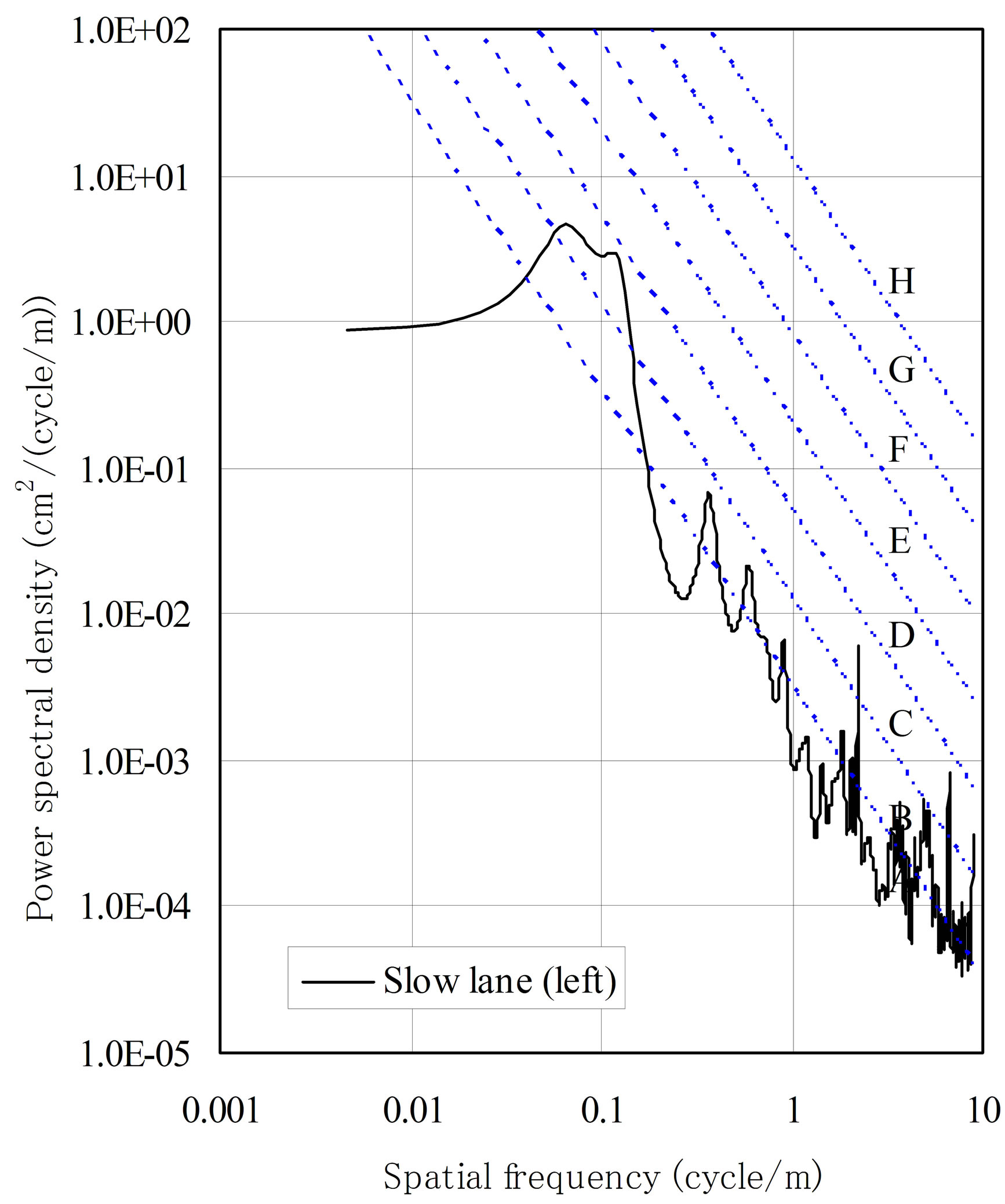 (b)
(b)
Figure 8. Power spectral density of road roughness using ISO 8608 (slow lane). (a) Westbound bridge; (b) Eastbound bridge.
in each spatial frequency. The road roughness of these bridges is estimated as class C at a spatial frequency of 0.1 - 0.14 cycle/m (7.0 - 10.0 m/cycle).
A calculation of the relationships among the vehicle speed, spatial period, and loading time frequency by the vehicle and roughness using a one-degree-of-freedom system car model as shown in Figure 9 clearly shows that the bridge with the roughness of spatial period being 7.0 - 10.0 m/cycle receives vibrations at a frequency of about 3.0 Hz generated by the trucks when they run at a speed of 80 - 110 km/h, as shown in Table 3. Because the object bridge has bending vibration modes at a frequency of about 3.0 Hz, and the trucks’ rear leaf suspendsion spring vibration also has a frequency of about 3.0 Hz, the bridge resonates more strongly with the trucks’ vibration when they run at a speed of 80 - 110 km/h.
7.4. Validity of Dynamic Response
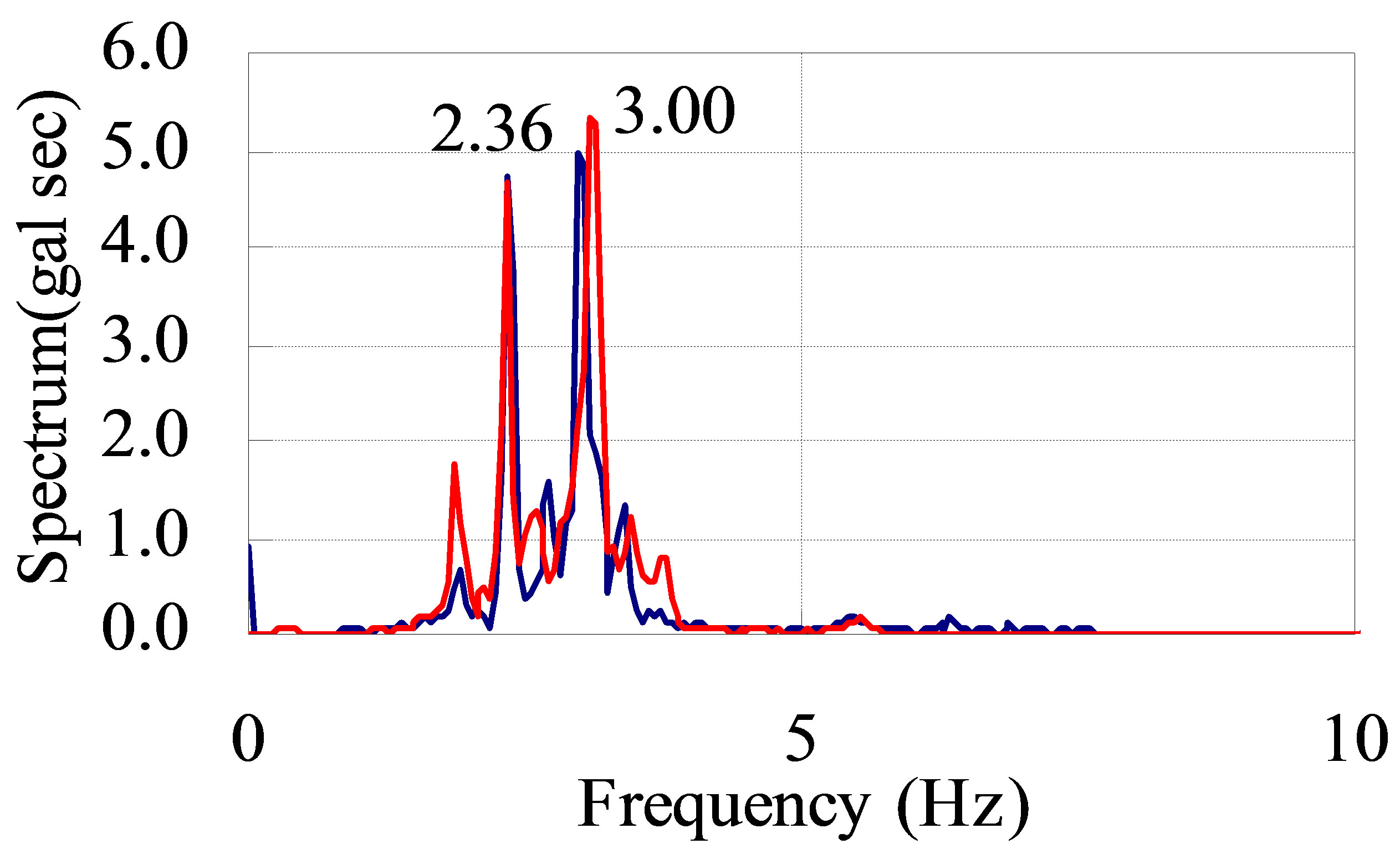
When the test truck ran in the slow lane of both bridges at 80 km/h, the analytical and experimental accelerations were compared. The object points are the girder (mid span of A1 - P1 and P1 - P2 in both bridges, vertical direction) and each spectrum, as shown in Figure 10.
The analytical acceleration resembles the experimental acceleration in the girder. The frequencies of the test truck’s rear leaf suspension spring vibration (3 Hz) and bending modes (2 - 4 Hz) appear in the experimental and analytical spectrums of the girder. The validity of the dynamic response analysis is estimated by comparing the experimental and analytical results.
8. Vibration Measures and Modeling
Various prevention vibration measures were considered

Figure 9. Outline of loading time frequency, speed, and spatial period.
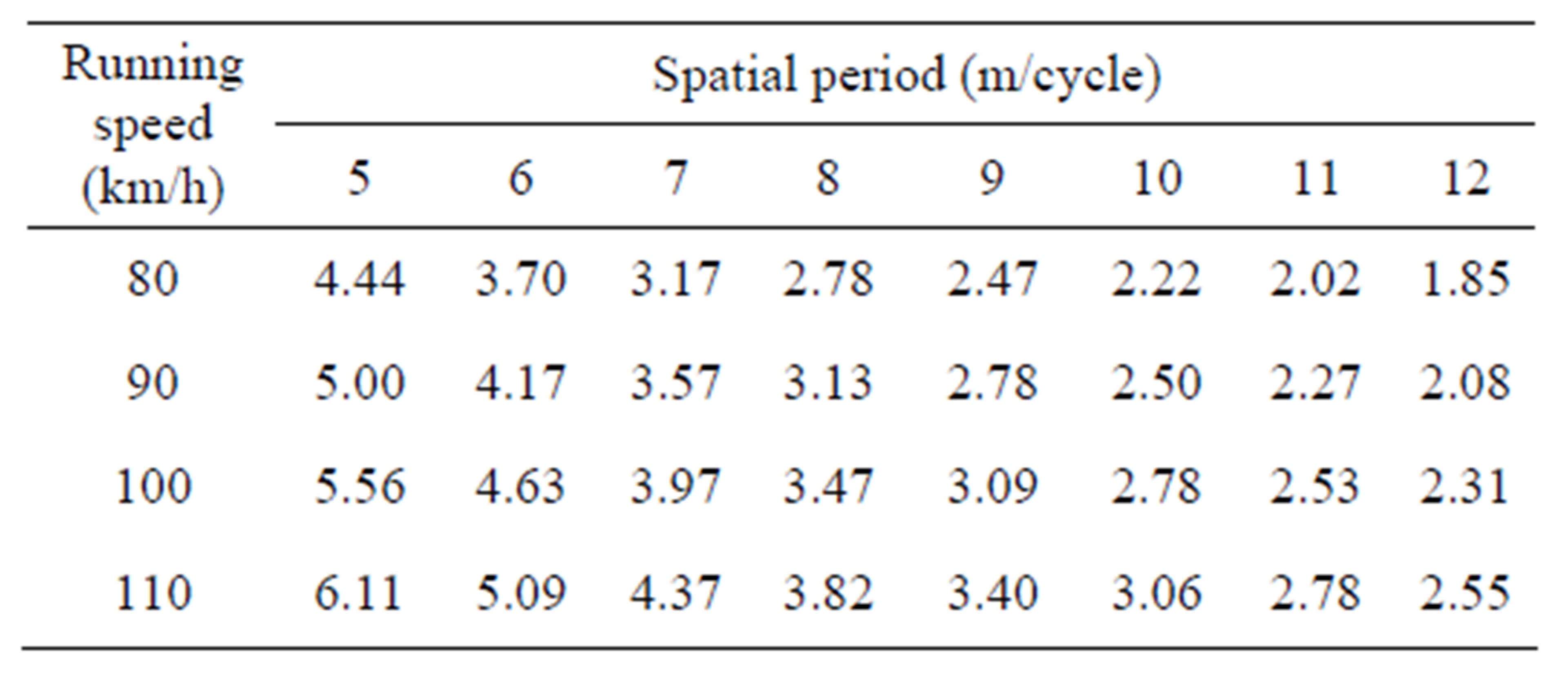
Table 3. Relation of loading time frequency [Hz], speed [km/h], and spatial period [m/cycle].
 (a)
(a)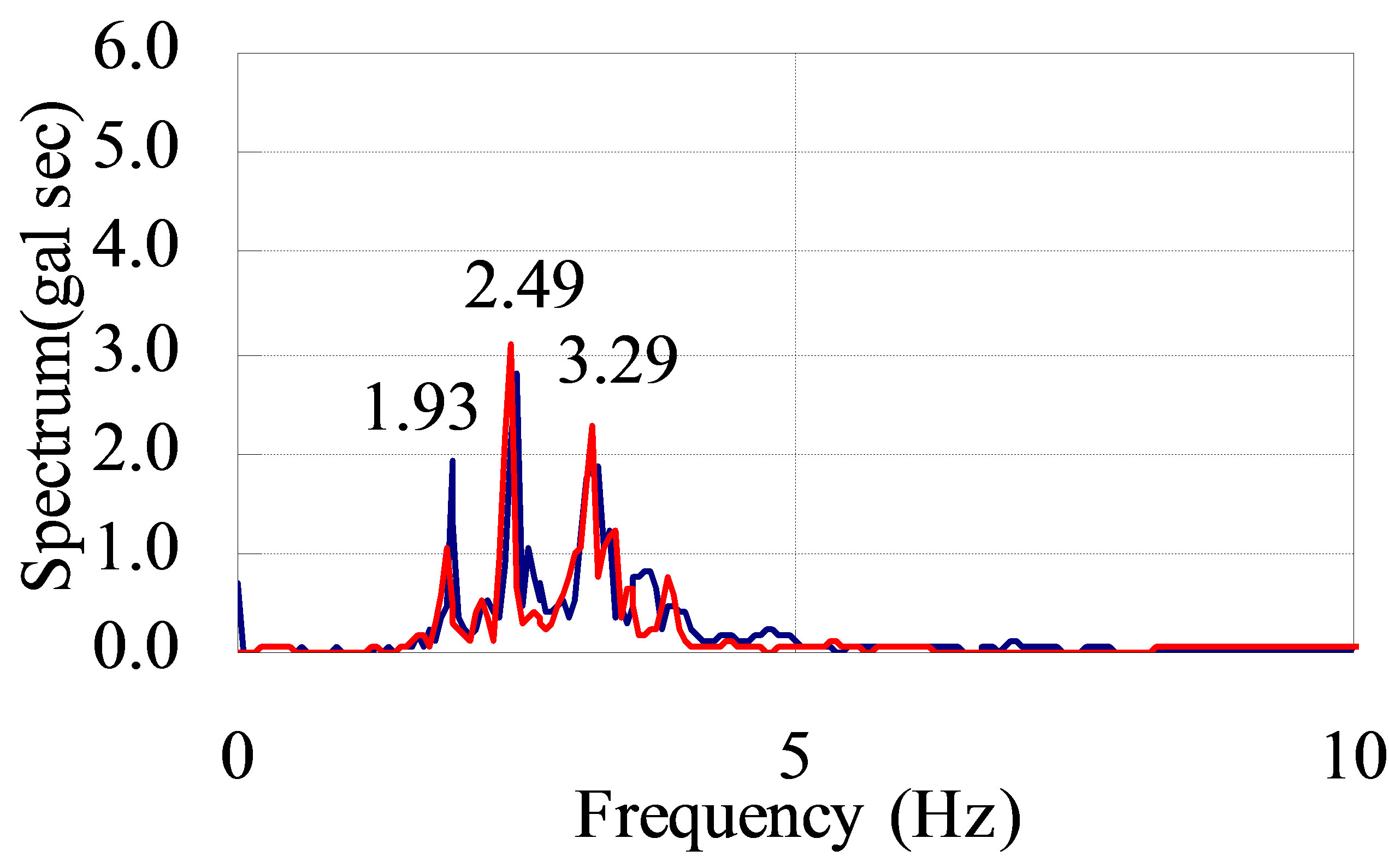 (b)
(b)
Figure 10. Acceleration and spectrum in analysis and experiment. (a) Eastbound bridge, slow lane, P1 - P2, G3, 1/2; (b) Westbound bridge, slow lane, P1 - P2, G1, 1/2.
to reduce the vibration amplitude of both bridges at frequencies of 2.5 - 4.0 Hz. The analytical cases of prevention measures with object installation points are shown in Table 4.
8.1. Extended Deck
The extended deck method [8,9] is used to reduce the vibration of 10 - 20 Hz caused by tire spring vibrations at the A1 joint of the eastbound and westbound bridges. The side view of the extended deck is shown in Figure 11. In the extended deck method, the existing reinforced concrete deck is extended in the direction of the embankment. The expansion joint is moved on the approach embankment. The length of the extended deck is set at 10 m considering the time of damping in the truck’s tire

Table 4. Analytical cases of prevention measures.
spring vibration. As another measure, the road roughness is improved with the construction of the extended deck at the A1 joint.
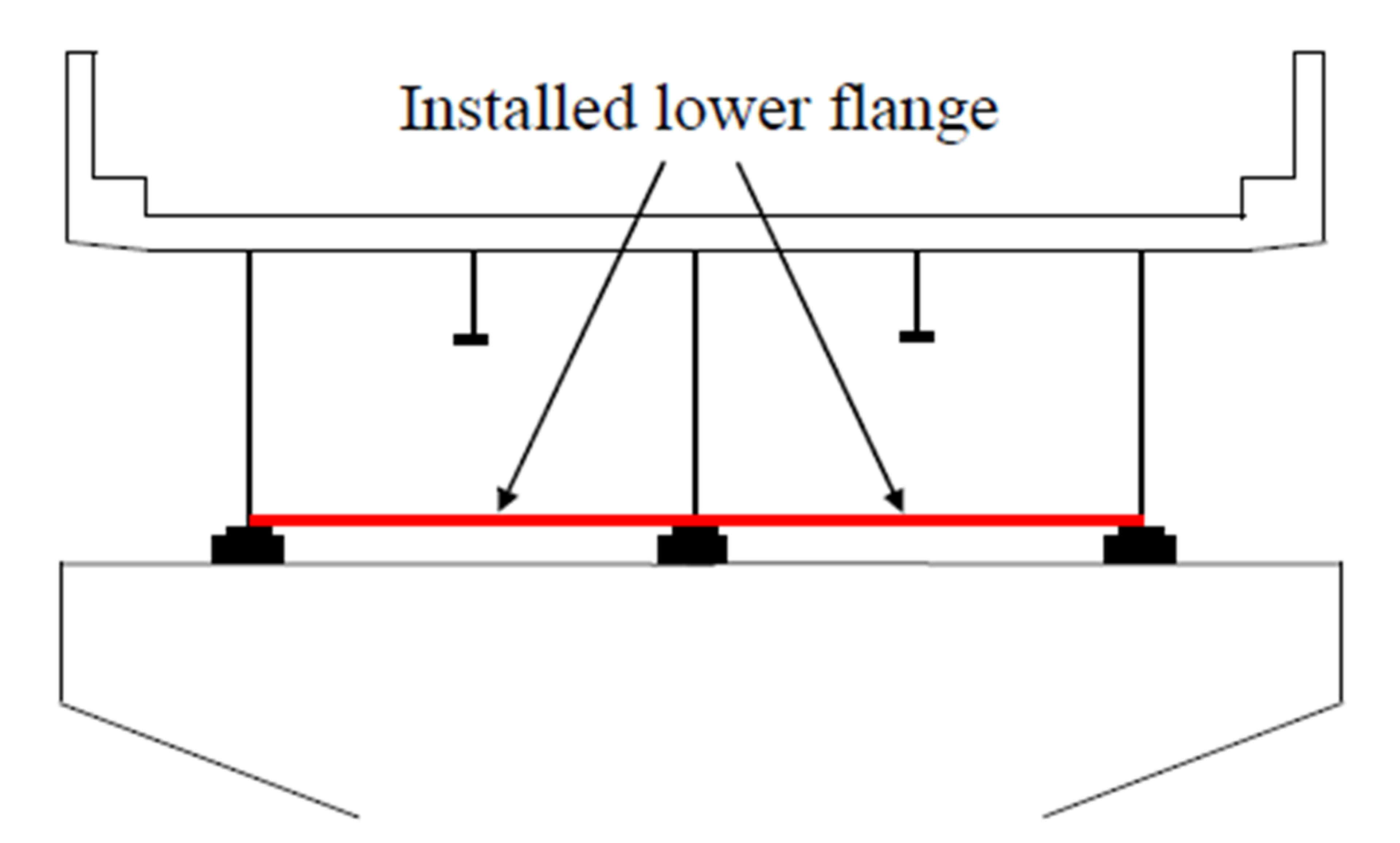
8.2. Viscoelastic Damper
A viscoelastic damper [15] consists of three plates and a viscoelastic material. One plate is installed in the lower flange of the girder, and it is sandwiched by the two plates cantilevered from the pier. The viscoelastic material is also installed between these two plates. This damper functions by changing the rotation angle at the ends of girders into shear deformation of the viscoelastic material.
The viscoelastic damper was modeled using spring and dashpot elements, as shown in Figure 12. This damper can be adjusted to add damping by changing the cross section, thickness, and loss coefficient in the viscoelastic material. In this case, the spring constant and damping coefficient of one damper is set as 9.00E4 (kN/m) and
2.00E3 (kNs/m), respectively, to add 4% damping for the bridge vibration mode at 4 Hz. The damper is installed at the ends of girders in the A1 - P1, P1 - P2, or P2 - P3 spans or the combination of each span.
8.3. Increase in Stiffness with Box Girders
To increase the bending and torsion stiffness of the existing bridge, this plate girder bridge is converted to a box girder bridge in which the existing lower flanges are connected to 24-mm-thick steel plates, as shown in Figure 13.
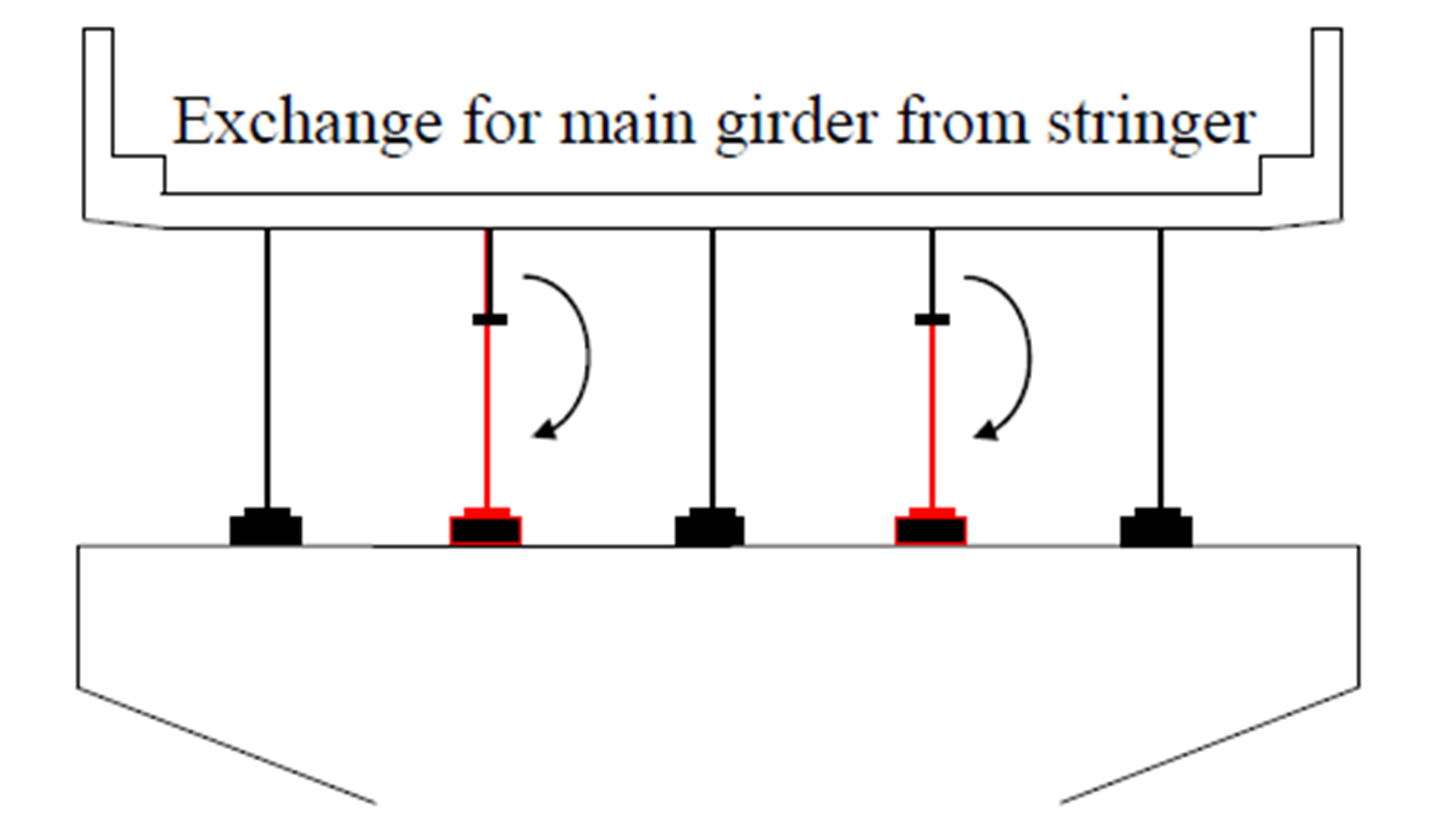
8.4. Increase in Stiffness by Exchanging for Main Girder from Stringer
To increase the bending stiffness of the existing bridge, the existing stringers are exchanged to main girders, as shown in Figure 14. The stiffness of the new main girder is the same as that of the existing main girder.
8.5. Arch Support Method
To reduce the amplitude of the object bending vibration at the mid span, the existing girders are supported at the mid span by arch structures, as shown in Figure 15. The arch members used have a diameter of 812.8 mm with a thickness of 16 mm.
8.6. Comparison of Frequencies for Each Measure
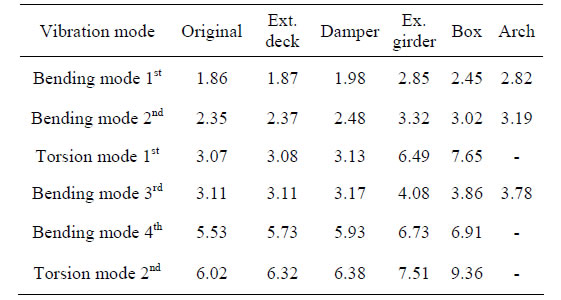
Table 5 shows the frequencies of each vibration mode for each measure in both bridges. These mode shapes of the eastbound and westbound bridges correspond to Figures 4 and 5, respectively. The frequencies of the extended deck in each line are almost the same as those of the original bridge without measures. The frequencies of the viscoelastic damper in each bridge are slightly greater than those of the original bridge without measures, because the stiffness of the spring in the viscoelastic damper affects the bending or torsion modes. Moreover, the frequencies of the exchange for main
 (a)
(a) (b)
(b)
Figure 13. Box girder structure. (a) Eastbound bridge; (b) Westbound bridge.
 (a)
(a) (b)
(b)
Figure 14. Exchange for main girder from stringer. (a) Eastbound bridge; (b) Westbound bridge.
girder from stringer, box structure, and arch support are much greater than those of the original bridge without measures, because the bending stiffness of the bridge structure increases. There are a few modes in box structure or arch support in which the frequencies of the original bridge do not appear.
9. Acoustic Analyses
The characteristics of the velocity response in the bridge
 (a)
(a) 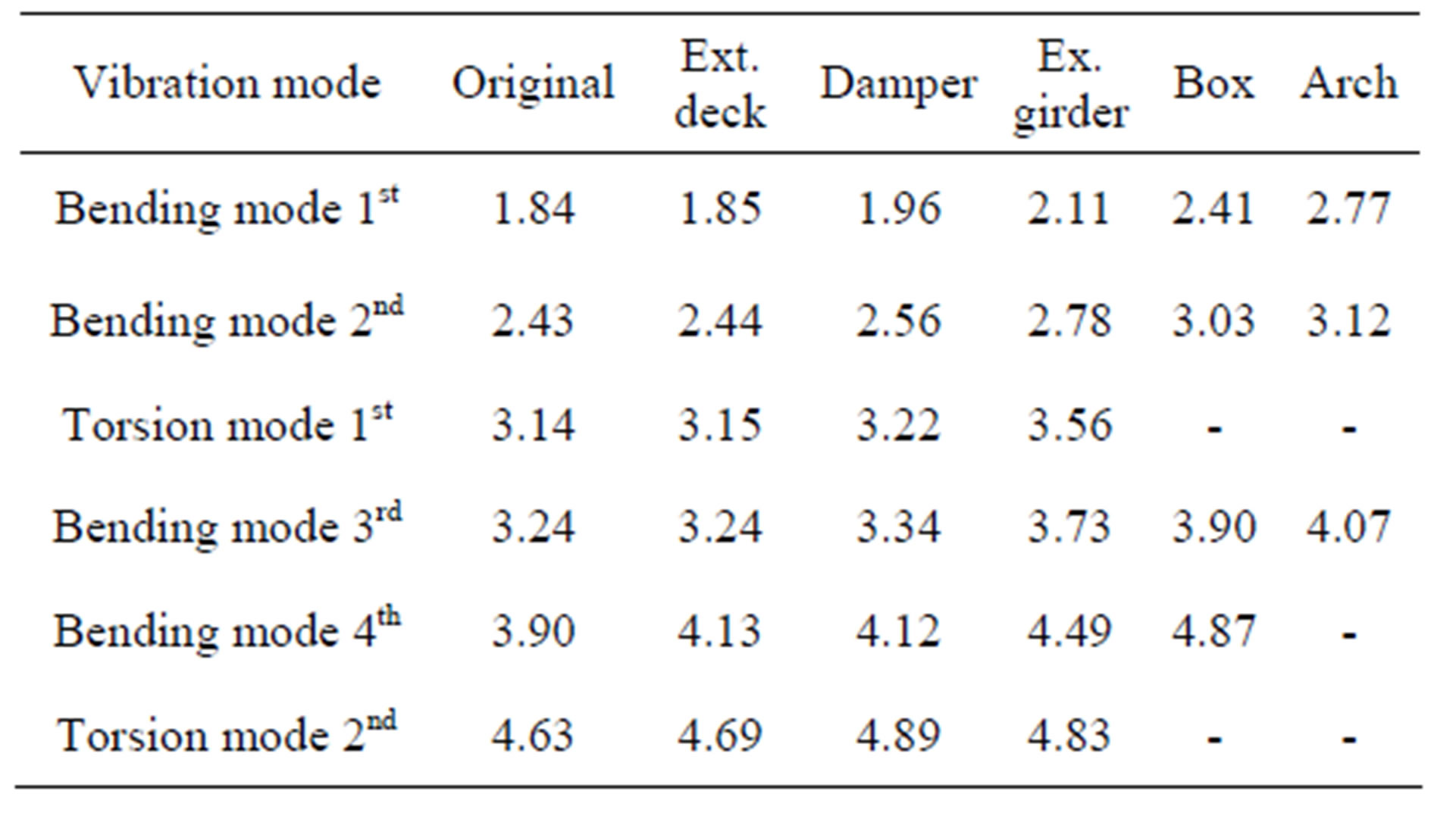 (b)
(b)
Table 5. Comparison of frequencies in each measure. (a) Eastbound bridge [Unit: Hz]; (b) Westbound bridge [Unit: Hz].
are known to be related to those of the infrasound response under the deck [5]. The relation of the velocity response in the bridge and the infrasound response under the deck are shown in Equation (2).
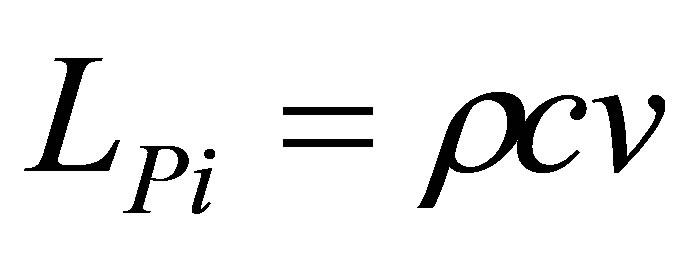 (2)
(2)
where LPi is the effective value of the sound pressure level; ρ, the density (ρ = 12.005 N/m3); c, the speed of sound (c = 340 m/s); and v, the velocity of the deck elements.
The predictions of infrasound have been investigated using a theoretical analysis [16] and by FEM and BEM [17-19]. In this study, the simple prediction method was used for this purpose. The infrasound response can be evaluated by the sound power level using the velocity response obtained by the simulation of the dynamic response analysis for the running truck model. The sound power levels are calculated by Equation (3) using the velocity response of the deck elements in the vertical direction, as shown in Figure 16.
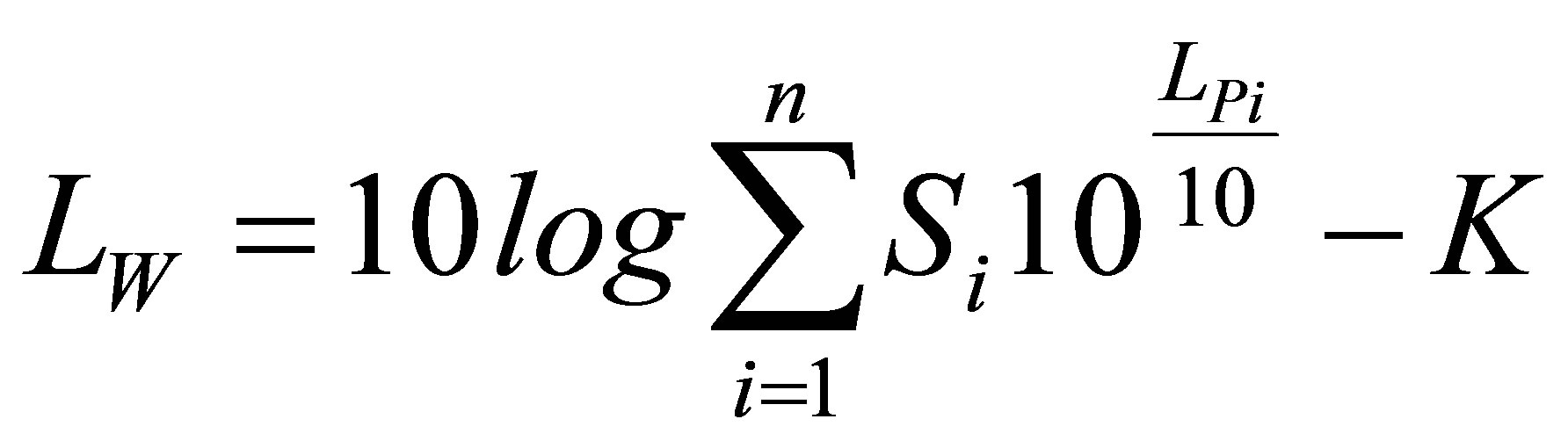 (3)
(3)
where LW is the sound power level; Si, the area of each deck element; and K, the compensation of the air impedance.
Furthermore, the sound pressure level at House A (Figure 16), which is at a distance r (m) from the sound source (each mid span), can be calculated by Equation (4) using the above sound power level. Equation (4) is described in detail in the Appendix.
 (4)
(4)
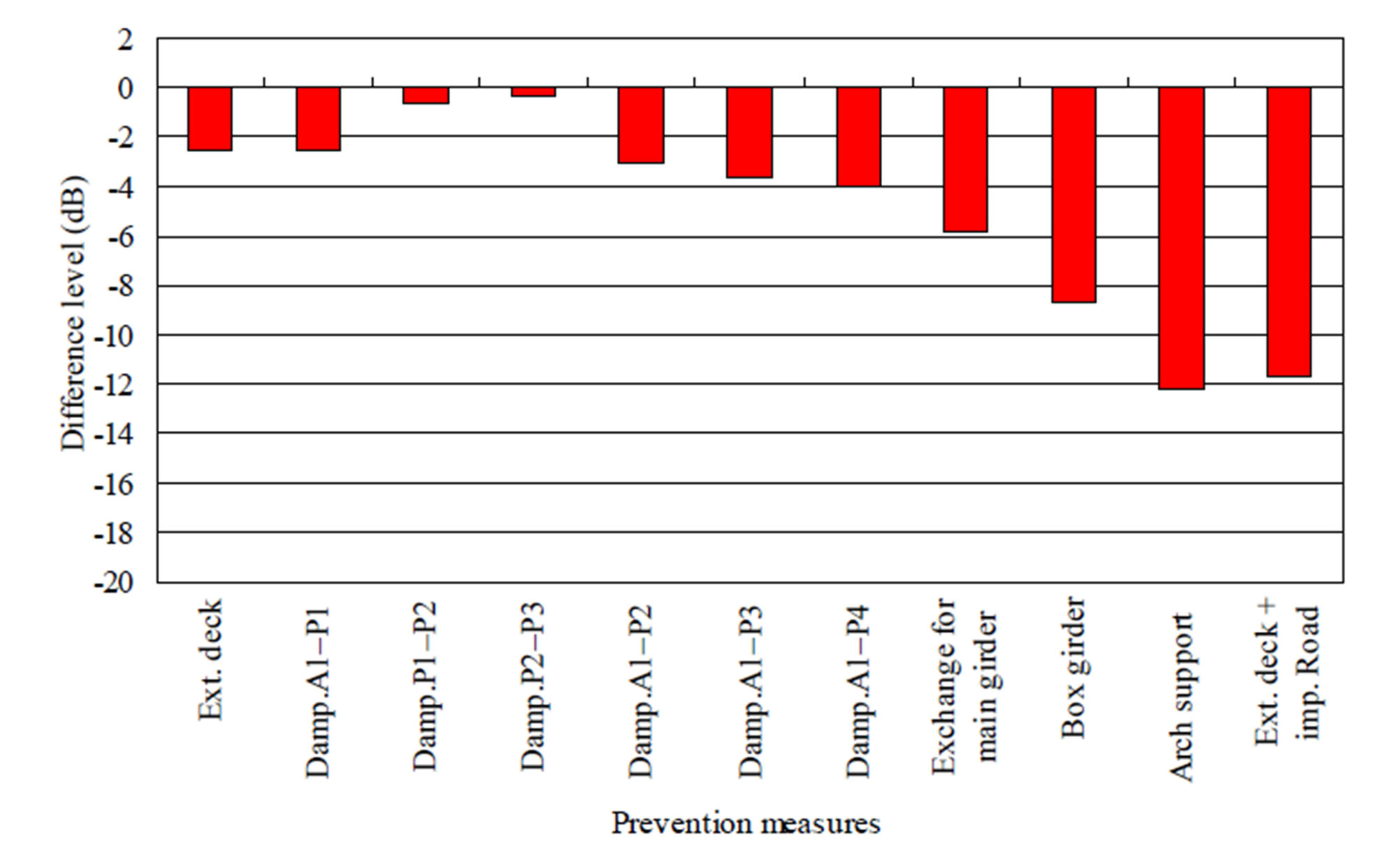
Figure 17 shows the analytical differences [each measure−original without measure (dB)] of the sound pressure levels with and without each prevention measure (Table 4) when the analytical truck model runs in each lane (estimation obtained by average of the fast and the slow lanes) at 80 km/h on both bridges. Here, the analytical results are evaluated under consideration of the effect on House A by A1 - P2, as shown in Figure 16.
The simulation results show that the most effective prevention measure for the infrasound transmitted from the westbound bridge to House A is the arch support
 (a)
(a)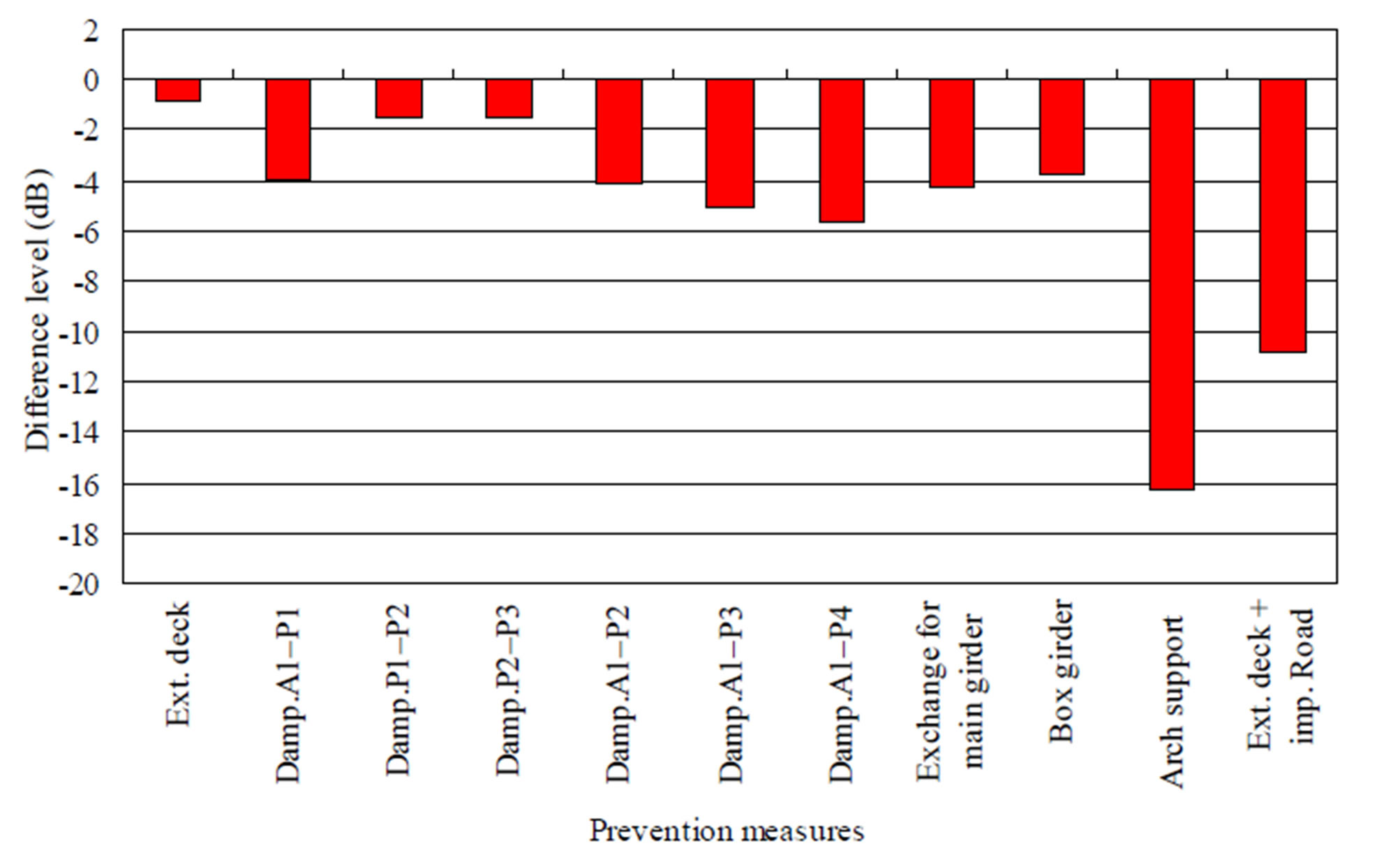 (b)
(b)
Figure 17. Analytical differences between sound pressure levels with and without each measure. (a) Eastbound bridge— House A; (b) Westbound bridge—House A.
method. This is because an object bridge with the addition of the arch support has the greatest bending stiffness. The second most effective method is the extended deck and improvement of the road roughness. Although the effectiveness of the former is small, the latter affects the reduction of sound pressure levels. The third most effective method is the viscoelastic damper (A1 - P4). The viscoelastic damper installed at the mid span of A1 - P4 is most effective compared to the viscoelastic dampers installed at the other spans. However, the effectiveness of the viscoelastic damper installed at the mid span of A1 - P2 or A1 - P3 is almost the same as that installed at the mid span of A1 - P4.
On the other hand, in the case of the eastbound bridge, the most effective prevention measure is the arch support method. The second most effective method is the extended deck and improvement of the road roughness. The third most effective method is the box structure method.
When deciding the prevention vibration measure, it is necessary to consider the above results in terms of the construction cost and working difficulty. Various measures are rearranged in order of construction cost as follows: Arch support > Box structure > Exchange for main girder from stringer > Viscoelastic damper > Extended deck and improvement of the road roughness. Furthermore, they are rearranged in order of working difficulty as follows: Arch support > Exchange for main girder from stringer = Box structure > Extended deck and improvement of the road roughness > Viscoelastic damper.
Therefore, the viscoelastic damper or the extended deck and improvement of the road roughness are recommended as vibration prevention measures for object bridges in consideration of the reduction of the sound pressure level, construction cost, and working difficulty.
The proposed method, which considered the effecttiveness of various measures through simulations, can also be useful for the assessment of other bridges with vibration problems such as infrasound.
10. Conclusions
In this study, bridge vibrations were studied through experiments and simulations using a test truck to investigate the causes of rattling sounds. Various preventive measures for the infrasound radiated from bridges were considered. The effectiveness of each preventive measure was investigated by simulating the dynamic response using a running truck.
The following conclusions were drawn from this study.
1) A comparison of the 1/3 octave band frequencies of the infrasound for both bridges showed that the object houses—Houses A and B—are affected by frequencies of 2.5 - 4.0 and 12.5 Hz. In particular, Houses A and B are affected to a greater extent by infrasound with frequencies of 2.5 - 4.0 Hz that is radiated from both bridges.
2) Both bridges have many similar vibration modes at frequencies of 2 - 5 Hz. Moreover, the bending vibration modes with the same phase at each span in the westbound bridge at a frequency of 2.5 - 4.0 Hz affect Houses A and B. Because each span vibrates with the same phase, the most powerful sound pressure appears to be caused by the infrasound transmitted to Houses A and B.
3) From ISO 8608 classification, the road roughness of these bridges is estimated as class C at a spatial frequency of 0.1 - 0.14 cycle/m (7.0 - 10.0 m/cycle).
4) Object bridges with the roughness of spatial period being 7.0 - 10.0 m/cycle receive vibration at a frequency of about 3.0 Hz owing to the trucks when they run at a speed of 80 - 110 km/h.
5) Various vibration prevention measures (extended deck, viscoelastic damper, box structure, exchange for main girders from stringer, arch support) were proposed to reduce the vibration amplitude of the object highway bridge at frequencies of 2.5 - 4.0 Hz.
6) The viscoelastic damper or the extended deck and improvement of the road roughness are recommended as vibration prevention measures for the object bridges in consideration of the reduction of the sound pressure level, construction cost, and working difficulty.
Appendix A [20]
The standard reference sound intensity that is equivalent to the standard reference sound pressure 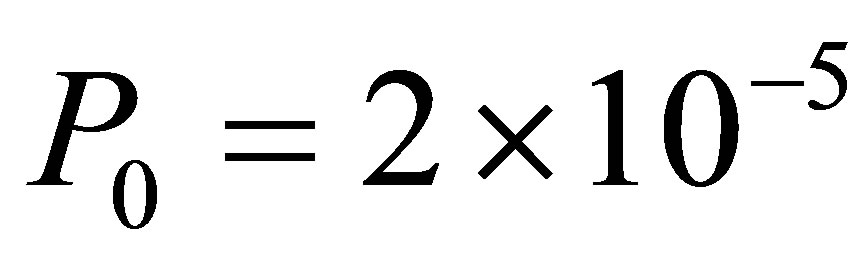 [N/m2] is shown in Equation (A1).
[N/m2] is shown in Equation (A1).
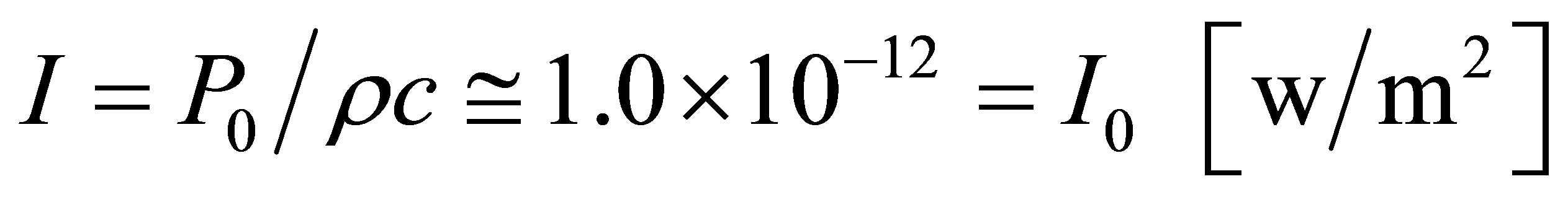 (A1)
(A1)
where ρ is the density of air and c, the speed of sound.
The sound intensity level LI is nearly equal to the sound pressure level using the standard reference sound intensity I0.
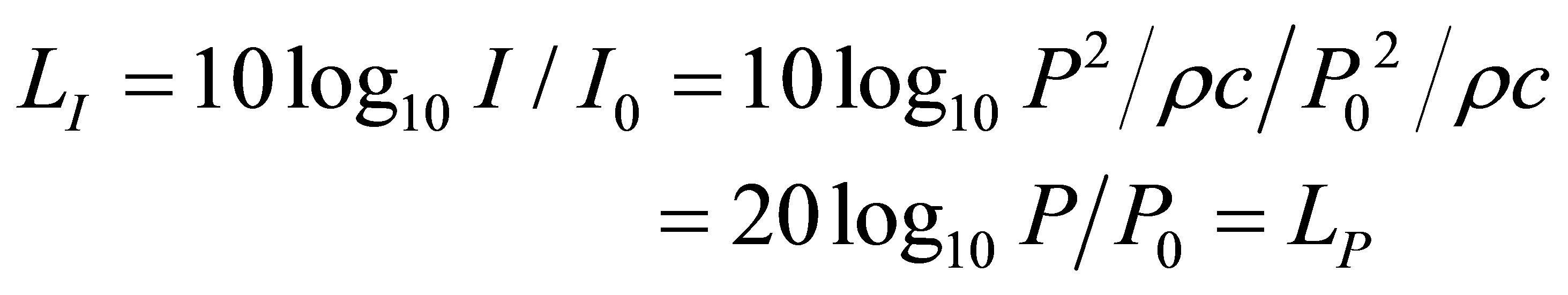 (A2)
(A2)
The sound intensity that penetrates the spherical surface from a sound source is given by Equation (A3).
 (A3)
(A3)
where Ep is the energy radiated from a sound source and r (radius), the distance from a sound source.
The sound intensity level LI is given by Equation (A4) using the standard reference sound intensity I0.
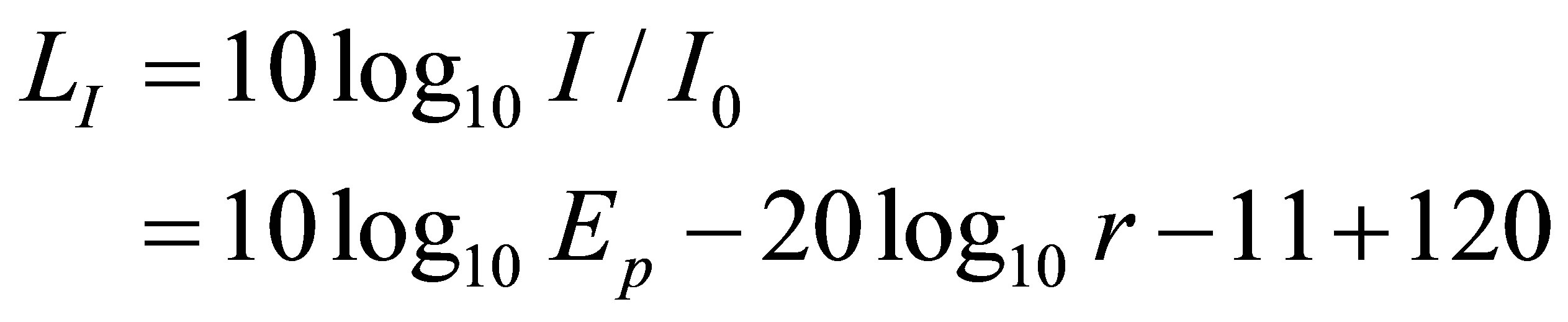 (A4)
(A4)
On the other hand, the sound power level LW is given by Equation (A5) using the standard reference sound power level EP0 = 10−12 [W].
 (A5)
(A5)
By considering Equation (A2), the sound intensity level LI is given by Equation (A6) using Equation (A4) and Equation (A5).
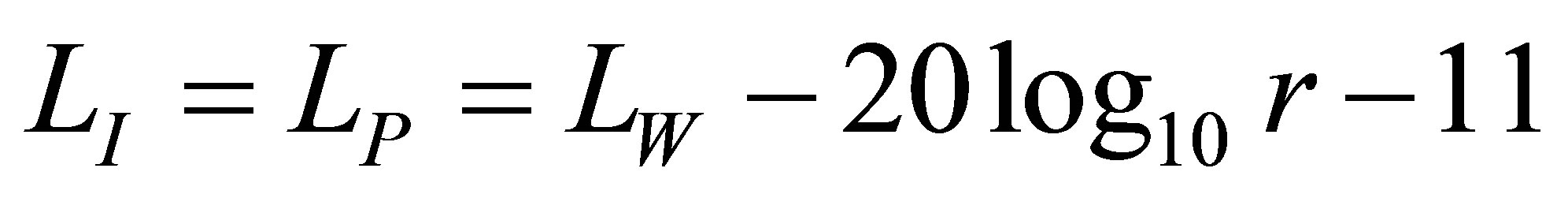 (A6)
(A6)