1. Introduction
In recent years, the role of topology is of fundamental importance in quantum particle physics and in logic programming semantics (see, e.g. [2-6]). Dislocated metrics were studied under the name of metric domains in the context of domain theory (see, [7]). Dislocated topologies were introduced and studied by Hitzler and Seda [1].
Now, we recall some definitions and a proposition due to Hitzler and Seda [1] as follows.
Definition 1.1. Let  be a set.
be a set.  is called a distance function. Consider the following conditions, for all
is called a distance function. Consider the following conditions, for all ,
,
(d1) ;
;
(d2) if , then
, then ;
;
(d3) ;
;
(d4) .
.
If  satisfies conditions (d1) - (d4), then it is called a metric on
satisfies conditions (d1) - (d4), then it is called a metric on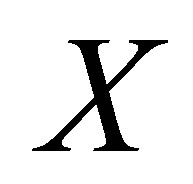 . If it satisfies conditions (d2) - (d4), then it is called a dislocated metric (or simply d-metric) on
. If it satisfies conditions (d2) - (d4), then it is called a dislocated metric (or simply d-metric) on .
.
Definition 1.2. Let  be a set. A distance function
be a set. A distance function  is called a partial metric on
is called a partial metric on 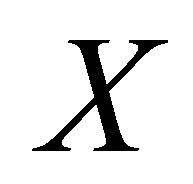 if it satisfies (d3) and the conditions:
if it satisfies (d3) and the conditions:
(d5) 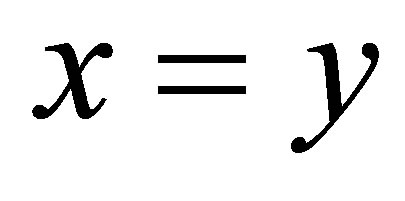 if and only if
if and only if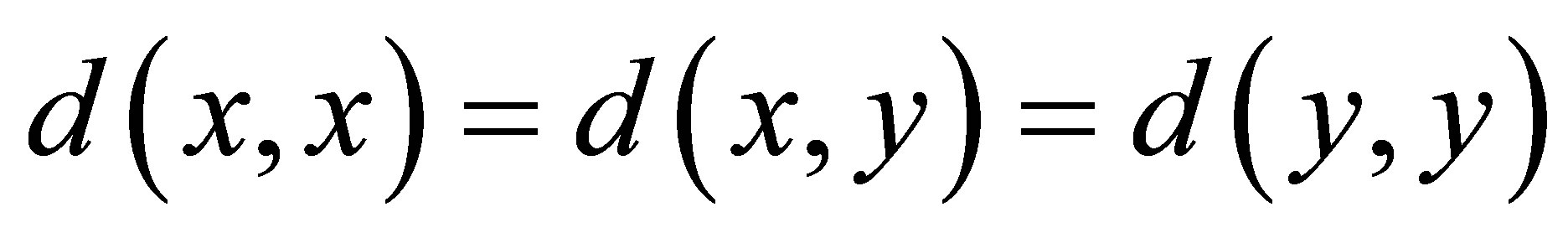 ;
;
(d6) ;
;
(d7)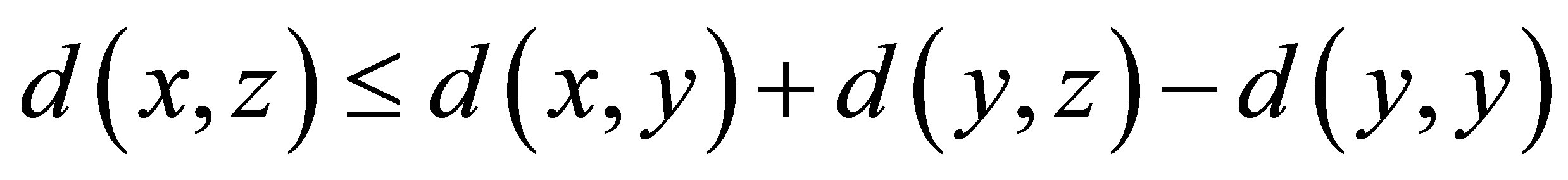 for each
for each .
.
It is obvious that any partial metric is a d-metric.
Definition 1.3. An (open ) ball in a d-metric space
) ball in a d-metric space 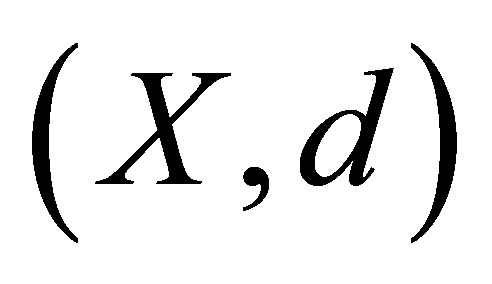 with centre
with centre  is a set of the form
is a set of the form , where
, where .
.
It is clear that 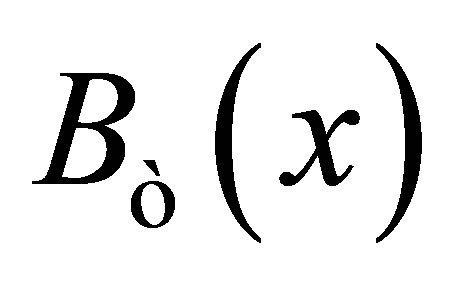 may be empty in a d-metric space
may be empty in a d-metric space 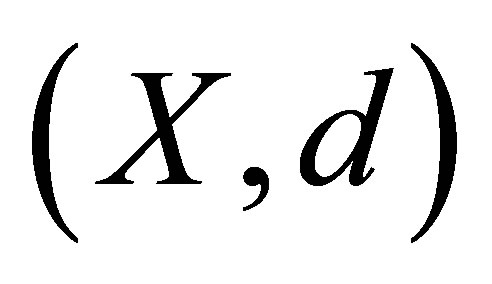 because the centre
because the centre  of the ball
of the ball  doesn’t belong to
doesn’t belong to .
.
Definition 1.4. Let  be set. A relation
be set. A relation  is called a d-membership relation(on
is called a d-membership relation(on ) if it satisfies the following property for all
) if it satisfies the following property for all  and
and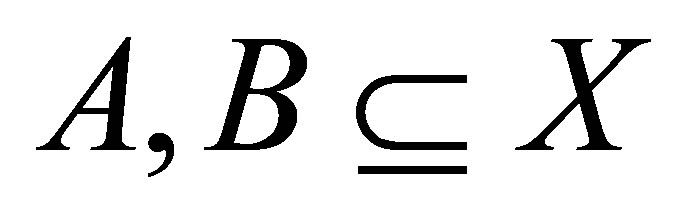 :
:  and
and  implies
implies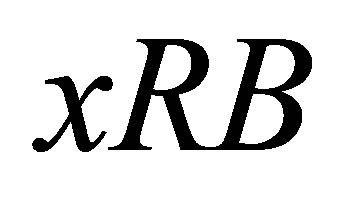 .
.
It is noted that the “d-membership”-relation is a generalization of the membership relation from the set theory.
In the sequel, any concept due to Hitzler and Seda will be denoted by “HS”.
Definition 1.5.Let  be a nonempty set. Suppose that
be a nonempty set. Suppose that  is a d-membership relation on
is a d-membership relation on  and
and  is a collection of subsets of
is a collection of subsets of  for each
for each . We call
. We call  a d-neighbourhood system (d-nbhood system) for
a d-neighbourhood system (d-nbhood system) for 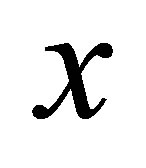 if it satisfies the following conditions:
if it satisfies the following conditions:
(Ni) if , then
, then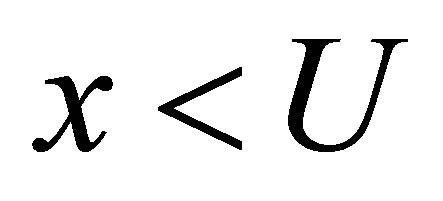 ;
;
(Nii) if , then
, then ;
;
(Niii) if , then there is a
, then there is a  with
with  such that for all
such that for all  we have
we have ;
;
(Niv) if 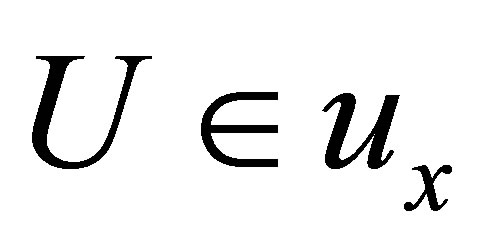 and
and  then
then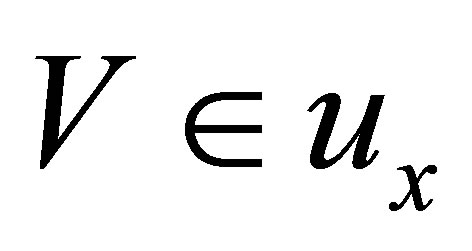 .
.
Each  is called an HS-d-neighborhood (HS d-nbhood) of
is called an HS-d-neighborhood (HS d-nbhood) of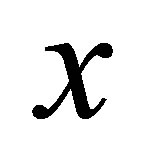 . The ordered triple
. The ordered triple  is called an HS-d-topological space where
is called an HS-d-topological space where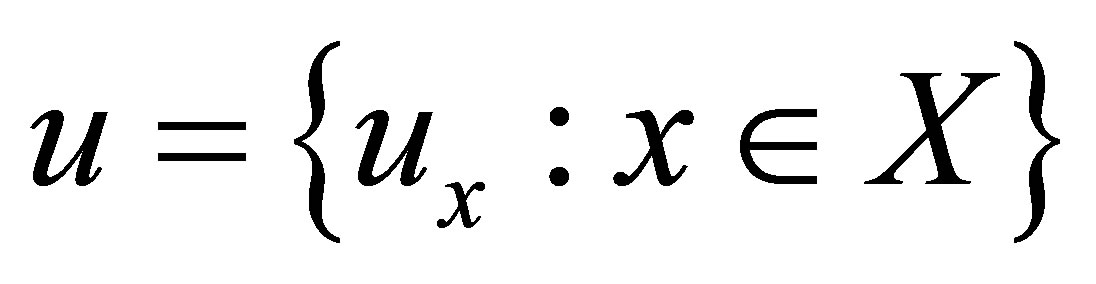 .
.
Proposition 1.1. Let  be a d-metric space. Define the d-membership relation
be a d-metric space. Define the d-membership relation 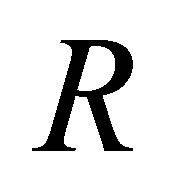 as the relation
as the relation . For each
. For each , let
, let 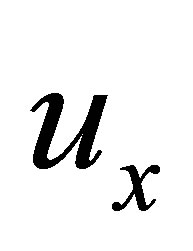 be the collection of all subsets
be the collection of all subsets  of
of 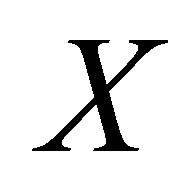 such that
such that . Then
. Then 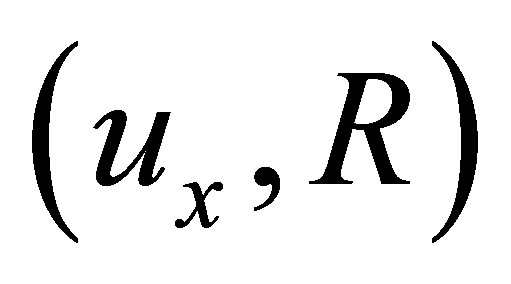 is an HS d-nbhood system for
is an HS d-nbhood system for  for each
for each , i.e.,
, i.e.,  is an HS d-topological neighbourhood space.
is an HS d-topological neighbourhood space.
The present paper is organized as follows. In Section 2, we redefine the dislocated neighbourhood systems given due to Hitzler and Seda [1]. Section 3 is devoted to define the concept of dislocated topological space by open sets. In Section 4, we study topological properties of dislocated closure and dislocated interior operation of a set using the concept of open sets. Finally, in Section 5, we study some further properties of the well-known notions of dislocated continuous functions and dislocated convergence sequence via d-topologies.
2. Redefinition of Definition 1.5.
In Proposition 1.1, it is proved that  is an HS d-topological neighbourhood space. We remark that Property (Niii) can be replaced by the following condition:
is an HS d-topological neighbourhood space. We remark that Property (Niii) can be replaced by the following condition:
(Niii) * If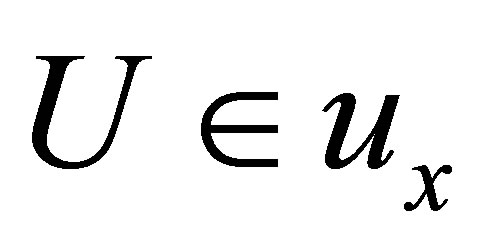 , then for each
, then for each .
.
One can easily verifies that 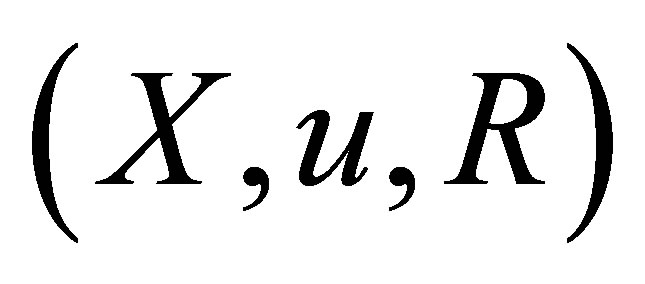 satisfies (Niii) *.
satisfies (Niii) *.
According to the above comment, we introduce a redefinition of the concept of the dislocated-neighbourhood systems due to Hitzler and Seda [1] as follows.
Definition 2.1. Let  be a nonempty set. Suppose that
be a nonempty set. Suppose that  is a d-membership relation on
is a d-membership relation on 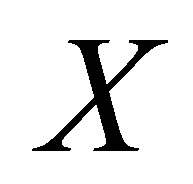 and
and  be a collection of subsets of
be a collection of subsets of 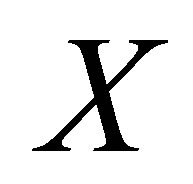 for each
for each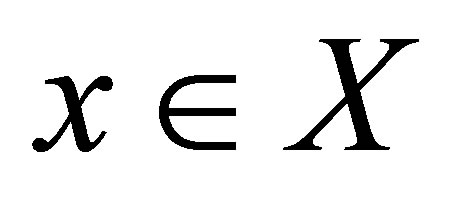 . We call
. We call  a d*-neighbourhood system (d*-nbhood system) for
a d*-neighbourhood system (d*-nbhood system) for  if it satisfies the following conditions:
if it satisfies the following conditions:
(Ni) if , then
, then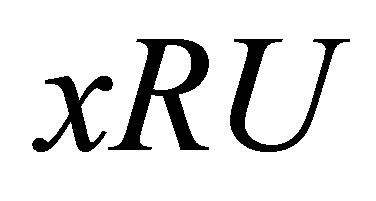 ;
;
(Nii) if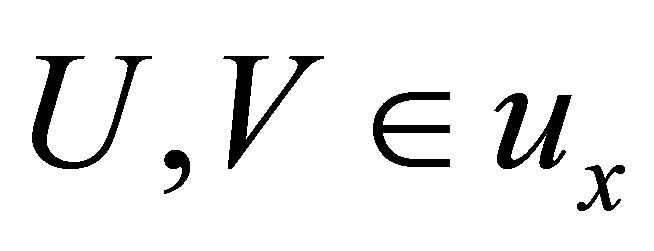 , then
, then ;
;
(Niii)* if  and
and , then
, then ;
;
(Niv) if  and
and , then
, then .
.
Each  is called a d*-neighborhood of
is called a d*-neighborhood of . If
. If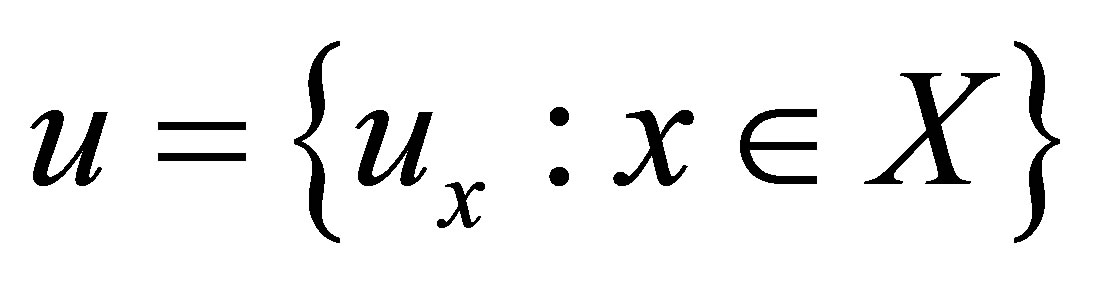 , then
, then 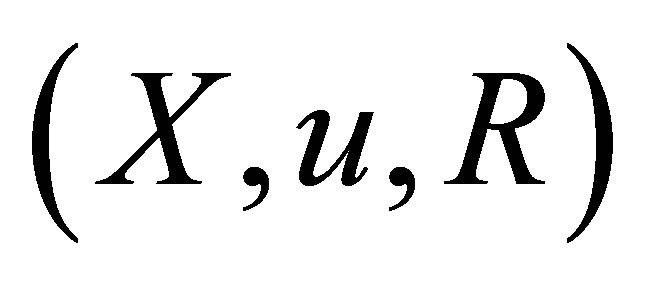 is called a d*-topological neighborhood space.
is called a d*-topological neighborhood space.
Now, we state the following theorem without proof.
Theorem 2.1. Let 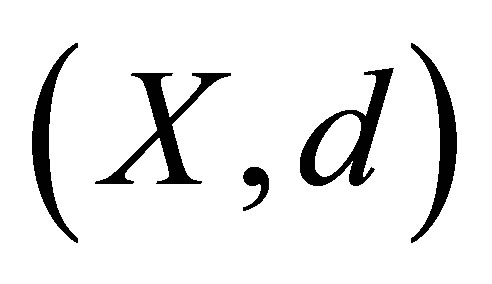 be a d-metric space. Define the d-membership relation
be a d-metric space. Define the d-membership relation  as the relation
as the relation  iff there exists
iff there exists  for which
for which . Assume that
. Assume that  and
and . Then
. Then 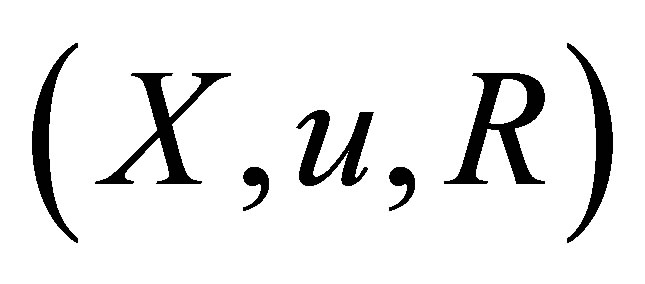 is a d*-topological neighborhood space.
is a d*-topological neighborhood space.
3. Dislocated-Topological Space
In what follows we define the concept of dislocatedtopological space (for short, d-topological space) by the open sets and prove that this concept and the concept of d*-topological neighborhood space are the same.
Definition 3.1. Let 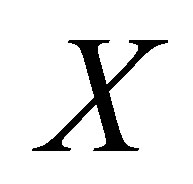 be a nonempty set. Suppose that
be a nonempty set. Suppose that 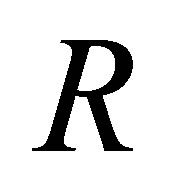 is a d-membership relation and
is a d-membership relation and  for each
for each . We call
. We call  an
an  -topology on
-topology on 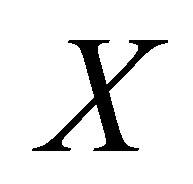 iff it satisfies the following conditions:
iff it satisfies the following conditions:
(dτx1) 
(dτx2) 
(dτx3)  and
and .
.
Each  is called a
is called a  -open set. If
-open set. If  is an
is an  -topology on
-topology on  for each
for each , then
, then  is called a d-topology on
is called a d-topology on . The triple
. The triple  is called an
is called an  -topological space and the triple
-topological space and the triple  is called a d-topological space.
is called a d-topological space.
Definition 3.2. Let 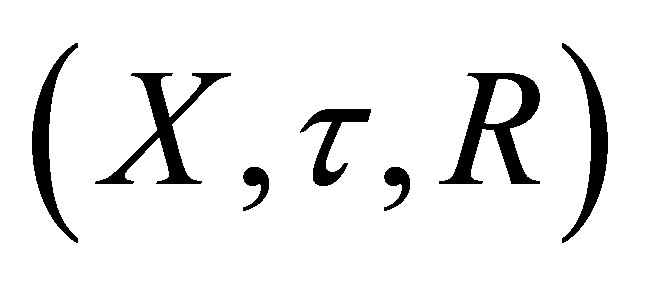 be an
be an  -topological space.
-topological space.  is called a
is called a  -closed iff
-closed iff  is a
is a  - open..
- open..
Theorem 3.1. The concepts of d*-topological neighborhood space and d-topological space are the same.
Proof. Let 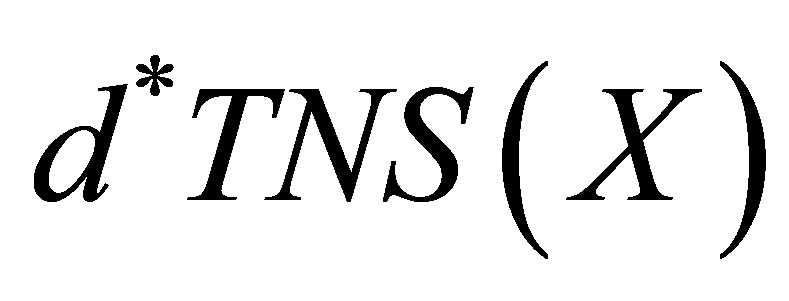 be the family of all d*- topological neighbourhood systems on
be the family of all d*- topological neighbourhood systems on 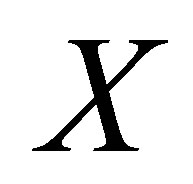 and let
and let  be the family of all d-topologies on
be the family of all d-topologies on . The proof is complete if we point out a bijection between
. The proof is complete if we point out a bijection between 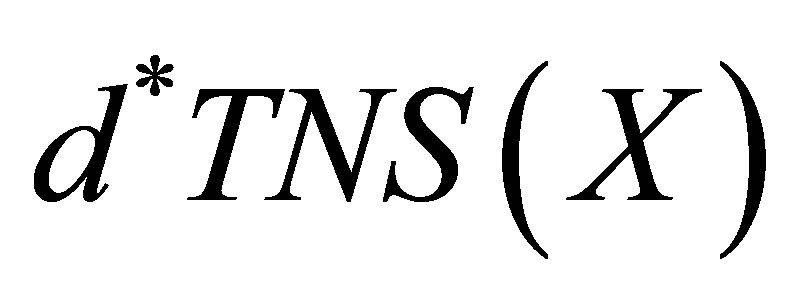 and
and . Let
. Let  and
and  be functions defined as follows:
be functions defined as follows: , where
, where  for each
for each  and
and , where
, where  for each
for each . One can easily verifies that these functions are well defined,
. One can easily verifies that these functions are well defined,  and
and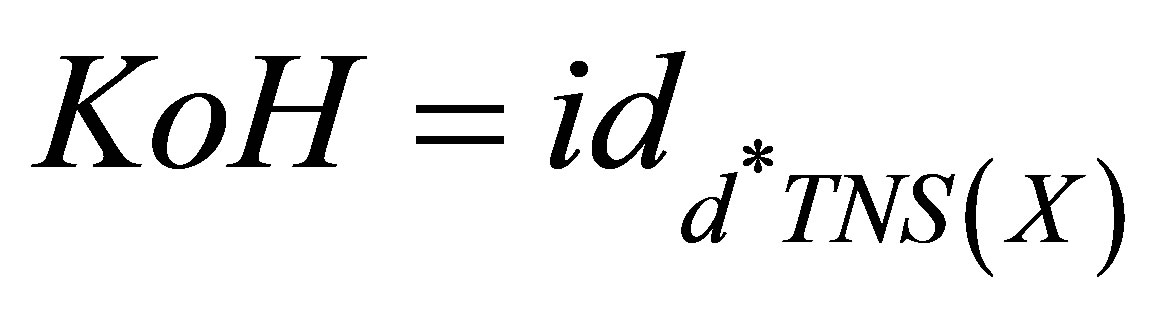 .
.
The following counterexample illustrates that the statement:  iff
iff  may not be true.
may not be true.
Counterexample 3.1. Let  and
and
 .
.
Then
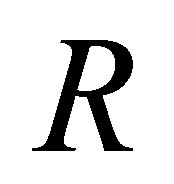
is a d-membership relation. Since
 , then
, then , i.e.
, i.e. 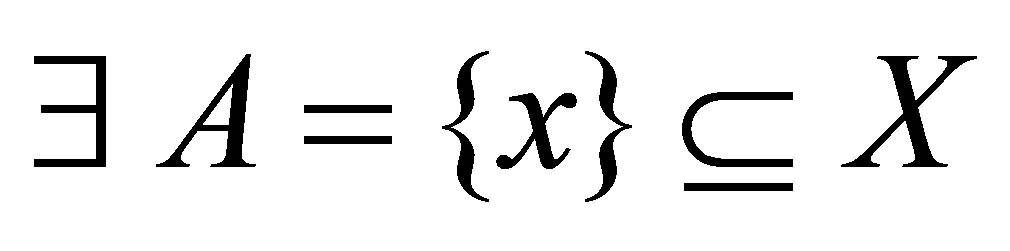 such that
such that  and
and .
.
We get the following theorem without proof.
Theorem 3.2. Let 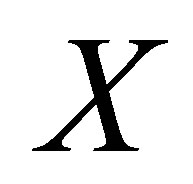 be a nonempty set. Suppose that
be a nonempty set. Suppose that  is a d-membership relation and
is a d-membership relation and  for each
for each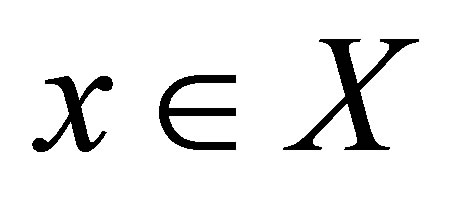 . Assume that
. Assume that  satisfies the following conditions:
satisfies the following conditions:
(dFx1)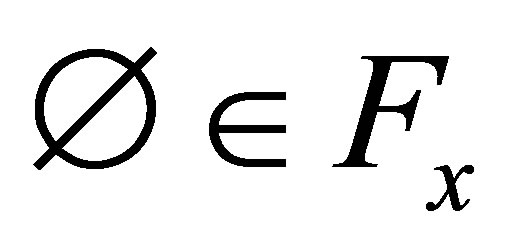 ;
;
(dFx2) ;
;
(dFx3)  and
and .
.
Then  is a d-topology on
is a d-topology on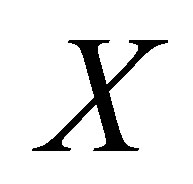 , where
, where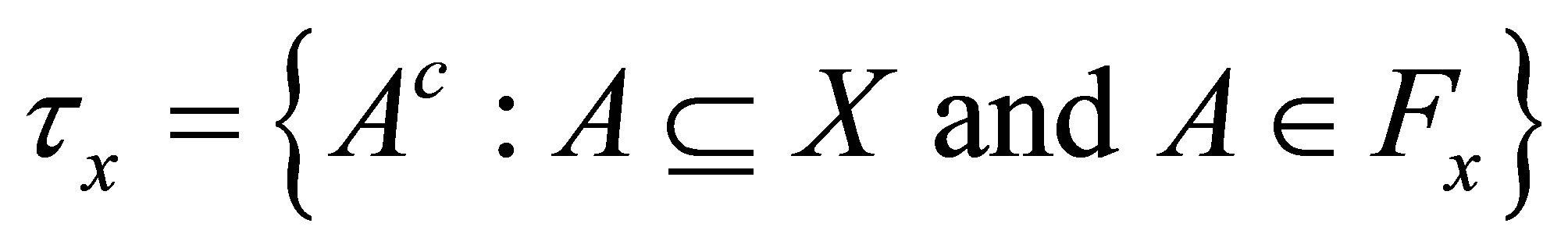 . If
. If 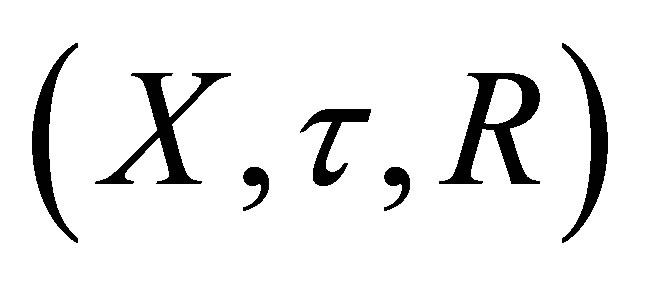 is a dtopological space, then for each
is a dtopological space, then for each  the family
the family  of all
of all  -closed sets satisfies the conditions (dFx1)- (dFx3).
-closed sets satisfies the conditions (dFx1)- (dFx3).
4. Dislocated Closure and Dislocated Interior Operations
In the sequel we define the dislocated closure and dislocated interior operations of a set and study some topological properties of dislocated closure and dislocated interior operation.
Definition 4.1. Let 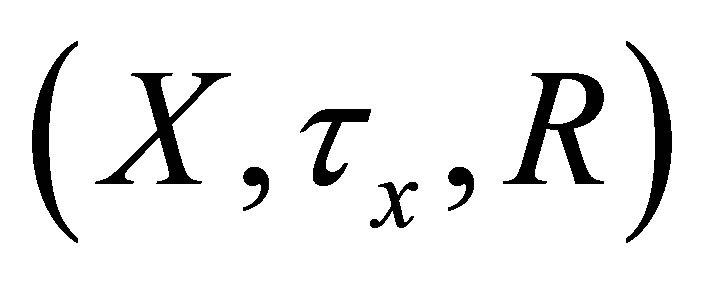 be an
be an  -topological space. The
-topological space. The  -interior of a subset
-interior of a subset  of
of 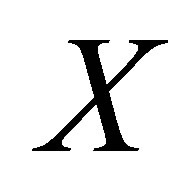 is denoted and defined by:
is denoted and defined by: .
.
Remark 4.1. From Definition 4.1, if , then
, then  is undefined. If
is undefined. If , then
, then  is defined.
is defined.
Theorem 4.1. Let 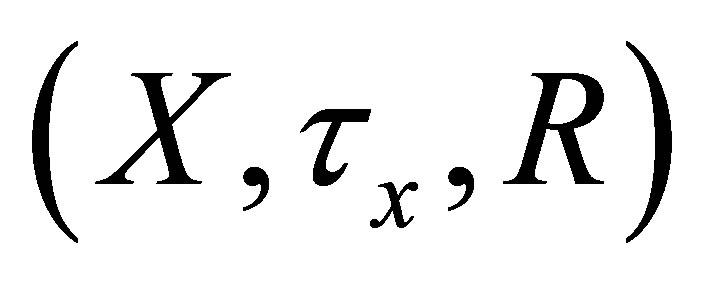 be an
be an  -topological space.
-topological space.
(A) If , then
, then  for each
for each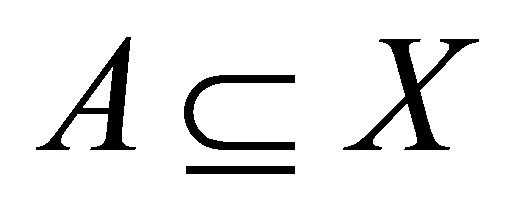 .
.
(B) If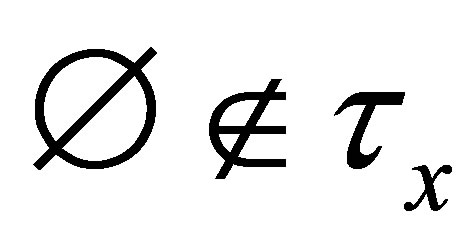 , then
, then
(i) ;
;
(ii)  for each
for each ;
;
(iii)  for each
for each ;
;
(iv)  or
or  for each
for each .
.
(v)  if
if 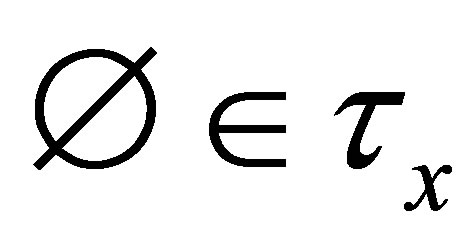 or
or .
.
Corollary 4.1. (1) If , then
, then  is a
is a  -open.
-open.
(2) If , then
, then .
.
Theorem 4.2. If  such that the conditions B(i), B(iii) and B(iv) are satisfied then
such that the conditions B(i), B(iii) and B(iv) are satisfied then
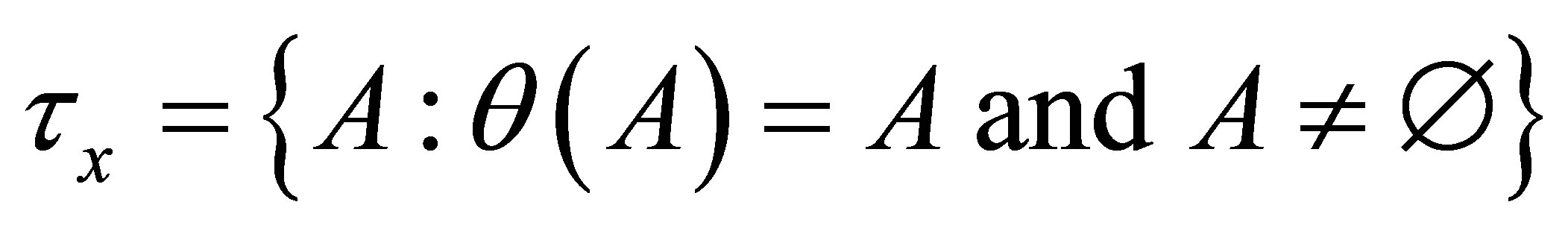 is an
is an  -topology on
-topology on . The
. The  -membership relation is defined as
-membership relation is defined as  iff
iff .
.
Proof. The desired result is obtained from the following:
(I) (dτx1)  since
since ;
;
(dτx2)  and
and
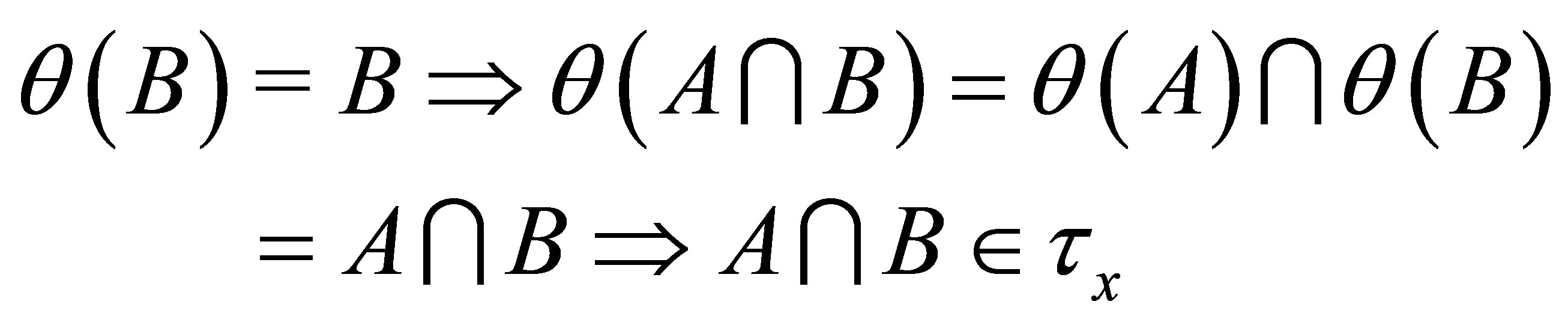 ;
;
(dτx3)  and
and ,
,  (from B(iii)-(iv)).
(from B(iii)-(iv)).
(II)  and
and  and
and  (from I
(from I ).
).
Definition 4.2. Let  be an
be an  -topological space. The
-topological space. The 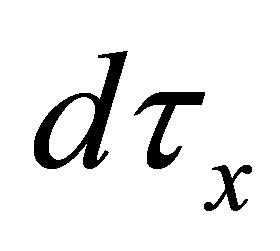 -closure of a subset
-closure of a subset  of
of  is denoted and defined by:
is denoted and defined by: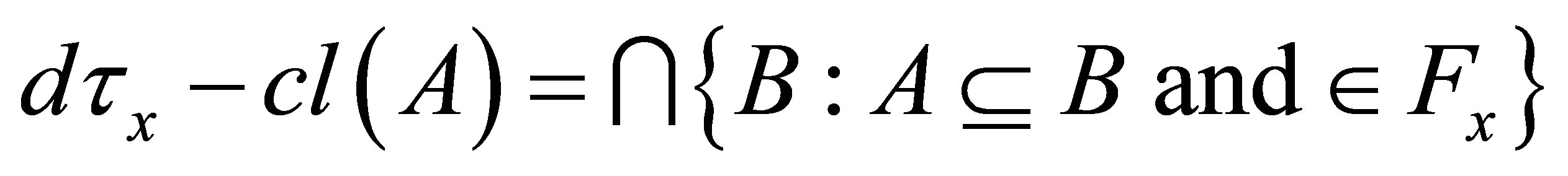 .
.
If , then
, then  is undefined but if
is undefined but if , then
, then  is defined.
is defined.
Theorem 4.3. Let  be an
be an  -topological space. Then for each
-topological space. Then for each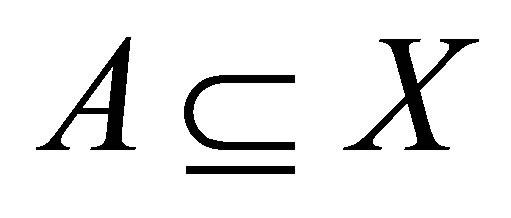 ,
,
 .
.
Proof.

From Theorems 4.1 and 4.3, we obtain the following theorem without proof.
Theorem 4.4. Let  be an
be an  -topological space.
-topological space.
(A) If , then
, then  for each
for each .
.
(B) If , then
, then
(i) ;
;
(ii)  for each
for each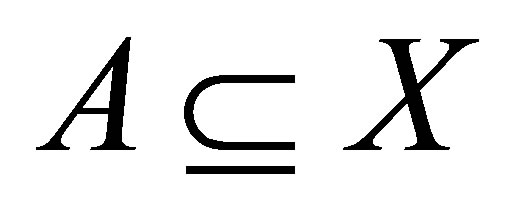 ;
;
(iii)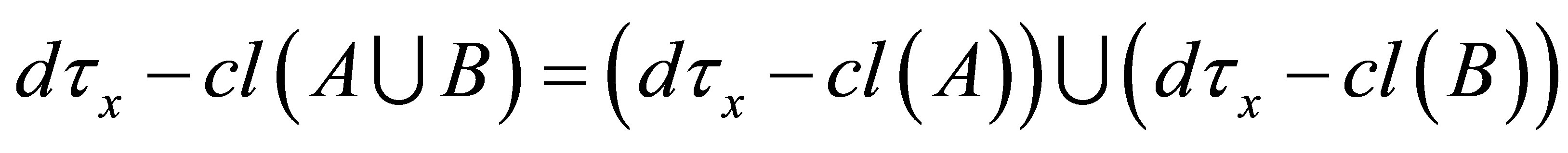 ;
;
(iv)  or
or  for each
for each ;
;
(v)  if
if 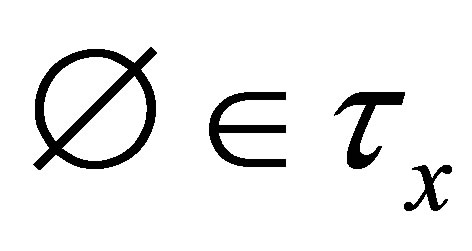 or
or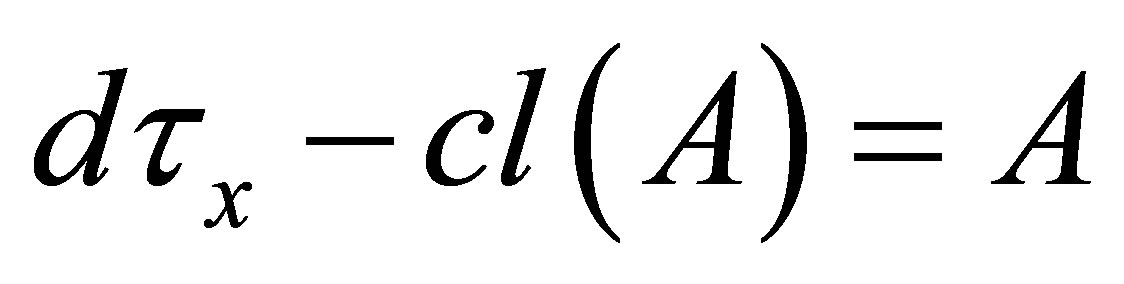 .
.
Corollary 4.2. (1) If , then
, then  is a
is a  -closed.
-closed.
(2) If , then
, then .
.
5. Dislocated Continuous Functions and Dislocated Convergence Sequences via d-Topologies
Now, we define the dislocated continuous functions and dislocated convergence sequences. We also obtain a decomposition of dislocated continuous function and dislocated convergence sequences.
Definition 5.1. Let  and
and  be dislocated-metric spaces. A function
be dislocated-metric spaces. A function 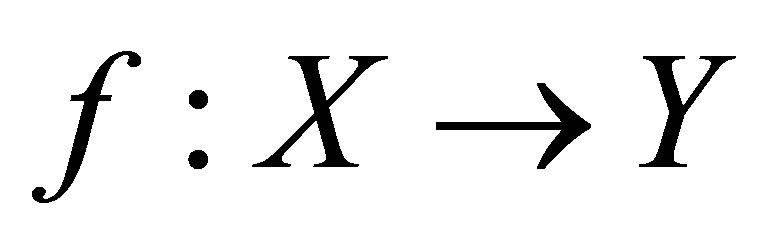 is called d-continuous at
is called d-continuous at  iff
iff  such that
such that . We say
. We say 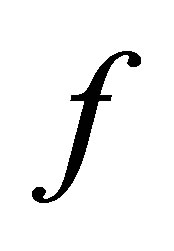 is d-continuous iff
is d-continuous iff  is d-continuous at each
is d-continuous at each 
Theorem 5.1. Let  and
and  be dislocated-metric spaces and
be dislocated-metric spaces and  be any function. Assume that
be any function. Assume that 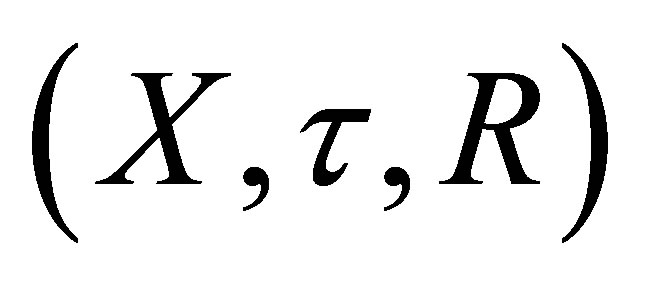 (resp.
(resp. ) be the d-topological space obtained from
) be the d-topological space obtained from  (resp.
(resp. ). Then the following statements are equivalent:
). Then the following statements are equivalent:
(1)  is d-continuous at
is d-continuous at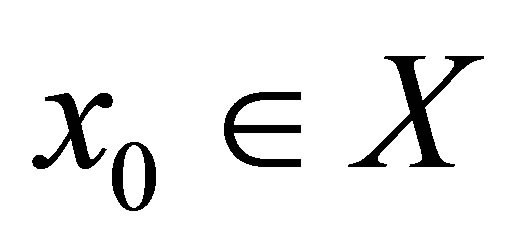 .
.
(2) 
(3)  such that
such that , where
, where 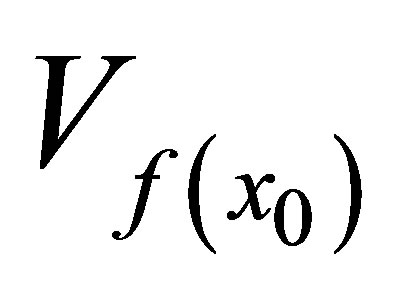 and
and 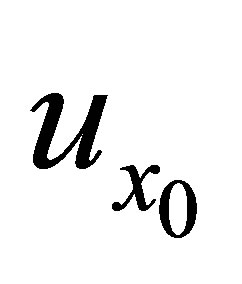 are the d*-topological neighborhood systems obtained from
are the d*-topological neighborhood systems obtained from  and
and 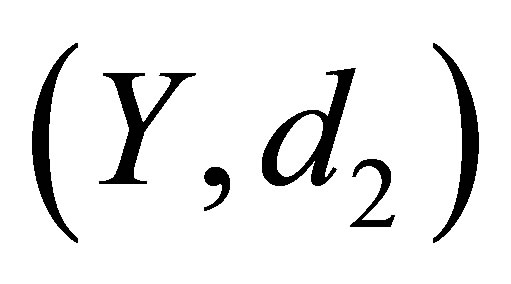 respectively.
respectively.
(4)  such that
such that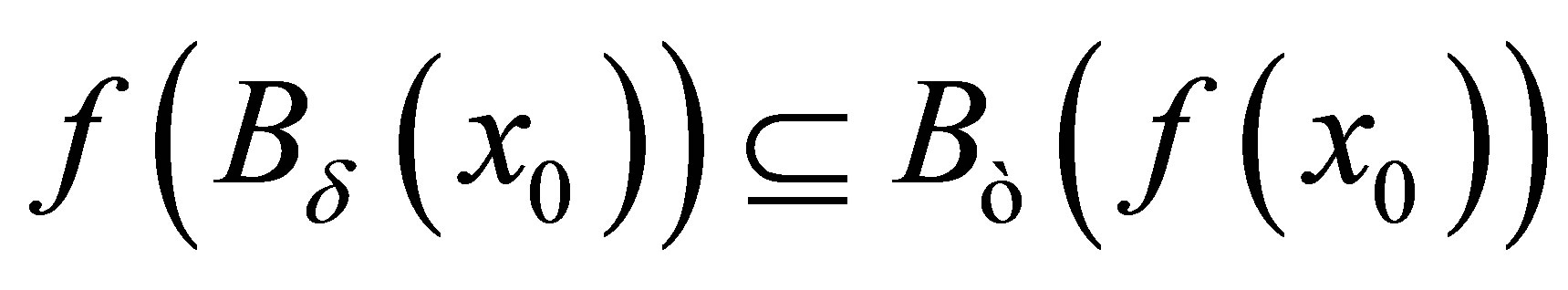 .
.
Proof. ((1)Þ(2)): Let . Then
. Then 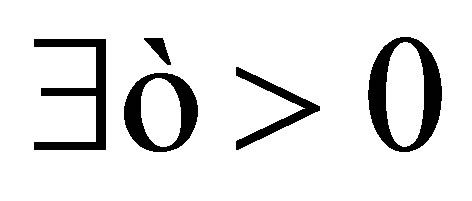 such that
such that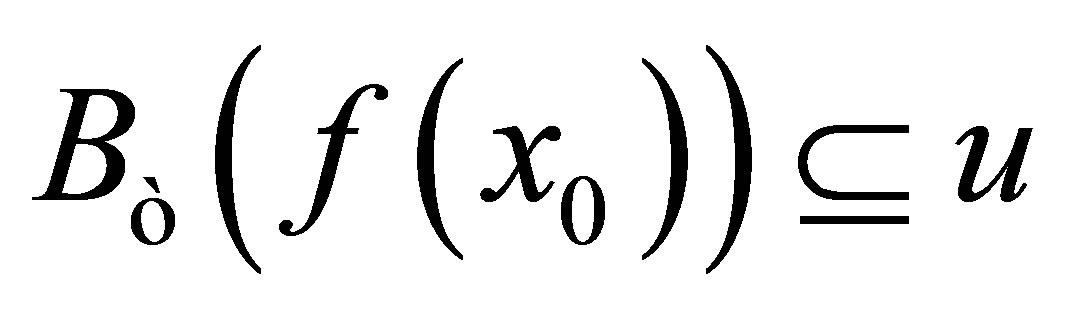 . Thus
. Thus  such that
such that , i.e.,
, i.e., 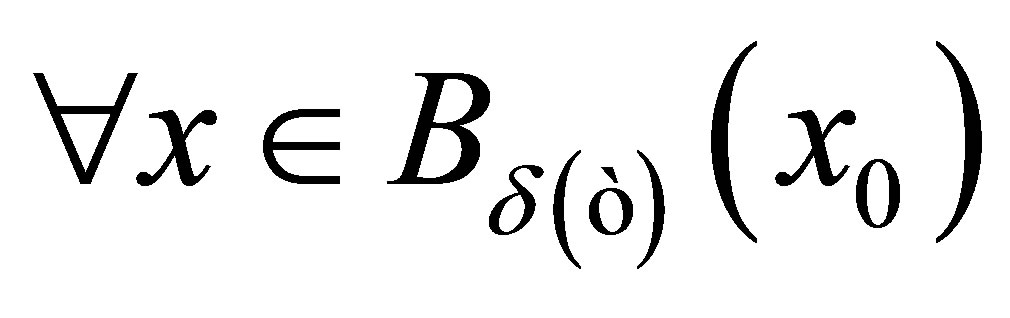 ,
,  , then
, then . Hence
. Hence .
.
((2)Þ(1)): Let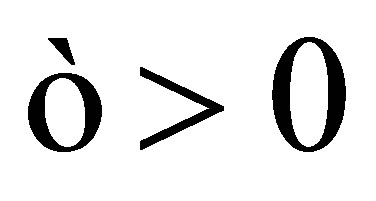 . Suppose that for each
. Suppose that for each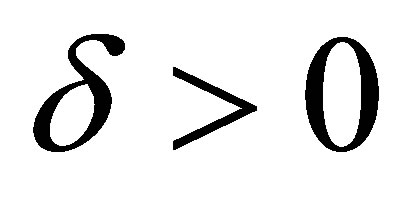 ,
, 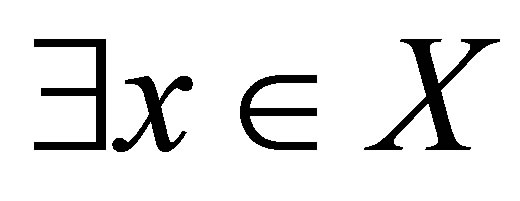 such that
such that . Now,
. Now, . From the assumption
. From the assumption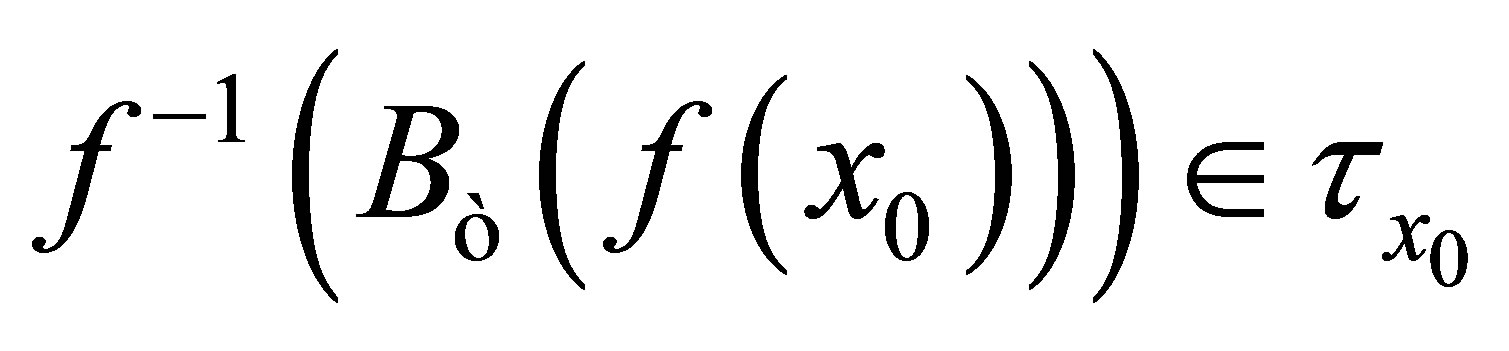 , i.e.,
, i.e., 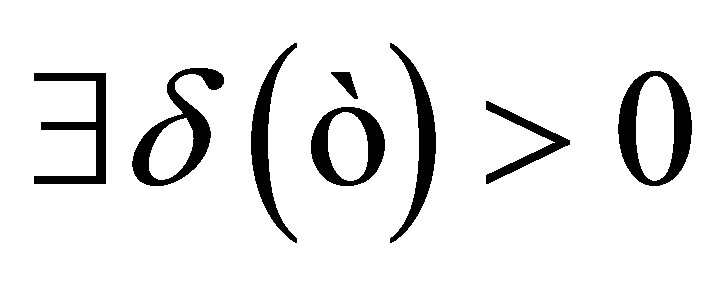 such that
such that . Then
. Then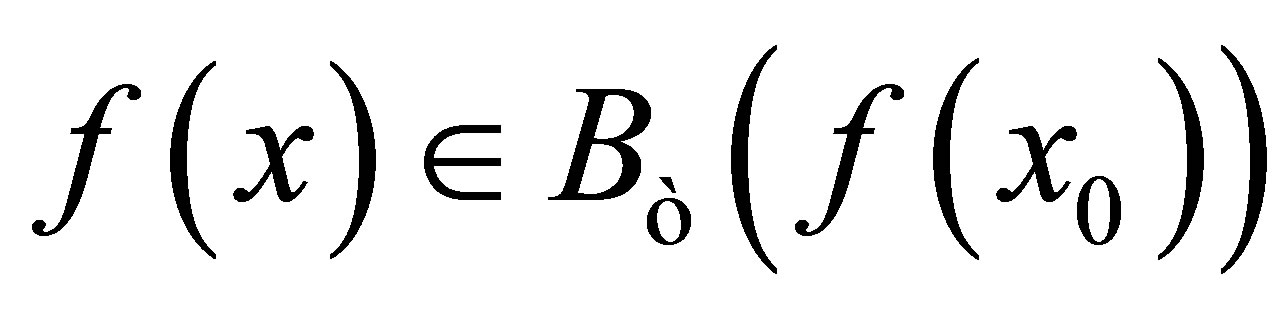 . The contradiction demands that
. The contradiction demands that  is d-continuous at
is d-continuous at .
.
(1) Û (4) and (2) Û (3) are immediate.
Definition 5.2. Let  be a d-metric space. A sequence
be a d-metric space. A sequence 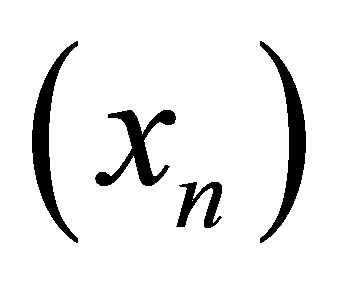 d-converges to
d-converges to 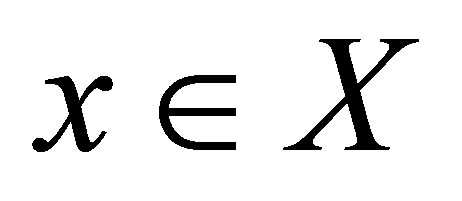 if
if  such that
such that ,
,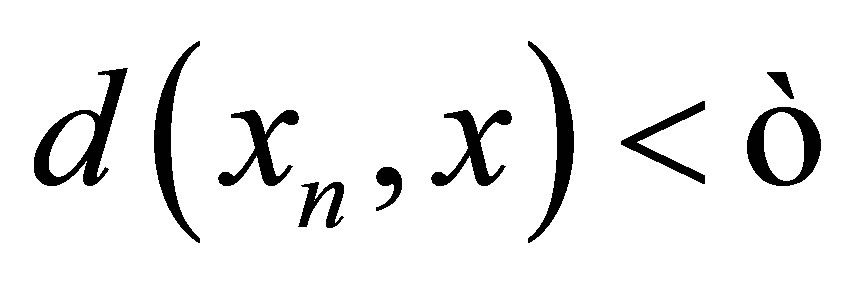 .
.
Theorem 5.2. Let 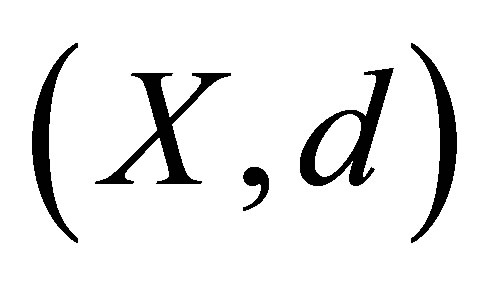 be a d-metric space and
be a d-metric space and  be the d-topological space obtained from it. Then the sequence
be the d-topological space obtained from it. Then the sequence  d-converges to
d-converges to 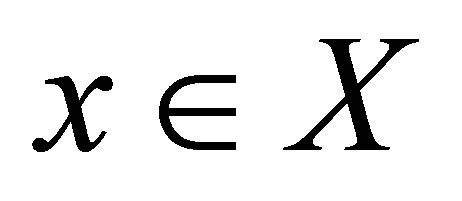 iff
iff 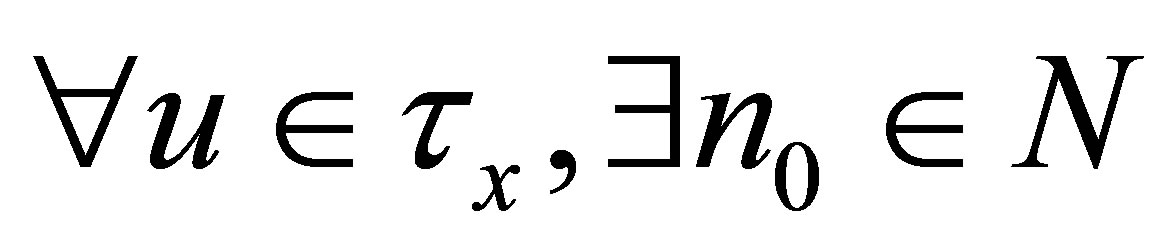 such that for each
such that for each .
.
Proof. (Þ:) Let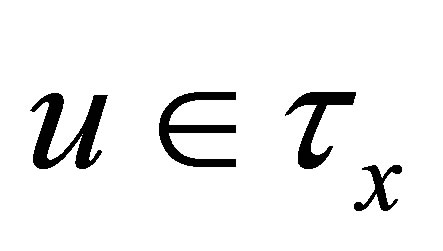 . Then there exists
. Then there exists  such that
such that . From the assumption
. From the assumption  such that
such that . Thus
. Thus 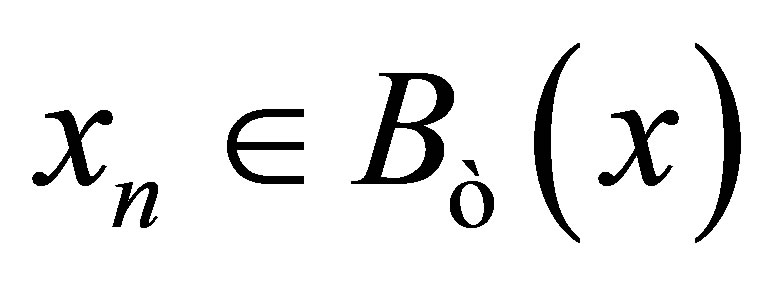 for each
for each . So
. So  for each
for each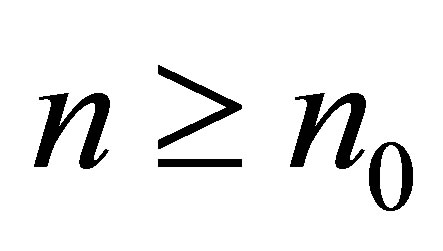 .
.
(Ü:) Let . Since
. Since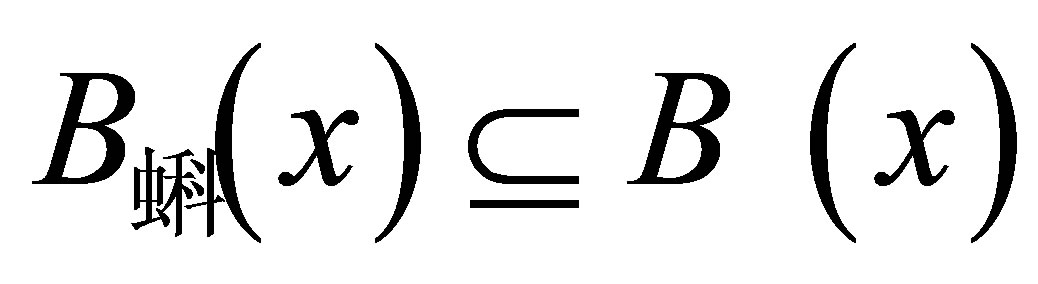 , then
, then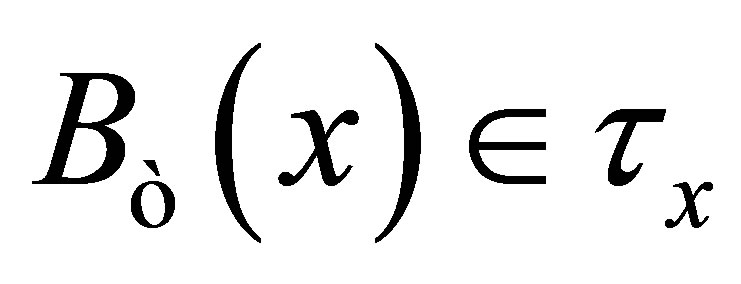 . Thus
. Thus  such that for each
such that for each 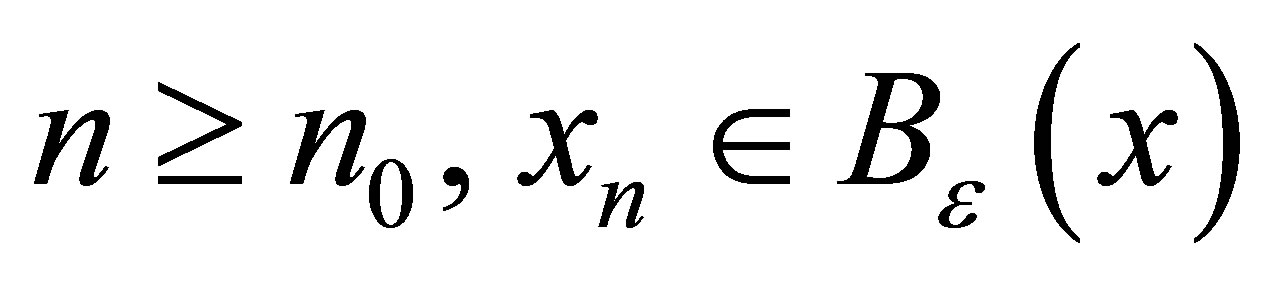 ,i.e.,
,i.e., 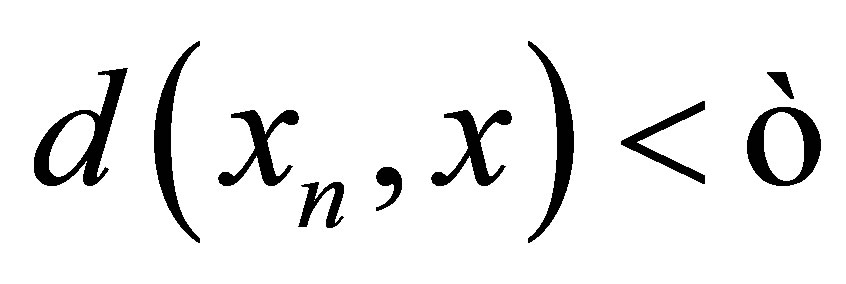 for each
for each . Hence
. Hence .
.
NOTES