1. Introduction
The Fickian first law and second law have been accepted as an independent one respectively since 1855 [1]. They have been thus widely applied to various diffusion problems. The Fickian second law is obtained by applying the Fickian first law to the well-known divergence theorem. The Fickian second law is also obtained from the provability of differential equation [2]. In mathematics, the Fickian first law is obtained by integrating the Fickian second law with respect to nabla operator  [3]. Therefore, it is considered that the Fickian law is only one, i.e., the Fickian second law.
[3]. Therefore, it is considered that the Fickian law is only one, i.e., the Fickian second law.
In the previous work, it was revealed that the Fikian first law is incomplete without an initial value for the Fickian second law [3]. At the same time, this indirectly means that the Darken equation is mathematically incorrect [4]. Nevertheless, a lot of interdiffusion researchers still believe that the Darken equation is valid. In the present work, therefore, we directly reveal that the Darken equation is mathematically and physically invalid.
The concentration profile depends on the diffusivity in the diffusion equation. The diffusivity is defined as an interaction between a single diffusion particle and the diffusion field around it. Therefore, the diffusivity should be originally discussed by using the well-known Schrödinger equation [5]. Based on the physical theory, the interaction does not depend on the motion of diffusion system. Thus, this indicates that there is no such an intrinsic diffusion coefficient.
The misjudged theory of Darken equation is caused by considering a partial differential equation as an ordinary differential equation [4]. It is revealed that the Darken equation is thus mathematically invalid and also the intrinsic diffusion concept is an illusion in contradiction to the fundamental principle in physics.
The well-known Kirkendall effect shows the following [6].
1) The diffusion mechanism of the metal atoms in metal crystal is the vacancy one.
2) The Kirkendall effect occurs in accordance with the parabolic law.
In the previous study, we can reasonably explain it using the new diffusion flux regardless of the intrinsic diffusion concept [3].
The Darken theory attendant on the Kirkendall effect and the Fickian first law appear in almost existing text books. A lot of previous diffusivity data analyzed by the invalid Darken equation have been accumulated since 1948. Further, the researchers still perform the study relevant to interdiffusion problems and also the student education is performed in accordance with the misjudged descriptions in existing text books. Therefore, the present brief report will have a great influence on their matters not only in future but also in past. The accumulated diffusivity data should be thus reexamined by using the new analytical method. The misjudged descriptions in existing text books should be also revised in accordance with the present theory. Therefore, we believe that it is extremely dominant to make the new theory universally known as soon as possible in this field.
2. Misjudgment of Darken Theory
In the previous works, the interdiffusion problems were reasonably solved regardless of the intrinsic diffusion concept [7,8]. This indicates that the intrinsic diffusion concept is needless in the analysis of interdiffusion problems. In the following, we reveal that the well-known Darken equation is incorrect in mathematics.
The diffusion equation of concentration C(t, x) in the moving coordinate system (t, x) yielding
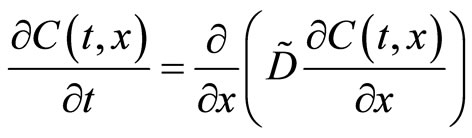 (1)
(1)
is transformed into one of the fixed coordinate system  in the following, where the diffusion time is t = τ in the usual procedure. As usually accepted in this field, Figure 1 shows that the cross section S of a diffusion couple of binary system, which is composed of the diffusion particles I and II, is approximately a constant value. In other words, this means
in the following, where the diffusion time is t = τ in the usual procedure. As usually accepted in this field, Figure 1 shows that the cross section S of a diffusion couple of binary system, which is composed of the diffusion particles I and II, is approximately a constant value. In other words, this means
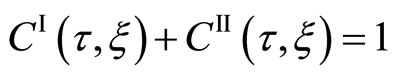 , (2)
, (2)
where  and
and  are the normalized concentrations of diffusion particles I and II, respectively. We set the initial state so the origin of coordinate system
are the normalized concentrations of diffusion particles I and II, respectively. We set the initial state so the origin of coordinate system  corresponds to that of
corresponds to that of .
.
If the velocity of  is
is  against
against 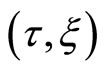
 , the relation of
, the relation of
 (3)
(3)
is valid. Therefore, the relations between the differential operators of
 (4)
(4)
are valid. Using (4) for (1), the diffusion equations of diffusion particles I and II in the fixed coordinate system are given as:
 (5)
(5)
where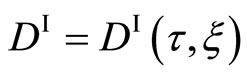 ,
, 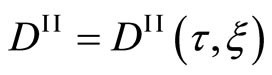 ,
,  and
and
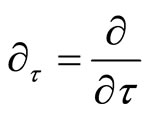 . From the divergence theorem, (5) shows that the diffusion fluxes in the fixed coordinate system are expressed as;
. From the divergence theorem, (5) shows that the diffusion fluxes in the fixed coordinate system are expressed as;
 (6)
(6)
Here, (2), (5) and (6) yield the relation of
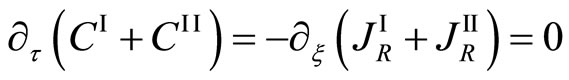 . (7)
. (7)
In accordance with the mathematical theory of a partial differential equation, (7) shows that 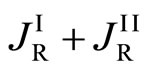 does not depend on
does not depend on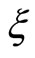 . Using a function of
. Using a function of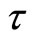 , i.e.,
, i.e.,  , the relation of
, the relation of
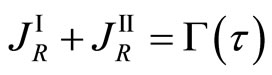 (8)
(8)
is thus mathematically valid. In other words, when the diffusion system moves, (8) indicates that the Fickian first law is not valid in the fixed coordinate system because of 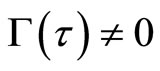 in the general case [3]. The new diffusion flux JR = J + J0(t) defined by the previous work corresponds to
in the general case [3]. The new diffusion flux JR = J + J0(t) defined by the previous work corresponds to , as given by
, as given by
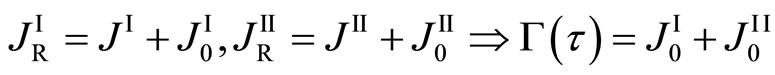 .
.
Here after, we discuss  independent of
independent of . Using (2), (6) and (7) for (8), the identical equation with respect to
. Using (2), (6) and (7) for (8), the identical equation with respect to 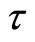 yielding
yielding
 (9)
(9)
is obtained. Since it is clear that 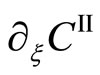 depends on the space coordinate
depends on the space coordinate 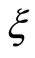 and that
and that 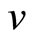 is independent of
is independent of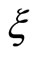 , it is necessary that the relation of
, it is necessary that the relation of
 (10)
(10)
is valid. Equation (10) is consistent with the physical principle which the physical relation does not depend on the given coordinate system. It is a common sense in physics that  is valid in the present case, if
is valid in the present case, if 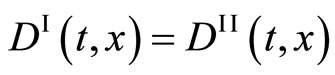 is valid in the moving coordinate system. The interdiffusion coefficient is thus defined as
is valid in the moving coordinate system. The interdiffusion coefficient is thus defined as
 (11)
(11)
in the fixed coordinate system.
Here, the Darken theory is discussed as follows. Substituting (6) into (7) yields
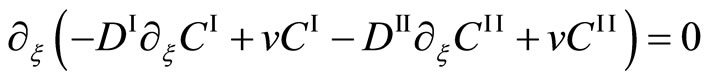 . (12)
. (12)
In contradiction to the mathematical theory of a partial differential equation, Darken solved (12) as an ordinary differential equation with respect to . In other words, using k as an integral constant value in stead of the above
. In other words, using k as an integral constant value in stead of the above , he thought that the relation of
, he thought that the relation of

is valid, although it is contradictory to the mathematical theory. Using the initial condition of k = 0 and (2), (12) is rewritten as
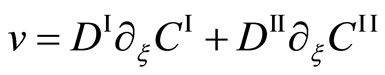 . (13)
. (13)
Here, (13) is an identical equation which the left-hand side does not depend on  and the right-hand side depends on
and the right-hand side depends on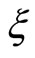 . Therefore, using (2) for (13), the relation of
. Therefore, using (2) for (13), the relation of
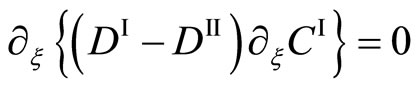 (14)
(14)
is obtained. It is apparent that (14) is identically valid only under the condition of . Thus, Darken again failed to notice the misunderstanding of fundamental theory in mathematics.
. Thus, Darken again failed to notice the misunderstanding of fundamental theory in mathematics.
In any case, if we substitute (13) into 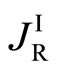 in (6), the relation of
in (6), the relation of
 (15)
(15)
is obtained. From comparing (15) with the Fickian first law of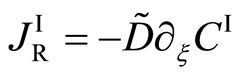 , the so-called Darken equation of
, the so-called Darken equation of
 (16)
(16)
is perfunctorily derived.
Darken failed to notice that (13) corresponds to the identical (14). He thus misunderstood  and
and 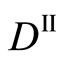 in (15) in the analytical process as if they are independent each other, although it is invalid. In any case, the
in (15) in the analytical process as if they are independent each other, although it is invalid. In any case, the 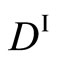 and
and 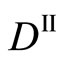 in (15) are symbolically rewritten as
in (15) are symbolically rewritten as  and
and 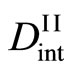 in (16) in order to distinguish from ones of (10). Further,
in (16) in order to distinguish from ones of (10). Further,  and
and  were defined as the intrinsic diffusion coefficients then.
were defined as the intrinsic diffusion coefficients then.
Hereinbefore, the Darken theory is apparently inconsistent with the mathematical theory. Equation (16) is thus entirely meaningless and at the same time the concept of intrinsic diffusion is an illusion.
3. Conclusions
The present brief report reveals that the Darken equation is apparently incorrect and the concept of intrinsic diffusion is meaningless. Nevertheless, the Darken theory has been widely applied to the interdiffusion problems for such a long time since 1948. The main reasons are as follows.
The derivation process of (16) shows that 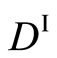 and
and , i.e.,
, i.e.,  and
and 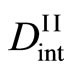 are independent of each other, although it is essentially incorrect. Researchers relevant to the interdiffusion problems have failed to notice the misjudgment of Darken equation (16). Based on the intrinsic diffusion concept, the Darken theory has been applied to the relation of
are independent of each other, although it is essentially incorrect. Researchers relevant to the interdiffusion problems have failed to notice the misjudgment of Darken equation (16). Based on the intrinsic diffusion concept, the Darken theory has been applied to the relation of

in order to understand the well-known Kirkendall effect. It has been thus considered that the Kikendall effect is caused by the relation of
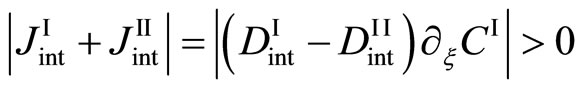
for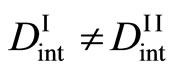 . However, this is a misjudged theory as can be seen from (11). Therefore, we cannot understand the Kirkendall effect by using the Darken theory. On the other hand, it is revealed that the Kirkendall effect is reasonably understood by using the new diffusion flux [3].
. However, this is a misjudged theory as can be seen from (11). Therefore, we cannot understand the Kirkendall effect by using the Darken theory. On the other hand, it is revealed that the Kirkendall effect is reasonably understood by using the new diffusion flux [3].
The concentration profile can be investigated by the experimental procedure, but the diffusivity profile cannot be experimentally obtained. The validity of diffusivity profile has been neglected by the reason why there is no experimental method to confirm it. It is revealed that the diffusivity profile must have an inflection point with respect to  in accordance with the mathematical theory [7]. On the contrary, some of their profiles obtained previously do not have it because of the mathematically incorrect analysis.
in accordance with the mathematical theory [7]. On the contrary, some of their profiles obtained previously do not have it because of the mathematically incorrect analysis.
In any case, the interdiffusion problems have been numerically investigated after the Darken theory, using 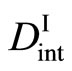 and
and 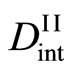 in (16) for the simulation as parameters. As a matter of course, the arbitrary concentration profile is perfunctorily reproducible then. However, those investigations are entirely meaningless in accordance with the above theory. It will be thus necessary to reexamine the validity of previous diffusivity data in accordance with the new diffusion theory [3,5,7,8].
in (16) for the simulation as parameters. As a matter of course, the arbitrary concentration profile is perfunctorily reproducible then. However, those investigations are entirely meaningless in accordance with the above theory. It will be thus necessary to reexamine the validity of previous diffusivity data in accordance with the new diffusion theory [3,5,7,8].
As a result, the misjudged Darken equation is caused by the incompleteness of the Fickian first law [3]. If we consider that a lot of diffusion researchers still perform the study for interdiffusion problems and also educate their students about diffusion theory, using the Fickian first law and/or the Darken equation, we strongly propose to make the new diffusion theory universally known as soon as possible for young researchers.
It is an extremely seldom example in science technology history that the misjudged theory has been accepted for such a long time, i.e., the Fickian first law since 1855 and the Darken theory since 1948. Researchers should deeply accept these events as a precept of the method and attitude of study. Hereafter, the terminologies of the Darken equation, the intrinsic diffusion and/or the Fickian first law will gradually disappear in the diffusion field.