A Theoretical Foundation for the Widely Linear Processing of Quaternion-Valued Data ()
1. Introduction
The widely linear (WL) estimation method has been proved mathematically to be effective for estimation problems using complex-valued data. Estimation using WL uses complex conjugate parameters in addition to complex-valued parameters [1]. It has been applied to communications [2,3] and adaptive filters [4], together with so-called augmented complex statistics, a concept introduced by Picinbono et al. Moreover, an extension of the WL method to quaternion-valued case has been presented [5], which fully exploits available statistical information. A quaternion, a four-dimensional number invented by W. R. Hamilton in 1843, is an extension of a complex number. Let  be a four-dimensional vector space over
be a four-dimensional vector space over  with an ordered basis, denoted by
with an ordered basis, denoted by  and
and  where
where  is a set of real numbers. Any quarternion
is a set of real numbers. Any quarternion  is expressed as
is expressed as  where
where . The three basis elements
. The three basis elements  satisfy the relations
satisfy the relations
 (1)
(1)
 (2)
(2)
Quaternion algebra has been used in fields such as robotics, computer vision, neural networks, signal processing, and communications (e.g. [6-8]).
In this paper, we present a theoretical foundation for quaternion-valued WL estimation: it is proved that the estimation error obtained using the quaternion-valued WL estimation method is smaller than that obtained using the usual quaternion-valued estimation method [9].
2. The WL Model
In this section, the complex-valued WL model and the quaternion-valued WL model are reviewed.
2.1. The Complex-Valued WL Model
Let  be a scalar complex-valued random variable to be estimated in terms of an observation that is a complex-valued random vector
be a scalar complex-valued random variable to be estimated in terms of an observation that is a complex-valued random vector  where
where  is a set of complex numbers, and
is a set of complex numbers, and 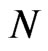 is a natural number. That is,
is a natural number. That is, 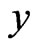 is a true value and
is a true value and  is an observed value. In complex-valued linear mean square estimation (LMSE), the problem is to find an estimate written as
is an observed value. In complex-valued linear mean square estimation (LMSE), the problem is to find an estimate written as
 (3)
(3)
where , and
, and  represents the complex conjugation and transposition. Then, the objective of the problem is to find the parameter
represents the complex conjugation and transposition. Then, the objective of the problem is to find the parameter  that minimizes the estimation error
that minimizes the estimation error .
.
In the meantime, the complex-valued widely linear mean square estimation (WLMSE) problem can be stated as follows: Consider the scalar  defined as
defined as
 (4)
(4)
where , and
, and  is the complex conjugate of
is the complex conjugate of . Then, the objective of the problem is to find parameters
. Then, the objective of the problem is to find parameters  that minimize the estimation error
that minimize the estimation error  .
.
Picinbono et al. gave a theoretical foundation for the complex-valued WLMSE described above: it was proved that the estimation error obtained using the complexvalued WLMSE method is smaller than that obtained using the usual complex-valued LMSE method:  where the equality holds only in exceptional cases [1].
where the equality holds only in exceptional cases [1].
Figures 1 and 2 demonstrate the effectiveness of complex-valued widely linear estimation. Samples of complex-valued random variable x and y are axisymmetric about the broken line: the white circle, the black circle, and the christcross in Figure 1 correspond to the white circle, the black circle, and the christcross in Figure 2, respectively, and the three marks in Figure 1 and the three marks in Figure 2 are all axisymmetric about the broken line. It is therefore difficult to estimate the three samples in Figure 1 by performing rotation, reduction, or expansion of the three samples in Figure 2 about the origin. Nevertheless, inversion of the samples about the real axis, i.e., assuming it as the samples of conjugate complex-valued random variable, allows to be estimated by rotation, reduction, and expansion about the origin. This is an intuitive explanation that the complex-valued widely linear estimation is superior to the conventional linear estimation method.

Figure 1. Three samples of a complex-valued random variable x.

Figure 2. Three samples of a complex-valued random variable y.
2.2. The Quaternion-Valued WL Model
The quaternion-valued WL model is a natural extension of the complex-valued WL model described in Section 2.1. Let  be a scalar quaternion-valued random variable to be estimated in terms of an observation that is a quaternion-valued random vector
be a scalar quaternion-valued random variable to be estimated in terms of an observation that is a quaternion-valued random vector . That is, y is a true value and
. That is, y is a true value and 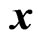 is an observed value.
is an observed value.
In quaternion-valued linear mean square estimation (LMSE), the problem is to find an estimate written as
 (5)
(5)
where , N is a natural number, and H represents the quaternionic conjugation and transposition.
, N is a natural number, and H represents the quaternionic conjugation and transposition.
The quaternion-valued widely linear mean square estimation (WLMSE) problem can be stated as follows: Consider the scalar 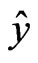 defined as
defined as
 (6)
(6)
where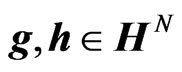 , N is a natural number, H represents the quaternionic conjugation and transposition, and
, N is a natural number, H represents the quaternionic conjugation and transposition, and  is the quaternionic conjugate of
is the quaternionic conjugate of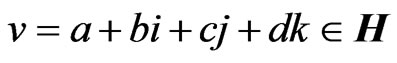 . Then, the objective of the problem is to find parameters
. Then, the objective of the problem is to find parameters  that minimize
that minimize  .
.
Took and Mandic derived an augmented quaternion least mean squares (AQLMS) algorithm for quaternion valued adaptive filters based on the quaternion-valued WL model, and confirmed its effectiveness via computer simulations [5]. Actually, the experimental results on the Lorenz attractor, real-world wind forecasting, and data fusion via quaternion spaces support the approach. Consequently, computer simulations proved that the quarternion-valued WL estimation method is superior to the usual quaternion-valued linear estimation method.
Moreover, the three perpendicular quaternion involutions can be introduced into the quaternion-valued WLMSE, which are given by
 (7)
(7)
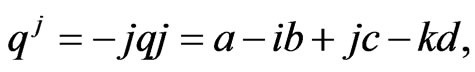 (8)
(8)
 (9)
(9)
where  [10-12]. The quarternion-valued WLMSE using (6) is an initial insight. However, in order to achieve the complete description of the second order statistics in
[10-12]. The quarternion-valued WLMSE using (6) is an initial insight. However, in order to achieve the complete description of the second order statistics in , we need to consider the involutions ((7)-(9)). Actually, the quaternion-valued widely linear mean square estimation (WLMSE) problem using the involutions has been formulated as follows [12]: Consider the scalar
, we need to consider the involutions ((7)-(9)). Actually, the quaternion-valued widely linear mean square estimation (WLMSE) problem using the involutions has been formulated as follows [12]: Consider the scalar 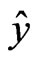 defined as
defined as
 (10)
(10)
where . Then, the objective of the problem is to find parameters
. Then, the objective of the problem is to find parameters  that minimize
that minimize .
.
However, no theoretical proof for the superiority of the quaternion-valued WL estimation method on estimation errors has been given to date, as it has been for the complex-valued WL estimation method. In the complexvalued setting, Picinbono et al. proved that the estimation error obtained with the complex-valued WLMSE is smaller than the error obtained using the complex-valued LMSE [1].
3. A Theoretical Foundation of the Quaternion-Valued WL Model
In this section, we show the superiority of the quarternion-valued WLMSE method. The main result is as follows: the estimation error obtained using the quarternionvalued WL estimation method based on (6) is smaller than that obtained using the usual quarternion-valued linear estimation method, except in rare cases. The result is obtainable in the same manner described by [1]. However, the noncommutativity of the quaternion products must be considered during the analysis ( for any
for any ).
).
Define

Therein, X is a set of scalar quaternion-valued random variables that constitutes a linear space, and which becomes a Hilbert subspace of the one-dimensional quarternion-valued Hilbert space 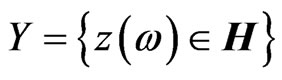 with the scalar product
with the scalar product . Then, for a true value
. Then, for a true value , an observed value
, an observed value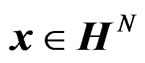 , and the estimate
, and the estimate , the following equations hold:
, the following equations hold:
 (12)
(12)
 (13)
(13)
where  means that all the components of
means that all the components of  are orthogonal to u with the scalar product
are orthogonal to u with the scalar product 
 . From (12) and (13), we obtain
. From (12) and (13), we obtain
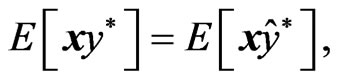 (14)
(14)
 (15)
(15)
Consequently, from (6), (14), (15), the following equations hold (see the appendices for the detail of the derivation):
 (16)
(16)
 (17)
(17)
where 



 Equations (16) and (17) yield
Equations (16) and (17) yield
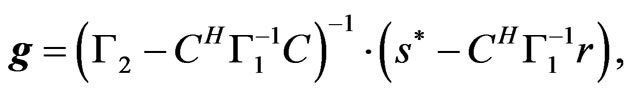 (18)
(18)
 (19)
(19)
where we assume that 
 and
and  exist (see the appendices for the detail of the derivation). Then, the estimation error
exist (see the appendices for the detail of the derivation). Then, the estimation error  is calculated from (6), (16), and (17) as follows:
is calculated from (6), (16), and (17) as follows:
 (20)
(20)
The estimation error  in the quaternion-valued LMSE can be obtained using (5) as shown below.
in the quaternion-valued LMSE can be obtained using (5) as shown below.
 (21)
(21)
Then, from (16) and (18), (20), (21), the quantity  can be expressed as
can be expressed as
 (22)
(22)
which is the difference between the estimation error of the quaternion-valued LMSE and that of the quarternion-valued WLMSE. Equation (22) is nonnegative because the matrix  is positive-semidefinite (see the appendices for the proof). Furthermore, (22) is equal to zero only when one of the following conditions holds:
is positive-semidefinite (see the appendices for the proof). Furthermore, (22) is equal to zero only when one of the following conditions holds:
 (23)
(23)
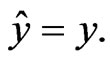 (24)
(24)
Equation (23) is an exceptional case, and (24) means that the true value y can be estimated with probability of one, which is a rare case.
4. Discussions
In the previous section, a theoretical foundation of the quaternion-valued WL model based on (6) is given, which guarantees the superiority of the quaternion-valued WLMSE method. It is difficult to analyze the quaternion-value WLMSE method using (7)-(9) which contains all the necessary second order statistical information because the process of the analysis is very complicated due to the three involutions if we adopt the way of proof used in [1]. To solve the problem, another approach would be needed.
5. Conclusion
We have presented a theoretical foundation for the quaternion-valued WL estimation method. It was proved that the estimation error obtained using the quaternion-valued WL estimation method is smaller than that obtained using the usual quaternion-valued linear estimation method, except in rare cases. In our future studies, we will proceed with analyses of the WL estimation based on the Clifford algebra [13].
6. Acknowledgements
The author extends special thanks to Prof. B. Picinbono, the Laboratoire des Signaux et Systèmes, Supélec, Gifsur Yvette, France for help in resolving several questions, and the anonymous reviewers for valuable comments.
Appendices
Proof of Equations (16) and (17):
 (25)
(25)
So, we obtain
 (26)
(26)
Similarly, from Equation (13) we obtain
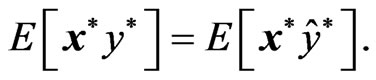 (27)
(27)
Here,
 (28)
(28)
Note that 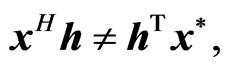
 due to the noncommutativity of the quaternion products. Thus, from Equations (26) and (28),
due to the noncommutativity of the quaternion products. Thus, from Equations (26) and (28),
 (29)
(29)
which means that Equation (16) holds.
It also follows from Equations (27) and (28),
 (30)
(30)
The left hand side of Equation (30) is given as:
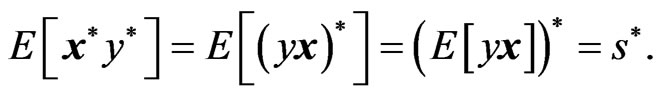 (31)
(31)
Equations (30) and (31) complete the proof of Equation (17). ■
Proof of Equations (18) and (19):
From Equation (16), we obtain
 (32)
(32)
Equations (17) and (34) lead Equation (18). And also, from Equation (17), we obtain
 (33)
(33)
Equations (16) and (33) lead Equation (19). ■
Proof that the matrix 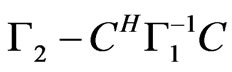 is positivesemidefinite:
is positivesemidefinite:
Consider the following problem. Let 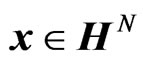 and
and  be two random vectors such that
be two random vectors such that . The problem is to estimate linearly
. The problem is to estimate linearly  in terms of
in terms of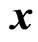 , which means to find the N-dimensional quaternion valued matrix M such that
, which means to find the N-dimensional quaternion valued matrix M such that 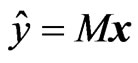 is the best linear mean square (LMS) estimation of
is the best linear mean square (LMS) estimation of  in terms of
in terms of . The solution is given by the orthogonality principle saying that
. The solution is given by the orthogonality principle saying that  is orthogonal to the observation
is orthogonal to the observation  or
or 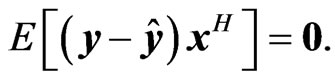 That is,
That is,  where
where  and
and  . Assuming that
. Assuming that  exists, the solution is obviously
exists, the solution is obviously
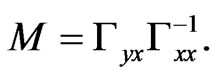 (34)
(34)
Here, the matrix  is positivesemidefinite because for any
is positivesemidefinite because for any  such that
such that ,
,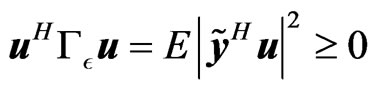 . Using the definition
. Using the definition  and Equation (34) yield by simple algebra
and Equation (34) yield by simple algebra
 (35)
(35)
where  and
and .
.
Suppose now that . This yields
. This yields ,
,  ,
, 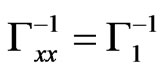 and
and . Thus we obtain from Equation (35)
. Thus we obtain from Equation (35)
 (36)
(36)
As seen above, since  is positive-semidefinite, the right-hand side of Equation (36) is positive-semidefinite. ■
is positive-semidefinite, the right-hand side of Equation (36) is positive-semidefinite. ■