Quantum of the Magnetic Flux Characteristic forExperiments Performed on the Integer and Fractional Quantum Hall Effects ()
1. Introduction
Experimentally the discovery of the integer quantum Hall effect for the planar metallic-like crystals led to a result that the magnetic flux in such crystals is quantized with a very high accuracy by the values equal to
 (1)
(1)
determined from the Bohr-Sommerfeld quantization condition imposed on the orbital motion of a charged particle in the magnetic field (see e.g. [1]). Equation (1) gives a tool in obtaining the effective charge e* of that particle. A well-known result for  in case of the superconducting systems is [2,3]
in case of the superconducting systems is [2,3]
 (2)
(2)
Result in (2) implies that the effective charge carried in superconductors is a double of the electron charge, i.e.
 (3)
(3)
leading to an idea of the coupled electron pairs as the particles providing the electric current. More recently, a source of interest in  is raised by the fractional quantum Hall effect in which e* is considered as a fraction of
is raised by the fractional quantum Hall effect in which e* is considered as a fraction of  [4,5].
[4,5].
Our aim is to examine the 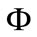 in the quantum Hall effect beginning with the integer form of that effect:
in the quantum Hall effect beginning with the integer form of that effect:
 (4)
(4)
In Section 2, we show that the flux in (2) leads to the result presented in (4).
The formula of (4) is characteristic for the magnetoresistance of the integer quantum Hall effect, but also the magnetoresistance values
 (5)
(5)
specific for the fractional quantum Hall effect can be obtained [6-8]. Here the coefficient  is a simple fraction like
is a simple fraction like
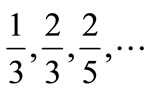 (6)
(6)
A predominant feature of (6) is that any fraction has an odd integer number in its denominator.
As a rule the experiments leading to (4)-(6) were performed for some definite value of the magnetic field induction , or some plateau of these values. The
, or some plateau of these values. The  directed, say, parallelly to the axis
directed, say, parallelly to the axis  were assumed to be normal to the planar crystalline samples, so each experiment concerned a specific concentration
were assumed to be normal to the planar crystalline samples, so each experiment concerned a specific concentration 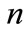 of the electric carriers (electrons or holes) present in the sample plane.
of the electric carriers (electrons or holes) present in the sample plane.
Theoretically an approach to the quanta of (4) and (5) can be attained by calculating the magnetoresistance of a metal on the basis of a single free-electron like band of states [9-12]. Here the off-diagonal Hall resistance and diagonal resistance can be considered.The change  of the diagonal tensor component of the electric resistance
of the diagonal tensor component of the electric resistance  upon the action of the magnetic field is represented by the formula
upon the action of the magnetic field is represented by the formula
 (7)
(7)
Expression (7) holds because [9-12]
 (8)
(8)
and
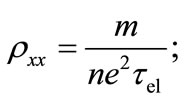 (9)
(9)
see e.g. [13]. The  is the relaxation time for the electric resistance,
is the relaxation time for the electric resistance,
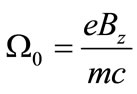 (10)
(10)
is the electron gyration frequency in the field ,
,
 (11)
(11)
is the relaxation time due to the presence of the magnetic field,
 (12)
(12)
is a constant number entering formula (11) obtained on the basis of a quantum-mechanical calculation [9,11]. Because of (12) we obtain from (7):
 (13)
(13)
Expression (13) is equal to the double absolute value of the Hall resistance:
 (14)
(14)
The formula (14) remains unmodified in comparison with the well-known result obtained before (see e.g. [14]) without any use of . The lack of change is due to the property of the tensor which is representing the modification of the electric resistance given by the presence of the magnetic field: the tensor contains
. The lack of change is due to the property of the tensor which is representing the modification of the electric resistance given by the presence of the magnetic field: the tensor contains  both in the numerator and denominator of the off-diagonal matrix element representing the Hall effect, so [9,11]:
both in the numerator and denominator of the off-diagonal matrix element representing the Hall effect, so [9,11]:
 (15)
(15)
on condition we note that
 (16)
(16)
because of the formula (11) for . In the last step of (15), a conventional notation for the Hall resistance is applied. A similar property of independence on the relaxation time has the Hall matrix element of the original tensor for the magnetoresistance [13], but this concerns the relaxation time
. In the last step of (15), a conventional notation for the Hall resistance is applied. A similar property of independence on the relaxation time has the Hall matrix element of the original tensor for the magnetoresistance [13], but this concerns the relaxation time 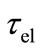 due to the electric field and not
due to the electric field and not  for the magnetic field.
for the magnetic field.
The plateaus of magnetoresistance which signalize the presence of the integer quantum Hall effect refer to some definite experimental values of  and
and . Because of the ratio
. Because of the ratio
 (17)
(17)
entering (13), (14) and (15) our aim is to examine (17) in some detail.
2. Electron Population of the Landau Levels Provides Us with the Quanta of Magnetoresistance and Those of the Magnetic Flux
For the magnetic field  strong enough to collect all electrons on a single Landau level, the number of electron orbits occupying that level is equal to [14]
strong enough to collect all electrons on a single Landau level, the number of electron orbits occupying that level is equal to [14]
 (18)
(18)
In the second step of (18) the spin degeneracy of the orbits is explicitly taken into account,  is the edge of the square occupied by the planar metallic-like sample. In a situation represented by (18) the ratio (17) becomes:
is the edge of the square occupied by the planar metallic-like sample. In a situation represented by (18) the ratio (17) becomes:
 (19)
(19)
which is identical with (2); see also [13]. The ratio of (19) can be substituted to the formulae (13) and (14)-(15). In the first case the result
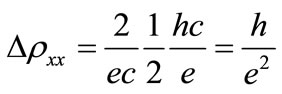 (20)
(20)
is identical to (4); in the second case we obtain
 (21)
(21)
which is a half of the diagonal magnetoresistance in (20). Henceforth we consider (21) as a quantum of the Hall resistance given by a fully occupied single Landau level.
An application of the formalism can be done for a textbook example of the experimental presentations of 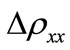 and
and 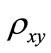 for which, however, no carrier concentration
for which, however, no carrier concentration  for the examined two-dimensional system has been given [15]. The obtacle can be avoided when, in the first step, the equivalence of (14) and (21) for a completely filled Landau level is taken into account. In this case
for the examined two-dimensional system has been given [15]. The obtacle can be avoided when, in the first step, the equivalence of (14) and (21) for a completely filled Landau level is taken into account. In this case
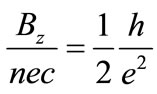 (22)
(22)
so
 (23)
(23)
Experimentally the quantum Hall plateau corresponding to the Hall resistance (21) begins at Bz = 4T = 4 × 104 gauss. Therefore from (23)
 (24)
(24)
This  provides us with the ratio
provides us with the ratio
 (25)
(25)
being in a perfect agreeement with (19); see (2).
The end point of the plateau is at 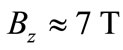 and this gives the magnetic flux per electron
and this gives the magnetic flux per electron
 (26)
(26)
therefore dispersion of 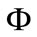 for a given
for a given  can be large.
can be large.
3. Calculation of the Magnetic Flux from the Experimental Data for Bz and n
Rather surprisingly the ratio (17) leading to the quantum (21) of the Hall resistance seems to be not very extensively examined on the experimental basis. In Table 1 we present a list of the values of ,
,  and ratios
and ratios  associated with the plateaus of the quantum Hall resistance observed in different compounds; see [16-41]. This study shows that the experimental data for
associated with the plateaus of the quantum Hall resistance observed in different compounds; see [16-41]. This study shows that the experimental data for  approach the quantum value obtained for (2) and in (19). The dispersion of the data in Table 1 is not much diffe
approach the quantum value obtained for (2) and in (19). The dispersion of the data in Table 1 is not much diffe
rent from that observed in superconducting cyllinders [42].
For some experiments the ratio

[see (20) and (21)] could find its confirmation in the observed data obtained for almost the same induction value  [29,39].
[29,39].
4. Discussion: Reference to the Fractional Quantum Hall Effect
A natural extension of the problem of  considered for the integer quantum Hall effect concerns the fractional version of that effect. In this case the orbit population (18) a Landau level is changed by a factor of
considered for the integer quantum Hall effect concerns the fractional version of that effect. In this case the orbit population (18) a Landau level is changed by a factor of  giving the relation
giving the relation
 (27)
(27)
Evidently in this case we obtain the formula
 (28)
(28)
instead of (19), so the expected magnetic flux per one carrier unit becomes
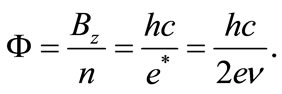 (29)
(29)
Here it should be noted that only a substitution of 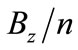 from the formula (29) into (13) can provide us with the result
from the formula (29) into (13) can provide us with the result
 (30)
(30)
in accordance with experiment; see (5). Since we have mainly , the formula (29) implies the presence of the carriers having their charge
, the formula (29) implies the presence of the carriers having their charge
 (31)
(31)
However, an alternative approach to  can be obtained on the basis of the assumption that no
can be obtained on the basis of the assumption that no  are present but the number of the filled Landau levels which take part in experiment is increased from 1 to
are present but the number of the filled Landau levels which take part in experiment is increased from 1 to ; for the sake of simplicity we assume that
; for the sake of simplicity we assume that 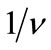 is an integer number [43]. An increase of the filled levels number can be attained by a corresponding change of
is an integer number [43]. An increase of the filled levels number can be attained by a corresponding change of  for a single filled level to
for a single filled level to 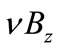 which makes on each level a decrease of the original concentration
which makes on each level a decrease of the original concentration 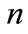 to
to . In effect we obtain
. In effect we obtain
 (32)
(32)
for each component level which is the same ratio as for a single filled Landau level; see (19). In result of that situation only a sum of  in (32) performed over all occupied
in (32) performed over all occupied 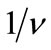 levels can give the magnetic flux equal to that presented in (29).
levels can give the magnetic flux equal to that presented in (29).
Since 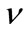 is a constant and
is a constant and  is a discrete integer parameter, the behaviour of the magnetic flux in the quantum Hall effects indicates that
is a discrete integer parameter, the behaviour of the magnetic flux in the quantum Hall effects indicates that  in (29) should be a quantized parameter. The quantum of
in (29) should be a quantized parameter. The quantum of 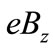 is expected to be the smallest experimentally acceptable number of
is expected to be the smallest experimentally acceptable number of
 (33)
(33)
obtained on condition we assume that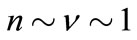 .
.
By considering 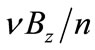 as the magnetic flux
as the magnetic flux  it can be noted that the following relation exists between
it can be noted that the following relation exists between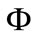 , the energy
, the energy 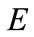 of the quantum state and current
of the quantum state and current  [44]:
[44]:
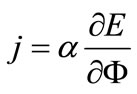 (34)
(34)
where  is a constant. In fact, for a one electron energy on the Landau level obtained by the change of
is a constant. In fact, for a one electron energy on the Landau level obtained by the change of  to
to , viz.
, viz.
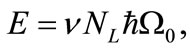 (35)
(35)
we obtain from (34) the relation:
 (36)
(36)
which gives
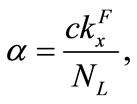 (37)
(37)
representing a number independent of ,
, 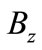 and
and . The
. The 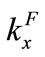 is a component of the Fermi wave vector,
is a component of the Fermi wave vector, 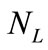 is the index of the Landau level.
is the index of the Landau level.
5. Examples of the Magnetic Flux Calculated for the Fractional Quantum Hall Effect
In Tables 2-4, we present several examples of the quanta of the magnetic flux obtained when the measured data for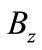 , n and
, n and  entering the experiments on the fractional quantum Hall effect are substituted on the left-hand side of the formula (28). These quanta approach evidently the result given in (2), as it could be expected on the basis of (28). Similar quanta of Table 1 are, in average, more distant from the result in (2) because the very existence of plateaus of
entering the experiments on the fractional quantum Hall effect are substituted on the left-hand side of the formula (28). These quanta approach evidently the result given in (2), as it could be expected on the basis of (28). Similar quanta of Table 1 are, in average, more distant from the result in (2) because the very existence of plateaus of  in the integer quantum Hall effect makes the calculations of
in the integer quantum Hall effect makes the calculations of  more uncertain than in
more uncertain than in

Table 4. The magnetic flux calculated from the experimental data for , Bz and n given in the diagrams of [45].
, Bz and n given in the diagrams of [45].
case of the fractional quantum Hall effect.