Conventional and Enhanced Canonical Quantizations, Application to Some Simple Manifolds ()
1. Introduction
Our understanding of the nature through the physics has significantly developed since the advent of the quantum theory and its quantization techniques known as conventional quantization methods, which are essentially the canonical and the path integral quantizations. However, we are far from the end of the story, since numerous questions that are usually called “difficult problems” still remain to be solved.
It’s well known that without geometrical and topological considerations, it is difficult to consistently quantize the physical models [1-3]. It’s thus indispensable to pay a particular attention to the geometry when one studies physical systems. Moreover, the relationship between interaction and topology is more and more clear [4,5]. Then, in the search of innovative methods of quantization, J. R. Klauder has proposed, by taking into account the topological and geometrical concepts, a new approach of quantization based on a subclass of quantum states, the coherent states [6,7]. These quantum states express themselves by means of classical phase space variables and thus constitute suitable mediators to realize the link between classical and quantum theories. Indeed, the canonical quantization rules associate to a given classical phase space variable, an operator belonging to a suitable Hilbert space, which must be at least hermitian or symmetric in mathematical parlance. The self-adjoint character is crucial for the observables and von Neumann was the first to put this foward, by proposing a formalism for systematically constructing self-adjoint operators by extensions [8]. However, after such conventional quantization, the quantum action which leads to the Schrödinger equation has nothing to do with the classical action which provides the Euler-Lagrange equations of movement and one thinks that it’s one of the causes of inadequacy of conventional quantization procedures.
The enhanced quantization procedure provides a new interpretation of the very process of quantization that encompasses the well-know conventional quantization formalism and offers additional features as well. Obviously, this enhanced quantization formalism aims at improving quantization techniques by means of simple mathematical tools associated to well-established physical concepts like the principle action at quantum level. It is to be noted that usually, this principle of the action is used in classical theory to determine the Euler-Lagrange equations of motion. Then, these classical variables are promoted to the rank of operators acting on appropriate Hilbert spaces. In the enhanced quantum process, once the domains of self-adjoint operators are well set, one constructs the quantum action that is restricted to the state spaces that are at reach of the real world observer.
In this paper, taking into account the canonical quantization procedure as well as the new method of quantization introduced in Ref. [6] and in the framework of the most general representations of the Heisenberg algebra, we solve two simple models: the particle on the segment and the particle on the two-sphere, with the intention of putting in evidence of the implications of these approaches. As far as the particle on the line is concerned, we first study the case of the free movement and then we consider the presence of a delta-point interaction located at the middle of the segment, making non simply-connected the associated manifold. Concerning the two-sphere model, only the conventional procedure is given by considering the topological (which is trivial here) and the geometrical implications of the Heisenberg algebra. Enhanced quantization on the two-sphere requires the construction of the canonical coherent states on this manifold and is postponed for later.
The paper is organized as follows. In the next section, we point out the topological classification stemming from the representations of the Heisenberg algebra on an arbitrary manifold. In Section 3, we briefly give the importance of representations of the Heisenberg algebra in quantization procedures. In Section 4, we develop the procedures of conventional and enhanced quantizations on the finite non-punctured and punctured lines. The spectrum of the free particle on the two-sphere is given in Section 5. Section 6 encloses the work with some discussions and outlooks.
2. Basics and Consequences of Representations of the Heisenberg Algebra
Let us sketch the results and then recall the main information stemming from the representations of the Heisenberg algebra over an arbitrary manifold: the topological classification of these representations. The results given hereafter are obtained from a purely algebraic analysis which is absolutely independent of the specific details and dynamics of a given physical system as defined through its classical Lagragian (see Ref. [1] for a detailed development); it solely relies on the existence of canonically conjugate pairs of phase space degrees of freedom.
The space of quantum states is assumed to be equipped with an hermitian inner product  and spanned by position eigenstates
and spanned by position eigenstates  of the position operators
of the position operators 
 for all the possible values of
for all the possible values of  as local coordinates over the manifold M so that
as local coordinates over the manifold M so that  . The general configuration space covariant representation of the Heisenberg algebra determined by the following relations,
. The general configuration space covariant representation of the Heisenberg algebra determined by the following relations,
 (1)
(1)
is constructed in terms of two structures defined over , namely its metric structure
, namely its metric structure  as well as a flat
as well as a flat  gauge connection
gauge connection .
.
The metric structure is required to specify the diffeomorphic covariant normalization of the position eigenstates,
 (2)
(2)
with
 (3)
(3)
 and
and  being the configuration space wave functions of the states
being the configuration space wave functions of the states  and
and . This parametrization of the inner product of the position eigenstate basis
. This parametrization of the inner product of the position eigenstate basis  comes about, since the consideration of the position matrix elements
comes about, since the consideration of the position matrix elements  of the coordinate operators
of the coordinate operators  as well as their hermiticity property
as well as their hermiticity property  implies the equations
implies the equations 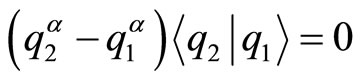 , while the choice of absolute normalization in terms of
, while the choice of absolute normalization in terms of  is made in so that configuration space wave functions
is made in so that configuration space wave functions  of states transform as scalar fields under diffeomorphisms in
of states transform as scalar fields under diffeomorphisms in .
.
The  gauge connection structure
gauge connection structure 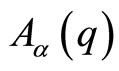 is related to the arbitrariness in the choice of phase for the position eigenstates
is related to the arbitrariness in the choice of phase for the position eigenstates , which is not yet fixed by the choice of normalization of their inner products
, which is not yet fixed by the choice of normalization of their inner products . In fact, a local change in this phase implies a local
. In fact, a local change in this phase implies a local  gauge transformation of
gauge transformation of ,
,
 (4)
(4)
The further restriction for the  connection to be flat, namely
connection to be flat, namely , stems from the condition that all momentum operators
, stems from the condition that all momentum operators 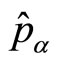 commute with one another, namely
commute with one another, namely . Indeed, the configuration space representation of these operators is constructed with the parametrization of their position matrix elements as
. Indeed, the configuration space representation of these operators is constructed with the parametrization of their position matrix elements as
 (5)
(5)
leading to the following representation in terms of configuration space wave functions of states and thus involving the  gauge covariant derivative,
gauge covariant derivative,
 (6)
(6)
Likewise, the configuration space representation of the position operators  is issued by
is issued by
 (7)
(7)
Consequently, by considering how the vector field  transforms under any local change (0.4) of phase in the position eigenstates
transforms under any local change (0.4) of phase in the position eigenstates , one finds that this field is actually a
, one finds that this field is actually a  gauge connection related to arbitrariness, whose field strength must be identically vanishing
gauge connection related to arbitrariness, whose field strength must be identically vanishing  so that the last set of commutation relations
so that the last set of commutation relations  defining the Heisenberg algebra will also be obeyed.
defining the Heisenberg algebra will also be obeyed.
In conclusion, all inequivalent unitary representations of the Heisenberg algebra are labeled by all possible gauge equivalence classes of flat  connections over the configuration manifold M. These inequivalent representations are thus in one-to-one correspondence with the
connections over the configuration manifold M. These inequivalent representations are thus in one-to-one correspondence with the  holonomies for all non contractible cycles in M. In the case of a simply-connected manifold, none of these cycles exist, and the Heisenberg algebra thus admits only a single covariant representation over M, which is associated to the trivial choice for a flat connection,
holonomies for all non contractible cycles in M. In the case of a simply-connected manifold, none of these cycles exist, and the Heisenberg algebra thus admits only a single covariant representation over M, which is associated to the trivial choice for a flat connection, . This result generalyzes to these kinds of curved manifolds, the well-known fact that over a flat Euclidean space, there only exists the usual von Neumann representation of the Heisenberg algebra. However, when the configuration space M is non simply-connected, including examples even as simple as a circle or a torus of arbitrary dimension, there exists an infinite number of inequivalent representations of the Heisenberg algebra, labeled by the
. This result generalyzes to these kinds of curved manifolds, the well-known fact that over a flat Euclidean space, there only exists the usual von Neumann representation of the Heisenberg algebra. However, when the configuration space M is non simply-connected, including examples even as simple as a circle or a torus of arbitrary dimension, there exists an infinite number of inequivalent representations of the Heisenberg algebra, labeled by the  holonomies for all non contractible cycles in M. This includes of course the possibility of vanishing holonomies for all cycles, a situation which then corresponds to the representation with
holonomies for all non contractible cycles in M. This includes of course the possibility of vanishing holonomies for all cycles, a situation which then corresponds to the representation with  up to the local arbitrariness in the phase of the position eigenstates
up to the local arbitrariness in the phase of the position eigenstates . When non vanishing, such
. When non vanishing, such  holonomies may be viewed as being associated to an AharonovBohm flux line threading the corresponding cycles in M. Clearly, even though the Heisenberg algebra is local as far as its characteristics are concerned, these results show that a consistent representation depends on the global topology structure of the configuration space manifold M as measured through its
holonomies may be viewed as being associated to an AharonovBohm flux line threading the corresponding cycles in M. Clearly, even though the Heisenberg algebra is local as far as its characteristics are concerned, these results show that a consistent representation depends on the global topology structure of the configuration space manifold M as measured through its  holonomies.
holonomies.
3. The Representations of the Heisenberg Algebra in Quantization Procedures
3.1. Conventional Quantization
Conventional quantization is the one to have been experimented since the very beginning of the modern quantization procedure. It links to classical phase space variables , quantum quantities which are required to be at least symmetric or straight out self-adjoint, denoted
, quantum quantities which are required to be at least symmetric or straight out self-adjoint, denoted  and belonging to specific Hilbert spaces. Dynamics in the classical space is expressed by means of the basic Poisson bracket1
and belonging to specific Hilbert spaces. Dynamics in the classical space is expressed by means of the basic Poisson bracket1  while at quantum level, the corresponding commutator is given by
while at quantum level, the corresponding commutator is given by .
.
The kinematical characterization of the quantized system given in the previous section still need to be completed with the specification of a quantum dynamics, namely a quantum Hamiltonian  in correspondence with the classical one, given by
in correspondence with the classical one, given by
 (8)
(8)
 being the phase space degrees of freedom conjugate to the local coordinates
being the phase space degrees of freedom conjugate to the local coordinates  through the usual canonical Poisson brackets.
through the usual canonical Poisson brackets.  is the mass of the particle. The only one possible choice for a diffeomorphic scalar quantum Hamiltonian is given by,
is the mass of the particle. The only one possible choice for a diffeomorphic scalar quantum Hamiltonian is given by,
 (9)
(9)
where the vector field  is given by the following representation
is given by the following representation
 (10)
(10)
Consequently, it’s important, taking into account the above topological classification, to pay a required attention to the character of the underlying manifolds to configuration spaces, theatre of physical phenomena. Finally, the quantum Hamiltonian which is the generator a the dynamics of the system admits the following configuration space representation, where we omit the hat over the quantum quantities,
 (11)
(11)
where the ordinary derivatives are replaced by U(1) covariant derivatives. Clearly, the presence of the topological quantum variable  shows that one must pay attention to the topological features of the manifold associated to the configuration space, for a given system.
shows that one must pay attention to the topological features of the manifold associated to the configuration space, for a given system.
3.2. Enhanced Quantization
Let’s now turn ourselves to the recently introduced enhanced canonical quantization2 procedure. We do not have the intention to give an exhaustive account on this specific and new method. We only want to sketch the ideas that span this quantization procedure and point out the place of the representations of the Heisenberg algebra in that quantization technique. For more details, the reader could consult the papers [6,7].
It aims at constructing a quantum action which will allow to consistently describe the system in the appropriate quantum space—a specific Hilbert space—as well as in the classical phase space. The ideal quantum space for this procedure is found to be the one spanned by the phase space coherent states which express themselves by means of conjugate quantum variables corresponding to the classical conjugate phase space degrees of freedom . Note that these variables are directly at the reach of a classical experimenter and then the corresponding quantum states are restricted to those that can be macroscopically created.
. Note that these variables are directly at the reach of a classical experimenter and then the corresponding quantum states are restricted to those that can be macroscopically created.
Taking into account the above, one also need to pay attention to the geometrical as well as the topological features of the considered manifold, since the general configuration space covariant representation of the momentum operator, given in the relation (6), is constructed in terms of a flat  gauge connection
gauge connection —a purely quantum degree of freedom—as well as the metric structure
—a purely quantum degree of freedom—as well as the metric structure  over this manifold.
over this manifold.
Finally, even if the topological degrees of freedom  are absent in the differential representations of the momenta and the Hamiltonians commonly encontered in the literature, this corresponds to the particular case of the trivial holonomy and is then included in the general case described above.
are absent in the differential representations of the momenta and the Hamiltonians commonly encontered in the literature, this corresponds to the particular case of the trivial holonomy and is then included in the general case described above.
4. Conventional and Enhanced Canonical Quantizations on the Line
4.1. Conventional Quantization on the Line
Let us concentrate our analysis on the case of a particle moving on a finite line represented by the interval . From the self-adjoint extensions point of view, it's the more general case; semi finite or infinite range domains being straightforward generalizations. Moreover, we shall include the situation in which the finite line is punctured at a spot standing for its middle. The physical interpretation of such model is the following: consider a quantum particle confined in a one-dimensional box submitted to a singular delta-point interaction localized at the center
. From the self-adjoint extensions point of view, it's the more general case; semi finite or infinite range domains being straightforward generalizations. Moreover, we shall include the situation in which the finite line is punctured at a spot standing for its middle. The physical interpretation of such model is the following: consider a quantum particle confined in a one-dimensional box submitted to a singular delta-point interaction localized at the center  if
if  and
and  if
if . The manifold linked to such a punctured line is no more simply-connected at the opposite of the non punctured line which is simply-connected. Consequently, we must consider the most general representations of operators
. The manifold linked to such a punctured line is no more simply-connected at the opposite of the non punctured line which is simply-connected. Consequently, we must consider the most general representations of operators  and
and  given by the relations (6) and (7).
given by the relations (6) and (7).
By exploiting the following property of the gauge field  on the line, where
on the line, where  is an a priori real parameter,
is an a priori real parameter,
 (12)
(12)
and taking into account the fact that  here, we get the following representation of the quantum momentum,
here, we get the following representation of the quantum momentum,
 (13)
(13)
while the spectrum of  is confined in the segment
is confined in the segment .
.
The property which is expressed by the relation (13) is interesting. It makes non explicit the presence of the gauge field  in the momentum and the hamiltonian operators
in the momentum and the hamiltonian operators  and
and , respectively. This gauge potential is represented by the useful quantum variable
, respectively. This gauge potential is represented by the useful quantum variable .
.
Let us continue our analysis by choosing the segment to be centered at the origin of the configuration space i.e. ,
,  , with
, with . Let's consider at quantum level the operators
. Let's consider at quantum level the operators  and
and  linked up to the classical phase space variables
linked up to the classical phase space variables  and
and  respectively, satisfying the commutation relation
respectively, satisfying the commutation relation . Moreover, these operators are required to be self-adjoint on the finite interval including its borders and the only possibility which is known to be safe to satisfy this requirement, is to extend these by the well-known means of the von Neumann self-adjoint extensions formalism. Consequently, let’s extend the momentum operator
. Moreover, these operators are required to be self-adjoint on the finite interval including its borders and the only possibility which is known to be safe to satisfy this requirement, is to extend these by the well-known means of the von Neumann self-adjoint extensions formalism. Consequently, let’s extend the momentum operator . It amounts firstly to find a domain
. It amounts firstly to find a domain  in which the operator
in which the operator  is symmetric and closed; secondly to determine its adjoint
is symmetric and closed; secondly to determine its adjoint  with the intention of calculating the deficiency indices of
with the intention of calculating the deficiency indices of ; and finally to characterize, if they do exist, the self-adjoint extensions of
; and finally to characterize, if they do exist, the self-adjoint extensions of .
.
 is densely defined, since the closure of
is densely defined, since the closure of  reads
reads , and is symmetric in the following domain
, and is symmetric in the following domain
 (14)
(14)
The adjoint of this momentum operator is formally given by . To determine the deficiency indice numbers, we must count the number of linearly independent solutions, belonging to
. To determine the deficiency indice numbers, we must count the number of linearly independent solutions, belonging to , of the following equation
, of the following equation
 (15)
(15)
where the quantity  is introduced for dimensional regularization. The solutions are readily found to be
is introduced for dimensional regularization. The solutions are readily found to be
 leading to
leading to .
.
Characterize the self-adjoint extensions boils down to determine the boundary conditions which make the operator  self-adjoint everywhere on the punctured segment, including its border. We know from the von Neumann’s theory [8-10] that self-adjoint extensions of
self-adjoint everywhere on the punctured segment, including its border. We know from the von Neumann’s theory [8-10] that self-adjoint extensions of  are parametrized by a
are parametrized by a  matrix, i.e. by a phase factor
matrix, i.e. by a phase factor ,
, . We have to enlarge
. We have to enlarge  and decrease
and decrease  so that they coincide. By denoting
so that they coincide. By denoting  the extended momentum operator, we get
the extended momentum operator, we get
 (16)
(16)
By considering the above, we readily find the spectrum of the momentum operator on the punctured segment where  is a non-vanishing constant:
is a non-vanishing constant:
 (17)
(17)
Note that in the absence of the point interaction, the purely topological quantum variable disappears, since the manifold associated to the segment is simply-connected. Consequently,  and the self-adjoint boundary condition reduces to
and the self-adjoint boundary condition reduces to  leading to the P-spectrum issued by
leading to the P-spectrum issued by 

 .
.
Let us deal with the determination of the spectrum of the Hamiltonian. The deficiency indices of this operator are finite and equal (2,2). All self-adjoint extensions of the hamiltonian are characterized by four parameters.
We pay attention to the parity symmetry whose the singular point interaction localized at xo = 0 must be respectful. This parity expresses as [11]: , where u stands for the space coordinate. It reduces the number of parameters of self-adjoint extensions. Consequently, the self-adjoint boundary conditions reduce to the following, with the condition
, where u stands for the space coordinate. It reduces the number of parameters of self-adjoint extensions. Consequently, the self-adjoint boundary conditions reduce to the following, with the condition 
 .
.
 (18)
(18)
In this notation, the wave functions  and
and  defined in
defined in  and
and  respectively, are given by the following expressions,
respectively, are given by the following expressions,
 (19)
(19)
The energy levels of the system are given by
 (20)
(20)
Finally, if we didn’t pay attention to the parity symmetry, the energy levels would be given by

and the self-adjoint boundary conditions would be written as follows, with 
 .
.
 (21)
(21)
The resulting spectrum in the absence of the point interaction (which means that the particle moves freely from  to
to ) is rather straightforward.
) is rather straightforward.
4.2. Enhanced Canonical Quantizations for the Free Particle on the Line
4.2.1. Coherent States-Restricted Quantum Action Functional
Let us define the eigenstates  and
and  related to the operators
related to the operators  and
and  respectively, satisfying the relations
respectively, satisfying the relations
 (22)
(22)
We have
 (23)
(23)
The canonical coherent states are introduced by the means of the following unitary operators
 (24)
(24)
These coherent states are given by the following relation [12],
 (25)
(25)
where  is a ket standing for the fiducial state. A straightforward computation shows that the states
is a ket standing for the fiducial state. A straightforward computation shows that the states  satisfy the following normalization and the unit resolution conditions
satisfy the following normalization and the unit resolution conditions
 (26)
(26)
 (27)
(27)
The set of states  provides a family of overcomplete normalized states and stands for the set of phase space coherent states.
provides a family of overcomplete normalized states and stands for the set of phase space coherent states.
We are now able to discuss the dynamics in the space spanned by these coherent states. Let us introduce the quantum generator that constitutes the Hamiltonian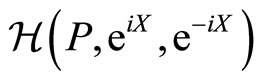 . Let’s also consider the quantum action restricted to the coherent states
. Let’s also consider the quantum action restricted to the coherent states  instead of arbitrary states
instead of arbitrary states , defined as follows
, defined as follows
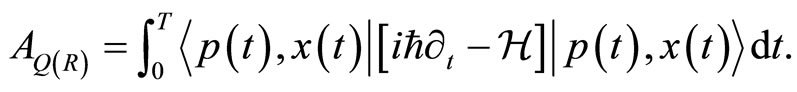 (28)
(28)
We chose a class of fiducial states satisfying  and
and , so that we have
, so that we have
 (29)
(29)
The restricted quantum action becomes
 (30)
(30)
where . In this equation,
. In this equation,  is the classical Hamiltonian. The quantum parameter
is the classical Hamiltonian. The quantum parameter  induces a surface term
induces a surface term  in
in  which does not have any influence on the classical equations of motion. Hence we may write
which does not have any influence on the classical equations of motion. Hence we may write
 (31)
(31)
The evaluation of the diagonal elements of the matrix representation of  in the coherent states basis, setting
in the coherent states basis, setting , gives
, gives
 (32)
(32)
where the constants  and
and  are included in
are included in . We deduce that
. We deduce that
 (33)
(33)
with the canonical following change of the momentum, 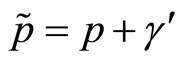 we finally obtain
we finally obtain
 (34)
(34)
Let us give the concrete example of the one-dimensional harmonic oscillator of mass . The restricted quantum action is the following,
. The restricted quantum action is the following,  being the Fock vacuum state,
being the Fock vacuum state,
 (35)
(35)
By the means of the Baker-Campbel-Hausdorf formula and after some lines of computation, one obtains
 (36)
(36)
which gives
 (37)
(37)
4.2.2. The Induced Coherent Phase Space Geometry
The geometrical characterization of the constructed coherent states phase space is encoded by the following metric [13]
 (38)
(38)
where , and
, and
 (39)
(39)
 (40)
(40)
 (41)
(41)
where  and
and  are constants. Finally, we get
are constants. Finally, we get
 (42)
(42)
and by setting
 (43)
(43)
the metric reads
 (44)
(44)
The metric  describes the geometry of an infinite range strip of width
describes the geometry of an infinite range strip of width  and can serve in a classical description as well as in a quantum description.
and can serve in a classical description as well as in a quantum description.
4.3. Enhanced Canonical Quantizations on the Line with a Point Interaction
Let us now apply the above formalism to a particle moving on a segment with a δ-point interaction at the right middle  of this finite line. The corresponding manifold which is non simply-connected is the one associated to the punctured line.
of this finite line. The corresponding manifold which is non simply-connected is the one associated to the punctured line.
The canonical coherent states are given by
 (45)
(45)
By choosing the fiducial orthonormilized states  such as
such as  and
and 
 , the coherent states quantum action restricted to the phase space is given by the following expression,
, the coherent states quantum action restricted to the phase space is given by the following expression,
 (46)
(46)
with the notation
 (47)
(47)
We recognize in the relation (0.46) the classical action  , while the surface term
, while the surface term  is characterized by the nontrivial holonomy parameter
is characterized by the nontrivial holonomy parameter  as well as the self-adjoint parameter
as well as the self-adjoint parameter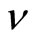 . We consequently have the expected relation which expresses the coexistence of classical as well as the quantum description of the considered system,
. We consequently have the expected relation which expresses the coexistence of classical as well as the quantum description of the considered system,
 (48)
(48)
The induced coherent phase space geometry is provided by the metric element
 (49)
(49)
After some lines of computations, one finds
 (50)
(50)
with the notations  and
and  . A redefinition of coordinates gives the metric on the subspace of coherent states,
. A redefinition of coordinates gives the metric on the subspace of coherent states,
 (51)
(51)
5. Eigenstates of a Free Particle on the Two-Sphere
As the simplest next example, in the same spirit, let us now consider the case of a particle moving freely on the two-sphere of radius R. Working in spherical coordinates  with
with  and
and , the invariant line element of this configuration space then reads
, the invariant line element of this configuration space then reads
 (52)
(52)
thereby defining the metric structure , such that
, such that
 (53)
(53)
This space being simply-connected, there only exists a single representation of the associated Heisenberg algebra, namely that in the trivial U(1) holonomy class . Consequently, the configuration space representation is given by the basis of positions eigenstates
. Consequently, the configuration space representation is given by the basis of positions eigenstates  such that
such that
 (54)
(54)
Thus implying the following inner product for configuration space wave functions of states,
 (55)
(55)
while the momentum operators are issued by the following configuration space representations,
 (56)
(56)
 (57)
(57)
Within this configuration space representation, the general diffeomorphic invariant quantum Hamiltonian in (9) corresponds in the present case to the following differential operator, acting on configuration space wave functions ,
,
 (58)
(58)
The configuration space wave functions of the energy eigenstates of this system are of course nothing else than the spherical harmonics, labeled by the angular momentum values  and the integer magnetic moment values
and the integer magnetic moment values  of its projection on the angular momentum quantization axis. The corresponding states
of its projection on the angular momentum quantization axis. The corresponding states  have their wave functions given by
have their wave functions given by  such as
such as
 (59)
(59)
 being the associated Legendre functions [14]. The normalization of these states is chosen such that
being the associated Legendre functions [14]. The normalization of these states is chosen such that , while their energy eigenvalues read
, while their energy eigenvalues read
 (60)
(60)
with the usual degeneracy in , due to the SO(3) symmetry of the sphere.
, due to the SO(3) symmetry of the sphere.
It is to be noted that if this spectrum is well known, the method used here which is based on the most general representation of the Heisenberg algebra is not common although it is associated to a trivial holonomy in this case.
Let us finally sketch the spectrum of the momentum operator . The corresponding wave function
. The corresponding wave function  is obtained by solving the following differencial equations,
is obtained by solving the following differencial equations,
 (61)
(61)
 (62)
(62)
which gives the following  -wave function, properly normalized by the means of conditions in (0.54),
-wave function, properly normalized by the means of conditions in (0.54),
 (63)
(63)
where  is an arbitrary function. The corresponding eigenvalues are given by
is an arbitrary function. The corresponding eigenvalues are given by
 (64)
(64)
6. Discussions and Outlooks
In this paper, we have constructed the spectra of some simple models, namely a particle on the line and on the two-sphere, within the framework of the well-known conventional quantization as well as that of the recently introduced promising enhanced quantization procedure. The model described by the particle on the finite line is extended by the addition of a delta-point interaction which, mathematically, boils down to consider a punctured line which is related to a non simply-connected manifold. It appeared that the representations of the Heisenberg algebra—with their topological classifications—are indissociable of such constructions if one needs to be exhaustive. We found that the quantum action functional restricted to phase space coherent states, is expressed as the classical action plus  -corrections. In this view, classical theory appears clearly as a subset of quantum theory, and they both co-exist as in the real world where
-corrections. In this view, classical theory appears clearly as a subset of quantum theory, and they both co-exist as in the real world where . Thus, the main result of the enhanced canonical quantization is that, we have constructed a set of coherent states which serve to remove the barrier between classical and quantum theories. This result adds an example to the existing ones [6,15], extending then the explorations of the implications of this new theory. Many confined systems could be concerned by our study like harmonic oscillators in the physical one-dimensional space.
. Thus, the main result of the enhanced canonical quantization is that, we have constructed a set of coherent states which serve to remove the barrier between classical and quantum theories. This result adds an example to the existing ones [6,15], extending then the explorations of the implications of this new theory. Many confined systems could be concerned by our study like harmonic oscillators in the physical one-dimensional space.
Let’s discuss some further potential applications of the new tool that constitutes the enhanced quantization, in providing some intuitive models that could be deciphered by the means of this procedure. Our first example is the famous Aharonov-Bohm (AB) effect. It’s well-known that this effect occurs only at quantum level and is essentially topological. Hence the enhanced canonical quantization that gives to a quantum action combining the classical as well as the quantum terms, could be useful to verify if this AB effect is only quantum and nonobservable at classical level and is topological. As a matter of fact, it is the case. Indeed, it has been proved in Refs. [1,5] that the quantum Hamiltonian recovered in paying the required attention to the nontrivial holonomy associated to the punctured Euclidean plane is mathematically equivalent to that associated to the AB effect and the suitable representation of the momentum operators is provided in polar coordinates  by
by ,
,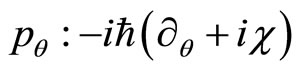 . The quantum parameter
. The quantum parameter  being the representative of the magnetic field or precisely the vector gauge potential. It appears that this physical phenomenon observes really only at quantum level. It suffices to observe the expression of the restricted to phase space quantum action obtained on the circle which has a similar topology to that of the punctured Euclidean plane [15]. Explicitly, the holonomy parameter
being the representative of the magnetic field or precisely the vector gauge potential. It appears that this physical phenomenon observes really only at quantum level. It suffices to observe the expression of the restricted to phase space quantum action obtained on the circle which has a similar topology to that of the punctured Euclidean plane [15]. Explicitly, the holonomy parameter  which induces the surface term in the restricted enhanced quantum action makes no influence on the enhanced classical equation of motion whatsoever (see P. 4 of Ref. [15]). Furthermore, this so-called enhanced quantization procedure has been conceived some years ago even though it has not been called enhanced quantization and its methods were applied to several physical systems (see Ref. [16] for an account).
which induces the surface term in the restricted enhanced quantum action makes no influence on the enhanced classical equation of motion whatsoever (see P. 4 of Ref. [15]). Furthermore, this so-called enhanced quantization procedure has been conceived some years ago even though it has not been called enhanced quantization and its methods were applied to several physical systems (see Ref. [16] for an account).
We note that the presence of certain interactions can change the considered topology of the manifold associated to a physical configuration space; this is actually the case of singular delta interactions as our study has shown. Among these, we also have the delta-sphere interactions. These interactions which were introduced first by Green and Moszowski [17] have intensively been used in nuclear, molecular as well as in solid states physics. Let us mention that one should study any Hamiltonian containing delta interactions by considering the most general diffeomorphic covariant representations of the momentum operator given in the relation (6). Ignoring this and using the commonly encontered textbook representation  , reduces the study to the trivial case
, reduces the study to the trivial case  . Likely, it has been proved [1,5] that a punctured hole in the bidimensional Euclidean plane induces mathematically, at quantum level, the AharonovBohm flux line threading this plane. This hole makes non simply-connected the manifold related to the plane and creates, at quantum level, a magnetic interaction via the nontrivial holonomy quantum variable which possesses the properties of the magnetic vector gauge potential. In this connection, let’s recall the spetrum on the circle[4, 15]. In conventional quantization, the
. Likely, it has been proved [1,5] that a punctured hole in the bidimensional Euclidean plane induces mathematically, at quantum level, the AharonovBohm flux line threading this plane. This hole makes non simply-connected the manifold related to the plane and creates, at quantum level, a magnetic interaction via the nontrivial holonomy quantum variable which possesses the properties of the magnetic vector gauge potential. In this connection, let’s recall the spetrum on the circle[4, 15]. In conventional quantization, the  -spectrum is given by
-spectrum is given by
 (65)
(65)
while the  -spectrum is issued by
-spectrum is issued by
 (66)
(66)
 being the circumference of this circle and
being the circumference of this circle and  are constants. At the beginning, the particle of mass
are constants. At the beginning, the particle of mass  is supposed to be free of any interaction. But after quantization, it occurs that the quantum parameter
is supposed to be free of any interaction. But after quantization, it occurs that the quantum parameter  in this spectrum which renders mathematically the influence of an Aharonov-Bohm flux line on this particle. The situation is analogous to that of the enhanced quantization on the circle [15]. It thus appears that the quantum mechanics on non simply-connected manifolds possesses hidden quantum degrees of freedom, which necessarily must also govern in an essential way the quatum physics properties of such systems. Finally, at quantum level, the topology is able to generate an interaction, and interactions can modify the topology. It would be worth looking at how the enhanced quantization applied to the two-sphere which is a system invariant under rotations in three dimensional physical space, whose quantum states thus fall into specific SO(3) spin representations, providing probably some complications in the phase space coherent states in this case. A small simulation leads us to the following steps. One has first to extend the operators
in this spectrum which renders mathematically the influence of an Aharonov-Bohm flux line on this particle. The situation is analogous to that of the enhanced quantization on the circle [15]. It thus appears that the quantum mechanics on non simply-connected manifolds possesses hidden quantum degrees of freedom, which necessarily must also govern in an essential way the quatum physics properties of such systems. Finally, at quantum level, the topology is able to generate an interaction, and interactions can modify the topology. It would be worth looking at how the enhanced quantization applied to the two-sphere which is a system invariant under rotations in three dimensional physical space, whose quantum states thus fall into specific SO(3) spin representations, providing probably some complications in the phase space coherent states in this case. A small simulation leads us to the following steps. One has first to extend the operators  and
and  which are the conjugate momenta associated to the position variables
which are the conjugate momenta associated to the position variables  and
and  respectively so that they are self-adjoint on the sphere. This first step is rather straightforward and
respectively so that they are self-adjoint on the sphere. This first step is rather straightforward and 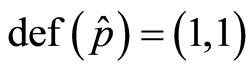 leading to a selfadjoint boundary condition characterized by a phase factor for this operator. The second step is the construction of the phase space coherent states, that could be noted
leading to a selfadjoint boundary condition characterized by a phase factor for this operator. The second step is the construction of the phase space coherent states, that could be noted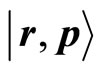 ,
,  ,
, . This crucial step could be made possible by inspiring oneself of the work by Kowalski et al. [18]. In this paper, the authors have discussed such a construction similarly to the case of the circle [15,19]. Then, the restricted quantum action could be computed for the model. The two-torus could also provide a good laboratory for testing these methods.
. This crucial step could be made possible by inspiring oneself of the work by Kowalski et al. [18]. In this paper, the authors have discussed such a construction similarly to the case of the circle [15,19]. Then, the restricted quantum action could be computed for the model. The two-torus could also provide a good laboratory for testing these methods.
7. Acknowledgements
Professor Jan Govaerts is warmly thanked for his kindly advice and for having sent us useful documents. Anselme F. Dossa is thanked for fruitful discussions.
NOTES
2Another alternative to the conventional quantization method has been introduced by the author, namely the affine quantization which is intended to play a role in Quantum Gravity.