Boundedness of Hyper-Singular Parametric Marcinkiewicz Integrals with Variable Kernels ()
1. Introduction
A function  defined on
defined on  is said to belong to
is said to belong to , if it satisfies the following three conditions:
, if it satisfies the following three conditions:
1)  for any
for any  and any
and any ;
;
2) 
3) , for any
, for any .
.
In [1], the authors considered the hyper-singular parametric Marcinkiewicz integral with variable kernel as follows:

where

When , we set
, we set , which is the parametric Marcinkiewicz integral with variable kernels considered in [2].
, which is the parametric Marcinkiewicz integral with variable kernels considered in [2].
For  the homogenous Lipschitz space
the homogenous Lipschitz space  is the space of function
is the space of function 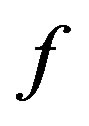 such that
such that

where  denotes
denotes  -th difference operator (see [3]).
-th difference operator (see [3]).
In 2006, Lu and Xu studied the boundedness of the commutator of  in [4]. They proved that:
in [4]. They proved that:
Theorem A [4]. Suppose 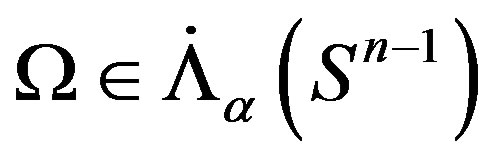 for
for  If
If  and
and , then
, then  maps
maps  continuously into
continuously into . Here
. Here  is defined as follows:
is defined as follows:
 (1)
(1)
where

Let 



 In this article, we mainly consider the commutator
In this article, we mainly consider the commutator  defined by
defined by
 (2)
(2)
where

Given any positive integer , for all
, for all , we denote by
, we denote by 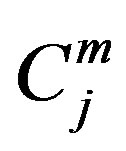 the family of all finite subsets
the family of all finite subsets  of
of  of
of  different elements. For any
different elements. For any , we associate the complementary sequence
, we associate the complementary sequence  given by
given by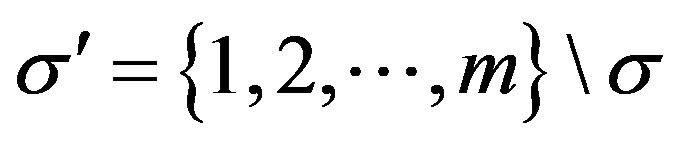 , (see [5]).
, (see [5]).
For any , we will denote
, we will denote  and the product
and the product  When
When , we have
, we have by definition, we have
by definition, we have . Similarly, when
. Similarly, when , we have
, we have  and
and . With this notation, if
. With this notation, if
 we write
we write 
When , we write
, we write 
Definition1.1.Let ,
, 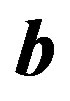 be defined as above such that
be defined as above such that .
.
A function 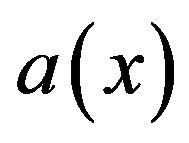 on
on  is called a
is called a  -atom if 1)
-atom if 1) , for some
, for some  and
and ;
;
2) 
3)  for any
for any
 and
and 
Definition 1.2. Let , we say that a distribution
, we say that a distribution  on
on  belongs to
belongs to  if and only if
if and only if 
can be written as  in the distributional sensewhere each
in the distributional sensewhere each  is a
is a 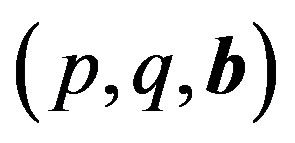 -atom and
-atom and
 Moreover,
Moreover,

with the infimum taken over all the above decompositions of  as above Definition 1.3. A function
as above Definition 1.3. A function  is said to satisfy the
is said to satisfy the  -Dini condition, if
-Dini condition, if
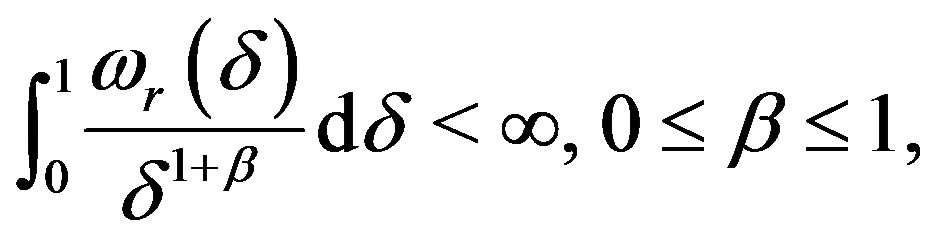 (3)
(3)
where  denotes the integral modulus of continuity of order
denotes the integral modulus of continuity of order  of
of  defined by
defined by

We will denote simply  -Dini condition for
-Dini condition for  - Dini condition when
- Dini condition when .
.
2. Main Theorem
Now let us formulate our main results as follows.
Theorem 2.1. Suppose that  is the commutator
is the commutator
(2), and let
 , then
, then  is bounded from
is bounded from  into
into . That is,
. That is,

Theorem 2.2. Suppose that  is the commutator
is the commutator
(2), and let  If
If
 satisfies the following two conditions:
satisfies the following two conditions:
1) 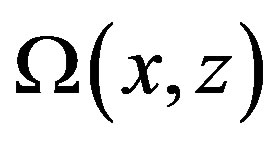 satisfies
satisfies 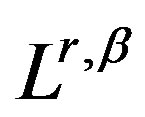 -Dini condition (3);
-Dini condition (3);
2) there exists
 such that
such that 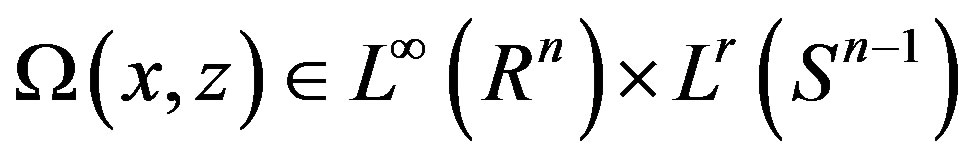 then
then  is bounded from
is bounded from 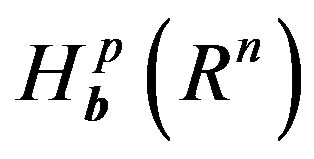 into
into . That is
. That is

Remark Obviously,  is the commutator of the operator
is the commutator of the operator  in [1]. At the same time, we change the course of the statement in [4].
in [1]. At the same time, we change the course of the statement in [4].
In order to prove our Theorems, we need several preliminary lemmas.
Lemma 2.1. [6] Let  and suppose
and suppose  If there exists a constant
If there exists a constant 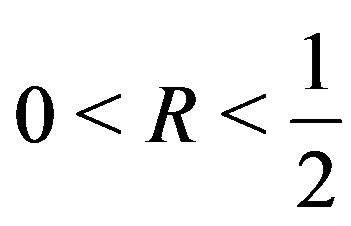 such that
such that , then for any
, then for any
 ,
,

where the constant  is independent of
is independent of 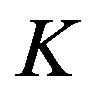 and
and .
.
lemma 2.2. [7] Let ,
, 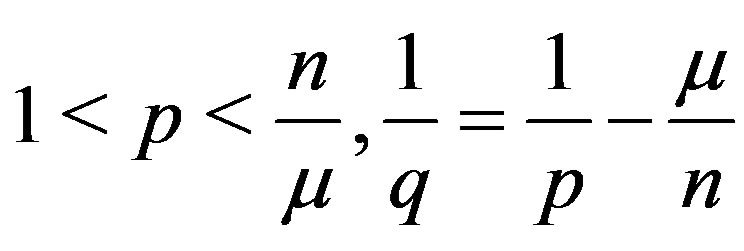 and
and 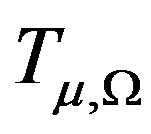 be defined as
be defined as  If there exists
If there exists
 , such that
, such that  then
then
 is bounded from
is bounded from 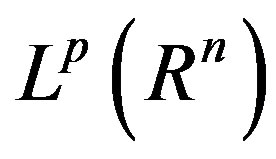 into
into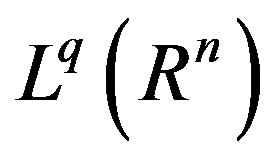 . That is
. That is

3. Proofs
3.1. Proof of Theorem 2.1.
Applying the Minkowski’ inequality, we can get

By Lemma 2.2 , we have

This completes the proof of Theorem 2.1.
3.2. Proof of Theorem 2.2.
Noting that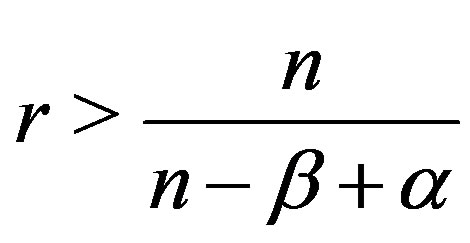 , we can choose
, we can choose  such that
such that . It is easy to see that
. It is easy to see that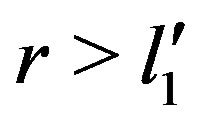 . Next , we choose
. Next , we choose  such that
such that 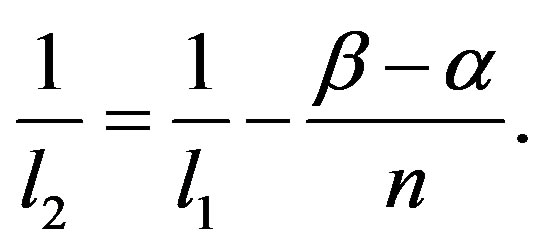 It follows from Theorem
It follows from Theorem  that
that  is bounded from
is bounded from 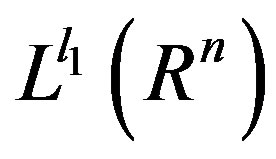 into
into . That is
. That is
 (4)
(4)
By the atomic decomposition theory on Hardy type space, it suffices to prove that there is a constant  such that for all
such that for all  -atom the following holds
-atom the following holds

Without loss of generality we may assume that
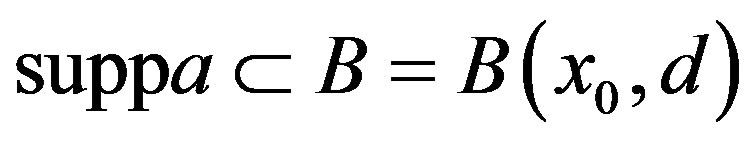 . We write
. We write  We split
We split
 into two parts as follows:
into two parts as follows:

We can easily see that . By (4) and the size condition of atom
. By (4) and the size condition of atom , we have
, we have

Next we estimate . Let us consider
. Let us consider :
:

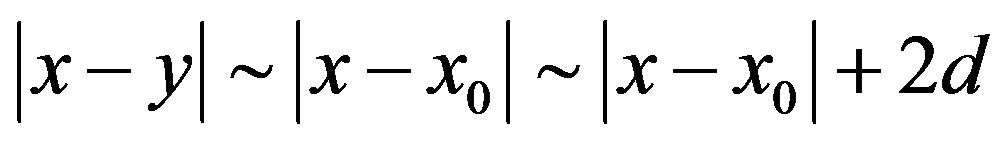 for
for
 . By the mean value theorem, we have
. By the mean value theorem, we have

Thus, by the Minkowski’s inequality for integrals,

Applying the Hölder inequality and the size condition of , we have
, we have

So we can get

Noting that  we have
we have

For , we write
, we write


So  is dominated by
is dominated by

Now let us estimate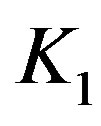 . By the vanishing condition of
. By the vanishing condition of , we have
, we have

where 
Since  we get from Hölder’s inequality and Lemma
we get from Hölder’s inequality and Lemma ,
,

Now we estimate . Applying Minkowski's inequality, the size condition of
. Applying Minkowski's inequality, the size condition of , we obtain
, we obtain

So we have

Thus

So when , we have
, we have

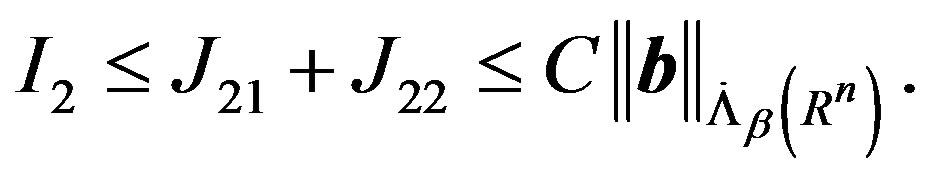
Combining the estimates for  and
and , we have
, we have

This completes the proof of Theorem 2.2.
4. Acknowledgements
The authors would like to thank anonymous reviewers for their comments and suggestions. The authors are partially supported by project 11226108, 11071065, 11171306 funded by NSF of China, project 20094306110004 funded by RFDP of high education of China.
NOTES