1. Introduction
The term auxetic is coming from the Greek word auxetos, meaning that which may be increased. Instead of getting thinner like an elongated elastic band when stretched, an auxetic material gains volume, expanding laterally [1]. For non-homogeneous linear elastic materials, it is demonstrated that even for the simplest loading case, i.e. quasi-static uniaxial, the Poisson’s ratio is spatial and temporal dependent and not a constant [2]. The Poisson’s ratio can be considered an auxetic descriptor only on such spatial and temporal domains where it gains negative values. Generally, the Poisson’s ratio is a function of the spatially and temporally changing moduli and stresses, and varies accordingly. For instance, we have
 (1.1)
(1.1)
Auxetic materials have a negative Poisson’s ratio for large spatial; and temporal domains and are expected to have interesting mechanical properties, such as high energy absorption, fracture toughness, indentation resistance and enhanced shear moduli, which may be useful in some applications [2-6]. Scientists have been aware of the existence of auxetic materials for over a hundred years, though without very special attention, and treating them as an accident or a curiosity. In the case of an isotropic material, the range of Poisson’s ratio is from –1.0 to 0.5, based on thermodynamic considerations of strain energy in the theory of elasticity. The auxetic behavior is found in materials from molecular and microscopic levels up to the macroscopic level. Love [7] presented an example of a cubic single crystal pyrite as having the Poisson’s ratio of –0.14, and he suggested that the effect may be caused by twinned crystals. Subsequently, an auxetic behavior has been observed in other naturally singlecrystal materials [8-10], in real materials with a high degree of anisotropy, such as conventional honeycomb network, re-entrant honeycomb and hexagonal structures (figure 1), reticulated metal foams, the skin covering a cow’s teats, certain rocks and minerals, living bone tissue, etc. In the auxetic materials the shear modulus is significantly greater then the elastic Young modulus It is well known that all major classes of materials (polymers, composites, metals and ceramics) can exist in auxetic form. A specific feature exhibeted by auxetic materials in comparison with other foams is their significant damping capacity at various loading levels, with increase up to 16 times compared to conventional foams [11-13]. The size-dependent theories of the damping capacity of auxetic foams have received increasing attention in recent years due to the need to model and analyse very small-sized mechanical interactions inn the rapid developments of micro-nanotechnologies [14-16]. The nonlocal theory becomes significant when dealing with such problems. The advantages of this theory over the classical local theory are in the high accuracy which can be obtained when employing the energy loss per unit volume versus the number of hysteretic cycles. The nonlocal estimation of the energy loss shows a better approximation of the experimental results than the local energy loss [15,16].
The starting point in the nonlocal damping theory of structures is the damping force which depends at a given point on the past history of a velocity field over a certain domain, through a kernel function. The nonlocal damping force is modeled as a weighted average of the velocity field over the spatial domain, and it is determined by a kernel function based on distance measures [17]. The damping capacity of the auxetic foam, in particular the conventional grey open-cells polyurethane foam [18], is tested by adding it under the form of the external elements to conventional materials [19-21].
Such models represent a generalization of the viscous damping, and examples include the beams and nanobeams with external patches [22,23], the auxetic composites [24-26], the micropaddles with the periodic auxetic cores [27], the multifunctional nanofoils based on the carbon nanotubes and the auxetic foams [14]. A nonlocal damping model including the time and spatial hysteresis effects for beams and plates is analysed in [14] by using the Galerkin method. The hysteresis in connection with PDEs and applicative problems are analyzed in [28-34]. Details on the nonlinear semigroups and differential equations in Banach spaces can be found in [35].
In this paper we apply the nonlocal theory to analyze the hysteretic behavior of the Euler-Bernoulli beams with external elements made from the auxetic material. The hysteresis operator is continuous and it is defined in connection with the motion equation of the beam.
2. Motion Equation with Hysteresis
Let us consider a beam of length L, in which a number  of external damping elements of thickness
of external damping elements of thickness  are attached at
are attached at 
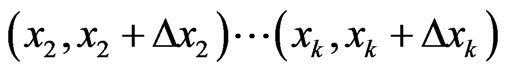 ,
,  ,
,  ,
,  as shown in figure 2. The length L, the transverse displacement
as shown in figure 2. The length L, the transverse displacement , and the coordinate x are non-dimensionalized by the length of the beam, so that dimensionless quantities
, and the coordinate x are non-dimensionalized by the length of the beam, so that dimensionless quantities  are given by
are given by 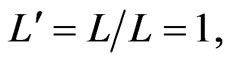


 .
.
The bending stiffness is , where E is the Young’s modulus of elasticity and
, where E is the Young’s modulus of elasticity and  the moment of inertia,
the moment of inertia,  is a constant moment of inertia, and
is a constant moment of inertia, and 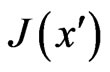 the dimensionless moment of inertia. The cross-sectional area A is non-dimensionalized by
the dimensionless moment of inertia. The cross-sectional area A is non-dimensionalized by , and the time t by
, and the time t by , where
, where  is the first natural frequency. The potential energy is non-dimensionalized by
is the first natural frequency. The potential energy is non-dimensionalized by , and the density of the bar
, and the density of the bar 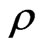 is non-dimensionalized by
is non-dimensionalized by . The virtual work due to the damping force per unit length is non-dimensionalizing by
. The virtual work due to the damping force per unit length is non-dimensionalizing by  and the damping force by
and the damping force by . The dimensionless non-conservative work is expressed as
. The dimensionless non-conservative work is expressed as
 , where
, where  is the external damping force per unit length defined over the spatial subdomains
is the external damping force per unit length defined over the spatial subdomains ,
, .
.


Figure 1. Conventional honeycomb network, re-entrant honeycomb and hexagonal structures, with negative Poisson’s ratio.

Figure 2. The beam with damping elements.
The state of the beam is characterized by two variables confined to a set : the external damping force
: the external damping force  acting over the spatial subdomains
acting over the spatial subdomains ,
,  , and the transverse displacement
, and the transverse displacement . Using the extended Hamilton’s principle, by including the non-conservative damping force
. Using the extended Hamilton’s principle, by including the non-conservative damping force , the equation of motion for the beam is written as, by omitting the prime
, the equation of motion for the beam is written as, by omitting the prime
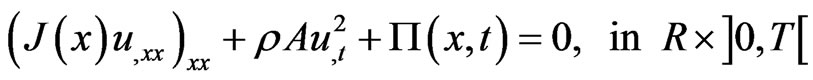 (2.1)
(2.1)
with
 (2.2)
(2.2)
The comma in (2.1) represents the differentiation with respect to the specified variable. The Poisson ratio is an important factor in defining the kernel , which is assumed to be separable in space and time
, which is assumed to be separable in space and time
 (2.3)
(2.3)
The expression (2.2) and (2.3) represent the general form of the nonlocal damping force. The Heaviside function  denotes the presence of damping. We have
denotes the presence of damping. We have  (constant) if x is within the patch, and
(constant) if x is within the patch, and  otherwise. The spatial kernel function
otherwise. The spatial kernel function 
is normalized to satisfy the condition .
.
A particular case of (2.3) refers to the spatial hysteresis with  where
where 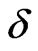 is the delta function in time. In this case, the force depends only on the instantaneous value of the velocity or strain rate, but depends on the spatial distribution of the velocities. Also, the velocities at different locations within a certain domain can affect the damping force at a given point.
is the delta function in time. In this case, the force depends only on the instantaneous value of the velocity or strain rate, but depends on the spatial distribution of the velocities. Also, the velocities at different locations within a certain domain can affect the damping force at a given point.
The external damping force  is related to the peculiar deformation mechanisms of the auxetic materials. In fact, the auxetic materials expand in all directions when pulled in only one, leading to an unusual volume change of the solid itself. The auxetic behaviour does not contradict the classical theory of elasticity. A homogeneous, isotropic material has a Poisson’s ratio range between –1.0 and 0.5, while the magnitude of the Poisson’s ratio can be even larger in the case of anisotropic solids. Negative Poisson’s ratio materials can exhibit slow decay of stress according to Saint-Venant’s principle. The choise of the function
is related to the peculiar deformation mechanisms of the auxetic materials. In fact, the auxetic materials expand in all directions when pulled in only one, leading to an unusual volume change of the solid itself. The auxetic behaviour does not contradict the classical theory of elasticity. A homogeneous, isotropic material has a Poisson’s ratio range between –1.0 and 0.5, while the magnitude of the Poisson’s ratio can be even larger in the case of anisotropic solids. Negative Poisson’s ratio materials can exhibit slow decay of stress according to Saint-Venant’s principle. The choise of the function  in (3) depends on the Poisson’s ratio. To understand this, some previous results are further presented [20,21]. The idea was to make a comparison between the non and auxetic grey open-cells polyurethane foams from the point of view of the damping capacities. The Poisson’s ratio values are all strain dependent, tending towards near-zero, negative or positive values depending on the pore dimensions. For example, the conventional foam has a Poisson’s ratio positive of 0.25 at compressive strain of 10%, which decreases sharply with the increase of compressive loading, to become slightly negative from 60 to 80% of tensile strain. The auxetic foam exhibits a negative Poisson’s ratio of –0.185 at compressive strain from 10 to 25%, showing a sharp increase for rising compressive strain, reaching then a zero value at 55% of compressive strain and a positive Poisson’s ratio of 1.33 at 80% [36]. Figure 3 shows the compressive constitutive law of the conventional and auxetic foams for cylinders having the diameter of 30 mm and length of 170 mm.
in (3) depends on the Poisson’s ratio. To understand this, some previous results are further presented [20,21]. The idea was to make a comparison between the non and auxetic grey open-cells polyurethane foams from the point of view of the damping capacities. The Poisson’s ratio values are all strain dependent, tending towards near-zero, negative or positive values depending on the pore dimensions. For example, the conventional foam has a Poisson’s ratio positive of 0.25 at compressive strain of 10%, which decreases sharply with the increase of compressive loading, to become slightly negative from 60 to 80% of tensile strain. The auxetic foam exhibits a negative Poisson’s ratio of –0.185 at compressive strain from 10 to 25%, showing a sharp increase for rising compressive strain, reaching then a zero value at 55% of compressive strain and a positive Poisson’s ratio of 1.33 at 80% [36]. Figure 3 shows the compressive constitutive law of the conventional and auxetic foams for cylinders having the diameter of 30 mm and length of 170 mm.
We determine the best form for  so that the variation of the energy loss per unit volume with respect to the number of compressive cyclic loadings is the closest to the experimental data [36,37]. The polyurethane sample is obtained from cylinders having the diameter of 30 mm and length of 170 mm. Then, it is compressed inside the mould obtaining a final nominal diameter of 20 mm and length of 100 mm. Figure 4 defines the compressive loading and displays the variation of the Poisson’s ratio with respect to compressive strain for this
so that the variation of the energy loss per unit volume with respect to the number of compressive cyclic loadings is the closest to the experimental data [36,37]. The polyurethane sample is obtained from cylinders having the diameter of 30 mm and length of 170 mm. Then, it is compressed inside the mould obtaining a final nominal diameter of 20 mm and length of 100 mm. Figure 4 defines the compressive loading and displays the variation of the Poisson’s ratio with respect to compressive strain for this

Figure 3. Comparison between compressive stress–strain curves of the considered types of foams.

Figure 4. Poisson’s ratio versus compressive strain for auxetic foam [21].
sample [21]. For any given loading cycle, the dissipated energy is , where
, where  and
and 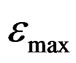 are the minimum and maximum strains, respectively, and
are the minimum and maximum strains, respectively, and . It is interesting to notice the higher energy absorption characteristics of the auxetic foam for the same strain ranges compared to the non-auxetic one.
. It is interesting to notice the higher energy absorption characteristics of the auxetic foam for the same strain ranges compared to the non-auxetic one.
Accordingly to [3], the calculations of the damping capacities for both non and auxetic foams are carried out on four forms of the spatial kernel : the exponential decay function,
: the exponential decay function,  the error function,
the error function,  , the hat function,
, the hat function,  for
for  and 0 otherwise, and the triangular function,
and 0 otherwise, and the triangular function,  for
for 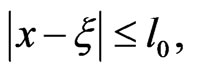
and 0 otherwise, respectively. In these expressions,  and
and 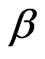 are characteristic parameters of the damping material, and
are characteristic parameters of the damping material, and  is the influence distance parameter. The numerical results are quite satisfying. The following conclusions can be drawn: 1) for nonauxetic foams the exponential decay function and triangular functions yield to similar values of energy loss per unit volume (15 mJ/cm3) after 20000 cycles; 2) all functions show a good correlation of the energy loss per unit volume with experimental data for auxetic materials; 3) while the hat and triangular functions yield to similar values of energy loss per unit volume (mJ/cm3) after 20000 cycles, the error function and respectively, exponential decay function are closer to an average value of 27 mJ/cm3, and respectively, 29 mJ/cm3. One feature of all results is the high energy dissipated by auxetic foam compared to the conventional foam for the same loading level.
is the influence distance parameter. The numerical results are quite satisfying. The following conclusions can be drawn: 1) for nonauxetic foams the exponential decay function and triangular functions yield to similar values of energy loss per unit volume (15 mJ/cm3) after 20000 cycles; 2) all functions show a good correlation of the energy loss per unit volume with experimental data for auxetic materials; 3) while the hat and triangular functions yield to similar values of energy loss per unit volume (mJ/cm3) after 20000 cycles, the error function and respectively, exponential decay function are closer to an average value of 27 mJ/cm3, and respectively, 29 mJ/cm3. One feature of all results is the high energy dissipated by auxetic foam compared to the conventional foam for the same loading level.
Therefore, we choose for the spatial kernel function the exponential decay with  and
and 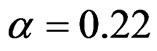
 (2.4)
(2.4)
The reacting character of the damping of the auxetic foams suggests to consider another particular case of (2.3), i.e. the temporal hysteresis, in which 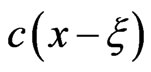 may be the Dirac delta function
may be the Dirac delta function , which reflects the reacting character of the damping force
, which reflects the reacting character of the damping force
 (2.5)
(2.5)
In this case we
 (2.6)
(2.6)
The ability to dissipate energy is one of the main reasons for using auxetic materials. Stress relaxation refers to the behavior of stress reaching a peak and then decreasing or relaxing over time under a fixed level of strain. For the kernel function  depending on the past time histories, we consider
depending on the past time histories, we consider
 (2.7)
(2.7)
with  the time relaxation constant of the auxetic foams and
the time relaxation constant of the auxetic foams and  a constant. Both constants depend on the Poisson’s ratio (figure 5).
a constant. Both constants depend on the Poisson’s ratio (figure 5).
In this paper we deal with the Euler-Bernouli problem (2.1) and (2.2) that contain a continuous hysteresis operator 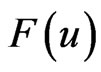
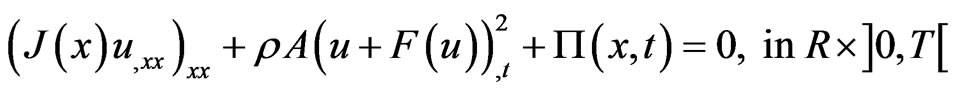 (2.8)
(2.8)
 (2.9)
(2.9)
The initial conditions attached to (2.8) are given by
 (2.10)
(2.10)
The boundary conditions are written, for example, for a simple supported beam
 (2.11)
(2.11)
In view of inserting of the delayed relay operator in (2.1) as expressed in (2.8), let us fix any pair 
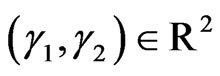 with
with  (figure 6). This operator is not closed. For any continuous function
(figure 6). This operator is not closed. For any continuous function  is uniformly continuous, hence it may have a finite number of oscillations between the thresholds
is uniformly continuous, hence it may have a finite number of oscillations between the thresholds . For any
. For any  and
and , we set
, we set 
 and
and
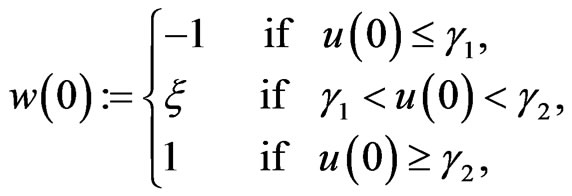 (2.12)
(2.12)
 (2.13)
(2.13)
with 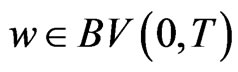 [29-31]. We define the rate-independent hysteresis operator
[29-31]. We define the rate-independent hysteresis operator 

in the sense of Visintin [29-31]. For any increasing continuous function , if
, if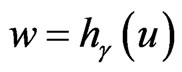 .we have
.we have .
.
Visintin has defined the completed relay operator , where
, where  is the set of parts of
is the set of parts of  (figure 7). This operator is defines as follows. For any
(figure 7). This operator is defines as follows. For any  and any
and any , we set
, we set  if and only if
if and only if  is measurable in
is measurable in 
 (2.14)
(2.14)
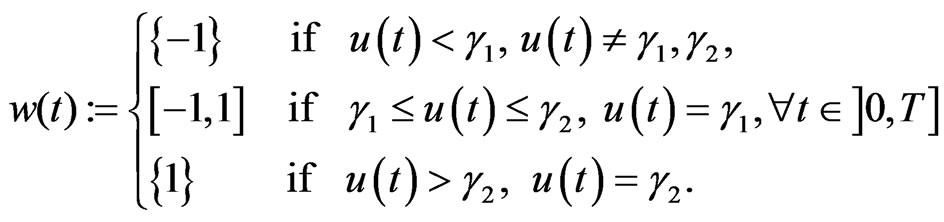 (2.15)
(2.15)
In conformity to (3.4), w is constant in a neighbourhood of t in the first case, w is nonincreasing in a neighbourhood of t in the second case, and w is nondecreasing in a neighbourhood of t in the last case.
The completed relay operator can be regularized by a regularized relay operator 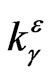
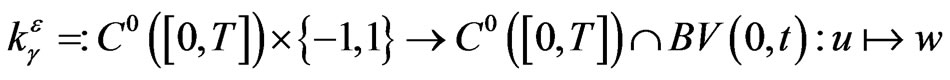
The regularized relay operator  may be written an the weak form
may be written an the weak form
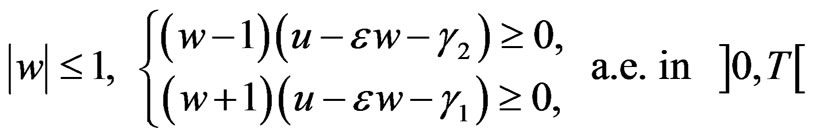 (2.16)
(2.16)
 (2.17)
(2.17)
or
 (2.18)
(2.18)
The hysteresis motion Equation (2.8) may be rewritten, by taking
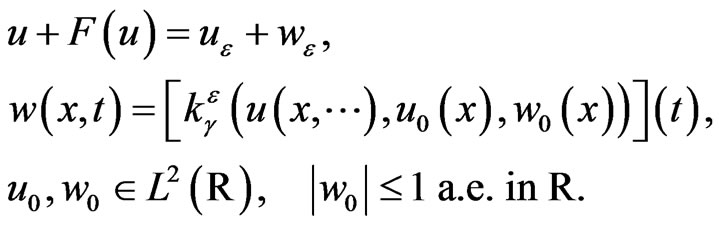 (2.19)
(2.19)
We also assume that , and provide a unified formulation of our problem for both the completed relay operator
, and provide a unified formulation of our problem for both the completed relay operator 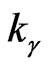 and its regularization
and its regularization  with
with . In this way, the problem can be formulated as Find
. In this way, the problem can be formulated as Find  and
and 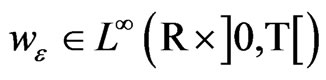 such that
such that  a.e. in
a.e. in 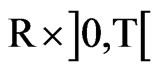 and
and
 (2.20)
(2.20)
 (2.21)
(2.21)
This problem may then be interpreted as a weak formulation of the problem (2.8), (2.9). Henceforth we shall write  in place of
in place of .
.
The hysteresis relay operator can be either continuous or discontinuous, but in this paper only the continuous case is studied.
3. Results and Conclusions
In what follows, the example refers to a simply supported aluminum beam with constant diameter d = 0.0025, with a single auxetic element ,
,  ,
, 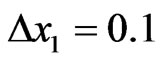 , and respectively, two auxetic elements
, and respectively, two auxetic elements 
 ,
,  ,
, 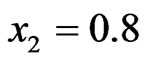 ,
, 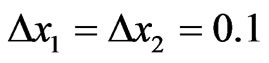 , with thickness
, with thickness . The auxetic material has the density
. The auxetic material has the density , the Poisson’s ratio
, the Poisson’s ratio  and the elastic modulus E = 259.93 MPa.
and the elastic modulus E = 259.93 MPa.
Tables 1 and 2 tabulate the lower estimates for the first five eigenvalues for the beam with a single and respectively, two damping elements. It is observed that the temporal hysteresis gives larger damping ratios then the spatial hysteresis. These results agree to the previous results reported in [21,22].
It is the purpose of this section to present the per-formance of the method of including the relay operator into the Euler-Bernoulli beam with auxetic external elements. To do this, we solve numerically the system of differential inclusions associated to the (2.20) and (2.21). As shown in figures 8 and 9, the hysteresis loops for the ratios  for a cyclic variation of u are displayed for both cases of spatial and the temporal hysteresis, respecttively. The calculations are carried out for
for a cyclic variation of u are displayed for both cases of spatial and the temporal hysteresis, respecttively. The calculations are carried out for  and
and  in the middle of the beam, for the first four vibration modes in the case of the spatial hysteresis and respectively, for first four vibration modes in the case of the temporal hysteresis.
in the middle of the beam, for the first four vibration modes in the case of the spatial hysteresis and respectively, for first four vibration modes in the case of the temporal hysteresis.
According to figures 8 and 9, it should be mentioned that the temporal hysteresis gives larger hysteresis loops then the spatial hysteresis. Moreover, the spatial loops look to be in some way to be stretched in the vertical direction.

Table 1. First five eigenvalues for a simply supported beam (spatial hysteresis).

Table 2. First five eigenvalues for a simply supported beam (temporal hysteresis).
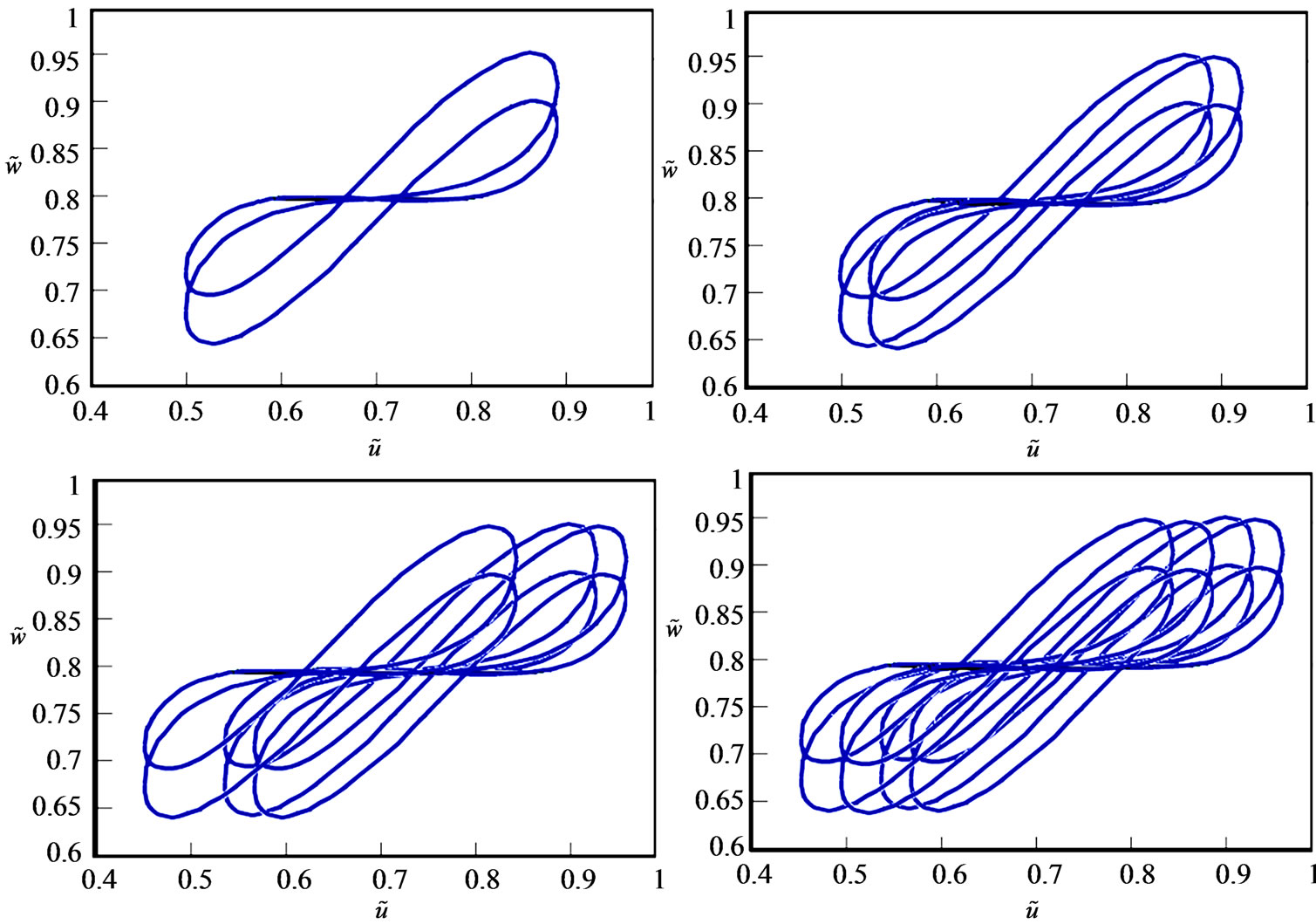
Figure 8. The temporal hysteresis for four vibration modes.

Figure 9. The spatial hysteresis for four vibration modes.
A possible drawback of this method is the difficulty in extending the method to deal with discontinuous relay hysteresis operator. The main idea is to explain some features of the experimental results in which the singularities of the hysteresis loops and the presence of the unclosed loops are reported.
For instance, in the figure 10 we see that the displacement drift, the force relaxation and non-closure of hysteretic loops are present [38]. We remember that the displacement drift appears when cycled between two unequal forces, the force relaxation appears when cycled between two unequal displacements. We must specify that such responses exhibit multiple reversals of small amplitude and are experimentally put into evidence [39].

Figure 10. The displacement drift and force relaxation [38].
4. Conclusions
In this paper, the continuous relay hysteresis operator is illustrated, and a weak formulation is studied for the nonlocal Euler-Bernoulli equation of the beam with external elements made from auxetic materials. The damping force is modeled as a weighted average of the velocity field over the temporal and spatial domains, determined by a kernel function based on distance measures. The spatial and temporal hysteresis are defined when employing the presence of the auxetic elements. The problem is solved by reducing it to a system of differential inclusions. From the numerical results presented in this study, we can conclude that the temporal hysteresis is associated with the larger hysteresis loops then in the case of the spatial hysteresis.
5. Acknowledgements
This research was financially supported by the National Authority for Scientific Research (ANCS, UEFISCSU), Romania, through PN2 project ID_1391/2008.