Characterization of Negative Exponential Distribution through Expectation ()
1. Introduction
Knowing characterizing property may provide unexpectedly accurate information about distributions and one can recognize a class of distributions before any statistical inference is made. This feature of characterization of probability distributions is peculiar to characterizing property and attracted attention of both theoretician and applied workers but there is no general theory of it.
Various approaches were used for characterization of negative exponential distribution. Among many other people, Fisz [1], Tanis [2], Rogers [3] and Fergusion [4] used properties of identical distributions, absolute continuity, constant regression of adjacent order statistics, linear regression of adjacent order statistics of random variables and characterized negative exponential distribution. Using independent and non-degenerate random variables Fergusion ([5,6]) and Crawford [7] characterized negative exponential distribution. Linear regression of two adjacent record values used by Nagaraja ([8,9],) were different from two conditional expectations, conditioned on a non-adjacent order statistics used by Khan [10] to characterize negative exponential distribution.
In this research note section 2 is devoted for characterization based on identity of distribution and equality of expectation function randomly variable for a negative exponential distribution with probability density function (pdf).
 (1.1)
(1.1)
where  are known as constants,
are known as constants,  is positive absolute continuous function and
is positive absolute continuous function and  is everywhere differentiable function. Since derivative of
is everywhere differentiable function. Since derivative of  is positive, the range is truncated by
is positive, the range is truncated by  from left
from left .
.
2. Characterization
Theorem 2.1 Let  be a random variable with distribution function
be a random variable with distribution function . Assume that
. Assume that is continuous on the interval
is continuous on the interval , where
, where . Let
. Let  and
and 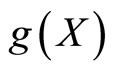 be two distinct differentiable and intregrable functions of X on the interval
be two distinct differentiable and intregrable functions of X on the interval  where
where  and moreover
and moreover  be non constant. Then
be non constant. Then
 (2.1)
(2.1)
is the necessary and sufficient condition for pdf  of
of  to be
to be  defined in (1.1).
defined in (1.1).
Proof Given  defined in (1.1), for necessity of (2.1) if
defined in (1.1), for necessity of (2.1) if  is such that
is such that  where
where  is differentiable function then
is differentiable function then
 (2.2)
(2.2)
Differentiating with respect to  on both sides of (2.2), replacing
on both sides of (2.2), replacing  for
for  and simplifying one gets
and simplifying one gets
 (2.3)
(2.3)
which establishes necessity of (2.1). Conversely given (2.1), let  be such that
be such that
 (2.4)
(2.4)
which can be rewritten as
 (2.5)
(2.5)
which reduces to
 (2.6)
(2.6)
Hence
 . (2.7)
. (2.7)
Since  is increasing integrable and differentiable function on the interval
is increasing integrable and differentiable function on the interval  with
with  the following identity holds
the following identity holds
 . (2.8)
. (2.8)
Differentiating  with respect to
with respect to and simplifying (2.8) after taking
and simplifying (2.8) after taking  as one factor, (2.8) reduces to
as one factor, (2.8) reduces to
 , (2.9)
, (2.9)
where  is a function of
is a function of  only derived in (2.3) and
only derived in (2.3) and  is a function of
is a function of  and
and  only derived in (2.7).
only derived in (2.7).
Since  be increasing integrable and differentiable function on the interval
be increasing integrable and differentiable function on the interval  where
where  and since
and since  is positive intregrable function on the interval
is positive intregrable function on the interval  where
where  with
with  and integrating (2.7) over the interval
and integrating (2.7) over the interval  on both sides, one gets (2.7) as
on both sides, one gets (2.7) as
 (2.10)
(2.10)
and
 .
.
Substituting  in
in  derived in (2.10),
derived in (2.10),  reduces to
reduces to  defined in (1.1) which establishes sufficiency of (2.1).
defined in (1.1) which establishes sufficiency of (2.1).
Remark 2.1 Using  derived in (2.3), the
derived in (2.3), the  given in (1.1) can be determined by
given in (1.1) can be determined by
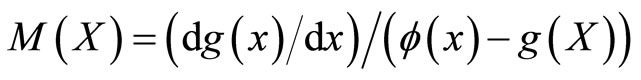 (2.11)
(2.11)
and pdf is given by
 (2.12)
(2.12)
where  is decreasing function for
is decreasing function for  with
with  such that it satisfies
such that it satisfies
 . (2.13)
. (2.13)
Illustrative Example: Using method described in the remark characterization of negative exponential distribution through survival function  is illustrated.
is illustrated.
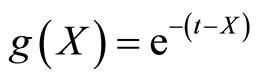
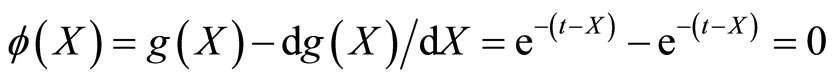
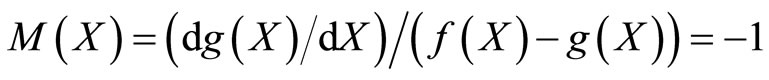
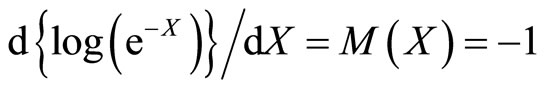
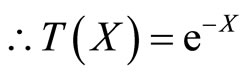
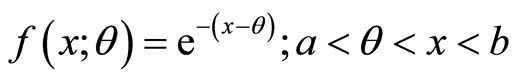
3. Conclusion
To characterize pdf defined in (1.1) one needs any arbitrary non-constant function of  which should only be differentiable and integrable.
which should only be differentiable and integrable.
NOTES