An Exactly Solvable Algebraic Model for Single Quantum Well Treatments ()
1. Introduction
Recently much interest has been drawn on the fabrication technology of semiconductor nanostructures. At this scale, it is well known that electronic properties are dominated by quantum effects, until at some points these effects become essential for device operation. For instance, the electronic states in highly confined semiconductor structures like quantum dots are entirely controlled by quantum mechanical size quantization, which can be exploited for entirely new device designs like quantum well or quantum dot lasers. However, the physical equations that describe these quantum systems are much too complex to be solved analytically and in general efficient numerical solution methods need to be used instead. As a consequence different numerical methods have been developed, which allow for reasonably efficient computer simulations in many cases of practical relevance. In particular, a large number of papers in the literature deal with the self-consistent solution of onedimensional Schrödinger-Poisson equations ([1], and the related references therein). In such methods, a trial potential distribution is used to solve the conventional Schrödinger equation and the resulting wavefunctions together with the energy eigenvalues are used to calculate the charge density in the quantum well regions. Poisson equation is then solved using this charge density to get the new potential distribution. For the solution of Schrödinger equation in the next iteration, a linear combination of these both, sum of the original and new additional potentials, are used as the new input potential and the whole procedure is repeated until the corresponding total energy is converged.
On the other side we stress that a key element of theoretical physics is the conceptualisation of physical phenomena in terms of models, which are then investigated by the tools at hand. For quantum many-body systems, some models can be exactly solved and their physical properties can be calculated in an exact fashion. To emphasize the relevance of exact models in physics, chemistry and engineering the reader is referred to [2] in order to see briefly general literature containing some important examples of exactly soluble models in quantum mechanics. Along this line, the ongoing miniaturization of semiconductor devices has prompted a shift of the focus of the modelling research [3], since the related algebraic models available in the literature do not account well some of the topics needed to be clarified in ultra-integrated devices.
Within this context, here we describe a new algebraic technique, in the light of previously reported exactly solvable models mentioned above, to propose a novel recipe in a different manner now to solve self-consistently the quantum (stationary Schrödinger’s equation) and the electrostatic (Poisson’s equation) for confined charges. This consideration of course constrains us in choosing the more physically acceptable forms for the particle mass and band edge potential functions in theoretical treatments. Nevertheless, the novel approach presented in this article would lead to more powerful algebraic discussions of the coupled Schrödinger-Poisson equations in the near future. A quite extended mathematical framework, relevant for the study of semiconductor heterostructures modelling, is in fact required for understanding and analysing in detail mathematical aspects of such calculations.
The present model uses an effective mass-Hamiltonian involving two potentials: a conventional finite well potential with different inside and outside masses for describing the band edge potential at zero doping and the additional potential due to the non-zero number of carriers i.e. the charge density. In order to decide whether or not typical carrier densities would give rise to a significant additional potential on top of the usual band edge potential term (which will be labelled specifically as ), it then becomes necessary to solve the electrostatics describing the system. For this reason, the relevant Schrödinger equation including the whole potential is split carefully in two parts which individually yield, in closed forms, the solutions for the unperturbed massdependent band edge potential and the corrections to the solutions due to the charge density in the system undertaken. Interestingly, the present formalism reveals that this second equation, which is responsible for the modifications brought to the unperturbed piece of the solutions, are exactly another form of the related Poisson equation. This significant observation makes clear the inter-relation between the Schrödinger and Poisson equations characterizing the system and suggests directly the modifications without solving the required equation. The necessary justifications for the results obtained by the present model and the assumptions used in the formalism, together with their validity and accuracy, are well discussed in the following sections. Although the literature covered similar works, to our knowledge an investigation such as the one we have discussed in this paper was missing.
), it then becomes necessary to solve the electrostatics describing the system. For this reason, the relevant Schrödinger equation including the whole potential is split carefully in two parts which individually yield, in closed forms, the solutions for the unperturbed massdependent band edge potential and the corrections to the solutions due to the charge density in the system undertaken. Interestingly, the present formalism reveals that this second equation, which is responsible for the modifications brought to the unperturbed piece of the solutions, are exactly another form of the related Poisson equation. This significant observation makes clear the inter-relation between the Schrödinger and Poisson equations characterizing the system and suggests directly the modifications without solving the required equation. The necessary justifications for the results obtained by the present model and the assumptions used in the formalism, together with their validity and accuracy, are well discussed in the following sections. Although the literature covered similar works, to our knowledge an investigation such as the one we have discussed in this paper was missing.
The paper is organized herewith as follows: In Section 2, we provide first a brief review of the Schrödinger equation for systems with a position-dependent effective mass. Later, the corresponding equation is decomposed meticulously in two pieces to have a clear observation on the contributions due to the different interactions in the system underlined. Section 3 deals with the application of the new formalism involving analytical treatments of the coupled equations in the model for a specifically chosen mass and potential profile. The significant relationship between seemingly distinct Poisson and Schrö- dinger equations is also discussed in this section, leading to the exact solutions in terms of the quantum mechanical results, for the Poisson equation, instead of the expressions in electrostatic. Finally, some conclusions are drawn in Section 4.
2. Formalism
An interesting question arises when one tries to formulate the correct Hamiltonian for a particle with spatially dependent mass in an arbitrary potential well. This problem often arises in the calculation of confined energy states for carriers in semiconductor quantum well structures under the envelope-function and the effective-mass approximations where the effective mass of a carrier is spatially dependent on the graded composition of the semiconductor alloys used in the barrier and the well region of the nanostructures. Since the mass and the momentum operators no longer commute, the correct ordering of these operators within the kinetic energy operator cannot be trivially assigned. This problem of ordering ambiguity is a long standing one in quantum mechanics, see for instance [4] for the recent review. Particular interest has been given to physical systems with positiondependent mass in recent years. It appears that a consensus was made in the majority of these works about the following form of the Hamiltonian
 (1)
(1)
All of the techniques are now in place to be able to solve the Schrödinger equation for any heterostructure for which the band edge potential profile defining the structure is known. However, all of the theoretical methods and examples described so far have concentrated solely on solving systems for a single charge carrier. In many devices such models would be inadequate as large numbers of charge carriers, e.g. electrons, can be present in the conduction band. Therefore, the additional potential term  arising from this charge distribution can be expressed by using Poisson’s equation
arising from this charge distribution can be expressed by using Poisson’s equation
 (2)
(2)
where  is the permittivity of the material, i.e.,
is the permittivity of the material, i.e.,  with
with  being material dependent. The solution is generally obtained via the electric field strength
being material dependent. The solution is generally obtained via the electric field strength
 (3)
(3)
Given the potential profiles,  for example, is one-dimensional, and then it will also produce a one dimensional charge distribution. In this case, Equation (1) reads
for example, is one-dimensional, and then it will also produce a one dimensional charge distribution. In this case, Equation (1) reads
 (4)
(4)
where . Making a new definition for the wavefunction
. Making a new definition for the wavefunction
 (5)
(5)
one gets a differential equation in a more familiar form
 (6)
(6)
in which
 (7)
(7)
where the primes denote the first and second derivatives of the mass function with respect to the variable .
.
Considering the structure of the full potential profile, we need at this stage to redefine  in (6) as
in (6) as
 (8)
(8)
The functions  and
and  are the solutions corresponding to
are the solutions corresponding to  and
and  potentials, respectively. The substitution of (8) into (6) produces coupled equations
potentials, respectively. The substitution of (8) into (6) produces coupled equations
 (9)
(9)
and
 (10)
(10)
where . It is obvious that the individual solutions of Equations (9) and (10) provide the needful solutions for (6) and, consequently, for the original spectra in Equation (4). The following section, which is the significant piece of the present work, focuses on the analytical solutions of these equations for a single quantum well.
. It is obvious that the individual solutions of Equations (9) and (10) provide the needful solutions for (6) and, consequently, for the original spectra in Equation (4). The following section, which is the significant piece of the present work, focuses on the analytical solutions of these equations for a single quantum well.
3. Application
We are fully aware of the crudeness of the formalism introduced above, but reasons will be given through this section for the belief that the solutions will come out fairly correctly from this picture, although the physical frame of a more realistic solution will differ greatly from the one presented here.
3.1. Solution of Equation (9)
Here, we first deal with the solution of Equation (9) by adopting a finite potential well for the conduction band edge and a piecewise flat mass distribution for the particles such as
 (11)
(11)
where  is the width of the well. The spatially variable effective mass is
is the width of the well. The spatially variable effective mass is
 (12)
(12)
in which  and
and  are constant, being the convenient masses of particles in the well and on the barrier.
are constant, being the convenient masses of particles in the well and on the barrier.
Within this simple, but physically reasonable, consideration the wavefunctions inside and outside the well can be obtained easily via Equation (9)
 (13)
(13)
and
 (14)
(14)
Following the usual procedure, the unnormalized (odd and even) solutions inside the well are
 (15)
(15)
while the wavefunction outside has the appearance
 (16)
(16)
where
 (17)
(17)
Remembering the wavefunction connection rules across an abrupt interface (i.e., discontinuity in the effective mass) associated to the Schrödinger equation in (4),
 (18)
(18)
the boundary conditions at  give
give
 (19)
(19)
for the odd solutions, and
 (20)
(20)
for the even solutions. These results, which are compatible with those of [5], lead us to

and
 (21)
(21)
The solutions of (21) provide the energies associated with the confined states of odd and even parities, respectively. In the particular case of , Equation (21) reduce to the familiar transcendental equations determining the bound eigenvalues of a finite square well.
, Equation (21) reduce to the familiar transcendental equations determining the bound eigenvalues of a finite square well.
3.2. Solution of Equation (10)
This formula contains the fundamental result of our calculations. The following discussion, down to the end of this section, clarifies a novel representation of the refinements to the solutions of Equation (9). For this reason, we first concentrate here on convencing the reader for the hidden relation between the Poisson equation concerning with the electrostatic potential  due to the charge distribution, which will be treated in a different manner from the previous convential ones, and Equation (10) though they have different appearance in their present forms. This point clarifies one of significant considerations in the related self-consistent calculations that the pertinent wavefunction
due to the charge distribution, which will be treated in a different manner from the previous convential ones, and Equation (10) though they have different appearance in their present forms. This point clarifies one of significant considerations in the related self-consistent calculations that the pertinent wavefunction  solely is simultaneously solution to both Schrödinger’s and Poisson’s equations.
solely is simultaneously solution to both Schrödinger’s and Poisson’s equations.
Considering the structure of the full wavefunction for the entire system, which is introduced by Equation (8), and using the spirit of the excellent recent work [6], we suggest a reasonable form for the electrostatic potential
 (22)
(22)
in which  is a constant. The unit analysis of (22) implies that
is a constant. The unit analysis of (22) implies that , being as another constant, should has a dimension like
, being as another constant, should has a dimension like , the physics behind of which will be disclosed below. It will also prove convenient for our forthcoming discussion to express
, the physics behind of which will be disclosed below. It will also prove convenient for our forthcoming discussion to express  with such a constant. This definition transforms smoothly the Poisson equation to the Schrödinger equation, explicitly, with a constant mass
with such a constant. This definition transforms smoothly the Poisson equation to the Schrödinger equation, explicitly, with a constant mass . Note that the proper mass
. Note that the proper mass  and material permittivity
and material permittivity , which is also constant for the present consideration although
, which is also constant for the present consideration although , are used throughout the discussion here since the only contribution to the energy of the whole system comes from the attractive part of the electrostatic potential, though they will disappear automatically at the end of the calculations.
, are used throughout the discussion here since the only contribution to the energy of the whole system comes from the attractive part of the electrostatic potential, though they will disappear automatically at the end of the calculations.
By substituting (22) into the one-dimensional form of (2), the Poisson equation turns out to be
 (23)
(23)
where
 (24)
(24)
is the electric field strength which is constant, as discussed comprehensively in Refs. [6,7]. Additionally, the natural verification of this concept through the analytical structure of  will appear spontaneously at the end of this section. A brief discussion related to this topic is also presented below. From the comparison of (23) with Equation (10), it is clear that
will appear spontaneously at the end of this section. A brief discussion related to this topic is also presented below. From the comparison of (23) with Equation (10), it is clear that
 (25)
(25)
from which and Equation (22),  has the unit of
has the unit of .
.
In the light of all these, and bearing in mind the onedimensional potential profile  and one-dimensional charge distribution discussed in the previous section, together with remembering that the quantum wells are assumed infinite in the
and one-dimensional charge distribution discussed in the previous section, together with remembering that the quantum wells are assumed infinite in the  plane, then any charge density
plane, then any charge density  can be thought of as an infinite plane, i.e. a sheet, with areal charge density
can be thought of as an infinite plane, i.e. a sheet, with areal charge density . Such an infinite plane of charge produces an electric field perpendicular to it, and with a strength
. Such an infinite plane of charge produces an electric field perpendicular to it, and with a strength
 (26)
(26)
at any space point. Note that as the sheet is infinite in the plane, then the field strength is constant for all distances from the plane. Thus, this theoretical consideration supports the reliability of Equation (23). For the total electric field strength due to many of these planes of charge, one needs of course to take the sum of the individual contributions, if required.
Further, the determinative factor in such electrostatic expressions is the form of . An extensive analytical solution of such an equation is presented by Ref. [6], from which we stress that the only charge distribution to produce a uniform electrostatic field are an odd number of parallel infinite sheets with opposite electric charge densities
. An extensive analytical solution of such an equation is presented by Ref. [6], from which we stress that the only charge distribution to produce a uniform electrostatic field are an odd number of parallel infinite sheets with opposite electric charge densities . Hence the analogy of the Poisson and Schrödinger equations argued above works only with a charge density given by
. Hence the analogy of the Poisson and Schrödinger equations argued above works only with a charge density given by
 (27)
(27)
where  is the Dirac delta function at the position
is the Dirac delta function at the position . The symmetry of the original heterostructure and doping profiles is reflected by the shape of
. The symmetry of the original heterostructure and doping profiles is reflected by the shape of  in (25). The electrostatic potential is positive at the center of the well since the system under consideration consists of electrons in the conduction band, so any test charge in the well-used to probe the potential is also electron which would be repelled by the existing charge. Similarly, it is attractive in the outside region (or through the barrier) due to many ionized donors in the system, though we expect that it is almost negligible when compared to its repulsive part. This observation explains the individual contributions having opposite signs in the whole structure of
in (25). The electrostatic potential is positive at the center of the well since the system under consideration consists of electrons in the conduction band, so any test charge in the well-used to probe the potential is also electron which would be repelled by the existing charge. Similarly, it is attractive in the outside region (or through the barrier) due to many ionized donors in the system, though we expect that it is almost negligible when compared to its repulsive part. This observation explains the individual contributions having opposite signs in the whole structure of 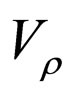 in (25) and of
in (25) and of  in (27). Note further that, when considering the case of for instance a
in (27). Note further that, when considering the case of for instance a  -type material, it is worth stating that the number of free electrons in the conduction band is equal to the number of positively charged ionized donors in the heterostructure. Thus, due to this charge neutrality, the electric field and
-type material, it is worth stating that the number of free electrons in the conduction band is equal to the number of positively charged ionized donors in the heterostructure. Thus, due to this charge neutrality, the electric field and  go to zero at large distances from the charge distribution.
go to zero at large distances from the charge distribution.
Consequently, the exact solutions of Equation (23), in connection with Equation (10), for the electrostatic potential in there
 (28)
(28)
are
 (29)
(29)
within the consideration of Equations (22), (25) and (27), and the single bound eigenvalue regarding the weak attractive pieces of  mentioned above penetrating to the barriers
mentioned above penetrating to the barriers
 (30)
(30)
by means of Equations (25) and (26). For the sake of clarity, we remind again that structure of the functions above do not cause any trouble in the frame of physics as this term as a whole yields a constant contributing to , which will be clear below. The significant point here is that the solutions above are obtained without solving Equation (23), which is another form the related Poisson equation for an appropriate definition of
, which will be clear below. The significant point here is that the solutions above are obtained without solving Equation (23), which is another form the related Poisson equation for an appropriate definition of . The same is valid Equation (10), as well. The results obtained are in agreement with those of Ref. [6].
. The same is valid Equation (10), as well. The results obtained are in agreement with those of Ref. [6].
For precise calculations, however, we should now proceed with reducing the present consideration to a wellknown case. For instance, Equation (27) takes the form of  for the case
for the case  and
and . In this perspective, it is not hard to see that the classical electrostatic potential in (28) resembles to the quantum mechanical attractive delta function potential
. In this perspective, it is not hard to see that the classical electrostatic potential in (28) resembles to the quantum mechanical attractive delta function potential
 (31)
(31)
where  has the units of
has the units of  and depends on the mass and doping properties. The expression above enables us to express the strengths of the potentials in terms of each other. In this case, taking Equations (3), (22), (26) and (31) into account, one can easily make a mapping between different frames, namely
and depends on the mass and doping properties. The expression above enables us to express the strengths of the potentials in terms of each other. In this case, taking Equations (3), (22), (26) and (31) into account, one can easily make a mapping between different frames, namely
 (32)
(32)
Similarly, for a given  and
and  profile, Equation (30) turns out to be
profile, Equation (30) turns out to be
 (33)
(33)
which, together with (32), coincide with the solutions for the attractive delta function potential in [8] in case of course , justifying the credibility of our findings. Moreover, the potential in (28) possesses only one exponentially localized bound state for all values of
, justifying the credibility of our findings. Moreover, the potential in (28) possesses only one exponentially localized bound state for all values of , with exactly the same energy.
, with exactly the same energy.
Nevertheless, we need one more equation to be able to express  in the quantum mechanical frame, which is vague in its present form, in terms of
in the quantum mechanical frame, which is vague in its present form, in terms of  that has a certain value given by (17). This means that the corrections, because of the charge density, to the unperturbed energy of the conduction band can be denoted purely by the quantum mechanical expressions without a need of classical datum. Within this context our exhaustive analysis (see the Appendix) puts forward that
that has a certain value given by (17). This means that the corrections, because of the charge density, to the unperturbed energy of the conduction band can be denoted purely by the quantum mechanical expressions without a need of classical datum. Within this context our exhaustive analysis (see the Appendix) puts forward that
 (34)
(34)
which is crucial for the exact computations in (33). Therefore, the required expression for the full energy of the system is transformed to its final form
 (35)
(35)
We close this section with a simple but realistic example for a deep understanding of the all theoretical considerations, in brief, introduced and discussed throughout the work presented here. Recalling the significant steps in the present framework:
1) Determine first  and
and  for a given system, together with
for a given system, together with  and
and ;
;
2) Calculate  within the frame of Equations (17) and (21);
within the frame of Equations (17) and (21);
3) Finalize the calculations with the computation of the full energy via Equation (35).
One can readily evaluate the validity and accuracy of the present method. For this purpose, we consider here the eigenstates of an electron in a simple rectangular quantum well of  where
where  and
and  with
with  being the mass of the free carrier. The width of the well is chosen to be 100 Ǻ and the height of the potential barrier is
being the mass of the free carrier. The width of the well is chosen to be 100 Ǻ and the height of the potential barrier is . Although the magnitude of the electrostatic potential is small compared to the conduction band offset, it has a measurable effect on the energy eigenvalues of the quantum well. To observe the change in the energy level from the single carrier system, which are approximately
. Although the magnitude of the electrostatic potential is small compared to the conduction band offset, it has a measurable effect on the energy eigenvalues of the quantum well. To observe the change in the energy level from the single carrier system, which are approximately  (first even) and
(first even) and  (first odd) low-lying levels, to the doped system, one may compute precisely the value of
(first odd) low-lying levels, to the doped system, one may compute precisely the value of  with the help of (33). The shift in the energy levels of the conduction band, as the inherent nature of the model, due to the additional bound state owing to the attractive part of
with the help of (33). The shift in the energy levels of the conduction band, as the inherent nature of the model, due to the additional bound state owing to the attractive part of , which is
, which is , compels us to choose
, compels us to choose  as the ground-state eigenvalue of the single quantum well instead of the lowest one that is the case in general. Altogether the ground-state energy changes, through Equation (35), to almost
as the ground-state eigenvalue of the single quantum well instead of the lowest one that is the case in general. Altogether the ground-state energy changes, through Equation (35), to almost  when accounting for the finite charge density in (27). This observation is in well agreement with the numerical selfconsistent calculations, e.g. see Figure 3.37 in Ref. [7].
when accounting for the finite charge density in (27). This observation is in well agreement with the numerical selfconsistent calculations, e.g. see Figure 3.37 in Ref. [7].
4. Concluding Remarks
In this paper we present a simple procedure to solve the one-dimensional Poisson-Schrödinger equations, as an algebraic alternative treatment to the corresponding selfconsistent calculations. The Poisson equation is analyzed within the frame of quantum theory to find the modified conduction band solutions. Although we have only discussed the one-dimensional case, it is straightforward to extend this approach for the larger dimensions and different forms of charge densities. Along this line, the works are in progress. We foresee that the present simple model will find wide applications in the related area.
5. Acknowledgements
The authors wish to thank Gabriel Gonzalez for a helpful discussion on this subject.
Appendix: Derivation of Equation (34)
To find an appropriate relation between  and
and  as in (34), one needs to repeat the whole procedure used in section III-B considering the algorithm of the self-consistent calculations. Starting with a prescription similar to (22) for the electrostatic potential
as in (34), one needs to repeat the whole procedure used in section III-B considering the algorithm of the self-consistent calculations. Starting with a prescription similar to (22) for the electrostatic potential
 (A.1)
(A.1)
and substituting it into the one-dimensional Poisson equation one obtains
 (A.2)
(A.2)
As the definition of the electric field strength now takes a new form,
 (A.3)
(A.3)
the Poisson equation in Equation (A.2) is then reduced to
 (A.4)
(A.4)
Keeping the discussion in section III-B in mind, and reminding the interplay between (A.4) and Equation (10), we offer (for a closed solution) that
 (A.5)
(A.5)
which does not cause any inconvenience in the calculations. This plausible recognition has a power of predicting the correct behavior of  without solving (A.4), which also serves as a benchmark for testing the present calculations. Consequently, as the behaviour of
without solving (A.4), which also serves as a benchmark for testing the present calculations. Consequently, as the behaviour of  is known, the use of (A.5) reveals smoothly the behaviour of the wavefunction responsible for the refinement
is known, the use of (A.5) reveals smoothly the behaviour of the wavefunction responsible for the refinement  and the comparison of the structure of the total wavefunction with the right hand side of (32)
and the comparison of the structure of the total wavefunction with the right hand side of (32)
 (A.6)
(A.6)
produces directly Equation (34). Remarkably, the whole solution in (A.6) is the product of growing  and decaying
and decaying  exponential functions as in (29). This clarifies the inter-relation between the electrostatic and related quantum mechanical solutions.
exponential functions as in (29). This clarifies the inter-relation between the electrostatic and related quantum mechanical solutions.