1. Introduction
The possibility to interpret unstable phenomena becomes very topical. In particular, the reason is conditioned by visualized increase in the intensity of disasters in nature. Experiment expects that the phenomenon of vortex shedding is the example of unstable process. Vortex shedding behind bluff bodies has been studied systematically at least since the days of Strouhal. Vortex shedding is welldefined instability development regime, which is fairly extended along the Reynolds scale. Sometimes, the phenomenon of vortex shedding is called the von Karman instability. Sometimes, the phenomenon is called the Kelvin-Helmholtz instability. However, the study of evolution of solution, after losing the stability, by means of direct numerical integration of the Navier-Stokes equations became feasible comparatively recently.
The phenomenon of vortex shedding behind bluff bodies is taken for evaluation of the results of direct numerical integration of the Navier-Stokes equations against experimental data [1,2]. In Section 2, the analysis of numerous divergences between the results of numerical integration of the Navier-Stokes equations and the experiment is given. The analysis is accompanied by corresponding conclusions. In Section 3, the concepts that lie in foundation of the multimoment hydrodynamics [3] are discussed. The characteristic features of unstable solution to the multimoment hydrodynamics equations in the problem on flow around a sphere [4,5] are considered.
2. Evaluating the Results of Numerical Integration against Experiment
In each of the problems on flow around a bluff bodies experiment records several independent directions of instability development. For 3D flow past a sphere experiment records three stable medium states. The  stable stationary flow consists of an axisymmetric toroidal recirculating zone in the near wake, which originates a single rectilinear thread in the far wake, see Figure 1(g) in [6]. The
stable stationary flow consists of an axisymmetric toroidal recirculating zone in the near wake, which originates a single rectilinear thread in the far wake, see Figure 1(g) in [6]. The  stable nonaxisymmetric flow consists of two weakly asymmetric halves in the near wake, which originate two rectilinear threads in the far wake, see Figure 12(a) in [7]. The
stable nonaxisymmetric flow consists of two weakly asymmetric halves in the near wake, which originate two rectilinear threads in the far wake, see Figure 12(a) in [7]. The  central-type stable state is characterized by periodic restructuring in the near non-axisymmetric wake, which causes wavy motion in the far wake without vortex shedding, see Figure 12(b) in [7].
central-type stable state is characterized by periodic restructuring in the near non-axisymmetric wake, which causes wavy motion in the far wake without vortex shedding, see Figure 12(b) in [7].
Each of these three states,  ,
,  , and
, and , after losing the stability, starts to evolve in its own direction qualitatively different from the others [2]. These directions are schematically shown by three horizontal branches in Figure 1. Instability begins to develop upon the attainment of critical Reynolds number values,
, after losing the stability, starts to evolve in its own direction qualitatively different from the others [2]. These directions are schematically shown by three horizontal branches in Figure 1. Instability begins to develop upon the attainment of critical Reynolds number values, 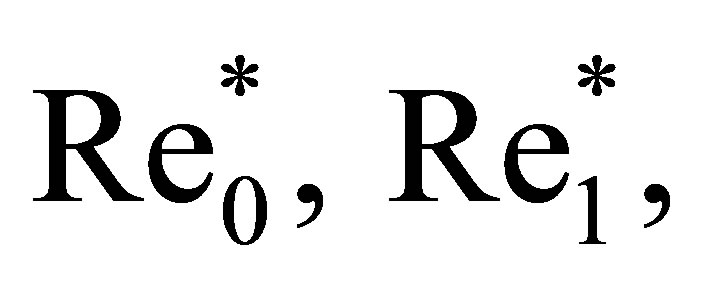 and
and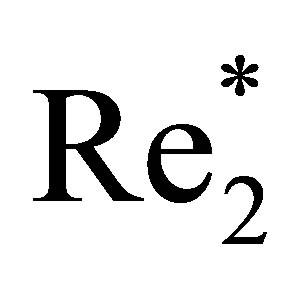 , respectively. Instability development inevitably involves periodic vortex shedding modes. Each of the three turbulence development directions has vortex shedding features of its own only characteristic of the given direction. No matter what direction is selected by experiments, periodic vortex shedding is, however, an unavoidable, well-defined instability-development mode.
, respectively. Instability development inevitably involves periodic vortex shedding modes. Each of the three turbulence development directions has vortex shedding features of its own only characteristic of the given direction. No matter what direction is selected by experiments, periodic vortex shedding is, however, an unavoidable, well-defined instability-development mode.
After the attainment of a certain critical Reynolds number value , the
, the  one-periodic vortex loop street appears in the wake behind a sphere, the upper branch in Figure 1. The periphery of the recirculating zone is periodically detached from the core and moves downstream in the form of hairpin vortex loop. The vortex loops move uniformly along one of the paths of the double undulated thread, which forms the far wake [7]. According to experiment, two vortex shedding modes existed at
one-periodic vortex loop street appears in the wake behind a sphere, the upper branch in Figure 1. The periphery of the recirculating zone is periodically detached from the core and moves downstream in the form of hairpin vortex loop. The vortex loops move uniformly along one of the paths of the double undulated thread, which forms the far wake [7]. According to experiment, two vortex shedding modes existed at . In the
. In the  twoperiodic mode, hairpin vortex loops are shed, whereas the
twoperiodic mode, hairpin vortex loops are shed, whereas the  two-periodic mode is characterized by vortex ring shedding. As with
two-periodic mode is characterized by vortex ring shedding. As with , the
, the  vortex rings are alternately shed from two symmetry related recirculating zone points and rush downstream along different double undulated thread paths [7,8], the upper branch in Figure 1.
vortex rings are alternately shed from two symmetry related recirculating zone points and rush downstream along different double undulated thread paths [7,8], the upper branch in Figure 1.
Above some critical  value, the
value, the 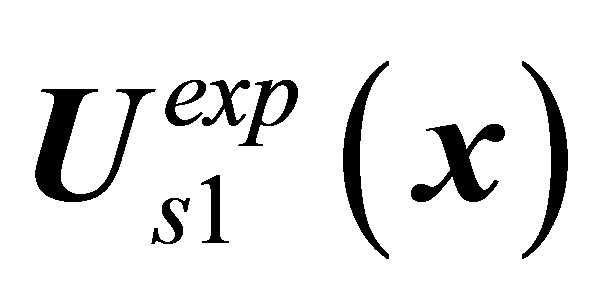 flow loses stability, the middle branch in Figure 1. The periphery of the recirculating zone of the
flow loses stability, the middle branch in Figure 1. The periphery of the recirculating zone of the 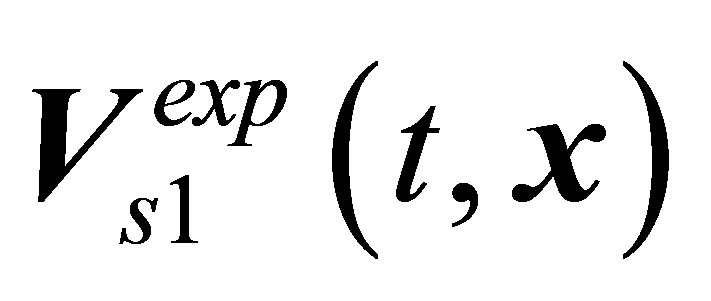 oneperiodic flow separates from its core and moves downstream along one of the double rectilinear thread paths in the form of hairpin vortex loop [9].
oneperiodic flow separates from its core and moves downstream along one of the double rectilinear thread paths in the form of hairpin vortex loop [9].
After the attainment of a certain critical Reynolds number  the
the 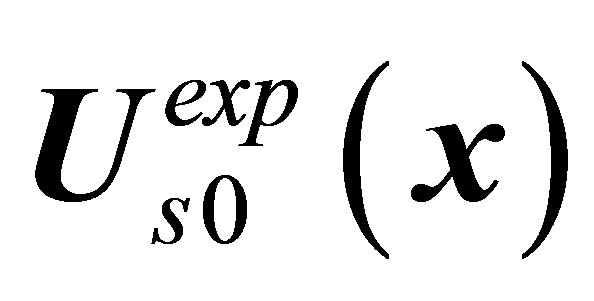 toroidal recirculating zone in the near wake behind a sphere begins to pulsate periodically, the lower branch in Figure 1. The frequency of pulsations is anomalously low. The
toroidal recirculating zone in the near wake behind a sphere begins to pulsate periodically, the lower branch in Figure 1. The frequency of pulsations is anomalously low. The  pulsating flow remains axisymmetric [6,10]. After the passage of
pulsating flow remains axisymmetric [6,10]. After the passage of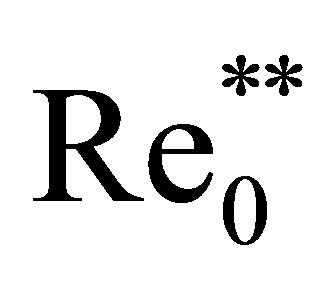 , vortex rings depart from a sphere downstream and move along the spiral path, that is, the
, vortex rings depart from a sphere downstream and move along the spiral path, that is, the  one-periodic flow becomes nonaxisymmetric [10]. The attainment of
one-periodic flow becomes nonaxisymmetric [10]. The attainment of  is accompanied by a change in the regime of vortex shedding from a sphere. Vortex rings penetrate into each other and form the
is accompanied by a change in the regime of vortex shedding from a sphere. Vortex rings penetrate into each other and form the  twoperiodic continuous spiral sheet in the wake behind a sphere [10], the lower branch in Figure 1.
twoperiodic continuous spiral sheet in the wake behind a sphere [10], the lower branch in Figure 1.
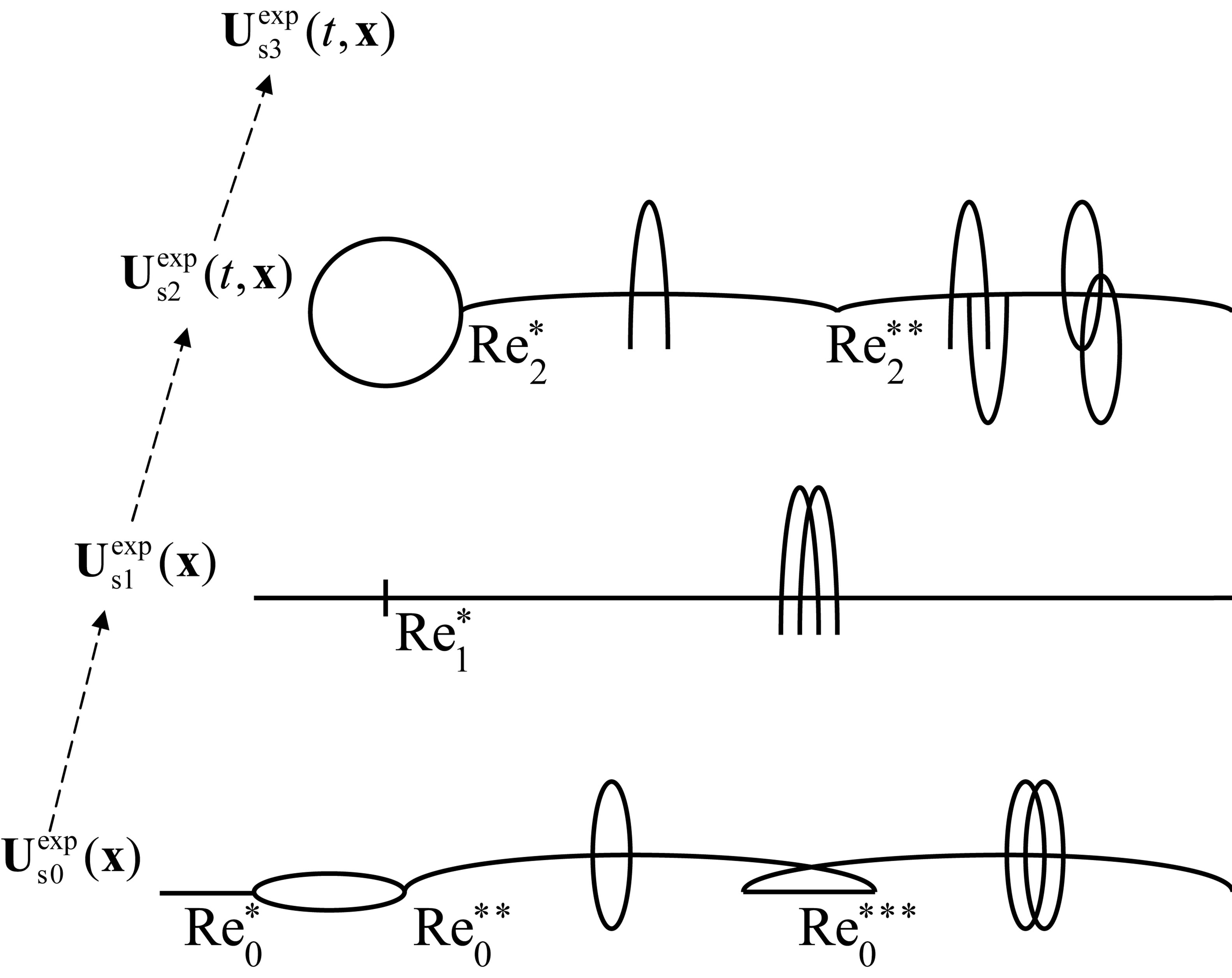
Figure 1. Three stable medium states originating three turbulence development directions for flow past a sphere. The lower branch corresponds to the evolution of stationary axisymmetric flow :
: ;
;  , periodic pulsations of the axisymmetric recirculating zone in the wake behind a sphere
, periodic pulsations of the axisymmetric recirculating zone in the wake behind a sphere , see Figure 1(h) in [6];
, see Figure 1(h) in [6]; , vortex ring shedding along a spiral path
, vortex ring shedding along a spiral path , see Figure 2" target="_self"> Figure 2(a) in [10]; and
, see Figure 2" target="_self"> Figure 2(a) in [10]; and , helicoidal vortex sheet
, helicoidal vortex sheet , see Figure 2(b) in [10]. The middle branch corresponds to the evolution of stable steady nonaxisymmetric flow
, see Figure 2(b) in [10]. The middle branch corresponds to the evolution of stable steady nonaxisymmetric flow :
: ;
; , periodic horseshoe-shaped vortex loop shedding along a rectilinear path
, periodic horseshoe-shaped vortex loop shedding along a rectilinear path , see Figure 6 in [9]. The upper branch corresponds to the evolution of a stable central-type state
, see Figure 6 in [9]. The upper branch corresponds to the evolution of a stable central-type state  :
: ;
; , periodic horseshoe-shaped vortex loop shedding along one of the double undulated thread branches
, periodic horseshoe-shaped vortex loop shedding along one of the double undulated thread branches , see Figure 7(a,i) in [7]; and
, see Figure 7(a,i) in [7]; and , periodic vortex loop shedding along both double undulated thread branches
, periodic vortex loop shedding along both double undulated thread branches , see Figure 4" target="_self"> Figure 4 in [8] and Figure 7(a,iii) in [7], or periodic vortex ring shedding
, see Figure 4" target="_self"> Figure 4 in [8] and Figure 7(a,iii) in [7], or periodic vortex ring shedding , see Figure 6 in [8].
, see Figure 6 in [8].
For 2D flow past a circular cylinder experiment records two stable medium states. The  stable stationary flow is characterized by axisymmetric recirculating zone in the near wake. The
stable stationary flow is characterized by axisymmetric recirculating zone in the near wake. The 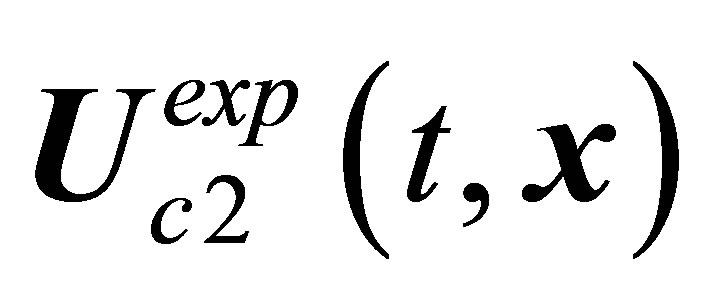 centraltype stable state is characterized by periodic restructuring in the near nonaxisymmetric wake without vortex shedding. Experiment finds at least two independent directions of instability development. Vortex shedding along each of the two directions,
centraltype stable state is characterized by periodic restructuring in the near nonaxisymmetric wake without vortex shedding. Experiment finds at least two independent directions of instability development. Vortex shedding along each of the two directions, 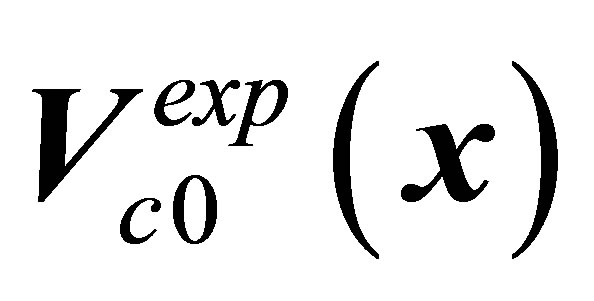 and
and  [11,12], is characterized by its own characteristic features intrinsic in it.
[11,12], is characterized by its own characteristic features intrinsic in it.
Evaluating the results of the direct numerical integration of the Navier-Stokes equations against experiment for unstable flows became feasible only recent twentyfive years, thanks to the vigorous development of computer facilities. As distinct from the earlier studies, the direct numerical integrations of the Navier-Stokes equations performed recently directly reproduce unstable flow conditions without artificially introducing non-stationary features into the stationary problem. Under artificial modeling a problem with time independent boundary conditions after stability loss is substituted by non-stationary stable problem [13,14]. Such substitution is need of initial conditions for non-stationary problem. The initial conditions consist of a solution for a fully developed vortex-shedding flow field. It is necessary to attract experimental data to construct such conditions. In particular, experiment must give eddy sizes and eddy positions in space, initial eddy velocities and vortex shedding frequency, beginning and completion of vortex shedding process at the Reynolds scale. To summarize, such modeling draws a picture of eddies movement. It is incapable of showing the direction of instability development.
Under the linear analysis of stability, the NavierStokes equations are linearized for small hydrodynamic values perturbations. Perturbations are expanded in Fourier series in time [15,16]. The linear character of studies does not allow evolution calculations to be extended to long times. That is, the linear analysis is incapable of defining the final stable saturated state. However, the linear analysis predicts characteristics of final solution, in particular, the oscillation frequencies around a stable position.
The direct numerical integration of the Navier-Stokes equations gives three stable solutions for flow around a sphere,  ,
,  , and
, and . These solutions reproduced three stable flows observed experimentally,
. These solutions reproduced three stable flows observed experimentally,  ,
, 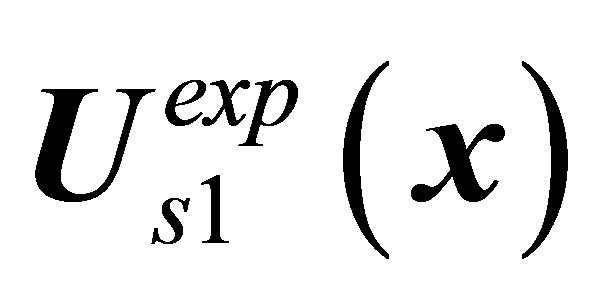 , and
, and , correspondently. In all calculations without exception performed by the direct numerical integration of the NavierStokes equations, instability development occurs in strict correspondence to classic Landau-Hopf scenario [17]. The calculation leads the instability development process in the direction given by dashed slanting line in Figure 1. The
, correspondently. In all calculations without exception performed by the direct numerical integration of the NavierStokes equations, instability development occurs in strict correspondence to classic Landau-Hopf scenario [17]. The calculation leads the instability development process in the direction given by dashed slanting line in Figure 1. The 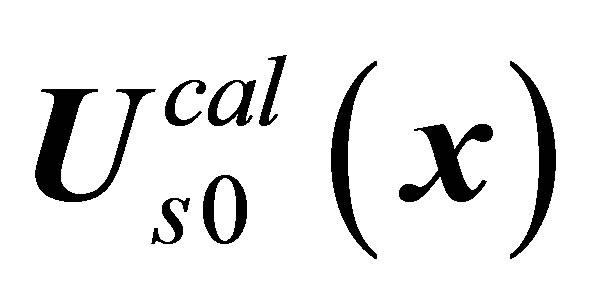 solution, when loses stability, experiences bifurcation to the
solution, when loses stability, experiences bifurcation to the 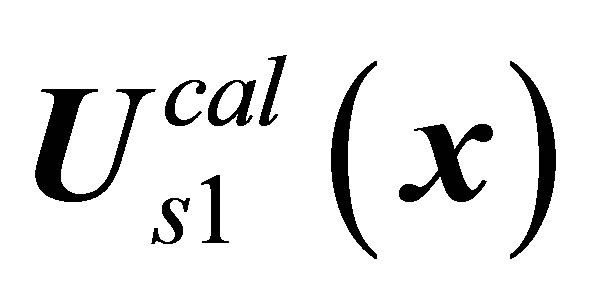 solution (regular bifurcation), and the
solution (regular bifurcation), and the  solution after stability loss experiences bifurcation to the
solution after stability loss experiences bifurcation to the 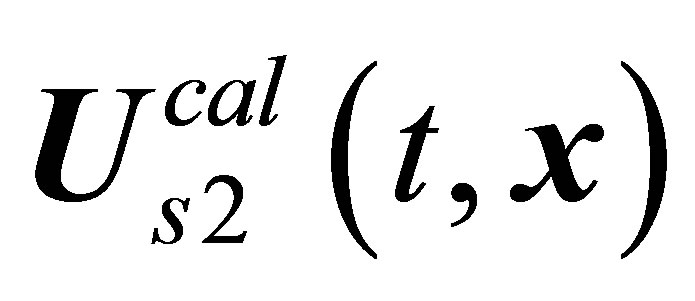 limiting cycle (Hopf bifurcation). The
limiting cycle (Hopf bifurcation). The 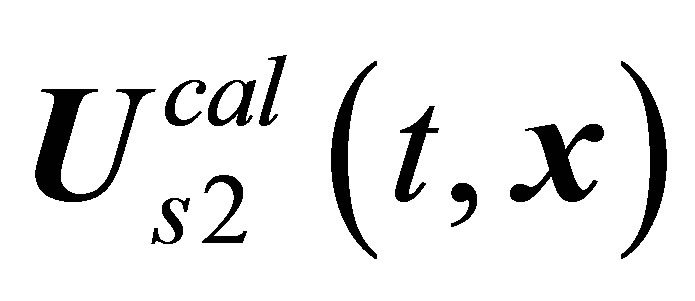 solution loses stability to be replaced by the
solution loses stability to be replaced by the  chaotic solution [18-21].
chaotic solution [18-21].
The direct numerical integration of the Navier-Stokes equations gives two stable solutions for flow around a cylinder, 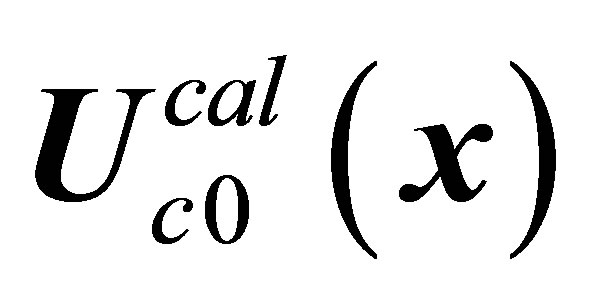 and
and . These solutions reproduced two stable flows observed experimentally,
. These solutions reproduced two stable flows observed experimentally,  and
and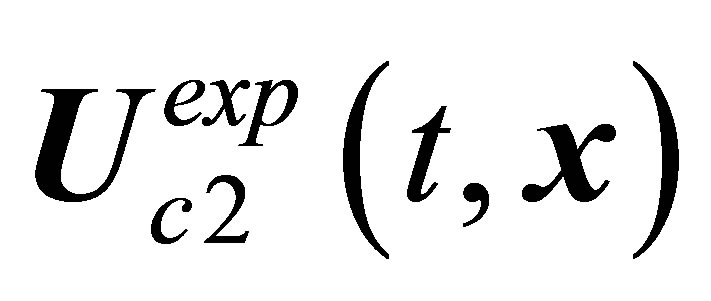 , correspondently. In accordance with Landau-Hopf scenario, the
, correspondently. In accordance with Landau-Hopf scenario, the  solution, when loses stability, experiences bifurcation to the
solution, when loses stability, experiences bifurcation to the 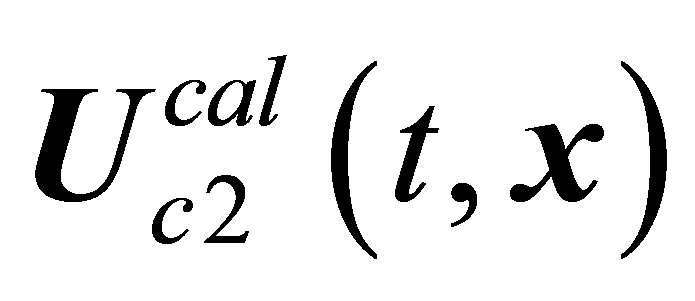 limiting cycle. The
limiting cycle. The 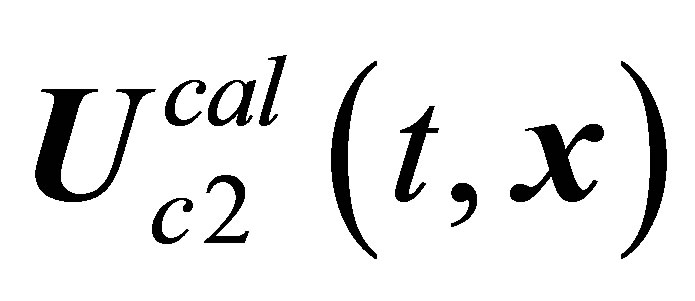 solution loses stability to be replaced by the
solution loses stability to be replaced by the 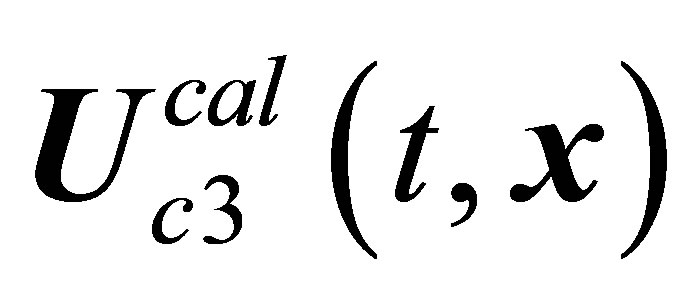 chaotic solution [22].
chaotic solution [22].
The bifurcation of a stationary state after stability loss to a limiting cycle is represented in Figure 2. The Figure 2" target="_self"> Figure 2 was drawn for a flat plate [23]. Later, qualitatively analogous pictures were drawn for different bluff bodies [24]. The Figure 2 gives the temporal development of the  absolute value of the velocity disturbance amplitude at an isolated point in the wake of a bluff body. After the attainment of the time moment
absolute value of the velocity disturbance amplitude at an isolated point in the wake of a bluff body. After the attainment of the time moment  lower solution loses its stability. They are the
lower solution loses its stability. They are the  solution for a cylinder and the
solution for a cylinder and the  solution for a sphere. By the time moment
solution for a sphere. By the time moment  increasing of disturbances results in saturation of a new stable solution, namely, the non-stationary periodic limiting cycle. They are the
increasing of disturbances results in saturation of a new stable solution, namely, the non-stationary periodic limiting cycle. They are the  solution for a cylinder and the
solution for a cylinder and the 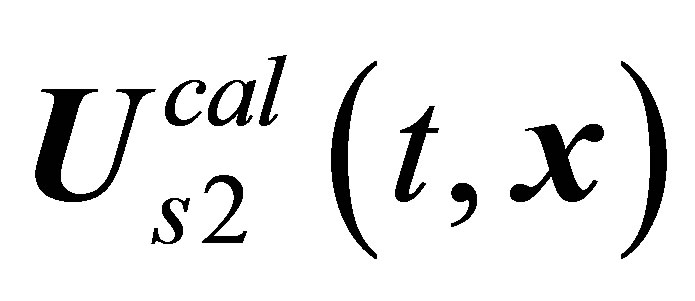 solution for a sphere. In accordance with definition [23], unstable regime is placed within the time interval between
solution for a sphere. In accordance with definition [23], unstable regime is placed within the time interval between 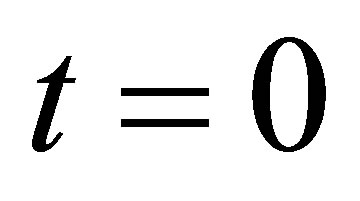 and
and . So, unstable regime is limited at time. On the contrary, the visualized process of vortex shedding is not limited at time. That is, experiment records a vortex street as long as investigator wants. Moreover, unstable regime, Figure 2, is not a periodic one, because the A disturbance amplitude grows. As a result, time limited non-periodic unstable regime can not be put in correspondence to strictly periodic phenomenon of vortex shedding which has no time frameworks. So, classic hydrodynamics is incapable to come up the expectations of experiment on unstable nature of vortex shedding phenomenon.
. So, unstable regime is limited at time. On the contrary, the visualized process of vortex shedding is not limited at time. That is, experiment records a vortex street as long as investigator wants. Moreover, unstable regime, Figure 2, is not a periodic one, because the A disturbance amplitude grows. As a result, time limited non-periodic unstable regime can not be put in correspondence to strictly periodic phenomenon of vortex shedding which has no time frameworks. So, classic hydrodynamics is incapable to come up the expectations of experiment on unstable nature of vortex shedding phenomenon.
The classic calculation can put only stable solution in correspondence to vortex shedding phenomenon. As noted above, the classic hydrodynamics equations in problem on flow past a sphere have four solutions, 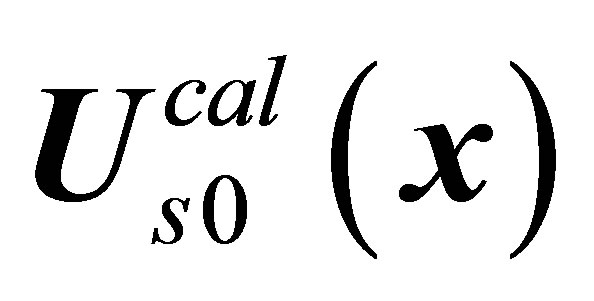 ,
,  ,
, 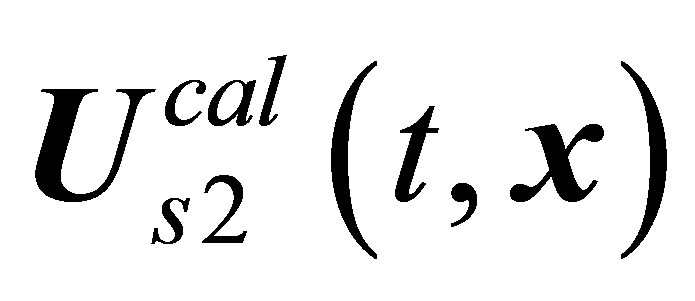 and
and . And these four solutions must describe ten observed modes,
. And these four solutions must describe ten observed modes, 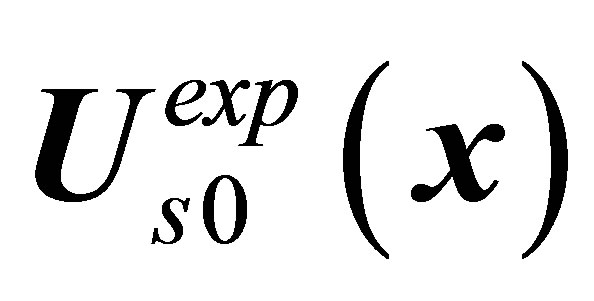 ,
, 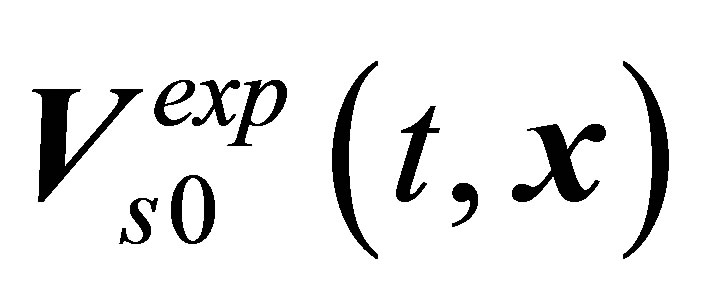 ,
,  and
and ;
;
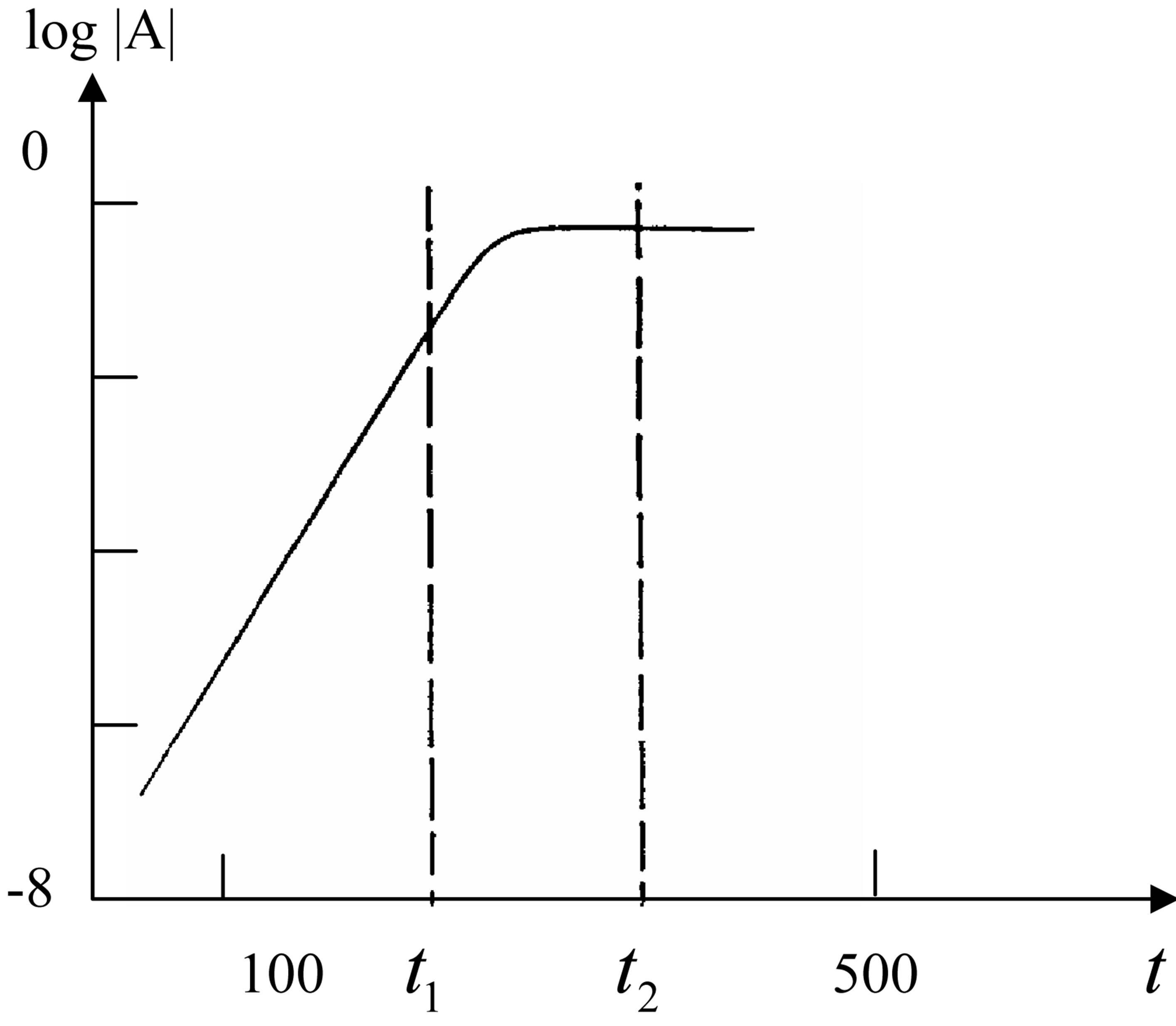
Figure 2. The temporal development of the absolute value of the velocity disturbance amplitude A: 0 < t < t1- exponential growth; t1 < t < t2- onset of nonlinearity; t > t2- saturation state. Figure 2 was drawn using the data from [23].
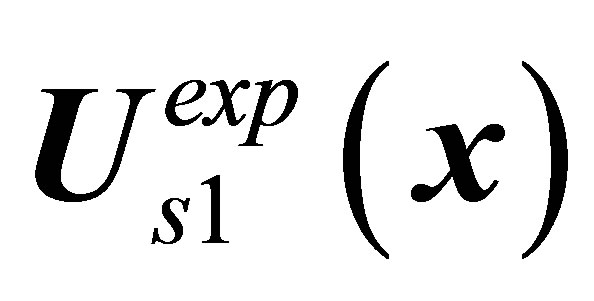 and
and ;
;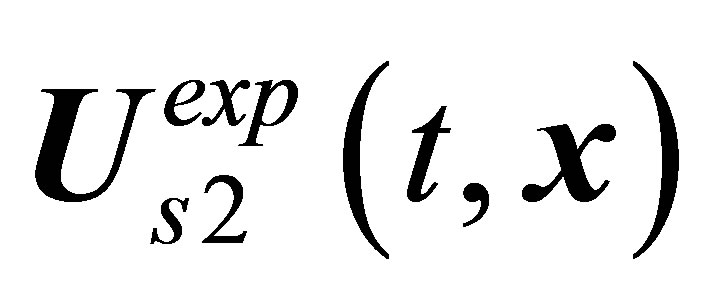 ,
,  ,
,
 and
and . The
. The  solution that succeeds the
solution that succeeds the 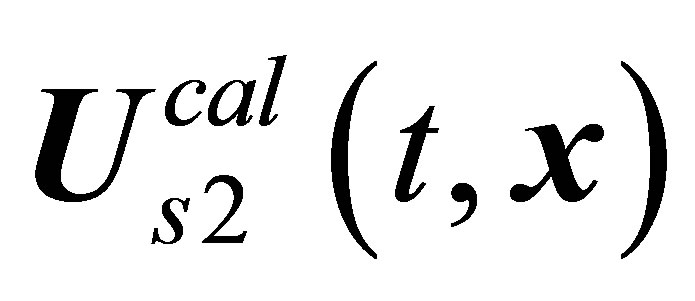 one-period mode is multiperiodic, that is, chaotic in essence. Attempts at correlating the
one-period mode is multiperiodic, that is, chaotic in essence. Attempts at correlating the 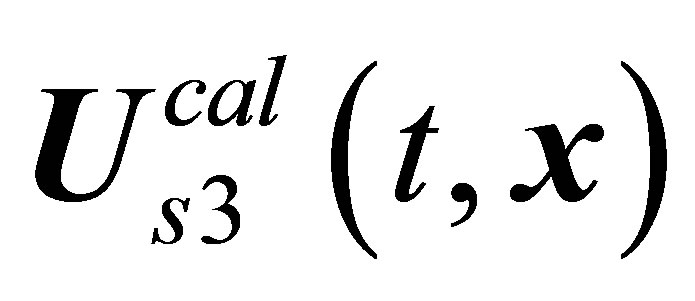 mode with the observed strictly periodic vortex shedding modes seem to have no prospects. The
mode with the observed strictly periodic vortex shedding modes seem to have no prospects. The  solution and the
solution and the  solution are stationary. That is why, the
solution are stationary. That is why, the 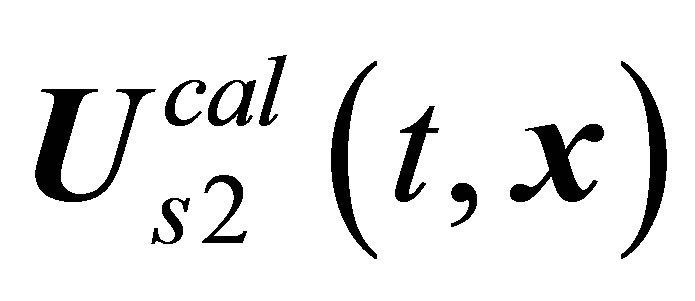 limiting cycle is the only case where it is possible to correlate the observed vortex shedding from a sphere to calculation results.
limiting cycle is the only case where it is possible to correlate the observed vortex shedding from a sphere to calculation results.
Let two experimental modes have pretensions to be described by the  limiting cycle. They are the
limiting cycle. They are the 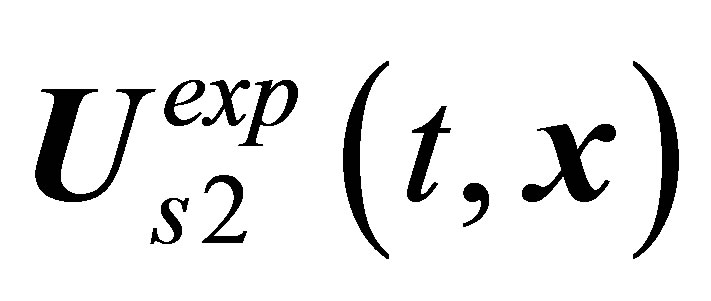 central-type stable state, which characterizes itself by wavy motion in the far wake without vortex shedding, and the
central-type stable state, which characterizes itself by wavy motion in the far wake without vortex shedding, and the  one-period vortex shedding mode, which manifests itself as a vortex loop street. Then, the
one-period vortex shedding mode, which manifests itself as a vortex loop street. Then, the  central-type state does not stand out as a separate regime when the experimental data are interpreted in [18-21]. The
central-type state does not stand out as a separate regime when the experimental data are interpreted in [18-21]. The  central-type regime is combined with the
central-type regime is combined with the  regime of periodic vortex shedding from a sphere. According to [18-21], vortex shedding does occur over the Reynolds number range
regime of periodic vortex shedding from a sphere. According to [18-21], vortex shedding does occur over the Reynolds number range , but its manifestations are exceedingly indistinct; the intensity of vortex shedding monotonically increases as Re grows. Earlier, this point of view was formulated in [25]. An attempt was made [18-21] to put the flow picture representing the
, but its manifestations are exceedingly indistinct; the intensity of vortex shedding monotonically increases as Re grows. Earlier, this point of view was formulated in [25]. An attempt was made [18-21] to put the flow picture representing the 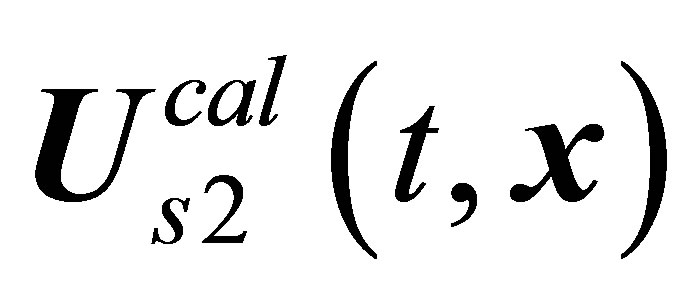 limiting process in correspondence with the observed
limiting process in correspondence with the observed 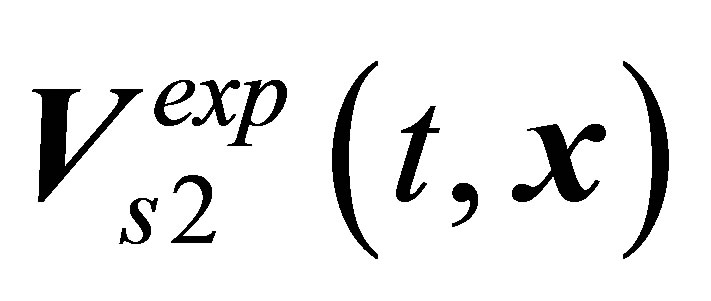 periodic vortex shedding combined with the
periodic vortex shedding combined with the 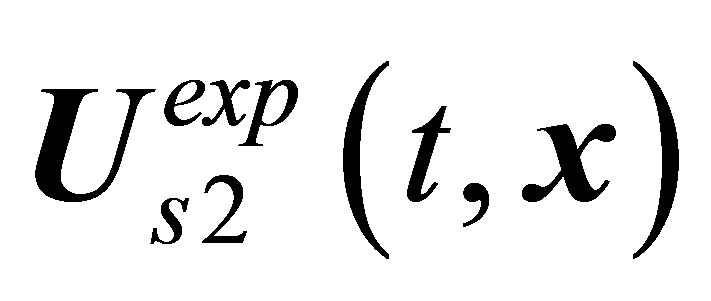 central-type mode.
central-type mode.
Attempts at correlating the  solution with observed vortex shedding modes initially seem to have no prospects. The reasons are as follows. First, the suggestion of a monotonic increase in the intensity of vortex shedding [18-21] is at variance with experiment (see Figures 12(b)-12(d) in [7]). According to Figure 12(c) from [7], the vortex structure appears in the wake suddenly and is fairly well defined starting with the moment of its origination. Secondly, in accordance with calculations, the
solution with observed vortex shedding modes initially seem to have no prospects. The reasons are as follows. First, the suggestion of a monotonic increase in the intensity of vortex shedding [18-21] is at variance with experiment (see Figures 12(b)-12(d) in [7]). According to Figure 12(c) from [7], the vortex structure appears in the wake suddenly and is fairly well defined starting with the moment of its origination. Secondly, in accordance with calculations, the 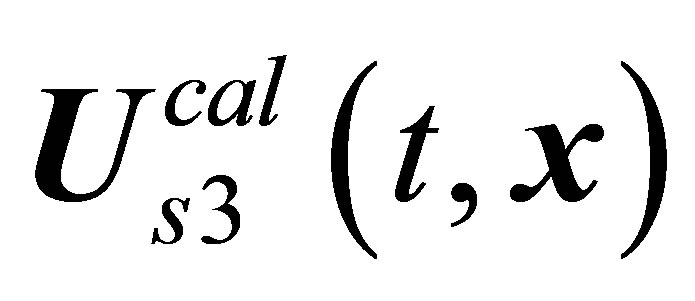 chaotic solution replaces the
chaotic solution replaces the 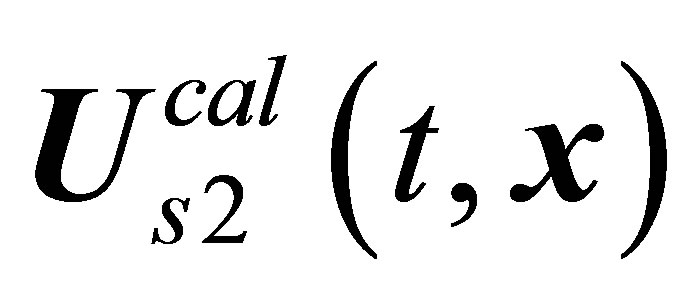 solution after the attainment of the Reynolds number value approximately equals to 500 [21]. However, in accordance with experiment, periodic vortex shedding is a well-defined mode, which is fairly extended along the Reynolds scale. In the experiments when a sphere was towed through an unperturbed medium vortex shedding was observed over the whole range of Reynolds numbers studied, up to Re = 30000 [10]. i.e., calculation predicts the early transition to chaos. This prediction is, however, at variance with experiment. Thirdly, three regimes of the six vortex shedding regimes actually observed are the one-period modes. These include
solution after the attainment of the Reynolds number value approximately equals to 500 [21]. However, in accordance with experiment, periodic vortex shedding is a well-defined mode, which is fairly extended along the Reynolds scale. In the experiments when a sphere was towed through an unperturbed medium vortex shedding was observed over the whole range of Reynolds numbers studied, up to Re = 30000 [10]. i.e., calculation predicts the early transition to chaos. This prediction is, however, at variance with experiment. Thirdly, three regimes of the six vortex shedding regimes actually observed are the one-period modes. These include ,
,
 , and
, and  regimes. Three regimes of vortex shedding are the two-period modes. These include
regimes. Three regimes of vortex shedding are the two-period modes. These include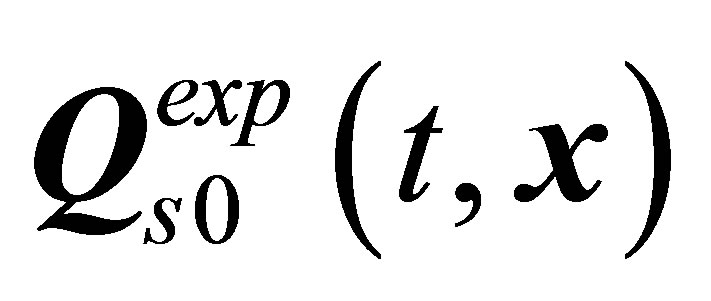 ,
,  , and
, and  regimes. Attempts at correlating the one-period
regimes. Attempts at correlating the one-period  solution with the observed two-period vortex shedding regimes seem to have no prospects. And at last, the
solution with the observed two-period vortex shedding regimes seem to have no prospects. And at last, the 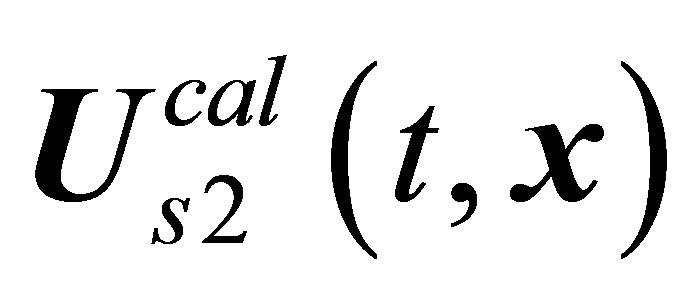 solution must be put in correspondence to several modes of vortex shedding simultaneously. For example, at some
solution must be put in correspondence to several modes of vortex shedding simultaneously. For example, at some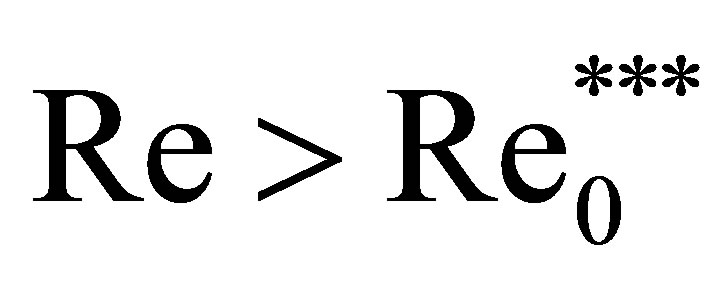 , experiment records four different regimes of vortex shedding: the
, experiment records four different regimes of vortex shedding: the  mode at the lower branch, the
mode at the lower branch, the 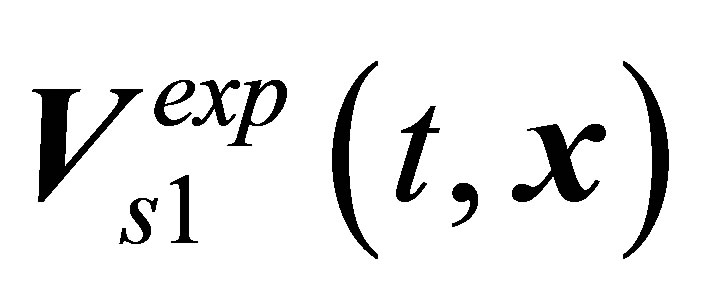 mode at the middle branch, the
mode at the middle branch, the 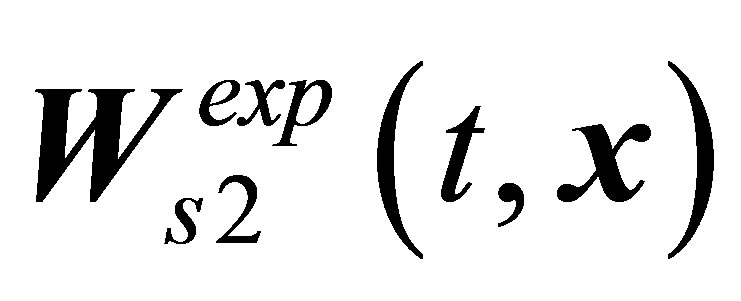 and the
and the 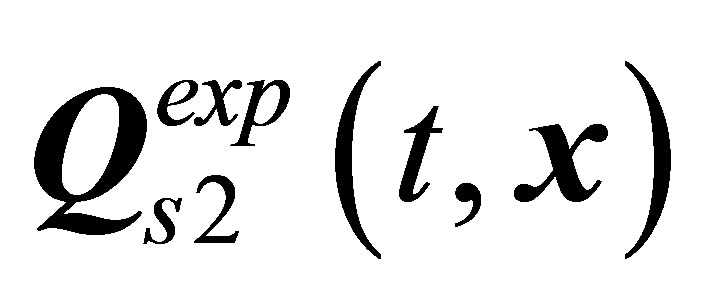 modes at the upper branch, Figure 1. However, the only
modes at the upper branch, Figure 1. However, the only 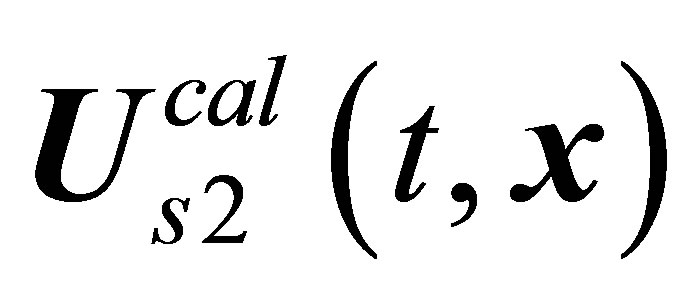 solution is incapable of reproducing four different modes simultaneously.
solution is incapable of reproducing four different modes simultaneously.
The streamline flow pictures for every quarter of the period of oscillations (Figure 25 in [20]) give an idea of the total period of recirculating zone oscillations in the 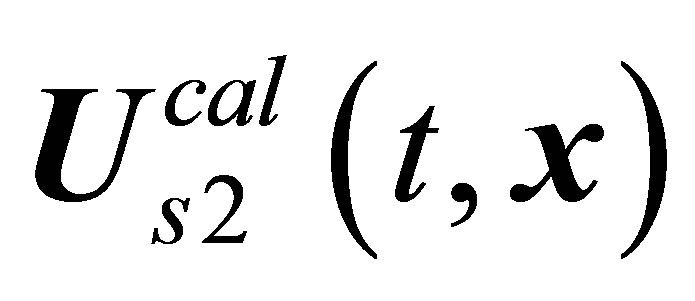 wake behind a sphere after the passage of the
wake behind a sphere after the passage of the 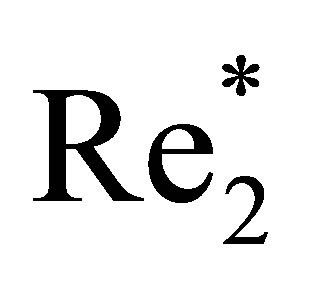 critical value. A detailed examination of these flow pictures was executed in [2,20]. To summarize, after the appearance in the wake behind a sphere, the size of the vortex structure becomes substantial at the surface of the sphere. Subsequently, the structure moves toward the periphery of the recirculating zone, which is accompanied by its continuous dissipation. Lastly, it fully disappears at the periphery of the recirculating zone.
critical value. A detailed examination of these flow pictures was executed in [2,20]. To summarize, after the appearance in the wake behind a sphere, the size of the vortex structure becomes substantial at the surface of the sphere. Subsequently, the structure moves toward the periphery of the recirculating zone, which is accompanied by its continuous dissipation. Lastly, it fully disappears at the periphery of the recirculating zone.
This picture is qualitatively different from the observed full period of oscillation of the recirculating zone. As in calculations, the experimental vortex structure engendered begins to expand and move downstream. After reaching the periphery of the recirculating zone, this vortex structure, however, acquires a maximum size rather than dissipates as predicted by calculations. At the end of the period, the vortex localized at the periphery of the recirculating zone separates from this zone. The separation of the shed vortex from the recirculating zone is very clearly shown in Figure 40 in [20]. The periphery of the recirculating zone, which is periodically shed from the recirculating zone, rushes downstream and forms a vortex street  (Figure 7(a,i) in [7]).
(Figure 7(a,i) in [7]).
Because of the absence of the detachment of the recirculating zone periphery in Figure 25 in the calculation [20], there is no vortex loop street in the wake behind a sphere. This is an essential difference between calculation and experiment. Analyzed Figure 25 from [20], the authors confirmed the disappearance of the vortex structure at the periphery of the recirculating zone. They note that the vortex structure “loses its spiral shape” at the periphery of the recirculating zone.
So, combining of the  and the
and the  did not give the desired result, because it did not allow the calculated
did not give the desired result, because it did not allow the calculated 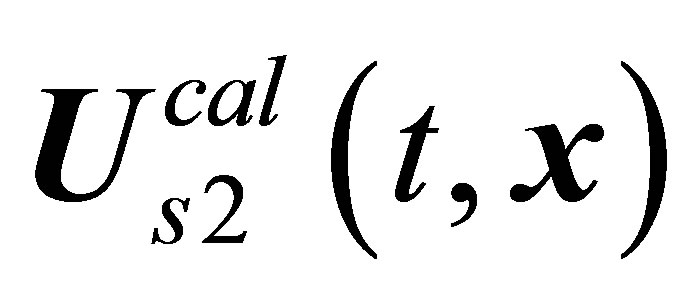 mode to be put in correspondence to the observed
mode to be put in correspondence to the observed 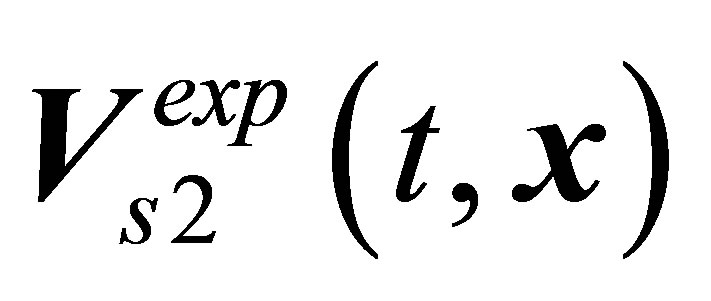 vortex shedding mode. Indeed, the calculated
vortex shedding mode. Indeed, the calculated  limiting cycle satisfactorily reproduces the stable central-type position
limiting cycle satisfactorily reproduces the stable central-type position 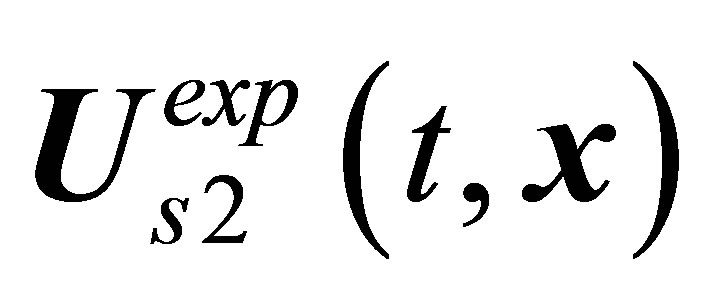 at
at  but proves a complete failure when attempts are made to reproduce the
but proves a complete failure when attempts are made to reproduce the  vortex shedding mode at
vortex shedding mode at 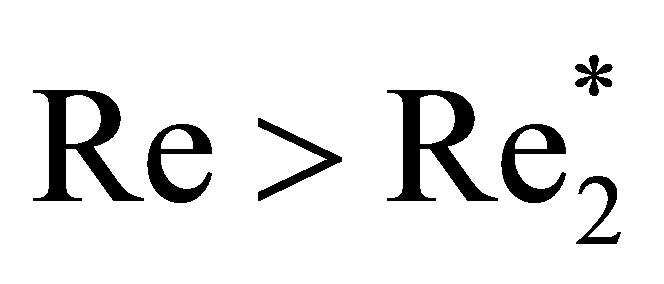 [18-21].
[18-21].
The 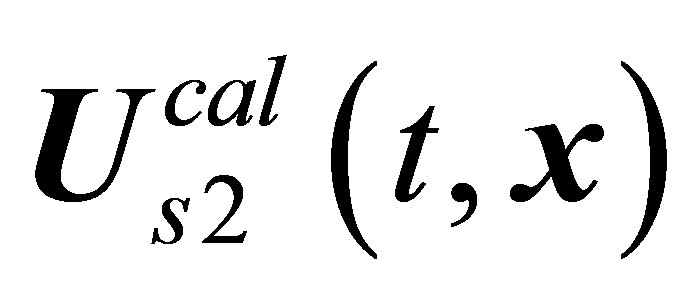 wake behind a sphere is drawn in [20] both by streamline flow pictures and by streakline flow pictures. On the flow pictures presented by streaklines, the lines having a form of hairpin vortices appear in near wake behind a sphere. However, a vortex street is absent too in the far wake on flow pictures presented by streaklines.
wake behind a sphere is drawn in [20] both by streamline flow pictures and by streakline flow pictures. On the flow pictures presented by streaklines, the lines having a form of hairpin vortices appear in near wake behind a sphere. However, a vortex street is absent too in the far wake on flow pictures presented by streaklines.
The authors of all the numerical experiments without exception discover the evident absence of a vortex street in the wake behind different bluff bodies on flow pictures. Numerical simulations were performed both for 2D and for 3D problems on flow around a circular cylinder and a flat plate, around a sphere and a disk, and so on. However, passed years gave no numerical experiments in which stability loss results in a periodic vortex shedding mode. Then, the conclusion of agreement between calculation and experiment is based in early direct numerical simulations on a comparison of the calculated vorticity distributions with visual observation results [18,21]. However, even insignificant twist in a streamline can create closed curves in the vorticity distribution pictures. And, really, the comparison of streamline flow pictures with the vorticity distributions (Figures 25 and 29 in [20]) shows that closed curves in the vorticity pictures correspond to wavy motion in the far wake behind a sphere rather than vortex structures. So, there is no reason at all for identifying the closed vorticity distribution curves in the wake with vortex structures.
That is why, Johnson and Patel [20] do not confine to drawing of streamline curves, streakline curves and vorticity distribution curves. To interpret the obvious contradiction between the observed vortex shedding and calculation results they put the regions of the supposed existence of vortex structures  in correspondence to the observed vortex shedding. The latter direct numerical simulations select namely this way to interpret the discrepancies between calculation and experiment [26,27]. The sense is that both calculated and experimental flow pictures are known to change qualitatively depending on the system of coordinates used to observe or calculate flows. Flow pictures represented by streamlines are not invariant with respect to the Galilean transformation. Vortex structures can be absent in a certain system and well defined in another. It follows that the uniform motion of a coordinate system can mask the vortex structure which, in reality, exists.
in correspondence to the observed vortex shedding. The latter direct numerical simulations select namely this way to interpret the discrepancies between calculation and experiment [26,27]. The sense is that both calculated and experimental flow pictures are known to change qualitatively depending on the system of coordinates used to observe or calculate flows. Flow pictures represented by streamlines are not invariant with respect to the Galilean transformation. Vortex structures can be absent in a certain system and well defined in another. It follows that the uniform motion of a coordinate system can mask the vortex structure which, in reality, exists.
Taking this into consideration, Jeong and Hussian developed a method for distinguishing space regions  in which vortex structures can hypothetically exist [28]. The study performed in [28] showed that the
in which vortex structures can hypothetically exist [28]. The study performed in [28] showed that the 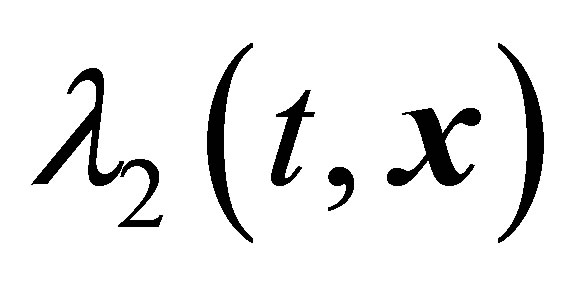 regions were indeed capable of predicting the position of vortex structures in space. These predictions are, however, fairly approximate.
regions were indeed capable of predicting the position of vortex structures in space. These predictions are, however, fairly approximate.
Namely, streamline flow pictures can contain regions with vortex structures that are undetectable by the JeongHussian method. Conversely, this method can show the regions of existence for vortex structures where, according to the streamline flow pictures, vortex structures are absent. Moreover, the Jeong-Hussian method outlines the  contours of the supposed existence of vortex structures but does not indicate the particular coordinate system in which these vortex structures are to be sought. The Jeong-Hussian method cannot be used to correct flow pictures. On the contrary, the correctness of this method is evaluated by comparing the hypothetical regions where vortex structures with calculated flow pictures exist.
contours of the supposed existence of vortex structures but does not indicate the particular coordinate system in which these vortex structures are to be sought. The Jeong-Hussian method cannot be used to correct flow pictures. On the contrary, the correctness of this method is evaluated by comparing the hypothetical regions where vortex structures with calculated flow pictures exist.
Once more, the Jeong-Hussian method [28] outlines only the boundaries of the  regions. The boundaries of the
regions. The boundaries of the  regions are very widespread, because vortex structures from all the reference systems without exception must find a place within these
regions are very widespread, because vortex structures from all the reference systems without exception must find a place within these  regions. The method is incapable of penetrating the
regions. The method is incapable of penetrating the 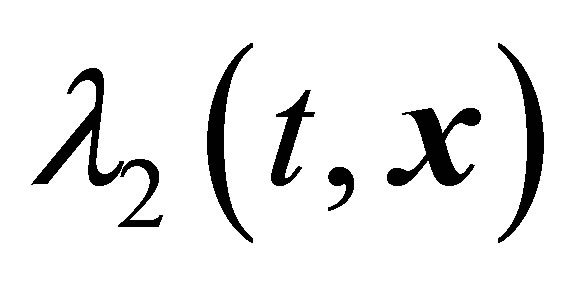 region. As a consequence, the method is incapable of revealing the presence or the absence of vortex structure within the
region. As a consequence, the method is incapable of revealing the presence or the absence of vortex structure within the  region. Nevertheless, namely boundaries of the
region. Nevertheless, namely boundaries of the 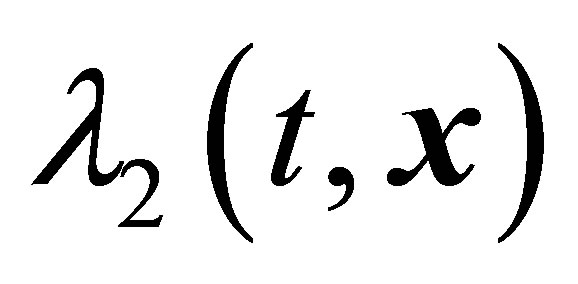 regions are put in correspondence to observed vortex structures. The ideas of appearance of vortex structures are based on the appearance of boundaries of the
regions are put in correspondence to observed vortex structures. The ideas of appearance of vortex structures are based on the appearance of boundaries of the 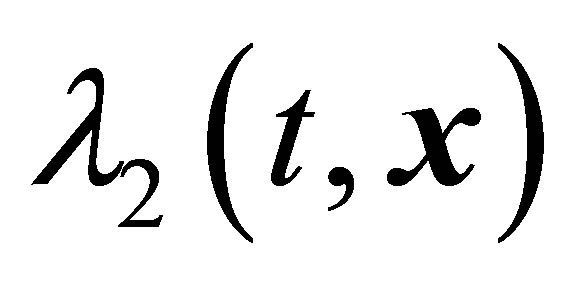 regions. The ideas of temporal evolution of vortex structures are based on temporal evolution of boundaries of the
regions. The ideas of temporal evolution of vortex structures are based on temporal evolution of boundaries of the 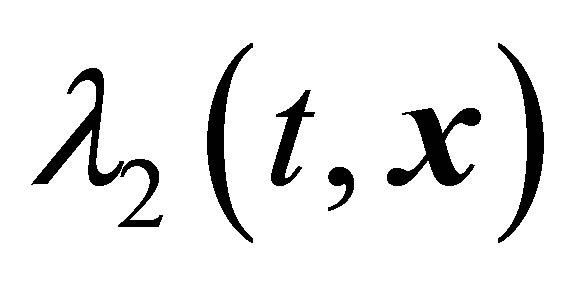 regions too.
regions too.
The 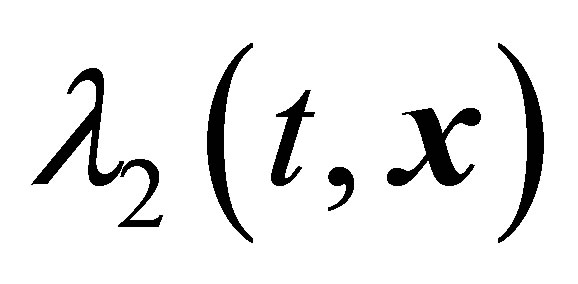 region of the supposed existence of vortex structures represented in Figure 31 from [20] extends in the wake behind a sphere to distances much larger than the sphere diameter. However, in the spherefixed
region of the supposed existence of vortex structures represented in Figure 31 from [20] extends in the wake behind a sphere to distances much larger than the sphere diameter. However, in the spherefixed  coordinate system the calculation does not find any vortex structures within the
coordinate system the calculation does not find any vortex structures within the 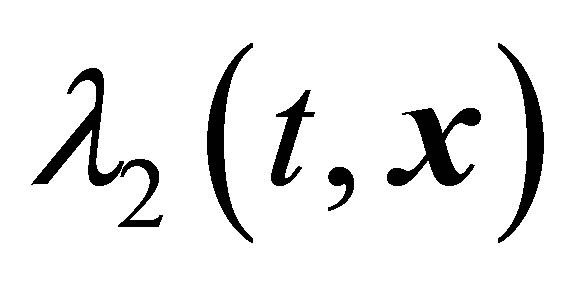 region (Figure 25 in [20]). To summarize, the
region (Figure 25 in [20]). To summarize, the  region pattern does not remove the discrepancy between the streamline flow picture calculated in the
region pattern does not remove the discrepancy between the streamline flow picture calculated in the  system of coordinates and the flow picture observed in the same system. Really, the experiment records the hairpin vortex shedding in the wake behind a sphere (Figure 7(a,i) in [7]). The streamline flow picture draws the periodic restructuring in the near wake, which causes wavy motion in the far wake without vortex shedding (Figure 25 in [20]).
system of coordinates and the flow picture observed in the same system. Really, the experiment records the hairpin vortex shedding in the wake behind a sphere (Figure 7(a,i) in [7]). The streamline flow picture draws the periodic restructuring in the near wake, which causes wavy motion in the far wake without vortex shedding (Figure 25 in [20]).
There may exist such reference system  in which the vortex shedding appears in the calculated flow picture. Possibly, the flow picture calculated in the
in which the vortex shedding appears in the calculated flow picture. Possibly, the flow picture calculated in the  system will be identical to the photographs of the flow obtained in the same
system will be identical to the photographs of the flow obtained in the same  system. Today, calculation does not discover such reference system
system. Today, calculation does not discover such reference system .
.
The possibilities of variation the boundary and initial conditions of calculations to bring it in strict correspondence to the experimental boundary and initial conditions are not very narrowly, the possibilities of perfecting the numerical procedure applied in recent simulations are boundless. Nevertheless, there are almost no prospects for a cardinal change in the calculated flow pictures [2]. It is therefore very improbable that the instability development direction calculated in [15,16,18-21] can change and new solutions to the Navier-Stokes equations other than ,
,  ,
, 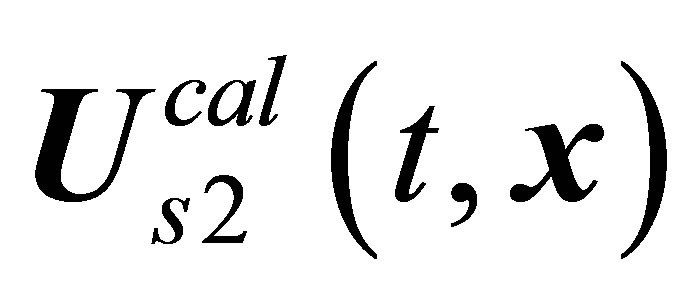 , and
, and 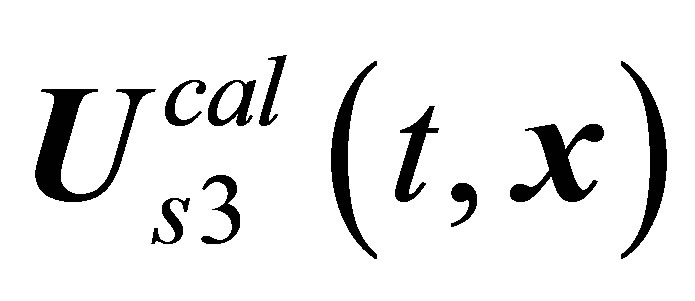 can appear.
can appear.
It may well be that the interpretation of experimental results presented in Section 2 is not ultimate. Possibly, the directions presented will be augmented by new modes that have not been recorded up to now. It is also possible that the modes that have been recorded will be differently distributed over the three directions shown in Figure 1, and new modes will force us to modify the concepts upon which the three turbulence development directions are based. However, irrespective of any modifications of the scheme shown in Figure 1, it is very improbable that one of the conclusions drawn from comparing it with experiment will change. Namely, calculations are incapable of reproducing any of the six periodical vortex shedding modes observed along the three turbulence development directions (Figure 1). Most likely [1,2], the reason for simulation failure is the NavierStokes equations themselves.
3. Increase in the Number of Principal Hydrodynamic Values
Classic hydrodynamics equations exist for about two centuries. By definition, these equations are valid for the description of arbitrary continuous media corresponding to continuity and unlimited deformability principles [29]. Statistically grounded hydrodynamics equations are, however, far from being completely established. The greatest progress in this direction was made for one of continuous medium states, namely, for the rarefied gas state, where the characteristic free path 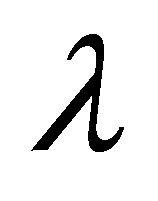 far exceeded the characteristic size of particles
far exceeded the characteristic size of particles . In a rarefied gas, that is, at
. In a rarefied gas, that is, at , the path from classic mechanics equations written separately for each of the
, the path from classic mechanics equations written separately for each of the 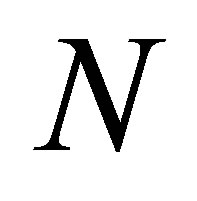 medium particle to classic hydrodynamics equations was passed without additional assumptions. The only exception was the Boltzmann hypothesis of molecular chaos “Stosszahlansatz” (Figure 3).
medium particle to classic hydrodynamics equations was passed without additional assumptions. The only exception was the Boltzmann hypothesis of molecular chaos “Stosszahlansatz” (Figure 3).
Classic direction and pair-multimoment direction are two independent branches of the statistical deterministic approach to medium description. Classic kinetics and classic hydrodynamics are direct corollaries to the first equation of the Bogolyubov-Born-Green-Kirkwood-Yvon

Figure 3. The scheme of the statistical deterministic approach.
chain of equations, i.e., the BBGKY hierarchy [30]. The kinetic equations for pair functions and the multimoment hydrodynamics equations are derived from the second of these equations. The BBGKY hierarchy is closed by the Liouville equation (Figure 3). To pass from the classical mechanics equations to the Liouville equation, the concept of the Gibbs ensemble is invoked. The Gibbs concept is the connecting link between the dynamical deterministic approach and the statistical deterministic approach [30].
The 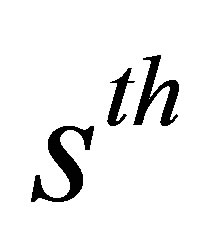 equation of the BBGKY hierarchy has the form,
equation of the BBGKY hierarchy has the form,
 (1)
(1)
where  is the mass of the particle;
is the mass of the particle;  is the force of the action of the
is the force of the action of the  on
on  particle; and
particle; and  are the spatial coordinate and velocity of the
are the spatial coordinate and velocity of the  particle, respectively. The
particle, respectively. The  s-particle distribution function has the meaning of the probability that at time
s-particle distribution function has the meaning of the probability that at time  particle 1 finds itself in unit element of the phase space near point
particle 1 finds itself in unit element of the phase space near point  and particle s near point
and particle s near point ,
,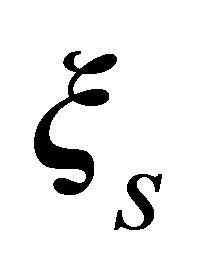 . The
. The 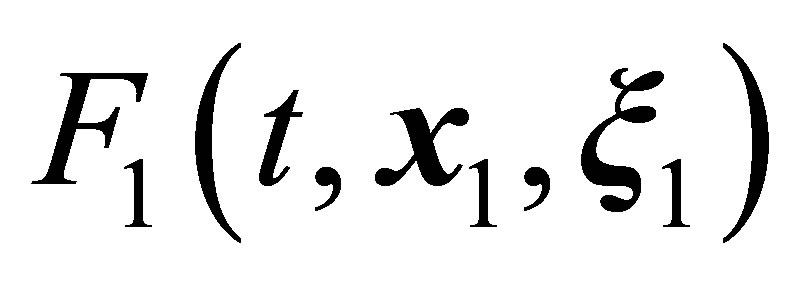 one-particle distribution function obeys the first equation of the BBGKY hierarchy (1). The first equation is not closed. The term on the right hand side of Equation (1) that contains the
one-particle distribution function obeys the first equation of the BBGKY hierarchy (1). The first equation is not closed. The term on the right hand side of Equation (1) that contains the 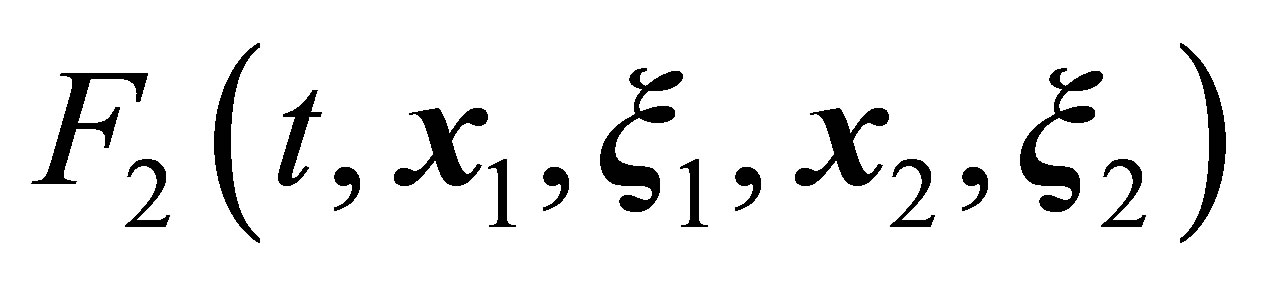 two-particle function is responsible for the interaction of particle 1 with some particle 2.
two-particle function is responsible for the interaction of particle 1 with some particle 2.
There are several variants of the derivation of the Boltzmann equation directly from the first equation of the BBGKY hierarchy [30]. Each of them reaches the equation,
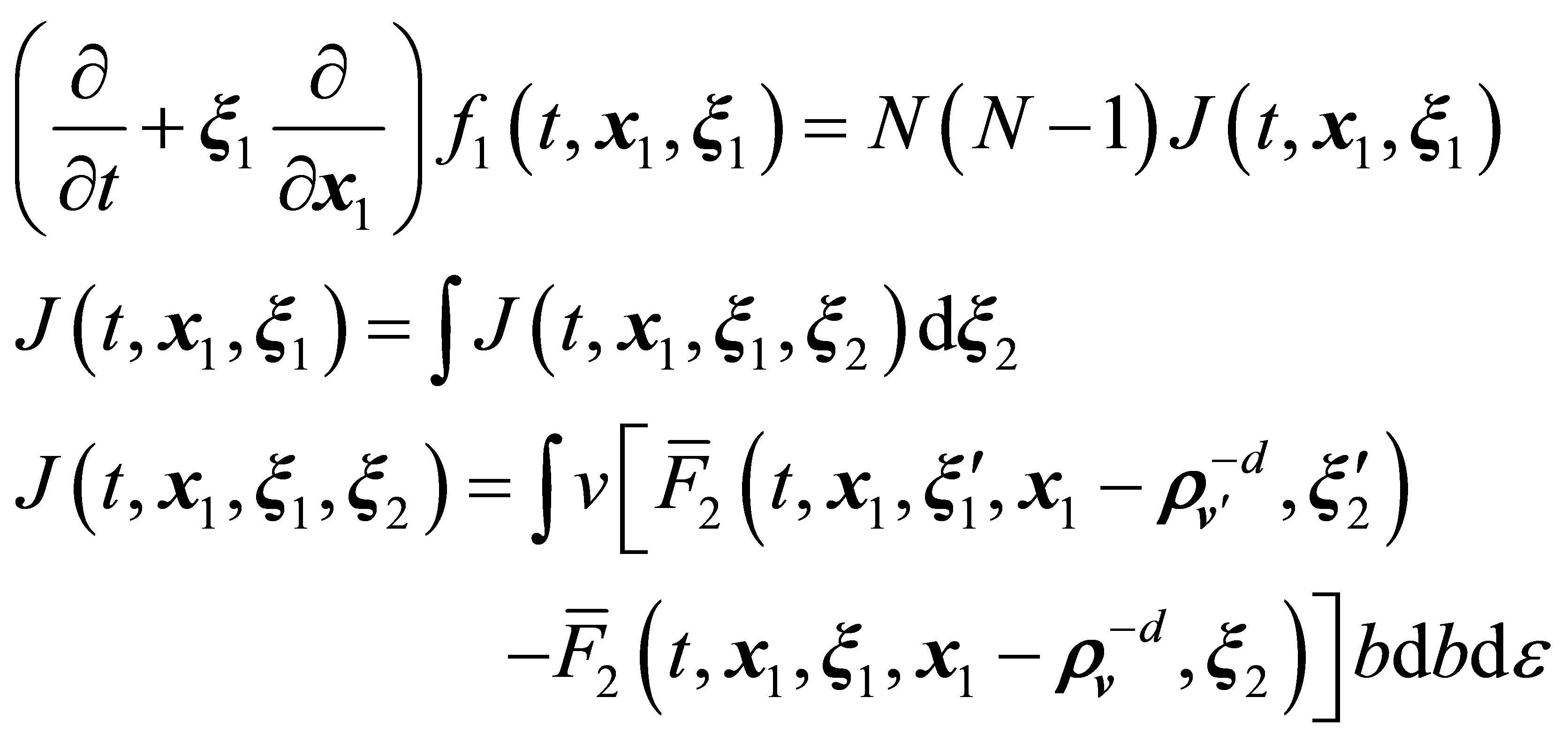 (2)
(2)
Equation (2) is valid for a rarefied gas, that is, at ,
,
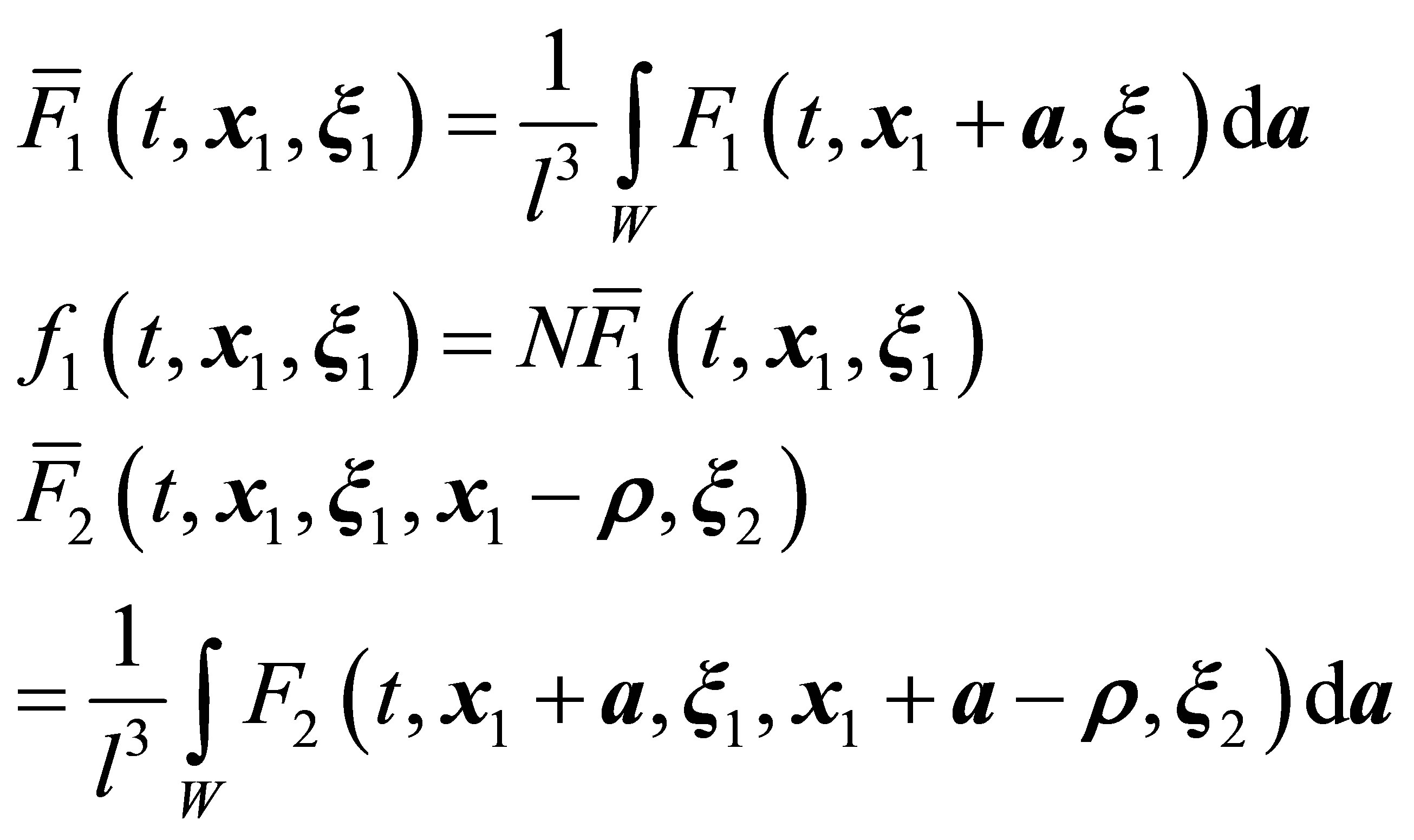 (3)
(3)
The one-particle distribution function  in Equations (2), (3) has the meaning of the probable number of particles situated at time
in Equations (2), (3) has the meaning of the probable number of particles situated at time  in unit volume element near point
in unit volume element near point  and having velocities in unit interval near the
and having velocities in unit interval near the  point. The spatial integration in Equation (3) is performed within the W region having the characteristic linear size
point. The spatial integration in Equation (3) is performed within the W region having the characteristic linear size ,
, . The averaged
. The averaged  and
and 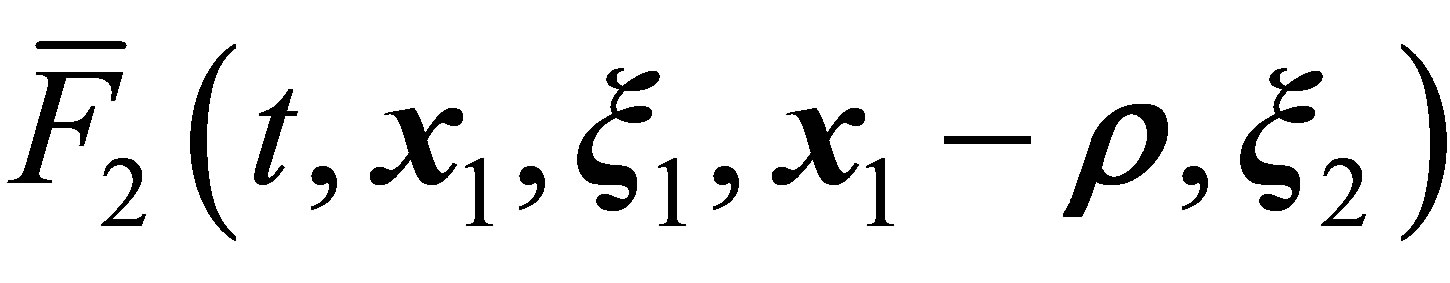 functions weakly change on the scale of particle size
functions weakly change on the scale of particle size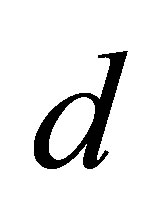 .
.
The  function on the right hand side of Equation (2) corresponds to a pair of particles 1 and 2, which enter the region of their interaction
function on the right hand side of Equation (2) corresponds to a pair of particles 1 and 2, which enter the region of their interaction  at velocities
at velocities  and
and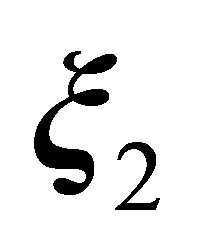 , respectively;
, respectively; , and
, and 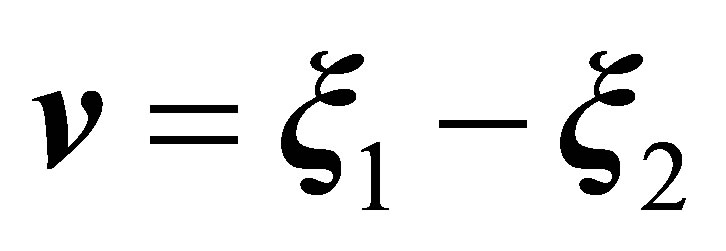 (Figure 4). The
(Figure 4). The  vector has the coordinates
vector has the coordinates  in the cylindrical system of coordinates with the z axis parallel to the
in the cylindrical system of coordinates with the z axis parallel to the  vector,
vector,  is the impact parameter, and
is the impact parameter, and  is the azimuthal angle. That is, the second term on the right hand side of Equation (2) is responsible for a decrease in the number of
is the azimuthal angle. That is, the second term on the right hand side of Equation (2) is responsible for a decrease in the number of  -particles in collisions with other particles. The
-particles in collisions with other particles. The
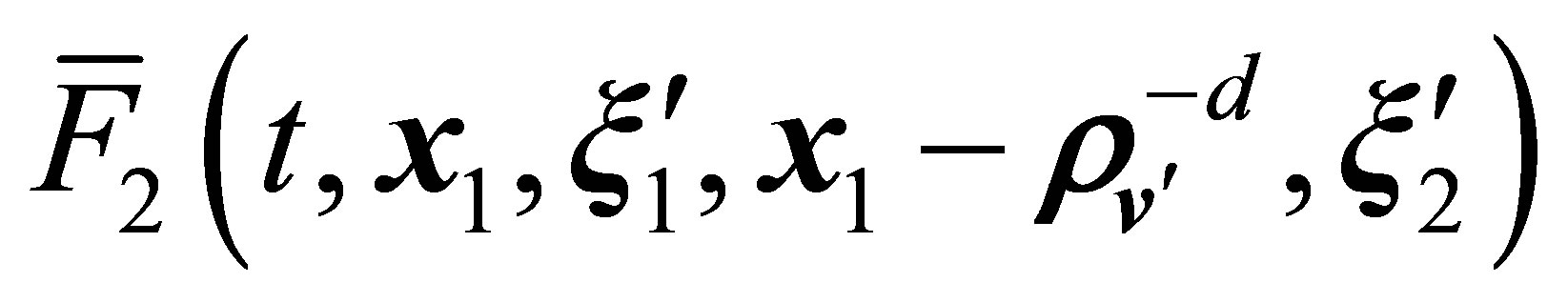 function corresponds to a pair of particles 1 and 2, which enter the region of their interaction
function corresponds to a pair of particles 1 and 2, which enter the region of their interaction 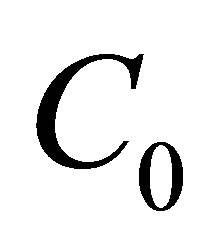 at velocities
at velocities  and
and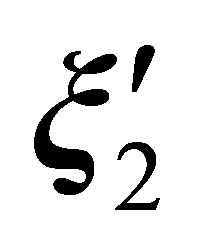 , respectively,
, respectively,
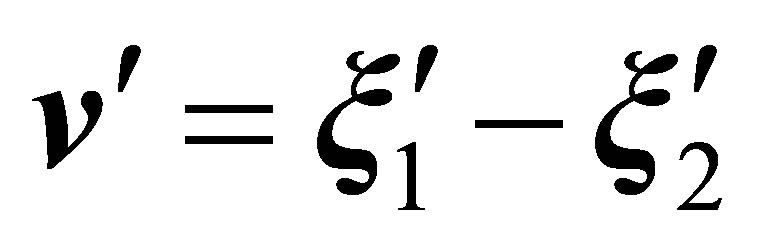 . The coordinates of the
. The coordinates of the 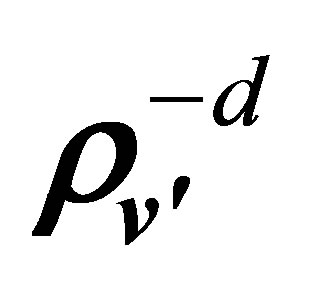 vector are
vector are
 in the cylindrical system coordinates with the
in the cylindrical system coordinates with the  axis parallel to
axis parallel to . At the exit of the region of their interaction, particles 1 and 2 then have velocities
. At the exit of the region of their interaction, particles 1 and 2 then have velocities  and
and  respectively (Figure 4), that is, the first term on the right hand side of (2) is responsible for an increase in the number of
respectively (Figure 4), that is, the first term on the right hand side of (2) is responsible for an increase in the number of  -particles caused by collisions.
-particles caused by collisions.
The factorization of two-particle distribution functions in  from Equation (2), that is, their representation in the form of the product of two one-particle functions,
from Equation (2), that is, their representation in the form of the product of two one-particle functions,
 (4)
(4)
leads to a closed Boltzmann classic kinetic equation,
 (5)
(5)
The approximation that we use was called the molecular chaos hypothesis “Stosszahlansatz” [31]. Classic hydrodynamics equations follow directly from the Boltzmann equation (Figure 3) and, naturally, include errors made in the derivation of the classic kinetic equation. Let us elucidate the physical meaning of the error introduced by the Boltzmann hypothesis into hydrodynamics.
Let us pass in Equation (2) from  functions written in and
functions written in and  variables to
variables to  functions written in
functions written in ,
,  ,
,  , and
, and  variables,
variables,
 (6)
(6)
The velocity of the center of mass of pair particles,  , and the modulus
, and the modulus  of the relative velocity of particles
of the relative velocity of particles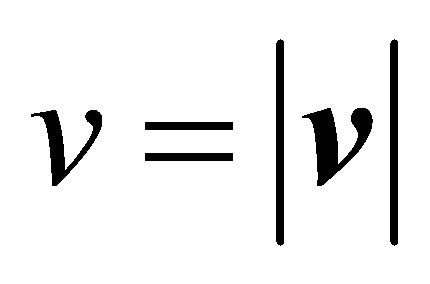 , are invariants of a binary particle collision. The enumeration of all the admissible target parameter values b and
, are invariants of a binary particle collision. The enumeration of all the admissible target parameter values b and  and relative motion velocity directions v at fixed
and relative motion velocity directions v at fixed  and
and  values then gives all the possible velocity directions
values then gives all the possible velocity directions . It follows that a collision-caused decrease in the number of pairs of particles from a unit phase volume interval near the
. It follows that a collision-caused decrease in the number of pairs of particles from a unit phase volume interval near the  point characterized by all the admissible b and
point characterized by all the admissible b and  parameter values and relative motion
parameter values and relative motion  orientations is strictly balanced by a collision induced increase in the number of pairs of particles in this interval with these parameters,
orientations is strictly balanced by a collision induced increase in the number of pairs of particles in this interval with these parameters,
 (7)
(7)
Here , and
, and  and
and  are the spherical coordinates of the
are the spherical coordinates of the  vector.
vector.
Suppose that ,
, 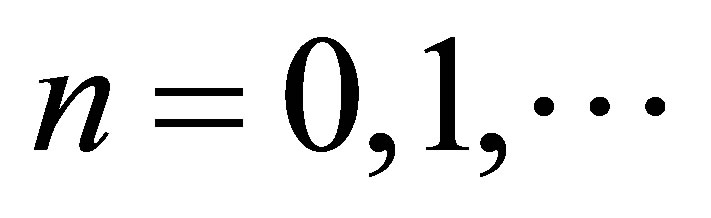 , is an arbitrary weight function of velocities
, is an arbitrary weight function of velocities  and
and . The properties of the
. The properties of the ,
, 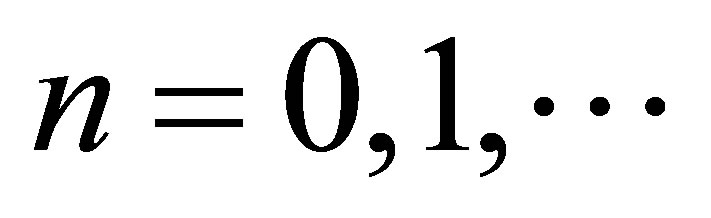 , pair are invariants of a particle binary collision. Let us multiply the
, pair are invariants of a particle binary collision. Let us multiply the  collision integral determined by Equation (6) by
collision integral determined by Equation (6) by ,
, 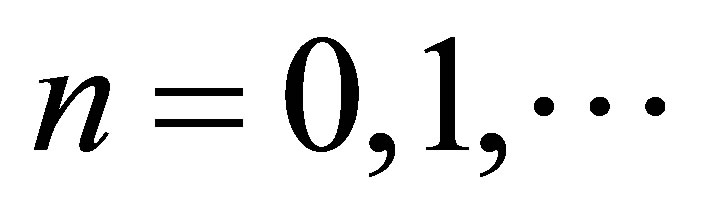 , and integrate the result with respect to velocities. By virtue of Equation (7), we then have,
, and integrate the result with respect to velocities. By virtue of Equation (7), we then have,
 (8)
(8)
This means that particle collisions cannot influence the formation of hydrodynamic values constructed on the properties of the ,
,  , pair. In other words, particle collisions cannot tune the distributions of all these hydrodynamic values to distributions of some other hydrodynamic values. That is, the set of hydrodynamic values constructed on the property of
, pair. In other words, particle collisions cannot tune the distributions of all these hydrodynamic values to distributions of some other hydrodynamic values. That is, the set of hydrodynamic values constructed on the property of ,
,  ,
,
 (9)
(9)
is a set of the principal hydrodynamic values, the  is local proportionality coefficient. Set (9) contains not only the lower
is local proportionality coefficient. Set (9) contains not only the lower  function moments but also all the higher moments without exception. To summarize, our analysis of the properties of the
function moments but also all the higher moments without exception. To summarize, our analysis of the properties of the  collision integral reveals the existence of an infinite number of principal hydrodynamic values.
collision integral reveals the existence of an infinite number of principal hydrodynamic values.
Under free molecular conditions, when , particle collisions do not participate in the formation of distributions of hydrodynamic values. These distributions are formed under the influence of the initial and boundary problem conditions, that is, each hydrodynamic value is principal. As the density of medium increases, the influence of intermolecular collisions on the formation of hydrodynamic value distributions increases. In a continuous medium,
, particle collisions do not participate in the formation of distributions of hydrodynamic values. These distributions are formed under the influence of the initial and boundary problem conditions, that is, each hydrodynamic value is principal. As the density of medium increases, the influence of intermolecular collisions on the formation of hydrodynamic value distributions increases. In a continuous medium,  , this influence becomes predominant. Namely, binary particle collisions tune the distributions of all the function moments to distribution of moments (9). The velocities
, this influence becomes predominant. Namely, binary particle collisions tune the distributions of all the function moments to distribution of moments (9). The velocities  and
and  are invariants of a particle binary collision. That is why, according to Equation (8), moments (9), as previously, do not experience the influence of binary particle collisions. As in the free molecular mode, that is, at
are invariants of a particle binary collision. That is why, according to Equation (8), moments (9), as previously, do not experience the influence of binary particle collisions. As in the free molecular mode, that is, at , moments (9) remain principal hydrodynamic values.
, moments (9) remain principal hydrodynamic values.
The equation for the  one-particle distribution function is written in a six-dimensional phase space of one particle (
one-particle distribution function is written in a six-dimensional phase space of one particle ( space). The dimensionality of the
space). The dimensionality of the 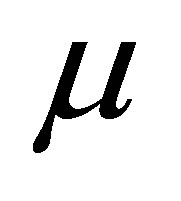 space allows only the properties of particle
space allows only the properties of particle ,
,  , to be accommodated in it; binary particle collision invariants, that is,
, to be accommodated in it; binary particle collision invariants, that is,  ,
,  , do not fit into the
, do not fit into the  space. The symmetry properties of the
space. The symmetry properties of the  collision integral strictly correspond to the symmetry properties of the Boltzmann collision integral (5), [31]. It follows that only three lower particle properties, namely
collision integral strictly correspond to the symmetry properties of the Boltzmann collision integral (5), [31]. It follows that only three lower particle properties, namely , can lead to the disappearance of the
, can lead to the disappearance of the  collision integral. Let us sequentially accommodate three lower properties of a particle in the
collision integral. Let us sequentially accommodate three lower properties of a particle in the  space. We then have,
space. We then have,
 (10)
(10)
Equations (10) are valid because of symmetry of the partial distribution function  with respect to the permutation of the phase coordinates of two particles [3]. The symmetry properties allow all the moments of the two-particle distribution functions odd with respect to
with respect to the permutation of the phase coordinates of two particles [3]. The symmetry properties allow all the moments of the two-particle distribution functions odd with respect to  to be removed from (10), [32].
to be removed from (10), [32].
It follows that the integrals that contain the lower particle properties , as weight functions are strictly reduced to the integrals with the
, as weight functions are strictly reduced to the integrals with the  weight functions belonging to
weight functions belonging to 
 , invariants. Three lower particle properties
, invariants. Three lower particle properties 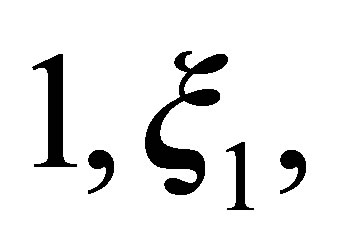 and
and  give three lower
give three lower  one-particle distribution function moments, the density of the number of particles
one-particle distribution function moments, the density of the number of particles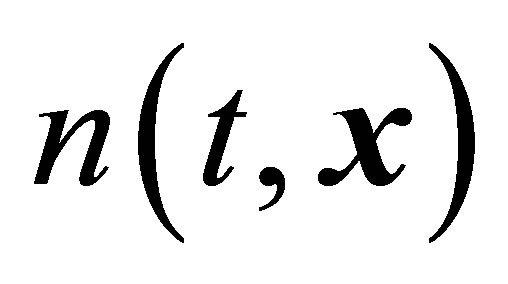 , medium velocity
, medium velocity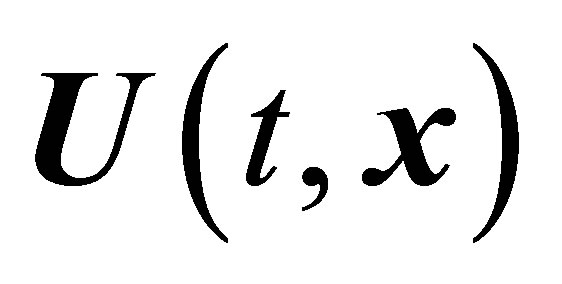 , and medium pressure
, and medium pressure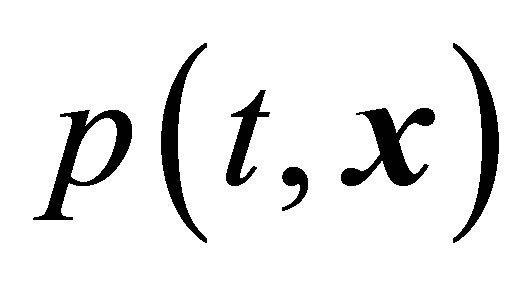 . It follows that, when we pass to the hydrodynamic stage from the phase space of one particle, such hydrodynamics equations cannot be constructed using more than three lower principal hydrodynamic values corresponding to the
. It follows that, when we pass to the hydrodynamic stage from the phase space of one particle, such hydrodynamics equations cannot be constructed using more than three lower principal hydrodynamic values corresponding to the  particle properties. The transition to the hydrodynamic stage from the phase space of one particle excludes higher principal hydrodynamic values (9) from participation in the construction of hydrodynamics equations. However, there is no rigorous passage to hydrodynamics from the
particle properties. The transition to the hydrodynamic stage from the phase space of one particle excludes higher principal hydrodynamic values (9) from participation in the construction of hydrodynamics equations. However, there is no rigorous passage to hydrodynamics from the  space. This passage is closed because Equation (2) is not closed.
space. This passage is closed because Equation (2) is not closed.
The use of the Boltzmann hypothesis (“Stosszahlansatz”) (4) opens up the possibility of approximate passage to hydrodynamics. So, the physical meaning of the error introduced by the Boltzmann hypothesis into hydrodynamics is as follows. It follows that just Boltzmann hypothesis allows us to construct hydrodynamics on only three lower principal hydrodynamic values. It follows that the use of the Boltzmann hypothesis excludes higher principal hydrodynamic values (9) from the participation in the formation of classic hydrodynamics equations. Since the classic three-moment hydrodynamics is constructed without the use of values (9), its applicability range is limited to states that are only weakly removed from the statistical equilibrium state. To substantiate this conclusion, we must find passage to hydrodynamics from the phase space capable of accommodateing the whole set of binary particle collision 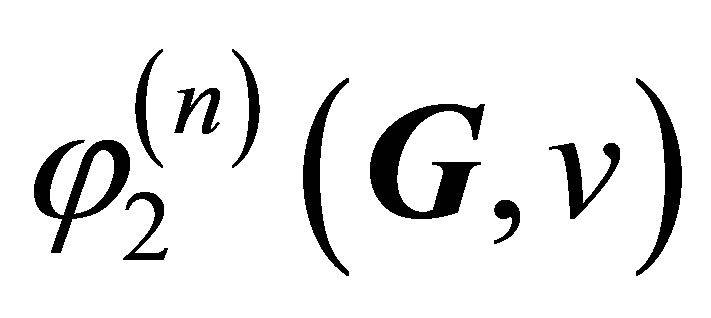
 , invariants.
, invariants.
The  two-particle distribution function obeys the second equation of the BBGKY hierarchy (1). The second equation is valid for arbitrary positions of particles 1 and 2 in space with respect to each other. It is not closed. There are, however, positions of particles 1 and 2 for which the second equation is considerably simplified.
two-particle distribution function obeys the second equation of the BBGKY hierarchy (1). The second equation is valid for arbitrary positions of particles 1 and 2 in space with respect to each other. It is not closed. There are, however, positions of particles 1 and 2 for which the second equation is considerably simplified.
The left hand side of the second equation of the BBGKY hierarchy (1),
 (11)
(11)
describes the free movement of particles 1 and 2 and the interaction between the particles 1 and 2. The integral terms containing the 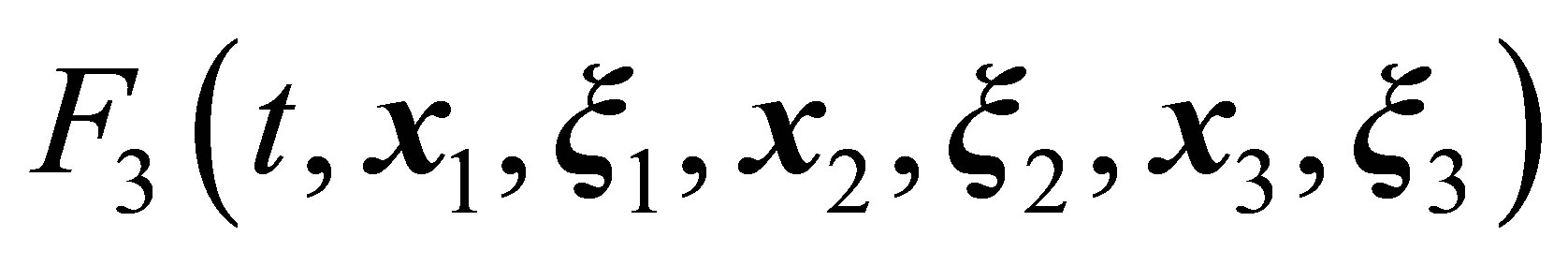 threeparticle distribution function are responsible for the interaction of particles 1 and 2 with some third particle 3. Presuming that a particle may be present at all phase space locations with equal probabilities, introduce the dimensionless quantities,
threeparticle distribution function are responsible for the interaction of particles 1 and 2 with some third particle 3. Presuming that a particle may be present at all phase space locations with equal probabilities, introduce the dimensionless quantities,
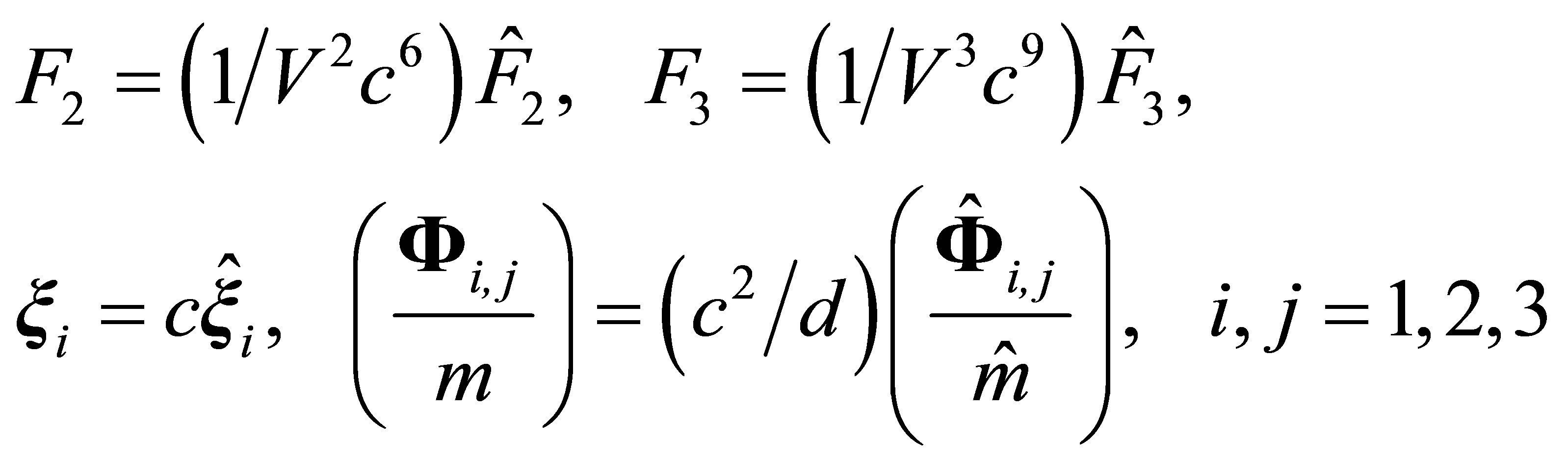 (12)
(12)
In Equation (12) the hat appears above the dimensionless quantities,  is the characteristic velocity of the particle, the ratio of the system volume
is the characteristic velocity of the particle, the ratio of the system volume 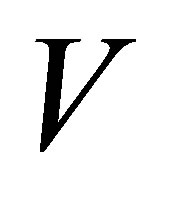 to the characteristic volume
to the characteristic volume 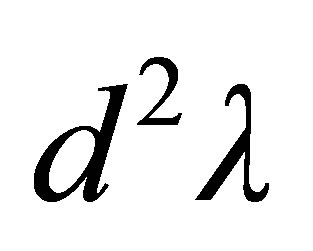 occupied by one particle is used as an estimation for
occupied by one particle is used as an estimation for . In the thermodynamic limit,
. In the thermodynamic limit,  ,
,  , yet,
, yet, 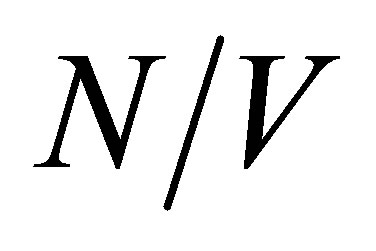 is finite.
is finite.
Let us bring the convective terms in the left hand side of Equation (11) into dimensionless form on the scale of particle size,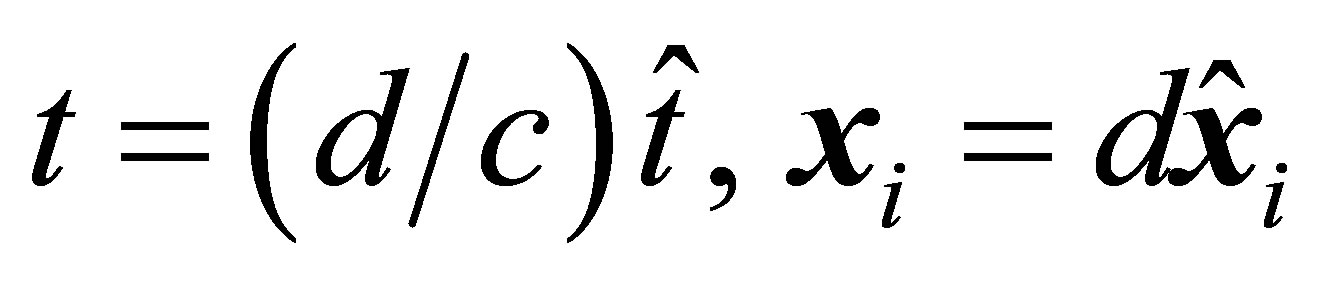 . In this case, the ratio of order of the right hand side terms to order of the left hand side terms of Equation (11) is of the order of
. In this case, the ratio of order of the right hand side terms to order of the left hand side terms of Equation (11) is of the order of . It means that the interaction with third particle has a very weak influence on the free movement of particles 1 and 2 and the interaction between the particles 1 and 2 at times, proportional to
. It means that the interaction with third particle has a very weak influence on the free movement of particles 1 and 2 and the interaction between the particles 1 and 2 at times, proportional to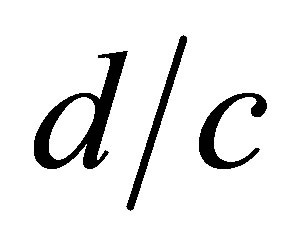 . The right hand side terms of Equation (11) receive the fundamental order only at times, proportional to
. The right hand side terms of Equation (11) receive the fundamental order only at times, proportional to .
.
Let us substitute the force term of the left hand side of the third equation of the BBGKY hierarchy (1) into the first term of the right hand side of Equation (11). Then,
 (13)
(13)
Here,
 ,
,
 ,
, . In the right hand side of Equation (13), the terms responsible for triple collisions of particles are omitted. The convective terms responsible for displacement of particles 1 and 2 during the time of interaction of particles 1 with particle 3 are omitted too. The omitted terms are negligible with respect to saved terms in the right hand side of Equation (13). The estimation of orders is carried out in accordance with Equation (12). As noted above, the order of the convective terms is estimated at times, proportional to
. In the right hand side of Equation (13), the terms responsible for triple collisions of particles are omitted. The convective terms responsible for displacement of particles 1 and 2 during the time of interaction of particles 1 with particle 3 are omitted too. The omitted terms are negligible with respect to saved terms in the right hand side of Equation (13). The estimation of orders is carried out in accordance with Equation (12). As noted above, the order of the convective terms is estimated at times, proportional to .
.
Positions of particles 1 and 3, described by the first and second terms of the right hand side of Equation (13), are depicted in Figure 4. However, when interpreting the collision integral (13) the vectors ,
,  ,
, 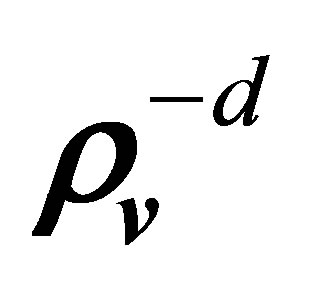 in Figure 4, should be replaced respectively by the vectors
in Figure 4, should be replaced respectively by the vectors ,
,  ,
,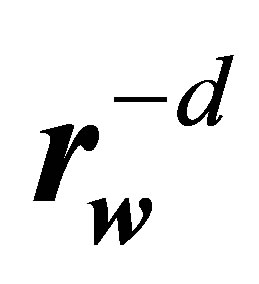 . The first term of the right hand side of Equation (13) is responsible for an increase in the number of
. The first term of the right hand side of Equation (13) is responsible for an increase in the number of  -particles caused by collisions with some third
-particles caused by collisions with some third  -particles
-particles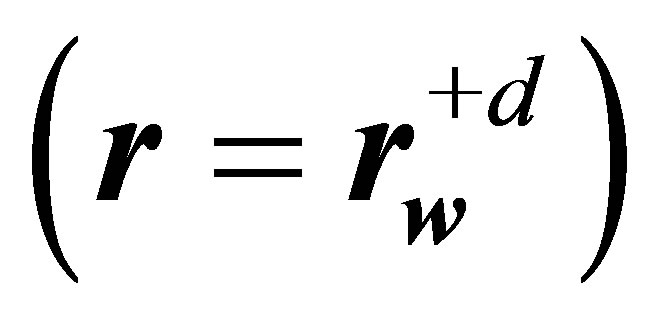 . If at time
. If at time  particles 1 and 3 leave the region of their interaction
particles 1 and 3 leave the region of their interaction , then later, within a time interval not exceeding
, then later, within a time interval not exceeding 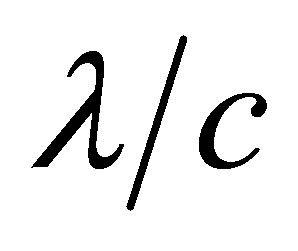 , they will be placed with respect to each other within the cylindrical volume oriented in the direction of vector
, they will be placed with respect to each other within the cylindrical volume oriented in the direction of vector  with bases area of
with bases area of  and height of
and height of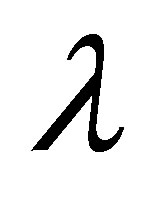 . I.e., these particles within a time interval of
. I.e., these particles within a time interval of 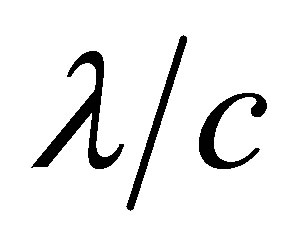 will be in the stage of departure from each other. The second term of the right hand side of Equation (13) is responsible for a decrease in the number of
will be in the stage of departure from each other. The second term of the right hand side of Equation (13) is responsible for a decrease in the number of  -particles in collisions with some third
-particles in collisions with some third  -particles
-particles . If at time
. If at time  particles 1 and 3 enter the region of their interaction
particles 1 and 3 enter the region of their interaction , then earlier, within a time interval not exceeding
, then earlier, within a time interval not exceeding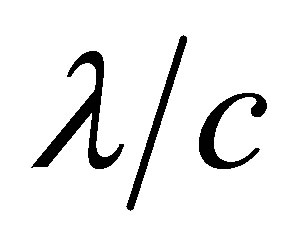 , they were placed with respect to each other within the cylindrical volume oriented in the direction of vector
, they were placed with respect to each other within the cylindrical volume oriented in the direction of vector  with bases area of
with bases area of  and height of
and height of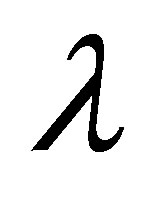 . i.e., these particles within a time interval of
. i.e., these particles within a time interval of 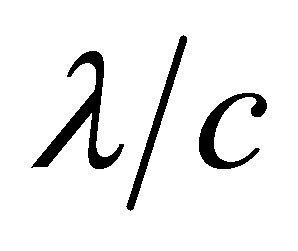 were in the stage of approaching with each other. Thus, the terms of the right hand side of Equation (13) at times, proportional to
were in the stage of approaching with each other. Thus, the terms of the right hand side of Equation (13) at times, proportional to , describe groups of three particles, in which two of three particles (1 and 3) find itself either at the stage of approaching before the collision with each other, or in the stage of departure from each other after collision. The second term of the right hand side of Equation (11) has the identical physical meaning.
, describe groups of three particles, in which two of three particles (1 and 3) find itself either at the stage of approaching before the collision with each other, or in the stage of departure from each other after collision. The second term of the right hand side of Equation (11) has the identical physical meaning.
The idea that leads to the concept of pair distribution functions is as follows. For instance, in a rarefied gas at each time moment, each particle after its last collision moves toward the next collision. This means that every particle 1 in a rarefied gas simultaneously flies away from some particle 2 with which it collided last at point D (Figure 5), and approaches some particle 2 with which it is to collide next at point B.
It follows that it is particle 2 plays the role of a third particle 3 for particle 1, with which particle 1 has already experienced a collision and will be in the stage of departure within a time interval not exceeding  (Figure 5(a)). At the same time, it is particle 1 plays the role of a third particle 3 for particle 2, with which the particle 2 has already experienced a collision and will be in the stage of departure within a time interval not exceeding
(Figure 5(a)). At the same time, it is particle 1 plays the role of a third particle 3 for particle 2, with which the particle 2 has already experienced a collision and will be in the stage of departure within a time interval not exceeding 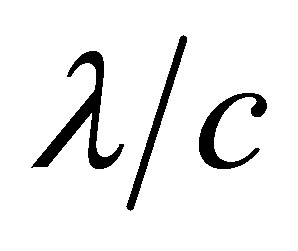 (Figure 5(a)). From the other hand, it is a particle 2 plays the role of a third particle 3 for particle 1, with which particle 1 should collide within a time interval not exceeding
(Figure 5(a)). From the other hand, it is a particle 2 plays the role of a third particle 3 for particle 1, with which particle 1 should collide within a time interval not exceeding 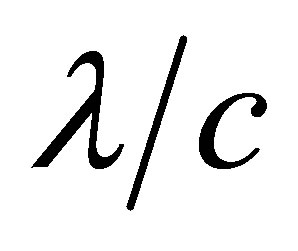 (Figure 5(b)). At the same time, it is particle 1 plays the role of a third particle 3 for particle 2,
(Figure 5(b)). At the same time, it is particle 1 plays the role of a third particle 3 for particle 2,

Figure 5. Graphic representation of a pair of particles.
with which the particle 2 should collide within a time interval not exceeding  (Figure 5(b)).
(Figure 5(b)).
The motion and interaction of particles 1 and 2 are, however, described by the left-hand side terms of the second equation of hierarchy (11) that are proportional to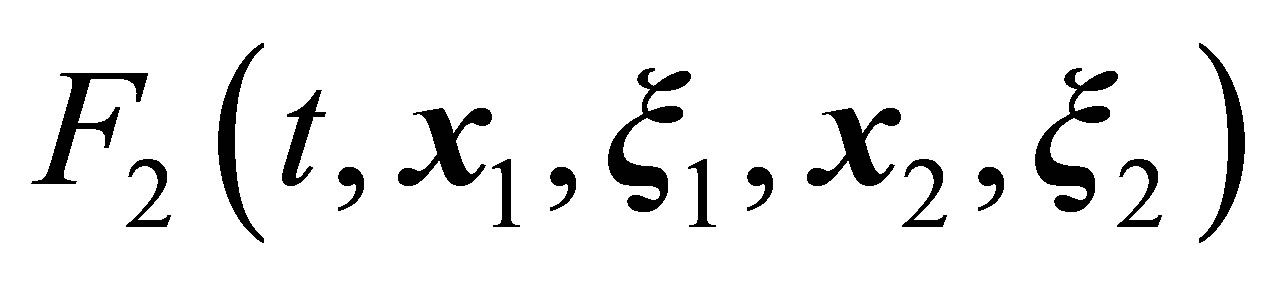 . For this reason, the terms containing
. For this reason, the terms containing 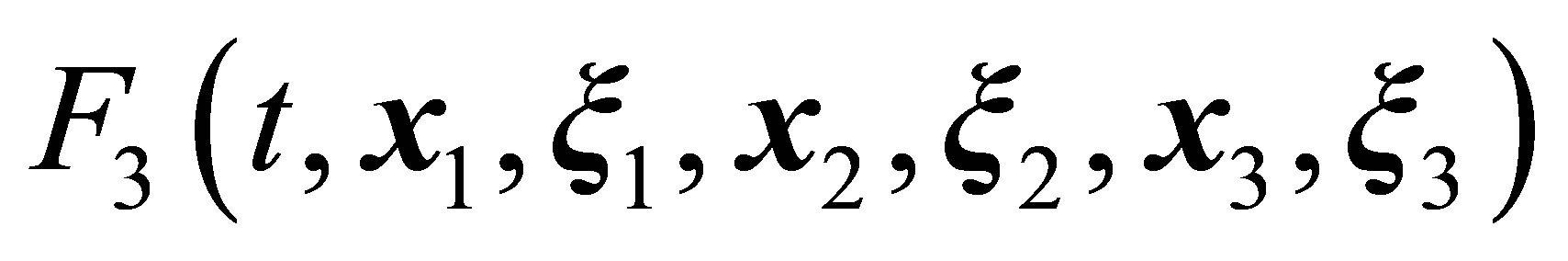 must be excluded for particles 1 and 2. The second equation of the BBGKY hierarchy (11) written for particles 1 and 2 (Figure 5), is therefore considerably simplified,
must be excluded for particles 1 and 2. The second equation of the BBGKY hierarchy (11) written for particles 1 and 2 (Figure 5), is therefore considerably simplified,
 (14)
(14)
Generally, any medium particle forms a pair with every other particle. A medium therefore contains  pairs of particles. All these pairs are described by the
pairs of particles. All these pairs are described by the  function, which obeys the second equation of hierarchy (11). If a single particle 2, which either flies away from (Figure 5(a)), or approaches (Figure 5(b)), some particle 1, is selected as a partner of this particle, this pair is described by the
function, which obeys the second equation of hierarchy (11). If a single particle 2, which either flies away from (Figure 5(a)), or approaches (Figure 5(b)), some particle 1, is selected as a partner of this particle, this pair is described by the 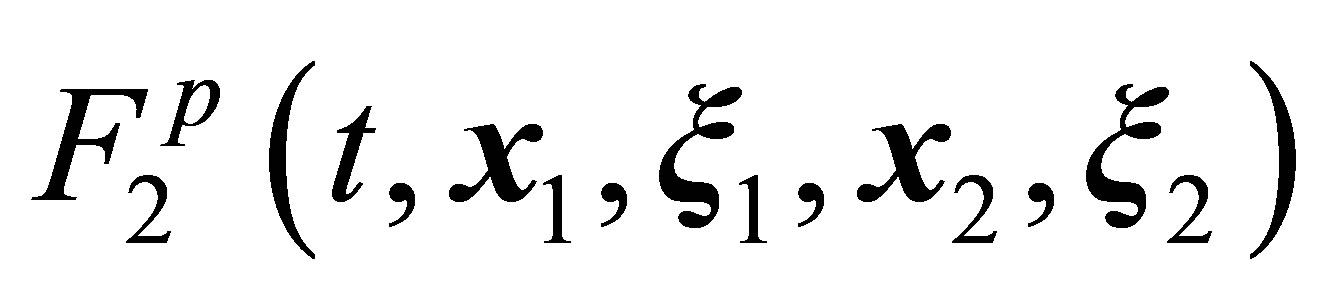 function that obeys Equation (14). Note that Equation (14) is valid for an arbitrary gas particle rather than some particular particle 1 (Figure 5). For this reason, Equation (14) is capable of describing the gas as a whole. A rigorous derivation of Equation (14) is given in [33]. There is an analogy between the derivation [33] and Grad method used in deriving the Boltzmann equation for a gas consisting of rigid spheres [30].
function that obeys Equation (14). Note that Equation (14) is valid for an arbitrary gas particle rather than some particular particle 1 (Figure 5). For this reason, Equation (14) is capable of describing the gas as a whole. A rigorous derivation of Equation (14) is given in [33]. There is an analogy between the derivation [33] and Grad method used in deriving the Boltzmann equation for a gas consisting of rigid spheres [30].
The arguments of the  function are
function are  and
and , which are the spatial coordinates of particles 1 and 2. Information about the position of a separate particle in space, however, becomes lost in kinetics and hydrodynamics. Classic kinetics and hydrodynamics deal with the place in space near which a set of particles are situated rather than with particle coordinates. It follows that a necessary condition for the transition from (14) to kinetics and hydrodynamics equations is getting rid of one of the spatial coordinates of the
, which are the spatial coordinates of particles 1 and 2. Information about the position of a separate particle in space, however, becomes lost in kinetics and hydrodynamics. Classic kinetics and hydrodynamics deal with the place in space near which a set of particles are situated rather than with particle coordinates. It follows that a necessary condition for the transition from (14) to kinetics and hydrodynamics equations is getting rid of one of the spatial coordinates of the  function. It was suggested in [33] that
function. It was suggested in [33] that 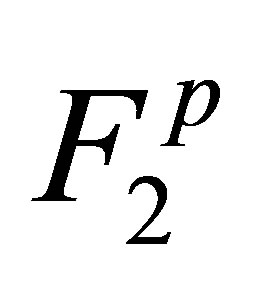 be integrated in one of its spatial coordinates within the cylinder of collisions. The
be integrated in one of its spatial coordinates within the cylinder of collisions. The  and
and  cylinders of collisions are oriented in the direction of the velocity
cylinders of collisions are oriented in the direction of the velocity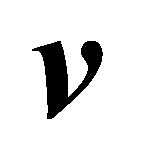 , the areas of their bases equal the collision cross section area
, the areas of their bases equal the collision cross section area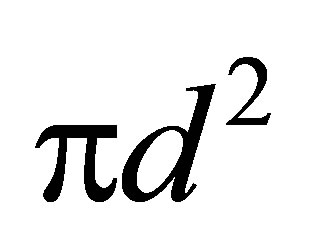 , and the heights of the cylinders equal the characteristic free path
, and the heights of the cylinders equal the characteristic free path . Let us pass from the 12-dimensional phase space of particles 1 and 2 constructed on the
. Let us pass from the 12-dimensional phase space of particles 1 and 2 constructed on the  vectors to the 12-dimensional space constructed on the
vectors to the 12-dimensional space constructed on the ,
,  ,
,  ,
,  vectors and produce pair distribution functions
vectors and produce pair distribution functions  and
and  ,
,
 (15)
(15)
Integration (15) collects all pairs of particles that either will inevitably collide during the time interval not exceeding the characteristic time between collisions 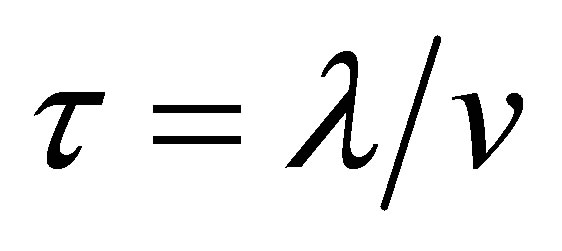 or fly away from each other after a collision that occurs during the time interval not exceeding
or fly away from each other after a collision that occurs during the time interval not exceeding . The integration with respect to
. The integration with respect to  within
within  region removes strong spatial dependence of the functions on the scale having the characteristic size of particles
region removes strong spatial dependence of the functions on the scale having the characteristic size of particles . The pair distribution function
. The pair distribution function 
 has the meaning of the probable number of pairs of particles approaching (diverging from) each other whose centers of mass are concentrated at time t in a unit volume element near point
has the meaning of the probable number of pairs of particles approaching (diverging from) each other whose centers of mass are concentrated at time t in a unit volume element near point  and the velocities of the centers of mass and relative particle velocities, in unit velocity elements near
and the velocities of the centers of mass and relative particle velocities, in unit velocity elements near  and
and , respectively. The relations between pair distribution functions (15) and
, respectively. The relations between pair distribution functions (15) and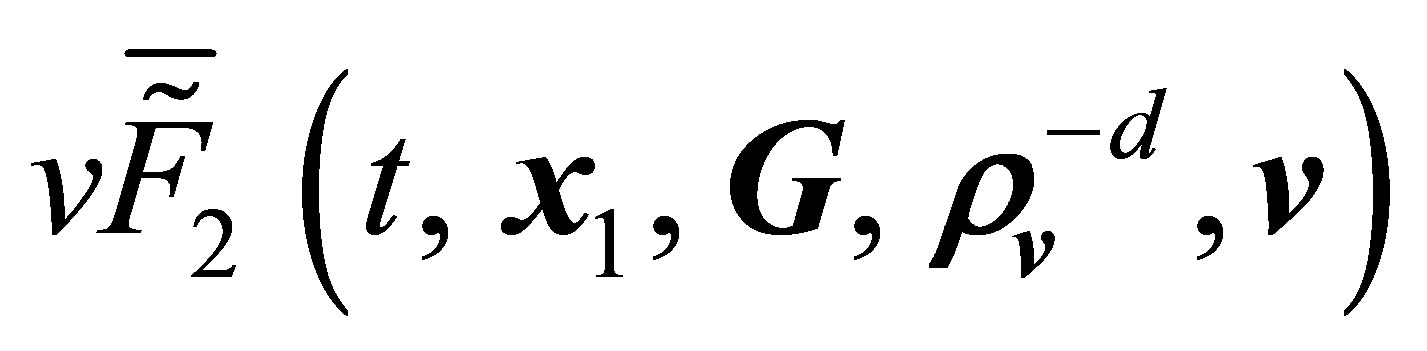 , and
, and 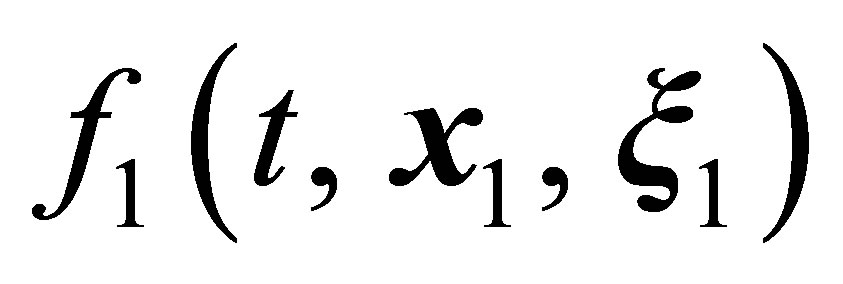
from [3] can be used to find the proportionality coefficient (9),
 (16)
(16)
Heuristic derivation of a system of kinetic equations for pair distribution functions 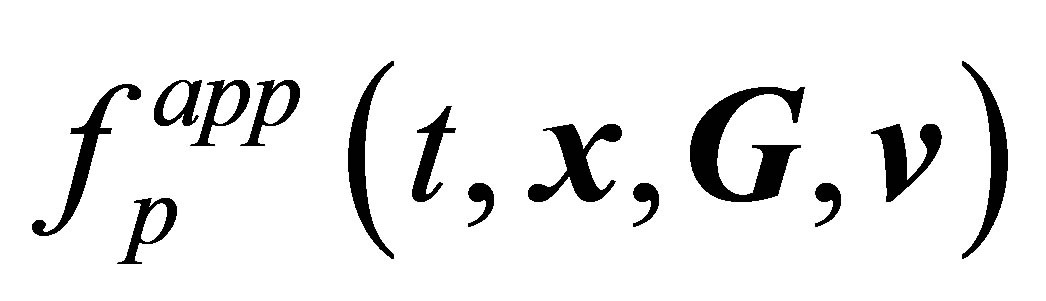 and
and  was given in [34]. In [33], equations for pair distribution functions (15) are derived directly from the fundamental statistical mechanics concepts. An analysis of the system of kinetic equations [33,34] reveals the most important property of
was given in [34]. In [33], equations for pair distribution functions (15) are derived directly from the fundamental statistical mechanics concepts. An analysis of the system of kinetic equations [33,34] reveals the most important property of  pair distribution function constructed on the velocity of the center of mass
pair distribution function constructed on the velocity of the center of mass  and the relative velocity modulus
and the relative velocity modulus ,
,
 (17)
(17)
Here,
 (18)
(18)
and 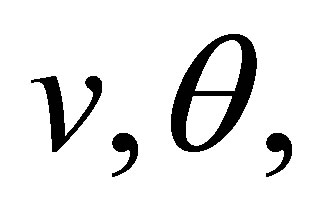 and
and  are the spherical coordinates of the
are the spherical coordinates of the 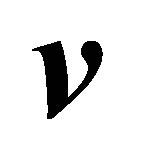 vector. According to Equation (17), the
vector. According to Equation (17), the 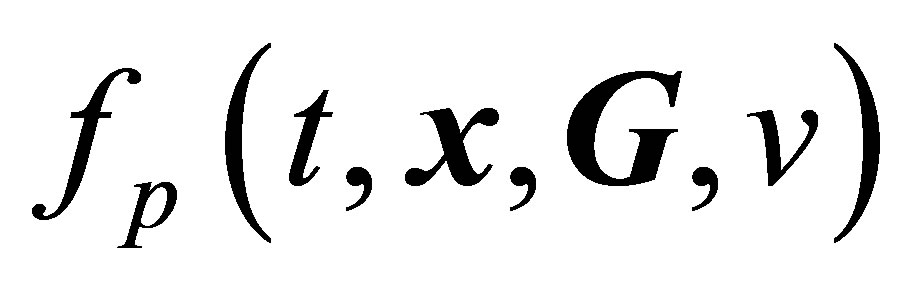 function remains unchanged at time along the trajectory of the center of mass of the pair.
function remains unchanged at time along the trajectory of the center of mass of the pair.
The lower moments of the pair distribution functions (18) are the local density of the number of pairs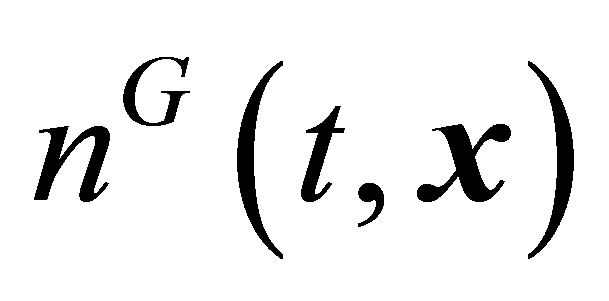 , the mean velocity of the centers of mass of pairs
, the mean velocity of the centers of mass of pairs , the
, the  tensor of stresses created as a result of movement of the centers of mass of pairs of particles, the
tensor of stresses created as a result of movement of the centers of mass of pairs of particles, the  tensor of stresses created because of relative movement of pair particles, the
tensor of stresses created because of relative movement of pair particles, the 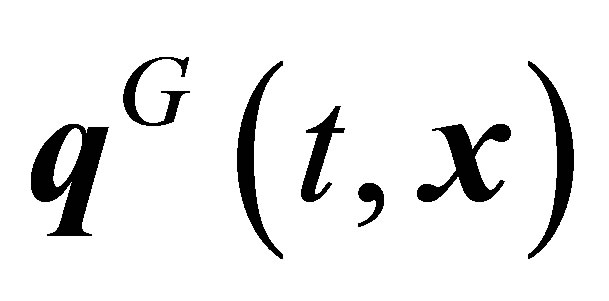 heat flux vector corresponding to the transfer of thermal energy because of movement of the centers of mass of pairs of particles,
heat flux vector corresponding to the transfer of thermal energy because of movement of the centers of mass of pairs of particles, 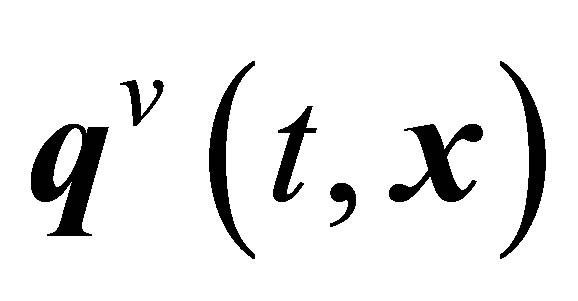 and
and  the and heat flux vectors corresponding to thermal energy transfer because of relative movement of particles in pairs. Along with
the and heat flux vectors corresponding to thermal energy transfer because of relative movement of particles in pairs. Along with 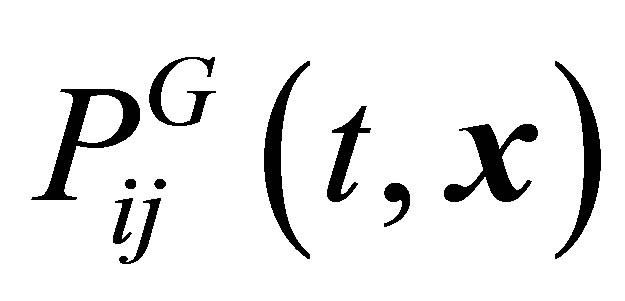 and
and 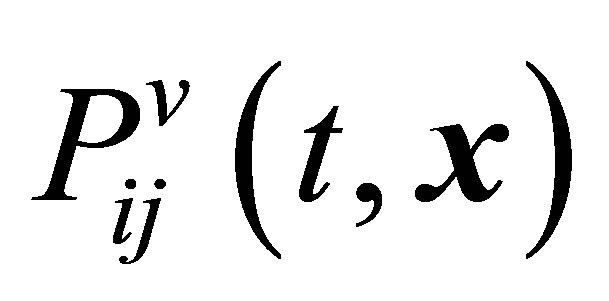 let us determine small stress tensors
let us determine small stress tensors 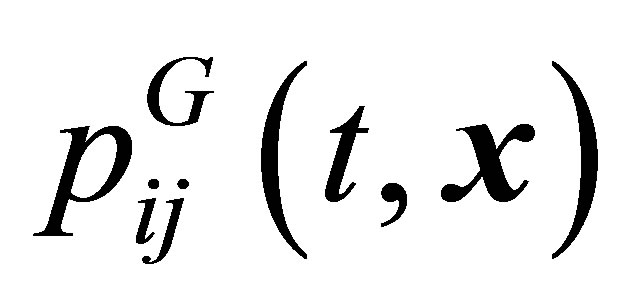 and
and , and
, and 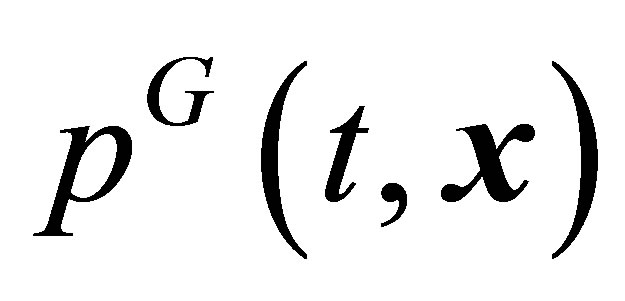 and
and 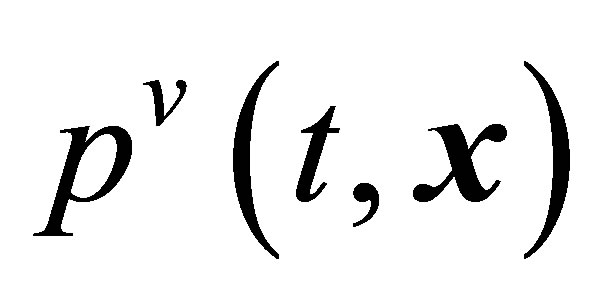 pressure, and
pressure, and  and
and 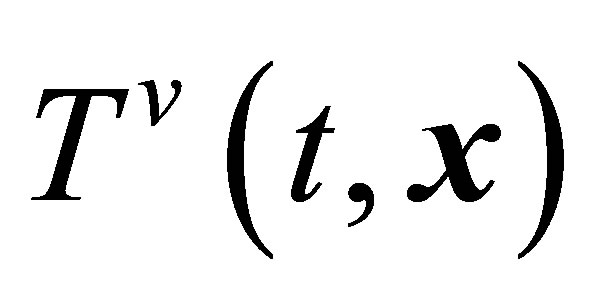 temperature,
temperature,  ,
, . The lower moments of the pair distribution functions (18) are determined by Equations (21)-(26) in [3]. The set of hydrodynamic values, namely,
. The lower moments of the pair distribution functions (18) are determined by Equations (21)-(26) in [3]. The set of hydrodynamic values, namely,  ,
,  ,
,
 ,
,  ,
,  ,
,  and
and
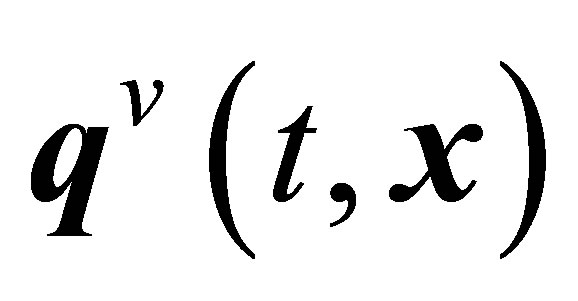 is constructed on the property of
is constructed on the property of 
 It is a set of the principal hydrodynamic values. The lower moments
It is a set of the principal hydrodynamic values. The lower moments 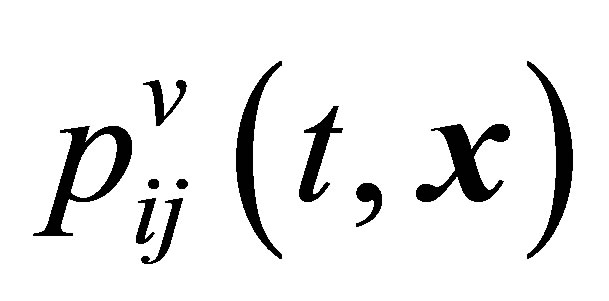 and
and  are not the principal hydrodynamic values.
are not the principal hydrodynamic values.
The relations between the 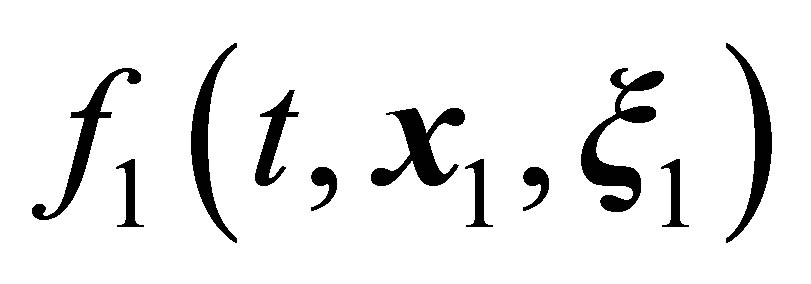 one-particle distribution function and the pair distribution functions (18) from [3] can be used to find a relation between the one-particle distribution function and the pair distribution functions moments,
one-particle distribution function and the pair distribution functions (18) from [3] can be used to find a relation between the one-particle distribution function and the pair distribution functions moments,
 (19)
(19)
Here,  denotes the number densities of particles,
denotes the number densities of particles, 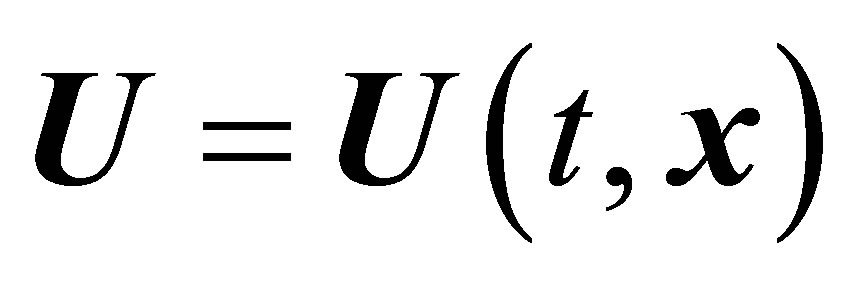 is the hydrodynamic velocity,
is the hydrodynamic velocity, 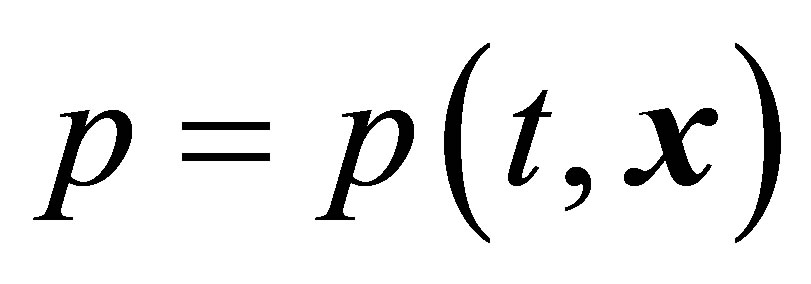 is the pressure,
is the pressure,  is the temperature,
is the temperature, 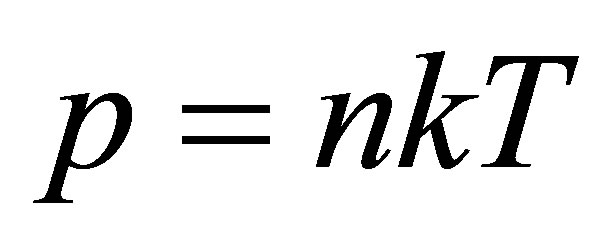 ,
,  and
and 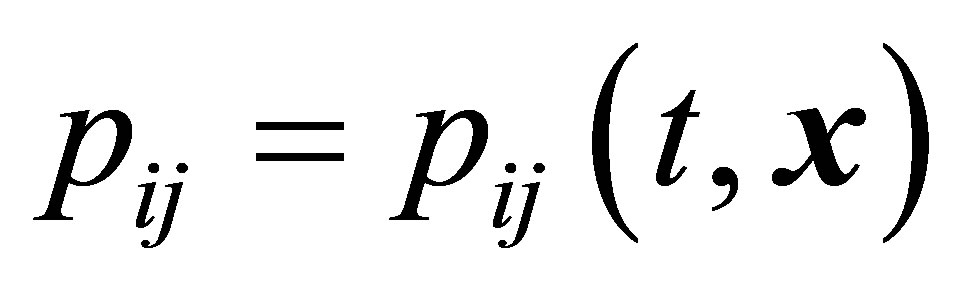 are the viscous stress tensors, and
are the viscous stress tensors, and  is the heat flux.
is the heat flux.
A derivation of equations determining lower moments of the pair distribution functions is given in [3]. In [32], these hydrodynamics equations are written in the form,
 (20a)
(20a)
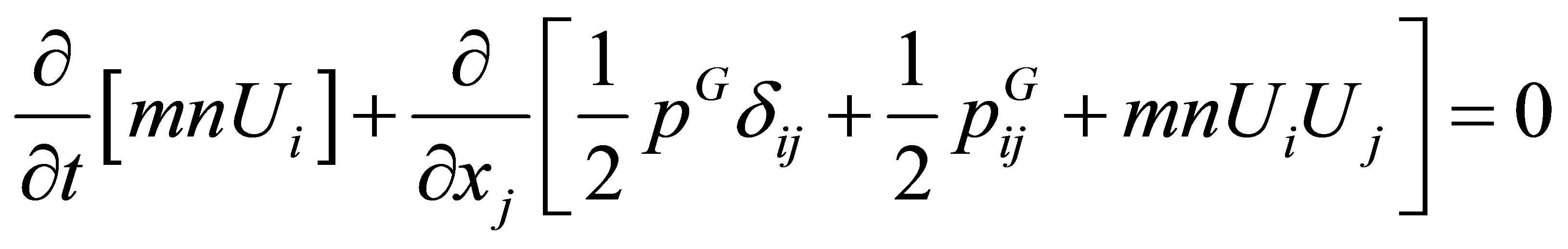 (20b)
(20b)
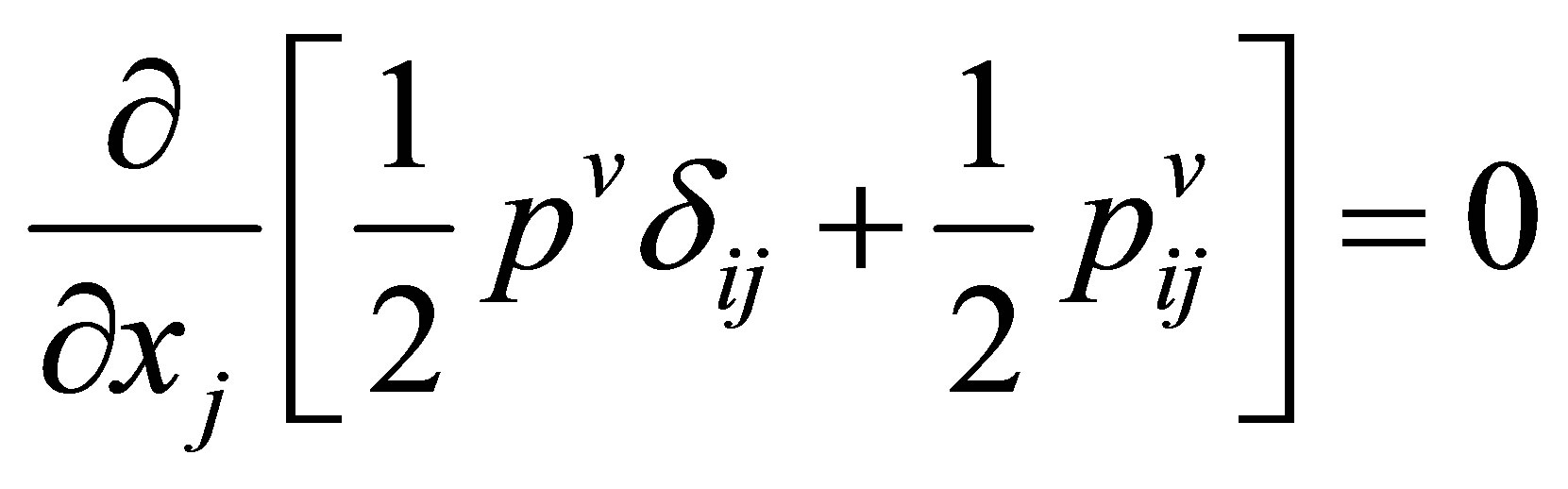 (20c)
(20c)
 (20d)
(20d)
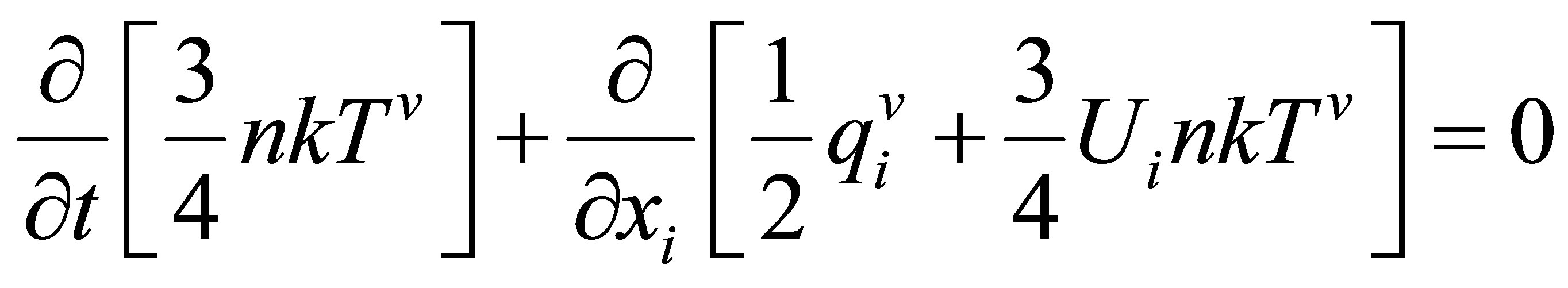 (20e)
(20e)
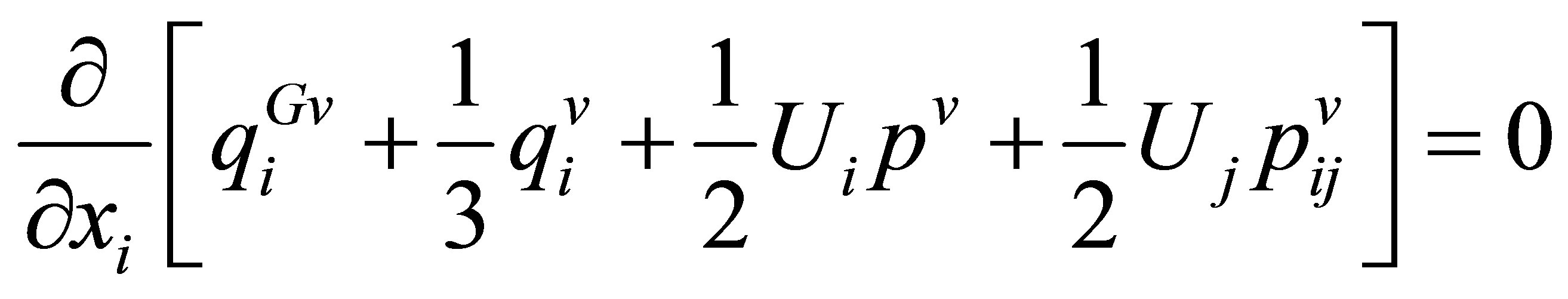 (20f)
(20f)
Taking (19) into account, we find that the sum of Equations (20b) and (20c) is none other than the equation of the conservation of momentum, and the sum of Equations (20d), (20e) and (20f) is none other than the equation of conservation of energy. Equation (20a) is the continuity equation. So, the equation for conservation of momentum separates into two equations, and the equation for conservation of energy, into three separate equations. In Equation (20), nonprincipal hydrodynamic values 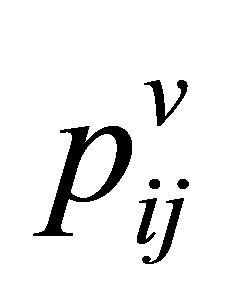 and
and  are given by the equations,
are given by the equations,
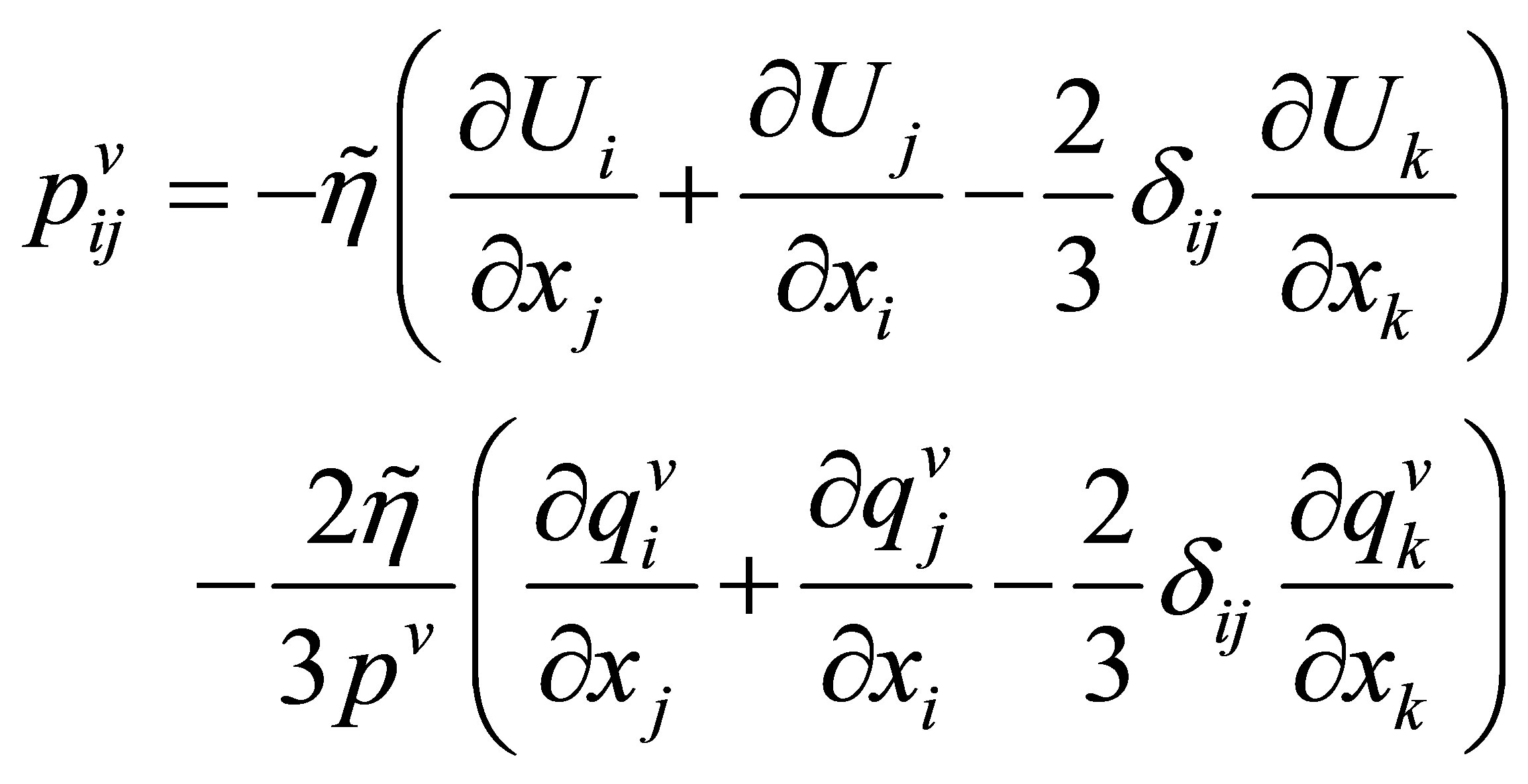 (21a)
(21a)
 (21b)
(21b)
Here,  is the dynamic viscosity coefficient and
is the dynamic viscosity coefficient and 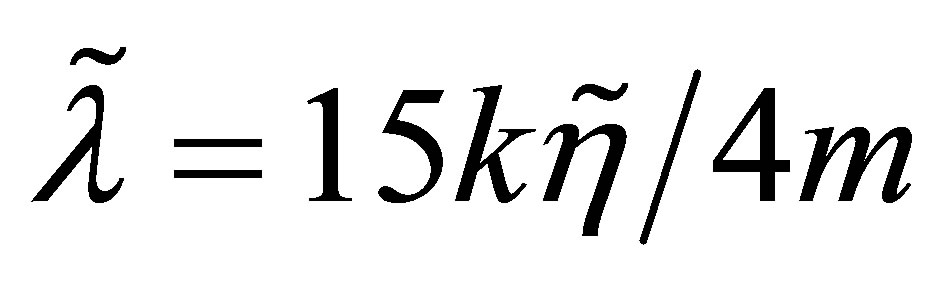 is the heat conductivity coefficient.
is the heat conductivity coefficient.
Relations (19) and Equations (20), (21) contain seven lower principal hydrodynamic values, namely, 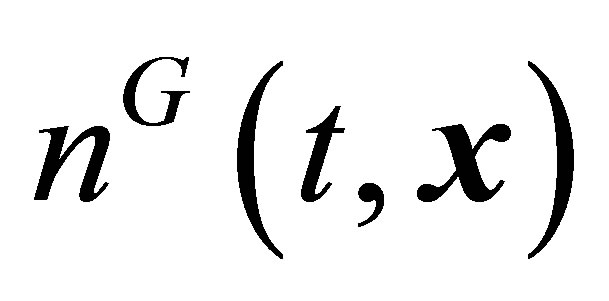 ,
,
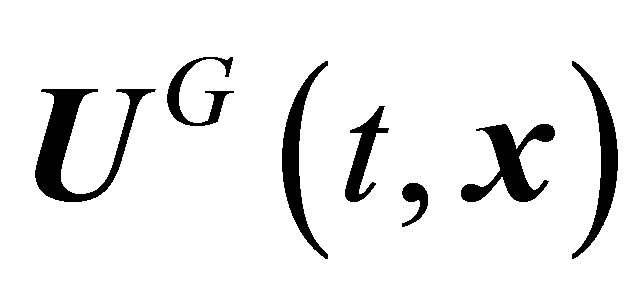 ,
, 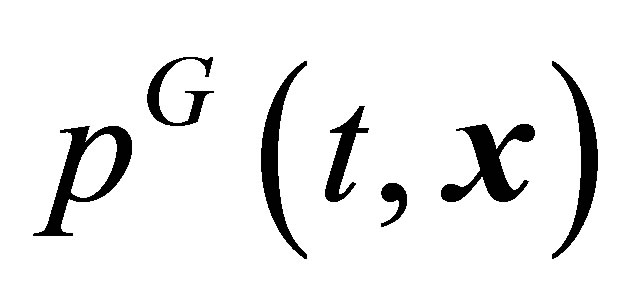 ,
,  ,
,  ,
,  and
and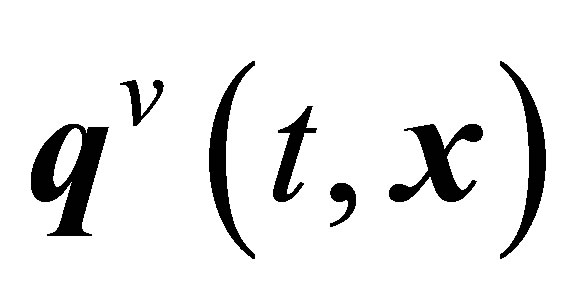 . Just these values dominate in equations for measurable one-particle function moments (19). All the other higher principal hydrodynamic values (9) were omitted in Equations (19)-(21). An increase in the number of principal hydrodynamic values taken into account will cause the additional appearance of derivatives of all the higher principal moments (9) taken into account in both definitions (19) and Equations (20), (21). The lower one particle distribution function moments
. Just these values dominate in equations for measurable one-particle function moments (19). All the other higher principal hydrodynamic values (9) were omitted in Equations (19)-(21). An increase in the number of principal hydrodynamic values taken into account will cause the additional appearance of derivatives of all the higher principal moments (9) taken into account in both definitions (19) and Equations (20), (21). The lower one particle distribution function moments ,
, 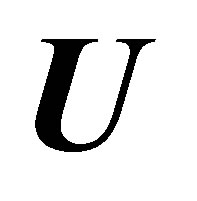 , and
, and 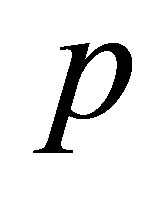 are written through the principal hydrodynamic values
are written through the principal hydrodynamic values ,
,  ,
,  and
and . The higher measurable moments
. The higher measurable moments  and
and  are represented by linear combinations of principal and non-principal hydrodynamic values. The
are represented by linear combinations of principal and non-principal hydrodynamic values. The 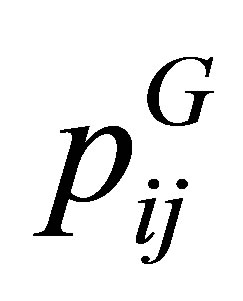 stress tensor component is a principal hydrodynamic value. The first term of the
stress tensor component is a principal hydrodynamic value. The first term of the  component is proportional to the tensor of deformation velocities
component is proportional to the tensor of deformation velocities  from Equation (21a), the remaining term of the component appears because of an increase in the number of principal hydrodynamic values. The first two components of the
from Equation (21a), the remaining term of the component appears because of an increase in the number of principal hydrodynamic values. The first two components of the  heat flux vector,
heat flux vector,  and
and , are principal hydrodynamic values. The first term of the third component,
, are principal hydrodynamic values. The first term of the third component, 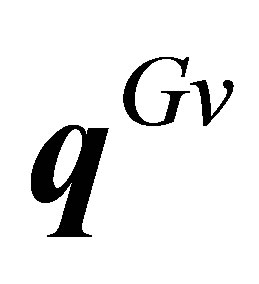 , is proportional to the temperature gradient from Equation (21b), and the other terms of the third component appear because of an increase in the number of principal hydrodynamic values.
, is proportional to the temperature gradient from Equation (21b), and the other terms of the third component appear because of an increase in the number of principal hydrodynamic values.
The upper indexes “div” and “app” were omitted in the 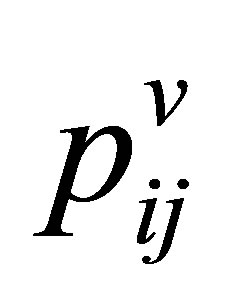 and
and  hydrodynamic values because the right hand sides of Equations (19) and (21) do not experience any changes in calculations of moments with pair functions corresponding either to particles that approach each other,
hydrodynamic values because the right hand sides of Equations (19) and (21) do not experience any changes in calculations of moments with pair functions corresponding either to particles that approach each other, 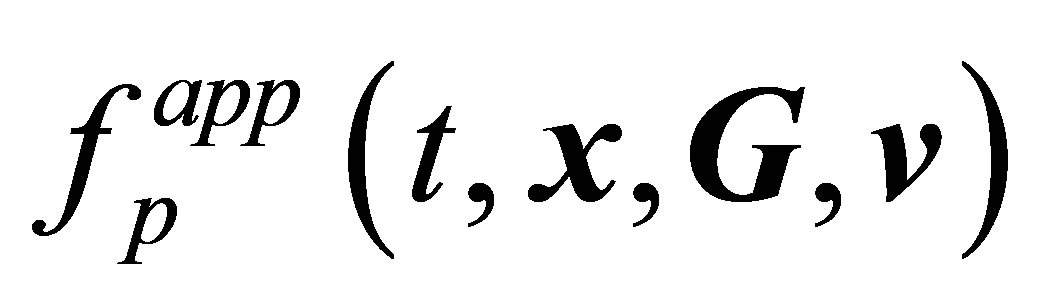 , or to particles that fly away from each other,
, or to particles that fly away from each other,  [3].
[3].
The analysis performed in [35] showed that hydrodynamic Equations (20), (21) could be rigorously reduced to classic hydrodynamics equations only when the state of the system weakly deviated from thermodynamic equilibrium. In particular, in the  limit, the
limit, the  main hydrodynamic value and the
main hydrodynamic value and the  value are equal. Moreover, the second term on the righthand side of Equation (21a), which is responsible for viscous stresses caused by heat fluxes, becomes negligibly small compared with the first term. It follows that, as is shown in [35], the Newton law [29] is only valid in the
value are equal. Moreover, the second term on the righthand side of Equation (21a), which is responsible for viscous stresses caused by heat fluxes, becomes negligibly small compared with the first term. It follows that, as is shown in [35], the Newton law [29] is only valid in the  limit.
limit.
An indefinite  parameter is the characteristic free path. An indefinite
parameter is the characteristic free path. An indefinite 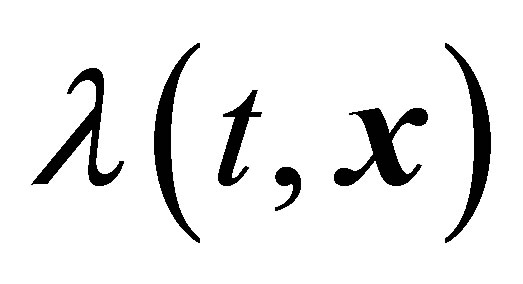 parameter is introduced at the stage of the formation of pair distribution functions (15). The characteristic time between collisions
parameter is introduced at the stage of the formation of pair distribution functions (15). The characteristic time between collisions
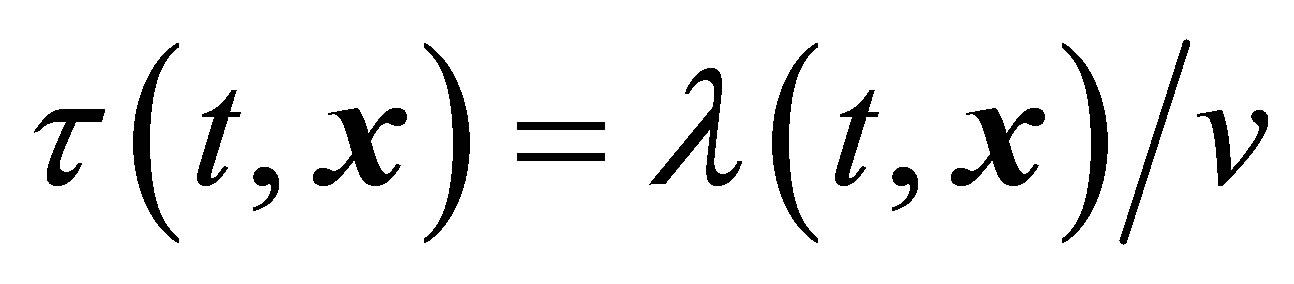 is contained in resulting kinetic equations and hydrodynamics equations [3]. The limit of weak non-equilibrium allows us to find the proportionality factor between the
is contained in resulting kinetic equations and hydrodynamics equations [3]. The limit of weak non-equilibrium allows us to find the proportionality factor between the  dynamic viscosity coefficient and
dynamic viscosity coefficient and ,
,
 (22)
(22)
The  coefficient can be calculated with arbitrary accuracy by solving the Boltzmann equation with the use of the Chapman–Enscog method for an arbitrary law of interparticle interactions [31].
coefficient can be calculated with arbitrary accuracy by solving the Boltzmann equation with the use of the Chapman–Enscog method for an arbitrary law of interparticle interactions [31].
In calculations of the right hand sides of the equations for the pair functions (18), collision integrals were calculated in [3] for a gas consisting of rigid spheres with diameter . This case has exceptional advantages, because, in integration in velocities
. This case has exceptional advantages, because, in integration in velocities  and
and  with the
with the 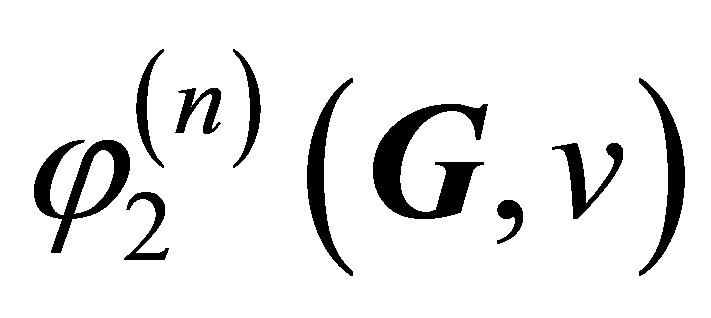
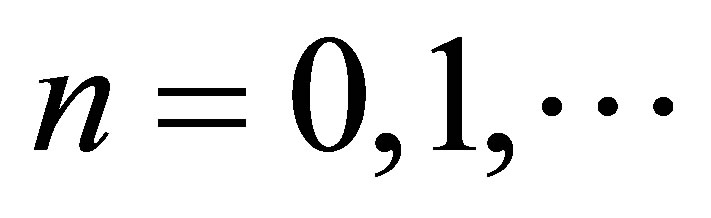 , weight function, the collision integrals of kinetic equations are expressed exactly in terms of the moments of pair distribution functions. The classic Boltzmann collision integral offers similar advantages to the case of so-called Maxwell molecules [36]. The structure of the derived hydrodynamics Equations (20) and (21) does not depend on the form of the law of structureless particle interactions. The interaction law only influences the values of transfer coefficients. It follows that system (20) and (21) is valid for the description of gas flows with an arbitrary law of interaction of structureless particles.
, weight function, the collision integrals of kinetic equations are expressed exactly in terms of the moments of pair distribution functions. The classic Boltzmann collision integral offers similar advantages to the case of so-called Maxwell molecules [36]. The structure of the derived hydrodynamics Equations (20) and (21) does not depend on the form of the law of structureless particle interactions. The interaction law only influences the values of transfer coefficients. It follows that system (20) and (21) is valid for the description of gas flows with an arbitrary law of interaction of structureless particles.
In the derivation of hydrodynamics Equations (19)- (21), only terms linear in  are retained. At the hydrodynamic description stage, the omitted terms correspond to so-called Barnett accuracy [31,36]. In follows that hydrodynamics Equations (20) and (21) presented above correspond to Navier-Stokes accuracy of description.
are retained. At the hydrodynamic description stage, the omitted terms correspond to so-called Barnett accuracy [31,36]. In follows that hydrodynamics Equations (20) and (21) presented above correspond to Navier-Stokes accuracy of description.
The system of equations determining lower moments of the pair distribution functions (20,21) is not closed. Let us multiply the Equation (17) for the  pair function by lower invariants of binary particle collision,
pair function by lower invariants of binary particle collision,  , and integrate the result with respect to velocities
, and integrate the result with respect to velocities  and
and . By virtue of definition of lower moments of pair functions [3], we then have hydrodynamic Equations (20a, b, d, e). Thus, Equation (17) is equivalent to several equations, namely, Equations (20a, b, d, e). According to (17), the
. By virtue of definition of lower moments of pair functions [3], we then have hydrodynamic Equations (20a, b, d, e). Thus, Equation (17) is equivalent to several equations, namely, Equations (20a, b, d, e). According to (17), the  function remains unchanged at time along the trajectory of the center of mass of the pair. This property creates the additional relations between the principal hydrodynamic values. The
function remains unchanged at time along the trajectory of the center of mass of the pair. This property creates the additional relations between the principal hydrodynamic values. The ,
,  and
and  vectors, and the
vectors, and the  tensor are multicomponent principal hydrodynamic values. It turned out that the use of the conservation property (17) is accompanied by the appearance of additional relations between each vector and tensor components. Generally, just these relations must close the system (20,21) of hydrodynamics equations.
tensor are multicomponent principal hydrodynamic values. It turned out that the use of the conservation property (17) is accompanied by the appearance of additional relations between each vector and tensor components. Generally, just these relations must close the system (20,21) of hydrodynamics equations.
However, a problem on flow around a fixed solid sphere was solved in [4,5] by another manner. In [4], the solution to Equation (17) was built. The first integrals of Equation (17) for a stationary system are the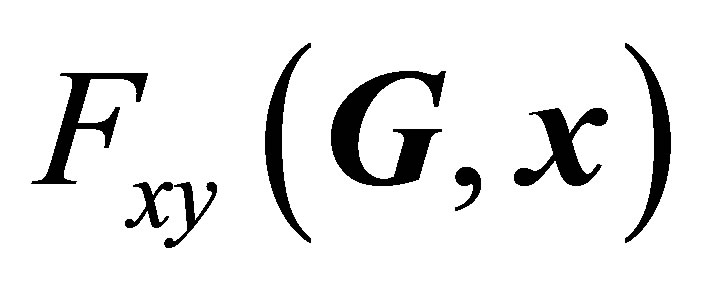 ,
, 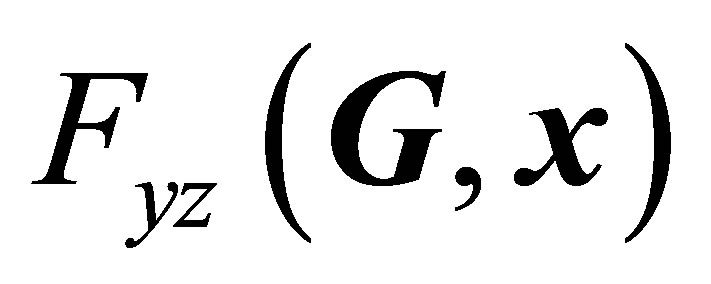 , and
, and  functions,
functions,
 (23)
(23)
According to [4], a solution to Equation (17) in the problem with time-independent boundary conditions should be sought in the form of a series of the products of the first integrals,
 (24)
(24)
Here,  is the temperature of the unperturbed medium and the
is the temperature of the unperturbed medium and the  coefficients generally depend on t. Substituting the distributions of the principal hydrodynamic values calculated by Equation (24) into the hydrodynamic Equations (20c, f) yields a nonlinear system of differential equations for the
coefficients generally depend on t. Substituting the distributions of the principal hydrodynamic values calculated by Equation (24) into the hydrodynamic Equations (20c, f) yields a nonlinear system of differential equations for the 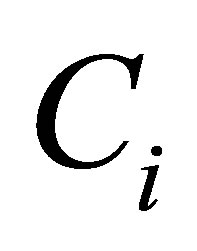 coefficients,
coefficients,
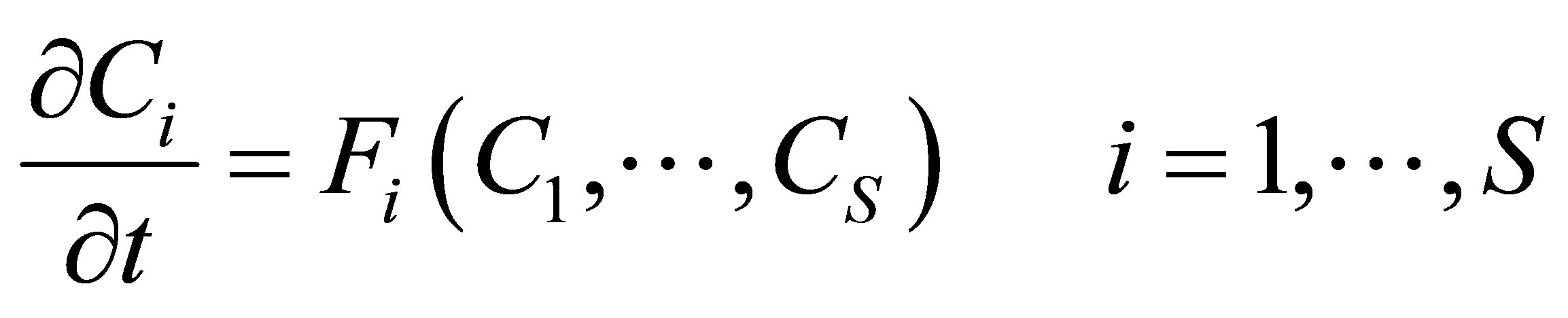 (25)
(25)
Relations between the  dimensionless coefficients and the
dimensionless coefficients and the 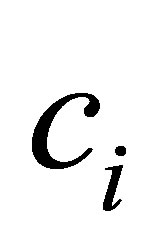 dimensional coefficients are given in [4].
dimensional coefficients are given in [4].
4. Conclusions
Figure 1 represents observed flow pictures around a sphere. Experiment records three stable flows: ,
, 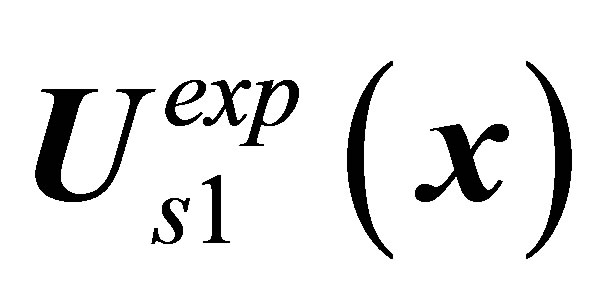 , and
, and . Each of these three flows after losing the stability starts to evolve in its own direction qualitatively different from the others. These directions are schematically shown by three horizontal branches. At these branches experiment records at least six vortex shedding modes:
. Each of these three flows after losing the stability starts to evolve in its own direction qualitatively different from the others. These directions are schematically shown by three horizontal branches. At these branches experiment records at least six vortex shedding modes: 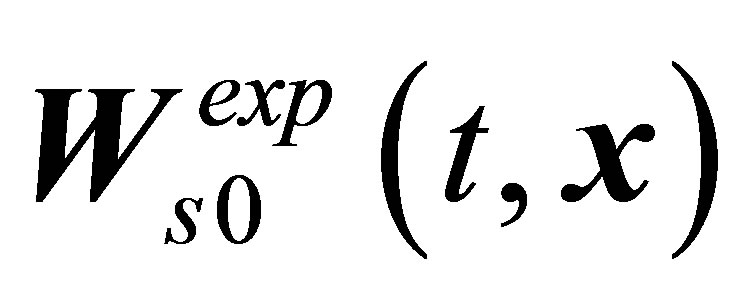 and
and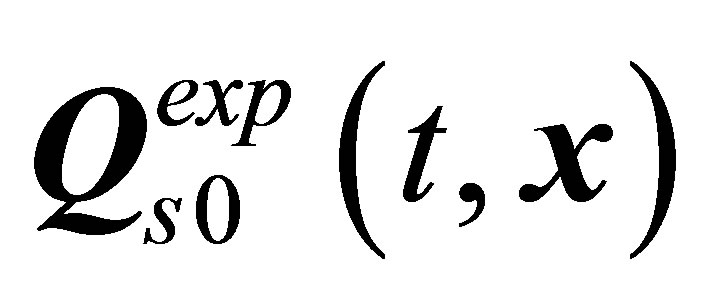 ;
;  ;
; ,
,  and
and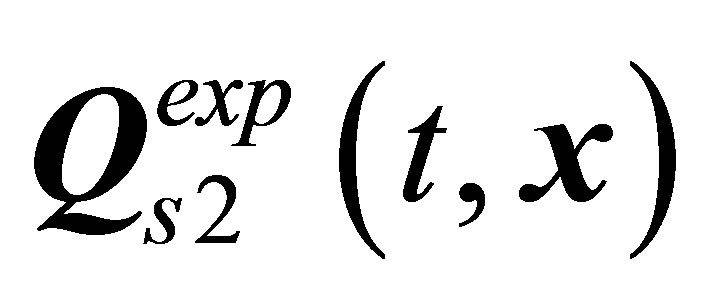 .
.
The integration of the Navier-Stokes equations for the problem of flow past a sphere [15,16,18-21] gives two stable solutions, 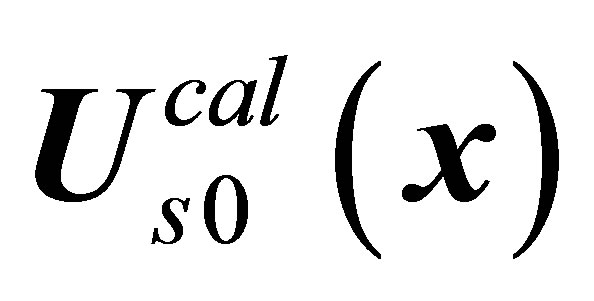 and
and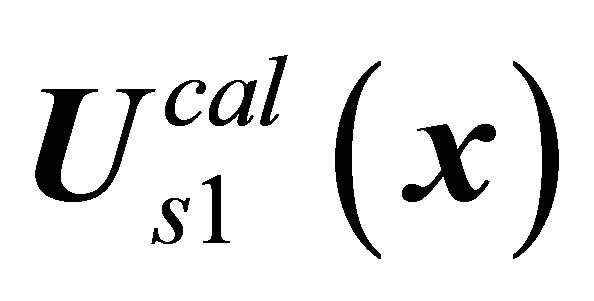 , and the
, and the
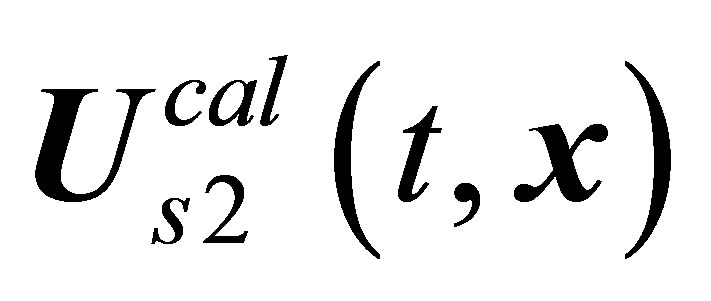 stable limiting cycle. These solutions satisfactorily reproduce three stable flows observed experimentally,
stable limiting cycle. These solutions satisfactorily reproduce three stable flows observed experimentally,  ,
,  , and
, and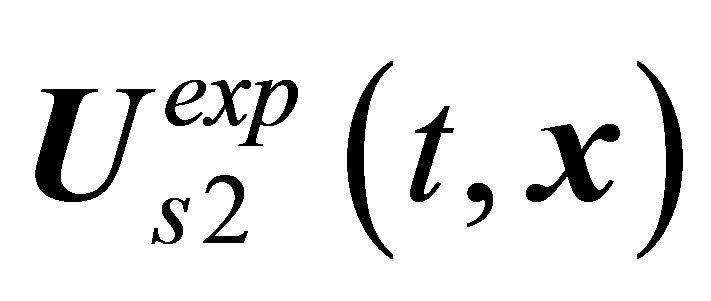 . Calculations were, however, incapable of reproducing any of the six vortex shedding modes. The calculation leads the instability development process in the direction given by dashed slanting line (Figure 1). The dashed slanting line separates stable solutions from unstable ones, that is, the dashed line gives the boundary of the instability field. So, solutions to the classic hydrodynamics equations successfully reach the boundary of the instability field. As Reynolds grows, these solutions move along the boundary of the field. However, the solutions to the classic hydrodynamics equations are unable to cross this boundary and to pass to the instability field. There are no numerical experiments on flow around different bluff bodies in which this boundary is crossed. Most likely, the reason for simulation failure is the Navier-Stokes equations themselves.
. Calculations were, however, incapable of reproducing any of the six vortex shedding modes. The calculation leads the instability development process in the direction given by dashed slanting line (Figure 1). The dashed slanting line separates stable solutions from unstable ones, that is, the dashed line gives the boundary of the instability field. So, solutions to the classic hydrodynamics equations successfully reach the boundary of the instability field. As Reynolds grows, these solutions move along the boundary of the field. However, the solutions to the classic hydrodynamics equations are unable to cross this boundary and to pass to the instability field. There are no numerical experiments on flow around different bluff bodies in which this boundary is crossed. Most likely, the reason for simulation failure is the Navier-Stokes equations themselves.
Analysis of the multimoment hydrodynamics equations [35] substantiates the suggestion that the applicability scope of classic hydrodynamics is limited, in particular, by small Reynolds number values, . Nevertheless, the calculated stable solutions to the NavierStokes equations,
. Nevertheless, the calculated stable solutions to the NavierStokes equations, 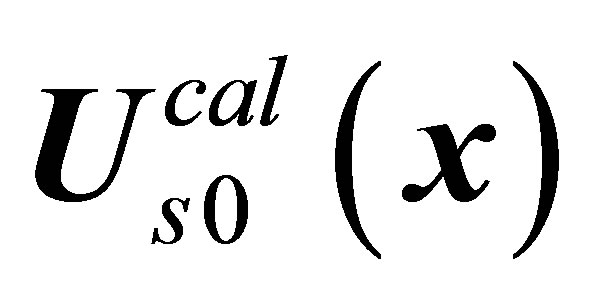 ,
, 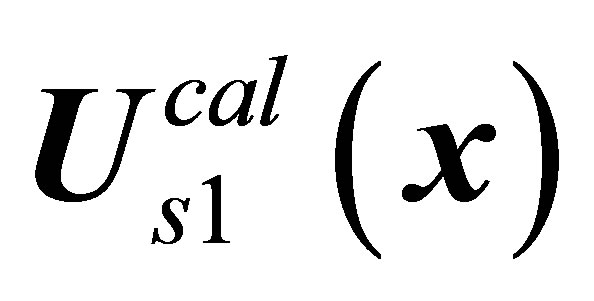 and
and , satisfactorily reproduce stable flows around a sphere
, satisfactorily reproduce stable flows around a sphere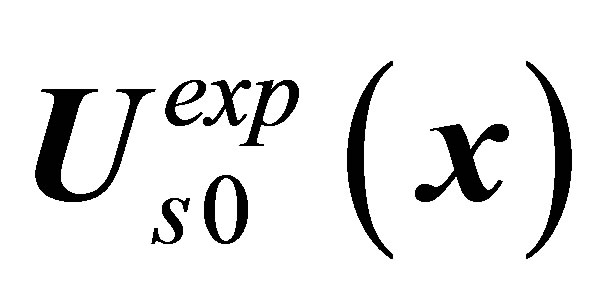 ,
, 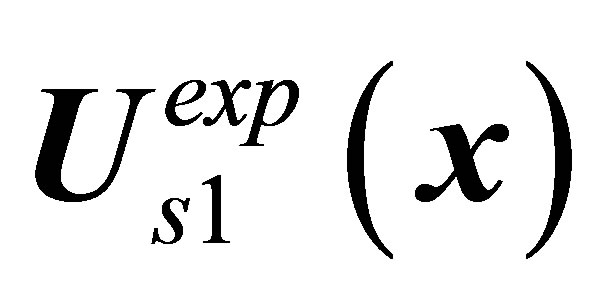 , and
, and  recorded experimentally at moderately high Reynolds number values, reaching a few hundreds. This means that the error in stable solutions to the Navier-Stokes equations is not large and cannot distort calculated flow pictures noticeably. This error, however, grows very rapidly after the loss of stability. This is explained by the tendency of nonlinear equations toward causing the divergence of close solutions even in a limited phase space region. This sensitivity to initial conditions was called the Lorentz butterfly effect. The loss of instability development direction is the result of error growth, i.e., the classic hydrodynamics equations become helpless in producing of regular nonstationary periodic flows appearing after the attainment of a certain critical Reynolds number value.
recorded experimentally at moderately high Reynolds number values, reaching a few hundreds. This means that the error in stable solutions to the Navier-Stokes equations is not large and cannot distort calculated flow pictures noticeably. This error, however, grows very rapidly after the loss of stability. This is explained by the tendency of nonlinear equations toward causing the divergence of close solutions even in a limited phase space region. This sensitivity to initial conditions was called the Lorentz butterfly effect. The loss of instability development direction is the result of error growth, i.e., the classic hydrodynamics equations become helpless in producing of regular nonstationary periodic flows appearing after the attainment of a certain critical Reynolds number value.
The numerical integration of the multimoment hydrodynamics equations in the problem on a flow past a sphere [4,5] shows that the solutions to these equations cross the boundary and enter the instability field. Let 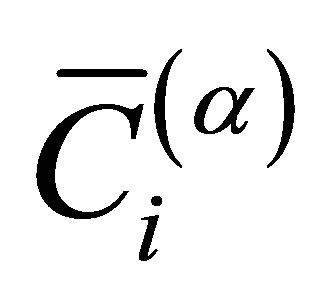 be a stationary
be a stationary  solution of the system (25) and
solution of the system (25) and  be a perturbation of the
be a perturbation of the 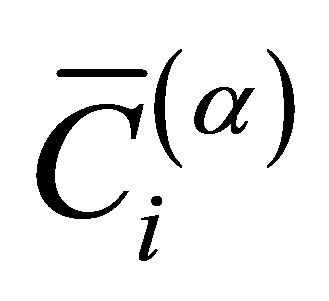 solution,
solution,
 . The retention of three-lower axisymmetric terms in expansion (24) leads to the classic Stokes solution valid in the
. The retention of three-lower axisymmetric terms in expansion (24) leads to the classic Stokes solution valid in the  limit [29]. For advancement up the Re scale, twenty lower axisymmetric expansion (24) terms are retained in [4]. The
limit [29]. For advancement up the Re scale, twenty lower axisymmetric expansion (24) terms are retained in [4]. The
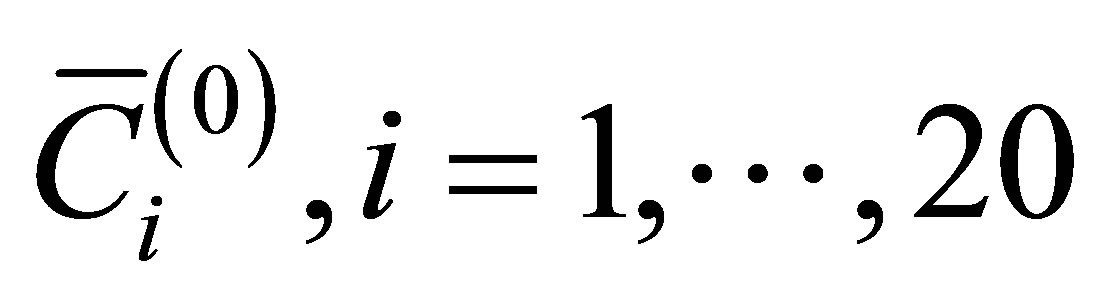 , stationary solution to the nonlinear algebraic system of twenty equations gives the stationary distribution of the hydrodynamic values (19). According to the
, stationary solution to the nonlinear algebraic system of twenty equations gives the stationary distribution of the hydrodynamic values (19). According to the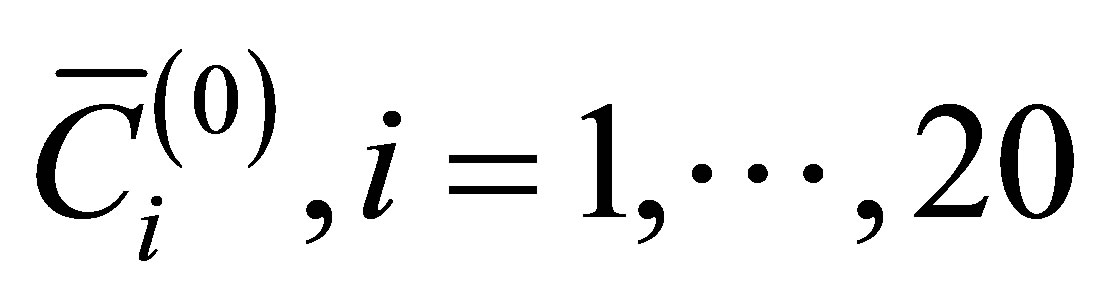 , solution, an axisymmetric recirculating zone is formed in the wake behind a sphere at Re ~ 20. This recirculating zone has the shape of an axisymmetric toroidal ring. It expands as Re grows but its shape remains unchanged. The calculated distribution
, solution, an axisymmetric recirculating zone is formed in the wake behind a sphere at Re ~ 20. This recirculating zone has the shape of an axisymmetric toroidal ring. It expands as Re grows but its shape remains unchanged. The calculated distribution  satisfactorily reproduces the
satisfactorily reproduces the  axisymmetric flow.
axisymmetric flow.
The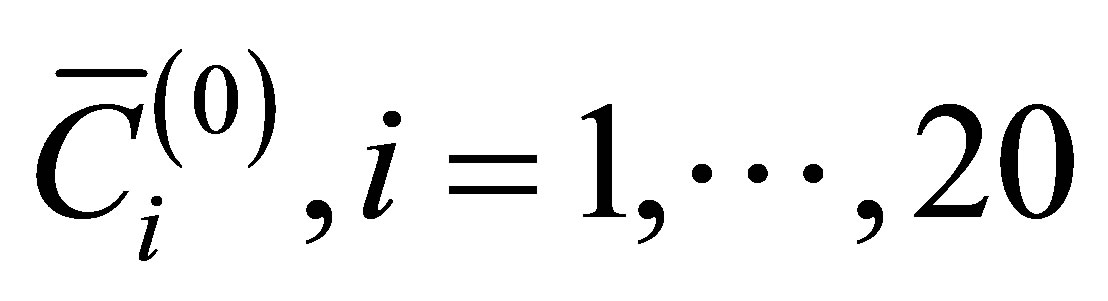 , solution remains stable up to a certain critical
, solution remains stable up to a certain critical  value. This means that the
value. This means that the
 small perturbations of the solution
small perturbations of the solution
 , are damped at
, are damped at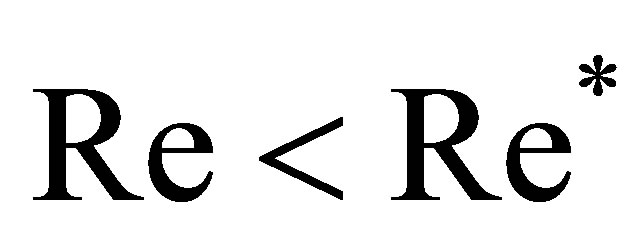 . The passage of
. The passage of 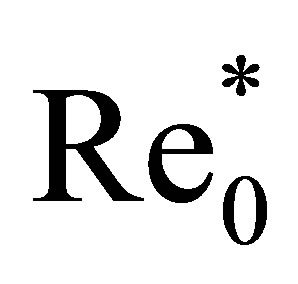 is accompanied by the
is accompanied by the , solution stability loss. Starting with
, solution stability loss. Starting with , the
, the
 small axisymmetric perturbations begin to increase exponentially at
small axisymmetric perturbations begin to increase exponentially at . The
. The  perturbations grow up to time
perturbations grow up to time . At
. At , the
, the 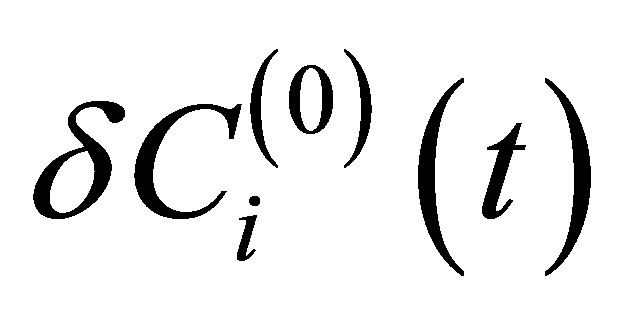 solution is cut off. The reason for this is analyzed in [4].
solution is cut off. The reason for this is analyzed in [4].
It turned out that another solution to the nonlinear system of differential Equations (25) existed in the neighborhood of the cut-off point. It is the
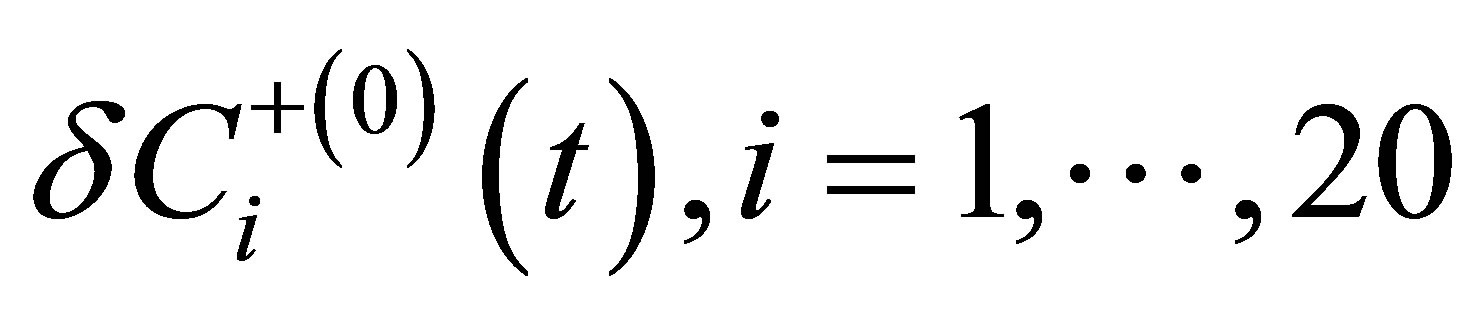 , solution of the so-called system of the reversed hydrodynamics equations [35]. According to [37], the law of large numbers is violated near singular points (bifurcations, regions of the coexistence of several stable solutions, etc.), and large fluctuations may appear in the system. In conformity with [37], a large fluctuation causes the transfer of the system from the cut-off point to the
, solution of the so-called system of the reversed hydrodynamics equations [35]. According to [37], the law of large numbers is violated near singular points (bifurcations, regions of the coexistence of several stable solutions, etc.), and large fluctuations may appear in the system. In conformity with [37], a large fluctuation causes the transfer of the system from the cut-off point to the , solution at time
, solution at time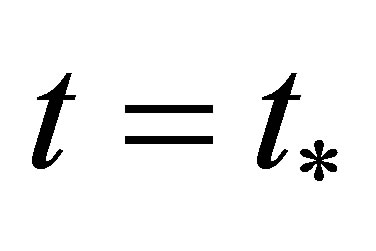 . At time
. At time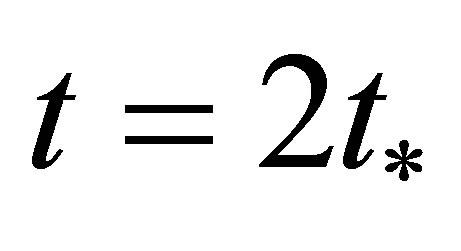 , the
, the 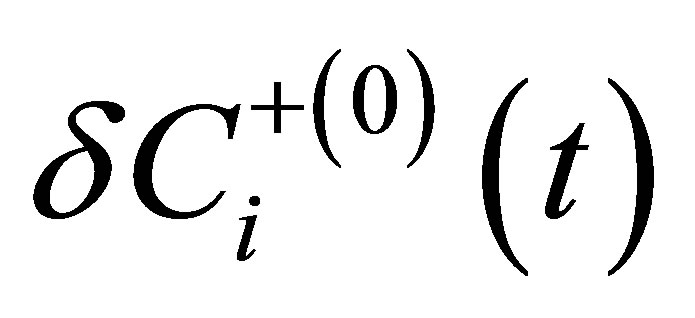 solution reaches the neighborhood of the
solution reaches the neighborhood of the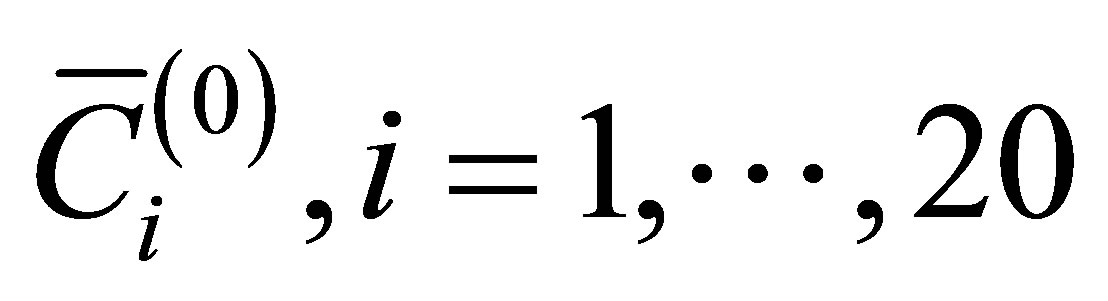 , stationary solution. At time
, stationary solution. At time  further evolution of the
further evolution of the
 , solution is finished. The
, solution is finished. The
 , solution exists at
, solution exists at , the
, the
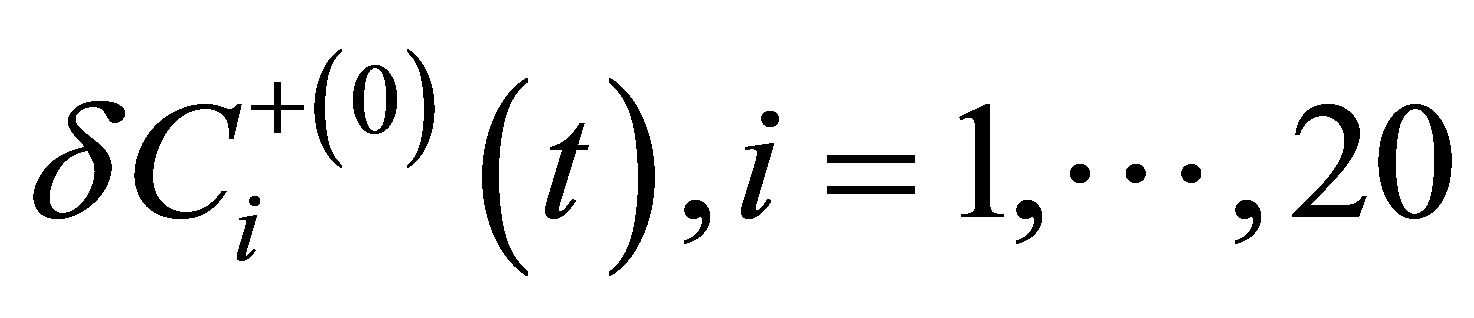 , solution exists at
, solution exists at . A fluctuation causes the transfer of the system from the
. A fluctuation causes the transfer of the system from the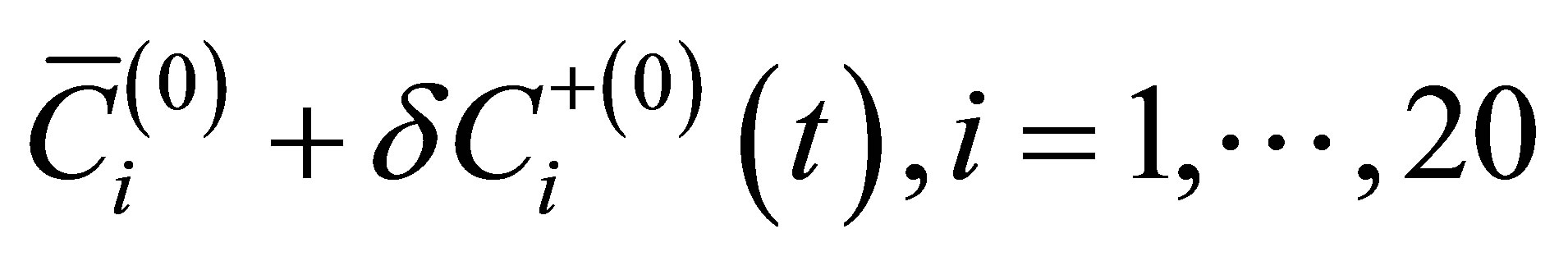 , solution to the
, solution to the
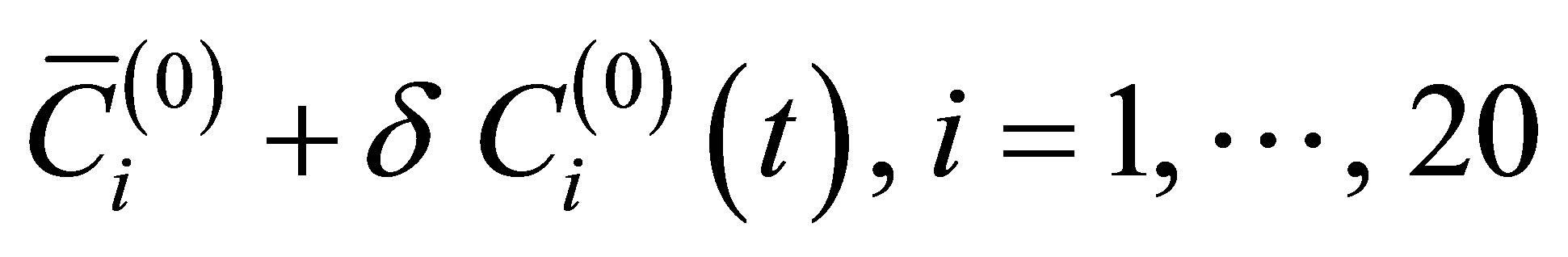 , solution at time
, solution at time .
.
The 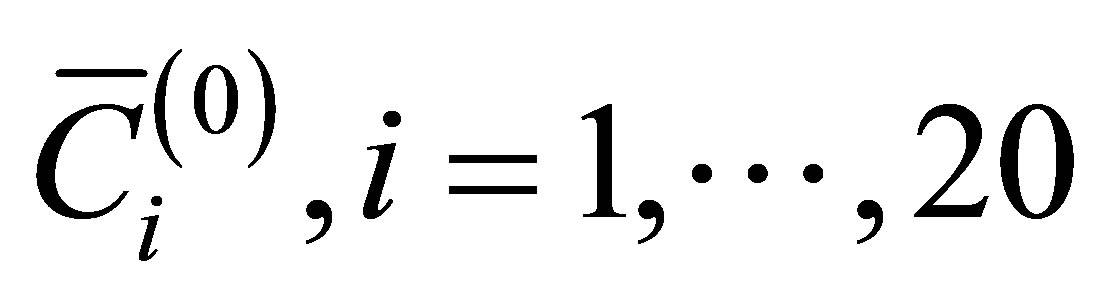 solution is unstable. It follows that small axisymmetric
solution is unstable. It follows that small axisymmetric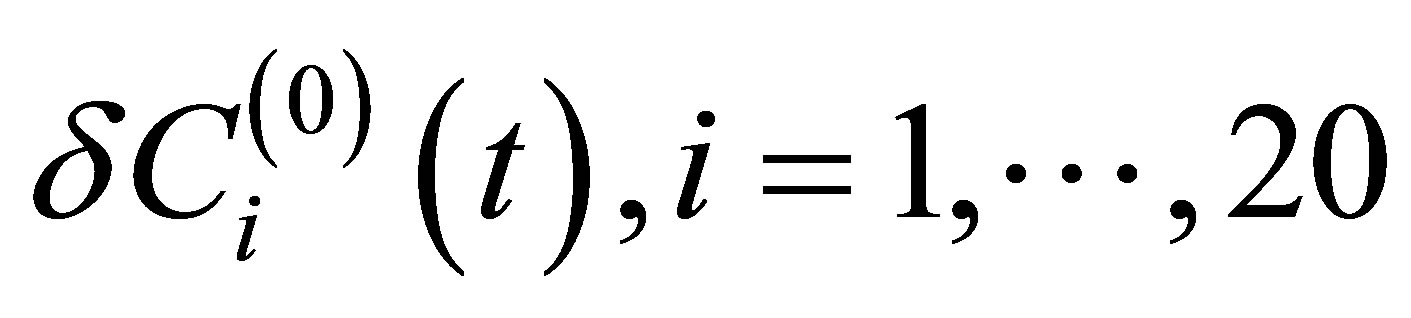 , perturbations begin to grow starting with time
, perturbations begin to grow starting with time . This process is repeated periodically.
. This process is repeated periodically.
The evolution of the  and
and
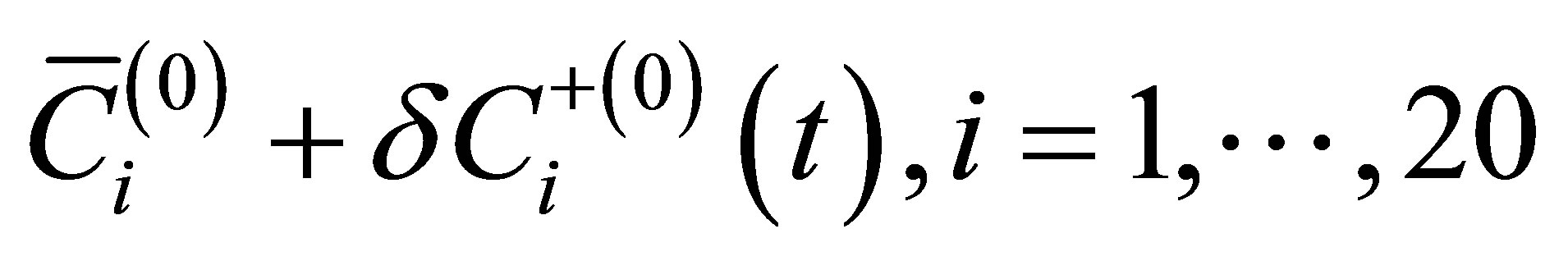 , solution satisfactorily reproduces the
, solution satisfactorily reproduces the  periodic axisymmetric pulsations from [6,10]. According to the
periodic axisymmetric pulsations from [6,10]. According to the 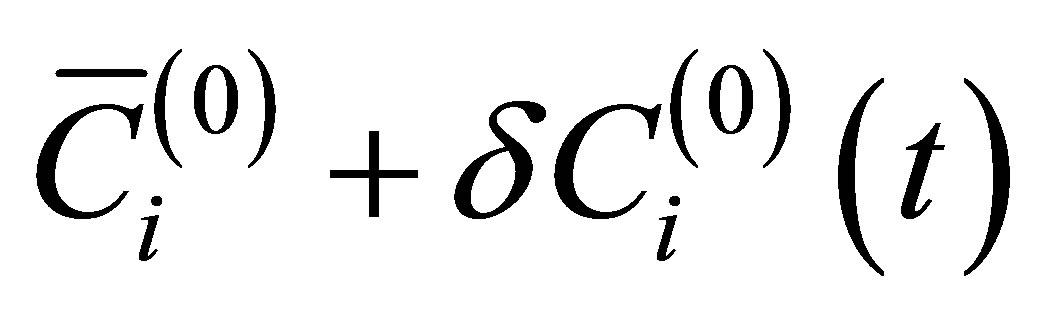 and
and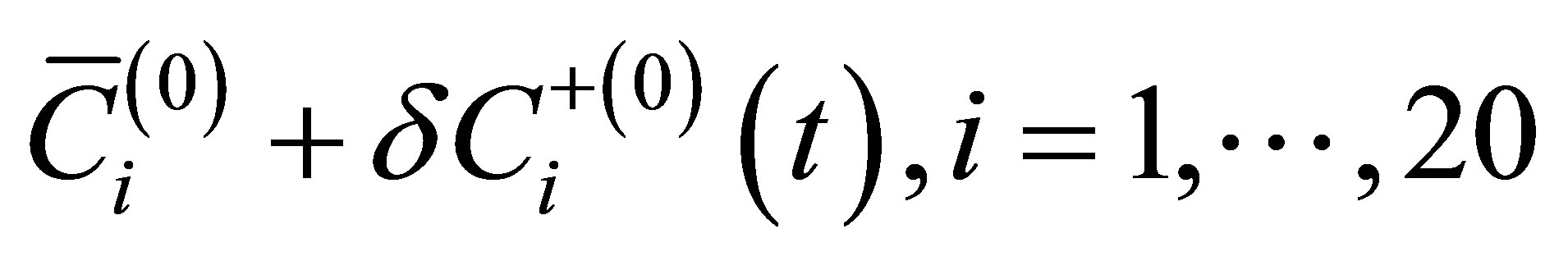 , solution, toroidal recirculating zone in the near wake behind a sphere begins to pulsate periodically after the attainment of the Reynolds number
, solution, toroidal recirculating zone in the near wake behind a sphere begins to pulsate periodically after the attainment of the Reynolds number . The recirculating zone remains toroidal during pulsations, and its forefront is firmly fixed on the sphere. The pulsating flow remains axisymmetric. Because of the absence of the detachment of the recirculating zone periphery, there is no vortex loop street in the far wake behind a sphere.
. The recirculating zone remains toroidal during pulsations, and its forefront is firmly fixed on the sphere. The pulsating flow remains axisymmetric. Because of the absence of the detachment of the recirculating zone periphery, there is no vortex loop street in the far wake behind a sphere.
The scenario of instability appearance,  , [4,5], has no analogues. Currently, we have no alternative to this scenario, because Landau’s scenario based on solutions to the Navier-Stokes equations [15,16,18-21] fails to describe experiment.
, [4,5], has no analogues. Currently, we have no alternative to this scenario, because Landau’s scenario based on solutions to the Navier-Stokes equations [15,16,18-21] fails to describe experiment.
The crossing of the instability field boundary is accompanied by the appearance of uncommon acts in the scenario of instability development. It turned out that the exponential growth of small perturbations of stationary unstable solution is not infinite. At some point the nonstationary solution is cut off and the growth of perturbations is completed. After the break the system finds extremely unlike direction of evolution. It starts a returning motion in the direction of the unstable stationary solution. As a result, the system after losing the stability does not find a new stable position, i.e., after crossing the boundary of the instability field, the evolution of the system takes place only within the instability field. Such a scenario differs from the ideas of classic hydrodynamics, which interprets the development of instability in terms of bifurcations from one stable state to another stable state.
The importance of the entropy in interpretation of instability is revealed in [5]. It turns out that the explanation of instability appearance lies in change in entropy balance. Namely, an open system with time-independent boundary conditions has a steady state while entropy production in it exceeds entropy outflow through the surface confining the system. Then, any fluctuation generated by the system fades out. As soon as the entropy is removed through the confining surface faster than it is produced in the system, any fluctuation generated by the system begins to grow. The system becomes unstable.
Further studies [38] show that reproduction of the  and
and  vortex shedding regimes,
vortex shedding regimes, 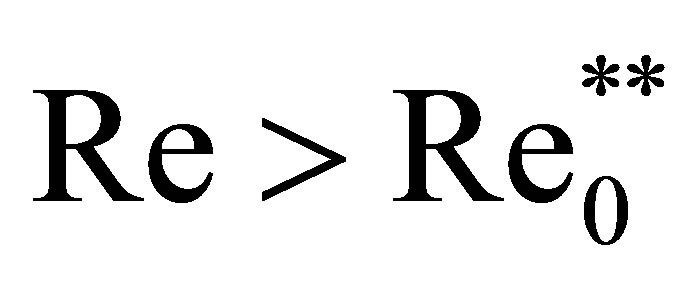 , leads to new scenario acts that do not have analogues. Moreover, the
, leads to new scenario acts that do not have analogues. Moreover, the 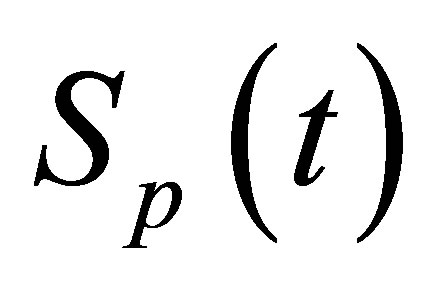 pair entropy of system begins to play the key role to predict the instability development direction. The calculation of the system evolution becomes impossible without participation of the entropy. The multimoment hydrodynamics equations find a large number of ways for system evolution. And the
pair entropy of system begins to play the key role to predict the instability development direction. The calculation of the system evolution becomes impossible without participation of the entropy. The multimoment hydrodynamics equations find a large number of ways for system evolution. And the 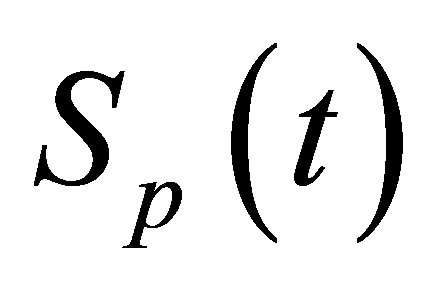 pair entropy shows the single way, in which the system evolution moves.
pair entropy shows the single way, in which the system evolution moves.
So, the perspectives for removal the discrepancies between calculations and experiment for unstable regimes are revealed along the direction on increase of the principal hydrodynamic values number when deriving the hydrodynamics equations.