A Study of the Factors Affecting Transporting Solid— Liquid Suspension through Pipelines ()
1. Introduction
The present study is originated in order to investigate the problem of blocking the pipelines that transport water and sold mixture. The slurry is the product of many industrial process like oxygen converter in iron and steel industries, and drilling industries.
These lines have a considerably low flow velocity, which leads to enhanced rate of deposition. As a result of this operation, pipeline systems suffer from fast blocking.
The present study is also of interest because it is applicable to problems related to the handling and transporting of solid raw materials and products, e.g. coal.
The experimental study for determining the pressure gradient and efficiency of transport is burdened by some different constraints arising mainly from the following three characteristics of the problem.
1) The abundance of variables which govern the flow.
2) The vast range over which most of the variables may vary.
3) The inherent limitation on accuracy and reproducibility of the data that can be obtained with heterogeneous settling slurries.
The basic problem in hydraulic transport of solids is the determination of the fluid forces acting upon the solid particles and the effects of these forces upon the behavior of such particles and upon the resultant energy losses.
The experimental results were compared with the correlations (13-15) developed later by other authors.
2. Literature Survey
2.1. Introduction
The transport of solid particles by a liquid flowing in a pipeline is governed by a number of parameters that can be classified as follows: pipeline parameters, liquid parameters, solid particle parameters and system parameters e.g. mixture flow velocity.
It would be useful to study the effects of these parameters upon the performance characteristics such as: the pressure gradient (∆P/L) and efficiency of transport (η).
During the last few years, there have been several investigations concerning the connections between these parameters with the pressure drops in addition to the effect of these parameters upon the characteristics of centrifugal pumps. The findings of the previous investigations for the flow of slurries are summarized in the following sections:
2.2. Flow Regimes and Critical Velocity
2.2.1. Flow Regimes
There are four distinct regimes of particle conveyance, (see Newit et al. [1]) who carried out experiments with solids of sizes from 0.062 to 4.67 mm. and specific gravity ranging between 1.18 and 4.6. The experiments were performed in a 2.54 cm. pipe and resulted in the following regimes.
1) Conveyance as a homogenous suspension in which mean mixture velocity is high to prevent sedimentation during transport process.
2) Conveyance as a heterogeneous suspension, which is maintained by turbulence heterogeneous flow.
3) Conveyance by saltation, in which the particles are alternatively picked up by the liquid and deposited further along the pipe.
4) Conveyance as a sliding bed, that is a regime in which the principal mechanism is sliding motion of solids along the bottom of the pipe.
Another classification of these regimes is derived by Durand [2]. This classification depends on particle size ranges as follows:
1) Particles of a size less than 40 µm, are transported as a homogenous suspension.
2) Particles of a size between 40 µm and 0.15 mm are transported as suspension that is maintained by turbulence.
3) Particles of a size among 0.15 and 1.5 mm are transported by a suspension and saltation.
4) Particles of a size greater than 1.5 mm are transported by saltation.
The flow regimes given in this classification are related having a specific gravity of 2.65.
2.2.2. Critical Velocity
The critical velocity conditions have been the study of extensive research effort and yet can still be confusing, as many definitions have been used for this term.
The most important critical velocities are those which another phase of flow is produced as laminar/turbulent transport velocity in case of homogenous slurry flow or the deposit velocity in case of settling slurry flow.
2.2.3. Critical Deposit Velocity
A further result of Durand’s work is an empirical equation for predicting the critical deposit velocity of slurry, i.e. the velocity below which a stationary deposit of solids forms in the pipe. The critical deposit velocity correlation is given by:
 (1)
(1)
where FL is a dimensionless function of particle diameter given by Durand and can be obtained using Figure 1, which requires only the mean particle size and concentration distribution of solids to find the value of FL. The result in equation is of considerable practical value for the critical velocity, if sufficiently high in a given case, may be the limiting parameter.
2.3. Pressure Drop through Slurry Pipeline
The need to predict pressure drop for flowing slurries is an eminently practical one.
2.3.1. Durand’s Equation for Pressure Losses in Horizontal Pipes
The empirical correlation published by DURAND [2] is related to the pressure drops associated with the flow of sand-water and gravel-water mixtures with particles of sizes ranging from 0.2 to 25 mm. and pipe diameters from 3.8 to 58 cm. with solids concentrations up to 60% by volume.
A principal result of the work by DURAND [2] is the correlations:
 (2)
(2)
where i and iw are the pressure drop of slurry and of water respectively, k is a constant and CD is the drag coefficient for the free failing particle at its terminal velocity in the stagnant unbounded liquid, assumed spherical and of diameter ds given by:
 (3)
(3)
The constant k is found to be 3.18 for sand slurry ac-

Figure 1. Values of FL (Durand et al. (1953)).
cording to WORSTER [3]. To account for the effect of particle density, moreover, a modification of Equation (1) is given by
 (4)
(4)
where S is the specific gravity of solid material.
In this equation Durand’s group used (S ‒ 1) = 1.65, and, by comparing Equation (2) and Equation (4) k = 150.
Durand’s correlation, Equation (2) gave 18.0% absolute average deviation when compared with data by Turain and Yuan [6].
2.3.2. Worster’s Equation for Pressure Losses in Horizontal Pipes
Worster [3] studied flow phenomena associated with large particles in particular coal particles, and produced a similar correlation to that of Durand and his coworkers except for the inclusion of a term in take account of specific gravity of the solid material and the absence of any parameter of particle size.
 (5)
(5)
2.3.3. Improved Durand—Equation for Multiple Applications
The applicability of Durand’s equation could be improved for general use by applying suitable parameters representing the grain size distribution. Thus, the Durand’s equation can not only describe polydisperse (pseudo)- homogenous or heterogeneous transportation, but also solidliquid mixtures containing a certain amount of fine particles. Even non Newtonian influences can be taken into account.
The applicability of the extended Durand’s equation for polydisperse mixtures was demonstrated by measurement data. With respect to this, the transition between pseudohomogeneous and heterogeneous transport has been considered on the basis of measured concentration profiles.
WAGNER [4] empirically could show with special polydisperse mixtures the grain size distribution can be taken into account more efficiently by using  and
and  in the following correlation factor, m; viz.
in the following correlation factor, m; viz.
 (6)
(6)
where  and
and  are particle diameter at 90% and 10% passing sieve, respectively.
are particle diameter at 90% and 10% passing sieve, respectively.
Thus the following extended version of Durand’s equation can be written for polydisperse-heterogenous Newtonian mixture:
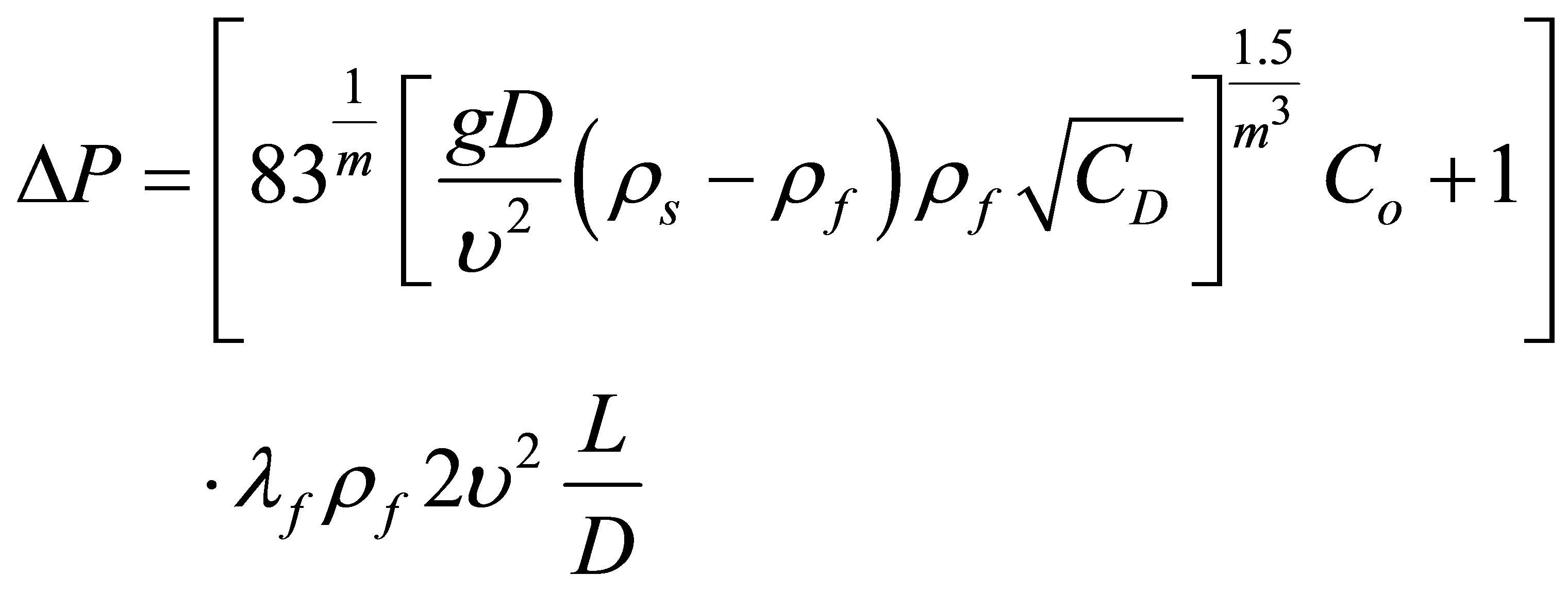 (7)
(7)
where  are solid and fluid densities, respectively.
are solid and fluid densities, respectively.
 is the delivered total concentration,
is the delivered total concentration,  is the pipe friction factor. Adapting this equation also to homogeneous mixtures by taking account of grain size distribution, the heterogeneous part of the equation can be partly or totally eliminated. This can be done by defining a homogeneous part ‘F’ of the grain size distribution, which is namely fine grain and a heterogeneous part (1 ‒ F).
is the pipe friction factor. Adapting this equation also to homogeneous mixtures by taking account of grain size distribution, the heterogeneous part of the equation can be partly or totally eliminated. This can be done by defining a homogeneous part ‘F’ of the grain size distribution, which is namely fine grain and a heterogeneous part (1 ‒ F).
The delivered concentration of the fine material could be represented as follows.
 (8)
(8)
The delivered concentration of the coarse material could be represented as follows.
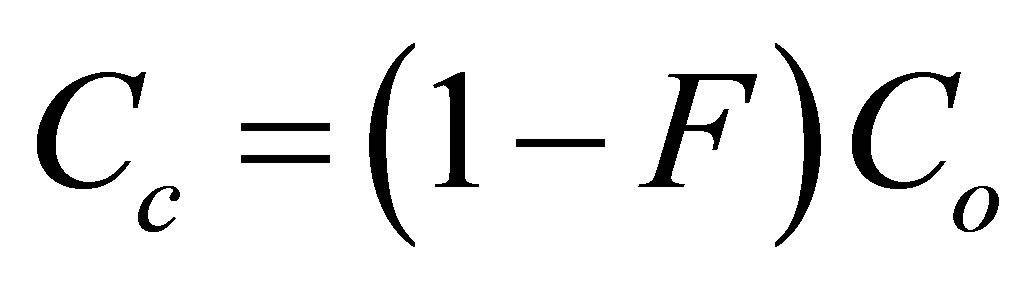 (9)
(9)
The density of the enriched carrier fluid is given by:
 (10)
(10)
Substituting  in Equation (7) by
in Equation (7) by  and adding (1 ‒ F) as a factor of
and adding (1 ‒ F) as a factor of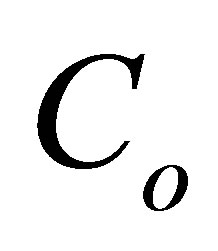 .
.
The generally valid equation for polydisperse heterogeneous and homogeneous Newtonian mixtures that was improved by M. WEBER, [5] can be stated as follows:
 (11)
(11)
 (12)
(12)
2.3.4. Turain’s Equation for Pressure Drop in Slurry Pipeline
The slurry flow correlation established in Turain and Yuan [6] is represented by relations:
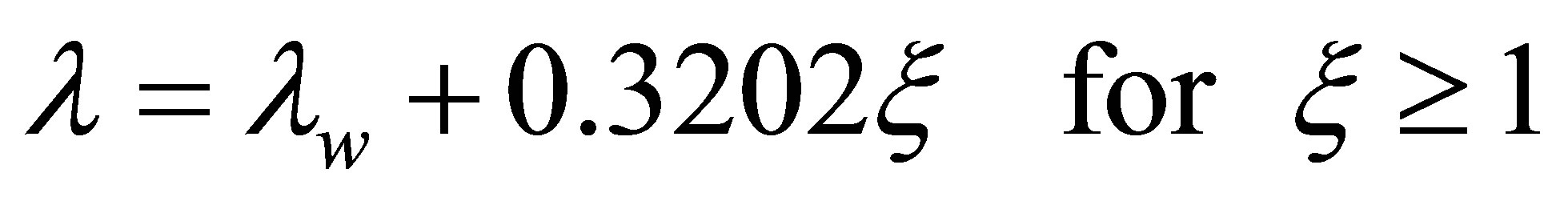 (13)
(13)
 (14)
(14)
where
 (15)
(15)
Co is the discharge concentration of solids, volume %.
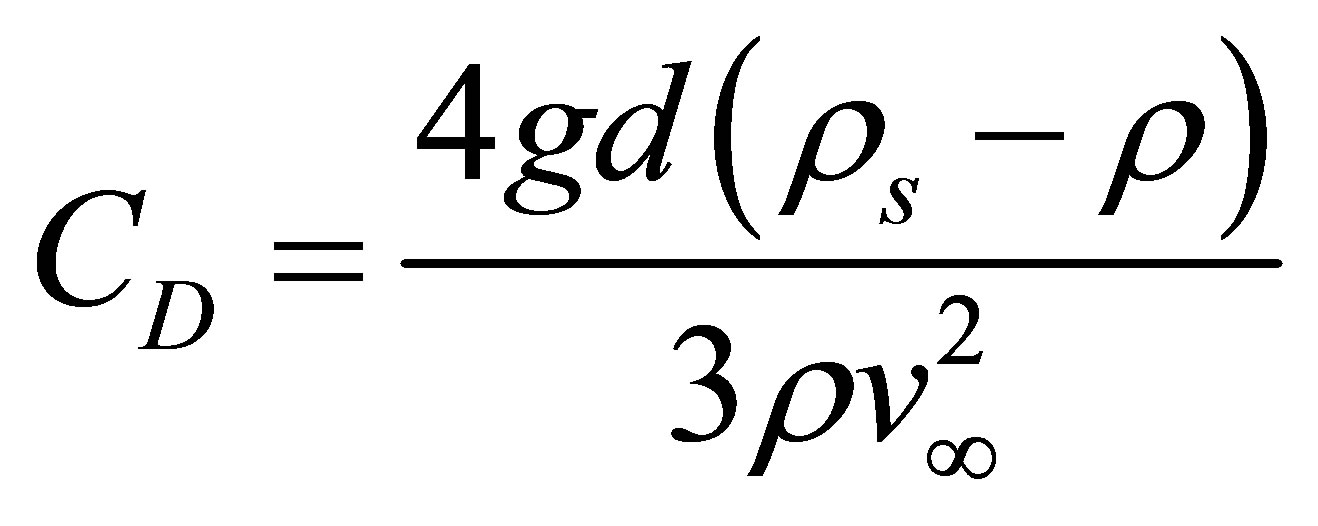 , Drag coefficient for free falling sphere, dimensionless, where S is the specific gravity of solids, D is the inside diameter of pipe, g is the gravitational constant,
, Drag coefficient for free falling sphere, dimensionless, where S is the specific gravity of solids, D is the inside diameter of pipe, g is the gravitational constant, 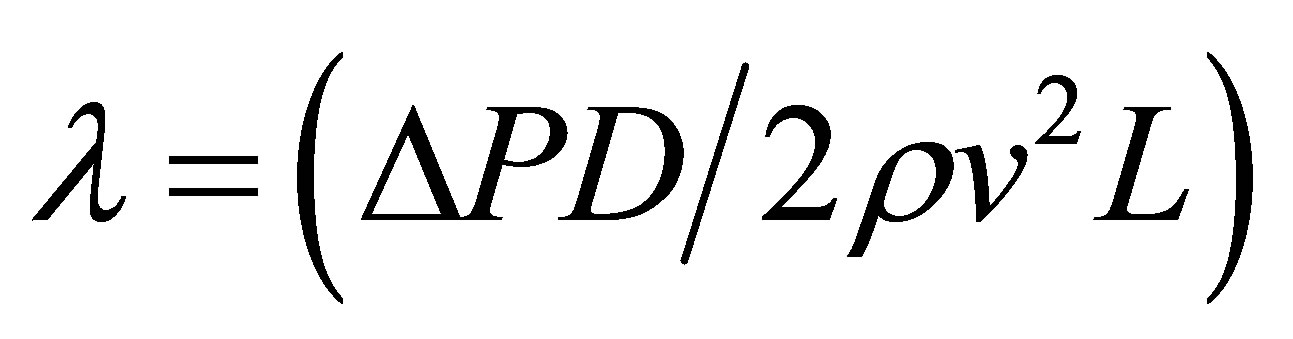 , friction factor for pipe flow of slurry, dimensionless, and
, friction factor for pipe flow of slurry, dimensionless, and
 , friction factor for pipe flow in absence of solids, dimensionless.
, friction factor for pipe flow in absence of solids, dimensionless.
This empirical correlation was based upon a collection of 1511 data points pertained to flow in 5.04, 2.54, and 1.27 on pipelines of water suspensions of twelve different sizes of solid particles ranging from 31 µm. to 4380 µm. and covering, in round figures, suspended solid densities of 2300, 3000, 4400, 7500, and 11300 kg/m3.
The correlation represented by Equation (8) and (9) predicts the slurry friction factor with absolute average deviations of 9.43% for all 1511 data points, with 76 points having deviations exceeding 30%, and only 9 points having deviations exceeding 50%.
2.4. Optimal Grain Distribution for Transport with High Concentration
Hydraulic conveying at high solid’s concentration is very attractive and a large amount of experimental data has accumulated to date, but many fundamental problems still need to be answered. H.C. HOU [7] carried out theoretical analysis and answered some questions dealing with concentration transport.
2.4.1. Two Forms of Flow
There are two forms of transport. The first case is the case of dilute concentration with fine and/or coarse materials, in which the solid particles are suspended individually in the flowing water. In this case the energy expenditure for suspension of particle is compensated by the turbulence energy, which is taken from the kinetic flow field with the result that the von Karman constant for flow with sediment suspension should be less than that for pure water. For a given particle—composition it was found that the higher the value of concentration, the lower the value of von Karman constant. The reduction of von Karman’s constant with the presence of sediment means that the increase of dissipated energy that is directly withdrawn from the mean flow field needs a corresponding increase in the energy-supply from outside the system. Therefore, the hydraulic conveying of solids by means of Newtonian fluids is not economic.
Another form of hydrotransport is the transport with hyper concentration including some of fine particles in the range . This forms a non-Newtonian system which is complex and requires thorough analysis.
. This forms a non-Newtonian system which is complex and requires thorough analysis.
2.4.2. Critical Volume Concentration
There are critical volume concentrations , by which the system—transfers from Newtonian fluid (dilute concentration) to hyper concentration i.e. nonNewtonian fluid. This limit was determined by H.C. HOU [7] after carrying some current experiments concerning solid-liquid mixture transport.
, by which the system—transfers from Newtonian fluid (dilute concentration) to hyper concentration i.e. nonNewtonian fluid. This limit was determined by H.C. HOU [7] after carrying some current experiments concerning solid-liquid mixture transport.
2.4.3. Specific Energy Consumption in the Slurry Pipelines
An experimental approach had been carried out by M.S. Lee, V. Matousek, C.K. Chung and Y.N. Lee [8] the results indicate that the specific energy consumption at velocities near the deposition limit is not very sensitive to the pipe size.
It also indicate that the low concentrated slurries of about 7% exhibit higher specific energy consumption values for all three pipes of diameters (155, 204, and 305 mm).
2.4.4. Closure
The above review has shown a lot of experimental data that have been accumulated during the last period. However most of these data concentrates on general flowtypes rather than on specific types. The present work, on the other hand concentrates on the special problem of transport slurry of the by-product solids of oxygen converter shop.
3. The Present Work
The present work divided into two branches; the first one was:
Theoretical and dimensional analysis, the second one was the experimental tests.
3.1. Theoretical and Dimensional Analysis
In this section the dimensional analysis is used to plan experiments and present data compactly. It is noteworthy to mention that many workers also used it in theoretical studies, as well.
Basically, dimensional analysis is a method for reducing the number and complexity of experimental variables that affect a given physical phenomenon, using a sort compacting technique. By applying this techniques for the problem of transporting solid-liquid mixture we proceed as follows:
Under isothermal conditions, at least 12 variables are needed to describe suspension flow behavior, provided that pipeline roughness and solids density distribution are excluded from consideration.
The input variables can be listed as follows:
Pipeline parameters:
1. Pipe diameter, assuming section to be circular D 2. Inclination to horizontal g 3. Pipe length. L Liquid parameters:
1. Density. ρ
2. Viscosity. µ
Solid particles parameters:
1. Density. 
2. Size distribution (dimensionless) 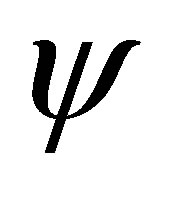
3. Shape factor 
System parameters:
1. Velocity of flow. 
2. Solid-liquid ratio of the flowing mixture at inlet. 
The output variables or the performance characteristic variables are:
1. The pressure drop for pipeline flow of solid – liquid suspension .
.
2. The efficiency of transport  defined as the ratio between output to input concentrations per unit volumeand can be represented as follows:
defined as the ratio between output to input concentrations per unit volumeand can be represented as follows: 
The total number of 12 variables can be reduced to 9 independent dimensionless groups by applying the conventional Π – theorem. One way of expressing this, is through a relation of the type.
 (16)
(16)
Under some conditions, certain simplifications can be made in Equation (16).
For example, if the pipe length is large the dependence on the  ratio becomes insignificant, and this term can be dropped, based on the measurement of the axial variations in pressure drop. Few other simplifications drop both
ratio becomes insignificant, and this term can be dropped, based on the measurement of the axial variations in pressure drop. Few other simplifications drop both  and
and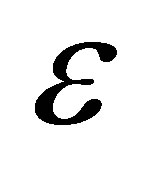 .
.
Accordingly, for this case Equation (16) takes the form:
 (17)
(17)
Despite the substantial reduction in the number of variables in going from Equation (16) to Equation (17), the functional dependence is still unknown.
3.2. Experimental Test Rig
To establish the relationship stated in Equation (17) a purely experimental approach designed. The model used for test is shown in Figure 2.
The model was chosen in such a way to permit the observation of effects of dimensionless groups that control the rate of deposition of solids and pressure gradient through pipeline system. These dimensionless groups are, Reynolds number, Froude number, relative density, particle grain size, and input concentration. The model consists of two cast steel reservoirs 6 cubic meter capacity each of conical-shaped bottom, and connected to a slurrytype centrifugal pump with diameters of 5.08 cm suction and 2.54 cm discharge pipes. The pumps are connected to 7.5 Kw. A/C induced motor with variable speeds. the pipeline is 285 meter long, and the solid concentration by volume was varied between 0.027% and 10%. Average grain size range between 0.25 mm and 1 mm and specific gravities ranging from 2.65 to 3.540 the Reynolds number was varied from 10907 to 63699.
The measured velocity was varied from 0.5 m/s to 2.5 m/s.
In the tests five variables were determined namely:
1. Pressure gradient along the pipeline system.
2. Flow rate measurements.
3. Input concentration to pipeline .
.
4. Output concentration from pipeline .
.
5. Input grain size.
3.2.1. Pressure Measurement
Pressure measurements were determined by means of bourdon tube manometers that were calibrated by means of dead weight testers. The bourdon gauges are fitted to the pipeline at an equal distance of 16 meter between any two successive manometers.
To avoid wrong readings of manometers as a result of existing solid material through the flow field, special connections were made by mounting a helical-shaped pipe full of oil that is lighter than water.
3.2.2. Flow Measurements
Flow measurements were determined by measuring the flow rate during one hour operation from suction tank to discharge tank.
During the experimental work, the flow rate controlled by means of adjustment of delivery valves only while keeping the suction valves fully opened.
3.2.3. Concentration Measurement
In this experimental work, the following steps have been carried out to determine the input and output concentrations1. Prepare a clean, empty bottle and weigh it.
2. Fill the empty bottle with 50 cm3 sample from the homogenous mixture of the suction tank.
3. Put the bottle on a heater until water is completely evaporated and hence the solids are completely dried.
4. Put the solid sample into cold dryer to cool it.
5. Weigh the solid sample.
6. Subtract the two weights in steps 5 and 1 respectively.

Figure 2. Schematic outline of experimental test rig.
The difference is the total solid existed in the sample (suspension solid + soluble solid).
7. Take another 50 cm3 sample from the same mixture of the suction tank and filter it, so as the water constitutes the soluble solids only.
8. Repeat the steps from (3 to 4) listed before to determine the weight of soluble solids.
9. Subtract the result of step number 8 from that of number 6 to obtain the T.S.M (Total Suspended Material) which represents the transported material through the pipeline system.
3.2.4. Input Grain Size Measurements
The input grain size was determined using a set of standard screen meshes that are available in the laboratories of the factory.
3.3. Experimental Procedure
Preliminary measurements were made to ensure that the system produces a stable (no pulsation), with no leakage from test devices. The Reynolds number (ReD) for the tests is varied from (10907 to 63699).
The model was provided with 18 pressure gauges, fitted at locations of equal distance of 16 meter apart to ensure precise plotting of the pressure drop variation with length and velocity.
4. Results and Discussions
In the present section the results obtained from the experimental model are presented and discussed.
4.1. Performance Characteristics of Water in Absence of Solids
From section (3) it was noted that the governing equation of slurry flow system may be written in the form:
 (17)
(17)
This equation can be reduced to the following equation for the clean water
: (18)
(18)
From this equation, the parameter describing the flow performance is represented by the pressure gradient, whereas the Reynolds number of clean water Rew is the only affecting variable.
4.2. Effect of Varying Reynolds Number Re and Froude Number upon the Performance Characteristics
In the present experimental work, it was found that the simplest way to vary the value of Reynolds number would be through adjustment of the flow velocity. Therefore, Reynolds number as well as Froude number vary together.
1) Effect of varying Re, Fr, upon pressure gradients
The Reynolds number has been varied from (10907 – 63699) and Froude number from (0.5 - 17).
It has been noted from Figures 3 to 8 that as Reynolds

Figure 3. Variation of slurry performance characteristics for sand slurry with solid concentration 1% by volume and particle diameter ds = 0.25 mm. versus mean mixture velocity.
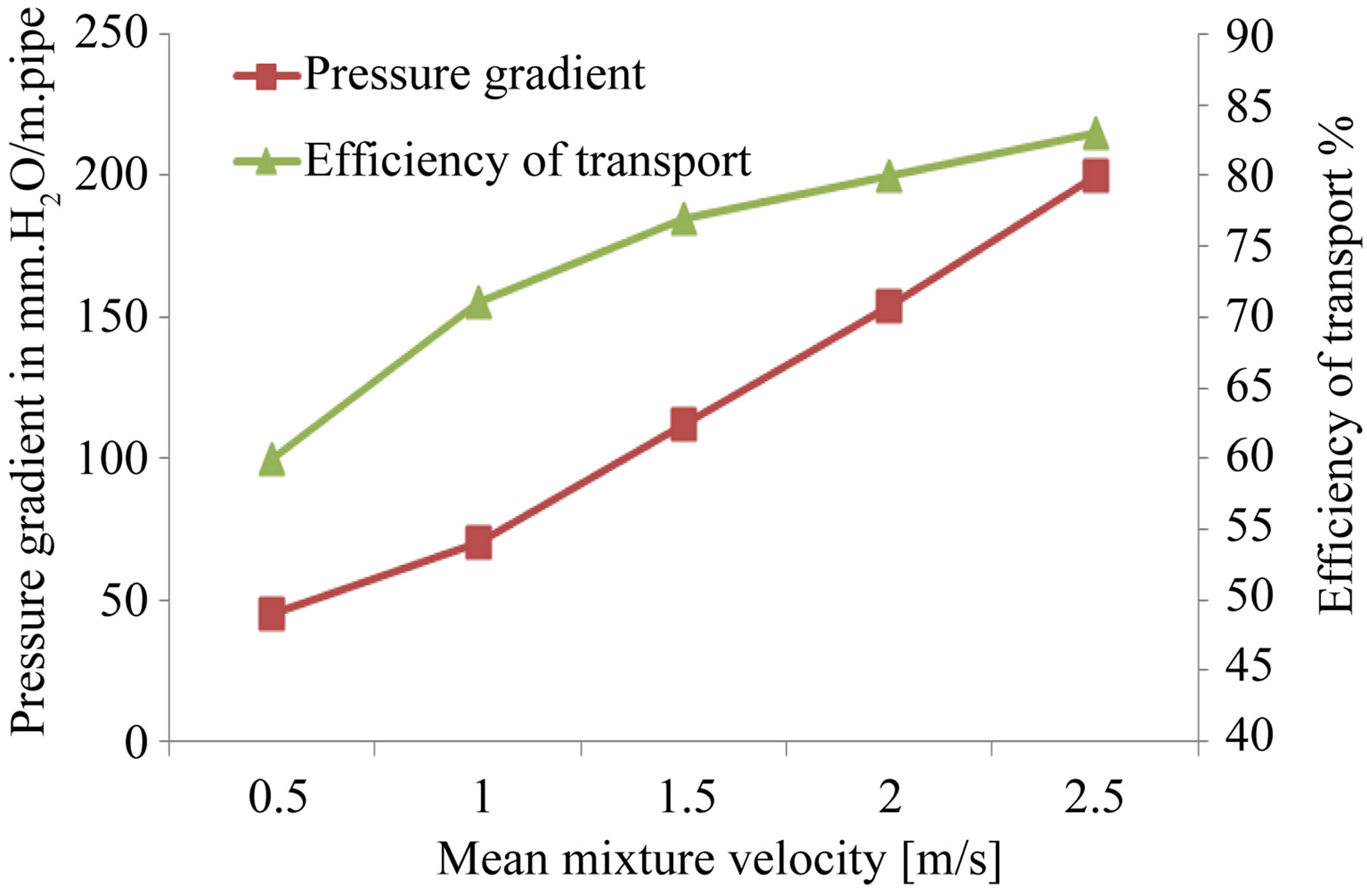
Figure 4. Variation of slurry performance characteristics for sand slurry with solid concentration 1% by volume and particle diameter ds = 0.5 mm. versus mean mixture velocity.
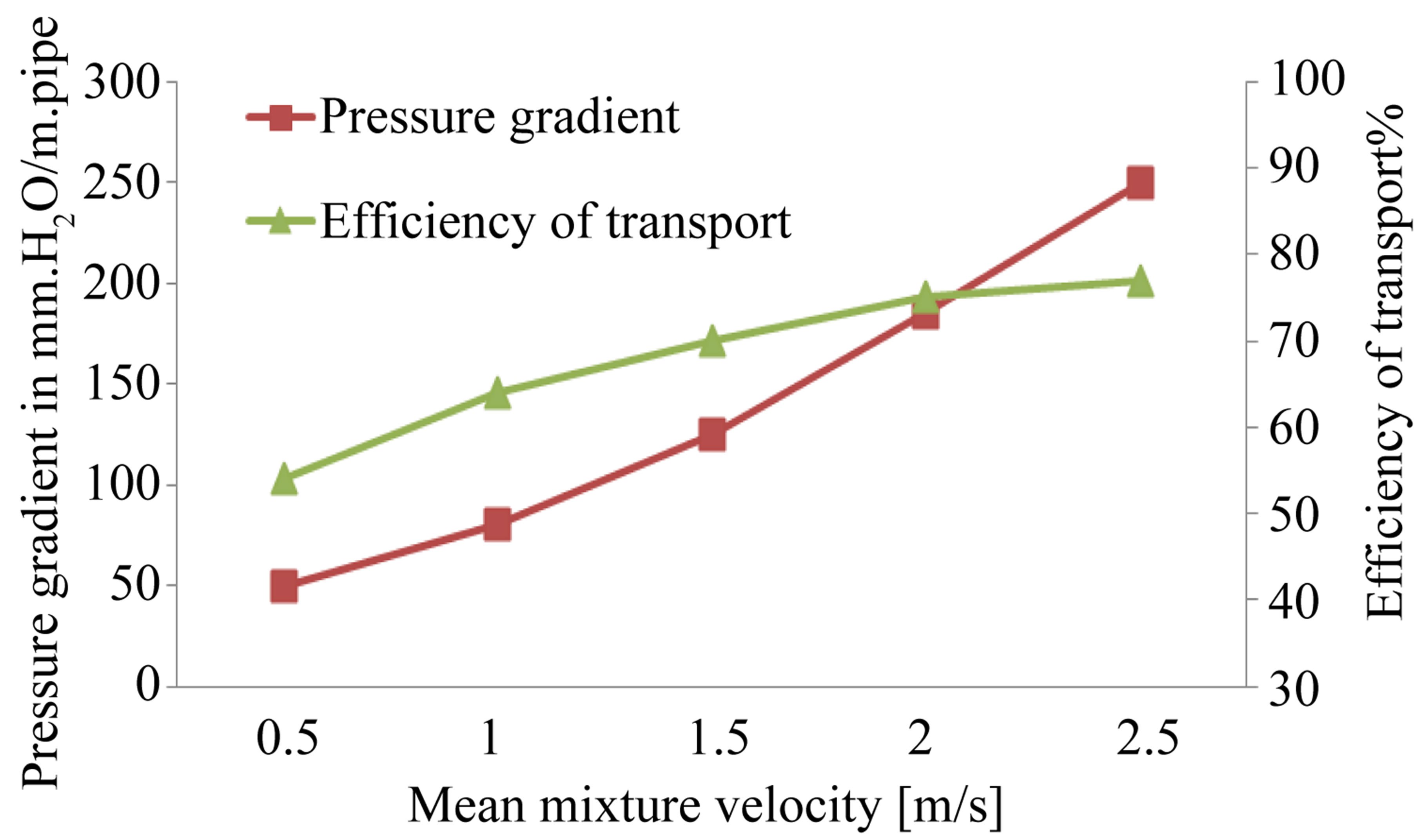
Figure 5. variation of slurry performance characteristics for sand slurry with solid concentration 1% by volume and particle diameter ds = 1 mm. versus mean mixture velocity.

Figure 6. Variation of slurry performance characteristics for slurry of iron oxide with solid concentration 1% by volume and particle diameter ds = 0.25 mm. versus mean mixture velocity.
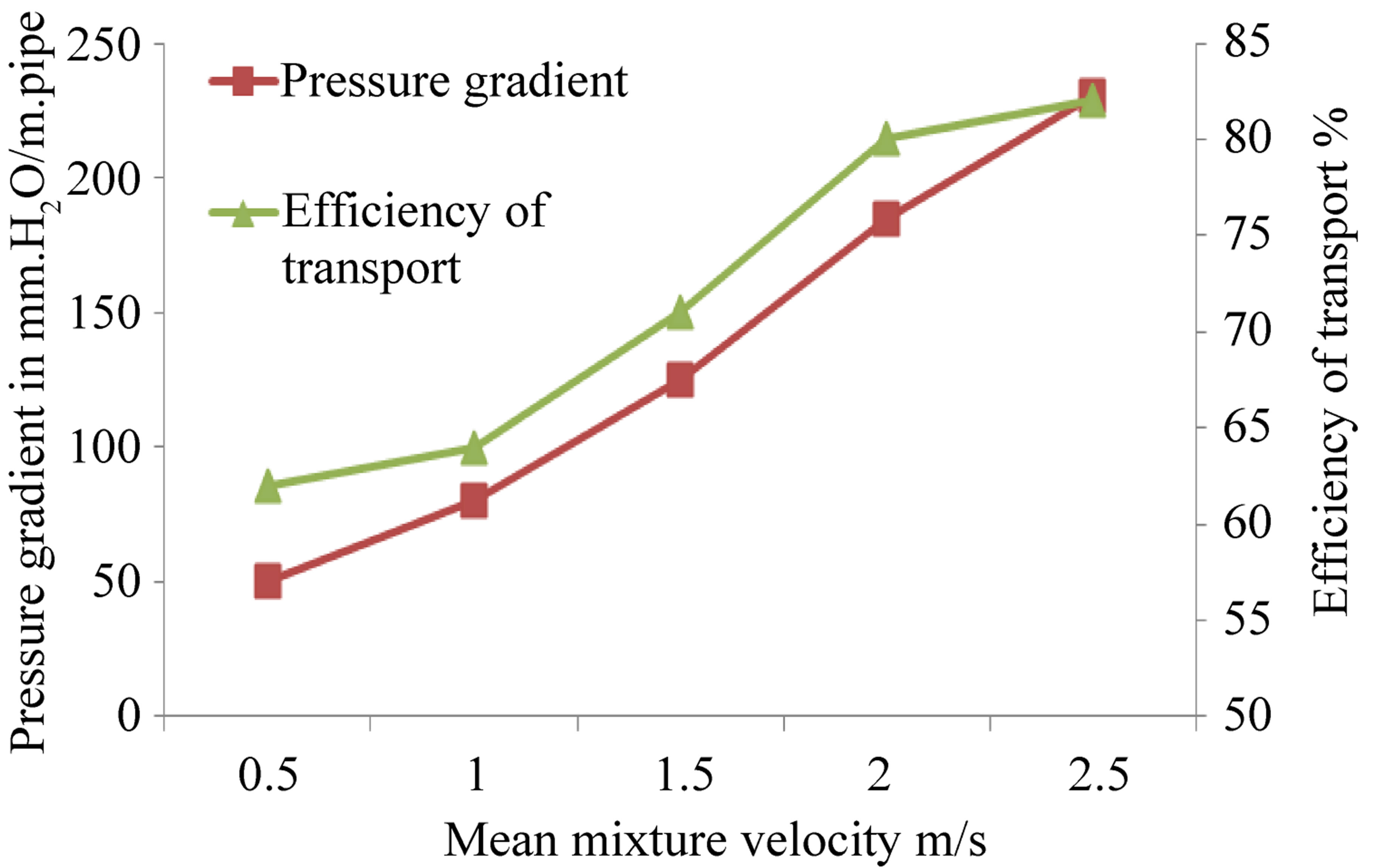
Figure 7. Variation of slurry performance characteristics for slurry of iron oxide with solid concentration 1% by volume and particle diameter ds = 0.5. mm. versus mean mixture velocity.
and Froude numbers increase the pressure gradient
 , which is a waste of power available increases.
, which is a waste of power available increases.
Also these experimental results concerning pressure gradient have close results in comparison to Turian and Yuan [6] correlations. this comparison is shown in Figures 9 and 10.

Figure 8. Variation of slurry performance characteristics for slurry of iron oxide with solid concentration 1% by volume and particle diameter ds = 1 mm. versus mean mixture velocity.

Figure 9. Comparison between experimental and theoretical pressure gradient for sand slurry with solid concentration 1% by volume with grain size diameter ds = 1 mm.

Figure 10. Comparison between experimental and theoretical pressure gradient for slurry of iron oxide with solid concentration 1% by volume with grain size diameter ds = 1 mm.
2) Effects of varying Re, Fr, upon efficiency of transport
The effect of varying Reynolds and Froude numbers upon the efficiency of slurry transport (η) is shown in Figures from 3 to 8. It can be noticed that as Reynolds and Froude numbers increases the efficiency of transport (η) is increased. This remark also encourages the use of high velocities to avoid blocking slurry pipelines.
4.3. Effect of Varying Particle Diameter (ds) upon Performance Characterstics of Slurry Pipeline
1) Effect of varying particle diameter (ds) upon pressure gradient :
:
Experimental tests have been carried out using samples of solid materials of arithmetic mean diameter from 0.25 mm to 1 mms. at the same input concentration by volume. The effects of changing particle diameter on pressure gradient are shown in Figures from 3 to 8 From these figures it was noticed that as the particle diameter increases the pressure drop increases slightly.
2) Effects of varying solid particle diameter (ds) upon efficiency of transport (η):
Figures from 3 to 8, indicates also the effects of varying particle grain diameter on efficiency of transport (η). As particle diameter increases the efficiency of transport (η) decreases.
4.4. Effect of Varying Specific Gravity of Particles upon Performance Characteristics
1) Effects of varying specific gravity upon pressure gradient:
The specific gravity was varied from 2.65 for sand and 3.540 for iron oxide.
Figure 11 indicates the effects of varying specific gravity upon the pressure drop . as specific gravity increases, the pressure drop increases; indicating the relative
. as specific gravity increases, the pressure drop increases; indicating the relative