Comparative Examinations of Single Bored Piles Using International Codes ()
1. Introduction
Settlement problems of soil containing clay layers extend deeply such as in Nile Delta and Port-Said regions are common. Although, rafts have been successfully used in many situations for diminishing settlement effects, pile foundations might not be avoided in other circumstances. Hossain et al. (2008) [5] presented the case study of a drilled shaft constructed in the Mid-Atlantic deposits in the USA, which was underlined by a bedrock present about 10 to 100 feet below the ground surface. They have determined the drilled shaft capacity experimentally to compare with the capacities calculated from empirical estimations computed by using the methods specified in the AASHTO Specifications and the FHWA Design Manual. Harraz et al. (2005) [6] compared the analysis results of fifty-six load test data with five different empirical methods, in order to determine the variation of the skin friction of drilled shaft in granular soils with high gravel content. According to Harraz et al. (2005), all the prediction methods under consideration were extremely conservative and the actual value of skin friction was under predicted by an average over 300%. Abdel Rahman et al. (2006) [7] presented a comparative study between the predicted ultimate bearing capacities of large diameter bored piles of the Egyptian code (ECP202/ 2005), DIN 4014 (1990) and AASHTO (1998). According to Abdel-Rahman et al. (2006) the Egyptian code predictions were found to be more conservative if compared to the indicated codes.
A numerical model for piled raft analysis has been proposed by El Gendy et al. [8] based on a technique combining both mathematical and empirical procedures. In the proposed model, the self-settlement of a pile was presented using the empirical nonlinear relation of loadsettlement according to DIN 4014 [2] while the settlements due to pile-pile, pile-raft and raft-soil interactions are determined using flexibility coefficients according to Mindlin’s solution [9]. In their work, the authors pointed out that the indicated model can accept any empirical load-settlement relation specified in other national standards instead of DIN 4014.
The main objective of this research is to compare the predicted axial ultimate load capacity of bored piles as is given by the Egyptian code [1] with the load test results obtained by the modified Chin (1970) method, in addition to the predictions of the following three international codes:
1) German Code DIN4014 (1990) [2];
2) AASHTO bridge design Specifications (2005) [3]; and
3) French code (Fascicule N˚ 62-Titre V) [4].
At first, a total of 38 drilled shaft load tests and their corresponding soil borings are described and classified according to their dimensions and locations. The load test data and soil properties for a selected sample of the examined bored piles are described. Then, background information on the code empirical methodologies used in this study for determining the ultimate capacity and loadsettlement curves of drilled shafts is introduced. Extensive comparisons are made between the predictions of the above mentioned codes regarding the total ultimate pile loads as well as the individual contributions of the tip and skin resistances. Finally, an empirical simplified load-settlement model deducted from code predictions of the ultimate load of large diameter bored piles is presented.
2. Description of Case Studies
A database consisting of 38 bored piles constructed and tested in Delta and Port Said areas in Egypt is taken as the basis of the present research [6]. The length of piles varies from 15 m to 70 m and diameters are 0.8 m to 1.2 m as shown in Figures 1-4. A sample of these case studies is shown in Table 1. These case studies are located in 8 different Egyptian cities with variable ground conditions. Careful review of geologic conditions of these sites reveals that no rocky bearing strata.
3. Pile Failure Load Evaluation
The pile failure load can be defined as the load limit beyond which a small increase in the load corresponds to a large increase in the tip settlement. It cannot be directly measured from a pile load test. Accordingly, ECP202 stipulated that the empirical pile capacity predicted by code methodology should be confirmed and verified with static load testing, following the modified Chin (1970) or Brinch-Hansen (1963) methods. Specifications regarding static load testing procedure are clearly specified in ECP202.
As stated earlier, the modified Chin (1970) method is chosen to verify the empirical ultimate pile capacities in this work. This method uses the different sloping gradient or tangent of test load-settlement curves. Figure 5 shows a typical sample of the regression analysis carried out for the test results of Case no. (27) of the present study database; from which the pile ultimate load is evaluated.
4. Estimation Methodologies of Pile Ultimate Bearing Capacity for Different Codes
4.1. Egyptian Code ECP202 (2005)
The design of piles with diameters greater than 60 [cm]

Figure 1. Lengths and diameters of case studies.

Figure 2. Case studies distribution according to site location.
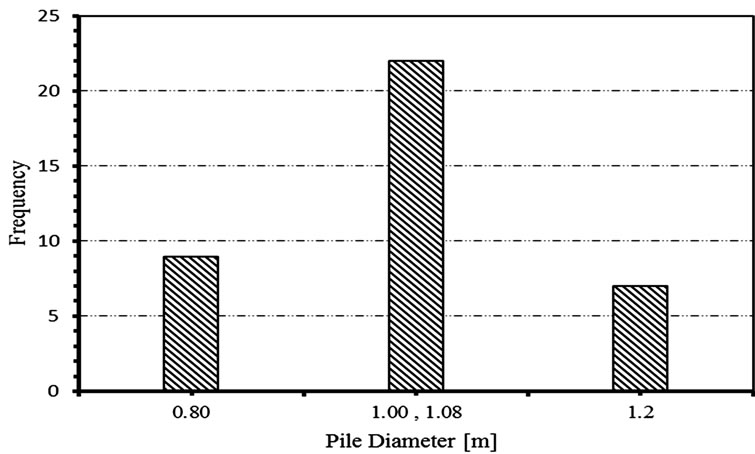
Figure 3. Case studies distribution according to diameters.

Figure 4. Case studies distribution according to lengths.


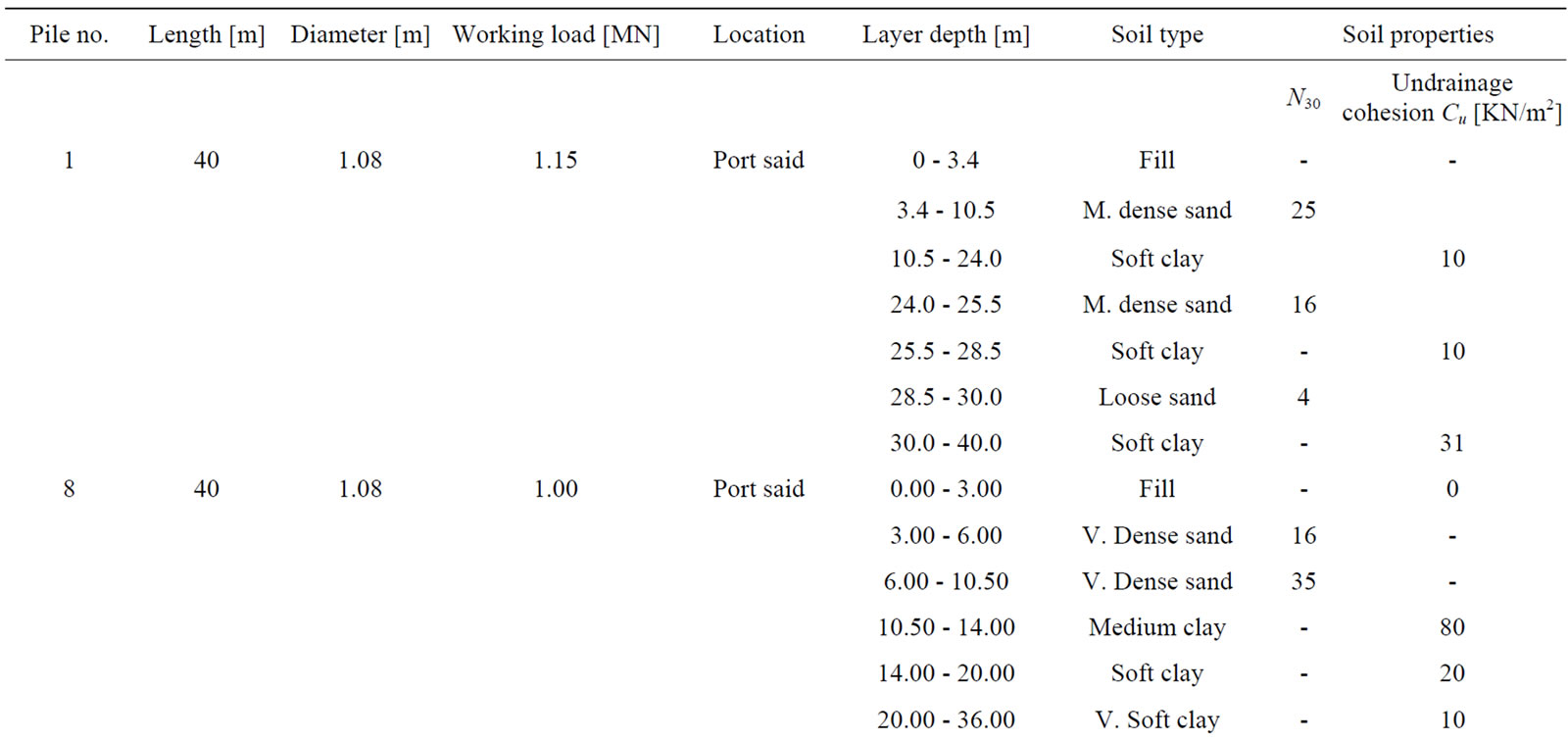
Table 1. Sample of soil properties and load test data of bored piles under examination [7].

Figure 5. Computation of ultimate load according to modified Chin (1970) method for Case (27).
and implemented by typical drilling and cast in place depends on the amount of settlement where the loadsettlement relationship is estimated from the results of pile load test. At initial design phases, where results from pile load tests are not available, the code presents a number of tabulated parameters for both cohesive and cohesion less soils to plot a multi-linear pile load-settlement relationship. Figure 6 shows a sample of estimated load-settlement curves for Case no. (20) of the present study database.
4.2. German Code DIN 4014
Regarding bored piles bearing capacity, the prediction of the German code, DIN 4014 [2] is based on the static cone penetrometer results and undrained shear stress. As the field measurements of penetrometer tip resistance qs were not available, the conversion factor qs/N30 is taken according to Table 2, as stipulated by DIN 4014. Figure 7 shows a sample of estimated load-settlement curves for Case no. (37) of the present study database.
4.3. AASHTO LRFD Bridge 2005
Among five different methods adopted in AASHTO, (2005) [3] for determining drilled shaft resistance in cohesionless soil, Reese and Wright (1977) method was selected for the present study. In this case, the ultimate load carrying capacities from the side shear and tip resistance in sand, both are estimated using the SPT blow count, N. On the other hand, Reese and O’Neill (1988) method was used in this work to estimate the ultimate capacities of drilled shafts in cohesive soils. Accordingly, the nominal unit side resistance, in MPa, was taken as a function of the adhesion factor α (0.55 ≥ α ≥ 0.31), and the undrained shear strength of cohesive layers Cu such that
 (1)
(1)
The nominal unit end bearing resistance for axially

Figure 6. ECP202 load-settlement curves for Case no. 20.

Figure 7. DIN 4014 load-settlement curves for Case no.37.

Table 2. Relation between cone penetration resistance and No. of blow counts (N30) (DIN 4014, 1990).
loaded drilled shaft in cohesive soil was taken as:
 (2)
(2)
in which:
 (3)
(3)
where:
Z = Penetration of shaft [mm].
D = Diameter of drilled shaft [mm].
Reese and O’Neill (1988) have sumarized loadsettlement data for drilled shafts in dimensionless form for both skin and tip resistances in the cases of cohesionless and cohesive soils. Those curves provide a usefull guide for estimating short-term settlement of drilled shafts, and they were used herein to estimate the loadsettlement curves for all case studies under examination. Figure 8 shows a sample of estimated load-settlement curves for Case no. (11) of the present study database.
4.4. French Code 1993
In this case, the results of the Ménard Pressuremeter Test (MPT) are used for determining the bearing capacity of piles (end bearing and skin friction). The French code [4] method depends on a tabulated tip bearing design factor kp, together with a chart for the ultimate unit skin friction qs. The ultimate unit skin friction resistance depends on soil properties, type of pile, and construction conditions. Unfortunately, the database of current study does not include any results for pressuremeter test. Therefore, for cohesionless soil, Baguelin et al. (1978) relationships [10] were used to convert the database available SPT results into MPT results. Moreover, Salencon (1966) equation was utilized for cohesive soil [10]. Finally, the French code recommends using MPT results for plotting the load-settlement curves for each soil layer separately as proposed by Frank and Zhao (1982). Figure 9 shows a sample of estimated load-settlement curves for Case no. (29) of the present study database.
5. Discussion of Results
The 38 pile case studies analyzed in the present research were selected fairly according to regional and availability
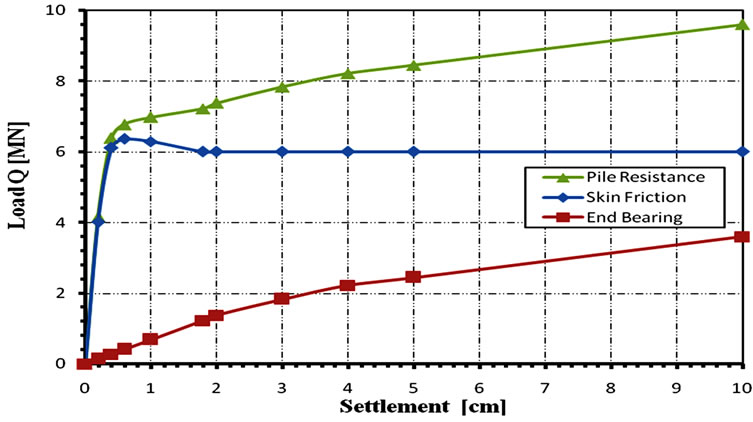
Figure 8. AASHTO load-settlement curves for Case no. 11.

Figure 9. Load-settlement curves according to Fascicule 62- V for Case no. 29.
basis to cover the Delta and Port Said areas. In general, every site location has special characteristics depending on its physical and Geotechnical properties. Consequently, the ultimate capacity of a drilled shaft Qu can be considered as a randomly selected variable. In this section, a comparitive study is made between the theoretical predictions of Qu as computed by the abovementioned four codes and Qu computed based on results of the pile load test using the modified Chin method. The comparisons are made for the total ultimate bearing resistance of the pile, as well as the separate resistance components (tip and skin resistances). Moreover, both the sandand clay skin resistances are dealt with individually. In a special subsection, the study is extended to compare the predictions of Egyptian code with their counterparts of the three other international codes.
5.1. Comparison of the Total Ultimate Pile Resistance
Statistical analyses are utilized herein to compare the total ultimate pile resistances Qu predicted by the mentioned codes and the results of the modified Chin method. Table 3 compares the main statistical parameters namely: the mean (μ), the median (Mdn), the standard deviation (σ), and the coefficient of variation (COV) for the four codes, with their counterparts computed based on the modified Chin’s method. Moreover, by plotting the probability distribution of the four theoretical predicted sets of ultimate pile capacity, together with the modified Chin’s method results, one gets the graphical presentation shown in Figure 10. It is clear that the five sets of results are normally distributed. It’s also clear from Table 3 that the arithmetic mean, and median are the most likely to coincide for every set of results, except for the modified Chin’s method. Moreover, the average total ultimate pile capacities estimated based on DIN 4014 and AASHTO codes are about 13 [%] higher-, while those of the Egyptian and French codes are about 11 [%] and 13 [%] respectively, lower than the load test results. Figure 10 also shows that the normal probability distributions of Qu for DIN 4014 and AASHTO codes are much closer to
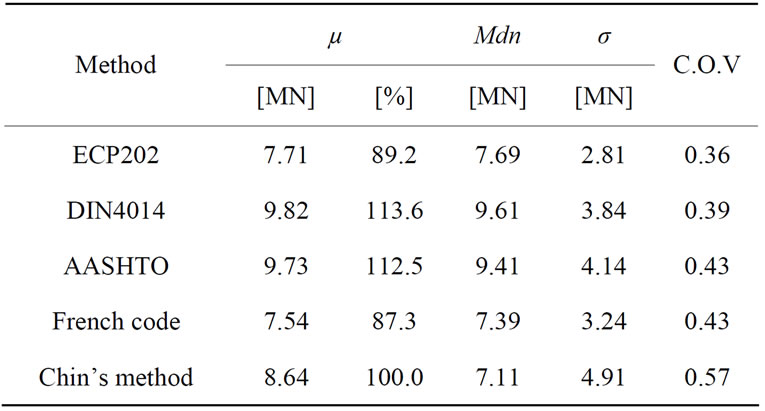
Table 3. Summary of statistical analysis of Qu results.
each other while those of the ECP202 and French codes are slightly different from one another.
As all five resulting sets of Qu are normally distributed, a statistical analysis of variance (ANOVA) was carried out to study the correlation between those sets. This type of statistical analysis explores the different kinds of variability among multiple data sets; based on the sums of variance squares. Table 4 gives the results of one-way ANOVA F-test (p-value, F, and Fcritical) for the comparisons between the predicted and measured Qu; for each of the four codes. It can be seen that all p-values resulting from the four separate comparisons are close to one another. As the p-value exceeds 0.05 and F < Fcritical for all codes, it can be concluded that the mean for all sets of predicted Qu are almost the same as that of the modified Chin results.
Figures 11 to 14 represent the best fit using regression analysis for the measured Qum versus the predicted ultimate pile loads Qup. On each figure, the coefficient of correlation R2 is given for each code. The coefficient of correlation, R2, is a measure that determines the degree to which Qum and Qup are associated. It gives a statistical correlation between the measured and predicted ultimate loads. This coefficient is unique in model evaluations. A higher value means a better model, with a value of unity indicating a perfect statistical correlation and a value of zero indicating there is no correlation. Table 5, summarizes the results of regression analysis for all codes. It is clear that the correlation coefficient R2 is al most equal

Figure 10. Probability distribution curves of Qu results.

Figure 11. Measured versus predicted Qu (Egyptian code).
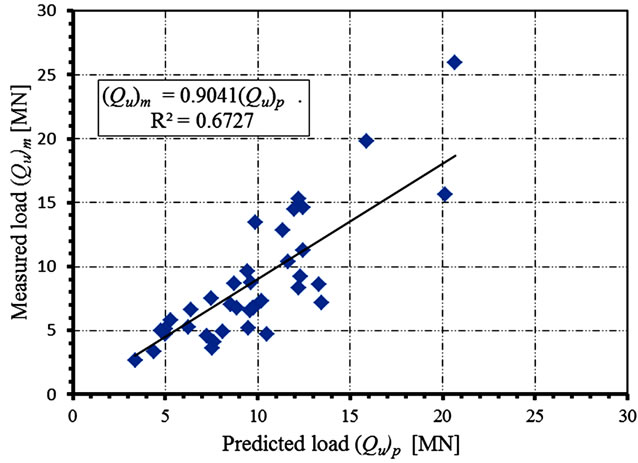
Figure 12. Measured versus predicted Qu (DIN 4014).
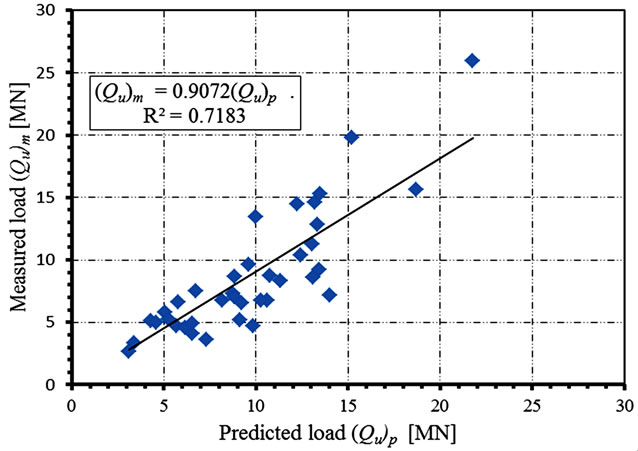
Figure 13. Measured versus predicted Qu (AASHTO).

Figure 14. Measured versus predicted Qu (French code).

Table 5. Summary of regression analysis results.
for all codes; which indicates that all code predictions are almost equally correlated to the test results. Both Egyptian and French codes under predict the measured pile capacity by about 14 [%]; while DIN 4014 and AASHTO over predict it by about 11 [%]. Consequently, it can be said that the performance of each of the four codes under consideration is as good as the others; regarding the estimation of ultimate load bearing capacity for large diameter bored piles.
5.2. Comparison of Separate Components of Pile Resistance
The analyses performed in the previous section showed significant differences between the maximum and minimum predicted total pile capacities among the codes under consideration. Moreover, a few exceptional cases were encountered where the code methodology excessively overestimates the pile bearing capacity. Therefore, it is essential to explore the reasons by analyzing each of the predicted pile resistance components individually. A number of comparative studies are carried out for code predictions of the tip and skin resistances individually. The separate contributions of sand and clay layers into the pile skin resistance are also investigated.
5.2.1. General Results for All Case Studies
Figures 15 to 18 show the separate components of pile resistance (given as a percentile of each pile total resistance) for all 38 case studies. For each code, the separate contributions (tip-, skin clay-, and skin sand resistance) are given as percentages. The average predicted ultimate tip resistance contribution ranges from 25% to 33% of the total pile resistance.
The predicted average shaft resistance is twice to three times as large as the predicted average tip resistance. It is also clear from Table 6 that the French code is considerably conservative regarding the predictions of clay skin resistance, if compared to any of the other three codes.
The mean (µ), stander deviation (σ) and COV for the different resistance components of the 38 case studies are summarized in Table 7 for all codes. It can be observed that the skin resistance components have larger variance, if compared to the variance of tip resistance for all codes.

Figure 15. Contribution of predicted side and tip resistances using ECP 202 design method.

Figure 16. Contribution of predicted side and tip resistances using DIN 4014 design method.
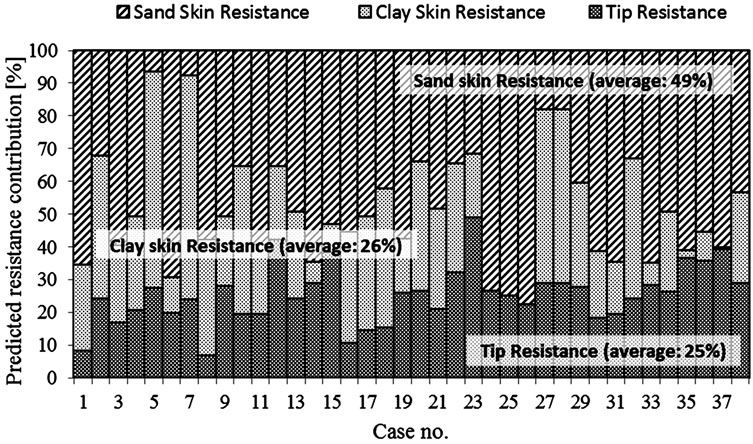
Figure 17. Contribution of predicted side and tip resistances using AASHTO design method.

Figure 18. Contribution of predicted side and tip resistances using French code design method.

Table 6. Average contributions of components resistance.

Table 7. Statistical analysis of resistance components for large diameter bored piles.
5.2.2. Code overestimation of Ultimate Pile Capacity
Among the 38 pile case studies under investigation, the total ultimate bearing resistance was over estimated by all codes for 13 case studies. It should be realized that this portion represents about one third of the total number of cases under examination. For a sample of those cases, Figure 19 compares the measured total pile loads to their counterparts estimated by both Egyptian and French codes; while Figure 20 compares them to the results of both DIN4014 and AASHTO codes. For those 13 case studies, the average predicted to measured Qu for Egyptian, DIN4014, AASHTO, and French codes, were found to be 134%, 167%, 158%, and 137%, respectively. These results prove that code predictions are not always sufficient for attaining a safe design; and performing a pile load test should be considered as a corner stone during the process of structural design.
It is noticed that the contribution of skin clay resistance in the French code is noticeably small, if compared to the other three codes. Thus, analysis of the different components of pile resistance herein focuses on all code predictions; except for the French code. Referring to Tables 6 and 8, it can be seen that the average tip as well as the average skin resistances for all 38 piles are almost the same as their counterparts for over predicted piles category; for the same code. Table 6 shows that for all 38 plies case studies, the average clay to total skin resistance is about 32 % to 36% (i.e. about one third roughly). However, for the cases with code over estimated Qu, this
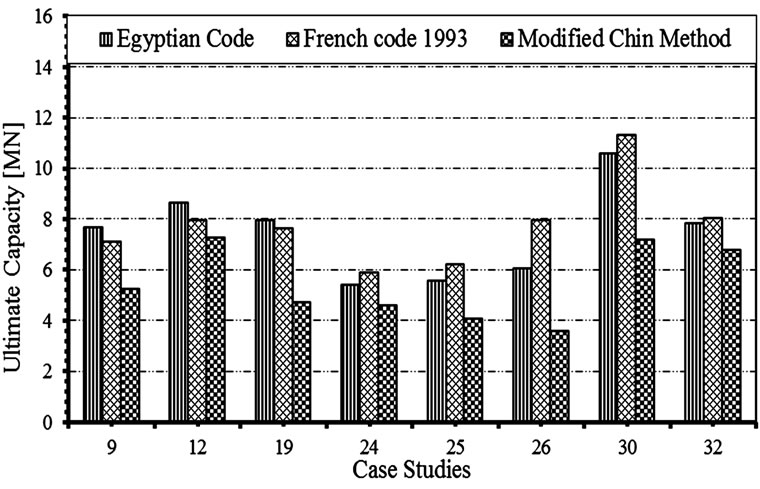
Figure 19. Overestimation of ultimate pile loads by Egyptian and French codes compared to test results.

Table 8. Average contributions of components resistance for cases with code over predicted pile loads.
contribution decrease to be lower than 23% of the pile total skin resistance as shown in Table 8. Therefor, it can be concluded that if the majority (about 77% or more) of shaft resistance is owing to sand friction, the code prediction for total pile bearing capacity would probably be over estimated.
5.3. Comparison of ECP 202 with Other International Codes
It was stated earlier that Qu predictions of the ECP202 are relatively conservative, if compared to those of DIN4014 and AASHTO codes, but they agree satisfactorily with the predictions of French code.
These correlations are studied in more details in this section. Table 9 gives a summary of results for some comparisons between the predictions of ECP202 and the other three codes; as percentiles. It should be noticed that the results given in the table are applicable for 92%, 85%, and 85% of the samples when compared to DIN4014, AASHTO, and French codes, respectively. For the pile samples which are not considered in the results given in the indicated table results, no correlation could be reached among the predictions of different codes. From the results given in Table 9, the following could be drawn:
1) Tip resistance of ECP202 reaches 85% of its counterpart in DIN4014, while it rises to 104% when compared to AASHTO and French codes.
2) Variations between skin resistances among the different codes are quite substantial.
3) Regarding the total pile capacity, ECP202 predictions are relatively conservative compared to DIN4014 and AASHTO, while they correlate well with the French code predictions.
Table 10 presents a comparison between the average predictions of ECP202 and the other three codes; for 2 of the 38 pile case studies examined in this research. In both cases, the pile was mostly embedded in lower layers of soft clay; which covers about 70% of the pile length. It is clear that the tip resistance prediction of the ECP202 code in this case was much more than the predictions of other codes; the worst case was a 415% over prediction (a factor of about 5.) In this case, the prediction of ECP202 code for total ultimate resistance of the pile was 24% to 80% higher than the predictions of other codes. In fact, ECP202 ignores the actual properties of cohesive end bearing soil and it does consider all cohesive base layers as hard clay.
6. Empirical Load-Settlement Curve
So far, the effort was devoted to study the correlation between code predictions and the measured ultimate bearing capacities for large diameter bored piles. In this section, the load-settlement relationships proposed by each of the four codes under consideration are compared in order to evaluate their performance. The load-settlement curves for ultimate end bearing, ultimate skin friction, and the total ultimate resistance of pile were determined separately for each of the 38 case studies under investigation. A sample is shown in Figure 21; which shows the load-settlement curves for case study no. 27. Figure 21(c) also presents two samples of a modified load-settlement model proposed by the authors, based on the comparative studies conducted herein. The proposed model depends on code prediction of the ultimate pile load bearing resistance (Qu), together with the corresponding settlement recommended by the code (Su). The proposed model can be considered as a general tool, because it can be equally applied using the predictions of any one of the four codes under consideration. The proposed load-settlement model is given by:

Figure 20. Overestimation of ultimate pile loads by DIN 4014 and AASHTO codes compared to test results.

Table 9. Comparisons of average resistances of ECP202 to other international codes predictions.

Table 10. ECP202 versus international codes predictions for weak cohesive end bearing layers (case studies no 1 and 8).
 (4)
(4)
where the coefficient C is taken as 8.66 for Egyptian and French codes, and it is taken as 11 for DIN 4014 and AASHTO codes. The two samples given in Figure 21(c) for the modified load-settlement curves are computed based on ECP 202 and AASHTO codes predictions for the ultimate pile loads. Similar modified curves can be simply plotted for the other two codes. The proposed closed form equation of the modified load-settlement curve might be very helpful for pile-raft analysis, as it would simplify to a great extent finding the pile settlement due to the load on pile itself. Accordingly, the flexibility coefficients can be directly evaluated in the piled-raft analysis with no necessity for numerical integration. The validity of the proposed modified load-settlement curve for pile-raft analysis will be the subject of a separate upcoming research.
7. Conclusions
This paper presents analyses 38 load test results for large diameter bored piles at eight different cities in northern Egypt. The analyses are based on four different international codes, namely: ECP202 (2005), DIN 4014 (1990), AASHTO (2005), and French Fascicule 62-V Code (1993). For each pile load test, the ultimate load bearing capacity and the load-settlement curve of the pile are found for all codes. Moreover, the modified Chin method dedicated by the Egyptian code for computing the experimental ultimate load of a bored pile is taken as a basis to evaluate the theoretical predictions given by different codes. Based on the analyses performed in this research, and keeping in mind that all conclusions given hereafter are related to the Nile Delta and Port Said regions in Egypt, the following conclusions could be drawn:
● Regarding the methodology for computing the ultimate load bearing capacity of a large diameter bored pile, the Egyptian and French codes are more conservative than DIN 4014 and AASHTO codes if compared to the modified Chin results (with a number of exceptions);
 (a)
(a) (b)
(b)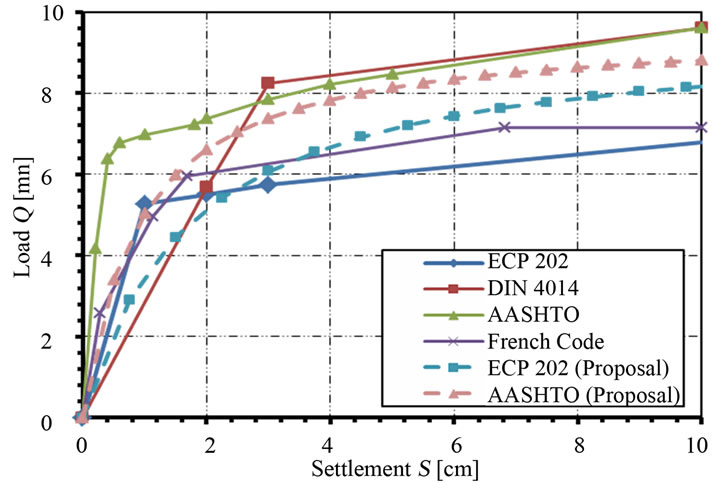 (c)
(c)
Figure 21. Empirical and modified load-settlement curves for Case no. 27. (a) Results of ultimate end bearing curves; (b) Results of ultimate skin friction curves; (c) Results of total pile resistance curves.
● In general, the average predicted ultimate tip resistance contribution was found to be 25% to 33% of the total ultimate pile resistance;
● In some exceptional situations, the Egyptian code may overestimate the total ultimate resistance of a bored pile, as the code methodology neglects the actual properties of end bearing soil;
● The pile load test is an irreplaceable process for determining the ultimate capacity of large diameter bored piles;
● Using the code prediction for the ultimate load bearing capacity of a bored pile, the research presents a useful simplified modified load-settlement curve to estimate the pile settlement for north Delta and Port Said regions in Egypt. The proposed modified loadsettlement curve will particularly be appreciated for piled-raft analysis, as it will be illustrated in a separate upcoming research.