Fuzzy Sliding Mode Observer for Vehicular Attitude Heading Reference System ()
1. Introduction
Considering Micro Electro-Mechanical System (MEMS) type sensors in an Attitude Heading Reference System (AHRS) to determine 3-axis orientations, a robust observer is introduced to handle modeling uncertainties and exogenous unknown inputs. Kalman filtering is widely used in state estimation problems, however, it is unable to treat large uncertainties with low-cost navigation equipment including 3-axis inclinometers (based on accelerometers), magnetometers and particularly gyroscopes in which noise effects are increased owing to integration of the sensor’s outputs.
Sliding mode observers (SMOs) have been developed to estimate the states of both linear and nonlinear variable structure systems which are affected by large uncertainties due to unknown bounded disturbances, modeling uncertainties and measurement noises. By use of a nonlinear discontinuous sign term, the SMO keeps the trajectory of estimation error remaining on a surface in the error space after a finite time. Therefore, the estimation errors become completely insensitive to the uncertainties [1]. Different variants of SMOs may be considered to robust state estimation in nonlinear systems. Based on Lyapunov’s direct method, design of an observer for nonlinear systems subjected to bounded nonlinearities and uncertainties has been suggested [2]. As another example, a numerical tractable algorithm for Walcott-Zak SMO has developed in [3,4]. Using equivalent control theory, other category of SMOs has been proposed in which the output estimation error and its higher derivatives are considered as sliding manifolds [5]. Furthermore, the idea of Utkin has been extended to a general class of nonlinear systems by [6].
Sliding mode systems suffer from chattering effects as their main drawback [7]. The chattering phenomenon is undesirable because it involves high control activity and furthermore may excite high frequency unmodeled dynamics. This difficulty of SMOs may be attenuated using different modifying techniques into the original observer. As the most common modification method to decrease chattering, a boundary layer neighboring the origin is considered. Therefore, a continuous term as a saturation function is replaced to the discontinuous sign term of the SMO inside the boundary layer [7]. Using the boundary layer method should result in a chattering-free performance; however, a finite steady-state error is generated. If the system’s uncertainties are large, the SMO would require a high switching gain with a thicker boundary layer to eliminate the resulted high chattering. However, if the boundary layer thickness continuously increases, the feedback system will reduce to a system without a sliding behavior. Thus, the application of a high gain feedback when the sliding variables reach the boundary layer results in a poor tracking and robust performance [8]. The fuzzy set theory is arisen from the desire of linguistic description for complex systems and can be used to formulate and translate the human experience to automatic control strategies, see for example, [9,10]. To tackle the above-mentioned difficulties of a SMO, a Mamdani type Fuzzy SMO (FSMO) is proposed for taking the discontinuous term of the SMO. Therefore, the knowledge and the experiences of expert engineers in the form of a fuzzy rule base are used to maintain the guaranteed tracking and robust performance of the observer as long as chattering free estimations.
First, in this paper, the design process of pure and fuzzy SMOs is proposed for a linearized MIMO system, which like an AHRS is affected by unknown uncertainties and exogenous inputs. Through adding a discontinuous term to the conventional Kalman estimator, both the SMO and the FSMO could be used as a complement term to the extended Kalman filter as a robust state estimator of uncertain systems. Second, the proposed estimation algorithms are implemented for an AHRS to estimate accurate orientations of ground vehicles even during accelerated maneuverings and under local magnetic disturbances. The performance of the proposed FSMO with respect to those of the SMO and the extended Kalman filter is evaluated through simulations and real tests of a low-cost AHRS including a TMS320VC5416 processor. The computer simulations and also the real experiments reveal that the tracking capability of FSMO on accurate estimation of vehicles’ attitude and heading is significantly better than those of the SMO and the extended Kalman filter.
The rest of the paper is organized as follows. In Section 2, design process of a SMO for uncertain MIMO systems is presented. FSMO is introduced in Section 3. Dynamical model of AHRS and its implementation by SMOs are presented in Section 4. Section 5 denotes results of simulations and real tests. Concluding remarks are made in Section 6.
2. Sliding Mode Observer
The general form of a continuous-time nonlinear uncertain system is considered as follows.
 (1)
(1)
 (2)
(2)
where,  and
and  are state and known input vectors, respectively;
are state and known input vectors, respectively;  represents a 2-norm bounded noise vector which stands for the uncertainties and the unknown inputs affecting a practical MEMS type AHRS; the measurement vector,
represents a 2-norm bounded noise vector which stands for the uncertainties and the unknown inputs affecting a practical MEMS type AHRS; the measurement vector,  is assumed to be completely known and measurable at each sample time, t;
is assumed to be completely known and measurable at each sample time, t; ,
,  and
and  are sufficiently smooth functions on the vector space, M.
are sufficiently smooth functions on the vector space, M.
To design a linear standard observer, the nonlinear system (1) and (2) is linearized as
 (3)
(3)
 (4)
(4)
 ,
,  ,
,  ,
,  (5)
(5)
where, A, B, G and C are fixed matrices which are resulted by linearization of system (1) and (2) at the current estimate, .
.
2.1. Observer Design
The following SMO based on the linearized model (3) and (4) of the nonlinear uncertain system is proposed for state estimation.
 (6)
(6)
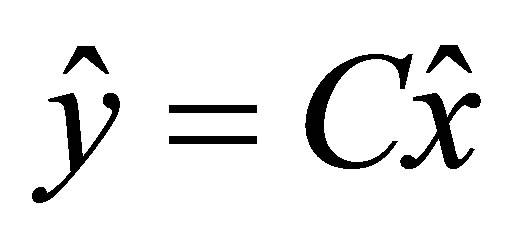 (7)
(7)
where, the estimated state vector is denoted by ;
;  is the well-known residual signal;
is the well-known residual signal;  and
and  are appropriately designed gain matrices; and
are appropriately designed gain matrices; and  represents the common sign function. In the proposed observer (6), the sign term is considered to compensate the effects of disturbance inputs of system (3). Therefore, the states of the system can be estimated using data given by the measured input vector,
represents the common sign function. In the proposed observer (6), the sign term is considered to compensate the effects of disturbance inputs of system (3). Therefore, the states of the system can be estimated using data given by the measured input vector,  and the system output,
and the system output, . Suitable design methods have been used to determine the observer gain L, ensuring the stability of the proposed estimator. For the designed SMO (6), the estimation gain of Kalman filter algorithm,
. Suitable design methods have been used to determine the observer gain L, ensuring the stability of the proposed estimator. For the designed SMO (6), the estimation gain of Kalman filter algorithm,  will be applied for L. Therefore, the proposed SMO includes Kalman filter’s term as well as the discontinuous sign term in which their corresponding gains are designed separately. Considering
will be applied for L. Therefore, the proposed SMO includes Kalman filter’s term as well as the discontinuous sign term in which their corresponding gains are designed separately. Considering  as a white Gaussian noise process, the well-known Kalman filter should result in unbiased estimations. However, due to the large uncertainties affecting the nonlinear system (1) and (2), Kalman filter results in biased and inaccurate estimations. Therefore, the proposed observer (6) is changed to the following mixed Kalman-SMO.
as a white Gaussian noise process, the well-known Kalman filter should result in unbiased estimations. However, due to the large uncertainties affecting the nonlinear system (1) and (2), Kalman filter results in biased and inaccurate estimations. Therefore, the proposed observer (6) is changed to the following mixed Kalman-SMO.
 (8)
(8)
2.2. Observer Stability
The main goal is to design  so that the discontinuous term,
so that the discontinuous term,  overcomes the parametric uncertainties assuring a stable dynamics of observer error. To prove the stability of the proposed SMO (8), the estimation error e is obtained as:
overcomes the parametric uncertainties assuring a stable dynamics of observer error. To prove the stability of the proposed SMO (8), the estimation error e is obtained as:
 (9)
(9)
The objective is to ensure that the estimation error is stable and independent of the unknown signals during the sliding motion. The stability of the SMO (8) is proven under the following assumptions.
Assumption 1: The pair  is assumed to be detectable so that there exist an observer gain,
is assumed to be detectable so that there exist an observer gain,  such that
such that  is a strictly Hurwitz matrix.
is a strictly Hurwitz matrix.
Assumption 2: The unknown disturbance,  is bounded, i.e. there exists a positive real value,
is bounded, i.e. there exists a positive real value,  such that
such that  where the symbols
where the symbols  and – stand for the 2-norm of vector/matrix and the upper bound value, respectively.
and – stand for the 2-norm of vector/matrix and the upper bound value, respectively.
Assumption 3: The 2-norm of the known term 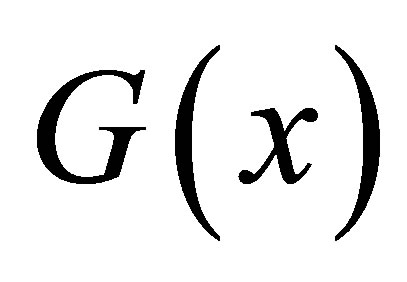 and the SMO gain matrix
and the SMO gain matrix  are bounded to corresponding upper bounds,
are bounded to corresponding upper bounds,  and
and  respectively.
respectively.
For a system satisfying assumptions 1 through 3, the stability of the SMO (8) can be investigated using the following Lyapunov candidate function.
 (10)
(10)
where, the unique positive symmetric matrix  is the solution of the following Lyapunov equation.
is the solution of the following Lyapunov equation.
 (11)
(11)
Taking the time derivative of (10) yields:
 (12)
(12)
Replacing (11) in (12) leads to:
 (13)
(13)
A negative definite,  requires that
requires that . Therefore, the bounded error dynamic will be guaranteed through the following gain condition.
. Therefore, the bounded error dynamic will be guaranteed through the following gain condition.
 (14)
(14)
Consequently, since , the estimation error of the SMO,
, the estimation error of the SMO,  converges to zero.
converges to zero.
3. Fuzzy Sliding Mode Observer
Chattering free estimations may be achieved using linguistic variables instead of fixed numerical values. Therefore, to enhance the performance of a classic SMO, a knowledge based Fuzzy logic SMO (FSMO) is designed. The intelligent FSMO maintain the robust property of the pure SMO while the chattering phenomenon is significantly decreased.
The fuzzy sliding mode observer is considered as:
 (15)
(15)
where, the crisp output of the FSMO,  is computed through the designed if then rule-base considering the tracking errors,
is computed through the designed if then rule-base considering the tracking errors,  and
and  as input variables of the fuzzy inference system. Compared with the SMO (8), the sign term of the observer is replaced by the output variable of the fuzzy inference system to construct the FSMO (15). Since the if-then rules of the fuzzy system are generated according to the properties of sign term, the FSMO is expected to be a robust observer.
as input variables of the fuzzy inference system. Compared with the SMO (8), the sign term of the observer is replaced by the output variable of the fuzzy inference system to construct the FSMO (15). Since the if-then rules of the fuzzy system are generated according to the properties of sign term, the FSMO is expected to be a robust observer.
The fuzzy if-then rules make a nonlinear mapping from the input linguistic variables  and
and  to the output linguistic variable,
to the output linguistic variable,  as:
as:
 (16)
(16)
The membership functions corresponding to the input and output fuzzy sets of ,
,  and
and  are represented in Figure 1, in which the linguistic labels P, N, ZE,
are represented in Figure 1, in which the linguistic labels P, N, ZE,
S, M and L stand for positive, negative, zero, small, medium and large, respectively and thereby for example, NL denotes a negative-large fuzzy set.
A simple fuzzy rule table is constructed considering the following reaching and stability requirements [11]:
1. The output fuzzy set,  is normalized in the interval
is normalized in the interval , therefore,
, therefore, .
.
2. When  becomes a positive value, the membership function of
becomes a positive value, the membership function of  is set in such a way that its sign becomes similar to that of
is set in such a way that its sign becomes similar to that of  and therefore,
and therefore, .
.
3. While  is a negative value, the reaching condition
is a negative value, the reaching condition  would be satisfied automatically. In this case, the membership function of
would be satisfied automatically. In this case, the membership function of  could be changed with negative or even positive sign to enhance the tracking performance.
could be changed with negative or even positive sign to enhance the tracking performance.
Regarding seven membership functions for each input variable of the fuzzy rule base, 49 if-then rules of Table 1 are obtained using expert engineering knowledge in the navigation field and satisfying the above-mentioned stability and reaching conditions.
Laypunov’s stability of the FSMO (15) is evaluated similar to that of the SMO using the following positive function.
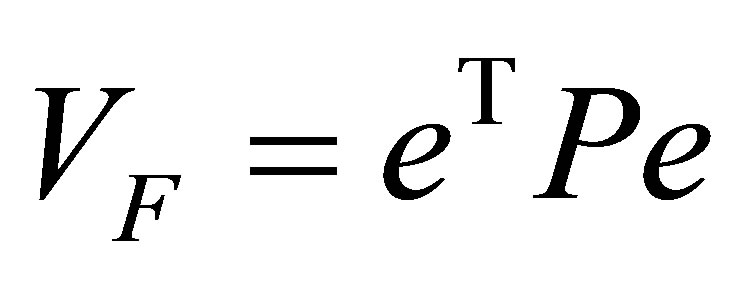 (17)
(17)
 (18)
(18)
Taking the time derivatives of  gives:
gives:
 (19)
(19)
Based on Lyapunov’ direct theory, if  (19) is negative for all
(19) is negative for all , then the reaching condition
, then the reaching condition  is satisfied. Therefore,
is satisfied. Therefore,  is designed to guarantee that the system tracking error asymptotically converges to zero.
is designed to guarantee that the system tracking error asymptotically converges to zero.
According to (12):
 (20)
(20)

Table 1. Rule bases of fuzzy logic observer.
Similar to (13), a negative definite,  requires that
requires that . Therefore, the bounded error dynamics and the reaching condition
. Therefore, the bounded error dynamics and the reaching condition  will be guaranteed using
will be guaranteed using  which, for example,
which, for example,  stands for the upper bound of
stands for the upper bound of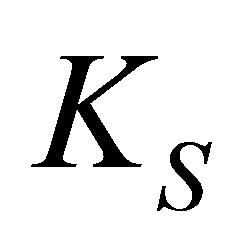 .
.
4. Observer Design for AHRS
4.1. Attitude Heading Reference System
Appearance of low-cost MEMS accelerometers and gyroscopes offers the opportunity of applying inertial navigation systems for ground vehicles. However, the navigation data obtained from MEMS equipment are subjected to random drifts due to large uncertainties affecting the sensors. In an AHRS, 3-axis gyroscopes, accelerometers and magnetometers measure the rotation rates of the system’s body, and the vectors of gravity and magnetic fields of the Earth all along the body axes, respectively. In this way, the measurements made by the 3-axis accelerometers are used to update the roll and pitch angles through vector matching between the measurements and the Earth’s gravity field vector in the reference North East Down (NED) frame. The matching vector based measurement system of accelerometers is integrated with the Euler angles dynamics including the measurements made by MEMS rate gyroscopes. Once the attitude is estimated, the measurements of a 3-Axis Magnetometer and the angular rate sensors will be integrated to update the heading angle [12]
4.2. Attitude
The following attitude dynamics determines the evolution of the roll and pitch angles, [13]:
 (21)
(21)
where, the evolution of the roll and pitch angles are expressed in terms of the body-referenced body to NED frame rotation vector,  and the measurement disturbance,
and the measurement disturbance, . The input angular rate to the AHRS includes also the rotation rate of the Earth and the transport rate of the vehicle which are smaller than the noise bound of the MEMS type gyroscopes. Therefore, the components of the rotation rate vector,
. The input angular rate to the AHRS includes also the rotation rate of the Earth and the transport rate of the vehicle which are smaller than the noise bound of the MEMS type gyroscopes. Therefore, the components of the rotation rate vector,  may simply be considered equal to the measured rates by the MEMS gyroscopes as follows.
may simply be considered equal to the measured rates by the MEMS gyroscopes as follows.
 (22)
(22)
where, the superscript, T stands for the transposed vector. The components of the measurement noise vector are defined as:
 (23)
(23)
According to the general nonlinear system (1) and (2), the nonlinear matrices ,
,  and
and  of the AHRS’s model are smooth functions of the state vector,
of the AHRS’s model are smooth functions of the state vector,  , the rate vector,
, the rate vector,  and the acceleration due to the Earth’s gravity,
and the acceleration due to the Earth’s gravity,  as:
as:
 (24)
(24)
 (25)
(25)
 (26)
(26)
The elements of the vector  are the Earth’s gravity field vector resolved along the body axes, for example as,
are the Earth’s gravity field vector resolved along the body axes, for example as,  which are ideally measured by the 3-axis accelerometers of the AHRS. Therefore, the attitude angles could be computed through the matching of the earth’s reference gravity vector in NED frame with the measurements of accelerometers along the body axes [14]. Hence, during initial alignment process, the AHRS should be unmoved to obtain the initial states of (21) as:
which are ideally measured by the 3-axis accelerometers of the AHRS. Therefore, the attitude angles could be computed through the matching of the earth’s reference gravity vector in NED frame with the measurements of accelerometers along the body axes [14]. Hence, during initial alignment process, the AHRS should be unmoved to obtain the initial states of (21) as:
 (27)
(27)
 (28)
(28)
where, the symbol,  denotes the average output of the inertial sensors over the alignment time. It is worth noting that the mathematical singularity of (28) at
denotes the average output of the inertial sensors over the alignment time. It is worth noting that the mathematical singularity of (28) at  does not occur in vehicular applications of the AHRS.
does not occur in vehicular applications of the AHRS.
4.3. Heading
The Earth’s magnetic field vector as a directional reference is generally used for alignment and monitoring of heading angle by the AHRS which includes MEMS gyroscopes. Once the roll and pitch angles are estimated, the measurements made by the magnetometers are used to make a vector matching with respect to the resolved components of the Earth’s magnetic field vector in the local level horizontal plane, [14]. Therefore, the following dynamics whose mathematical singularity at  my not occur due to the bounded attitude angles of car vehicles is considered to obtain the heading angle of the vehicle.
my not occur due to the bounded attitude angles of car vehicles is considered to obtain the heading angle of the vehicle.
 (29)
(29)
 (30)
(30)
 (31)
(31)
 (32)
(32)
 (33)
(33)
where,  is the magnetic heading angle. The horizontal component of the earth’s magnetic field vector,
is the magnetic heading angle. The horizontal component of the earth’s magnetic field vector,  is resolved to
is resolved to  and
and  along the local level axes. The components of the earth’s magnetic field vector along the body x-y-z axes are denoted by
along the local level axes. The components of the earth’s magnetic field vector along the body x-y-z axes are denoted by ,
,  and
and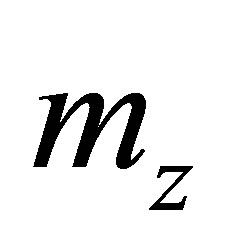 .
.
5. Observer for AHRS
The attitude estimation problem has received a lot of attentions especially in aerospace engineering fields. The Kalman filter (KF), extended Kalman filter (EKF) and its other variants are the most widely used approaches for estimating the states of a nonlinear system. In this paper, the proposed SMO and the FSMO are implemented in a strapdown AHRS on a ground vehicle.
5.1. Attitude Estimation
Considering (24) and (25) the matrices and
and  are obtained as:
are obtained as:
 (34)
(34)
 (35)
(35)
According to the observation vector (26), the observation matrix,  is constructed as:
is constructed as:
 (36)
(36)
Now, the following sliding mode and fuzzy sliding mode observers can be specialized for the proposed attitude dynamics using suitable estimation gains,  and
and  as:
as:
 (37)
(37)
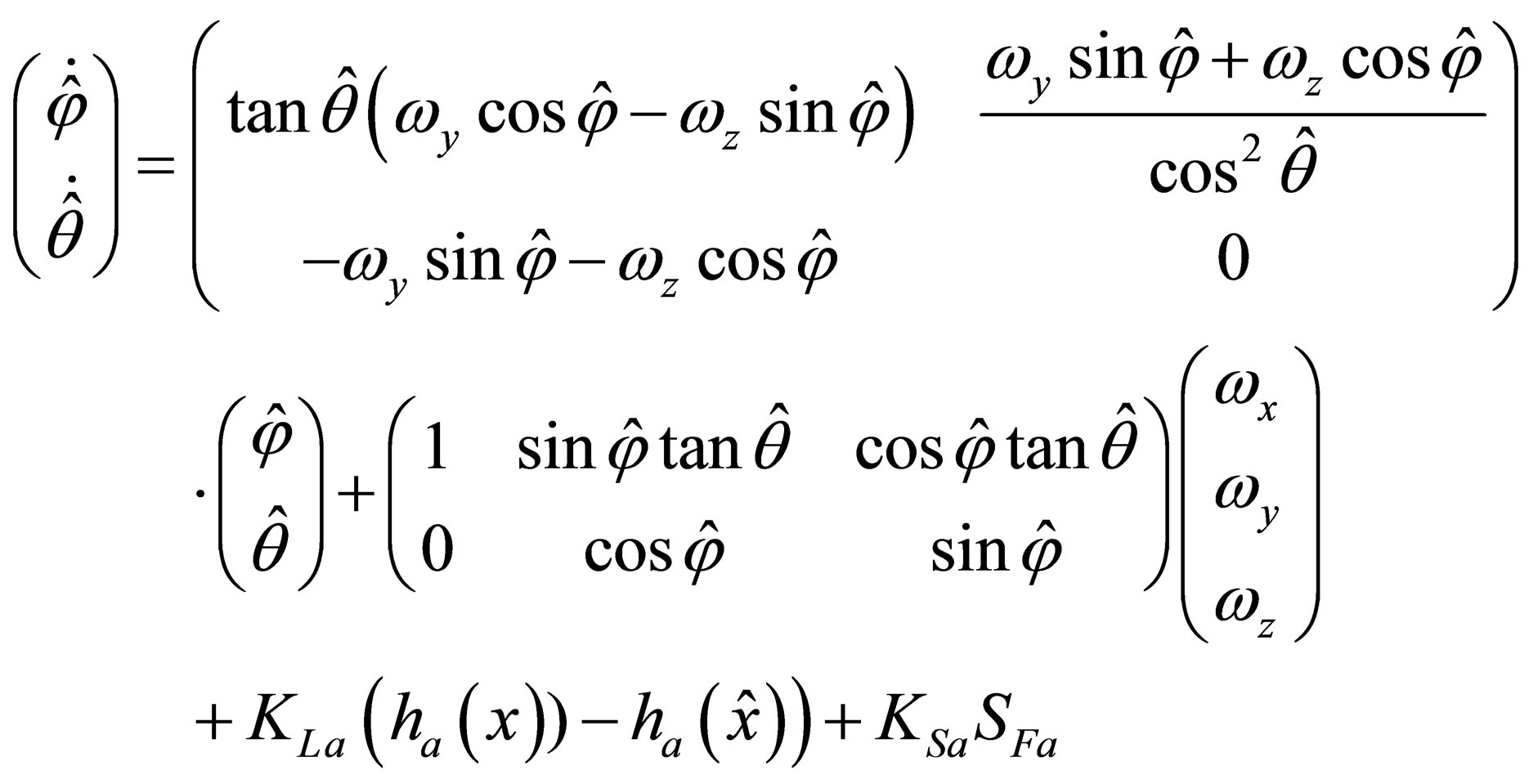 (38)
(38)
5.2. Heading Estimation
Considering the dynamic system (29) and (30), the corresponding matrices ,
,  and
and  are defined as:
are defined as:
 (39)
(39)
Similarly, the corresponding pure and fuzzy SMOs can now be rewritten for the proposed heading dynamics using proper estimation gains,  and
and  as:
as:
 (40)
(40)
 (41)
(41)
where,
 (42)
(42)
The observer is completed by designing suitable observer gains,  and
and  based on the information coming from the estimated attitude angles
based on the information coming from the estimated attitude angles  and
and .
.
6. Simulation and Test Results
In this section, first using software simulations, the estimation performance of the FSMO is assessed in comparison with that of the Kalman filter. The simulated vehicle is considered to be accelerated up to 0.5 g and affected by magnetic disturbances up to 1 μT (microTesla). The desired attitude and heading trajectories are generated by applying the ideal turn rates of a vehicle body axes in the simulated dynamics of Euler angles. Furthermore, the measurement equations of the AHRS are simulated based on the desired roll, pitch and heading angles. To evaluate the robust performance of the FSMO, stochastic uncertainties and measurement noises regarding the specifications of real MEMS gyroscopes in table 2 are considered in the simulations.
Figure 2 shows the tracking errors of estimated attitude-heading angles by the EKF with respect to the reference true values which are obtained through simulation without considered noise uncertainties. Similarly, using the proposed SMO, Figure 3 shows the corresponding tracking errors with respect to the reference values.
As the simulation results show, the EKF approximately yields the chattering-free estimation of attitude and heading angles. However, unlike the SMO, the EKF could not result in robust estimation in the presence of bias uncertainty and changing the intensity of noises. On the other hand, SMO results in fast convergence of initial alignment errors of the angles to zero, however, the chattering error of the SMO could not be perfectly removed. In addition, from Figures 2 and 3, the tracking performance of the SMO is significantly accurate and robust to the uncertainties compared with that of the EKF.
Using the FSMO, the estimated attitude-heading angles and the corresponding tracking errors with respect to the reference true values are shown in Figures 4 and 5, respectively. As shown in these figures, owing to the robustness of sliding mode structure, the FSMO results in a better tracking performance and yields less estimation errors of the attitude-heading angles compared to the EKF. Furthermore, by the proposed FSMO, the chattering phenomenon that frequently appears in the pure SMO is eliminated without deteriorating the system’s robustness in the presence of bias uncertainties of low-cost MEMS gyroscopes.
Next, the EKF, SMO and FSMO algorithms of the AHRS are experimentally verified using the vehicular tests data of a Vitans navigation system which is aided by a Garmin 35 GPS and a magnetic compass [15]. Table 2 shows the main specifications of the magnetic and inertial sensors of Vitans system.
The raw measurements of the 3-axis gyroscopes, magnetometers and accelerometers are processed in the FSMO, SMO and EKF algorithms implemented for the AHRS. Figure 6 shows the geographical latitude-longitude of the tracked path by the vehicle which conveys the AHRS during a highway test. Along the test path of Figure 6, compared with the reference attitude-heading of the integrated INS with GPS, Figures 7 and 8 show the attitude and heading angles of the vehicle, which have been obtained through the EKF and the SMO. Similarly, Figures 9 and 10 show the estimated angles and their tracking errors made by the FSMO. According Figure 10,

Figure 2. Tracking errors of estimated (a) roll; (b) pitch and (c) heading using EKF from true values.

Figure 3. Tracking errors of estimated (a) roll; (b) pitch and (c) heading using SMO from true values.

Figure 4. Estimation error of (a) roll; (b) pitch and (c) heading angles using FSMO from true values.

Figure 5. Tracking errors of estimated (a) roll; (b) pitch and (c) heading using FSMO from true values.

Figure 6. Vehicle tracked path during a highway test.
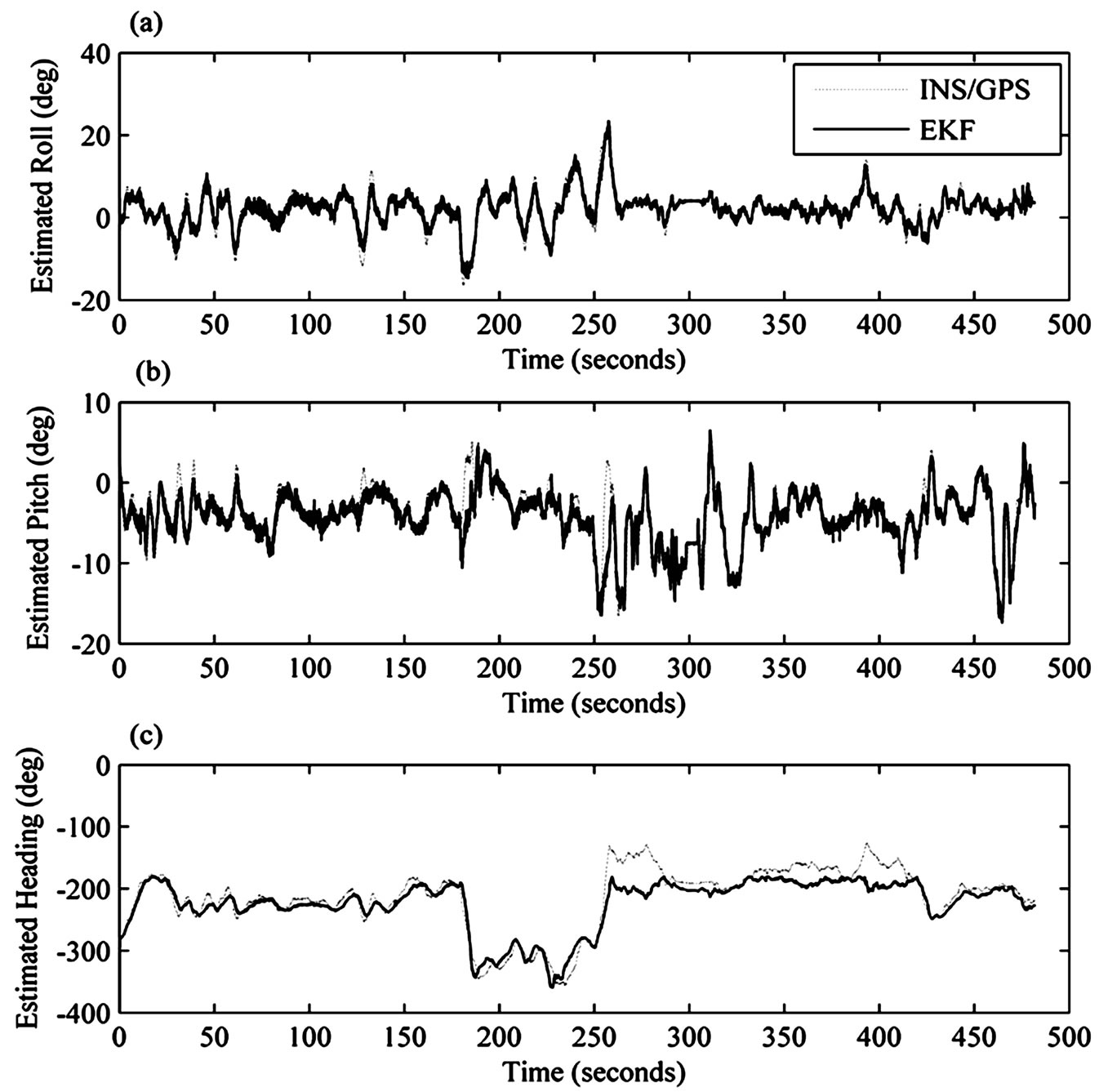
Figure 7. Estimation of (a) roll; (b) pitch and (c) heading angles using EKF compared with reference values of INS/GPS.

Figure 8. Estimation of (a) roll; (b) pitch and (c) heading angles using SMO compared with reference values of INS/GPS.

Figure 9. Estimation of (a) roll; (b) pitch and (c) heading angles using FSMO compared with reference values of INS/GPS.
considerable heading error in the interval 250 second and 280 second shows a little weakness of FSMO against abrupt changes of magnetic disturbances.
To legitimize the comparisons, the mean values and the standard deviations of the estimation errors of all the FSMO, SMO and EKF systems are represented in Tables 3 and 4. The tabled results show that the FSMO yields a superior estimation quality of the vehicle’s attitudeheading angles with respect to the SMO and the EKF. It should be noted that the heading angles of the AHRS’s algorithms are computed based on the measurements made by the magnetometers. However, the reference heading angle is given by the aiding GPS receiver with respect to the polar North of the Earth. Therefore, by removing the 7 ̊ declination angle between the magnetic and polar North axes of the Earth, the heading angle error in Tables 3 and 4 is about 2 ̊ which is a good estimation accuracy regarding the low-cost magnetometers.

Figure 10. Errors of estimated (a) roll; (b) pitch and (c) heading angles using FSMO with respect to reference INS/GPS values.

Table 2. Specifications of inertial and magnetic sensors.

Table 3. Mean values of estimation errors.

Table 4. Standard deviations of estimation errors.
6. Conclusion
In this paper, a Mamdani-type fuzzy logic based sliding mode observer including 49 if-then rules has been proposed. The designed intelligent reaching law of the FSMO improves its estimation performance with respect to that of the pure SMO of a low-cost AHRS which is affected by exogenous inputs and modeling uncertainties. Based on Lyapunov’s stability theory, the FSMO has been designed for regulation of the estimation error vector to the origin equilibrium point in the state space. Through gathering the robustness of SMOs and chattering cancellation property of the fuzzy boundary layer, the proposed FSMO is superior with respect to the EKF and the SMO in practical applications. Therefore, as both simulation and real test results show, the proposed estimation method is efficient against increasing uncertainties, unknown magnetic disturbances and non-gravitational accelerations affecting the AHRS. In the proposed FSMO, the chattering phenomenon that frequently appears in the pure SMO is eliminated without deteriorating the system robustness. Compared with the conventional EKF, both the SMO and the FSMO yield high convergence rates of estimation errors to zero. Furthermore, fast compensation of initial alignment errors of the attitude and heading angles is obtained by the fuzzy and pure SMOs. On the other hand, during affecting abrupt magnetic disturbances, the performance of the EKF is a little better with respect to the FSMO owing to the conservative nature of fuzzy systems. However, the overall performance of the FSMO is superior with respect to those of the EKF and the SMO. An adaptive fuzzy SMO could be developed in future to improve the performance of the fuzzy SMO during affecting abrupt changes of disturbances.