Holographic-Type Gravitation via Non-Differentiability in Weyl-Dirac Theory ()
1. Introduction
The General Relativity states that there is a reciprocal conditioning between geometry and matter so that the guiding mechanism is governed by the motions of the matter itself. However, the same guiding mechanism is neglected when it is used in the study of particle dynamics at microscopic scale. Such “apparent contradiction” is can be solved, for example by means of Weyl-Dirac (WD) theory [1-3].
After the development of general theory of relativity, Weyl extend this theory for electromagnetic processes, from the dominance of light rays for physical measurements, where the phenomena are also described geometrically. This theory had some features that not gain the general acceptance. Later, Dirac introduces some modifications which removed the theory difficulties and he made use of the theory to provide a framework to explain his large number hypothesis.
Different formalisms have been developed in WD theory. Among the most known and useful ones we mention the Gauss-Mainardi-Codazzi (GMC) formalism [4-6]. Using the GMC formalism in WD theory, important results were obtained (the particle is represented by a spherically symmetric thin-shell solution to Einstein’s equations; a geometric model with conformal invariance broken in the interior space; a new possibility to consider non-local effects, when the interior curved space—time has non causal properties, such as closed time-like curves; a transfer mechanism for energy—momentum between the thin shell and the Madelung fluid; a geometric guidance condition for the bubble at microscopic scale and a Hamilton-Jacobi equation that can be directly applied to the thin shell so that the bubble could move in step with the Madelung fluid) [4-6].
In [7-9] we have shown that the wave-particle duality may be associated with a phase transition of superconducting—normal state type. More recently [10], using the hydrodynamic model of the WD theory in the non-relativistic approach, we established some properties of vacuum states.
This paper analyzes the wave-particle duality in the WD non-relativistic hydrodynamics model from the perspective of the non-differentiability of motion curves of the WD non-relativistic fluid particles. The paper is structured as follows: in Section 2 the non-differentiability of the motion curves in the WD non-relativistic hydrodynamics model; in Section 3 the wave-particle duality through cnoidaloscillation modes of the states density.
2. Non-Differentiability of the Motion Curves in the WD Non-Relativistic Hydrodynamics
The way in which the geometry of space-time affects the dynamics of the particle in the WD theory is given by the covariant Equation [5]
 (1)
(1)
where  is the covariant derivative, R is the Ricci scalar, Λ is the cosmological constant and
is the covariant derivative, R is the Ricci scalar, Λ is the cosmological constant and 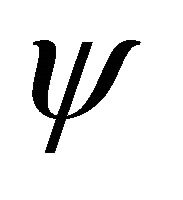 is the wave function associated of the particle. So, “it is considered a matter shell on a cosmological background described by the field
is the wave function associated of the particle. So, “it is considered a matter shell on a cosmological background described by the field  which is also a source of the wave function. The law of parallel transport common to this theory requires a vector to change not only in direction but also in magnitude, after transport along a closed space-time loop. This result is given by a quantum force due to both the curvature of space-time and wave function, and consequently, due to the loss of the microscopic distinguishability of the particle’s trajectories” [5]. Since
which is also a source of the wave function. The law of parallel transport common to this theory requires a vector to change not only in direction but also in magnitude, after transport along a closed space-time loop. This result is given by a quantum force due to both the curvature of space-time and wave function, and consequently, due to the loss of the microscopic distinguishability of the particle’s trajectories” [5]. Since  is taken to represent the probability density, Equation (1) enables the quantum mechanical interpretation of the WD theory in the sense of Bohm [11].
is taken to represent the probability density, Equation (1) enables the quantum mechanical interpretation of the WD theory in the sense of Bohm [11].
In the weak field approximation (WFA) [10,12-19] and low speeds as compared to speed of light in vacuumthe WD equation with  is reduced to the set of equations:
is reduced to the set of equations:
 (2a)
(2a)
 (2b)
(2b)
where
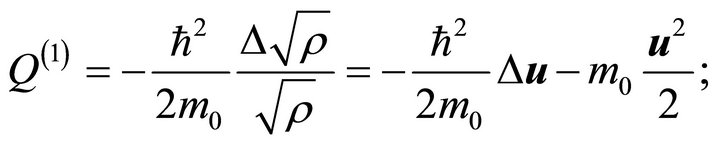 (3a)
(3a)
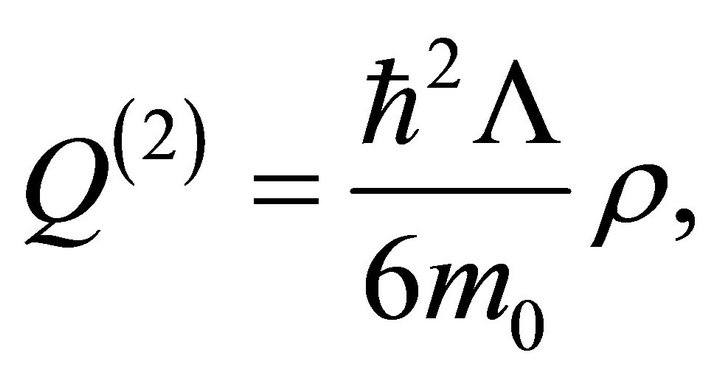 (3b)
(3b)
 (3c)
(3c)
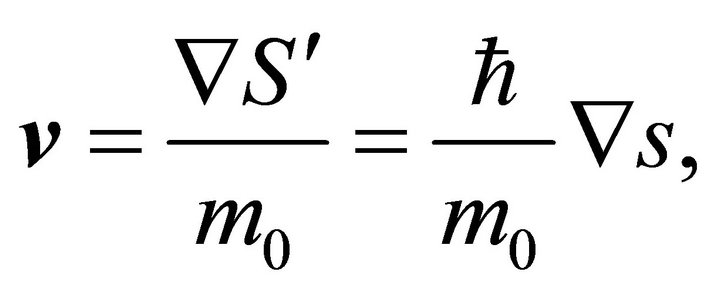 (3d)
(3d)
 (3e)
(3e)
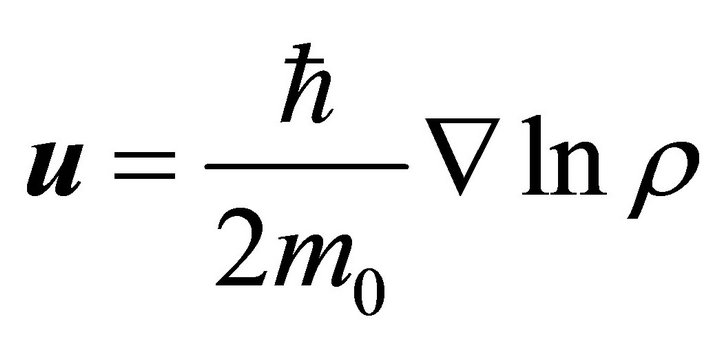 (3f)
(3f)
In (2a,b) and (3a-f),  is the states density,
is the states density, 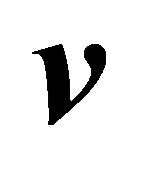 is the speed associated to classical phase
is the speed associated to classical phase ,
,  is the speed associated to state density,
is the speed associated to state density, 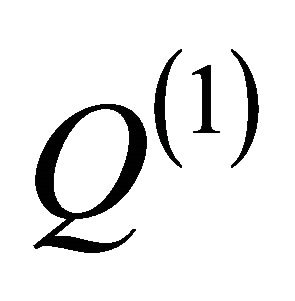 is the quantum potential,
is the quantum potential,  is the potential associated to space-time-sub-quantum medium interaction,
is the potential associated to space-time-sub-quantum medium interaction,  is the potential associated to space-time,
is the potential associated to space-time,  is the Ricci scalar in the WFA approach [12-19], ħ is Planck’s reduced constant, c is the light speed in vacuum,
is the Ricci scalar in the WFA approach [12-19], ħ is Planck’s reduced constant, c is the light speed in vacuum,  is the rest mass of material “entity” and t is the classical time.
is the rest mass of material “entity” and t is the classical time.
Now, certain conclusions are obvious: i) Any material “entity” is in a permanent interaction with the “subquantum level” through the quantum potential,  , as well as through the “perturbations” at the quantum potential as
, as well as through the “perturbations” at the quantum potential as  and
and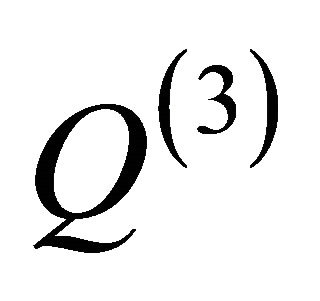 ; ii) The “sub-quantum level” is identified with a non-relativistic WD fluid described by the probability density and the momentum conservation laws, see (2a,b). These equations correspond to the generalised quantum hydrodynamics model (WD nonrelativistic hydrodynamics model); iii) In space-time topology.
; ii) The “sub-quantum level” is identified with a non-relativistic WD fluid described by the probability density and the momentum conservation laws, see (2a,b). These equations correspond to the generalised quantum hydrodynamics model (WD nonrelativistic hydrodynamics model); iii) In space-time topology.
 (4)
(4)
Equations (2a,b) become:
 (5a)
(5a)
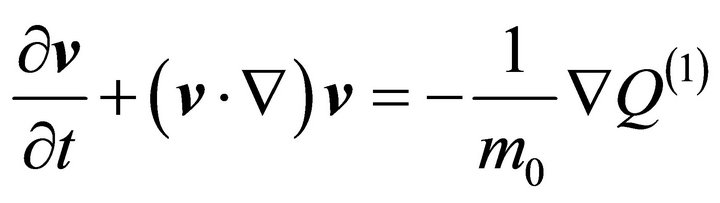 (5b)
(5b)
These equations define the standard model of quantum hydrodynamics [11];
iv) The Equation (2a) can be written under the form:
 (6)
(6)
This result is obtained through the following operations: multiplication with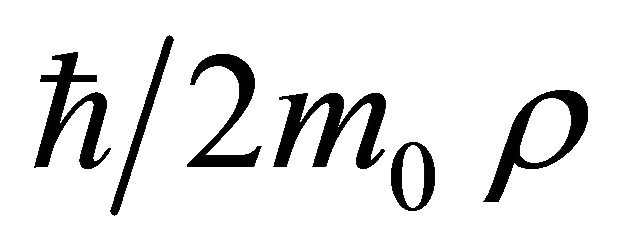 , integration with a null integration constant, applying the gradient and using the relation (3f).
, integration with a null integration constant, applying the gradient and using the relation (3f).
Let us multiply the relation (6) with  and also, let us multiply the Equation (2b) with
and also, let us multiply the Equation (2b) with . By summing them, the movement equation results:
. By summing them, the movement equation results:
 (7)
(7)
where  is the complex speed field (for similar results see [20-24])
is the complex speed field (for similar results see [20-24])
 (8a)
(8a)
 (8b)
(8b)
 (8c)
(8c)
 is the scalar potential of the complex speed and
is the scalar potential of the complex speed and  is the “covariant derivative”
is the “covariant derivative”
 (9)
(9)
Thus, the movements of material “entity” on continuous and non-differentiable curves (fractal curves with fractal dimension ) are proved by “activating” a space with a special topology, i.e. the fractal space [23-26]. Once such a space admitted, the following consequences result: iv1) The dynamics of physical system are described through fractal functions that depend both on space-time coordinates and on the de Broglie scale resolution. Thus the physical quantities, which define these dynamics of the physical system, are complex functions (for example the complex speed field (8a) and the pure imaginary coefficient
) are proved by “activating” a space with a special topology, i.e. the fractal space [23-26]. Once such a space admitted, the following consequences result: iv1) The dynamics of physical system are described through fractal functions that depend both on space-time coordinates and on the de Broglie scale resolution. Thus the physical quantities, which define these dynamics of the physical system, are complex functions (for example the complex speed field (8a) and the pure imaginary coefficient , corresponding to the fractal-non-fractal transition [23,24]). Moreover, the real parts of physical quantities are differentiable and independent on scale resolution, while the imaginary parts are non-differentiable and dependent on the resolution scale; iv2) The scale resolution reflects a certain degree of non-differentiability of the movement curve; iv3) The movement operatoris identified with the “covariant derivative”
, corresponding to the fractal-non-fractal transition [23,24]). Moreover, the real parts of physical quantities are differentiable and independent on scale resolution, while the imaginary parts are non-differentiable and dependent on the resolution scale; iv2) The scale resolution reflects a certain degree of non-differentiability of the movement curve; iv3) The movement operatoris identified with the “covariant derivative” ; iv4)The use of a generalized Newton principle turns the movement Equation (7) into geodesics of a fractal space; iv5) Chaoticity, either by turbulence as in the WD non-relativistic hydrodynamics approach, either by stochasticization as in the generalized Schrödinger approach, is achieved through non-differentiability of a fractal space. Indeed, by substituting (8a,b) in (7) and using the method described in [27,28], it results:
; iv4)The use of a generalized Newton principle turns the movement Equation (7) into geodesics of a fractal space; iv5) Chaoticity, either by turbulence as in the WD non-relativistic hydrodynamics approach, either by stochasticization as in the generalized Schrödinger approach, is achieved through non-differentiability of a fractal space. Indeed, by substituting (8a,b) in (7) and using the method described in [27,28], it results:
 (10)
(10)
Equation (10) can be integrated in a universal way and yields
 (11)
(11)
up to an arbitrary phase factor which may be set to zero by a suitable choice of the phase of . Thus, the nonlinear Schrödinger type equation (NSE) as fractal space geodesics is obtained. We note that in the WD non-relativistic hydrodynamics,
. Thus, the nonlinear Schrödinger type equation (NSE) as fractal space geodesics is obtained. We note that in the WD non-relativistic hydrodynamics, 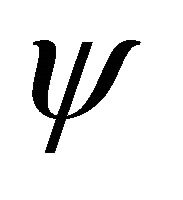 (through
(through ) is the scalar potential of the complex speed and in GSE is a wave function; iv6) The compatibility between the WD nonrelativistic hydrodynamics model and the wave mechanics (WM) implies, through the relation (3d) and (3e) the quantization conditions:
) is the scalar potential of the complex speed and in GSE is a wave function; iv6) The compatibility between the WD nonrelativistic hydrodynamics model and the wave mechanics (WM) implies, through the relation (3d) and (3e) the quantization conditions:
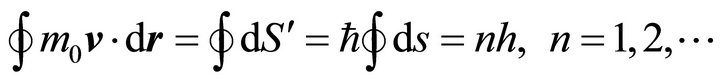 (12)
(12)
iv7) The mean value of the fractal potential (the imaginary part of the scalar potential of the complex speed) can be identified, without a constant factor, with the Shanon informational energy [24,29,30]
 (13)
(13)
Now, accepting a maximization principle for the informational energy in the form:
 (14)
(14)
for constrains with radial symmetry, we get  with
with . In the space-time topology (4), by substituting this value in the expression
. In the space-time topology (4), by substituting this value in the expression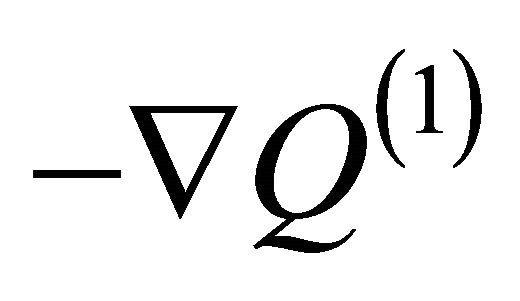 , the force is found
, the force is found
 (15)
(15)
Therefore, in the WD non relativistic hydrodynamics model and space-time topology (4), the information is “stored and transmitted” by the sub-quantum level as a force. The choice of  specifies the type of force “stored and “transmitted”.
specifies the type of force “stored and “transmitted”.
3. Wave-Particle Duality through Cnoidal Oscillations Modes of the States Density
In one-dimensional case, the Equations (2a,b)
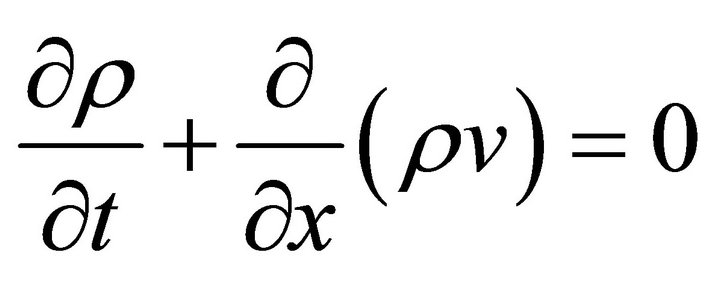 (16a)
(16a)
 (16b)
(16b)
in non-dimensional coordinates
 (17a)
(17a)
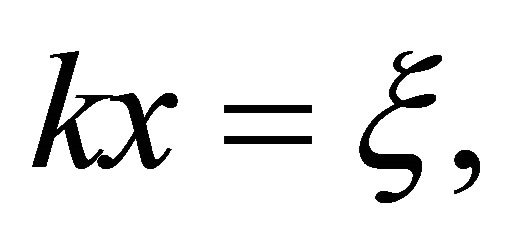 (17b)
(17b)
 (17c)
(17c)
and with the restriction , become
, become
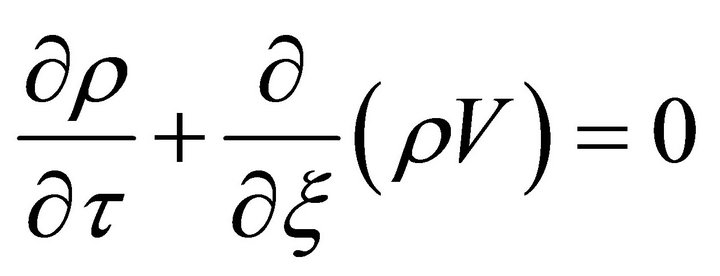 (18a)
(18a)
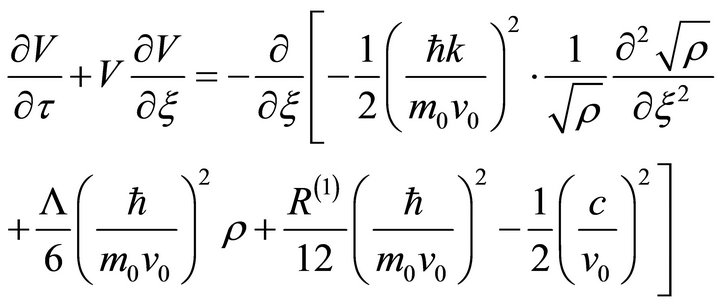 (18b)
(18b)
In the above relations  is a critical pulsation, k is the inverse of a critical length and
is a critical pulsation, k is the inverse of a critical length and  is a critical speed. These parameters are imposed both by the intrinsic properties of the “sub-quantum level” and by space topology specified through
is a critical speed. These parameters are imposed both by the intrinsic properties of the “sub-quantum level” and by space topology specified through  and
and .
.
The stationary case implies changing the variable 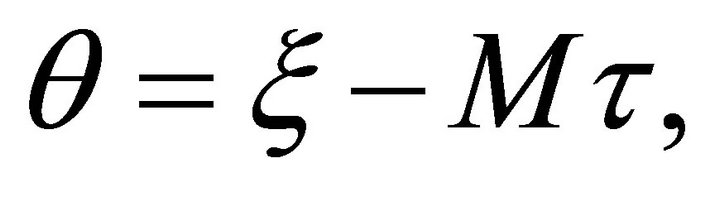 situation in which the Equations (18a,b) are written as follows:
situation in which the Equations (18a,b) are written as follows:
 (19a)
(19a)
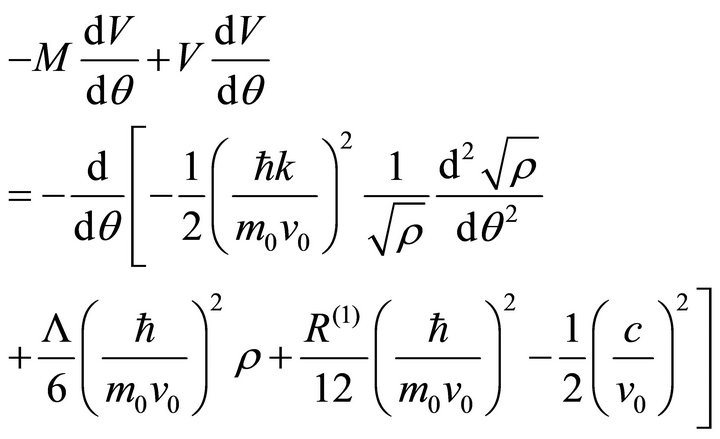 (19b)
(19b)
where M is equivalent with the Mach number. Hence, through integration, is found
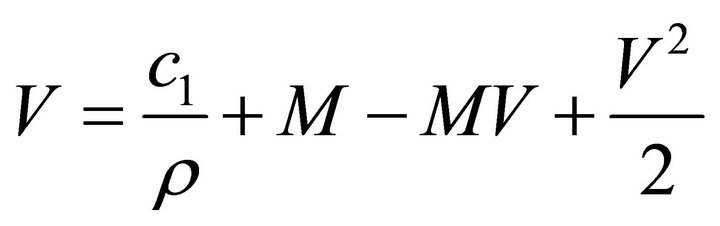 (20a)
(20a)
 (20b)
(20b)
or, by eliminating V from Equations (20a,b)
 (21)
(21)
where  and
and 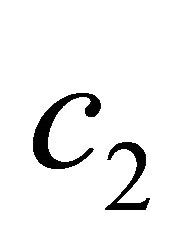 are integration constants.
are integration constants.
The solution of this equation has the expression
 (22)
(22)
where ,
,  are the complete elliptical integrals of first and second kindof modulus s, cn is the Jacobi elliptical function of argument
are the complete elliptical integrals of first and second kindof modulus s, cn is the Jacobi elliptical function of argument  and modulus s [31], a is an amplitude and
and modulus s [31], a is an amplitude and  is an average value of the states density. Details on defining parameters s, a and
is an average value of the states density. Details on defining parameters s, a and  can be found in [31]. Therefore the wave-particle duality is achieved through space-time cnoidal oscillation modes of the states density-see Figure 1. The oscillation modes are explained through modulus s of the elliptical function cn, non-linearity parameter depending among others space-time topology. Moreover, the oscillation modes are self-similar via the non-linearity parameter-see Figures 2(a)-(c), which specifies the fractal character of the space.
can be found in [31]. Therefore the wave-particle duality is achieved through space-time cnoidal oscillation modes of the states density-see Figure 1. The oscillation modes are explained through modulus s of the elliptical function cn, non-linearity parameter depending among others space-time topology. Moreover, the oscillation modes are self-similar via the non-linearity parameter-see Figures 2(a)-(c), which specifies the fractal character of the space.
The self-similarity of the cnoidal modes specifies the existence of some “cloning” mechanisms (full and fractional wavefunction revivals—a wave function evolves in time to a state describable as a collection of spatially distribuited sub-wave-functions that each closely reproduces the initial wave-function shape) [32]. All these show a direct connection between the fractal structure of space and holographic principle [23,24,30,33].
The space-time cnoidal oscillation modes have the following characteristics:
i) Wave number
 (23)
(23)
ii) Phase velocity

Figure 1. Space-time cnoidal oscillation modes of states density versus 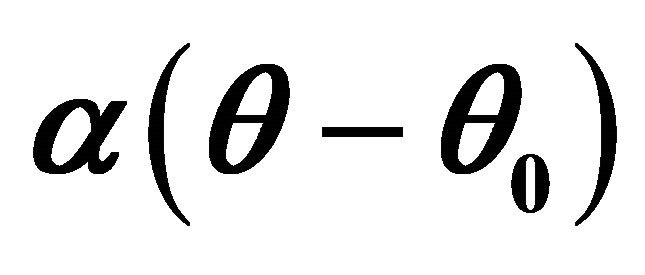 and non-linearity parameters s.
and non-linearity parameters s.

Figure 2. Self-similar contour curves of state density versus non-linearity parameters: (a) 0 ≤ s ≤ 1; (b) 1 ≤ s ≤ 0.5; (c) 0 < s ≤ 0.2.
 (24)
(24)
iii) Pulsation
 (25)
(25)
Various sequences are obtained through the following degenerations:
i) For s→0, (22) reduces to the harmonic wave packages
 (26)
(26)
characterized by wave number  phase velocity
phase velocity  and pulsation
and pulsation 
ii) For s→1, (22) reduces to the soliton-packages
 (27)
(27)
characterized by wave number  phase velocity
phase velocity
 and the pulsation
and the pulsation

iii) For s = 0, (22) reduces to the harmonic wave, while for s = 1 to the soliton one.
Eliminating the amplitude a, between (23) and (24) we obtain the relation
 (28a)
(28a)
 (28b)
(28b)
 (28c)
(28c)
Non-linearity s generates two distinct flow regimes of the non-relativistic WD fluid: non-quasi-autonomous flow regime (by harmonic wave, harmonic wave package, etc.) and quasi-autonomous flow regime (by soliton, soliton package). The dependence A(s), see Figure 3, specifies that the value  separates these two flow regimes. For
separates these two flow regimes. For , i.e. for non-quasi-autonomous flow regime,
, i.e. for non-quasi-autonomous flow regime,  , situation in which (28a) takes the form
, situation in which (28a) takes the form
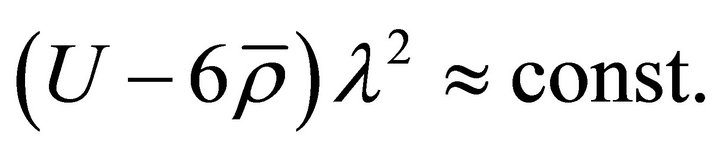 (29)
(29)
while for , i.e. for quasi-autonomous flow regime, the relation (29) loses its validity. The non-quasiautonomous regime will be associated to the wave characteristic while the quasi-autonomous regime to the corpuscular one.
, i.e. for quasi-autonomous flow regime, the relation (29) loses its validity. The non-quasiautonomous regime will be associated to the wave characteristic while the quasi-autonomous regime to the corpuscular one.

Figure 3. Flow regimes of the non-relativistic WD fluid versus λ and non-linearity parameters. It results the change of flow region for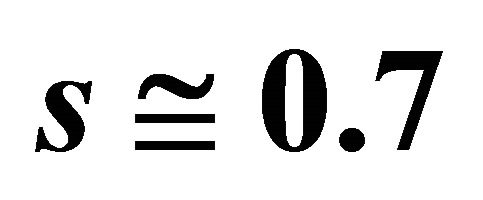 .
.
4. Conclusion
In the WD non-relativistic hydrodynamics model the non-linear interaction between the sub-quantum level and particles induces non-differentiable properties to the space. Thus: a) Particle movement takes place on continuum and non-differentiable curves (fractal curves); b) Particle dynamics are described by depending quantities both by spatial-temporal coordinates and scale resolution (de Broglie), fractal functions. They contain a real part, differentiable and independent on the de Broglie scale and an imaginary part, fractal and dependent on the de Broglie scale. An example of this kind is given by the complex speed field; c) Motion standard operator  is replaced by the covariant derivative
is replaced by the covariant derivative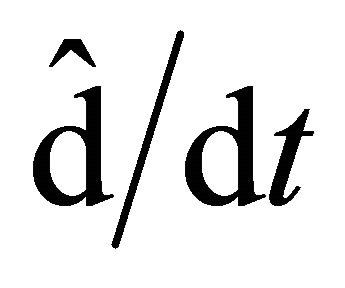 ; d) Applying the covariant derivative to a complex speed field, the particle’s motion equation become a geodesic of the fractal space. These are described by a non-linear Schrodinger equation; e) Chaoticity, either by turbulence like in the case of hydrodynamics, or by stocasticity like in Schrodinger representation, are induced by non-differentiability; f) Real part of the speed field assures through a quantification condition the compatibility between the WD non-relativistic hydrodynamics and wave mechanics; g) Average size of the fractal scalar potential of the complex speed field, without a certain constant factor, can be identified with informational Shanon energy. Accepting a maximization principle of the informational energy for constraints with radial symmetry, in a special topology, through quantum potential gradient, a force field results. Thus, the sub-quantum level will “store” and “transfer” informational energy as a force; h) In general, waveparticle duality is realised by cnoidal oscillation modes of the states density. These are characterized by two distinct flow regimes, one by non-quasi-autonomous structures (wave, wave package, etc.) which assures dominant undulatory character, and another one through quasiautonomous structures (soliton, soliton package, etc.) which assures dominant particle character. Moreover, the self-similarity of cnoidal oscillation modes specify a direct connection between the fractal structure of space and holographic principle, i.e. a holographic type gravitation.
; d) Applying the covariant derivative to a complex speed field, the particle’s motion equation become a geodesic of the fractal space. These are described by a non-linear Schrodinger equation; e) Chaoticity, either by turbulence like in the case of hydrodynamics, or by stocasticity like in Schrodinger representation, are induced by non-differentiability; f) Real part of the speed field assures through a quantification condition the compatibility between the WD non-relativistic hydrodynamics and wave mechanics; g) Average size of the fractal scalar potential of the complex speed field, without a certain constant factor, can be identified with informational Shanon energy. Accepting a maximization principle of the informational energy for constraints with radial symmetry, in a special topology, through quantum potential gradient, a force field results. Thus, the sub-quantum level will “store” and “transfer” informational energy as a force; h) In general, waveparticle duality is realised by cnoidal oscillation modes of the states density. These are characterized by two distinct flow regimes, one by non-quasi-autonomous structures (wave, wave package, etc.) which assures dominant undulatory character, and another one through quasiautonomous structures (soliton, soliton package, etc.) which assures dominant particle character. Moreover, the self-similarity of cnoidal oscillation modes specify a direct connection between the fractal structure of space and holographic principle, i.e. a holographic type gravitation.