Hints at Quantum Characteristics of Light Signals Measured from a Human Subject ()
1. Introduction
The phenomenon of spontaneous and incessant emission of, mainly visible range, photons by all living systems defies conventional interpretation. The phenomenon is called ultra-weak photon or biophoton emission and the emitted photon signals have been labeled biophoton signals [1]. A biophoton signal has many features which defy common interpretations in the living system. Two of these features are the visible range of photons (above the currency of biochemical energy) and non-decaying nature of signal. Both features make the incorporation of biophoton emission in the (semi)classical framework difficult.
The basic premises of the classical framework are composite structure of living system, contact interaction of constituents and preservation of the integrity (chemical and physical action) of constituents in biological processes. The constituents are the biomolecules. They cause and manifest all biological processes [2]. They emit photon signal in probabilistic transitions from higher to lower energy states. The probabilistic transitions of one type of biomolecules confer exponential decay shape to the emitted photon signal. Its wavelength, decay rate and strength are related to the properties of biomolecules emitting it [3]. The shape of signal emitted in the transitions of more than one type of biomolecules is the sum of exponential decay terms.
On the other hand, a non-decaying signal requires coordinated and continuous replenishing of the population of biomolecules in higher energy state through a mechanism, which in case of biophoton signals remains operative at all time. The absence of such a mechanism puts biophoton signals beyond the reach of classical framework. Visible range photons require a mechanism to supply more than 3 eV of energy to a biomolecule in one act for its transition from lower to higher energy state [4]. Cooperative occurrence of many chemical reactions can possibly upgrade their heat of reactions into an energy mode of more than 3 eV. The mechanism ensuring cooperative functioning of biomolecules is given the name coherence; the participating biomolecules cohere and the phenomena emanating from it are called coherent. The coherent phenomena need a different description using attributes that characterize synergetic/holistic functioning of biomolecules. The transfer of instructions/information between cohering biomolecules via interaction may or may not happen in coherent phenomena. If it happens or could happen, then it is classical coherence otherwise it is quantum coherence.
Both coherence and its nature are inferred from the properties of a phenomenon. The main objectives of biophoton research, therefore, have been to establish the coherence of biophoton signal, determine its nature, discover holistic attributes and identify cohering biomolecules. Progress has been made in fulfilling all but the last objective. The measurement of the conditional probability of not detecting subsequent photon in a small interval after the detection of a photon provided information on coherence in biophoton signals [5]. This probability behaves differently in coherent and incoherent signals when signal strength goes to zero. It was measured for intervals (10 μs-1 ms) in biophoton signals and signals emitted by a light emitting diode [6]. The measurements pointed towards the coherence of biophoton signals without information transfer to cohering biomolecules by molecular and sound signals. Progress achieved in fulfilling the other two objectives is presented in the next two sections. We present analysis of biophoton signal emitted either spontaneously or after chemically-induced stress.
2. Quantum Coherence of Spontaneous Biophoton Signals
The quantum nature of coherence is easier to establish in a spontaneous biophoton signal because its statistical properties can be determined with sufficient accuracy. We shall illustrate the procedure in human biophoton signals emitted from dorsal and palm sides of the hand. The human hand is selected as an in-vivo sample because it is easily measurable, it is without a substrate (no sample substrate interactions), its life time is much larger than the measuring time and the subject can provide feedback while measurements are performed.
Biophoton signals are usually detected with broadband photo multiplier tubes (Figure 1(a)) and have signal to noise ratio of around one, which necessitates background noise correction to the properties of the series of observed (obs) signal to obtain the properties of actual signal (sig) and makes the determination of spectral decomposition in human photon signal difficult. Experiments are performed by detecting spontaneous signals in intervals of 3 min by counting photons in 3600 contiguous intervals of 50 ms (bin size). The outcomes consitute a series of integer photon counts (0,1,2...) for bin size of 50 ms (Figure 1(b)).We then combine neighbouring bins together and form series of series with bin sizes that are integral multiples of 50 ms (obs) (Figure 1(c)). Similar series of series are generated with background noise (bg) in order to make background correction. The subscripts obs, bg and sig are added, both to the series and the properties, of observed, background noise and actual signals. The properties of a series are equated to those of its signal. This amounts to assuming that the series contains outcomes of repeated measurements of signal strength (ergodicity). The measured series determine the properties of background and observed signals. The signal properties are obtained from them by assuming that signal and background noise produce photons independently and no interference occurs in their detections. Our analysis requires photon count distribution, P, which is the set of probabilities of detecting different numbers of photons n = 0,1,2… for the bin size, Δ (Figure 1(c)). From it we obtain mean signal strength, k, and variance, V (Figure 1(d)). Signal properties (sig) are obtained from measured quantities by the following equations [7]:
 (1)
(1)
 (2)
(2)
An important intrinsic property of a signal is . It increases linearly with bin size in a series indicating that signal strength expressed in counts/s is the same in all series of signal. A nearly unchanging value of signal strength over macroscopic interval points towards a coherent mechanism for the origin of the signal [8].
. It increases linearly with bin size in a series indicating that signal strength expressed in counts/s is the same in all series of signal. A nearly unchanging value of signal strength over macroscopic interval points towards a coherent mechanism for the origin of the signal [8].  is different in different time series of a signal. In a classical signal, it merely determines the ensemble fluctuations in the signal strength and is not considered an intrinsic property. In contrast, in quantum signals, it is an intrinsic property and carries information about the signal. The existence of signal specific information in
is different in different time series of a signal. In a classical signal, it merely determines the ensemble fluctuations in the signal strength and is not considered an intrinsic property. In contrast, in quantum signals, it is an intrinsic property and carries information about the signal. The existence of signal specific information in  provides evidence of quantum coherence. In-depth analysis of this quantity has been performed in other studies [9]. Here we shall restrain ourselves to the analysis of variance normalised by signal strength (
provides evidence of quantum coherence. In-depth analysis of this quantity has been performed in other studies [9]. Here we shall restrain ourselves to the analysis of variance normalised by signal strength ( /
/ ) at different bin sizes and show that information is easily extracted from its attributes. The normalised variance is called Fano Factor [10],
) at different bin sizes and show that information is easily extracted from its attributes. The normalised variance is called Fano Factor [10],
 (3)
(3)
Fano Factor of a signal is different in its series at different bin sizes. It fluctuates around a point value in a classical signal but around a curve in a quantum signal. The curve contains signal specific information. In human biophoton signals, the curve is nearly a straight line (with a small curvature). The intercept and slope therefore characterize the curve. They are properties of signal and we identify them as holistic attributes of the biological object emitting the signal.
Figure 2 depicts the Fano Factor for 100 bin sizes in three signals: background noise (BG), spontaneous biophoton signal from palm side of a hand (SE) (and 3rd interval of signal emitted in response to stimulation of 500 mM hydrogen peroxide (H2O2) (3rd int, see Section 3). The intercepts of Fano Factor in the respective signals are 2.01, 1.31 and 1.01. The slope of Fano Factor is ill determined.

Figure 1. (a) Experimental setup: Human hands photo-emission is detected with photomultilier tubes; (b) Raw photon signal: Photo counts in 50 ms bin size; (c) Probability distributions: Pobs for original bin size (50 ms) and grouped bin sizes (200, 500 ms); (d) Background and spontaneous signal properties: We use observed and background means (kobs, kbg) and variances (Vobs, Vbg) to determine the properties of biophoton signals.
In a parallel study, we also analysed Fano Factor of 10 background noise and 60 spontaneous biophoton signals of 15 human subjects measured over a period of 30 min with two different photo multipliers tubes [11]. The intercept was around 2 and the slope was nearly zero in background signals. The intercept was around 1 in most biophoton signals but was also less than 1 in a few signals. The slope was usually positive and small. It was well determined among four subjects emitting relatively stronger signals. A Fano Factor less than one is a strong indicator of quantum coherence. The Fano Factor curve was below one in two weak biophoton signals for many bin sizes but the small value of signal strength diminishes its reliability.
The indication of quantum coherence in quantum optics is obtained from the value of second order correlation coefficient . One can show [12] that its relation to Fano Factor at zero bin size is given by
. One can show [12] that its relation to Fano Factor at zero bin size is given by
 (4)
(4)
The right hand side of Equation (4) is to be extrapolated towards its value when bin size tends to zero.
The value of  in respective signals (BG, SE, 3rd int) are 2.57, 0.17 and 0.029 for bin size of 50 ms and 0.026, 0.016 and 0.0003 at bin size of 5 s (Figure 2). Its value in two of the signals (SE, 3rd int) is much smalller than in background noise, an indication of quantum coherence.
in respective signals (BG, SE, 3rd int) are 2.57, 0.17 and 0.029 for bin size of 50 ms and 0.026, 0.016 and 0.0003 at bin size of 5 s (Figure 2). Its value in two of the signals (SE, 3rd int) is much smalller than in background noise, an indication of quantum coherence.
3. Quantum Coherence of Signals Emitted in Response to Stimulation
Additional information about quantum coherence in the

Figure 2. Fano Factor and [g(2)(0)−1] at different bin sizes: Two factors pointing to the possibility of classical or quantum signal are depicted at 100 bin sizes for the background noise (BG), spontaneous biophoton signal (SE) and 3rd 3 min interval emitted from the palm side in response to stimulation of 500 mM of H2O2 (3rd int, see Section 3). For the smallest of bin size, a value of [g(2)(0)−1] less than or nearly 0 points to a strong quantum component of the signal.
living system is provided by the photon signals emitted in response to small physical and chemical stimulations. The most extensively studied stimulation is exposure of a living system to light triggering the emission of a photon signal with the twin features of photons in the visible range and non-exponential decay [13]. These twin features again indicate coherence of photon signal and of biomolecules. The response signals have been called stimulated or light induced biophoton signals.
Investigations with the light induced biophoton signals have remained confined to models that aim to explain decay shape and extract strength parameters [10], and do not explicitly address the problem of coherence and its nature. The model analysed here addresses these important issues and is henceforth called quantum model [14, 15]. The quantum model does so explicitly by assigning an evolving quantum squeezed state to every response signal [16]. In light induced response signals of human subjects, the decay is obervable for less than a second, which is too small for verifying quantum coherence. Luckily however, human subjects respond to chemical stimulation by H2O2 on the skin by emitting photon signals with above mentioned twin features. These response signals are measurable for a much longer duration, which permits the verification of quantum coherence. When a small amount of mild concentration H2O2 (500 mM) is applied on human skin, the skin immediately starts emitting a response signal that decays continuously with decreasing decay rate [17-19] for the duration of nearly an hour (Figure 3). One can determine the statistical properties of the decay signal by dividing it in 3 min intervals

Figure 3. Decay of response signals: The strength of visible range photon signal emitted by a human subject in response to stimulation of skin by H2O2 is depicted for five concentrations of the chemical. Only one concentration was used on a portion of skin on the dorsal and palm sides of the left hand in one day. The signals were detected within 2 s of the applying of chemical. Background noise and observed spontaneous signals emitted prior to stimulation are also depicted on the figure.
during which its strength is nearly constant. The decay nature of the signal can be ignored in each 3 min interval. The photon count distribution (P) can then be used to ascertain the quantum coherence of the signal in the interval. The quantum coherence of response signal can be ascertained through 3 min intervals that scan the entire signal.
We measured ten response signals emitted within 2 s of applying 500 μl of five concentrations of H2O2 (100 mM - 500 mM) on an area of nearly 30 cm2 of the skin at the palm and dorsal sides of the left hand of a subject. Ninety-eight 3 min intervals were detected. The average strength in these intervals is depicted in Figure 3. We studied the behaviour of variance in all 3 min intervals to check if it indicated the possibility of quantum coherence. The signal decayed steeply during the first 3 min interval in all signals and in the subsequent interval in two intense signals. The decay in these twelve intervals could not be neglected, thereby preventing the determination of their statistical properties. The remaining eighty-six intervals indicated the possibility of quantum coherence. In Figure 2, we also depicted its characteristics for the interval with the highest signal strength (3rd int).
The long duration of response signal is suitable forchecking the robustness of signal specific parameters to change in the bin size. The parameters of valid description have to be robust. The checking of robustness brings out the absence of exponential decay character in response signals and points towards the validity of the quantum model. We present two models which use different functional forms for n(t), where n(t)∙Δt is the number of photons detected in a small interval Δt around t.
One model has a functional form which shows exponential decay character and is taken to be the sum of two exponential decay terms, for definiteness, but can also have more terms,
 (5)
(5)
It has five parameters ;
; ;
; ;
;  and
and . They specify strength of background noise, slow decay constant, strength of slow decay, fast decay constant and strength of fast decay, respectively. The parameter
. They specify strength of background noise, slow decay constant, strength of slow decay, fast decay constant and strength of fast decay, respectively. The parameter 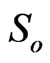 is not a property of signal and expected to be same in all signals. This model embraces a classical description [3].
is not a property of signal and expected to be same in all signals. This model embraces a classical description [3].
The functional form of n(t) in the quantum model [15] is
 (6)
(6)
which has four parameters ;
; ;
; 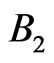 and
and . The background noise contribution,
. The background noise contribution, 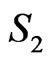 , is included in
, is included in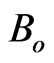 .
.
The nine parameters of the two models were estimated for each of the ten response signals with bin sizes varying from 50 ms to 3 min. The parameters ;
;  and
and  remained same for all bin sizes whereas the other parameters varied significantly with bin sizes. Figure 4 depicts the contributions of
remained same for all bin sizes whereas the other parameters varied significantly with bin sizes. Figure 4 depicts the contributions of ;
;  and
and  to the signal at t = 0 along with
to the signal at t = 0 along with  and
and  in the most intense response signal. The contribution of the
in the most intense response signal. The contribution of the  term is less than 1% and it further decreases for larger t which,
term is less than 1% and it further decreases for larger t which,

Figure 4. Robustness of the parameters of the quantum model: The contributions of B1; B2 and S2 at t = 0 in the signal emitted in response to 500 mM of H2O2 from the palm side of left hand are depicted against bin size. The figure also depicts the values of parameters to and λ2. These parameters provide the dominant contribution to the signal and are correctly estimated. S1 and λ1 are not depicted in order to avoid the clumsiness while the values of Bo and So are too small for depiction in the same figure. B1; to and Bo are robust and the contribution of B2 is less than 1% at all bin sizes.
probably, makes it ill determined as well as non-robust. Conversely, the contribution of  is insignificant at t = 0 but becomes significant at larger t which, probably, makes it well determined and robust. In the classical model, the dominant contribution to the signal comes from
is insignificant at t = 0 but becomes significant at larger t which, probably, makes it well determined and robust. In the classical model, the dominant contribution to the signal comes from  and
and . The figure (Figure 4), illustrates how the quantum based model provides the best picture of the decay. Similar figures of other response signals of this subject as well as two other subjects measured by us convey the same message.
. The figure (Figure 4), illustrates how the quantum based model provides the best picture of the decay. Similar figures of other response signals of this subject as well as two other subjects measured by us convey the same message.
4. A Quantum Framework to Understand the Living System?
Our analysis points towards statistical time coordination in fluctuations of spontaneously emitted photons. The classical interpretation of fluctuations is devoid of fundamental information. Statistical time coordination establishes their role in manifesting overall coordination, balance or equilibrium of the emitting system. Fano Factor brings out the coordination and quantifies it.
The holistic nature of the characteristics suggests the possibility of their correlation with other holistic features of human subjects e.g. with some qualitative aspects of health. If such a correlation is found then, their measureability makes those aspects quantitative and measurable.
It is suspected that other characteristics, such as quantum optics squeezed state index [20,21,16], individually or in combination can identify and measure physiological, pathological and psychological aspects of human health. The suspicion needs confirmation, it is planned to perform non-invasive measurements of few minutes in subjects recuperating from illnesses.
Determining the quantum state of a biophoton signal is a definite proof of its quantum coherence as well as the biomolecules implicated in its emission. Quantum biophoton signal can only be emitted by an assembly of biomolecules in a definite quantum state [9]. The confirmation can transform biophoton signals into potent clinical parameters [22].
Response signals manifested the coordination of human subject during oxidative stress. Even mild oxidative stress does not elicit a linear one dimensional response from human subject. Perhaps, it is true in other stresses encountered inadvertently and interventions made for managing health. The variation of signal strength from 11.1 to 0.84 counts/50 ms in different intervals showed the resilience of the quantum picture. The quantum mechanism is not overwhelmed with the abundance of oxidising molecules and continues operating efficiently. The study opens up new vistas of human response to explore and comprehend. This gives credence to the scenario of quantum coherence envisaged by Fröhlich [23] and searched by Popp [13]. It also presents enigmatic biophoton signal into a rich source of information.
NOTES