Effect of Non-Uniform Basic Temperature Gradient on the Onset of Rayleigh-Bénard-Marangoni Electro-Convectionin a Micropolar Fluid ()
1. Introduction
Convection due to variations of densities between two parallel plates caused by temperature difference and variations of temperature dependence surface tension in a horizontal fluid layer is of great importance because of its applications in science and engineering. Such convection in literature is known as Rayleigh-Bénard and Bé- nard-Maangoni convection. The developments of convection and corresponding heat transfer are examples of the physical phenomena to be encountered in these types of problems. The flow associated with Rayleigh-Bénard convection and Marangoni convection has been extensively reviewed in the literature. Particularly, Marangoni convection is found to be of importance in crystal growth melts and nucleate boiling. The problem of onset of convection driven by the combined effect of buoyancy and surface tension is also important in understanding many practical problems.
Pearson [1] was the first person to give a detailed mathematical analysis for the onset of convection driven by surface tension gradients. Nield [2] studied the problem of onset of convection driven by the combined effect of buoyancy and surface tension. Later many authors, Rudraiah [3], Maekawa and Tanasawa [4] studied the onset of convection in a horizontal layer of Newtonian fluid driven by both surface tension variations and buoyancy force by considering the non-deformable surfaces. The corresponding problem with deformable boundaries is studied by Sarma [5,6], Takashima [7], Wilson [8,9], Hashim and Wilson [10].
The application of strong electric field in a poorly conducting fluid can induce bulk motions. This phenomenon is known as Electro convection. In recent years, the study of the interaction of electromagnetic fields with fluid stated gain attention with the promise of new applications. Onset of natural convection in the presence of external electric field had been studied by Turnbull [11], Turnbull and Melcher [12], Takashima and Aldridge [13], Stiles [14], Stiles et al. [15], Siddheshwar [16], Siddheshwar and Abraham [17,18], Siddheshwar and Chan [19], Shivakumara et al. [20], Rudraiah et al. [21] and Siddheshwar and Radhakrishna [22].
Most of the previous studies were concerned with convection in Newtonian fluids. However, very less work has been done on convection in micropolar fluid with electric fields. The theory of micropolar fluids, developed by Eringen [23] is the best established theory of fluid with microstructure. Physically, the micropolar fluid consists of small, rigid, cylindrical suspended particles. Many classical flows were reexamined using the micropolar fluid to study the effect of fluid microstructures. Thermal convection in micropolar fluids with uniform and non-uniform temperature gradients was studied by many authors (Datta and Sastry [24], Siddheshwar and Pranesh [25-27] Pranesh and Riya Baby [28], Pranesh and Arun Kumar [29]). The main result of all these studies is that the micropolar fluid heated from below is more stable compared to the fluid without suspended particles. To the best of our knowledge not much work is done in this field, except the above mentioned.
The main objective of this paper is to provide the theoretical framework for studying the thermo capillary instabilities in the presence of buoyancy instability in earth laboratories for electrically conducting micropolar fluid layers under an AC electric field and non-uniform temperature gradients. Eigen value of the problem is obtained using single term Galerkin method.
2. Mathematical Formulation
Consider an infinite horizontal layer of a Boussinesquian micropolar fluid layer of depth “d”. The uniform electric field is directed along z-axis (see Figure 1). A Cartesian coordinate system is taken with the origin in the lower boundary and z-axis vertically up-wards. Let 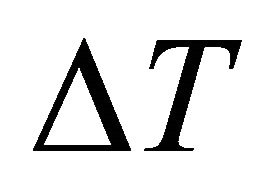 be the temperature difference between lower and upper boundaries of the fluid. The interface at the upper boundary has a temperature dependent surface tension
be the temperature difference between lower and upper boundaries of the fluid. The interface at the upper boundary has a temperature dependent surface tension 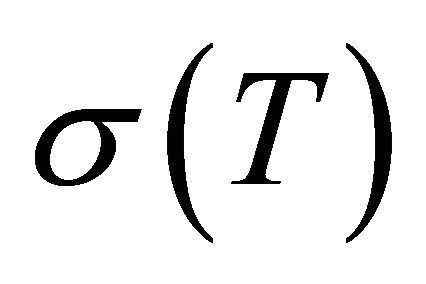 . Expanding
. Expanding  by Taylor series about T0, we get
by Taylor series about T0, we get
 (1)
(1)
where,  and
and . The form of
. The form of 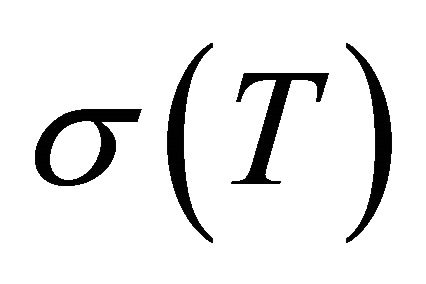 in Equation (1) was used by Pearson.
in Equation (1) was used by Pearson.
The governing equations for the problem are:
Equation of continuity:
 (2)
(2)
Conservation of Linear Momentum:
 (3)
(3)

Figure 1. Schematic diagram of Rayleigh-Bénard situation for a fluid with suspended particles.
Conservation of Angular Momentum:
 (4)
(4)
Conservation of Energy:
 (5)
(5)
Equation of State:
 (6)
(6)
Equation of State for Dielectric Constant:
 (7)
(7)
Faraday’s Law:
 (8)
(8)
Equation of Polarization Field:
 (9)
(9)
where,  is the velocity,
is the velocity,  is the spin,
is the spin,  is the hydrodynamic pressure, T is the temperature
is the hydrodynamic pressure, T is the temperature  is the density of the fluid at a reference temperature
is the density of the fluid at a reference temperature ,
,  is the coupling viscosity coefficient,
is the coupling viscosity coefficient,  is the shear kinematic viscosity coefficient, I is the moment of inertia,
is the shear kinematic viscosity coefficient, I is the moment of inertia,  and
and  are bulk and shear spin viscosity coefficients,
are bulk and shear spin viscosity coefficients,  is a Micropolar heat conduction coefficient,
is a Micropolar heat conduction coefficient,  is the specific heat,
is the specific heat,  is the thermal conductivity,
is the thermal conductivity,  is the coefficient of thermal expansion,
is the coefficient of thermal expansion,  is the electric field,
is the electric field,  is the dielectric polarization,
is the dielectric polarization,  is the electric permeability of free space and
is the electric permeability of free space and  is the dielectric constant.
is the dielectric constant.
The “Equations (2)-(9)” are solved subject to containment conditions appropriate for a rigid and thermally perfect conducting wall on the underside and a free surface on the upper side. This free surface is adjacent to a non-conducting medium and subject to a constant heat flux. Further, the no-spin boundary condition is assumed for micro-rotation. Since the shear stress for a non-classical fluid with suspended particles is no different from that of classical fluids, the boundary conditions for flat free boundaries used by Nield [2] in respect of Newtonian fluids are appropriate for micropolar fluids also.
In the quiescent state the velocity , the spin
, the spin , the temperature T, the electric field
, the temperature T, the electric field , the pressure
, the pressure , the density
, the density , the dielectric polarization
, the dielectric polarization 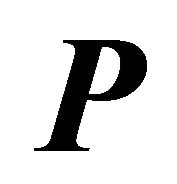 have the following solution:
have the following solution:
 (10)
(10)
where  is a non-dimensional basic temperature gradient, satisfying the condition
is a non-dimensional basic temperature gradient, satisfying the condition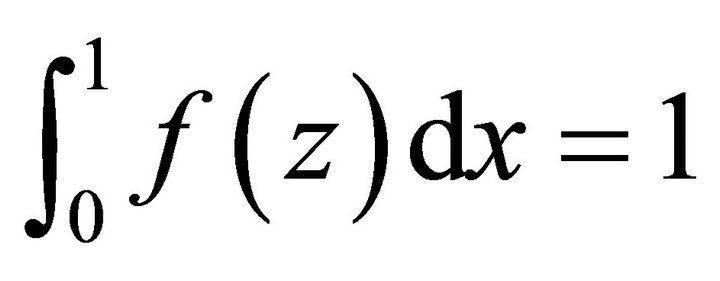 .
.
Since the aim of the present study is to understand control of convection in a micropolar fluid layer by different basic temperature profiles, the various non-uniform basic temperature gradients considered in this study are represented in Table 1.
This type of basic temperature gradients arises due to sudden heating or cooling, radiation, through flow, etc.
In order to investigate the stability of the basic solution, infinitesimal disturbances are introduced in the form:
 (11)
(11)
where the primes indicate that the quantities are infinitesimal perturbations assumed to be small and subscript ‘b’ indicates basic state value.
We assume the principal of exchange of stability to be valid and hence deal with only stationary convection. Introducing the electric potential  and substituting “(11)” into “(2)-(9)” and using the basic state solution (10), we get linearized equation governing the infinitesimal perturbations in the form:
and substituting “(11)” into “(2)-(9)” and using the basic state solution (10), we get linearized equation governing the infinitesimal perturbations in the form:
 (12)
(12)
 (13)
(13)
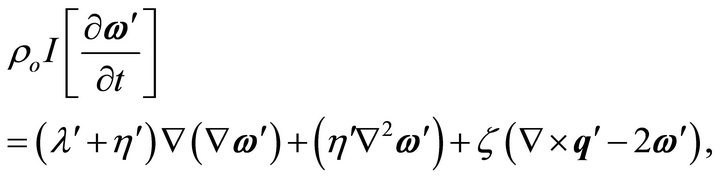 (14)
(14)
 , (15)
, (15)
 . (16)
. (16)

Table 1. Non-uniform basic temperature gradient profile.
The perturbation “(12)-(15)” are non-dimensionalised using the following definitions:
 (17)
(17)
Using “(16)” in “(13)”, operating curl twice on the resulting equation, operating curl on “(14)” and non-dimensionalising the two resulting equations and also “(15)”, we get
 (18)
(18)
 , (19)
, (19)
 , (20)
, (20)
 . (21)
. (21)
where the non-dimensional parameters N1, N3, N5, R and L are given by :
 (Coupling Parameter),
(Coupling Parameter),
 (Couple Stress Parameter),
(Couple Stress Parameter),
 (Micropolar Heat Conduction Parameter),
(Micropolar Heat Conduction Parameter),
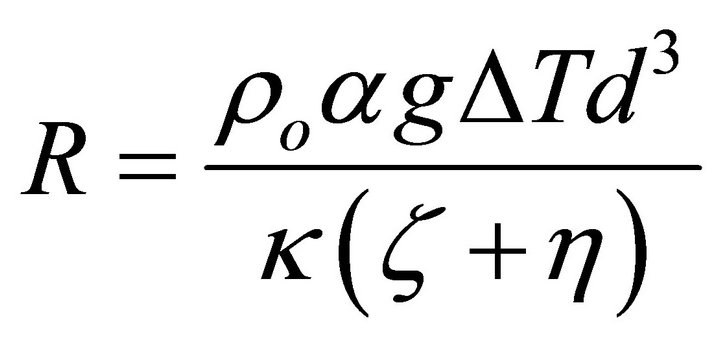 (Rayleigh number),
(Rayleigh number),
 (Electric Rayleigh number).
(Electric Rayleigh number).
The infinitesimal perturbations W, Ωz, T and ϕ are assumed to be periodic waves and hence these permits and normal mode solution in the following form:
 (22)
(22)
where l and m are the horizontal components of the wave number .
.
We substituting “(22)” into “(18)-(21)”, then we get
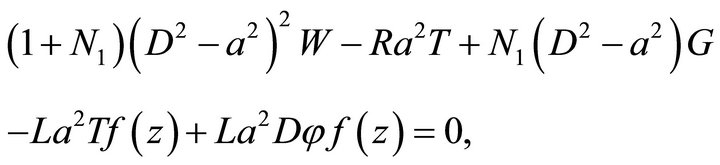 (23)
(23)
 (24)
(24)
 , (25)
, (25)
 , (26)
, (26)
where  and
and .
.
In “(23)-(26)”, the asterisks have been omitted.
“(23)” and “(26)” are solved subject to the following boundary conditions:
 (27)
(27)
where  is the Marangoni number.
is the Marangoni number.
“(27)” indicates the use of rigid, isothermal lower boundary and upper, free, thermally insulating boundary (with respect to perturbation). The condition on G is spin-vanishing boundary condition.
We now use the single term Galerkin expansion technique to find the critical eigenvalue. Multiplying “(23)” by W, “(24)” by G, “(25)” by T and “(26)” by , integrating the resulting equations by parts with respect to z from 0 to 1, using the boundary conditions “(27)” and using W = AW1, G = BG1, T = CT1 and
, integrating the resulting equations by parts with respect to z from 0 to 1, using the boundary conditions “(27)” and using W = AW1, G = BG1, T = CT1 and  in which A,B,C and E are constants and W1, G1, T1 and
in which A,B,C and E are constants and W1, G1, T1 and  are trial functions, yield the following equation for the Marangoni number M:
are trial functions, yield the following equation for the Marangoni number M:
 (28)
(28)
where,

In “(28)”,  denotes integration with respect to
denotes integration with respect to  between
between  and
and .
.
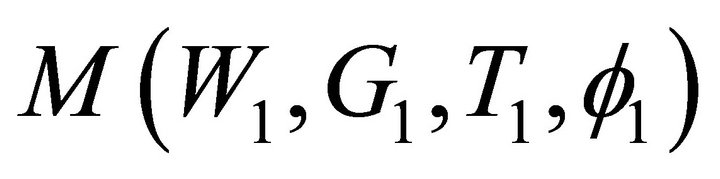 in “(28)” is a functional and EulerLagrange equations for the extremisation of M “(23)- (26)”.
in “(28)” is a functional and EulerLagrange equations for the extremisation of M “(23)- (26)”.
The trial functions satisfying “(27)” are
 (29)
(29)
such that they satisfy all the boundary conditions “(27)” except the one given by  at
at , but the residual from this is included in the residual from the differential equations. Substituting “(29)” in “(28)” and performing the integration, we can calculate the critical Marangoni number Mc which attains its minimum at
, but the residual from this is included in the residual from the differential equations. Substituting “(29)” in “(28)” and performing the integration, we can calculate the critical Marangoni number Mc which attains its minimum at .
.
3. Result and Discussion
As per the motivation stated in the introduction to the paper we consider the effects of electric Rayleigh number, micropolar fluid parameters and non-uniform basic temperature distribution on the onset of Rayleigh-Bé- nard-Marangoni convection in a micropolar fluid layer. These three effects are respectively represented by the L, (N1, N3 and N5) and f(z) in the Eigen value “(28)”. Due to the thermodynamics restrictions the following values of N1, N3 and N5 are chosen:

where, m and n are finite, positive real numbers (see Siddheshwar and Pranesh [29]) and the values of L are those chosen for Newtonian fluid problems. One linear and five non-linear basic temperature gradients are considered in the study (see Table 1). The results obtained in the study are depicted by the Figures 2-5. It is observed that for the critical Marangoni number, Mc, the following inequality holds for the six models chosen in the study:
 i.e., step function is the most destabilizing temperature profile and inverted parabolic temperature is the most stabilizing temperature profile. In the case of piecewise linear and step function profiles, the critical Marangoni number, Mc, depends on the thermal depth, ε, in addition to depending on the parameters of the problem. In the case of piecewise linear profile heating from below, cooling from above and step function profiles, the minimum value of Mc is attained at ε = 0.95, ε = 0.45 and ε = 0.75 respectively. With the above background and with the motive specified in the introduction we now discuss the results presented by the Figures 2-5.
i.e., step function is the most destabilizing temperature profile and inverted parabolic temperature is the most stabilizing temperature profile. In the case of piecewise linear and step function profiles, the critical Marangoni number, Mc, depends on the thermal depth, ε, in addition to depending on the parameters of the problem. In the case of piecewise linear profile heating from below, cooling from above and step function profiles, the minimum value of Mc is attained at ε = 0.95, ε = 0.45 and ε = 0.75 respectively. With the above background and with the motive specified in the introduction we now discuss the results presented by the Figures 2-5.
Figure 2 is the plot of critical Marangoni number Mc versus coupling parameter N1 for different non uniform temperature gradients and for different electric Rayleigh number L. Clearly Mc increases with N1. Increase in N1 indicates increase in the concentration of micro elements. These elements consume the greater part of the energy of

Figure 2. Plot of critical Maragoni number Mc versus coupling parameter N1 for different non -uniform temperature gradient and different electric Rayleigh Number L. (a) Linear, (b) Heating from below, (c) Cooling from above, (d) Step function, (e) Parabolic, (f) Inverted parabolic.

Figure 3. Plot of critical Maragoni number Mc versus coupling parameter N3 for different non-uniform temperature gradient and different Electric Rayleigh number L. (a) Linear, (b) Heating from below, (c) Cooling from above, (d) Step function, (e) Parabolic, (f) Inverted parabolic.

Figure 4. Plot of critical Maragoni number Mc versus coupling parameter N5 for different non-uniform temperature gradient and different Electric Rayleigh number L. (a) Linear, (b) Heating from below, (c) Cooling from above, (d) Step function, (e) Parabolic, (f) Inverted parabolic.

Figure 5. Plot of critical Maragoni number Mc versus coupling parameter N1 for different non-uniform temperature gradient and different Rayleigh number R. (a) Linear, (b) Heating from below, (c) Cooling from above, (d) Step function, (e) Parabolic, (f) Inverted parabolic.
the system in developing the gyrational velocity of the fluid and as a result the onset of convection is delayed. Therefore, the increase N1 is to stabilize the system. It is also observed that increase in electric Rayleigh number decreases the Mc. Electric Rayleigh number L is the ratio of electric force to gravitational force. Thus, L has a destabilizing effect on the system.
Figure 3 is the plot of Mc versus coupling stress parameter N3 for different non uniform temperature gradients and for different electric number L. Clearly Mc decreases with increase in N3. Increase in N3, decreases the couple stress of the fluid which causes a decrease in microrotation and hence makes the system more unstable.
Figure 4 is the plot of Mc versus micropolar heat conduction parameter N5 for different non uniform temperature profiles and for different electric number L. Clearly Mc increases with N5. When N5 increases, the heat induced in the fluid due to these microelements also increases which reduces the heat transfer from bottom to top. The decrease in heat transfer is responsible for delaying the onset of instability. Thus increase in N5 is to stabilize the system.
Figure 5 is the plot of Mc versus coupling parameter N1 for different non uniform temperature gradients and for different Rayleigh number R. Clearly Mc increases with N1. It is also observed that the increase in R decreases the Mc and ultimately we get the case of convection dominated by buoyancy force.
From the Table 2 it is clear that with an increase in N1, Mc becomes zero for higher values of R compared to Newtonian fluids. Similar results have been obtained in respect to the influences of N3 and N5. Treating Marangoni number as the critical parameter we find from the Table 3 that any particular infinitesimal disturbance can be destabilized with electric field. The results of the Table 3 are in respect of linear temperature gradient. This general observation on the destabilizing influence of electric field, however holds good for the other five temperature gradients as well. From Table 3 as well as Table 2, we also note that as R increases Mc decreases. From Table 4, it is found that the critical wave number is in general insensitive to the changes in the micropolar parameters but is influenced by the electric field. This indicates that, the convection cell at the onset increases in size with the increase in electric field. In the limit L tends to zero, we recover the results of Siddheshwar and Pranesh [29] for Chandrasekhar number tends to zero from the present study.
The above result indicates that externally applied electric field is an effective means of controlling, RayleighBénard-Marangoni convection in mircopolar fluids. The result also suggests that Rayleigh-Bénard-Marangoni convection in Newtonian fluids may be delayed by adding micron sized suspended particles. Further by creating

Table 2. Critical Marangoni number (Mc)j (j = 1 to 6 ) for different values of L, R and N1, L = 100, N3 = 2.0, N5 = 1.0.

Table 3. Critical Marangoni number Mc for different values of L and R with f(z) = 1, N1 = 0.5, N3 =2.0, N5 = 1.0.

Table 4. The values of critical wave number  for various values of N1, N3, N5 and L with f(z) = 1 and for all values of R.
for various values of N1, N3, N5 and L with f(z) = 1 and for all values of R.
conditions for an appropriate basic temperature gradient, we can also make an appropriate decision delaying the convection. It has been observed that parabolic temperature profile is the most stabilizing temperature profile and step function is the most destabilizing temperature profile.
4. Acknowledgements
The authors would like to thank their respective managements for the support in completing this work. One of the authors (TVJ) would like to acknowledge the support of the Christ University administration on deputing him to the Ph.D program.