Impact of Awareness on the Spread of Dengue Infection in Human Population ()
1. Introduction
Dengue is viral infection transmitted by the bite of an infected Aedes mosquito causing severe flu-like symptoms which may lead to potentially lethal complications. The disease affects infants, children and adults and could be fatal. The symptoms of dengue fever vary according to the age of the patient. Once infected, the human becomes the main carrier and multiplier of the virus, serving as a source of the virus for uninfected mosquitoes. The virus circulates in the blood of an infected person for 2 - 7 days, at approximately the same time that the person develops a fever. Patients who are already infected with the dengue virus can transmit the infection via Aedes mosquitoes after the first symptoms appear (during 4 - 5 days; maximum 12). Symptoms usually last for 2 - 7 days, after an incubation period of 4 - 10 days after the bite from an infected mosquito [1,2]. The only method of controlling or preventing dengue virus transmission is to effectively control the mosquitoes and their bites.
There are four distinct serotypes of the dengue virus (DEN 1, DEN 2, DEN 3 and DEN 4). In humans recovery from infection by one dengue virus provides lifelong immunity against that particular virus serotype. However, this immunity confers only partial protection against subsequent infection by the other three serotypes of the virus. Once infected, a mosquito remains infected for life, transmitting the virus to susceptible individuals during probing and feeding.
Different mathematical models have been proposed to study the spread of dengue. Host vector type models are generally considered. The host (human) population consists of susceptible, exposed, infectious and removed compartments. For the vector (mosquito), only susceptible and infective compartments are considered. Feng and Vealsco proposed and model to study the population dynamics of vector transmitted disease with two pathogen strains [3]. A model for the transmission of dengue fever in a constant human population and variable vector population is discussed by Estava and Vargas [4]. The same authors in [5] proposed another model considering vertical and mechanical transmission in the vector population, to study the effects on the dynamics of the disease. Some more mathematical models have been developed in the literature to gain insights into the transmission dynamics of dengue in a community (see, for instance, [6-11]).
The spread of the disease in the population make the people to change their behavior so as to protect themselves from the disease. Such change of attitude and behavior can be considered as awareness towards the disease. When the dengue infected person gets recovered from the disease, he takes all the necessary precautions not to experience its bitterness again. For this, he takes precautionary measures such as use of mosquito nets, repellents etc., eliminating the possibility of mosquito bite and hence dengue infection. To incorporate this idea, a separate class of aware individual is taken into consideration. The infective will become aware after recovery. Also, transitions from susceptible to aware class directly are possible. This is due to the fact that infection of one member makes the whole family and friends aware to take necessary steps to be protected against the disease. The preventive measures due to awareness may bring vital changes in the dimension of the epidemic. Keeping these in view, a dynamic model incorporating the awareness is proposed for the dengue infection.
2. Mathematical Model
The most important and responsible factor for the spread of the dengue fever (DF) in the human population is the mosquito population. Therefore to study and predict the control of the DF it is necessary to consider the dimension of the mosquito population along with the human population. The total human population of interest is divided into three mutually disjoint classes. The members of susceptible class  are at the risk of contracting DF. Each member of aware class
are at the risk of contracting DF. Each member of aware class  is very much cautious to protect themselves from the mosquito bites and hence from dengue also. The members of dengue infected class
is very much cautious to protect themselves from the mosquito bites and hence from dengue also. The members of dengue infected class  are getting infection due to infected mosquito bite. Let
are getting infection due to infected mosquito bite. Let  and
and  be the number of individuals in these three compartments respectively such that the total human population at time
be the number of individuals in these three compartments respectively such that the total human population at time  is
is .
.
Let 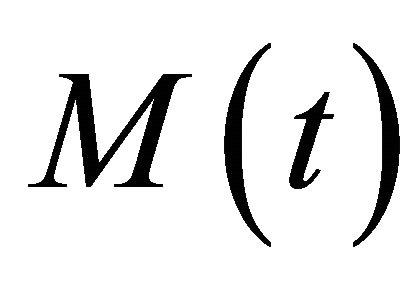 be the total population of mosquitoes which is divided into susceptible
be the total population of mosquitoes which is divided into susceptible  and infected population
and infected population  at time
at time  such that
such that . Further, for constructing the model the following assumptions are considered:
. Further, for constructing the model the following assumptions are considered:
Human susceptible become dengue infected following bite of the dengue infected mosquito. The infected individual may have any of the four serotypes of dengue virus. Some susceptible are becoming aware and are taking sufficient protection to avoid mosquito bites. After recovery, the lifelong immunity is achieved to the particular serotype. It is assumed that after recovery the infected person becomes aware as he or she understands the risk factors for the disease. Further, due to awareness all protections will be used by the recovered individual and he or she will not be then infected by any other serotype of dengue virus. The decay in the life expectancy of human population due to dengue virus is ignored.
Let  and
and 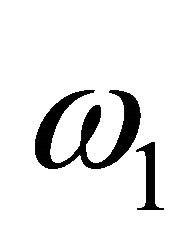 be the constant recruitment rates of two populations while
be the constant recruitment rates of two populations while 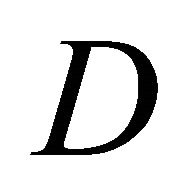 and
and  be the natural death rates in host (human) and vector (mosquito) populations respectively. Let
be the natural death rates in host (human) and vector (mosquito) populations respectively. Let  be the dengue infection transmission coefficient from mosquito to human. The awareness is spread in the susceptible population at the rate
be the dengue infection transmission coefficient from mosquito to human. The awareness is spread in the susceptible population at the rate . This incorporates the direct transfer from susceptible to aware class. Infected human are treated and recovered at the rate
. This incorporates the direct transfer from susceptible to aware class. Infected human are treated and recovered at the rate .
.
The susceptible mosquitoes are infected with the virus while probing or feeding the dengue infected individual and the transmission coefficient is . The infected mosquito transmits the virus to the susceptible person on biting. No vertical transmission of virus is considered for the mosquito population. No recovery is assumed in the vector population. Accordingly, the SI model is considered for the mosquito population. These assumptions lead to the following model:
. The infected mosquito transmits the virus to the susceptible person on biting. No vertical transmission of virus is considered for the mosquito population. No recovery is assumed in the vector population. Accordingly, the SI model is considered for the mosquito population. These assumptions lead to the following model:
 (5.1)
(5.1)
All parameters are assumed to be nonnegative. The following nonnegative initial conditions are associated with the system (5.1):
 (5.2)
(5.2)
It is easy to establish that the solution of the IVP (5.1)- (5.2) is positive. Further, the set
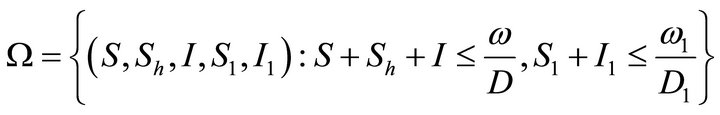
is found to be positive invariant.
Further, the dynamical system (5.1) can also be written as
 (5.3)
(5.3)
It may be observed that  does not appear explicitly in the system (5.1) except the second equation. Also, the limiting mosquito population is obtained as
does not appear explicitly in the system (5.1) except the second equation. Also, the limiting mosquito population is obtained as  . Accordingly, it is sufficient to consider only the first, third and the fifth equations to determine the dynamics of the system (5.1). Hence, the three-dimensional nonlinear system (5.4), given as follows, will be analyzed in the rest of this paper:
. Accordingly, it is sufficient to consider only the first, third and the fifth equations to determine the dynamics of the system (5.1). Hence, the three-dimensional nonlinear system (5.4), given as follows, will be analyzed in the rest of this paper:
 (5.4)
(5.4)
This system is positively invariant in the region

3. Equilibrium Points and Basic Reproduction Number
The non-linear dynamical system (5.4) always admits the disease-free equilibrium point , where
, where  . The basic reproduction number is obtained as the dominant eigenvalue of the next generation matrix [12]. It is important to distinguish new infections from all other class transitions in the population. Considering
. The basic reproduction number is obtained as the dominant eigenvalue of the next generation matrix [12]. It is important to distinguish new infections from all other class transitions in the population. Considering  where
where  and
and  are two infected classes, the system (5.4) can be written as
are two infected classes, the system (5.4) can be written as

The vector  is the rate of appearance of new infection in each class and
is the rate of appearance of new infection in each class and  is the difference of transfers out of compartment and into the compartments:
is the difference of transfers out of compartment and into the compartments:

The corresponding Jacobian matrices at disease freestate  are computed as
are computed as
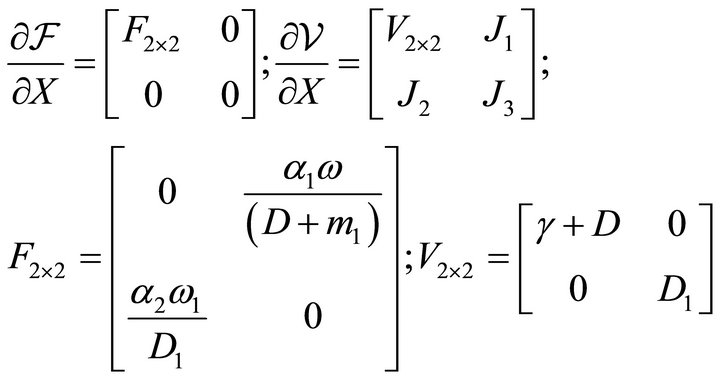
The basic reproduction number 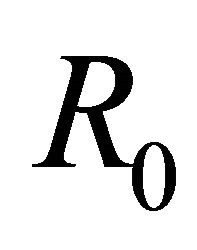 is obtained as the spectral radius of the next generation matrix
is obtained as the spectral radius of the next generation matrix  and is computed as
and is computed as
 (5.5)
(5.5)
The endemic equilibrium  is obtained by solving the system:
is obtained by solving the system:
 (5.6)
(5.6)
This gives

Since , the unique endemic equilibrium point exists when
, the unique endemic equilibrium point exists when
 (5.7)
(5.7)
Further, the equilibrium level of dengue infected human population  decreases if
decreases if 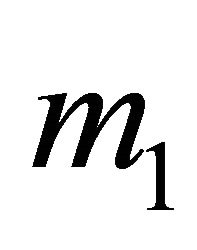 increases. Hence, the awareness reduces the severity of the epidemic.
increases. Hence, the awareness reduces the severity of the epidemic.
4. Stability Analysis
The local stability of different equilibrium points of (5.4) can be discussed on the basis of stability matrix at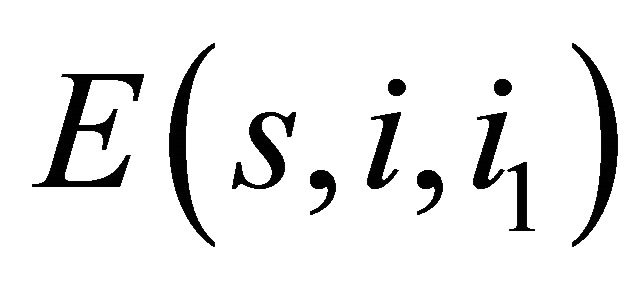 . It is computed as
. It is computed as

The stability results are stated below in the form of theorems.
Theorem 4.1. The disease-free state  is locally asymptotically stable when
is locally asymptotically stable when
 (5.8)
(5.8)
Proof: The characteristic equation of stability matrix at  is obtained as
is obtained as


Therefore, the characteristic equation has roots with negative real parts for .
.
Hence, the result is proved. □
Remark 1. Clearly, when  there will be no disease and when
there will be no disease and when  disease will persist in the population. Note that the awareness
disease will persist in the population. Note that the awareness  decreases the basic reproduction number
decreases the basic reproduction number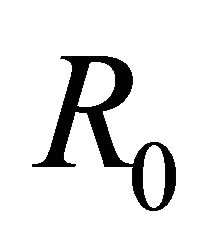 , thereby increasing the stability of
, thereby increasing the stability of . It can also be observed that
. It can also be observed that  decreases as the natural death rates
decreases as the natural death rates  and
and  increase.
increase.
Remark 2. It may be noted from (5.7) and (5.8) that the local stability of  ensures the non-existence of endemic equilibrium point
ensures the non-existence of endemic equilibrium point . This suggests that the disease-free state
. This suggests that the disease-free state  may be globally stable when
may be globally stable when . This is proved by using the geometric approach [13-15] for global stability in the next theorem.
. This is proved by using the geometric approach [13-15] for global stability in the next theorem.
Theorem 4.2. The locally stable disease-free equilibrium,  is globally asymptotically stable.
is globally asymptotically stable.
Proof: The Jacobean matrix and second additive compound matrix of the system (5.4) around the equilibrium point  are obtained as
are obtained as

Define a function ,
,  and let
and let  be a vector field of (5.4), it may be noted that
be a vector field of (5.4), it may be noted that

Taking , where the block matrix B is given as
, where the block matrix B is given as
 , with
, with
 ,
, 

Let  denote the Lozinski measure, then it is computed as:
denote the Lozinski measure, then it is computed as:

Now, when , there exists a number
, there exists a number  such that
such that  provided
provided
 (5.9)
(5.9)
Hence, .
.
Combining the two inequalities in (5.9) gives the condition

Observe that left side of inequality is always greater than unity while right side is less than unity. Therefore the condition is always true. Hence, the result is proved.
Theorem 4.3. The endemic state  if exists, is locally asymptotically stable.
if exists, is locally asymptotically stable.
Proof: When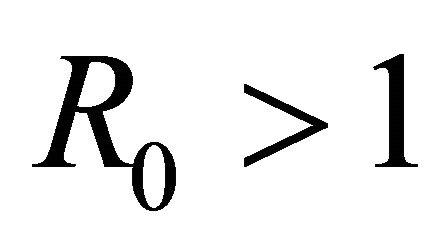 , the characteristic equation about
, the characteristic equation about  is obtained as
is obtained as

Since , the characteristic equation has roots with negative real parts. Hence, the result is proved.
, the characteristic equation has roots with negative real parts. Hence, the result is proved.
Theorem 4.4. The endemic state , if exists, is globally asymptotically stable if
, if exists, is globally asymptotically stable if
 (5.10)
(5.10)
Proof: Denote , the Jacobian matrix and second additive compound matrix of the system (5.4) around
, the Jacobian matrix and second additive compound matrix of the system (5.4) around  are
are



Using the same approach as in Theorem (4.2), the matrix B is computed as
 ,
,

 ,
,

The Lozinski measure  is computed as
is computed as


If the conditions in (5.10) are satisfied then there exist a number  such that
such that

This establishes the result.
However, the endemic state may be globally stable even when these conditions are not satisfied.
5. Numerical Simulations
The following data set is chosen to confirm different analytical results:

For the above dataset with  the basic reproduction number R0 is computed as 0.506414. Since R0 < 1, the disease free equilibrium point of the system (5.4) is computed as (198, 0, 0). The solution of system (5.1) is numerically obtained for this data set and with different initial conditions. It was observed that the solution converges to the disease free state after removing the initial transients. The endemic state does not exist in this case. However, for m1 = 0.00025 the basic reproduction number is computed as
the basic reproduction number R0 is computed as 0.506414. Since R0 < 1, the disease free equilibrium point of the system (5.4) is computed as (198, 0, 0). The solution of system (5.1) is numerically obtained for this data set and with different initial conditions. It was observed that the solution converges to the disease free state after removing the initial transients. The endemic state does not exist in this case. However, for m1 = 0.00025 the basic reproduction number is computed as . In this case, the endemic state is computed as (401, 24, 36). For these two values of awareness parameter m1, the time series for susceptible, infected human and infected mosquitoes is obtained in Figures 1 and 2. These time series confirms the analytical results.
. In this case, the endemic state is computed as (401, 24, 36). For these two values of awareness parameter m1, the time series for susceptible, infected human and infected mosquitoes is obtained in Figures 1 and 2. These time series confirms the analytical results.
6. Conclusion
A five dimensional model is proposed and analyzed to get insights of dengue transmission in the human population. It is assumed that due to awareness of the disease some susceptible take necessary precautionary measures to protect themselves from mosquito bite and joins aware class. It is also assumed that all the recovered individuals are convinced that the dengue re-infection is very dangerous so they take sufficient care to protect themselves from the mosquito bites so they also join the aware class after recovery. Increase in the awareness decreases density of infected human as well as infected mosquitoes. Also, increase in the rate of awareness decreases basic

Figure 1. Time series for m1 = 0.002. Blue: susceptible host, black: infective host, red: infective vector.

Figure 2. Time series for m1 = 0.00025. Blue: susceptible host, black: infective host, red: infective vector.
reproduction number. It also increases the stability of disease free state. Hence, it is concluded that sufficiently high rate of awareness plays a crucial role in reducing the menace of the disease.
NOTES