Thermal Activation of Asymetrical Composites for Vibration Control ()
1. Introduction
Smart materials can be defined as materials which are able to change their form, their mechanical or any physical properties to adapt to their background. They are more and more used for technical applications and particularly in the field of controlling structural deformations. In this case, main actuators use piezoelectric and shape memory alloys materials. To make an active composite, these actuators may be used at the scale of the fiber or the matrix [1,2], at the scale of the interface between the successive layers in a laminate [3,4] or at the scale of the linkage between the actuator and a passive composite structure [5,6]. However, the interface strength between the actuator and the composite plays a crucial role. It is a limit of such a technology for the time life of the structure, especially when the rigidity of the composite structure is high, because to deform the structure the actuator has to fight against this rigidity. The use of a thermal actuation, based on the bimetallic strip effect can be a solution to overcome the problems of bonding between the actuator and the structure. Indeed, the whole structure can be considered as an actuator and the problem of interface cohesion is not concentrated at the interface actuator/structure but distributed all along the interfaces of the laminated composite. For composite structures, the bimetallic strip effect can be obtained by coupling an internal heat source with an unsymmetrical laminate.
The concept of a thermal activation based on a bimetallic effect, CBCM effect [7,8] has been studied for morphing structure, the objective of this work is to show the ability of this technology in the field of vibration control of composite structures. For the control of vibration the main actuator remains the piezoelectric, for example the Macro Fiber Composite [9,10]. However in the literature, some application using SMA actuators can be found. The particular behavior of the SMA actuators inserted in the composite or fixed on the composite surface, leads to two technics of vibration control which lead to a frequency shift for different eigenvalue. The ASET technic (Active Strain Energy Tuning) [11], use the shape memory property of the SMA. A non-activated shape and an activated shape are programmed for the SMA actuator by a thermo mechanical cycle. SMA actuator is inserted in the composite have to be maintained during the manufacturing of the composite. During actuation the shape recovery of the SMA induces a stress field and modifies the dynamic behavior of the composite. To modify the dynamic behavior, the APT technic [12,13] uses the change of the SMA behavior during the phase transformation (variation of the Young’s modulus between austenitic and martensitic phase.
A CBCM combines these two actions, stress field increase and change for the behavior of the matrix, especially a loss of stiffness during heating.
After a presentation of the CBCM principle, the constitution of the different tested plates, the experimental procedure, boundary conditions and experimental apparatus will be totally described. In a first par for two kinds of boundary condition, free/free and embedded/embedded and for two CBCM, the influence of the plate rigidity on their dynamical response will be studied: for nonactivated and activated plates. The shift of frequency for the different eigenvalue will be highlighted. In the second part of this work, the influence of the loss of stiffness for the matrix will be studied for a CBCM plate and a symmetrical plate. An embedded/embedded boundary condition will be use and from the experimental date, the shape of the two first modes will be reconstructed.
2. Material and Methods
2.1. How CBCM Works
The bending or the warping is a well-known drawback of a dissymmetrical composite when submitted to temperature variations.
Two different manners to have a bending effect by heating the CBCM have been identified: one called “single effect” or “temperature effect”, another called “double effect” or “gradient effect”. The characterization between “single” or “double” is a reference to the possibility for CBCM plates to bend in one or two directions. The single effect is obtained thanks to an asymmetric laminate made of layers with different coefficients of thermal elongation in a given direction. The different coefficients can be obtained either by different materials or by different orientations of the reinforcement in the layers.
The double effect can be obtained with any composite structure containing an insulating layer, for instance a sandwich structure. If only one side of the composite is heated, the other side being insulated, a gradient of temperature appears within the structure. The result is, as previously shown, the bending of the plate Figure 1.
The thermal response time of the CBCM and conesquently the response time of the structure is the same order as the SMA one [14]. This response time is directly linked to the intensity of the current in the active layer.
2.2. Description of the CBCM Plates
The composite plates (395 × 125 × 2 mm3), prepared by compression moulding, are made of seven layers: two layers (2DG) of plain weave Glass fabric (196 g/m2), two layers (90G) of Glass unidirectional (588 g/m2), an active layer (AL) and two layers (2DA) of plain weave Aramid fabric (173 g/m2). Three constitutions of plates are studied: two CBCM plates SL = {(2DG)2/(0G)2/AL/(2DA)2} and ST = {(2DG)2/(90G)2/AL/(2DA)2}where 0˚ is along the longitudinal direction of the plate. The difference between the two CBCM plates becomes to the orientation of the main reinforcement, the glass unidirectional. The latest constitution is symmetrical SYM = {(2DG)1/(90G)1/ (2DA)1/AL/(2DA)1/(90G)1/(2DG)1}. The active layer is made of four parallel carbon yarns (6000 filament of 7 μm diameter) along the longitudinal direction of the plate. The yarns are connected to a DC generator and provide the internal heat source of the structure. The resin used for the matrix is an epoxy resin (Epolam 20 - 25 from Axson Corporation). The curing cycle followed is recommended by the manufacturer to obtain a glass transition temperature Tg of 130˚C.
2.3. Experimental Procedure
In this work two experimental procedures are used. The first procedure consists to characterize the influence of
the internal stress field induced by CBCM effect on the whole dynamic response of plates with different rigidity (SL and ST plates). Two kinds of boundary conditions are considered: free/free and embedded/embedded. To perform the dynamic analysis, the measuring systems is composed by a Brüel & Kjær acquisition system, an impact hammer (stress sensor PCB 086C05 # 13381), a piezoelectric accelerometer (Brüel & Kjaer 4393# 1803841, sensitivity 0319 pC/ms−2), an amplifier (Endevco 133 # BD69, gain 10 mV/ms−2) and a Pulse acquisition module with I/O 4/2 way 3109. For the value of a modal frequency, this set gives accuracy equal to ±2 Hz.
The second experimental procedure consists to highlight the influence of change of rigidity of the plates due to the mechanical softening of the matrix function due to the temperature increase. The plate is embedded on line A and B Figure 2. The measurement area (240 × 125 mm2) is discretized in 20 measurement nodes. The dynamic analysis is performed using a system acquisition, Brüel & Kjaer, an impact hammer (with force sensor PCB 086C05 # 13381), a front acquisition Pulse (Controller Module 7539 A). The speed of the plate is measured using a laser vibroscope (Ometron DV-500-D) in the node 1 as the reference node. During the test, the 20 nodes are successively affected by the hammer. The modal frequency accuracy is equal to 0.2 Hz. After treatment, in order to construct the shape of the different modes, experimental data are transferred to ME’scope VES software.
The temperature of the plate is measured by thermocouple on the upper side of the plate and a DAQ NX acquisition system of National Instrument.
3. Results and Discussion
3.1. Influence of the Plate Rigidity
The difference of rigidities between SL and ST plates is due to the orientation of the two glass unidirectional layers. The longitudinal rigidity is greater for the SL plate than the ST one; which is the opposite for the transversal rigidity.
For the free/free boundary conditions, Figure 3 shows the responses of the two plates at ambient temperature equal to 20˚C (without the activation of CBCM effect). The smaller longitudinal rigidity of the ST plate leads to a decreasing of the modal frequency. This result is in accordance with those obtained during the static characterization of plates for a free point bending test. For the SL and ST plates, the flexural modulus is 20 GPA and 16 GPA respectively. It can be noted that the morphing properties free displacement and blocking force given by the unconstrained and constrained test respectively are higher for the ST plate [14].
For a temperature of activation TA = 100˚C, Table 1 summarizes the results obtained for the first seven modes

Figure 3. SL and ST plates dynamical response at 20˚C (free/free boundary conditions).
of the plates. δ is the difference (in %) between the frequency modal values of the non-activated and activated plates. the non-indicated values correspond to a lower value than the accuracy of the measurement system (4 Hz). For the two plates, the CBCM effect affects the same values of modal frequency. The maximal values of δ are observed for the ST plate. For mode 1 and 3 no change of frequency may be observed.
For the free/free boundary conditions and due to the morphing property of the plates, the direction of curvature changes between the non-activated and activated plate Figure 4.
For the embedded/embedded test the change of curvature is cancelled by the boundary condition. At ambient temperature, the values of modal frequency Table 2 show the difference of dynamical response of the two plates. Contrary to the precedent results, the ST plate is more rigid than the SL one. This change of rigidity becomes to the boundary conditions, because due to the clamping an internal stress field appears in the plates, higher in the ST plates due to the higher value of the initial curvature.
For TA = 100˚C the CBCM effect can be observed for the SL plate Figure 5 and the ST plate Figure 6. The same kinds of previously results are obtained: no changes for certain frequency modal value and for the modes a lower value for the activated plates. After activation, the rigidity of the ST plate remains higher than the SL plate (Table 2), however the maximum values of δ are obtained for the ST plate. Depending of the glass unidirectional orientation, the CBCM effect not affects the same
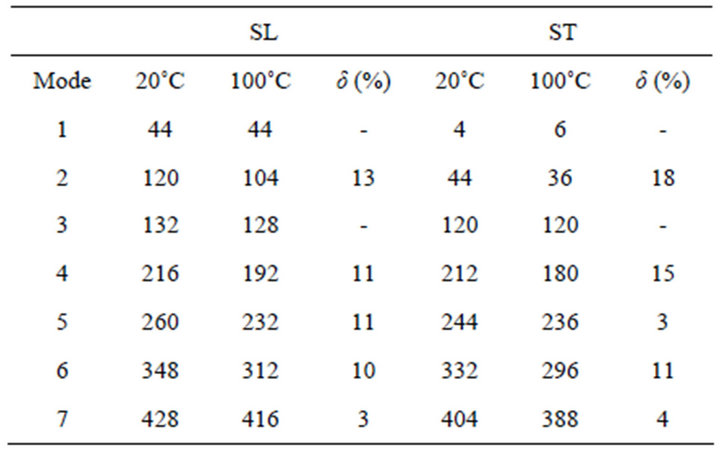
Table 1. Frequency modal value for free-free boundary conditions (Hz).

Figure 4. Curvature change for SL and ST plates.

Table 2. Frequency modal value for embedded/embedded boundary conditions (Hz).
nodal frequency values, and the influence of the CBCM effect is different depending on the frequency. The first three modes are unchanged for the SL plate; the third mode of the ST plate has the maximum value of δ. An opposite result is obtained for the fourth mode of the plate SL. This difference of dynamical behavior between SL and ST plates may be induced by the initial stress field due to the embedded boundary conditions. But the thermal activation has an influence on the mechanical property of the matrix and induces a loss of stiffness.
Thereby, when the plate is heating three phenomena are in competition. The initial stress field and the stress field induce by the CBCM effect. Linking to the asymmetry of the composite, these fields are higher for the ST plate and lead to an increase in stiffness along the longitudinal direction of the plate. The third phenomenon is the loss of stiffness and for the ST plate, due to the orientation of the glass unidirectional; this phenomenon’s effect is higher for the longitudinal direction.
3.2. Influence of the Matrix Loss Stiffness
For the embedded/embedded boundary conditions, the dynamic behavior of the thermal active plates is influenced by three coupled phenomena. The initial and thermal stress fields due to the curvature of the plate and the CBCM effect respectively, lead to an increase of the stiffness. On the opposite, the latest phenomenon induces a loss of rigidity linking to the matrix loss stiffness. To isolate this phenomenon, two plates are studied the ST plate and a symmetrical plate SYM. The dynamic analysis is made of two steps. The first is the determination of the modal frequency but only for the two first modes. The second step consists to reconstruct the associated modal shape of the modes.
For node 1, the reference point Figure 2, a change of modal frequency is observed for the SYM plate Figure 7. The value of δ between the plate at Tamb and the activated plate at TA = 100˚C is δ = 12% for the first mode (10.3

Figure 5. SL plate dynamical response (embedded/embedded boundary conditions).

Figure 6. ST plate dynamical response (embedded/embedded boundary conditions).
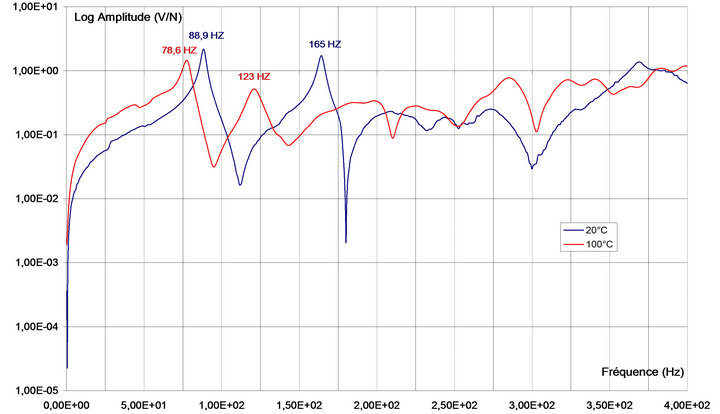
Figure 7. Dynamic response, SYM plate, embedded/embedded, at 20˚C and 100˚C.
Hz), and δ = 25% for the second mode (42 Hz). The corresponding damping coefficients are respectively, 1.72% and 1.15% for the non-activated plate and 3.22% and 3.35% for the activated plate.
The previous results obtained for the ST plate are confirmed Figure 8. The value of δ between the plate at Tamb and at TA = 100˚C is δ = 3% for the first mode (4 Hz) and δ =12% for the second mode (20 Hz). The corresponding damping coefficients are respectively, 1.35% and 1.14% for the non-activated plate and 2.48% and 2.39% for the activated plate.
For the two plates, the thermal activation leads to a decrease in the value of the frequency, and an increase of the damping coefficients. This result is consistent with the variation of the behavior of the epoxy depending to the temperature increase: loss of rigidity and increase of viscous properties.
However, for the asymmetrical plate ST, the changes of modal frequency and damping factor depending to the temperature are smaller than for the symmetrical plate. For the symmetrical plate, the changes are only due to the loss of stiffness of the epoxy resin depending to the temperature. For the ST plate, during the thermal activation, the competition between CBCM effect, and the loss of epoxy stiffness remains. For the two modes of the ST plate, the coupling between these opposite phenomena acts differently. For the first mode, the loss of stiffness is partly compensated by the CBCM effect.
This result may explain the dynamical behavior observed in Section 3.1 (Tables 1 and 2). For certain mode the loss of stiffness is totally compensated by the CBCM effect, and the value of the modal frequency remains the same. For the other modes the loss of stiffness is not compensated and a change of frequency is obtained. So depending on the shape of the mode, the coupling acts differently.
From experimental data, the shape of the two modes is reconstructed. For the SYM plate Figure 9, at ambient temperature the two modes are for the first a (2,1) mode and a (1,2) mode for the second. After the thermal activation, the same modal shapes are observed. The mode most affected by the loss stiffness (δ = 25%) is the second mode (1,2). This result is consistent with the orientation of the main reinforcement, the Glass unidirectional, along the transversal direction of the plate.
For ST plate Figure 10, the shape of the modes is conserved between the non-activated and activated structure. The modes are: (1,1) mode for the first and (1,2) for the second. As previously for the SYM plate, the second mode, the same that the SYM plate, is more affected by the loss stiffness (δ = 12%). However the first mode remains quasi constant (δ = 3%). The bending effect along the longitudinal direction of the plate due to CBCM effect affect mainly this first mode composed by a flexural mode along the longitudinal direction. Along this direction, the CBCM effect balances the loss of stiffness.
4. Conclusions
For the all modes, the softening of the matrix depending of the temperature increase induces an important change for their modal frequency. This result has been also observed for inserted SMA, for their temperature of activation. The loss of rigidity of the matrix is accompanied by an increase in its viscous properties. For a SYM plate, a thermal active layer may be used to change its dynamic behavior, but all modes will be modified by this thermal
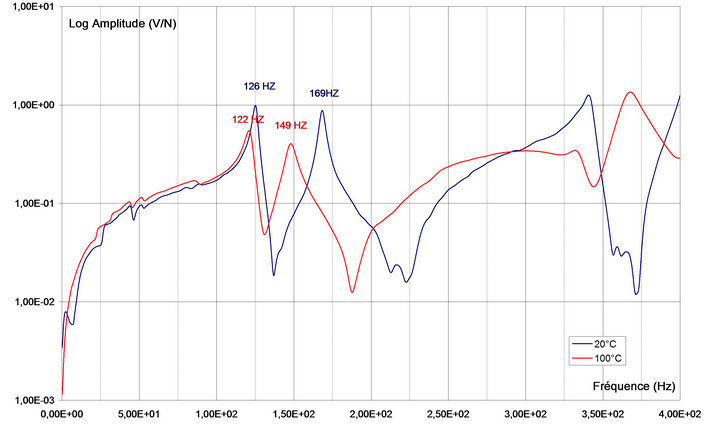
Figure 8. Dynamic response, ST plate, embedded/embedded/ at 20˚C and 100˚C.
activation. For the asymmetrical plate, the CBCM effect is added and for certain modes can be compensated the softening effect.
The softening is induced by the behavior of the matrix and is linked to the heat field in the composite plate. Depending to this thermal field, the softening can be local or global at the entire plate. The CBCM effect is also linked to the heat field; it can be local or global. However the CBCM effect depends also to the organization of the structure nature and orientation of the reinforcement. Therefore the coupling depending to the thermal field, between the loss of rigidity and the CBCM effect gives a wide field of possibility for the adaptation of the composite structures dynamic behavior.
Finally, one of the main advantages of the thermal activation compared to SMA or piezoelectric technologies is its simplicity of implementation in the process of composite structures manufacturing and this for any kinds of structure geometry.
NOTES