Pairing Effect on the Binding Energy Curve of N = Z Atomic Nuclei ()
1. Introduction
A nucleus is made of two types of discrete nucleons having practically the same mass, the neutron and the proton. Thus the binding energy of a nucleus is a discontinuous function of its mass. The shell model is quantized but unable to quantify the binding energies of the nuclei. It seems that it does not distinguish between unpaired nucleons, (odd-N, even-Z) from (odd-Z, evenN). The Bethe-Weizsäcker formula (Figure1) represents the binding energycurves. The even-odd phenomenon is expressed in the Bethe-Weizsäcker formula [3] by taking theodd-even nucleus as a reference point [4]. Only for heavy nuclides it is possible to use analytical functions to represent the binding energy. A, Z, and N are usually mixed in the equations as in the Wigner energy [3]. Also called liquid drop model, it is a collection of α-particles dissolving in a liquid drop, where these α-particles “form a relatively stable sub-nucleus” as proposed by Gamow in 1928 [5,6]. “This most-resilient of models” [7] has been developed by many others, forgetting the α-particles, replaced by the Pauli “four-shells” [8], partially compatible with the α-particle model because the neutron (and proton) magnetic moments, as the spins, are opposite.
Despite the fact that the neutron and proton electromagnetic properties are different, the usual assumption is that the nuclear interaction (called NN, 3N, Paris, Bonn, Nijmegen, Argonne...) is the same for the proton and the neutron, except for the long-range Coulomb repulsion, often disregarded. According to Weisskopf and Blatt [8], the discredited “naive ” α-particle model has no adequate method of treating the A = 4n + 2 nuclei. “Even in nonalpha-particle nuclei the average binding energy per nucleon has roughly the same value as in the alpha-
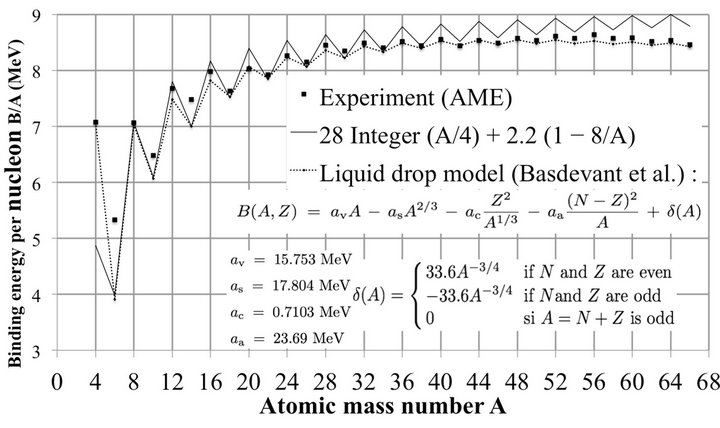
Figure 1Saw-tooth, even-odd, zig-zag, four-shells or pairing effect of the binding energy (absolute value) of N = Z nuclei. It “suggests an α model for light nuclei” [1]. An odd N = Z nucleus has almost the same total binding energy as its neighbors for unbound α-particles (28 MeV) with and without excess nucleons. Adding the binding energy of the α -α bonds as deuteron bonds (2.2 MeV) explains the mean increasing binding energy per nucleon with increasing A. The rms deviation between the calculated curve and the experimental curve from AME [2] is 0.25 MeV. Liquid drop model from [3].
particle. (...) A very strong experimental argument against the alpha-particle model comes from the scattering of alphaparticles in helium” [8]. Unfortunately, scattering data are measured with a “high-precision” of less than 2 digits without standardized experimental and interpretation method. Binding energies are known with high precision from mass spectrometer data with up to 8 digits for the 4He mass; thousands of data are recorded in standardized tables [2]. It is possible to extend the α- particle model to all N = Z nuclei as it will be shown thereafter. A recent update about various models and particularly the cluster and lattice models can be found [7].
2. Alpha-Cluster Model
According to Gamow [6], “Numerous attempts to compute the average interaction between nucleons moving in 1s and 2p orbits have all led to the result that, if the two-body forces are the same as evidenced in scattering and in the deuteron, the predicted binding energy in the nuclei between He and O is only a small fraction of the observed binding energies”. Gamow explains this discrepancy by α-particles “bound to each other by relatively weak forces of the van der Waals type”. He applied this idea to the nuclei containing only α-particles, that is, with N = Z even. The increase of the binding energy with the number of α-particles can be explained by the small contribution from the bonds between the α-particles.
The alpha-cluster model has been developed over a period of more than six decades. Binding energies and vibrational energies of certain of the small 4n-nuclei have been worked out in impressive detail. When the masses of the nuclear fragments are measured, an abundance of alpha particles or their multiples is consistently found. Alpha clustering is not only now well established in light nuclei [9,10] but also in all nuclei, as shown in this paper. MacGregor [7] “pointed out that there is a huge penalty paid by, particularly, the large nuclei for having a core region with equal numbers of protons and neutrons because that implies an abundance of proton charge in the nuclear interior”.
3. Other Models
Many theories have tried to explain the binding energy curve for the first N = Z nuclei (Independent Particle Model or Shell Model, Liquid Drop Model and the Face Centered Cubic Lattice Model). According to the Shell model, the nucleons fill shells within the nucleus.
“The existence of these peaks is a compelling experimental demonstration of the applicability of the Pauli exclusion principle in nuclei, because each four-shell contains just two neutrons (with spin upand spin down) and two protons (with spin upand spin down)” [1]. It distinguishes between even-Z even-N, odd-Z odd-N but not between mirror nuclei, (e.g. 6Li with B/A = 5.33 MeV) and even-Z odd-N (e.g. 6Be with B/A = 4.49 MeV) because they have both Jπ = 5/2+. The different binding energies of odd-Z even-N and odd-Z even-Z is attributed to the long range Coulomb repulsion energy.
4. Saw-Tooth Appearance
The peaks of the N = Z even nuclei (Figure 1 and Table 1) is general for all nuclei. There is no exception, with
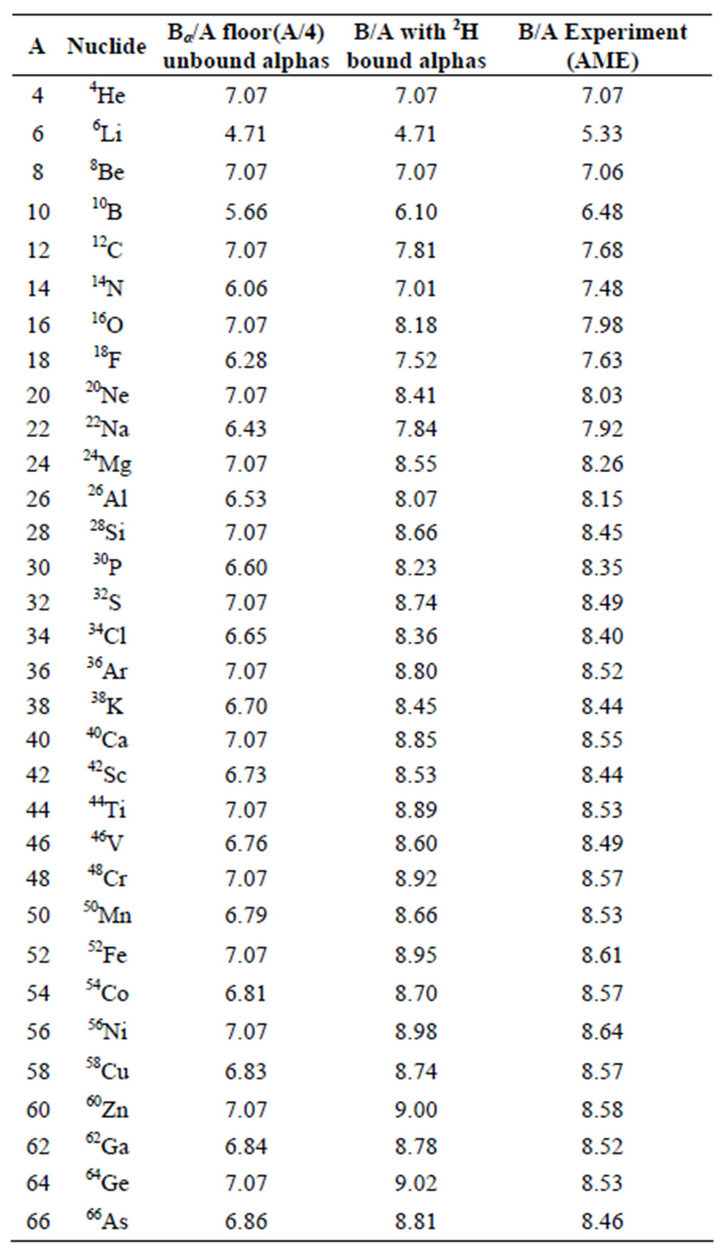
Table 1. Binding energies of N = Z nuclei. There are no α-α bonds for 4He, 6Liand 8Be, unstable. 4He and 8Be are forced to the α-particle binding energy. The total deuteron binding energy being small in comparison with that of the α-particle, the binding energy of an odd-odd N = Z nucleus is smaller because it is divided by A + 2 instead of A. The mean binding energy of the nuclei increases because the deuteron bonds between the α-particles remain although the deuterons are dissolved in the new α-particle. The rms deviation is 0.25 MeV and the greatest discrepancy is for 6Li where it is 13 %. Experimental data from AME [2].
completely regular periodic peaks on the binding energy curve of the nuclides. The atomic mass number A shows a periodicity of 4 (four-shells). The proton and neutron numbers Z and N show a periodicity of 2 observed for all chemical elements (Figures 2-4).
The peaks happen when N (or Z) is even, as may be seen on Figures 2 and 3, for all nuclei, as for heavy nuclei (Figure 4). For N = Z even the nucleus contains only α-particles. When N = Z is odd, the binding energy is lower, due to the presence of one proton and one neutron lightly bound to α-particles by two deuteron bonds of 2.225 MeV each, much less than that of the 28.28 MeV binding energy of α-particles. The saw-tooth behavior occurs in many nuclear phenomena such as neutron multiplicity, single-neutron separation, deepinelastic heavy-ion reactions, β decay, abundance.
5. Binding Energy of N = Z Nuclei Calculated from 4He and 2He
Adding one nucleon to a nucleus increases its mass. If the binding energy of a nucleon to a nucleus is negligible, the total binding energy remains the same. Therefore the binding energy per nucleon decreases. This is what happens when a neutron and a proton are added to an N = Z even nucleus, explaining qualitatively the saw-tooth phenomenon that will be now calculated.
In a first approximation, a nucleus is constituted only of unbound α-particles. The total binding energy is thus the sum of the binding energies of the sole α-particles:
 (1)
(1)
where Integer (x) is the integer part of x. This formula is partially equivalent to the δ(A) function (Figure 1) of the

Figure 2. Experimental binding energies of selected isotopes. The binding energy peaks are larger for both even Z and N. There is no clear evidence that even Z isotopes have a higher binding energy than their neighbors (see the curves of F, Ne and Na). The binding energy is parabolic, decreasing with a maximum around N ≈ 1.4 Z. Three Fe isomer steps are clearly visible.
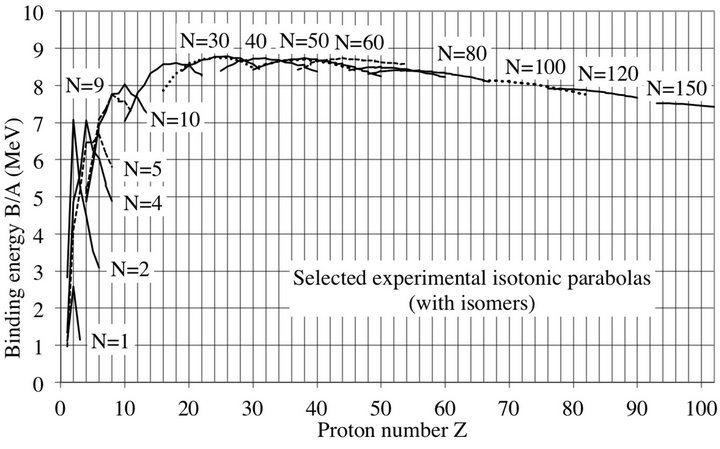
Figure 3. Experimental binding energies of selected isotones. The binding energy curves are similar for isotopes and isotones with peaks at even Z. Each inverted parabola shows a hump near N/Z between 1 and 1.4 as for the isotopes.

Figure 4. Experimental binding energies of some heavy nuclei. This figure shows that the α-particle cluster model is not limited to light nuclei. There is no significant difference between even and odd Z curves. The maximum value decreases with increasing Z, probably due to the long-range Coulomb repulsion between protons. One can see isomers at N = 126.
liquid drop model. The binding energy per nucleon of loose α-particles plus loose nucleons is thus, in this approximation:
 (2)
(2)
In a second approximation, let us begin with a nucleus containing only α-particles bound together. Two nucleons, one proton and one neutron have to be added to obtain an N = Z odd-odd nucleus. A proton will be attracted by a neutron of an α-particle to form a deuteron bond and vice versa. Two deuteron bonds are created to bind two α-particles, therefore the total binding energy increases by 2 × B(²H) = 2 × 2.225 MeV. Each time an α-particle is created and bonded to another one the total binding energy increases by 4.45 MeV. For each proton added, Z increasing by 1, the binding energy increases by 2.225 MeV, giving the formula:
 (3)
(3)
Number 8 comes from the experimental fact that the binding energy of 8Be is the same as that of the α- particle. Therefore the binding energy increases only for nuclides heavier than 8Be. Per nucleon we have:
 (4)
(4)
The binding energy per nucleon is the sum of the α-particle energy plus the α-α binding energy identified with that of two deuteron bonds, explaining the van der Waals bonds suspected by Gamow [6]. On Figure 1 the calculated curve is compared with the experimental curve. Adding successively one α-particle, one proton, one neutron, one α-particle, etc. resuming the 4-nucleon cycle.
When A increases indefinitely, the binding energy per nucleon attains asymptotically its maximum, the sum of the ⁴He and ²H binding energies per nucleon, according to formula (4). The long range Coulomb repulsive energy may be neglected here where light nuclei are considered. The corresponding data are shown on Table 1.
6. Conclusion
The binding energies of N = Z nuclei have been calculated in a way derived from the Gamow α-particle model [5,6] where the van der Waals forces are materialized as deuteron bonds between the α-particles. The ²H and ⁴He binding energies, calculated ab initio elsewhere [11], are the fundamental bricks of the N = Z nuclei and probably of all nuclei. The long-range Coulomb repulsion, small for light nuclides, is provisionally neglected. The rms deviation is 0.25 MeV and the maximum discrepancy between the calculated and experimental values is 0.5 MeV or 7% for 14 N. The rms deviation is twice that of the liquid drop model. Figures 2-4 prove that the saw-tooth pattern exists for all nuclei, from the lightest to the heaviest, even for the hydrogen isotopes although containing no α-particles, still to be clearly explained [12,13]. The saw-tooth phenomenon is due to the small binding energy of the neutron-proton bonds between the α-particles. Per nucleon, the maximum binding energy of any nucleus is shown to be the sum of the α-particle and deuteron binding energies.