1. Substitution of Formal Power Series
In this contribution we let  denote any field of characteristic zero. We recall some basic definitions from [1,2]. The algebra of formal power series in the variable
denote any field of characteristic zero. We recall some basic definitions from [1,2]. The algebra of formal power series in the variable  is denoted by
is denoted by . In what follows we sometimes use the notation
. In what follows we sometimes use the notation  for
for  to mean that
to mean that 
is a formal power series of the variable t. We recall that any formal power series of the form  for
for
 and
and  is invertible with respect to the usual product of series. Its inverse is denoted by
is invertible with respect to the usual product of series. Its inverse is denoted by  and has the form
and has the form  for some
for some . In particular, the set of all series of the form
. In particular, the set of all series of the form  forms a group under multiplication, called the group of unipotent series. For a series of the form
forms a group under multiplication, called the group of unipotent series. For a series of the form we may define for any other series
we may define for any other series  an operation of substitution given by
an operation of substitution given by . A unipotent substitution is a series of the form
. A unipotent substitution is a series of the form . Such series form a group under the operation of substitution, called the group of unipotent substitutions (whenever
. Such series form a group under the operation of substitution, called the group of unipotent substitutions (whenever , a series
, a series  is invertible under substitution, and the totality of such series forms a group under the operation of substitution called the group of substutions, and it is clear that the group of unipotent substitutions is a sub-group of this one). The inverse of
is invertible under substitution, and the totality of such series forms a group under the operation of substitution called the group of substutions, and it is clear that the group of unipotent substitutions is a sub-group of this one). The inverse of  is then denoted by
is then denoted by  and satisfies
and satisfies
 . Finally, it is possible to define a semi-direct product of groups by considering pairs
. Finally, it is possible to define a semi-direct product of groups by considering pairs  where
where  is a unipotent series, and
is a unipotent series, and  is a unipotent substitution, and the operation
is a unipotent substitution, and the operation 
 . The identity element is
. The identity element is
 . This group has been previously studied in [3-5], and is called the group of (unipotent) substitutions with pre-function. These substitutions with pre-function act on
. This group has been previously studied in [3-5], and is called the group of (unipotent) substitutions with pre-function. These substitutions with pre-function act on  as follows:
as follows:  for every series
for every series . In [3] is associated a doubly-infinite matrix
. In [3] is associated a doubly-infinite matrix  to each such operator which defines a matrix representation of the group of substitutions with prefunction, and it is proved that there exists a oneparameter sub-group
to each such operator which defines a matrix representation of the group of substitutions with prefunction, and it is proved that there exists a oneparameter sub-group . Therefore, it satisfies
. Therefore, it satisfies  for every
for every , and
, and
 is the usual
is the usual  -th power of
-th power of  whenever
whenever
 is an integer. It amounts that for every
is an integer. It amounts that for every ,
,  is the matrix representation of a substitution with prefunction say
is the matrix representation of a substitution with prefunction say 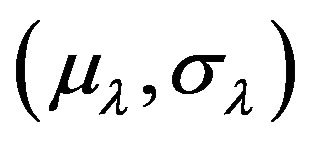 so that
so that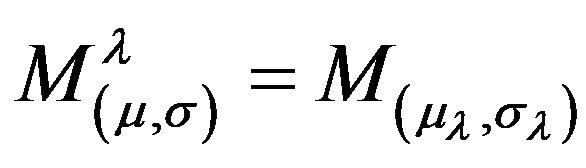 . The authors of [3] then define
. The authors of [3] then define . Actually in [3] no formal proof is given for the existence of such generalized powers for matrices or unipotent substitutions with pre-function.
. Actually in [3] no formal proof is given for the existence of such generalized powers for matrices or unipotent substitutions with pre-function.
In this contribution, we provide a combinatorial proof for the existence of these generalized powers for unipotent substitutions with pre-function, and we show that this even forms a one-parameter sub-group. To achieve this objective we use some ingredients well-known in combinatorics such as delta operators, Sheffer sequences and umbral composition which are briefly presented in what follows (Sections 2, 3, 4 and 5). The Section 6 contains the proof of our result.
2. Differential and Delta Operators, and Their Associated Polynomial Sequences
By operator we mean a linear endomorphism of the  -vector space of polynomials
-vector space of polynomials  (in one indeterminate
(in one indeterminate ). The composition of operators is denoted by a simple juxtaposition. If
). The composition of operators is denoted by a simple juxtaposition. If , then we sometimes write
, then we sometimes write 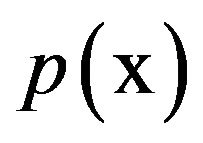 to mean that
to mean that  is a polynomial in the variable
is a polynomial in the variable .
.
Let 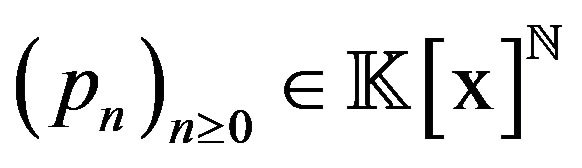 be a sequence of polynomials.
be a sequence of polynomials.
It is called a polynomial sequence if  for every
for every 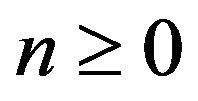 (in particular,
(in particular, ). It is clear that a polynomial sequence is thus a basis for
). It is clear that a polynomial sequence is thus a basis for .
.
An operator  is called a differential operator (see [6]) if 1)
is called a differential operator (see [6]) if 1)  for every
for every .
.
2)  for every non-constant polynomial
for every non-constant polynomial .
.
For instance, the usual derivation  of polynomials is a differential operator. Moreover, let
of polynomials is a differential operator. Moreover, let , and let us define the shift-invariant operator
, and let us define the shift-invariant operator  as the unique linear map such that
as the unique linear map such that 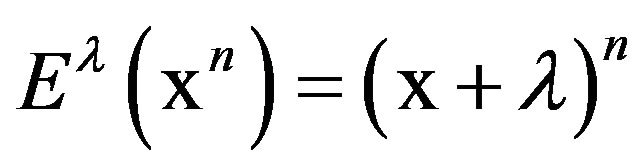 for every
for every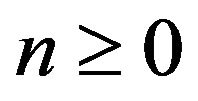 . Then,
. Then, 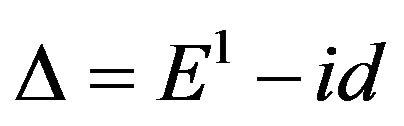 is also a differential operator.
is also a differential operator.
A polynomial sequence  is said to be a normal family if 1)
is said to be a normal family if 1) .
.
2) 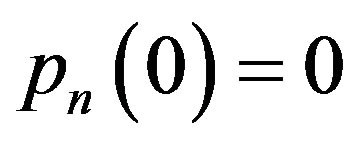 for every
for every .
.
Let  be a differential operator. A normal family
be a differential operator. A normal family 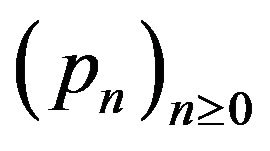 is said to be a basic family for
is said to be a basic family for  if
if

for every . It is proved in [6] that for any differential operator admits is one and only one basic family, and, conversely, any normal family is the basic family of a unique differential operator. As an example, the normal family
. It is proved in [6] that for any differential operator admits is one and only one basic family, and, conversely, any normal family is the basic family of a unique differential operator. As an example, the normal family 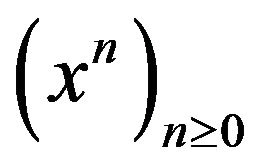 is the basic family of
is the basic family of .
.
Let 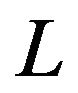 be an operator such that for every non-zero polynomial
be an operator such that for every non-zero polynomial ,
, 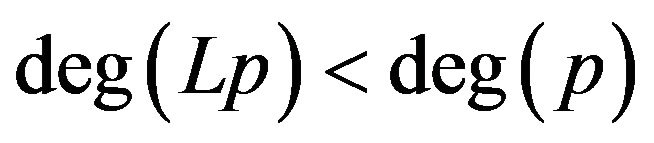 (in particular,
(in particular,  for every constant
for every constant ). Such an operator is called a lowering operator (see [7]). For instance any differential operator is a lowering operator. Then given a lowering operator
). Such an operator is called a lowering operator (see [7]). For instance any differential operator is a lowering operator. Then given a lowering operator , we may consider the algebra of formal power series
, we may consider the algebra of formal power series 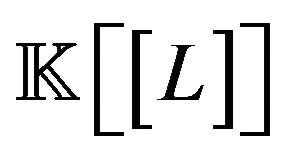 of operators of the form
of operators of the form  where
where  for every
for every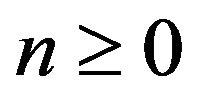 .
.
The series  converges to an operator of
converges to an operator of
 in the topology of simple convergence (when
in the topology of simple convergence (when  has the discrete topology) since for every
has the discrete topology) since for every , there exists
, there exists  such that for all
such that for all ,
,  , so that we may define
, so that we may define

According to [6], if  is a differential operator, then
is a differential operator, then
 if, and only if,
if, and only if,  commutes with
commutes with , i.e.,
, i.e.,
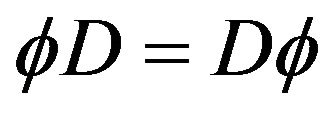 . Moreover, if
. Moreover, if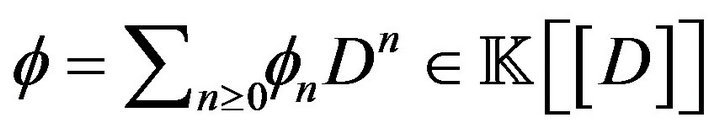 , then
, then
 is also a differential operator if, and only if,
is also a differential operator if, and only if,  and
and .
.
Following [1], let us define a sequence of polynomials
 by
by 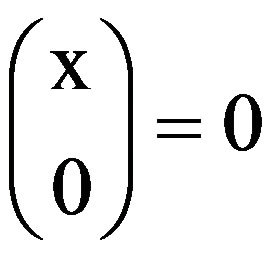 and
and 
for every integer . For
. For , we denote by
, we denote by  the value of the polynomial
the value of the polynomial  for
for . Let
. Let  be a lowering operator, and let
be a lowering operator, and let  be its unipotent part. Then we may consider generalized power
be its unipotent part. Then we may consider generalized power
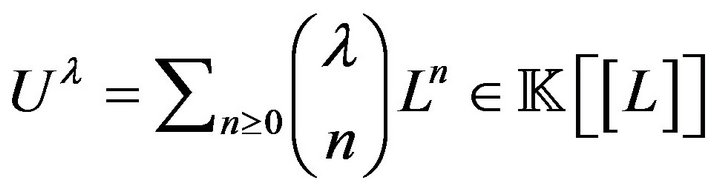 (in particular, this explains the notation
(in particular, this explains the notation  for the shift operator). We observe that for every integer
for the shift operator). We observe that for every integer ,
,  really coincides to the
really coincides to the  -th power
-th power  of
of . Moreover,
. Moreover,  for every
for every . We may also form
. We may also form

in such a way that for every ,
,
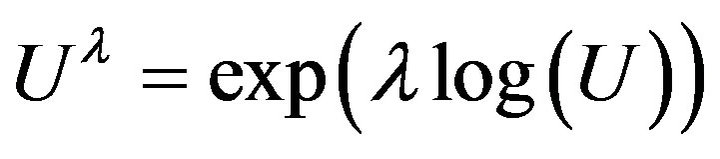
where for every  with
with ,
,  (it is a well-defined operator). This kind of generalized powers may be used to compute fractional power of the form
(it is a well-defined operator). This kind of generalized powers may be used to compute fractional power of the form  for every
for every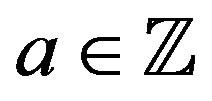 ,
, 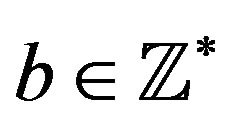 (for instance,
(for instance, ). They satisfy the usual properties of powers:
). They satisfy the usual properties of powers: ,
, . The objective of this contribution is to provide a proof of the existence of such generalized powers for unipotent substitutions with pre-function.
. The objective of this contribution is to provide a proof of the existence of such generalized powers for unipotent substitutions with pre-function.
Following [8], we may consider the following sub-set of differential operators, called delta operators. A polynomial sequence  is said to be of binomial-type if for every
is said to be of binomial-type if for every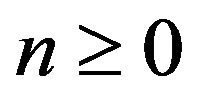 ,
,

An operator  is a shift-invariant operator if for every
is a shift-invariant operator if for every ,
, . Now, a delta operator
. Now, a delta operator  is a shift invariant operator such that
is a shift invariant operator such that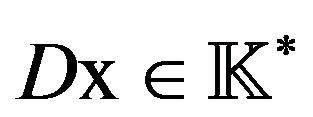 . For instance, the usual derivation
. For instance, the usual derivation  of polynomials is a delta operator. It can be proved that a delta operator is a differential operator. The basic family (uniquely) associated to a delta operator is called its basic set. Moreover, the basic set of a delta operator is of binomial-type, and to any polynomial sequence of binomial-type is uniquely associated a delta operator. If
of polynomials is a delta operator. It can be proved that a delta operator is a differential operator. The basic family (uniquely) associated to a delta operator is called its basic set. Moreover, the basic set of a delta operator is of binomial-type, and to any polynomial sequence of binomial-type is uniquely associated a delta operator. If  is a delta operator, then there exists a unique
is a delta operator, then there exists a unique  -algebra isomorphism from
-algebra isomorphism from  to the ring of shift-invariant operators
to the ring of shift-invariant operators 
that maps  to
to . In [8]
. In [8]
is proved that given a delta operator , and a series
, and a series 
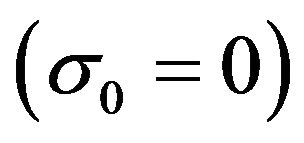 with
with , then
, then  is also a delta operator. Conversely, if
is also a delta operator. Conversely, if 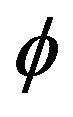 is a shift-invariant operator (so that
is a shift-invariant operator (so that ), then if it is a delta operator, the unique series
), then if it is a delta operator, the unique series

such that  satisfies
satisfies  and
and .
.
3. Sheffer Sequences
In this section, we also briefly recall some definitions and results from [8].
Let  be a sequence of polynomials in
be a sequence of polynomials in . We define the exponential generating function of
. We define the exponential generating function of  as
as

Let  be a delta operator and
be a delta operator and  be its basic set. Let
be its basic set. Let 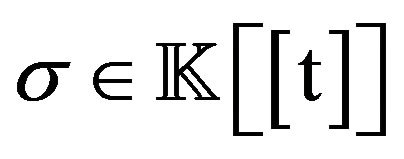 with
with  and
and  such that
such that . Then from [8],
. Then from [8],

A polynomial sequence  is said to be a Sheffer sequence (also called a polynomial sequence of type zero in [9] or a poweroid in [10]) if there exists a delta operator
is said to be a Sheffer sequence (also called a polynomial sequence of type zero in [9] or a poweroid in [10]) if there exists a delta operator  such that 1)
such that 1) 2)
2)  for every
for every .
.
Following [9], a polynomial sequence  is a Sheffer sequence if, and only if, there exists a pair
is a Sheffer sequence if, and only if, there exists a pair  of formal power series in
of formal power series in  with
with  invertible, and
invertible, and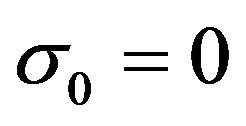 ,
,  , such that
, such that
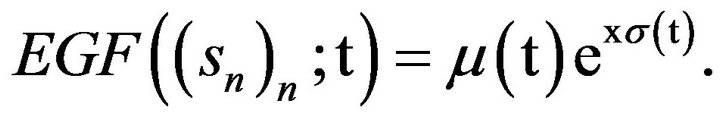
Remark 1. The basic set of a delta operator  is a Sheffer sequence.
is a Sheffer sequence.
Let  be a delta-operator with basic set
be a delta-operator with basic set . Following [8], the following result holds.
. Following [8], the following result holds.
Proposition 1. A polynomial sequence  is a Sheffer sequence if, and only if, there exists an invertible shift-invariant operator
is a Sheffer sequence if, and only if, there exists an invertible shift-invariant operator 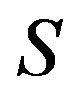 such that
such that  for each
for each . Moreover, let
. Moreover, let 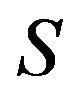 be an invertible shift-invariant operator. Let
be an invertible shift-invariant operator. Let  be the unique formal power series such that
be the unique formal power series such that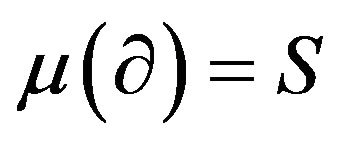 . Then,
. Then,  is invertible, and
is invertible, and

where  is the Sheffer sequence defined by
is the Sheffer sequence defined by
 for each
for each , and
, and  is the unique formal power series such that
is the unique formal power series such that . Finally we also have the following characterization.
. Finally we also have the following characterization.
Proposition 2. Let  be a polynomial sequence. It is a Sheffer sequence if, and only if, there exists a delta operator
be a polynomial sequence. It is a Sheffer sequence if, and only if, there exists a delta operator  with basic set
with basic set  such that
such that

4. Umbral Composition
This section is based on [11].
Let  be a fixed polynomial sequence. Let us define an operator
be a fixed polynomial sequence. Let us define an operator 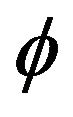 by
by  for each
for each .
.
Since  is a basis of
is a basis of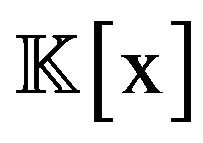 , this means that
, this means that 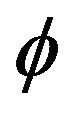 is a linear isomorphism of
is a linear isomorphism of . When
. When 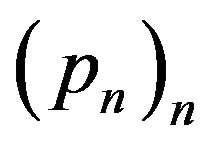 is the basic set of a delta operator, then
is the basic set of a delta operator, then  is referred to as an umbral operator, while if
is referred to as an umbral operator, while if  is a Sheffer sequence, then
is a Sheffer sequence, then  is said to be a Sheffer operator. An umbral operator maps basic sets to basic sets, while a Sheffer operator maps Sheffer sequences to Sheffer sequences.
is said to be a Sheffer operator. An umbral operator maps basic sets to basic sets, while a Sheffer operator maps Sheffer sequences to Sheffer sequences.
Let  be a polynomial sequence. For every
be a polynomial sequence. For every ,
,
 where
where  is the coefficient of
is the coefficient of  in the polynomial
in the polynomial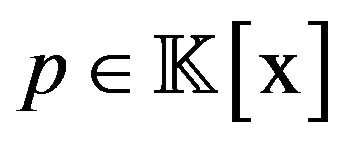 . Let
. Let 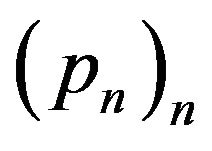 and
and 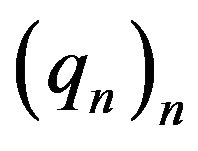 be two polynomial sequences. Their umbral composition is defined as the polynomial sequence
be two polynomial sequences. Their umbral composition is defined as the polynomial sequence 
 defined by
defined by

for each . By simple computations, it may be proved that
. By simple computations, it may be proved that . The set of all polynomial sequences becomes a (non-commutative) monoid under
. The set of all polynomial sequences becomes a (non-commutative) monoid under  with
with  as identity. We observe that if
as identity. We observe that if 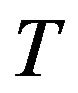 is the operator defined by
is the operator defined by  for each
for each
 , then
, then . More generally, we have
. More generally, we have  where
where  is the
is the
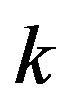 -th power of
-th power of  for the umbral composition (it is equal to a sequence say
for the umbral composition (it is equal to a sequence say  and we denote
and we denote 
by ). Under umbral composition, the set of all Sheffer sequences is a (non-commutative) group, called the Sheffer group ([12]), and the set of all basic sequences is a sub-group of the Sheffer group.
). Under umbral composition, the set of all Sheffer sequences is a (non-commutative) group, called the Sheffer group ([12]), and the set of all basic sequences is a sub-group of the Sheffer group.
From [8] we have the following result that combines delta operators, basis sets, Sheffer sequences and umbral composition.
Theorem 1. Let  and
and  be two delta operators with respective basic sets
be two delta operators with respective basic sets  and
and . Let
. Let  and
and  be two invertible shift-invariant operators. Let
be two invertible shift-invariant operators. Let  and
and  be the Sheffer sequences defined by
be the Sheffer sequences defined by  and
and  for each
for each . Let
. Let  be two invertible series such that
be two invertible series such that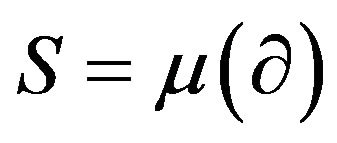 ,
, . Let
. Let  be two formal power series with
be two formal power series with ,
,  such that
such that  and
and . Then,
. Then,
 is a shift-invariant operator,
is a shift-invariant operator,  is a delta operator with basic sequence
is a delta operator with basic sequence
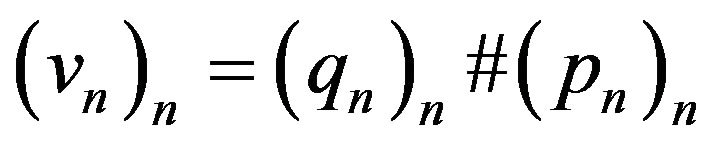 . Finally, let
. Finally, let  be the Sheffer sequence given by
be the Sheffer sequence given by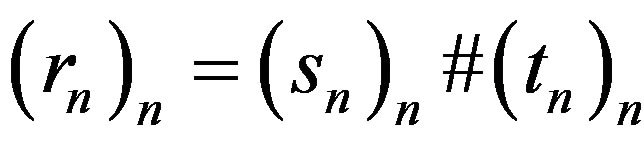 . Then,
. Then, 
for each .
.
It may be proved that if  is the Sheffer sequence obtained from the delta operator
is the Sheffer sequence obtained from the delta operator  with basic set
with basic set  and the invertible shift-invariant operator
and the invertible shift-invariant operator , i.e.,
, i.e., 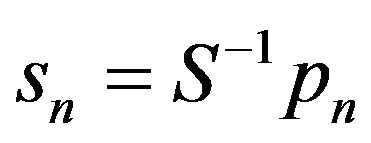 for each
for each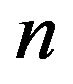 , then the inverse
, then the inverse
 of
of  with respect to the umbral composition is the basic set of the delta operator
with respect to the umbral composition is the basic set of the delta operator , the inverse
, the inverse
 of
of  with respect to the umbral composition is the Sheffer sequence
with respect to the umbral composition is the Sheffer sequence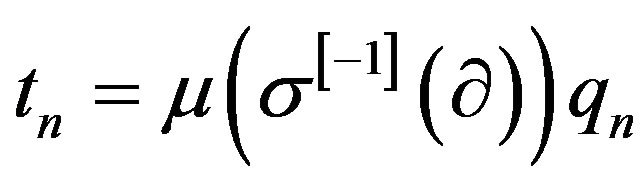 .
.
5. Unipotent Sequences
The basic set  of a delta operator
of a delta operator  is said to be unipotent if the unique series
is said to be unipotent if the unique series  such that
such that  satisfies
satisfies 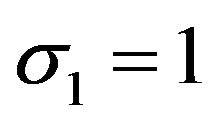 (and, obviously,
(and, obviously,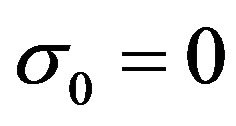 ), i.e.,
), i.e.,  is a unipotent substitution. A Sheffer sequence
is a unipotent substitution. A Sheffer sequence  associated to a delta operator
associated to a delta operator  (with
(with ,
, ) and an invertible shift-invariant operator
) and an invertible shift-invariant operator  (with
(with 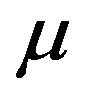 invertible), i.e.,
invertible), i.e., 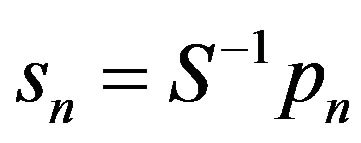 for every
for every  where
where 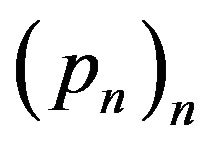 is the basic set of
is the basic set of , is said to be unipotent if
, is said to be unipotent if 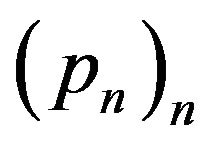 is unipotent, and if
is unipotent, and if 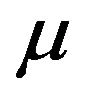 is unipotent, i.e.,
is unipotent, i.e., . It is also clear from the previous section (theorem 4) that the (umbral) inverse of a unipotent basic set is unipotent, and the (umbral) inverse of a Sheffer sequence is also unipotent.
. It is also clear from the previous section (theorem 4) that the (umbral) inverse of a unipotent basic set is unipotent, and the (umbral) inverse of a Sheffer sequence is also unipotent.
It is clear from theorem 4 that the group of basic sets under umbral composition is isomorphic to the group of substitutions. Moreover, the group of unipotent basic sets also is isomorphic to the group of unipotent substitutions. Likewise, the group of (unipotent) Sheffer sequences is isomorphic to the group of (unipotent) substitutions with pre-function (see also [12]).
Lemma 1. Let  be a substitution with prefunction, and let
be a substitution with prefunction, and let  be the Sheffer sequence and the basic set associated to the delta operator
be the Sheffer sequence and the basic set associated to the delta operator 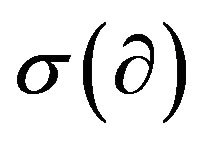 and the invertible shift-invariant operator
and the invertible shift-invariant operator  (this means that
(this means that  is the basic set of
is the basic set of , and
, and
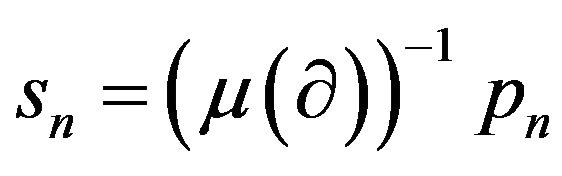 for each
for each ). Then,
). Then,  is a unipotent substitution with pre-function if, and only if,
is a unipotent substitution with pre-function if, and only if,  for every
for every .
.
Proof. Let us first assume that  is a unipotent substitution with prefunction. We have
is a unipotent substitution with prefunction. We have  for every basic set, so that
for every basic set, so that . Let
. Let . We have
. We have
 . Then,
. Then,  is equivalent to
is equivalent to
 .
.
By identification of the coefficient of  on both sideswe obtain
on both sideswe obtain 
(since  is assumed to be a unipotent substitution), and, by induction,
is assumed to be a unipotent substitution), and, by induction, . Besides, we have
. Besides, we have
 for each
for each . But
. But 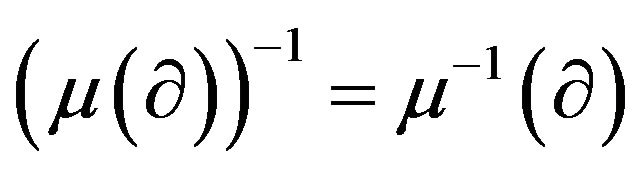
(because there is a ring isomorphism between 
and ), and
), and , where
, where .
.
Then, by identification of the coefficient of , we have
, we have
 for every
for every . Conversely, let us assume that
. Conversely, let us assume that 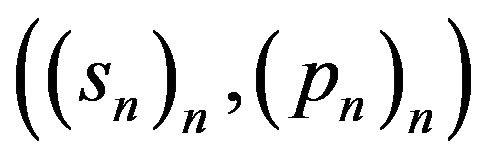 is the Sheffer sequence and the basic set associated to the delta operator
is the Sheffer sequence and the basic set associated to the delta operator  and the invertible shift-invariant operator
and the invertible shift-invariant operator  with
with
 for every
for every . By construction we have
. By construction we have  so that
so that . Likewise,
. Likewise,  , so that
, so that . □
. □
6. Generalized Powers of Unipotent Substitutions with Pre-Function
The purpose of this section is to define  for any
for any 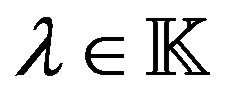 and any unipotent substitution with pre-function
and any unipotent substitution with pre-function , and to prove that it is also a unipotent substitution with pre-function. Moreover we show that
, and to prove that it is also a unipotent substitution with pre-function. Moreover we show that
 is a one-parameter sub-group, i.e.,
is a one-parameter sub-group, i.e.,
 for every
for every , and
, and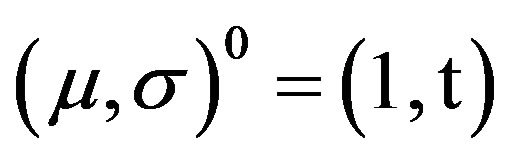 .
.
Let 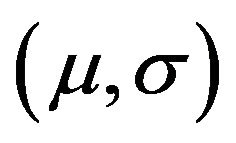 be a unipotent substitution with prefunction of
be a unipotent substitution with prefunction of . Let
. Let  be the unipotent basic set of the (unipotent) delta operator
be the unipotent basic set of the (unipotent) delta operator . Let
. Let 
be the unipotent Sheffer sequence associated to 
and the (unipotent) invertible shift-invariant operator . Let
. Let  be the umbral operator given by
be the umbral operator given by  for all
for all , and let
, and let  be the Sheffer operator defined by
be the Sheffer operator defined by 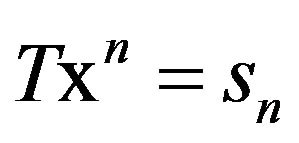 for all
for all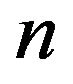 . It is easily checked that for every integer
. It is easily checked that for every integer ,
,  and
and . In particular, for each
. In particular, for each ,
, 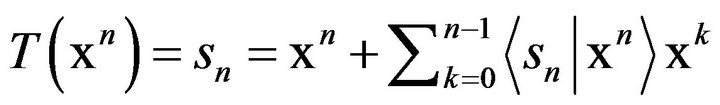
(by Lemma 5). Therefore,  , where
, where
 for each
for each . The operator
. The operator  is actually a lowering operator. Then according to section 2it is possible to define
is actually a lowering operator. Then according to section 2it is possible to define  for every
for every . Moreover, we have
. Moreover, we have .
.
For each , let us define
, let us define  for every
for every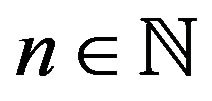 . When
. When , we have
, we have 
 . So that in this case,
. So that in this case, 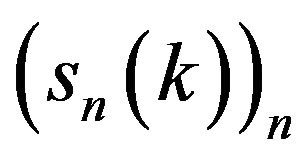 is the unipotent Sheffer sequence associated to
is the unipotent Sheffer sequence associated to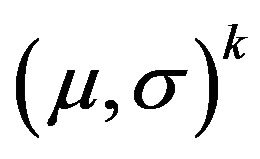 . This means that if
. This means that if , and
, and  is the unipotent basic set of the (unipotent) delta operator
is the unipotent basic set of the (unipotent) delta operator then
then  for each
for each . Similarly, let
. Similarly, let
 for every
for every . Therefore,
. Therefore,  , where
, where  is a lowering operator. Again for every
is a lowering operator. Again for every , we define
, we define
 . For each
. For each
 , we define
, we define 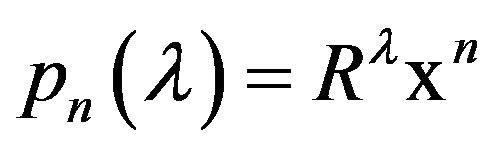 for each
for each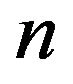 . In particular for
. In particular for ,
,  , so that it is the basic set of the unipotent delta operator
, so that it is the basic set of the unipotent delta operator . Clearly,
. Clearly,  for each
for each . Thus for every
. Thus for every , we have
, we have
 (1)
(1)
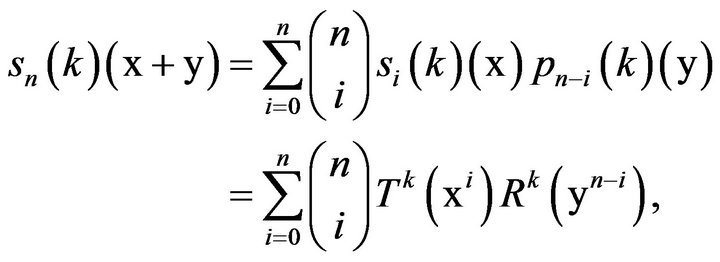 (2)
(2)
Now, let  be a variable commuting with
be a variable commuting with  and
and , and let us define
, and let us define
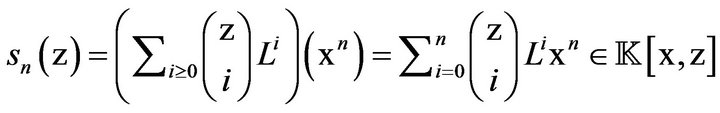
and similarly,
 for each
for each . As polynomials in the variable
. As polynomials in the variable , their degrees are at most
, their degrees are at most . As polynomials in the variable
. As polynomials in the variable ,
,  ,
,  ,
,
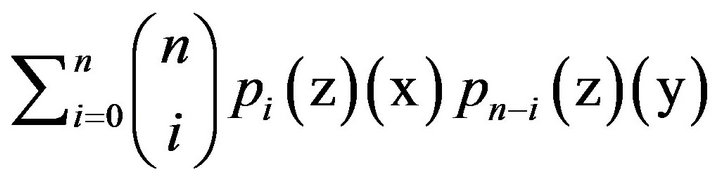
and

have also a degree at most . Because the equations (1) and (2) hold for every integer
. Because the equations (1) and (2) hold for every integer , the polynomials (in the variable
, the polynomials (in the variable )
)

and

are identically zero, and the above equations hold for every . Therefore,
. Therefore,  is a polynomial sequence of binomial-type, and
is a polynomial sequence of binomial-type, and  is a Sheffer sequence for every
is a Sheffer sequence for every . Moreover, for every
. Moreover, for every , we have
, we have

so that . Similarly,
. Similarly,
 for every
for every . Moreover,
. Moreover,
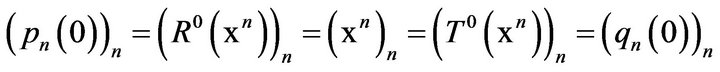 .
.
Therefore, 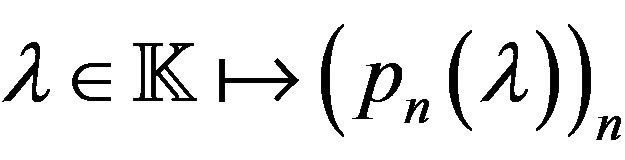 and
and  are one-parameter sub-groups. It follows that
are one-parameter sub-groups. It follows that

and

(inverses under umbral operation).
We define  as the pair of formal power series
as the pair of formal power series  such that
such that  is the substitution that defines the delta operator
is the substitution that defines the delta operator  with basic sequence
with basic sequence , and
, and  is the invertible series such that
is the invertible series such that

for each . Since
. Since  and
and 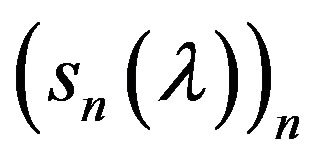 are unipotent sequences, it is clear that
are unipotent sequences, it is clear that 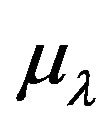 is unipotent, and
is unipotent, and  is a unipotent substitution. It is also clear that whenever
is a unipotent substitution. It is also clear that whenever , then
, then . Let us check that
. Let us check that  is a one-parameter subgroup of the group of unipotent substitutions with prefunction. This means that for every
is a one-parameter subgroup of the group of unipotent substitutions with prefunction. This means that for every ,
,

First of all, by definition,  is the unipotent substitution associated to the basic set
is the unipotent substitution associated to the basic set
 and therefore
and therefore . In a similar way, the series
. In a similar way, the series  is uniquely associated to the Sheffer sequence
is uniquely associated to the Sheffer sequence
 and to the basic set
and to the basic set
 . Again this means that
. Again this means that . Therefore, we obtain the expected result. It is also clear that
. Therefore, we obtain the expected result. It is also clear that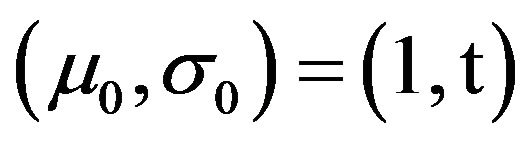 .
.
Remark 2. In particular, since  is a field of characteristic zero, for every
is a field of characteristic zero, for every , we may define fractional powers
, we may define fractional powers  such as for instance
such as for instance
for each integer .
.