1. Introduction
Tumour Control Probability (TCP) models have been widely used to compare different strategies in cancer therapy [1-4]. Some of these models have properties derived from multi-cellular biological systems approach and are analyzed either by continuum or cell-based models [5]. It has been shown recently that for the case of prostate cancer—and low proliferating tumours in general—diferent TCP models for radiotherapy lead practically to the same predictions regarding the TCP evolution in time [6], suggesting the use of simpler and more computationally feasible models in the clinic. However these simpler models tend to neglect the peculiar biological differences between tumours. The Monte Carlo method plays a fundamental role when one aims to include such differences into the TCP calculations.
The radiotherapy consists of depositing a certain amount of radiation dose into the tissue in order to kill the tumour cells. The dose is defined as the radiation energy deposited into the tissue per unit mass and is measured in units of gray (1 Gy = 1 Joule·kg−1). The treatment involves strategies which maximize the dose on the tumour while minimize it on the normal surrounding tissue [7]. Although the accuracy and precision of the dose have improved considerably due to technological advances [8], these are still limiting factors for a total success in radiotherapy [9,10]. Various studies have evaluated the effects of the non-uniformity of the dose deposition and heterogeneity of cancer cells in the same tumour [8,11]. Recently, the tumour control in radiation therapy was revised by Zaider and Hanin [12].
In this context, we propose a TCP model-based test for prediction of tumour erradication (cure) in radiotherapy. We obtain sampled data from Monte Carlo simulations of the two-compartment Dawson-Hillen (DH) model [1, 6]. We add a gaussian noise into the radiation dose in order to simulate the uncertainty on its deposition. Our simulations follow a particular protocol of radiation therapy for prostate cancer. A positive aspect of this procedure is that both diversity of patients and dose imprecision can be simulated. To determine the statistical power of the proposed test, we construct its receiver operating characteristic (ROC) curve from the probability distribution of the fraction of remaining tumour cells for simulated experiments that evolve either to cure or non-cure. ROC curve is an important tool which has been widely used in many research areas such as radiology [13] and signal analysis [14-16]. In a recent study [17] ROC curves were used in prediction procedures related to prostate disease.
Our study is based on simulations and a similar procedure may be applicable to clinical data. Specifically the clinical evaluation of tumour sizes may be used for shortterm prognosis in radiotherapy.
2. Monte Carlo Simulations for a TCP Model
2.1. The Dawson-Hillen TCP Model
As a generalization of the previous TCP model presented by Zaider and Minerbo [2], Dawson and Hillen developed a model [1] where the tumour cells are divided into two compartments, say active and quiescent. Cells from the quiescent compartment can migrate to the active one by an average rate 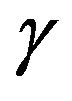 and undergo mitosis at constant rate
and undergo mitosis at constant rate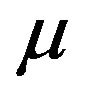 , thus giving rise to two identical cells. These two cells on their turn immediately become quiescent thus repeating the cycle. The dynamics is governed by the set of equations [1]
, thus giving rise to two identical cells. These two cells on their turn immediately become quiescent thus repeating the cycle. The dynamics is governed by the set of equations [1]
 (1)
(1)
where 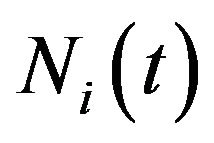 and
and 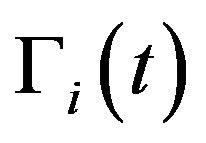 are respectively the number of cells and the mean death rates (caused by the radiation) in the active
are respectively the number of cells and the mean death rates (caused by the radiation) in the active 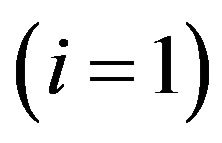 and quiescent
and quiescent  compartments at time
compartments at time . For our purposes, it is also usefull to define
. For our purposes, it is also usefull to define  as the total number of tumour cells (active and quiescent ones) at time
as the total number of tumour cells (active and quiescent ones) at time .
.
The mean death rate is related to the survival fraction [2] in the corresponding compartment. After receiving a certain amount of radiation dose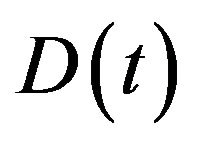 , acumulated in the time interval
, acumulated in the time interval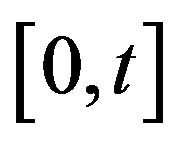 , the expected fraction of surviving cells
, the expected fraction of surviving cells 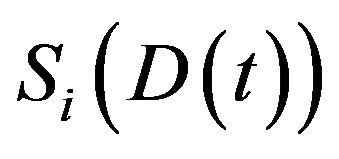 in the
in the  compartment is given by
compartment is given by  well known in the literature as the Linear-Quadratic Model [18], where
well known in the literature as the Linear-Quadratic Model [18], where 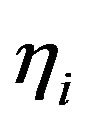 and
and 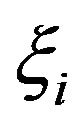 are parameters related to the radiosensitivities
are parameters related to the radiosensitivities  in the
in the 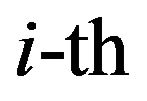 compartment. The derivative of
compartment. The derivative of 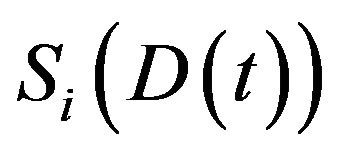 is expressed by
is expressed by
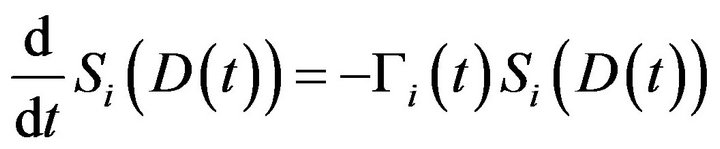 (2)
(2)
so that the time evolution of the mean death rate is written as [2]
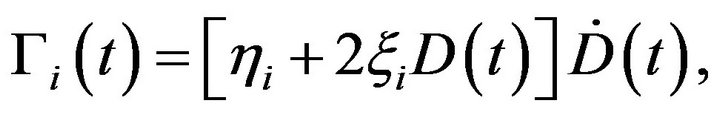 (3)
(3)
where 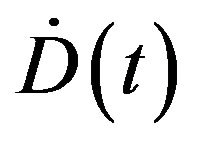 is the dose rate. Since dividing cells are more sensitive to radiation
is the dose rate. Since dividing cells are more sensitive to radiation 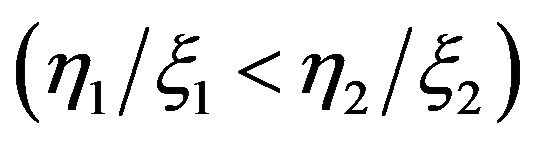 the death rate turns to be different for each compartment. From these equations Dawson and Hillen extended the ZiderMinerbo’s approach and obtained explicit expressions for the TCP which depend on the initial number of tumour cells in each compartment [1,2].
the death rate turns to be different for each compartment. From these equations Dawson and Hillen extended the ZiderMinerbo’s approach and obtained explicit expressions for the TCP which depend on the initial number of tumour cells in each compartment [1,2].
2.2. A Monte Carlo Implementation for Sampling
Gong et al. [6] compared different TCP models regarding to clinical treatment protocols for prostate cancer. In this study, the Monte Carlo method was used as a valid approach to determine the tumour survival for one and twocompartment models.
In the present study, we propose a TCP model-based test for radiotherapy and evaluate its statistical power. For this purpose, we now describe a general Monte Carlo procedure for sampling and constructing the ROC curve of the test.
In our approach, the dynamics of tumour growth and death is governed by Equations (1), (2) and (3) of the DH two-compartment TCP model. In this way, for a time step  each cancer cell can: 1) migrate from quiescent compartment to the active one with probability
each cancer cell can: 1) migrate from quiescent compartment to the active one with probability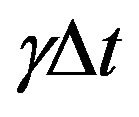 ; 2) divide by mitosis in the active compartment with probability
; 2) divide by mitosis in the active compartment with probability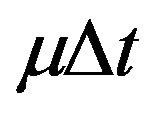 , thus originating two cells in the quiescent compartment; 3) be killed by radiation in the respective compartment with probability
, thus originating two cells in the quiescent compartment; 3) be killed by radiation in the respective compartment with probability 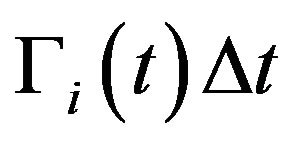 or; 4) remain unchanged otherwise. For each Monte Carlo experiment, the system evolves in time according to the above probabilistic rules. Clinically, the treatment is interrupted when the prescribed maximum dose
or; 4) remain unchanged otherwise. For each Monte Carlo experiment, the system evolves in time according to the above probabilistic rules. Clinically, the treatment is interrupted when the prescribed maximum dose 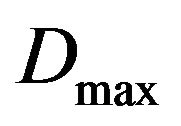 is reached.
is reached.
Table 1 shows a typical schedule for prostate cancer treatment used in our simulations: the nominal dose d received per fraction, the daily frequency of irradiation, the number of treatment days per week, the total number of treatment days and the corresponding nominal dose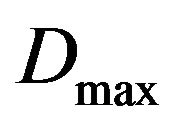 .
.
This protocol corresponds to the treatment schedule used by Parsons et al. [19] except for the number of treatment days per week. In Parsons’ protocol, no radiation dose is deposited on weekends so that such number is 5 as usual in standard treatments. Nevertheless, in our simulations the treatment is never interrupted so that the probability of tumour eradication can be continuously evaluated as function of time. In this way, statistical analysis is prevented from gaps in time if dose is deposited everyday. Naturally, such analysis can be extended to weekends off schedules.
Table 2 lists typical prostate cancer parameters used in our simulations: the initial number  of tumour cells (active and quiescent ones), the net mean rates for mitosis
of tumour cells (active and quiescent ones), the net mean rates for mitosis 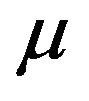 and migration
and migration 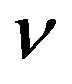 (both ones discounted
(both ones discounted