Homological Electromagnetism and Electromagnetic Demonstrations on the Existence of Superconducting Effects Necessaries to Magnetic Levitation/Suspension ()
1. Introduction
One of the main goals in the study of electromagnetic levitation/suspension of symmetrical objects was the demonstration of the inherent importance of the natural geometry required to the obtaining of prototypes designed with certain geometry. Also the use of superconductors and magnetic field to create the anti-gravitational effects of their impulse and movement [1], as is realized in sidereal bodies (stars, galaxies, molecular clouds, etc.) where the intersidereal magnetic fields and superconductor nucleus act in their center that generate the rotation and translation of these bodies in the universe [2], with an auto-sustainability almost inexhaustible of energy (Figure 1). In before papers was demonstrated that the geometry under certain symmetrizations of the superconductor electromagnetic field [3], is very important to risk the adequate characterizing of the superconducting process to levitation. The produced effects to their levitation/suspension defined for their Eddy currents and iso-rotations of magnetic origin are the required to can design a vehicle with impulse properties, exceptional displacement and auto-sustainability.
One of the problems that appear and that are intimately related to the transmission of these properties to a vehicle, is the design of a electromagnetic reactor that transmits the subjacent levitation effects in the interactions between their magnetic field and the Eddy currents from their inner and that and that in turn generate enough energy to the auto-sustainability of the vehicle in their functioning of all their systems (for example, the control panel, the impeller ring, the revetment of Eddy currents in their structure, the telemetry and localization systems of the vehicle, monitoring and communication systems, etc.) in permanent form, having energy to one thousand years. In this point we enounce the following postulates that must apply our vehicle:
Postulate 1.1. The vehicle must be auto-sustainable in all moment, circumstance and control process.
In it, we must consider that the operator  that establishes a condition of permanent electromagnetic field on all the trajectories
that establishes a condition of permanent electromagnetic field on all the trajectories , of field, involves the actions of magnetic field and the actions of the Eddy currents through the integral of total action of permanent magnetic field:
, of field, involves the actions of magnetic field and the actions of the Eddy currents through the integral of total action of permanent magnetic field:
 (1)
(1)

Figure 1. A vehicle seemed in behavior to a sidereal object or macro-particle. Images published in the proceedings of fluid flow, Heat Transfer Thermal Systems British Columbia Canada [3].
where , depends on the geometrical form of
, depends on the geometrical form of , in our case the design of the vehicle will be an ellipsoid or a disc, convenient geometries of the shape of the vehicle that were discussed before in [1] and that represent intermediate superconductors states in the region of interaction of field [4]. Furthermore, these states shape the specific topological transforms in the superconductor context [4], and by physic of superconductors are related [5].
, in our case the design of the vehicle will be an ellipsoid or a disc, convenient geometries of the shape of the vehicle that were discussed before in [1] and that represent intermediate superconductors states in the region of interaction of field [4]. Furthermore, these states shape the specific topological transforms in the superconductor context [4], and by physic of superconductors are related [5].
The term  explains the thermodynamics effects (see Figure 2) of the action of the field in the neighborhood of the reactor. If there are not these magnetic effects then
explains the thermodynamics effects (see Figure 2) of the action of the field in the neighborhood of the reactor. If there are not these magnetic effects then

and
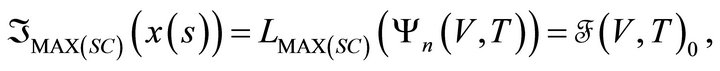
is the corresponding thermodynamic action that only depends on the volume (size of the reactor), and not of their form [5]. T is the temperature and this is an effect obtained by the reactor operation. Furthermore, in this same article, is demonstrated how can be used these heat effects to produce more electromagnetic energy.
All the energy that must be electromagnetic will have to be created in and from inner of the reactor and with the interaction of the magnetic iso-rotations that must cohelp to the diamagnetic obtaining of a part of the vehicle interacting with the impelled magnetic field, aspects that will generate the magnetic sustentation of the vehicle and their displacement as a galaxy or star (to see Figure 1). Of this way, is necessary demonstrate this auto-sustainability of the reactor, as well as the quantum transmission of the properties of levitation/suspension [6], that must be generated to create a “magnetic levitation conscience in all the vehicle”, in accordance with the geometrical design of the vehicle. The detached effects for the reactor functioning (heat, parasite currents, captive lines of the magnetic field, etc.) are re-used to the feeding of secondary systems.
Postulate 1.2. The orbits (or orbital spaces) signed in

Figure 2. Magnetic modeling of the prototype: as disc of the vehicle. The scale goes from the major intensity of the magnetic field (red color) to the absence of the magnetic field and revetment for the Eddy currents (diamagnetic effect: Scales that go from the green color to the turquoise blue). The rim effect debilitates substantially to the magnetic field (yellow trenches).
before studies (twistor of the magnetic field and the diamagnetic revetment due to the Eddy currents (skin effect)) must be invariants under any external transformation and only their transformation will must obey to the inner mechanisms of reactor control.
2. Homological Electrodynamics
The similarities of sidereal objects and the proposed vehicle must from comes similarities of effects created for electromagnetic characteristics that happen in both cases. In both cases the creation of the movement effects (displacement and rotation) effects of magnetic sustentation (levitation/suspension) and the permanent auto-sustainability (production of proper energy) must expire the realizations of the field given by certain integrals on orbital spaces created by the superconducting in the quantum electro-dynamical spaces satisfying the corresponding orbital integrals due [7] to cuspidal surfaces in the generation Chirality inversion through a Dirac node [7, 8]:
 (2)
(2)
which include the microscopic effects of the superconductor field on el magnetic field [9,10]. This last is consigned in the variation of the Eddy currents flux to a levitation disc [11].
Proposition (F Bulnes) 2.1. The lines of the magnetic field are to displacement of the vehicle through a twistor.
The integrals of line of the actions of field have their equivalents as contour integrals, which bears to isomorphism between the cohomological spaces of intersidereal fields (of a galaxy) and the displacement fields of a twistor produced for iso-rotation (Lemma [3]). This is not a mere coincidence, since the space of differential forms to the Maxwell tensors like 2-form, and the potentials (as well as the quantum densities of energy that they produce ) like 1-form, admit a geometrical modeling through vector of lines that can establish the structural equivalence in the complex ambit given for (ver [12,13]):
) like 1-form, admit a geometrical modeling through vector of lines that can establish the structural equivalence in the complex ambit given for (ver [12,13]):
 (3)
(3)
Here there arise an endless number of transformations that can explain from a point of topological view very of the geometrical phenomena that are caused in the universe and that can be copied inside the electromagnetic context to the designs and obtaining of prototypes of our ship. The space  defines a set of singularities that from a point of view of our prototype represents the source or reactor of the vehicle. Then the equivalences given by the homology Equivalence (3) demonstrate the superconductor-magnetic field interrelation to the levitation and movement in levitation of our vehicle. Here
defines a set of singularities that from a point of view of our prototype represents the source or reactor of the vehicle. Then the equivalences given by the homology Equivalence (3) demonstrate the superconductor-magnetic field interrelation to the levitation and movement in levitation of our vehicle. Here  is the homogeneous vector bundle of lines that considers the lines of magnetic field in the twistor generated for the magnetic field in movement (rotation ring of the vehicle) (see Figure 3(a)).
is the homogeneous vector bundle of lines that considers the lines of magnetic field in the twistor generated for the magnetic field in movement (rotation ring of the vehicle) (see Figure 3(a)).
3. Iso-Rotations
If we define as a reactor to the Levitron, the topological space could be written as [3]:
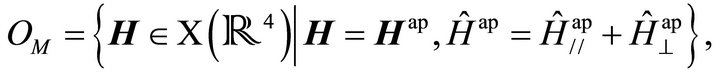 (4)
(4)
Then , in the center of the imam. The magnetic iso-rotations are reached with the moment of rotation created by the alternation of two rotational operators (one for each of the components of the Levitron)
, in the center of the imam. The magnetic iso-rotations are reached with the moment of rotation created by the alternation of two rotational operators (one for each of the components of the Levitron)
 (5)
(5)
Then there is a magnetic potential function , such that in the limit of the magnetic bounder satisfies
, such that in the limit of the magnetic bounder satisfies
 (6)
(6)
The magnetic energy is conserved through their magnetic moment which is uniform for the geometrical design [3].
This conclusion is deduced to set off the magnetostatic study of the levitron, which establish as conservation law the law of their magnetic momentum as conesquence of the iso-rotations (rotations in a parallel plane to the base). These must realize in very high frequency and under a constant magnetic momentum. If this thin condition is fulfilled the levitation of the levitron will be more prolonged. What happens with the model of variable magnetic field as the given in the Figure 2? What happen when both orbits must be levitated by the current of the superconductor?
Lemma (Bulnes, F) 3.1. Be  with
with , a space of orbits (hypersurfaces), generates in
, a space of orbits (hypersurfaces), generates in , by the realization of movements given for
, by the realization of movements given for  through of the action of their Maxwell fields
through of the action of their Maxwell fields  given
given

Figure 3. (a) The magnetic field generates in the blue central part of the vehicle (reactor) establishes the spin direction of the movement geodesics of the vehicle to displace it, very similar to the realized for the lines orientation of magnetic field of a galaxy that it makes her rotate and create their displacement through of the universe [2]. Is necessary to be careful in not confusing the fact of that these lines of magnetic field have their begin in the reactor (centre of the vehicle) and they end in the exterior of the vehicle, translating to all the vehicle by electromagnetic homology between the generated orbit for the magnetic field and the superconductor orbit; (b) Sidereal homology of the superconductor and magnetic fields in a galaxy; (c) The colors in the multi-physics modeling, corresponding to the heat concentration by the interaction between the magnetic field and superconductor currents.
by the Equation (1), in the superconductor. Then the orbits engendered by the actions , on
, on  are magnetic torus engendered by rotations
are magnetic torus engendered by rotations  generated by fluxoids
generated by fluxoids , in the vortex zone [6]. Details of the lemma mathematical demonstration, please to see [3].
, in the vortex zone [6]. Details of the lemma mathematical demonstration, please to see [3].
From the lemma 2.1, and considering the regime of energy given by , the magnetic rotation actions takes the form
, the magnetic rotation actions takes the form
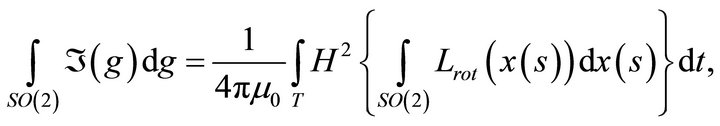 (7)
(7)
where  is the special orthogonal group of the rotations of range two.
is the special orthogonal group of the rotations of range two.
But we want that the penetration longitude let bigger in the area of superconducting transition of our vehicle to transform it as perfect diamagnetic, then by superconducting
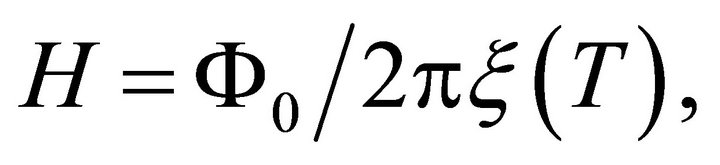 (8)
(8)
This involves implicitly geometry of symmetrical body that helps to these iso-rotations.
4. Re-Producing the Superconductor Effects from Pure Electromagnetism (Existence Demonstration of the Eddy Currents)
We consider the following experiment [4], to demonstrate the existence of parasite currents that with big amperage can be induced in a wire winding with geometrical shape a torus like the given in the Figure 4 B to create levitation. Remember that this geometrical shape is recurrent because is an orbit of the involved inside the space  (see lemma 3.1, and Table 1) [3] also (Figure 5).
(see lemma 3.1, and Table 1) [3] also (Figure 5).
The explaining to these phenomena is inside the Foucault or Eddy currents that are induced in the non-magnetic plate due to the variation of magnetic flux that on she produces the bobbin. These currents give origin in turn a magnetic field that creates the repulsion force on the bobbin. If this force overcomes their weight, the bobbin Levite, and is necessary that the plate do not be magnetic material, since it can dominate the attraction effect due to the orientation of the magnetic dipoles of the material (Figure 6).
The interesting conclusion rests on the fact that we might install an amplifier of current type microchip inside the reactor that not necessary uses material superconductors. With a small amplified current we can create the necessary force on the vehicle so that this levite

Figure 4. (a) Experiments with homade levitron have managed ten minutes (10 min) of levitation due to their dimensions. We cannot do that the spinning-top haves a inferior velocity to the 19 rpm, not even Superior to the 25 rpm, this fact due to the equilibrium of iso-rotations, that is to say, considering that the rotation plane of the spinning-top must be parallel to the base (the saucer must auto-generates their magnetic field, and their impulse must be a combination of their magnetic field and their iso-rotations [3,11]). Concerning to the launching base, is demonstrated that to a levitation design must be considered a exact and proportional geometry between the spinning-top and the base to avoid insufficiency of the magnetic force (this is traduced to our design as: the vehicle obeys to symmetrical designs and topological transformations of a superconductor ellipsoid (Landau theorem [14])); (b) Two orbital spaces shape the Levitron, although one space is the fixed base. These two orbital spaces define the levitation in a geometrical sense. To a levitation model with superconductor, the two orbital spaces are positioned both in concentric shape [3]. The inner torus is the generator of the magnetic twistor. The exterior torus is the generator of movement.
without need for an exterior base making use also of their symmetry of spherical type [1]. The shape of the useful Eddy currents for their auto-suspension might be regulated by a device that controls the flow of magnetic field and the diamagnetic flow created by these currents.
Using the homology principle developed for the Equivalence (3) we can establish that the two orbits given inside a magnetic levitron come superposes in only

Figure 5. Rotating magnetic ring. Multi-physics simulations published in [3].
 (a) (b)
(a) (b)
Figure 6. (a) Eddy currents producing diamagnetismo on the surface of ferromagnetic material; (b) Electro-antigravity device showing the Eddy currents from usually electrical current and their levitation effect [11].

Table 1. Orbital regions obtained in the superconducting process.
one orbit (fiber electric torus) and their superposing is equivalent to the levitation created for the feeding of the winding for a current of the space . This is not mere coincidence, since is demonstrated that the effect of levitation is the resulted of two effects acting in synergicform [15], to the securing of the vehicle movement in magnetic levitation [3].
. This is not mere coincidence, since is demonstrated that the effect of levitation is the resulted of two effects acting in synergicform [15], to the securing of the vehicle movement in magnetic levitation [3].
5. Design of the Electromagnetic Reactor
We consider as  to the reactor of our vehicle or flying ship
to the reactor of our vehicle or flying ship , under the electromagnetic principles already mentioned. This comes determined by two fundamental parts: the rotational part and the superconductor part. In the superconductor part, it is wanted to obtain a diamagnetic state of the whole structure of the vehicle
, under the electromagnetic principles already mentioned. This comes determined by two fundamental parts: the rotational part and the superconductor part. In the superconductor part, it is wanted to obtain a diamagnetic state of the whole structure of the vehicle  (effect skin obtained through Eddy’s currents).
(effect skin obtained through Eddy’s currents).
Likewise, let us define as reactor to the vector topological space to the superconducting process, then:
 (9)
(9)
where , and
, and , are the applied magnetic field (field engendered by a magnetic component just as a permanent imam or electromagnet) and the field engendered by the superconducting currents. We can also decompose also the total magnetic field in their perpendicular components H^, and tangent H//, to the surface of the superconductor that should be the whole vehicle due to Eddy’s currents or superconducting currents in this case. Then each component of the reactor
, are the applied magnetic field (field engendered by a magnetic component just as a permanent imam or electromagnet) and the field engendered by the superconducting currents. We can also decompose also the total magnetic field in their perpendicular components H^, and tangent H//, to the surface of the superconductor that should be the whole vehicle due to Eddy’s currents or superconducting currents in this case. Then each component of the reactor , is induced in each perpendicular component and tangent of the total magnetic field, that is
, is induced in each perpendicular component and tangent of the total magnetic field, that is
 (10)
(10)
and
 (11)
(11)
In the superconductor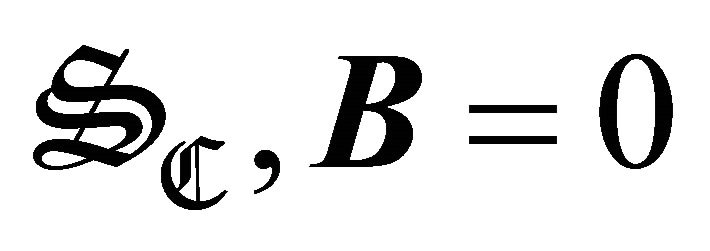 , then
, then  and
and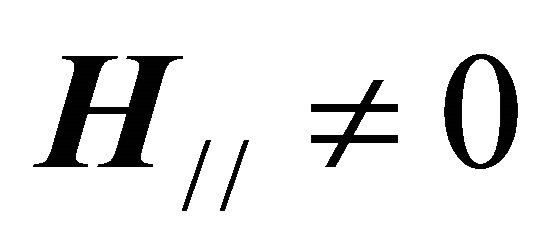 , that is to say; the field of force of the superconductor should be tangent everywhere to its surface being had that the magnetic lines of force have to the surface like its encircling one, which is determined by the superficial currents defined by the density js (to see Figure 7).
, that is to say; the field of force of the superconductor should be tangent everywhere to its surface being had that the magnetic lines of force have to the surface like its encircling one, which is determined by the superficial currents defined by the density js (to see Figure 7).
What others possibilities of superconductor materials or non-superconductor materials (that under an electromagnetic process obtain the same superconductor effects) can be used inside the reactor ?
?
The center of the reactor might be designed by a superconductor ring where turned at very high speed (like part of a gyroscopic stabilizer effect demonstrated in the lemma 3.1) a conductive metal to which an electric current is applied as the established in the experiments exhibited in the Section 4, and by means of an operational amplifier (microchip) installed in the same reactor to amplify the electric currents produced inside the reactor. The remaining energy in every process might be accumulated in cells similar to the made solar cells of crystal of high resonance, remaining ready this additional energy for processes of emplacement of the vehicle (to see Figure 8).
6. Results: Electrodynamical Measurements and Dynamical Analysis of Fields
6.1. Behavior of the Magnetic Field with Some Thermal Conditions to Superconducting
One of the aspects that appears in the phenomenon of superconducting and ligature with the diamagnetic effects that are wanted to obtain by Eddy’s currents for the proper microscopic effects of the superconducting, is the appearance of Fermi flows for the interaction electronfonon-electron in this phenomenon, which also produces the trenches in the band of conduction due to the conductivity . But all this, is linked to the energy of the excited states that appear in the trenches that make change the critical magnetic field (magnetic field produced in the bosom of the space
. But all this, is linked to the energy of the excited states that appear in the trenches that make change the critical magnetic field (magnetic field produced in the bosom of the space  on the quasi-particles space (liquid of Fermi)) in function to the temperature
on the quasi-particles space (liquid of Fermi)) in function to the temperature  which must not exceed to a critical temperature
which must not exceed to a critical temperature 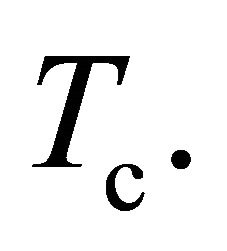
The variation of temperature inside of range  (Figures 9), to the trenches was predicted in the Abriko-
(Figures 9), to the trenches was predicted in the Abriko-
zov effect (Figure 10) and after by Cooper [6,17].
6.2. Quantum Levitation Will (Magnetic Levitation Conscience): The Ship like Macro-Particle
The necessary levitation effects to the displacement of the vehicle on the space , require of the transmission of the Field projection effect in a position of the space that is determined for a quantum operator
, require of the transmission of the Field projection effect in a position of the space that is determined for a quantum operator 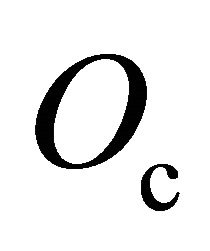 (intention operator [15]), that realize the transformation of the particles in the immediate enthrone of the vehicle flight space, that is determinate for a levitation state
(intention operator [15]), that realize the transformation of the particles in the immediate enthrone of the vehicle flight space, that is determinate for a levitation state . This projectivization of the field obeys to the realization of the quantum operator
. This projectivization of the field obeys to the realization of the quantum operator . For this, is necessary consider to
. For this, is necessary consider to  like the quantum space-time perse of the transformation
like the quantum space-time perse of the transformation .
.
How to measure this transference of conscience of transformation due to the field , inside of the ship reactor on an object defined by a portion of the space
, inside of the ship reactor on an object defined by a portion of the space ? What is the limit of this supported action or transference of conscience so that it supplies effect in the portion of the space
? What is the limit of this supported action or transference of conscience so that it supplies effect in the portion of the space , and the temporary or instantaneous actions for every particle
, and the temporary or instantaneous actions for every particle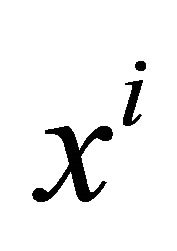 , are founded on an only one global synergic action on
, are founded on an only one global synergic action on ?
?
We measure this transference of conscience (or intention) of , on a particle
, on a particle , through the value of the integral of the spilled intelligence (magnetic conscience) given as [18]:
, through the value of the integral of the spilled intelligence (magnetic conscience) given as [18]:
 (a) (b) (c)
(a) (b) (c)
Figure 8. Central part of the Reactor: (a) Magnetic field (blue color) concentration; (b) Temperature in a plate inside the reactor; (c) Set of crystal plates of high resonance in a disc format (COMSOL Multi-physics [16]).
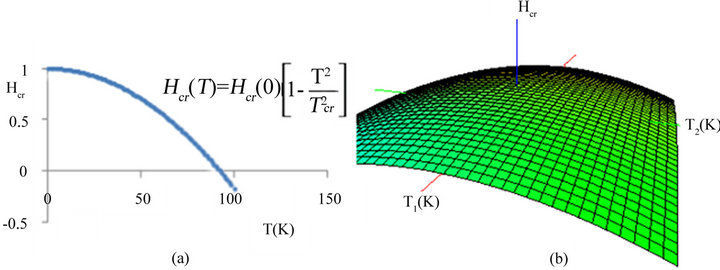
Figure 9. (a) The critical magnetic field versus the temperature (b) Surface of critical magnetic field given in the computational program space-time 4.0, .
.

Figure 10. Variation of fluxoids due the temperature variation inside the range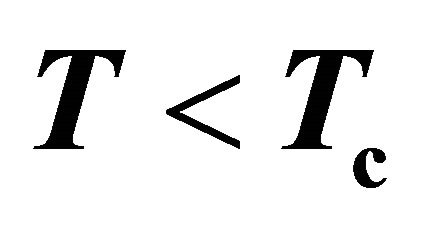 . This fluxoids explain the electro-anti-gravitational effects obtained by superconducting to levitation. Therefore in the vertical axis the values are negatives. Among fluxoids there are superconductor electrons [17].
. This fluxoids explain the electro-anti-gravitational effects obtained by superconducting to levitation. Therefore in the vertical axis the values are negatives. Among fluxoids there are superconductor electrons [17].
 (12)
(12)
where  is the transference from the quantum state
is the transference from the quantum state  to the quantum state
to the quantum state  due to the voltage increased by the one amplifier. By the nanotechnology theory [15], this increasing obeys to a behavior of logarithmic type [15]. We leave at level conjecture and based on our researches of nanotechnology and advanced quantum mechanics [15], that a sensor for the quantum sensitization of any particle that receives an instruction given by a field
due to the voltage increased by the one amplifier. By the nanotechnology theory [15], this increasing obeys to a behavior of logarithmic type [15]. We leave at level conjecture and based on our researches of nanotechnology and advanced quantum mechanics [15], that a sensor for the quantum sensitization of any particle that receives an instruction given by a field , it must satisfy the inequality of Hilbert type [19], for this transference of conscience defined in (13) on the region
, it must satisfy the inequality of Hilbert type [19], for this transference of conscience defined in (13) on the region , to know [20] (see Figure 3 de [18])):
, to know [20] (see Figure 3 de [18])):
 (13)
(13)
which in the magnetic context is the inequality obtained in [21], and given by (theorem of F. Bulnes [3])
 (14)
(14)
The conscience transference demands a synchronization of events that it answers to an effect of simultaneity and coordination of temporary actions on a set of parti-
 (a) (b)
(a) (b)
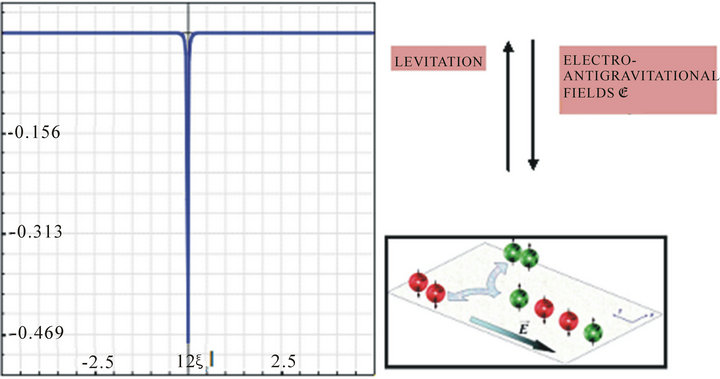
Figure 11. (a) Graph of spins versus distribution of particles to Electro-Anti-Gravitational effects (levitation). In the simulation was used the model of LEVITATION studied in the experiments of levitation mentioned in the Section 4, where the solution in a dynamical analysis is . The curve of blue, is a vortex in the Abrikosov mixed. The parameter , is the coherent length; (b) Positioning of particles to create the micro-vortexes (fluxoids).
. The curve of blue, is a vortex in the Abrikosov mixed. The parameter , is the coherent length; (b) Positioning of particles to create the micro-vortexes (fluxoids).

Figure 12. The microscopic effects of the electromagnetic fields (quantum densities of field) created in the bosom of the algebra 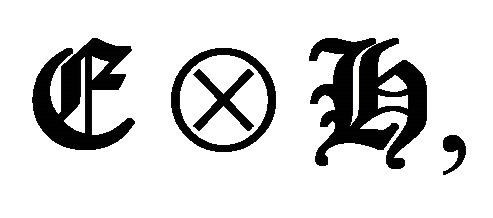 create an effect of macro-particle of the vehicle (the vehicle and their electromagnetic revetment behaves like a particle) where their displacement is realized in instantaneous form and its direction is a macro-spin projected from the magnetic conscious operator of the ship which defines their angular moment [26-28]. The aptitude to transform to the ship for any type of anti-gravitational flight will be recorded in the law of quantum transformation for the microscopic effects obtained by the macroscopic effects (theorem). These laws obey the integrals of quantum transformation of the particles that are a source of the microscopic effects obtained by the macroscopic causes of the superconducting effect.
create an effect of macro-particle of the vehicle (the vehicle and their electromagnetic revetment behaves like a particle) where their displacement is realized in instantaneous form and its direction is a macro-spin projected from the magnetic conscious operator of the ship which defines their angular moment [26-28]. The aptitude to transform to the ship for any type of anti-gravitational flight will be recorded in the law of quantum transformation for the microscopic effects obtained by the macroscopic effects (theorem). These laws obey the integrals of quantum transformation of the particles that are a source of the microscopic effects obtained by the macroscopic causes of the superconducting effect.
cles that must behave under the same intensity that could be programmed through “revisited” path integrals [8,15], producing a joint effect called synergy (22 (to see Figures 11 and 12).
Theorem on quantum levitation transformation (F. Bulnes) 6.2.1. Considering the two orbital spaces created by the superconducting given in the space  [13], and supposing that the electro-anti-gravitational effect are defined by the generation Chirality inversion through a Dirac node then are satisfied the orbital integrals of (2) and where E, is the total Fermi energy in all the Fermi surface including the proper kinetic energies,
[13], and supposing that the electro-anti-gravitational effect are defined by the generation Chirality inversion through a Dirac node then are satisfied the orbital integrals of (2) and where E, is the total Fermi energy in all the Fermi surface including the proper kinetic energies,  is the momentum created in the chirality inversion through the node of automorphism
is the momentum created in the chirality inversion through the node of automorphism where the space
where the space  is the normal group defined to the action created by the fermions in the transit electronphonon-electron, which is normed by the product of logarithms given by (7).
is the normal group defined to the action created by the fermions in the transit electronphonon-electron, which is normed by the product of logarithms given by (7).
Proof. By [7,8,23] and applying the integral to electrical current in their extension of the photon sources to electromagnetic interactions ([24], pp. 265-277).
Then is possible to control and direct the Eddy’s currents from the center of the reactor, producing the levitation effect searched in the design and development of the electromagnetic vehicle with the microscopic properties due to the macroscopic effects produced by the reactor characterizing the quantum densities of field  (to superconductor electrons
(to superconductor electrons  [3,25] (Figure 11)).
[3,25] (Figure 11)).
6.3. System Analysis: Energy Production and Reactor Auto-Sustainability Unit (More Experiments)
One of the aspects that will characterize our vehicle is their autonomy of functioning and self-sustainability, aspects that must be consequences of their physical principles that govern it and characterize. But it is a consequence of the relations of equivalence given through the electromagnetic field cohomology that can be reproduced with superconductive properties, as it is established in the Equivalence (3) considering their microscopic effects.
For other side, the relation of isomorphism between the different classified electromagnetic spaces in the Table 1, for the electromagnetic effects that appear in the creation of magnetic levitation and using cohomological classes as the given in the Equivalence (3), give place to that the orbits (orbital spaces) of the topological group that includes all this effects and electromagnetic phenomena (which is  [13,26-28]), derive relations of equivalence where the description “potential modulo calibrates” of the same fields on
[13,26-28]), derive relations of equivalence where the description “potential modulo calibrates” of the same fields on , or
, or , let be part of the magnetic twistor and their intensity of magnetic field go to the recycling of their thermal dissipation and voltages, being able to store and transform the above mentioned dissipation as a bonus (plus) of energy that will serve for the re-light of the vehicle in levitation and feeding of secondary systems.
, let be part of the magnetic twistor and their intensity of magnetic field go to the recycling of their thermal dissipation and voltages, being able to store and transform the above mentioned dissipation as a bonus (plus) of energy that will serve for the re-light of the vehicle in levitation and feeding of secondary systems.
A simple form to demonstrate the feedback of the magnetic field and their effects, is through a rectifier of current and the law of Faraday-Henri (Figure 13(a)).
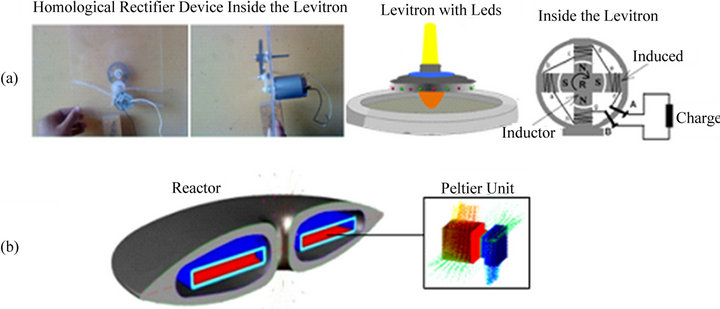
Figure 13. (a) Electromagnetism-temperature relation to the feedback energy inside of the reactor. Possibly let necessary involves the Peltier units to recover this heat energy and transducer her in electromagnetic energy; (b) Peltier plates inside the reactor unit.
Then the electromagnetic dissipation can be used like an energy feedback for the system.
7. Conclusions
The study of magnetic levitation necessarily establishes a relation of field-space (Figure 12) this last to particle level, that is inherent to the geometry of certain “orbital spaces” that are generated naturally by the super-currents and whose immediate effects are consequence of this relation that is established to quantum level (Abrikosov effect, Cooper effect, and more). Then the integral of the superconducting given in the Integral Orbital (2) determines the transit of the super-currents to quantum level establishing the action electron-phonon-electron [8,28] that can be obtained for condensation of a fermion flux whose macroscopic image produce the skin effect that is necessary cover or to the vehicle to create a opposite to the critical magnetic field Hcr, that must be expelled for the ship in their rotation ring situated inferiorly. This difference of magnetic-diamagnetic property contemplated in the Integral (1) and discussed in [1] is the electromagnetic analogous that is wanted to create for example, to the sustentation of a airplane with foundation in the aerodynamics, where the difference of pressures (a very big pressure below of an airplane and a little pressure in the top of the same one provoke their sustentation) create their sustentation. In our case, the elevation of our vehicle is not the sustentation of the same one, but yes their levitation or magnetic suspension.
The demonstrations realized along our work are directed to prove for electromagnetic homology from the topological point of view and of interactions of 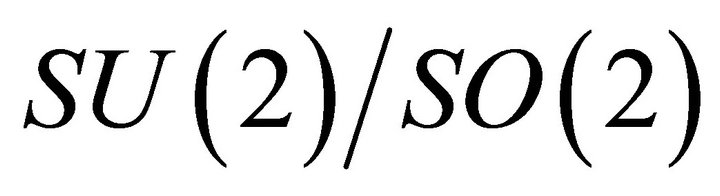 , of the existence of the Eddy currents to the diamagnetic effect that must interacts with Hcr, to produce the levitation, the creation of the magnetic twistor to the displacement (Figure 8) and the feedback and storing of energy to the self-sustainability of energy of our vehicle (Figure 14).
, of the existence of the Eddy currents to the diamagnetic effect that must interacts with Hcr, to produce the levitation, the creation of the magnetic twistor to the displacement (Figure 8) and the feedback and storing of energy to the self-sustainability of energy of our vehicle (Figure 14).

Figure 14. Direct piezoelectricity of some substances, like quartz, can generate potential differences of thousands of volts. In the piezo-electrical materials theory [29] there are crystal of high resonance that with the presence of magnetic field or electric field can to obtain a considerable electric field or magnetic field respectively. The feedback in the block diagram haves two levels of feedback; one is developed to the increasing of the supercurrent and Eddy currents. The other level or exterior circuit of the block diagram is developed to re-use the thermal dissipative energy produced for the magnetic field and voltage like a plus energy that cans useful to re-charge of the reactor. One time that again let use the reactor, this will begin with this plus energy stored in the crystal units.
This machine must be capable of generating large quantities of electric power without depending on any natural or artificial energy source (wind energy, hydraulic energy, solar energy, atomic energy of nuclear fission, etc) really only it will have to use a part of the electric energy that will produce herself. Like that we will have the vehicle that the humanity needs a vehicle with energy of one thousand years.
8. Acknowledgements
We thank to Demetrio Moreno-Àrcega, Master in L, Principal of TESCHA and Rodolfo Martìnez-Calles, B. L. sub-Director of Financing Department, TESCHA, the financial and moral support for this scientific publication.