Numerical Solution for Accelerated Rotating Disk in a Viscous Fluid ()
1. Introduction
The flow of an incompressible viscous fluid past an infinitely rotating disk was first studied by Von Karman [1] who reduced the necessary Navier-Stokes equations to self-similar form by means of some transformations and derived approximate solutions. Different physical situations were studied in this area by Dolidge [2], Sparrow & Gregg [3] and Benton [4]. Watson et al. [5] considered the flow past a decelerating porous rotating disk and they studied the effects of time dependent suction or injection velocity on the flow of a viscous fluid. Watson et al. [6] considered the two dimensional channel flow symmetrically driven by accelerating walls. Ariel [7] studied the problem of steady laminar flow of a second grade fluid near a rotating disk. The motion of an electrically conducting fluid film squeezed between two parallel disks in the presence of a transverse magnetic field was studied by Hamza [8]. MHD flow due to non coaxial rotations of an accelerated disk and a fluid at infinity was analyzed by Asghar et al. [9].
Unsteady flows are of importance from the practical point of view and full unsteady Navier-Stokes equations with all the unsteady, nonlinear and viscous terms are difficult to solve whereas exact solutions are rare. However, similarity solution to the governing equations is of special interest in case of fluid flow along a rotating disk. Wang [10] studied a viscous fluid between two parallel plates, which are being squeezed or separated with normal velocity proportional to 
and found similarity solutions of the unsteady Navier-Stocks equations. Ishizawa [11] derived a similarity solution to the case of the unsteady laminar flow between two parallel disks. Pop [12] investigated the problem of unsteady flow past a wall which starts impulsively to stretch from rest. Nazar et al. [13] investigated unsteady boundary layer flow due to a rotating fluid. Xu et al. [14] considered unsteady three dimensional MHD flow and heat transfer in boundary layer over an impulsively stretching plate.
Watson and Wang [15] solved the problem for decaleration of a rotating disk in a viscous fluid for the range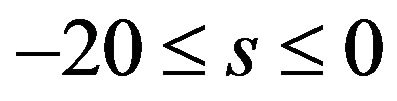
. They also viewed that similarity solution do not exist for 
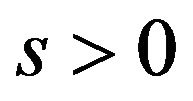which corresponds to the accelerated rotating disk. In the present work, the numerical solutions have been found for an accelerated 
rotating disk in a viscous fluid. The case 
corresponds to steady rotation of a disk in a fluid.
2. Mathematical Analysis
The fluid flow is unsteady and incompressible. u, v, w are velocity components in cylindrical polar coordinates (r, θz). The z-axis is the axis of rotation of the disk, with 
on the surface of the disk. The following similarity transformations are used:
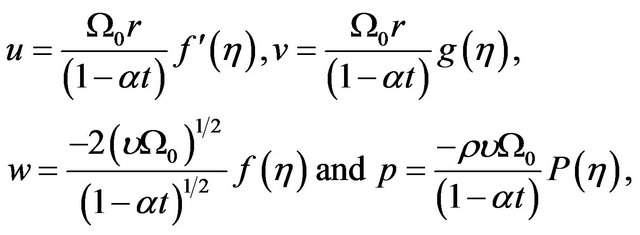(1)
where 
is the dimensionless variable, 
is non dimensional constant and 
is a positive constant. When
, the problem reduces to the case of the steady rotation of a disk in a fluid. We shall study the case when
. By using Equation (1), Navier-Stokes equations reduce to a set of nonlinear ordinary differential equations
(2)
(3)
where prime denote differentiation with respect to 
and 
is non-dimensional parameter which measures unsteadiness.
The associated boundary conditions are
(5)
Let 
(6)
The Equations (2) and (3) become:
(7)
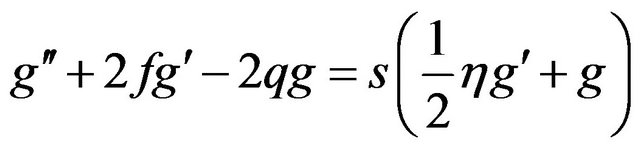(8)
The boundary conditions (5) take the form:
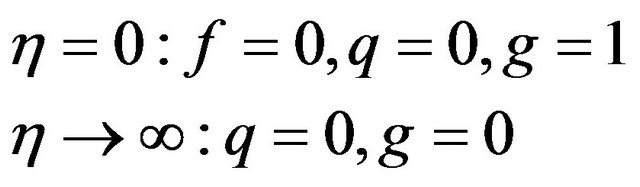(9)
In order to obtain the numerical solutions of nonlinear ordinary differential Equations (7) and (8), we approximate these equations by central difference approximation at a typical point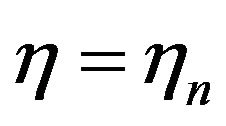 
of the interval
, we obtain
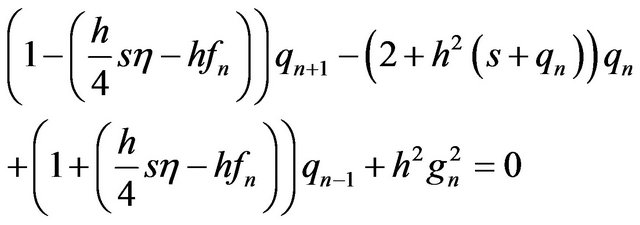(10)
(11)
where h denotes a grid size and Equation (6) is integrated numerically. Also, the symbols used denote 
and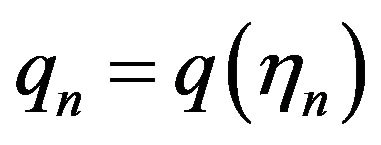
. For computational purpose, we shall replace the interval 
by 
where β is a sufficiently large.
3. Computational Procedure
Finite difference Equations (10) and (11) and the first order ordinary differential Equation (6) are solved simultaneously by using SOR method, Smith [16] and Simpson’s (1/3) rule, Gerald [17] with the formula given in Milne [18] respectively subject to the appropriate boundary conditions.
The order of the sequence of iterations is as follows:
1) The Equations (10) and (11) for the solution of q and g are solved subject to the following boundary conditions:
2) For the solution of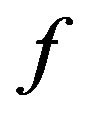
, we use the computed values q from above step in to Equation (6) and integrate by Simpson’s (1/3) rule subject to the following initial conditions:
3) The optimum value of the relaxation parameter 
is estimated, to accelerate the convergence of the SOR method.
4) The SOR procedure is terminated when the following criterion is satisfied for each of q and g:
where n denotes the number of iterations and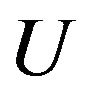 
stands for each of 
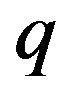and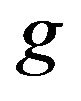
.
The above steps 1 to 4 are repeated for higher grid levels 
and
. The SOR procedure gives the solution of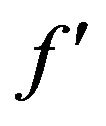 
and 
of order of accuracy 
due to second order finite differences used for finite-difference equations. While, the Simpson’s (1/3) rule gives the order of accuracy 
in the solution of f. Higher order accuracy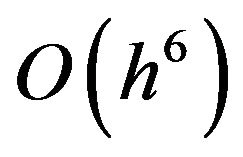 
on the basis of above solutions is achieved by using Richardson’s extrapolation, Burden [19].
4. Numerical Results and Discussion
The numerical results have been found for the values of parameter s for range
. In order to check the accuracy of the results, calculation have been made on three different grid sizes namely 
and 0.0125. The results for skin friction coefficient 
and torque 
are presented in Table 1. It is observed from the values given in the Table No. 1 that skin friction coefficient 
decreases with increasing values of s.
Also, the torque experienced by the disk 
becomes more negative with increasing values of s > 0. It means that rotating disk experiences increasing resistance with increasing values of s.
It is imperative to describe the effect of the parameter s on the flow pattern. So the graphical results of the velocity components have been exhibited in the Figures 1-3. Figure 1 shows the axial velocity distribution
. Figure 2 elucidates the circumferential velocity distribution
. The radial velocity distribution 
has been depicted in Figure 3. It is observed that all the velocity components decrease by increasing s.
The torque T experienced by the disk of radius R, may
Table 1. Data of skin friction coefficient & torque.
Figure 1. Graph of the axial velocity distribution 
for different values of s.
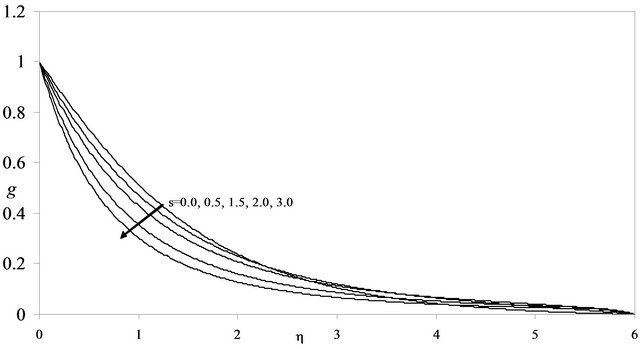
Figure 2. Graph of the circumferential velocity 
for different values of s.
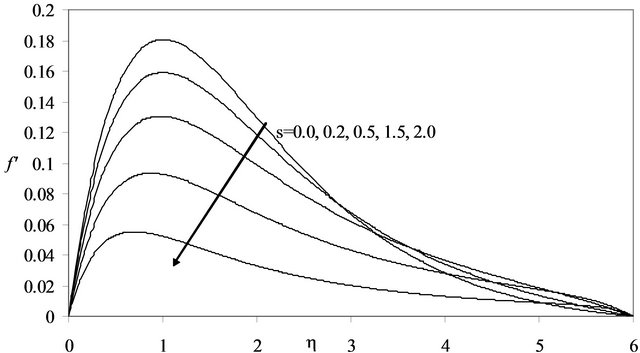
Figure 3. Graph of radial velocity distribution
for different values of s.
be written as:
For positive values of s, the rotating disk experiences a resistance, hence 
is negative as shown in Table 1.
NOTES