Three Dimensional Evolution of SN 1987A in a Self-Gravitating Disk ()
1. Introduction
The expansion of supernova remnant (SNR) is usually explained by the theory of the shock waves, as an example [1,2], which analyzes self-similar solutions with varying inverse power law exponents for the density profile of the advancing matter,  , and ambient medium,
, and ambient medium, . The SNRs conversely often present a weak departure from the circular symmetry, as an example, in SN 1006 1006 a ratio of 1.2 between maximum and minimum radius which has been measured, see [3] or great asymmetry as the triple ring of SN 1987A 1987a, see [4,5].
. The SNRs conversely often present a weak departure from the circular symmetry, as an example, in SN 1006 1006 a ratio of 1.2 between maximum and minimum radius which has been measured, see [3] or great asymmetry as the triple ring of SN 1987A 1987a, see [4,5].
The asymmetries of SNRs are hardly explained by the shock theory which is usually developed in spherical or planar symmetry. The presence of gradients in the density of the medium allows to explain such asymmetries when the conservation of the momentum is adopted. As an example an exponential decay allows to model SN1006 1006 and SN 1987A 1987a, see [6]. At the same time the various gradients that can be adopted such as Gaussian, power law and exponential do not have a precise physical basis. The auto-gravitating Maxwellian medium provides a gradient given by the secant law. In this paper we will answer the following questions.
• Is it possible to deduce an analytical formula for the temporal evolution of an SN in the presence of a vertical profile density as given by an ISD?
• Is it possible to deduce an equation of motion for SN with an adjustable parameter that can be found from a numerical analysis of the diameter—time relationship?
• Is it possible to simulate the appearance of the triple ring system of SN 1987A 1987a?
2. A Modified Thin Layer Approximation
The thin layer approximation with non cubic dependence (NCD), 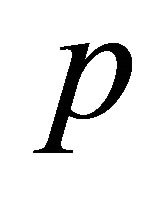 , in classical physics assumes that only a fraction of the total mass enclosed in the volume of the expansion accumulates in a thin shell just after the shock front. The global mass between 0 and
, in classical physics assumes that only a fraction of the total mass enclosed in the volume of the expansion accumulates in a thin shell just after the shock front. The global mass between 0 and 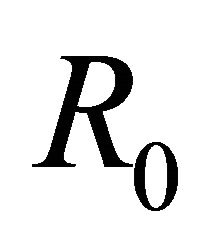 is
is 
where  is the density of the ambient medium. The swept mass included in the thin layer which characterizes the expansion is
is the density of the ambient medium. The swept mass included in the thin layer which characterizes the expansion is
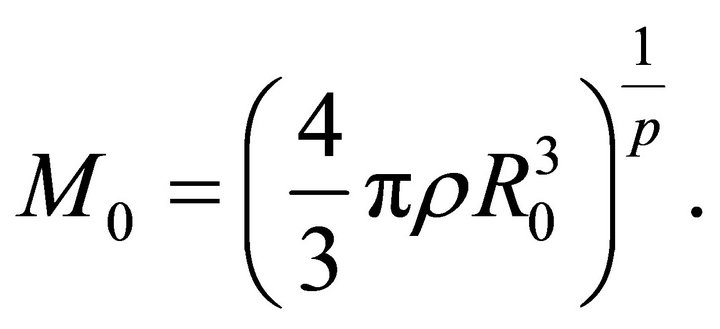 (1)
(1)
The mass swept between 0 and 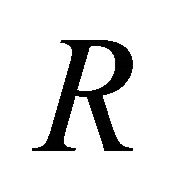 is
is
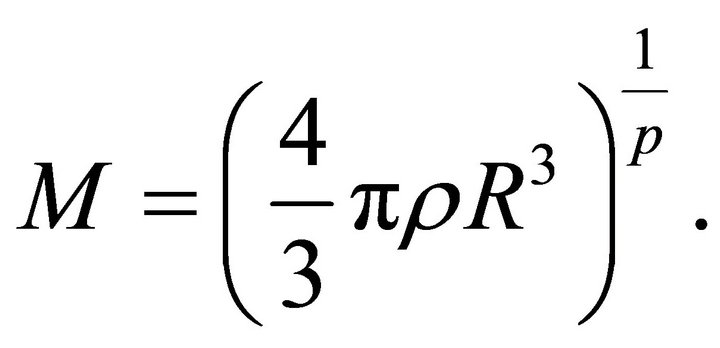 (2)
(2)
The conservation of radial momentum requires that, after the initial radius ,
,
 (3)
(3)
where  and
and 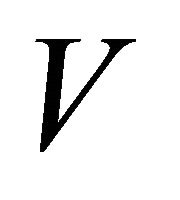 are the radius and velocity of the advancing shock. The velocity is
are the radius and velocity of the advancing shock. The velocity is
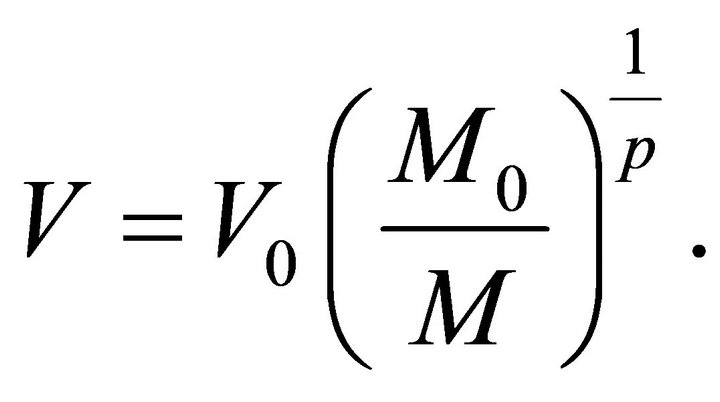 (4)
(4)
The velocity as a function of the radius when the expansion starts at the origin of the coordinates is:
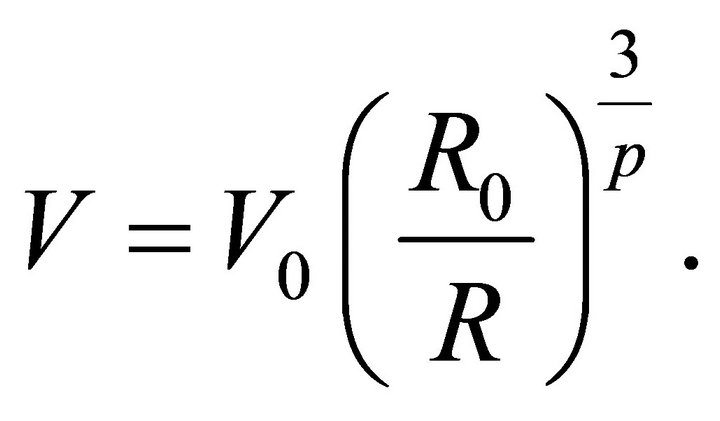 (5)
(5)
The velocity can be expressed as
 (6)
(6)
and the integration between ,
,  and
and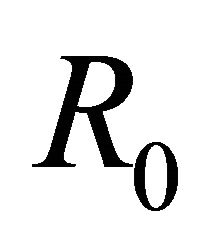 ,
, 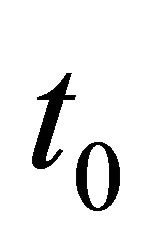 gives
gives
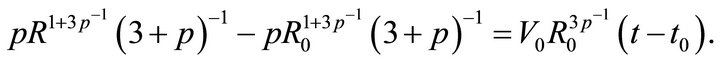 (7)
(7)
We solve the previous equation for  and we obtain
and we obtain
 (8)
(8)
The velocity is:
 (9)
(9)
where


Equation (8) can also be solved with a solution of type ,
, 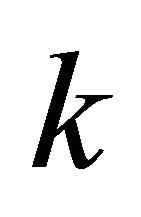 being a constant, and the asymptotic result is:
being a constant, and the asymptotic result is:
 (10)
(10)
The asymptotic solution for the velocity is
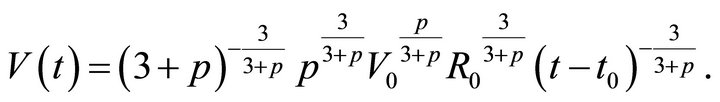 (11)
(11)
3. Asymmetrical Law of Motion with NCD
Given the Cartesian coordinate system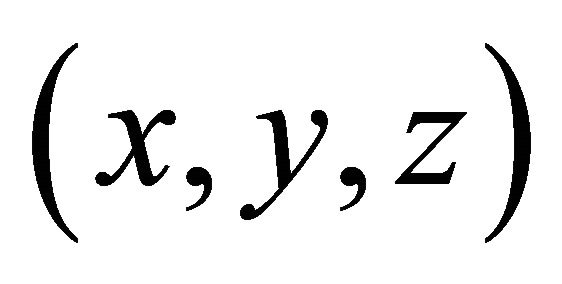 , the plane
, the plane 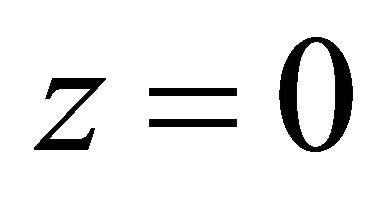 will be called the equatorial plane,
will be called the equatorial plane,  , where
, where  is the latitude angle which has range
is the latitude angle which has range , and
, and 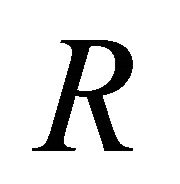 is the distance from the origin. In our framework, the polar angle of the spherical coordinate system is
is the distance from the origin. In our framework, the polar angle of the spherical coordinate system is . Here we adopt the density profile of a thin self-gravitating disk of gas which is characterized by a Maxwellian distribution in velocity and distribution which varies only in the z-direction (ISD). The number density distribution is
. Here we adopt the density profile of a thin self-gravitating disk of gas which is characterized by a Maxwellian distribution in velocity and distribution which varies only in the z-direction (ISD). The number density distribution is
 (12)
(12)
where  is the density at
is the density at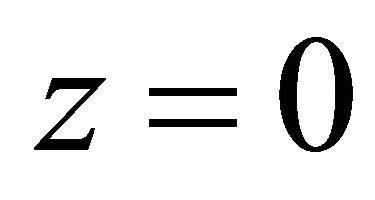 ,
, 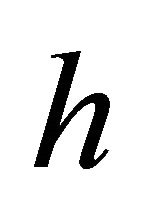 is a scaling parameter and
is a scaling parameter and 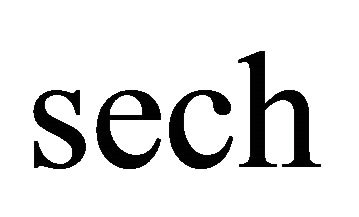 is the hyperbolic secant ([7,8]). On assuming that the expansion starts at
is the hyperbolic secant ([7,8]). On assuming that the expansion starts at , we can write
, we can write  and therefore
and therefore
 (13)
(13)
where  is the radius of the advancing shell.
is the radius of the advancing shell.
The 3D expansion that starts at the origin of the coordinates will be characterized by the following properties
• Dependence of the momentary radius of the shell on the polar angle  that has a range
that has a range .
.
• Independence of the momentary radius of the shell from , the azimuthal angle in the x-y plane, that has a range
, the azimuthal angle in the x-y plane, that has a range .
.
The mass swept,  , along the solid angle
, along the solid angle , between 0 and
, between 0 and 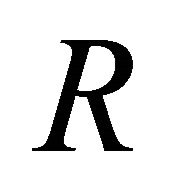 is
is
 (14)
(14)
where
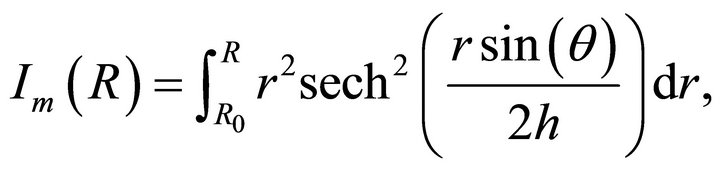 (15)
(15)
where  is the initial radius and
is the initial radius and 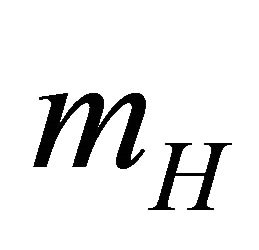 the mass of the hydrogen. The integral is
the mass of the hydrogen. The integral is

 (16)
(16)
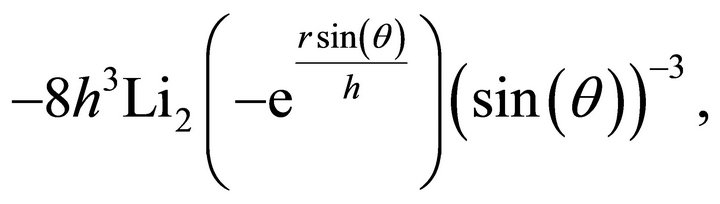 (17)
(17)
where
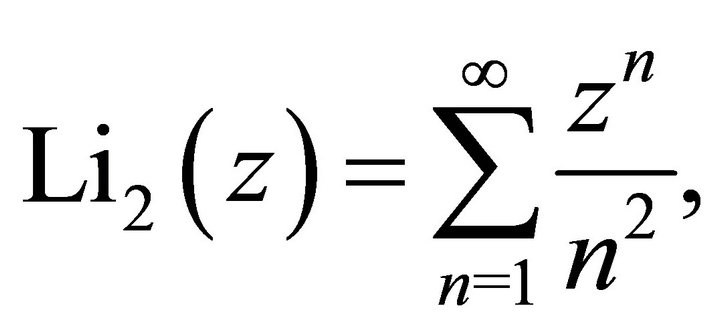 (18)
(18)
is the dilogarithm, see [9-11].
The conservation of the momentum gives
 (19)
(19)
where 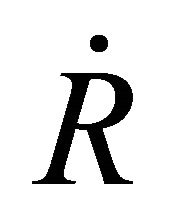 is the velocity at
is the velocity at 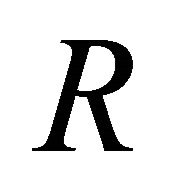 and
and  is the initial velocity at
is the initial velocity at 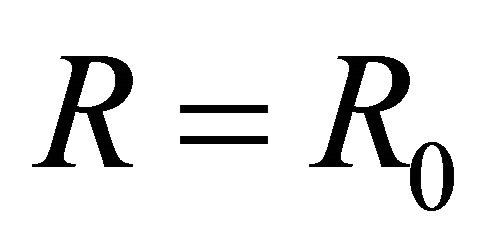 where
where 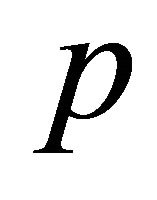 is the NCD parameter. This means that only a fraction of the total mass enclosed in the volume of the expansion accumulates in a thin shell just after the shock front. The emission of photons produces losses in the momentum carried by the advancing shell here assumed to be proportional to
is the NCD parameter. This means that only a fraction of the total mass enclosed in the volume of the expansion accumulates in a thin shell just after the shock front. The emission of photons produces losses in the momentum carried by the advancing shell here assumed to be proportional to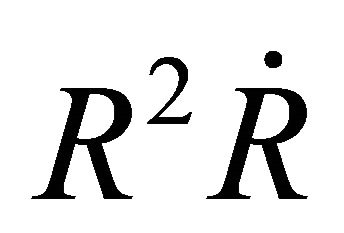 . The generalized conservation law is now
. The generalized conservation law is now
 (20)
(20)
where 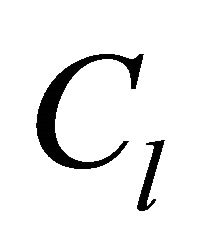 is a constant. At the moment of writing is not possible to deduce the parameter
is a constant. At the moment of writing is not possible to deduce the parameter  which controls the quantity of momentum carried away by the photons due to the presence of the parameter
which controls the quantity of momentum carried away by the photons due to the presence of the parameter  which controls the quantity of swept mass during the expansion. According to the previous generalized Equation (20) an analytical expression for
which controls the quantity of swept mass during the expansion. According to the previous generalized Equation (20) an analytical expression for  can be found but it is complex and therefore we omit it. In this differential equation of the first order in
can be found but it is complex and therefore we omit it. In this differential equation of the first order in 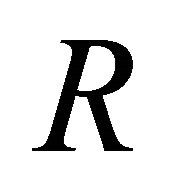 the variable can be separated and the integration term by term gives
the variable can be separated and the integration term by term gives
 (21)
(21)
where  is the time and
is the time and 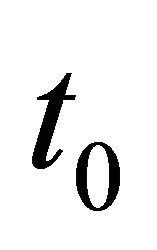 the time at
the time at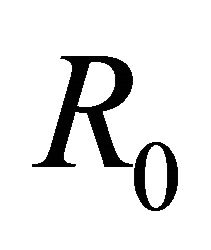 . We therefore have an equation of the type
. We therefore have an equation of the type
 (22)
(22)
where  has an analytical but complex form. In our case in order to find the root of the nonlinear Equation (22) the FORTRAN SUBROUTINE ZRIDDR from [12] has been used.
has an analytical but complex form. In our case in order to find the root of the nonlinear Equation (22) the FORTRAN SUBROUTINE ZRIDDR from [12] has been used.
The physical units have not yet been specified, 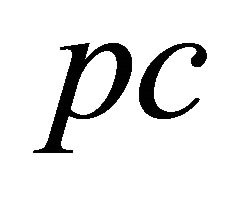 for length and
for length and  for time are perhaps an acceptable astrophysical choice. On adopting the previous units, the initial velocity
for time are perhaps an acceptable astrophysical choice. On adopting the previous units, the initial velocity 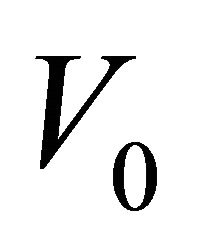 is expressed in pc/yr and should be converted into
is expressed in pc/yr and should be converted into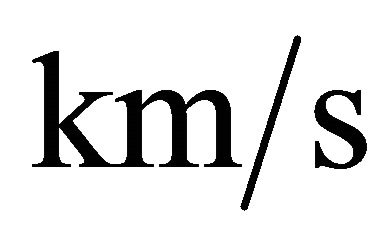 ; this means that V0 = 1.020738 × 10−6V1 where
; this means that V0 = 1.020738 × 10−6V1 where 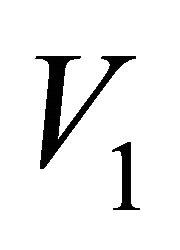 is the initial velocity expressed in
is the initial velocity expressed in .
.
4. Application to SN 1987A
4.1. The Simulation
The SN 1987A exploded in the Large Magellanic Cloud in 1987. The observed image is complex and we will follow the nomenclature of [13] which distinguish between torus only, torus +2 lobes and torus +4 lobes. In particular we concentrate on the torus which is characterized by a distance from the center of the tube and the radius of the tube. Table 2 of [13] reports the relationship between distance of the torus in arcsec and time since the explosion in days. Figure 3 in [14] reports diameter in pc versus year when the counting pixels is adopted. Table 1 reports the data used in the simulation, Figures 1 and 2 report the diameter and the velocity in the equatorial plane respectively as well the observational data as found by the counting pixels method, see [14]. Figure 3 reports the asymmetric expansion in a section crossing the center, Figures 4 and 5 report the radius and the velocity respectively as a function of the position angle θ.
The swept mass in our model is not constant but varies with the value of latitude, see Figure 6.
4.2. The Image
We assume that the emissivity is proportional to the number density.
 (23)
(23)
where  is the emission coefficient and
is the emission coefficient and 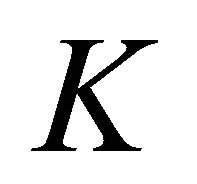 is a constant function. This can be the case of synchrotron radiation in presence of an isotropic distribution of electrons with a power law distribution in energy,
is a constant function. This can be the case of synchrotron radiation in presence of an isotropic distribution of electrons with a power law distribution in energy, 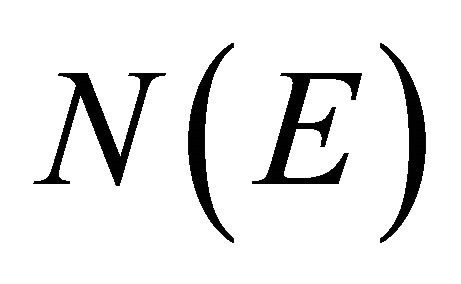 ,
,

Table 1. Numerical value of the parameters of the simulation for SN 1987A.
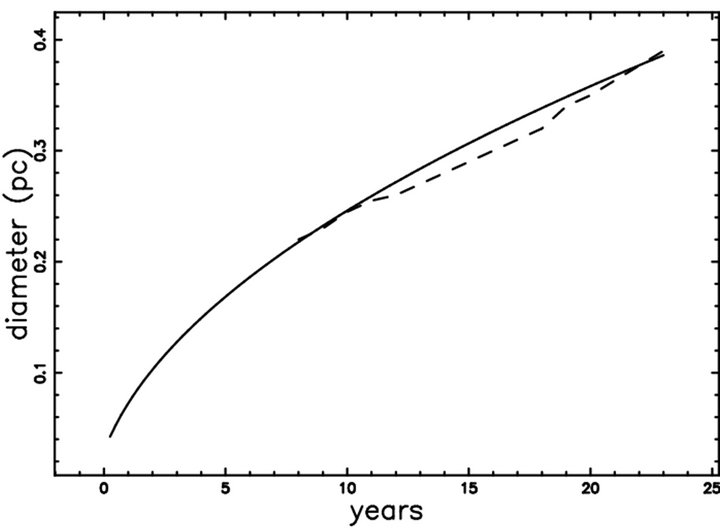
Figure 1. Diameter as a function of time for a self-gravitating medium (full line) when θ = 0.001 (equatorial plane) and astronomical data of torus only as extracted from Figure 3 in [14] (dashed line). Physical parameters as in Table 1.
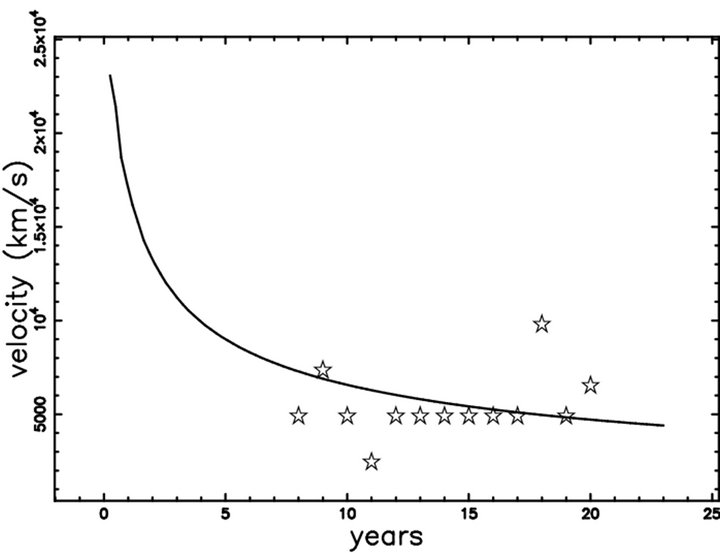
Figure 2. Velocity as a function of time for a self-gravitating medium (full line) when θ = 0.001 (equatorial plane) and astronomical data of torus only as extracted from Figure 3 in [14] (empty stars). Physical parameters as in Table 1.

Figure 3. Section of SN 1987A in the x-z plane. The horizontal and vertical axis are in pc. Physical parameters as in Table 1.

Figure 4. Radius in pc of SN 1987A as a function of the position angle in degrees for a self-gravitating medium. Physical parameters as in Table 1.

Figure 5. Velocity in km/s of SN 1987A as a function of the position angle in degrees for a self-gravitating medium. Physical parameters as in Table 1.

Figure 6. Swept mass of SN 1987A in arbitrary units as a function of the position angle in degrees, for a self-gravitating medium. Physical parameters as in Table 1.
 (24)
(24)
where 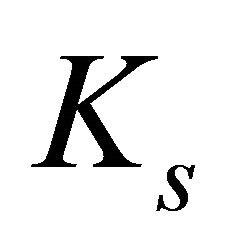 is a constant. The source of synchrotron luminosity is assumed here to be the flux of kinetic energy,
is a constant. The source of synchrotron luminosity is assumed here to be the flux of kinetic energy, 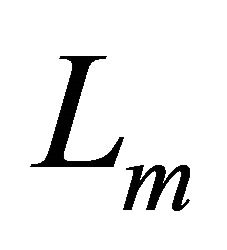 ,
,
 (25)
(25)
where  is the considered area, see formula (A28) in [15]. In our case
is the considered area, see formula (A28) in [15]. In our case , which means
, which means
 (26)
(26)
where  is the instantaneous radius of the SNR and
is the instantaneous radius of the SNR and 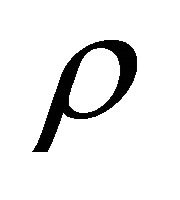 is the density in the advancing layer in which the synchrotron emission takes place. The total observed luminosity can be expressed as
is the density in the advancing layer in which the synchrotron emission takes place. The total observed luminosity can be expressed as
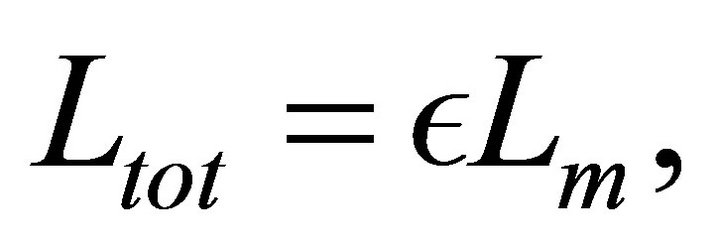 (27)
(27)
where  is a constant of conversion from the mechanical luminosity to the total observed luminosity in synchrotron emission.
is a constant of conversion from the mechanical luminosity to the total observed luminosity in synchrotron emission.
The numerical algorithm which allows us to build a complex image is now outlined.
• An empty (value = 0) memory grid  which contains
which contains  pixels is considered
pixels is considered
• We first generate an internal 3D surface by rotating the ideal image  around the polar direction and a second external surface at a fixed distance
around the polar direction and a second external surface at a fixed distance  from the first surface. As an example, we fixed
from the first surface. As an example, we fixed , where
, where  is the momentary radius of expansion. The points on the memory grid which lie between the internal and external surfaces are memorized on
is the momentary radius of expansion. The points on the memory grid which lie between the internal and external surfaces are memorized on  with a variable integer number according to formula (26) and density
with a variable integer number according to formula (26) and density  proportional to the swept mass, see Figure 6.
proportional to the swept mass, see Figure 6.
• Each point of 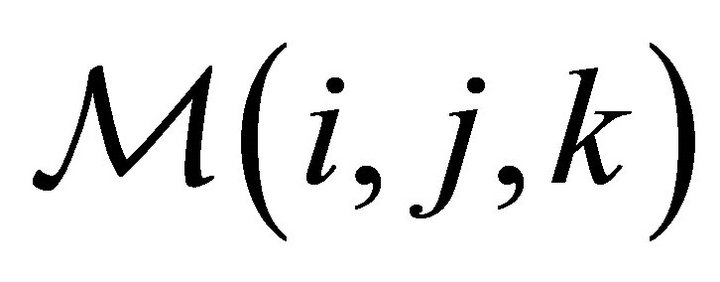 has spatial coordinates
has spatial coordinates  which can be represented by the following
which can be represented by the following  matrix,
matrix,  ,
,
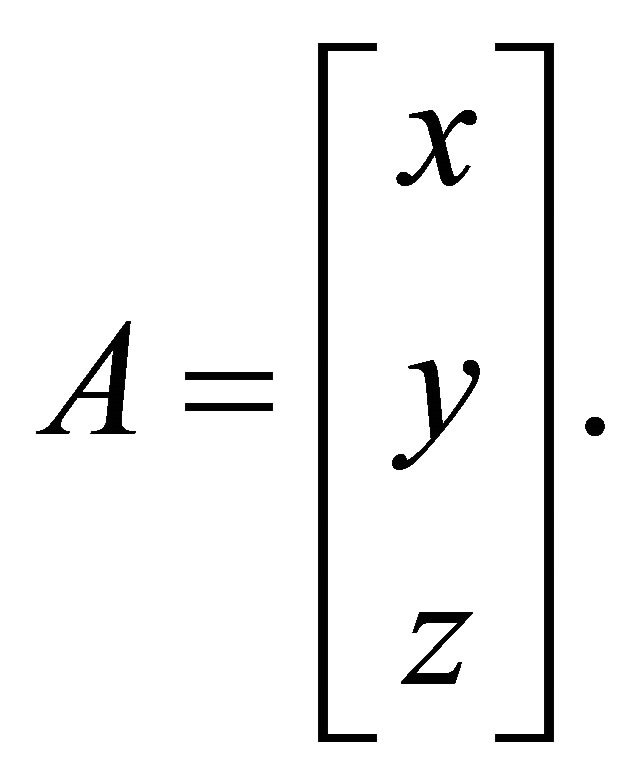 (28)
(28)
The orientation of the object is characterized by the Euler angles 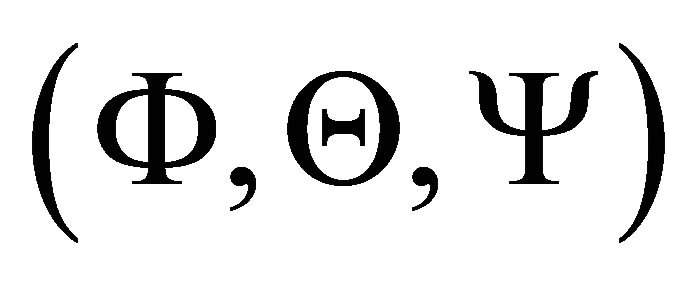 and therefore by a total
and therefore by a total 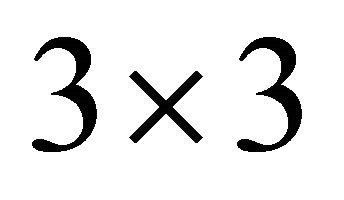 rotation matrix,
rotation matrix, 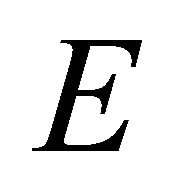 , see [16]. The matrix point is represented by the following
, see [16]. The matrix point is represented by the following  matrix,
matrix,  ,
,
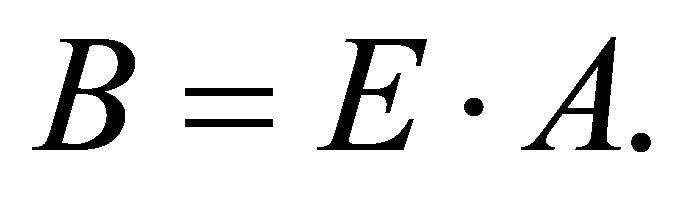 (29)
(29)
• The intensity map is obtained by summing the points of the rotated images along a particular direction.
• The effect of the insertion of a threshold intensity,  , given by the observational techniques, is now analyzed. The threshold intensity can be parametrized to
, given by the observational techniques, is now analyzed. The threshold intensity can be parametrized to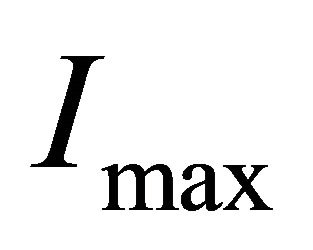 , the maximum value of intensity characterizing the map.
, the maximum value of intensity characterizing the map.
The image of SN 1987A having polar axis along the z-direction, is shown in Figure 7. The image for a realistically rotated SN 1987A is shown in Figure 8 and a comparison should be done with the observed triple ring system as reported in Figure 1 of [5] where the outer lobes are explained by light-echo effects.
Two cuts of intensity are reported in Figure 9, and is interesting to note that the polar cut is characterized by four spikes. Here conversely the two outer lobes are explained by the image theory applied to a thin advancing shell.
5. Conclusions
5.1. Law of Motion
The presence of a thin self-gravitating disk of gas which is characterized by a Maxwellian distribution in velocity

Figure 7. Map of the theoretical intensity of SN 1987A in the presence of a self-gravitating medium. Physical parameters as in Table 1. The three Euler angles characterizing the orientation are Φ = 180˚, Θ = 90˚ and Ψ = 0˚. This combination of Euler angles corresponds to the rotated image with the polar axis along the z-axis.

Figure 8. Model map of SN 1987A 1987a rotated in accordance with the observations, for a self-gravitating medium. Physical parameters as in Table 1. the orientation of the observer are Φ = 105˚, Θ = 55˚ and Ψ = −165˚. This combination of Euler angles corresponds to the observed image. In this map .
.
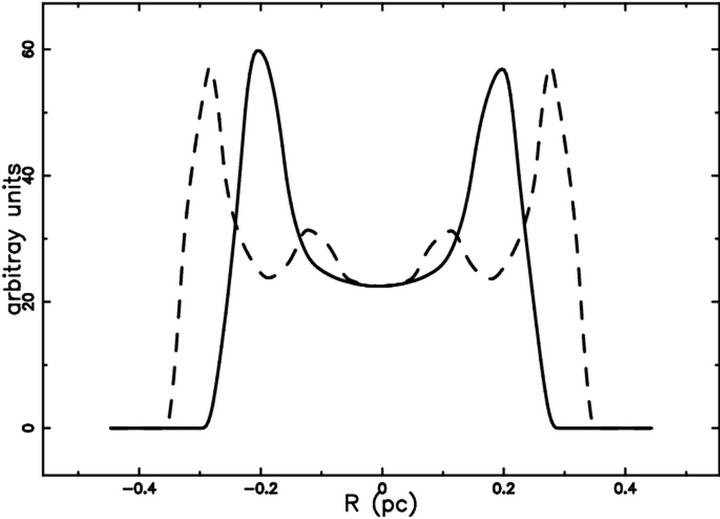
Figure 9. Two cuts of the model intensity across the center of the realistically rotated SN 1987A: equatorial cut (full line) and polar cut (dotted line).
and distribution of density which varies only in the zdirection produces an axial symmetry in the temporal evolution of a SN. The resulting Equation (22) has a form which can be solved numerically. The results depend from the chosen latitude and more precisely the radius as function of the time is maximum at the poles and minimum at the equator. A comparison between the observed radius and the velocity at the equator, see [14], gives an agreement of 92% for the theoretical versus observed radius and of 62% for the theoretical versus observed velocity. This is the first result that confirms the rationality of the method here presented. The momentum carried away by the photons can be modeled by introducing a reasonable form for the photon’s losses, see Equation (20).
5.2. Images
The combination of different processes such as the bipolar 3D shape , the thin layer approximation (which means advancing layer having thickness  of the momentary radius), the conversion of the rate of kinetic energy into luminosity and the observer’s point of view allows to simulate the observed triple ring morphology of SN 1987A 1987a. The framework here adopted is similar to that adopted to explain the asymmetric shape of the nebula around
of the momentary radius), the conversion of the rate of kinetic energy into luminosity and the observer’s point of view allows to simulate the observed triple ring morphology of SN 1987A 1987a. The framework here adopted is similar to that adopted to explain the asymmetric shape of the nebula around  -Carinae (Homunculus), see [17,18]. We therefore suggest that the astronomers should map the non rotated radius and velocity of SN 1987A 1987a following the outlines of Table 1 in [19]. These maps, if realized, will produce a clearer framework for the observed triple ring. The suggested similarity of the triple ring system of SN 1987A 1987a with
-Carinae (Homunculus), see [17,18]. We therefore suggest that the astronomers should map the non rotated radius and velocity of SN 1987A 1987a following the outlines of Table 1 in [19]. These maps, if realized, will produce a clearer framework for the observed triple ring. The suggested similarity of the triple ring system of SN 1987A 1987a with  -Carinae is the second result which ensures the rationality of the method here presented.
-Carinae is the second result which ensures the rationality of the method here presented.