Fuzzy Set Based Models and Methods of Decision Making and Power Engineering Problems ()
1. Introduction
Diverse types of uncertainty [1] are commonly encountered in a wide range of optimization and decision making problems related to planning and operation of power systems and subsystems. The incorporation of the uncertainty factor in the construction of mathematical models serves for increasing their adequacy and, as a result, the credibility and factual efficiency of decisions based on their analysis. Investigations of recent years show the benefits of applying fuzzy set theory [2,3] to deal with diverse types of uncertainty. Its use offers advantages of both a fundamental nature (the possibility of obtaining more effective, less “cautious” solutions as well as considering simultaneously different types of uncertainty) and a computational character [4,5]
The uncertainty of goals is an essential kind of uncertainty related to a multicriteria nature of many power engineering problems. Issues related to the classification of situations which need the use of a multicriteria approach are discussed in [6]. However, from the substantial point of view, it is possible to identify the following classes of situations [5,7] which need the application of a multicriteria approach:
• problems whose solution consequences cannot be estimated on the basis of a single criterion: these problems are associated with the analysis of models which include economic as well as physical indices (when alternatives cannot be reduced to comparable form) and also by the need to consider indices whose cost estimations are hampered or impossible;
• problems that may be solved on the basis of a single criterion or several criteria. However, if the uncertainty of information does not permit one to obtain unique solutions, it is possible to solve these problems, applying additional criteria, including criteria of qualitative character (whose utilization is based on knowledge, experience, and intuition of involved experts).
Therefore, two classes of models, so-called 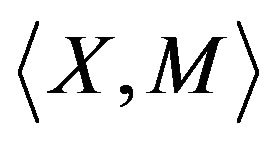 models and
models and  models may be constructed [5,7]. The present paper briefly describes these models as well as methods of their analysis (based on the use of the Bellman-Zadeh approach to decision making in a fuzzy environment and the application of techniques involving fuzzy preference modeling, respectively).
models may be constructed [5,7]. The present paper briefly describes these models as well as methods of their analysis (based on the use of the Bellman-Zadeh approach to decision making in a fuzzy environment and the application of techniques involving fuzzy preference modeling, respectively).
The paper includes a review of the authors’ results related to using 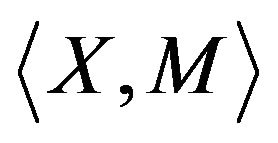 and
and 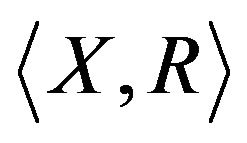 models and methods of their analysis to solve diverse problems of power systems and subsystems. The recent results associated with their utilization for the allocation of reactive power sources in distribution systems and the prioritization in maintenance planning in distribution systems are considered in more detail.
models and methods of their analysis to solve diverse problems of power systems and subsystems. The recent results associated with their utilization for the allocation of reactive power sources in distribution systems and the prioritization in maintenance planning in distribution systems are considered in more detail.
2. 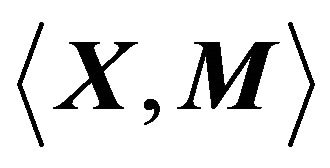 Models, Their Analysis, and Applications
Models, Their Analysis, and Applications
When analyzing  models, a vector of objective functions
models, a vector of objective functions 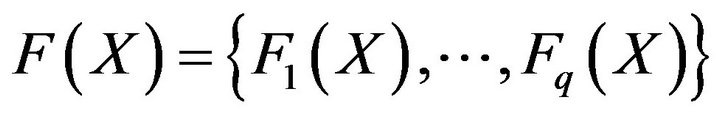 is considered, and the problem consists of optimizing all of them, i.e.,
is considered, and the problem consists of optimizing all of them, i.e.,
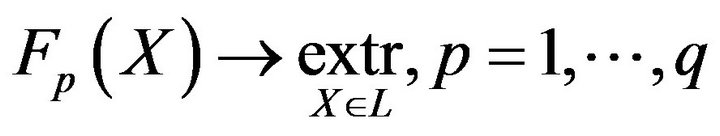 (1)
(1)
where 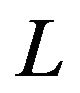 is a feasible region in
is a feasible region in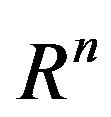 .
.
The first step in solving the problem (1) is associated with determining a set of Pareto solutions 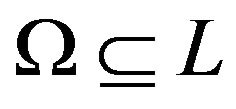 [8]. This step is useful; however it does not permit one to obtain unique solutions. It is necessary to choose a particular Pareto solution on the basis of information of a decision maker (DM). There are three approaches to using this information [5]: a priori, a posteriori, and adaptive. The most preferable approach is the adaptive one. When using this approach, the procedure of successive improving the solution quality is realized as a transition from
[8]. This step is useful; however it does not permit one to obtain unique solutions. It is necessary to choose a particular Pareto solution on the basis of information of a decision maker (DM). There are three approaches to using this information [5]: a priori, a posteriori, and adaptive. The most preferable approach is the adaptive one. When using this approach, the procedure of successive improving the solution quality is realized as a transition from 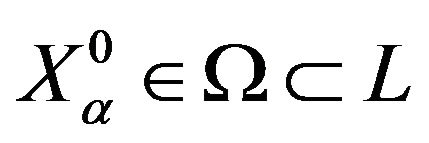 to
to 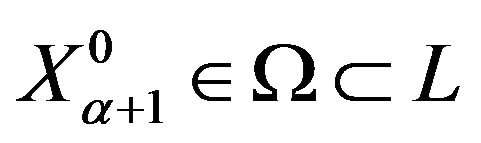 with considering information
with considering information 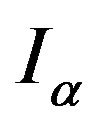 of DM (
of DM (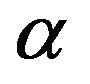 is a number step of the decision making process). The solution search may be presented in the following form:
is a number step of the decision making process). The solution search may be presented in the following form:
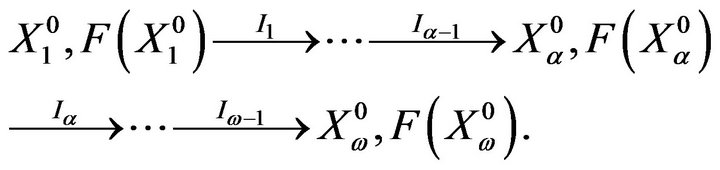 (2)
(2)
The process (2) serves for two types of adaptation: computer to preferences of DM and DM to the problem. The first type of adaptation is based on information received from DM. The second type of adaptation is realized as a result of carrying out several steps
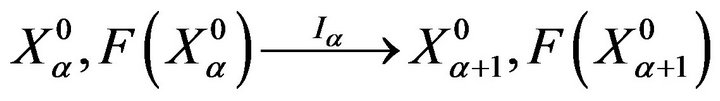 which permit DM to understand the correlation between own needs and possibilities of their satisfaction by the model (1).
which permit DM to understand the correlation between own needs and possibilities of their satisfaction by the model (1).
When analyzing multiobjective problems, it is necessary to solve some questions related to normalizing objective functions, selecting principles of optimality, and considering priorities of objective. Their solution and, therefore, development of multiobjective methods is carried out in the following directions [9-11]: scalarization techniques, imposing constraints on objectives, utility function method, goal programming, and using the principle of guaranteed result. Without discussing these directions, it is necessary to point out that an important question in multiobjective analysis is the solution quality. It is considered high if levels of satisfying objective functions are equal or close to each other (harmonious solutions) if we do not differentiate their importance [5,12] (other directions may lead to solutions with high levels of satisfying some objectives that is reached by low levels of satisfying other objectives, for instance [12,13]). From this point of view, it should be recorded the validity and advisability of the direction related to the principle of guaranteed result.
The lack of clarity in the concept of “optimal solution” is the basic methodological complexity in solving multiobjective problems. When applying the Bellman-Zadeh approach to decision making in a fuzzy environment [14], this concept is defined with reasonable validity: the maximum degree of implementing goals serves as a criterion of optimality. This conforms to the principle of guaranteed result and provides constructive lines in obtaining harmonious solutions. The use of the Bellman-Zadeh approach permits one to realize an effective (from the computational standpoint) as well as rigorous (from the standpoint of obtaining solutions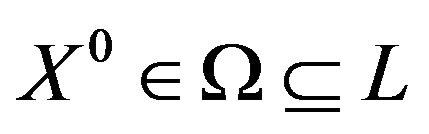 ) method of analyzing multicriteria models [5,7]. Finally, its use allows one to preserve a natural measure of uncertainty in decision making and to consider indices, criteria, and constraints of qualitative character.
) method of analyzing multicriteria models [5,7]. Finally, its use allows one to preserve a natural measure of uncertainty in decision making and to consider indices, criteria, and constraints of qualitative character.
When using the Bellman-Zadeh approach, each objective function  is replaced by a fuzzy set
is replaced by a fuzzy set
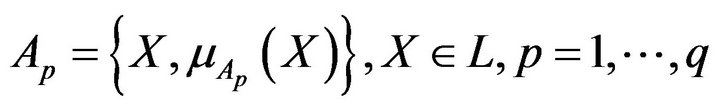 (3)
(3)
where  is a membership function of
is a membership function of 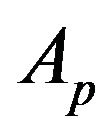 [2,3].
[2,3].
A fuzzy solution  with setting up the fuzzy sets (3)
with setting up the fuzzy sets (3)
is obtained as a result of the intersection 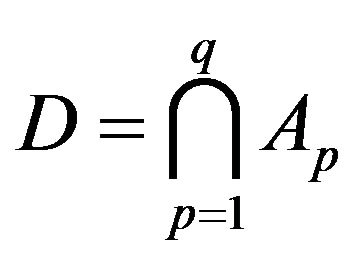
with a membership function
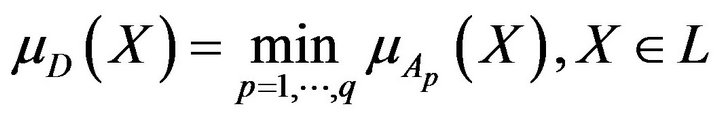 . (4)
. (4)
Its use permits one to obtain the solution proving the maximum degree
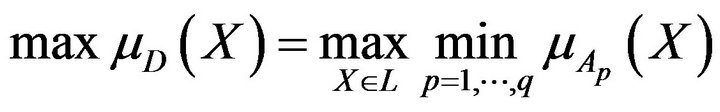 (5)
(5)
of belonging to the fuzzy solution  and reduced the problem (1) to
and reduced the problem (1) to
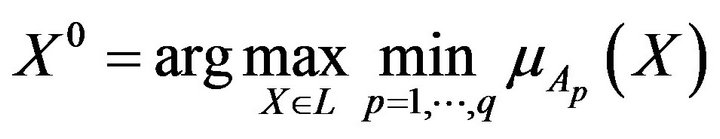 . (6)
. (6)
The use of (6) requires to build membership functions
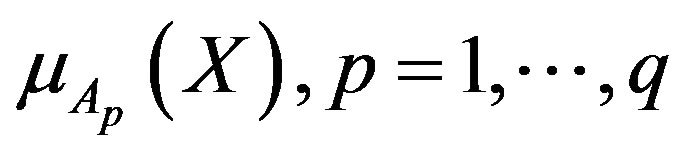 reflecting a degree of achieving
reflecting a degree of achieving
“own” optima by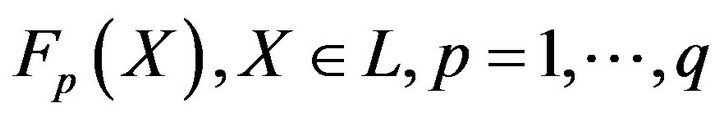 . This condition is satisfied by the use of membership functions
. This condition is satisfied by the use of membership functions
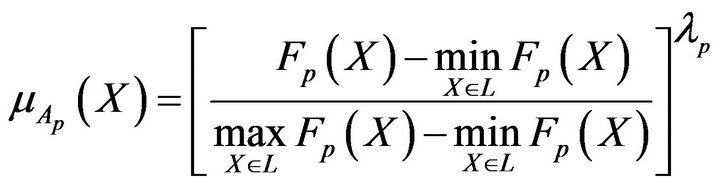 (7)
(7)
for maximized objective functions or by the use of membership functions
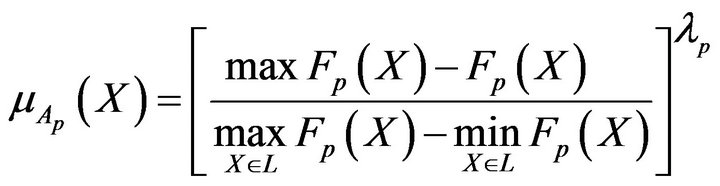 (8)
(8)
for minimized objective functions. In (7) and (8), 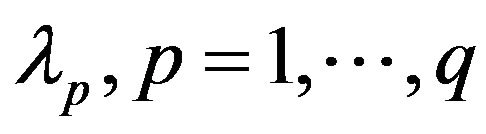 are importance factors for the corresponding objective functions (they are not to be normalized because it is important the relationship between different
are importance factors for the corresponding objective functions (they are not to be normalized because it is important the relationship between different  but not their absolute values).
but not their absolute values).
The construction of (7) or (8) demands the solution of the following problems:
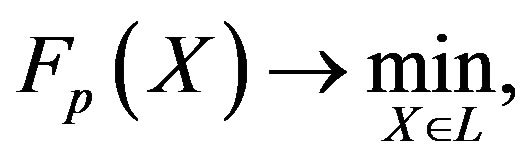 (9)
(9)
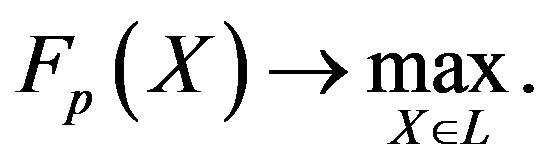 (10)
(10)
Thus, the solution of the problem (1) on the basis of the Bellman-Zadeh approach demands analysis of 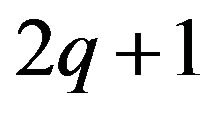 monocriteria problems (9), (10), and (5), respectively.
monocriteria problems (9), (10), and (5), respectively.
Since 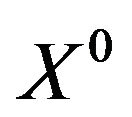 is to belong to
is to belong to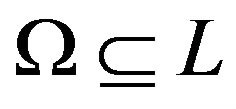 , it is necessary to build
, it is necessary to build
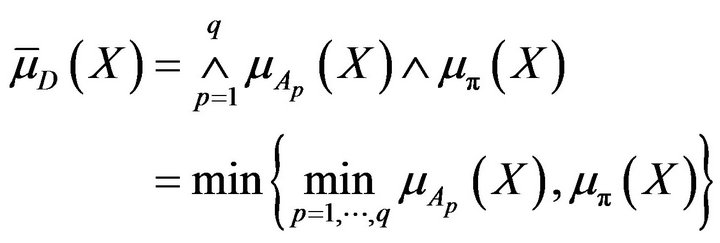 (11)
(11)
where 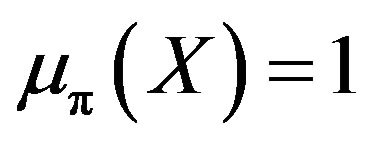 if
if 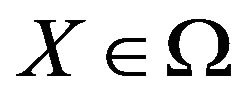 and
and 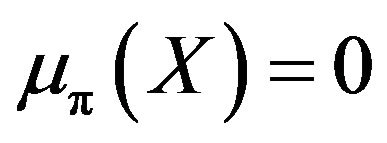 if
if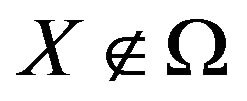 .
.
Finally, the existence of additional conditions (indices, criteria or constraints) of qualitative character, defined by linguistic variables [2,3], reduces (6) to
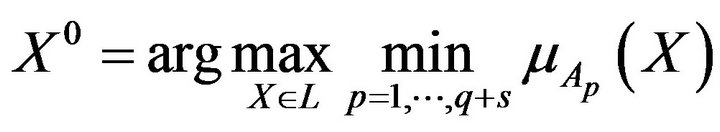 (12)
(12)
where 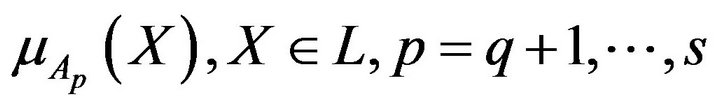 are membership functions of fuzzy values of linguistic variables which reflect these additional conditions.
are membership functions of fuzzy values of linguistic variables which reflect these additional conditions.
There are theoretical bases (for example, [15]) of the validity of applying min operator in (4)-(6). However, there exist several families of aggregation operators [2,16] that may be used in place of min operator. Considering this, it is possible to generalize (4) as follows:
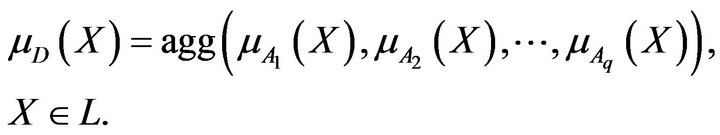 (13)
(13)
Despite that some properties of the aggregation operators have been established, there is no clear and intuitive interpretation of these properties, nor unifying interpretation of the operators themselves [16]. It is possible to state the following question: among many types of aggregation operators, how is one selected, which is adequate for a particular problem? Although some selection criteria are suggested in [2], the majority of them deal with empirical fit. Thus, it is possible to assert that the selection of the operators, in large measure, is based on experience. Considering this, below we discuss computing experiments with using not only min operators but product operator as well. The last operator has found wide applications in solving decision making problems, reduces (4) to
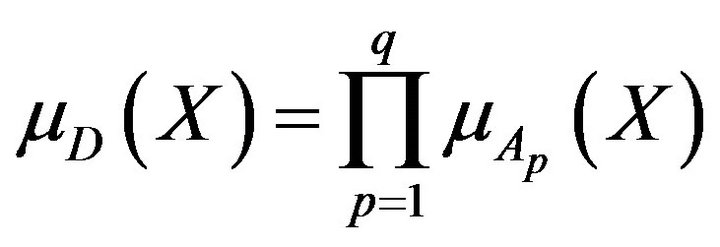 (14)
(14)
and permits one to construct the problem
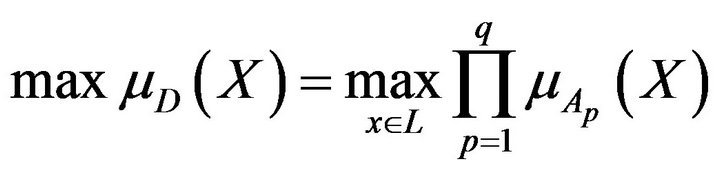 (15)
(15)
to find
 (16)
(16)
2.1. Power and Energy Shortage Allocation as Applied to Load Management
The statement of the problem of multicriteria allocation of resources or their shortages (these problems are equivalent from the general, mathematical, and information points of view) among consumers supposes the possibility to use diverse types of objective functions (linear, fractional, quadratic, etc. [17]) in (1) defined in a feasible region
 (17)
(17)
where 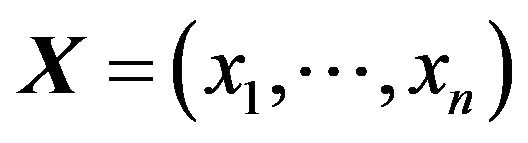 is a vector of limitations (for definiteness) for consumers,
is a vector of limitations (for definiteness) for consumers,  is a permissible value of limitation for the ith consumer,
is a permissible value of limitation for the ith consumer,  is a total value of limitations for all involved consumers.
is a total value of limitations for all involved consumers.
A general scheme for solving the problem formalized within the framework of the model (1), (17) is given in [5]. It has served for developing an adaptive interactive decision making system AIDMS1.
The problems of power and energy shortage allocation are of a fundamental importance in a family of load management problems. They are to be analyzed not only from the economical and technological, but also from social and ecological points of view. Besides, when solving these problems, it is necessary to account for considerations of creating incentive influences for consumers. Taking this into account, methods of power and energy shortage allocation, based on fundamental principles of allocating resources have drawbacks [18]. Their overcoming is possible by formulating and solving the problems within the framework of multiobjective models. This permits one to consider and to minimize diverse consequences of shortage allocation and to create incentive influences for consumers (the first attempts to apply the models (1), (17) were associated with the necessity to overcome the situation in the USSR energy sector emerged after the Chernobyl accident).
A substantial analysis of problems of power and energy shortage allocation, systems of economics management, and real, readily available reported and planned information has permitted the construction of a general set of goals. Without listing all of them, it is possible to indicate the following goals:
1. Primary limitation of consumer with more low cost of produced production or given services on consumed 1 kWh of energy (achievement of a minimal drop in total produced production or given services);
12. Primary limitation of consumers with a more high level of the coefficient of energy possession of work on consumed 1 kWh of energy (achievement of maximal reduction in the number of workers, whose productivity and, consequently, wage is diminished);
15. Primary limitation of consumers with a more low value of the demand coefficient (primary limitation of consumers with greater possibilities of production out the peak time);
16. Primary limitation of consumers with a more low duration of using maximum load in 24 h (primary limitation of consumers with greater possibilities in transferring maximum load in the 24 h interval).
The general set of goals is directed at decreasing diverse negative consequences for consumers and creating incentive influences for them. This set is universal because can serve as the basis for models at different levels of load management hierarchy by aggregation of information and posterior decomposition of the problems. The concrete list of goals can be defined at every case by DM, who can be individual or group.
Consider the solution of problems of power shortage allocation formalized within the framework of the model (1), (17) for six consumers with 
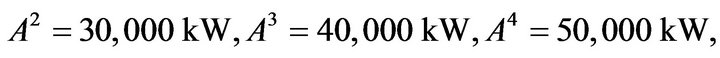 and
and  with using min operator and in comparison with using product operator as well as the wellknown Boldur’s method (the scalarization method) [19], considering the goals listed above, described by objective functions
with using min operator and in comparison with using product operator as well as the wellknown Boldur’s method (the scalarization method) [19], considering the goals listed above, described by objective functions
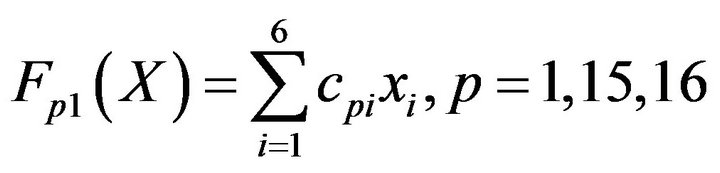 (18)
(18)
that are to be minimized and
 (19)
(19)
that is to be maximized. Here 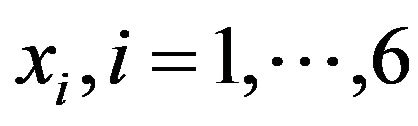 are limitations for consumers. The coefficients
are limitations for consumers. The coefficients 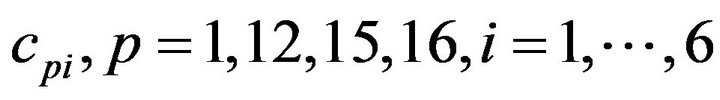 defined by specific characteristics of consumers are given in Table 1.
defined by specific characteristics of consumers are given in Table 1.
The results obtained on the basis of applying min operator , product operator
, product operator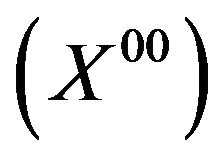 , and the Boldur’s method
, and the Boldur’s method 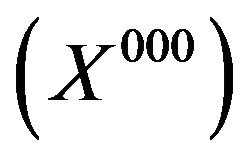 are presented in Table 2 and Table 3
are presented in Table 2 and Table 3
for  and
and .
.
To reflect the quality of solutions obtained on the basis

Table 2. Power shortage allocation.
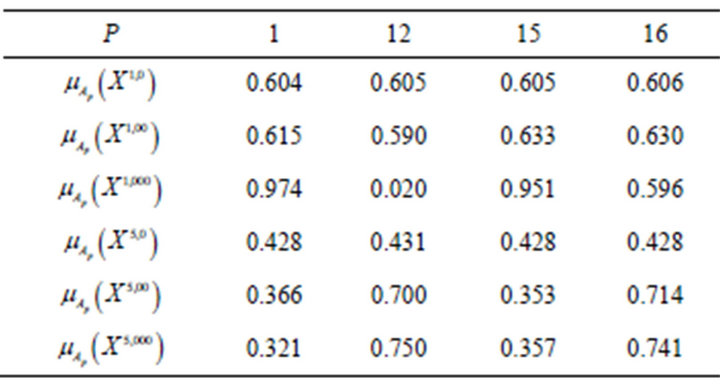
Table 3. Membership function levels.
of different approaches, Table 4 includes the mean magnitudes of absolute values 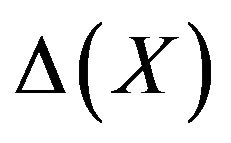 of deviations of membership function levels (satisfaction levels)
of deviations of membership function levels (satisfaction levels)
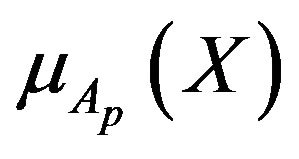 from their mean values
from their mean values 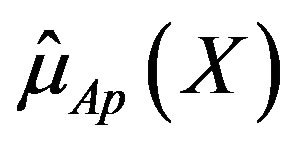 calculated as follows:
calculated as follows:
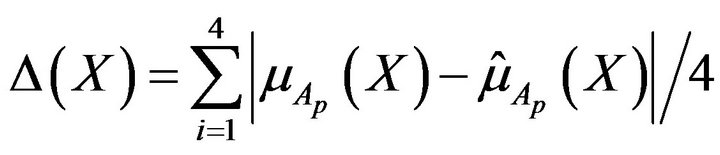 (20)
(20)
where
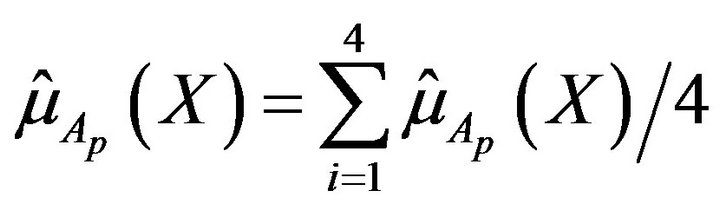 . (21)
. (21)
Table 4 covers the cases presented in Tables 2 and 3 as well as those computed for ,
, 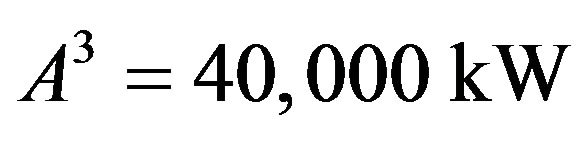 , and
, and 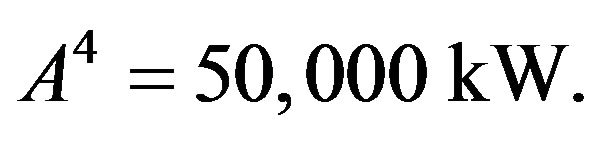 The data of Table 4 bring out that
The data of Table 4 bring out that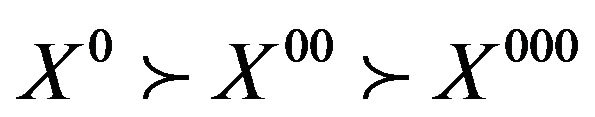 . The high quality of the solutions
. The high quality of the solutions 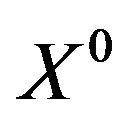 is also confirmed by inequalities
is also confirmed by inequalities
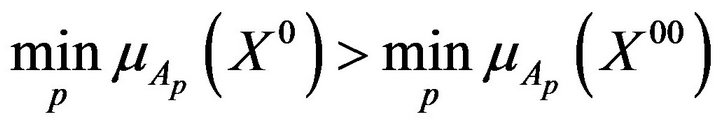 and
and
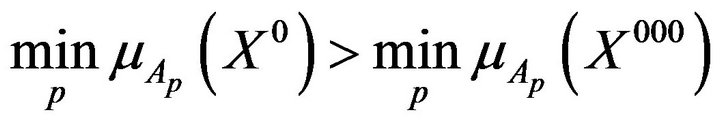 observed for all cases. The inequalities
observed for all cases. The inequalities  are also observed for all cases. Thus, the use of product operator leads to solutions more harmonious than solutions obtained on the basis of the scalarization approach.
are also observed for all cases. Thus, the use of product operator leads to solutions more harmonious than solutions obtained on the basis of the scalarization approach.
2.2. Multicriteria Power System Operation
The use of the results described above permits one to apply the multicriteria approach to power system operation to realize dispatch on several objectives. In [20], this is exemplified by a case study with the standard IEEE 30-bus system, where three objective functions are to be minimized: losses, sulfur oxide emissions, and nitrogen oxide emissions.
The consideration of the objective functions of emissions creates no difficulties at all. However, the presentation of the objective function of losses gives rise to difficulties. One possible workaround is the application of sequential multicriteria optimization procedures [5] with using sensitivity models reflecting the loss changes at each optimization step [20].
2.3. Optimization of Network Configuration and Voltage Control in Distribution Systems
The most important functions of Distribution Manage-
ment Systems are implemented on the basis of solution of problems of optimal network configuration (network reconfiguration) and optimal voltage control in distribution systems [20].
The problems of optimal network configuration are associated with altering network topology by changing locations of their disconnections. Works dedicated to the analysis of such problems seem to “compete” for achieving “more optimal” solutions. However, this competition is not convincing, considering that a combination of the information uncertainty and relative stability of optimal solutions produces uncertainty regions of indistinguishable solutions. Besides, these works do not permit one to consider a power system reaction (the results of [21] allow one to overcome this drawback on the basis of constructing so-called functionally oriented equivalents). Furthermore, the majority of results in this field is directed at the solution of problems which are defined under a monocriteria statement (usually, power or energy losses are minimized). However, reconfiguration problems are multicriteria in nature because they have an impact on reliability, service quality, and economical feasibility of power supply. Considering this, the developed computing system DNOS permits one to consider and to minimize objective functions of power losses, energy losses, system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), undersupply energy, poor quality energy consumption (consumption of energy outside of permissible voltage limits), and integrated overload of network elements in diverse combinations. Examples of solving reconfiguration problems are given in [5,20]. They show that the use of the multicriteria approach leads to the harmonious solution with small deviations from locally optimal solutions.
The techniques for optimal voltage control, which are implemented within the framework of the computing system VCOS, are directed at minimizing poor quality energy consumption. However, in accordance with a situational hierarchy, it may be necessary to implement an energetically efficient control, which considers the static characteristics of loads. Thus, it becomes necessary to speak about the second statement directed at the minimization of poor quality energy consumption and the reduction of peak load and/or energy consumption. This consideration is also implemented as a function of VCOS. Examples of its applications are given in [5,20].
2.4. Reactive Power Compensation in Distribution Systems
Traditionally, problems of reactive power compensation in distribution systems are associated with the selection of the locations, sizes, and types of capacitors to minimize the objective function of economical nature, while the constraints on upper and lower voltage limits at different load levels are satisfied.
Considering the discrete nature of such problems, the generalized algorithms of discrete optimization [22,23] can be applied for their solution. These algorithms combine formal procedures (related to the method of normalized functions) and informal procedures (based on greedy heuristics) and allow one to obtain quasi-optimal solutions after a small number of steps, overcoming the NP-completeness. They do not require an analytical description of objective functions and constraints, ensuring the flexibility and the possibility to correctly reflect diverse types of initial data using so called discrete sequences [22,23]. However, our experience in solving problems of reactive power compensation shows that the necessity to simultaneously observe constraints on upper and lower voltage limits at different buses creates essential obstacles. It is not uncommon to face situations when these constraints induce an empty feasible region. These obstacles can be avoided by minimizing the objective function of an economical nature as well as the objective function which reflects a volume of poor quality energy consumption. Besides, if the problem is associated with the determination of capacitor types (fixed or switched), the quantity of objectives should be increased.
Taking the above into account, the algorithms [22,23] have been modified to solve discrete multicriteria problems considering the results presented above.
The computing platform EPODIAN was developed to solve reactive power compensation problems in monocriteria and multicriteria settings for large-scale distribution networks.
As an example, Table 5 demonstrates the results of the application of EPODIAN for the allocation of reactive power sources in a distribution network 13.8/0.22 kV of one of substations of the Energy Company of Minas Gerais (CEMIG). This network includes 2 feeders with more than 5000 consumers connected to them. The total length of feeders is 729 km. They are modeled by 9660 electrical nodes. In Table 5, I is an initial state, A is a monocriteria solution minimizing the objective function of the economical nature, B is a monocriteria solution minimizing the objective function which reflects a volume of poor quality energy consumption, and C is a multicriteria solution providing a compromise between the solutions A and B. Figure 1 shows the EPODIAN screen demonstrating resulting reactive power flow for the solution C. All solutions were obtained less than 30 s on a conventional dual-core desktop PC.
Although the presented results do not take into account the uncertainty of initial information (associated with power demand curves, energy tariffs, etc.), EPODIAN allows their consideration into a general scheme of mul-
ticriteria analysis under information uncertainty [5,24] with evaluation of particular (monocriteria) and aggregated (multicriteria) risks in multiple scenarios.
3. 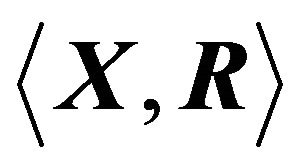 Models, Their Analysis, and Applications
Models, Their Analysis, and Applications
Some criteria considered in the process of decision making can be reflected only in a qualitative (semantic, contextual) manner. For instance, concepts such as “flexibility of development”, “investment utility”, etc. are based on experience, knowledge, and intuition of experts. This generates the necessity of the evaluation, comparison, choice, prioritization and/or ordering of alternatives in strong correspondence with the preferences of DM.
The application of fuzzy set theory to preference modeling [25] provides a flexible framework for dealing with “fuzziness” of the assessments which incorporates human consistency into the applied models. Next we briefly discuss three basic techniques for processing fuzzy preferences.
Assume we are given a set 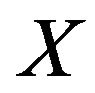 of alternatives which are to be examined according to q criteria of quantitative and/or qualitative nature. The decision making problem can be represented as a pair
of alternatives which are to be examined according to q criteria of quantitative and/or qualitative nature. The decision making problem can be represented as a pair 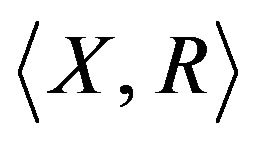 where
where 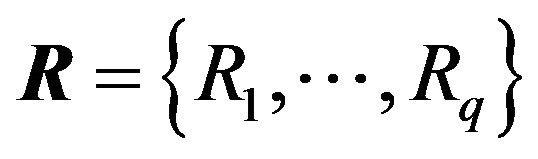 is a vector of fuzzy preference relations [5,26]. In this case, we have
is a vector of fuzzy preference relations [5,26]. In this case, we have
 (22)
(22)
where 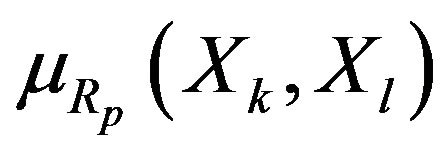 is a membership function of nonstrict fuzzy preference relation, which represents the degree to which
is a membership function of nonstrict fuzzy preference relation, which represents the degree to which 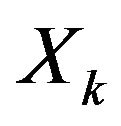 weakly dominates
weakly dominates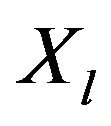 , i.e., the degree to which
, i.e., the degree to which  is at least as good as
is at least as good as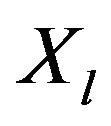 , according to the pth criterion.
, according to the pth criterion.
The availability of fuzzy or linguistic estimates
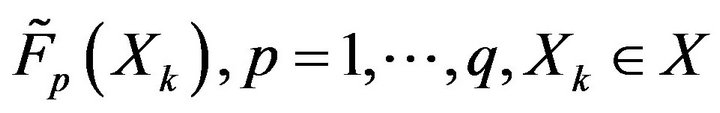 with membership functions
with membership functions
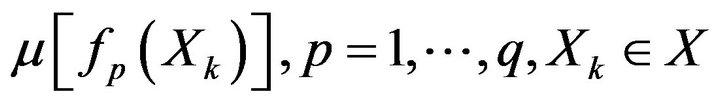 permits one [5,26] to construct elements of
permits one [5,26] to construct elements of 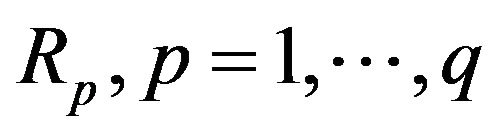 as follows:
as follows:
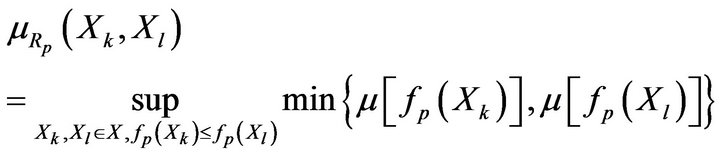 (23)
(23)
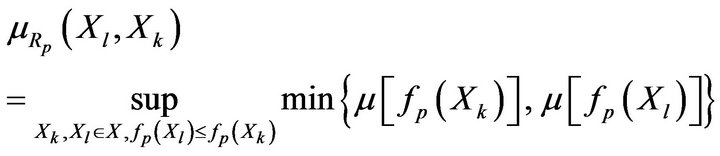 (24)
(24)
if the pth criterion is associated with minimization. If it is associated with maximization, then the domain conditions of suprema in (23) and (24) should be changed to  and
and 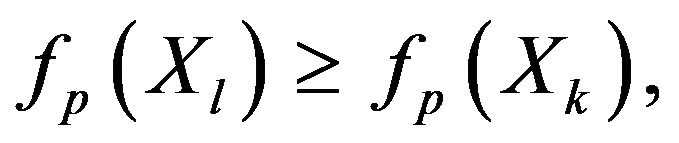 respectively.
respectively.
However, fuzzy preference relations are not a unique form of preference representation. For instance, the authors of [27] indicate eight formats which can be used to establish preferences among analyzed alternatives. It is natural that application of multiple preference formats demands a subsequent conversion to a unique format which can be processed and analyzed. Considering the advantages and rationality of the use of fuzzy preference relations for this objective, the results of [5], for instance, permit one to construct so-called transformation functions to convert different formats to fuzzy preference relations.
Let us consider the situation of setting up a single nonstrict preference relation 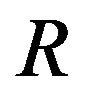 defined as follows:
defined as follows:
• 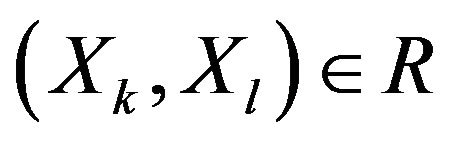 means “
means “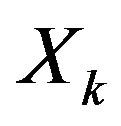 is not worse than
is not worse than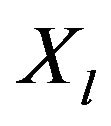 ”•
”• 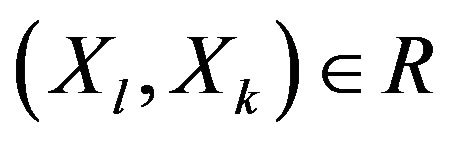 means “
means “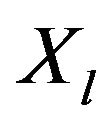 is not worse than
is not worse than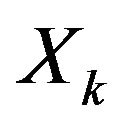 ”•
”•  or
or 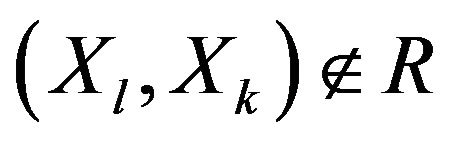 means “
means “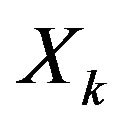 and
and  are not comparable”.
are not comparable”.
The nonstrict fuzzy preference relation  can be represented [5,28] by a strict fuzzy preference relation
can be represented [5,28] by a strict fuzzy preference relation 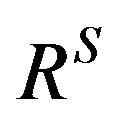 and an indifference relation
and an indifference relation 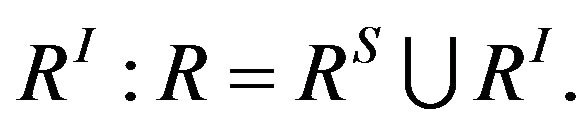 The strict preference relation
The strict preference relation 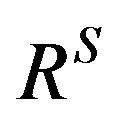 is constituted by all pairs of alternatives that satisfy the conditions
is constituted by all pairs of alternatives that satisfy the conditions 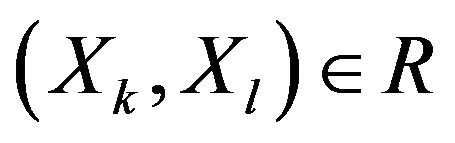 and
and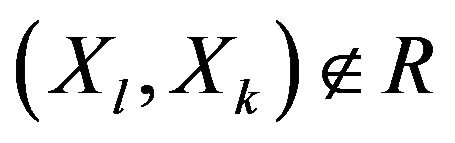 . If
. If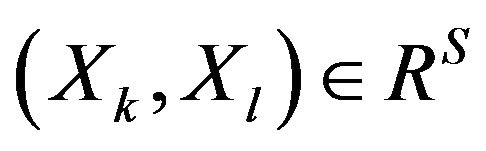 , it can be said that
, it can be said that  is strictly better than
is strictly better than 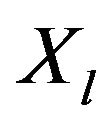 (or
(or 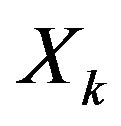 dominates
dominates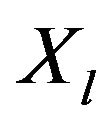 ). The indifference relation is constituted by all pairs of alternatives that simultaneously satisfy the conditions:
). The indifference relation is constituted by all pairs of alternatives that simultaneously satisfy the conditions: 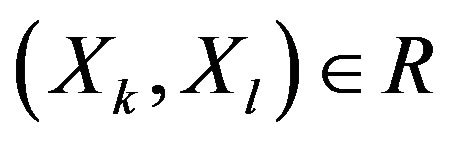 and
and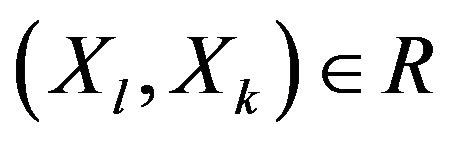 . If
. If , it can be said that
, it can be said that 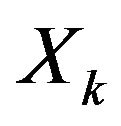 is indifferent to
is indifferent to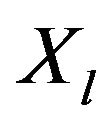 .
.
With the use of the inverse relation 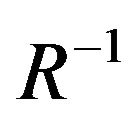 the strict preference relation
the strict preference relation 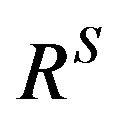 can be defined as
can be defined as  with
with
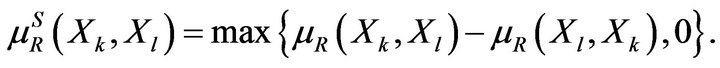 (25)
(25)
The expression (25) serves as the basis for the choice procedure which has been studied by many authors (its properties as well as its axiomatic characterization are discussed, for instance, in [29,30]).
If 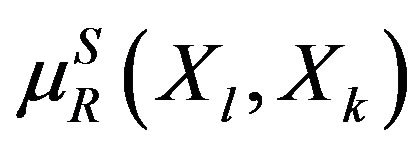 is the membership function of the fuzzy set of all
is the membership function of the fuzzy set of all  which are strictly dominated by
which are strictly dominated by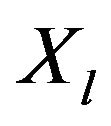 , then the complementary relation
, then the complementary relation 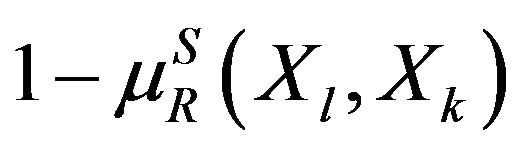 gives the fuzzy set of alternatives which are not dominated by other alternatives from
gives the fuzzy set of alternatives which are not dominated by other alternatives from 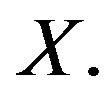 Therefore, in order to meet the set of alternatives from X that are not dominated by other alternatives, it is sufficient to find the intersection of all
Therefore, in order to meet the set of alternatives from X that are not dominated by other alternatives, it is sufficient to find the intersection of all 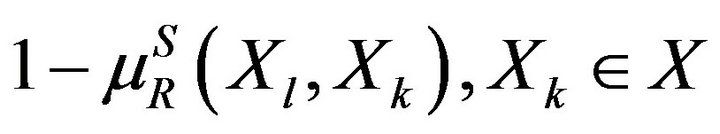 on all
on all 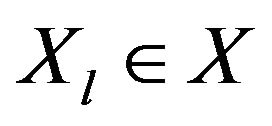 [28]. This intersection is the fuzzy set of nondominated alternatives with a membership function
[28]. This intersection is the fuzzy set of nondominated alternatives with a membership function
 (26)
(26)
Considering that a rational criterion for choice is to select a solution providing the highest level of nondominance, one can choose alternatives as follows:
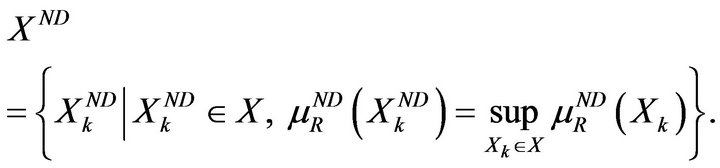 (27)
(27)
Let us consider the first procedure [28] to deal with multiple criteria, when preferences are modeled as a vector 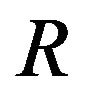 of fuzzy preference relations. The expressions
of fuzzy preference relations. The expressions
(25)-(27) are applicable if we take 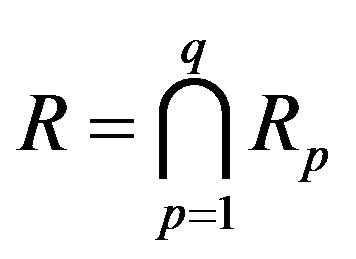 with
with
 (28)
(28)
When using (28), 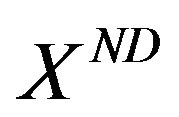 fulfils the role of a Pareto set. Its contraction is possible on the basis of distinguishing the importance of each
fulfils the role of a Pareto set. Its contraction is possible on the basis of distinguishing the importance of each 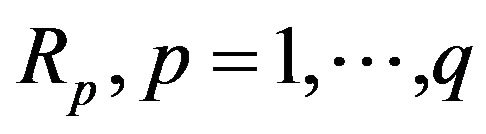 by means of the convolution:
by means of the convolution:
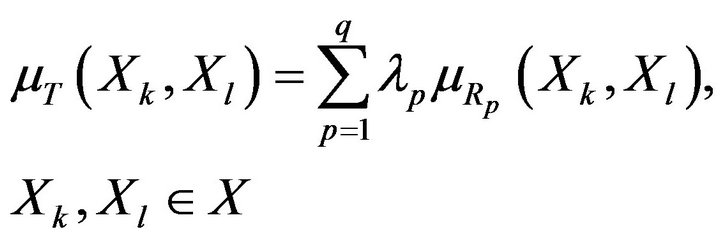 (29)
(29)
where 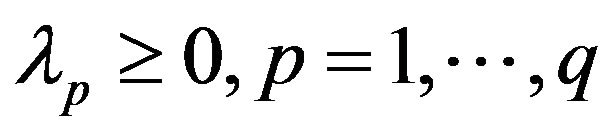 are importance factors normalized as
are importance factors normalized as
 . (30)
. (30)
The construction of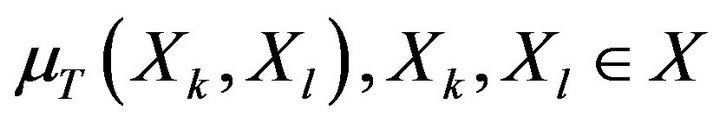 allows one to obtain the membership function
allows one to obtain the membership function  of the set of nondominated alternatives according to an expression similar to (25). The intersection
of the set of nondominated alternatives according to an expression similar to (25). The intersection
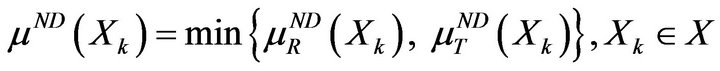 (31)
(31)
provides us with
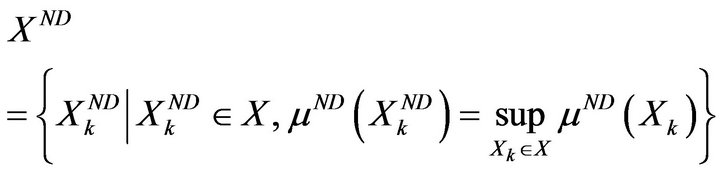 (32)
(32)
The expressions (26) and (27) can serve as the basis for the second procedure [5,7], which has a lexicographic character. It is based on the step-by-step application of criteria for comparing alternatives. The procedure permits one to build a sequence 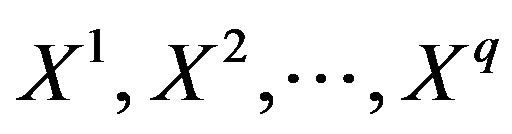 so that
so that  by applying the following expressions:
by applying the following expressions:
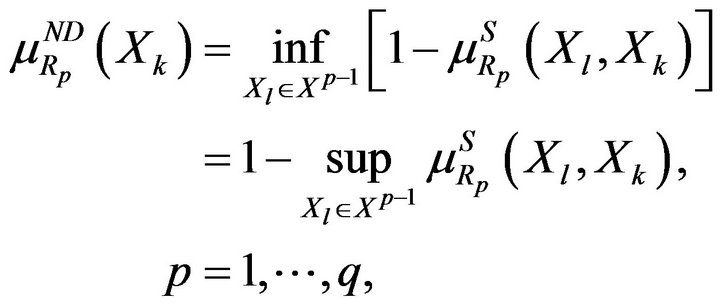 (33)
(33)
 (34)
(34)
Finally, let us consider the third technique [5,22]. The application of (26) in the form
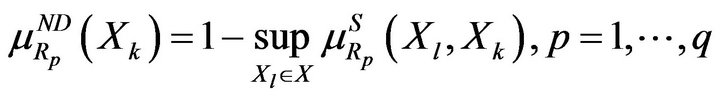 (35)
(35)
permits one to construct the membership functions of the set of nondominated alternatives for each fuzzy preference relation. The membership functions
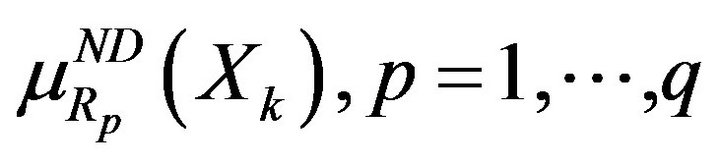 play a similar role to the membership functions which replace objective functions
play a similar role to the membership functions which replace objective functions
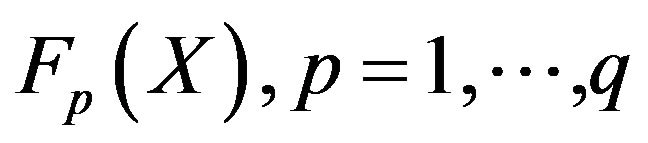 in
in  model analysis. Therefore, it is possible to construct
model analysis. Therefore, it is possible to construct
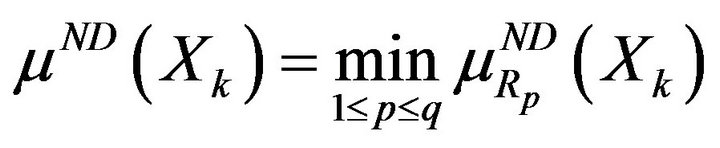 (36)
(36)
to obtain 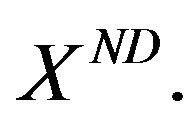 If it is necessary to distinguish the importance of preference relations, it is possible to extend (36) to
If it is necessary to distinguish the importance of preference relations, it is possible to extend (36) to
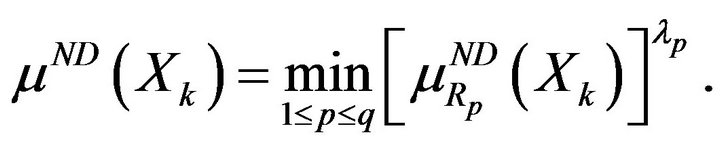 (37)
(37)
The use of (37) does not require the normalization of 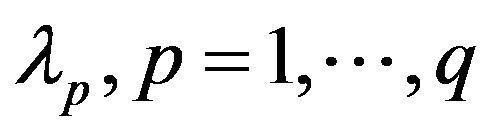 in the way similar to (30).
in the way similar to (30).
The application of the second procedure may lead to solutions different from the results obtained on the basis of the first procedure. Besides, solutions based on the first procedure and the third procedure having a single generic basis, may also be different. At the same time, the third procedure is preferable from the substantial point of view. In particular, the first procedure may lead to the choice of alternatives with unit degree of nondominance, though these alternatives are not the best ones from the point of view of all preference relations. The third procedure provides this result only for those alternatives which are the best from the point of view of all preference relations. The possibility to obtain different solutions on the basis of different approaches is considered natural, and the choice of an approach is a prerogative of DM.
The presented procedures have been implemented within the framework of an interactive decision making system MDMS1 [5].
The described techniques, as it was indicated above, are considered as the basic ones. They have served for developing other techniques:
• analysis of alternatives with fuzzy ordering of criteria [5,28];
• analysis of alternatives based on the concept of fuzzy majority (based on the application of the so-called OWA operator, originally proposed in [31]) [5];
• analysis of alternatives based on an outranking approach (by a means of a fuzzy version of the PROMETHEE [32]) [5].
The results described above have also served as a basis for developing and improving methods for multicriteria group decision making ([5,33-35], for instance).
3.1. Substation Planning in Power Systems
Among a family of power system expansion problems, the problem of substation planning is of a fundamental importance. The paper [36] discusses how to consider the uncertainty factor in the solution of this problem. In [36], the analysis of a power utility group of substations is carried out to select a solution among three alternatives, considering their total costs with the uncertainty of interest rates modeled as trapezoidal fuzzy numbers [2,3]. However, as it is shown in [5], this analysis does not give ground to proceed with a convincing decision. One possible way to overcome this difficulty is the application of the well-established approach in decision making practice: the multicriteria analysis of alternatives in a fuzzy environment [5], when the application of additional criteria, including criteria of qualitative character, serves as convincing means to contract the decision uncertainty regions. In [5], the use of this approach is exemplified by analysing the same power utility group of substations as [36], with the use of the three basic techniques for decision-making described above.
3.2. Local Reactive Power Source Choice
The problem of choosing a local reactive power source at a power system bus with reactive power shortage on the basis of applying the criteria of reliability, investment level, and control rapidity is considered in [37]. Its solution is associated with the construction and analysis of the 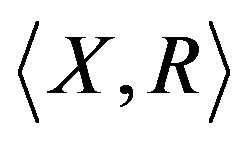 models with fuzzy ordering of the considered criteria [5,28].
models with fuzzy ordering of the considered criteria [5,28].
3.3. Selection of Technology in Renewable Energy Diffusion Plan
The problem of selecting the appropriated technology in a renewable energy diffusion plan for the Sardinia region is stated in [38]. In [5], this problem is resolved on the basis of analyzing alternatives with using the concept of fuzzy majority. In particular, the following options of energy sources have been considered as alternatives: 1) solar (domestic solar water heaters), 2) wind (wind turbines of type grid connected), 3) hydraulic (hydro plants in derivation schemes), and 4) biomass (combined heat and power plants fed by agricultural wastes or energy crops).
The following criteria have been considered: 1) targets of primary energy saving in a regional scale, 2) sustainability according to Greenhouse pollutant emissions, 3) consistence of installation and maintenance requirements with local technical conditions, 4) continuity and predictability of performances, 5) market maturity, and 6) compatibility with political, legislative, and administrative situation.
The first two criteria are of a quantitative character. The third, fourth, and sixth criteria are of a qualitative character and have been evaluated through the set of three fuzzy values. The fifth criterion is also of a qualitative character and has been evaluated through the set of five fuzzy values.
3.4. Prioritization in Distribution System Maintenance Planning
The problem of prioritization in maintenance planning aims at assuring reliability and service quality of power supply through network and equipment preventive maintenance. CEMIG implements a strategy to realize the maintenance in distribution systems according to the plans suggested by manufacturers of network elements and equipment.
The prioritization techniques allow one to take into account not only parameters of network elements and equipment, but also factors related to the conditions of
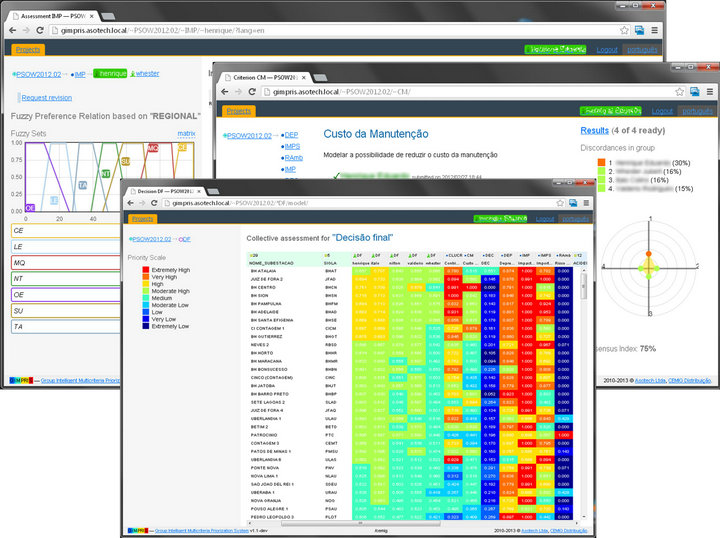
Figure 2. Web-based group decision making environment for prioritization in distribution system maintenance planning.
their operation. In addition to the failure risks, which can be assessed through the statistical analysis, factors associated with the impact of these failures are considered in the prioritization process. Among them it is possible to mention quantitative factors (number of consumers, energy demands, etc.) as well as qualitative factors (political impact, maintenance complexity, etc.).
The computing system for prioritization in maintenance planning GIMPRIS implemented for CEMIG provides group decision making environment in the webbased platform (Figure 2). The flexible tools for preference and aggregation modeling are designed to extend the capabilities of 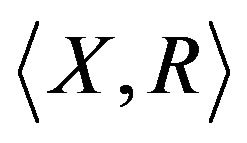 models for prioritization of more than 50,000 equipment items. The dynamic group management scheme implemented within the system allows a supervisor to efficiently control the process of convergence to consensus, while moderating up to 10 experts simultaneously.
models for prioritization of more than 50,000 equipment items. The dynamic group management scheme implemented within the system allows a supervisor to efficiently control the process of convergence to consensus, while moderating up to 10 experts simultaneously.
4. Acknowledgements
This research was supported by the National Council for Scientific and Technological Development of Brazil (CNPq)—grants 305036/2011-4 and 307466/2011-6, the State of Minas Gerais Research Foundation (FAPEMIG) —grant TEC-BPD-00235-10, and the Energy Company of Minas Gerais (CEMIG)—contract 4570022632-530 and R&D ANEEL Program projects.