Oscillations of a Punctual Charge in the Electric Field of a Charged Ring: A Comparative Study ()
1. Introduction
Nonlinear oscillators play a pivotal role in physics and engineering. Recently, considerable attention has been directed towards analytical/numerical solutions of nonlinear equations. Many new techniques have been appeared in writing, for example, max-min approach [1-3], frequency amplitude formulation [4], homotopy methods [5-7], harmonic balance method [8], parameter-expanding method [9], variational approach [10-11], Hamiltonian methods [12-14] and Lindstedt-Poincaré methods with modification etc. [15-16].
In this paper, we consider a generalized nonlinear oscillator
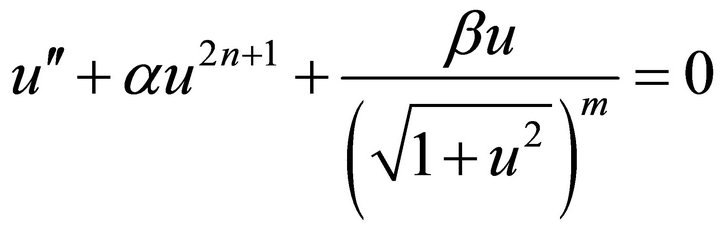 (1)
(1)
with initial conditions
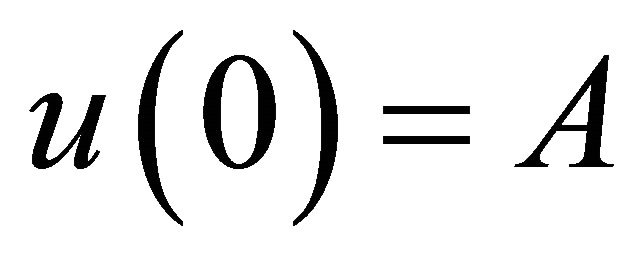 and
and  (2)
(2)
This equation occurs in certain phenomenon in relativistic physics, vibration of a stretched elastic wire due to mass attached to the centre and oscillation of a punctual charge in the electric field of charged ring. This equation has been investigated by various authors [17,18] for special cases.
It is interesting to note that  reduce to the oscillations of a charge in the electric field of a charged ring equation. This connection is given as follows: We consider a ring of radius r with a charge
reduce to the oscillations of a charge in the electric field of a charged ring equation. This connection is given as follows: We consider a ring of radius r with a charge 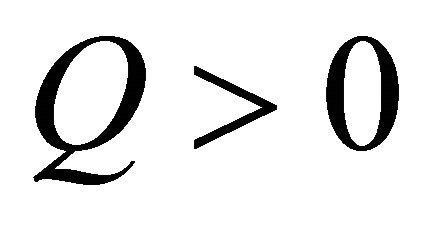 spread uniformly around the ring. The electric field E on the x-axis of the ring is given by
spread uniformly around the ring. The electric field E on the x-axis of the ring is given by
 (3)
(3)
where x is the distance along the axis. If a negative punctual charge 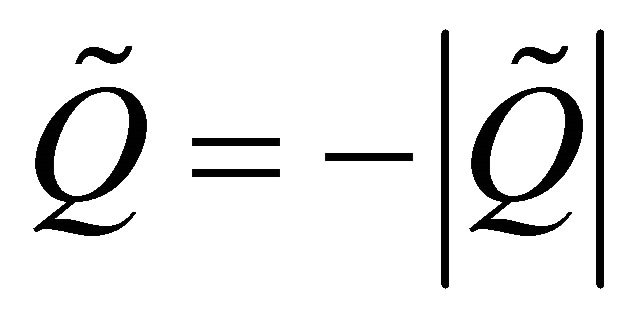 is placed at a point on the ring axis, the charge will experience a force
is placed at a point on the ring axis, the charge will experience a force
 (4)
(4)
The equation of motion of the punctual charge  is given by the following nonlinear differential equation
is given by the following nonlinear differential equation
 (5)
(5)
Equation (5) can be written as
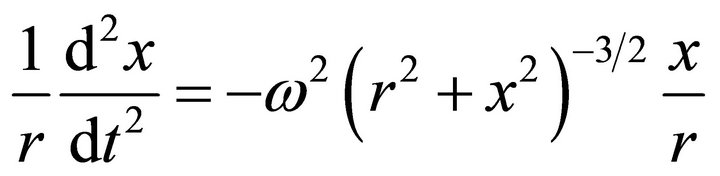 (6)
(6)
where
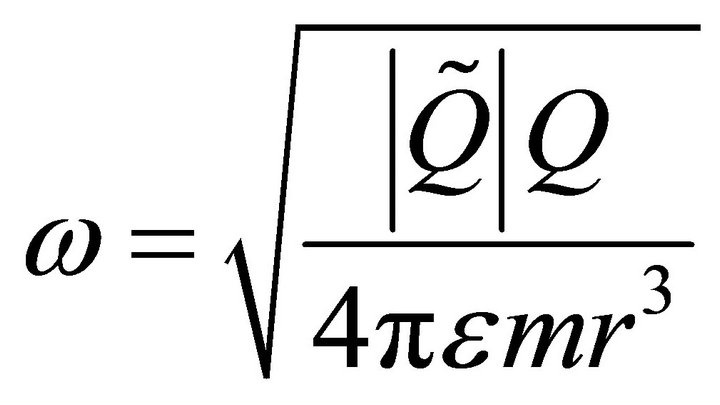
Now, dimensionlize the Equation (6) by taking
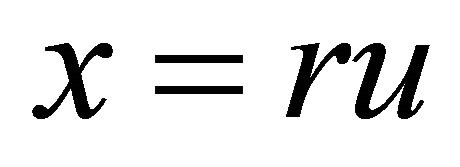 and
and  (7)
(7)
Substituting these dimensionless variables into Equation (6) gives
 (8)
(8)
This is a special case of generalized oscillator Equaiton (1).
We assume the solution in the following form:
 (9)
(9)
where 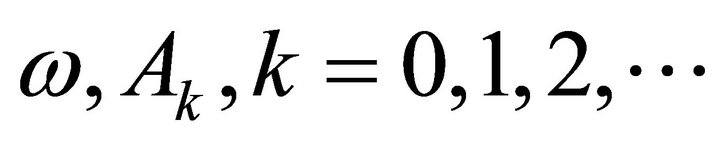 are the angular frequency of motion and Fourier coefficients, respectively.
are the angular frequency of motion and Fourier coefficients, respectively.
2. Governing Equation
Consider the following nonlinear equation:
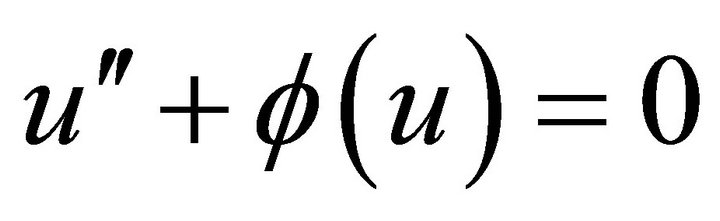 (10)
(10)
where 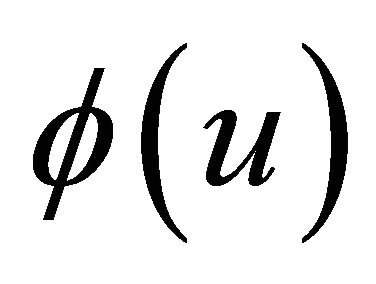 a rational function and u is the displacement. The imposed initial conditions take the forms
a rational function and u is the displacement. The imposed initial conditions take the forms
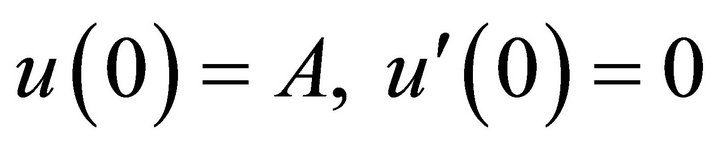 (11)
(11)
After multiplying both sides of Equation (10) by , integrating and using the initial condition (11), we obtain
, integrating and using the initial condition (11), we obtain
 (12)
(12)
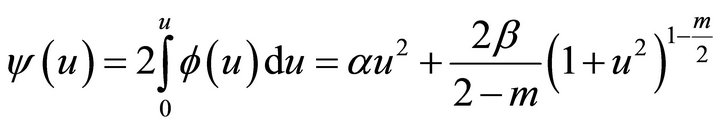 (13)
(13)
The exact frequency of the motion  can be expressed by the relation (see Equation (14)).
can be expressed by the relation (see Equation (14)).
A general scheme of the procedure of three and four parameters is depicted in Figures 1 and 2.
3. Applications of MPM to Oscillators with Rational Restoring Force
3.1. Example for 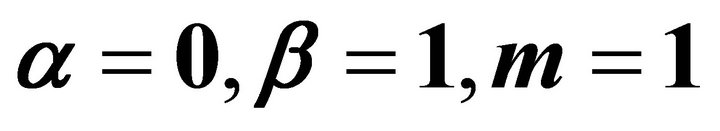
In this case, the nonlinear equation reduces to equation of relativistic oscillator
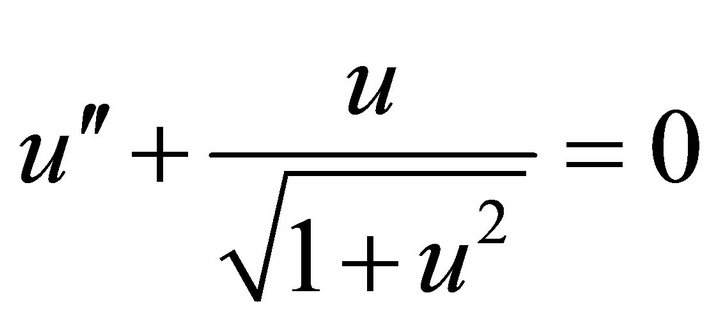 (15)
(15)
with initial conditions
 and
and 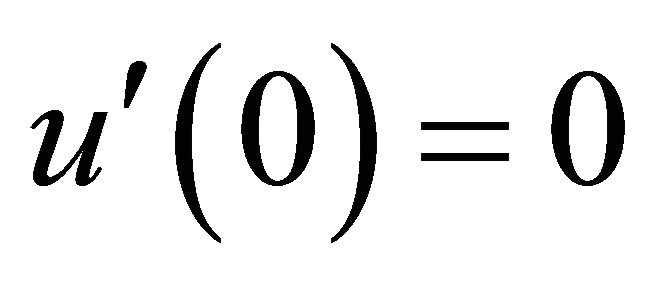 (16)
(16)
Multiplying both sides of Equation (15) by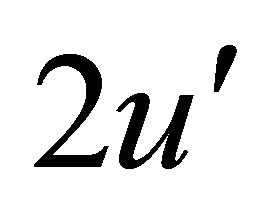 and integrating, with initial conditions, we get
and integrating, with initial conditions, we get
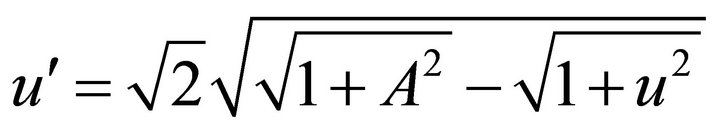 (17)
(17)
In MPM the solution of the problem is assumed to be
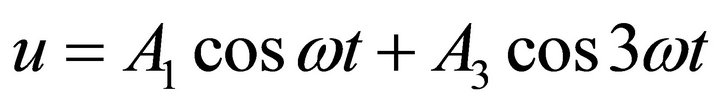 (18)
(18)
Differentiating Equation (18) leads to the results
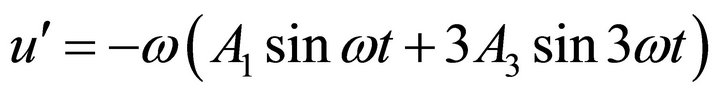 (19)
(19)
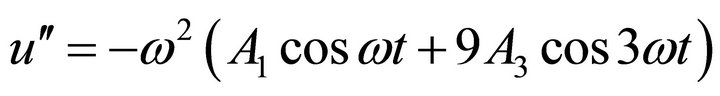 (20)
(20)
From the initial condition Equations (16) and (18), we have
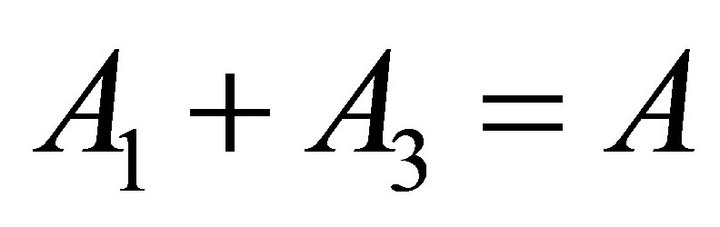 (21)
(21)
Substituting Equations (18) and (19) into Equaiton
(17) at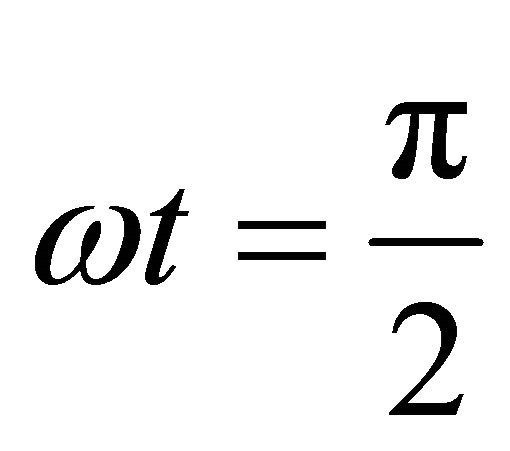 , we will find the following equation:
, we will find the following equation:
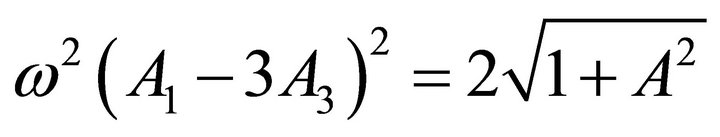 (22)
(22)
Considering the acceleration at the time , from Equations (15), (16) and (20), we get the following equation
, from Equations (15), (16) and (20), we get the following equation
 (23)
(23)
From the three Equations (21)-(23), three unknowns 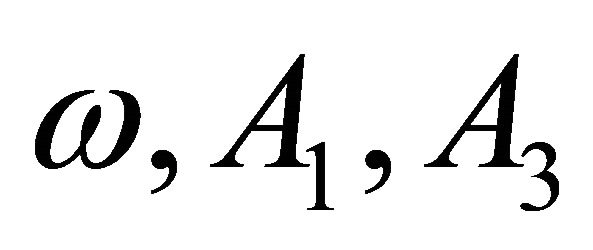 can be solved analytically/ numerically.
can be solved analytically/ numerically.
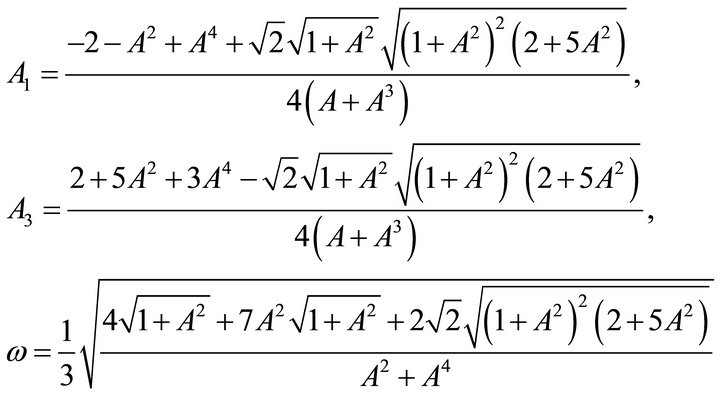
(24)
The computed results of three parameters methodsfor 
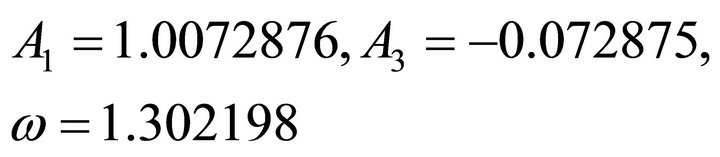 (25)
(25)
 (14)
(14)
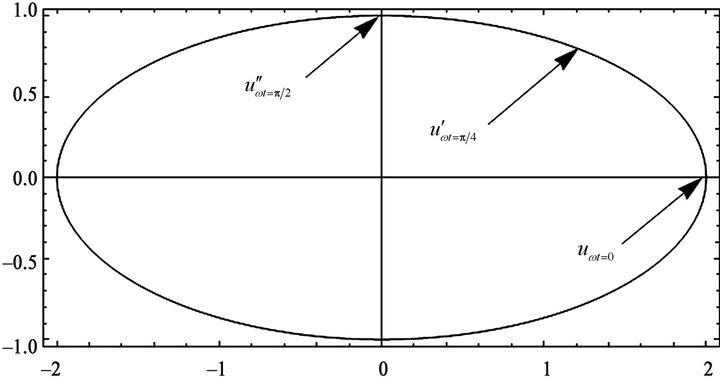
Figure 1. A genral scheme for the solution of nonlinear oscillator problem (three parameters case).
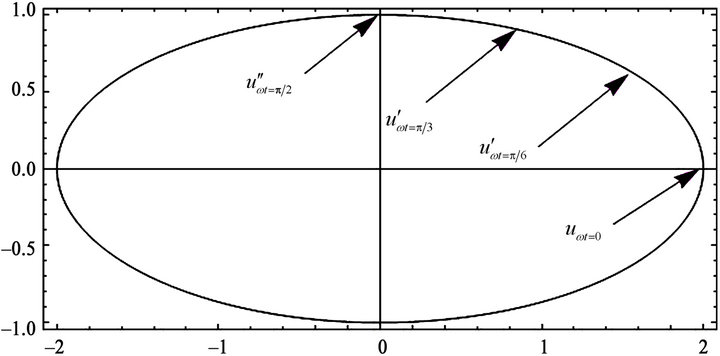
Figure 2. A general scheme for the solution of nonlinear oscillator problem (four parameters case).
The frequency of three parameters method is not highly perfect. In order to find more accuracy of the solution the four parameters technique is introduce
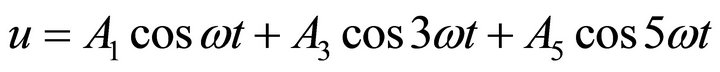 (26)
(26)
According to the initial conditions:
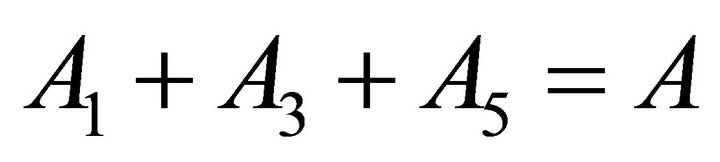 (27)
(27)
Substituting Equation (26) and its derivative at  and
and , the following equations are obtained
, the following equations are obtained
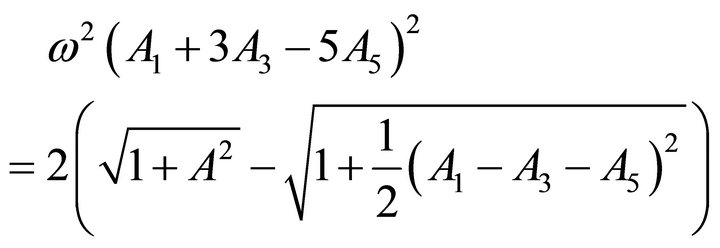 (28)
(28)
 (29)
(29)
The acceleration at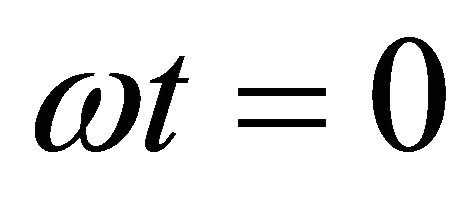 , from Equaiton (15), we will find the following equation:
, from Equaiton (15), we will find the following equation:
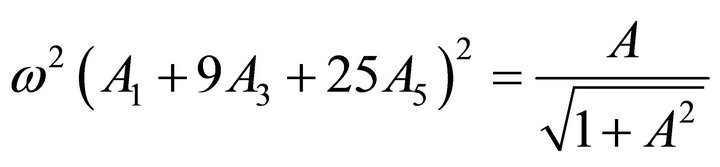 (30)
(30)
After some mathematical simplification with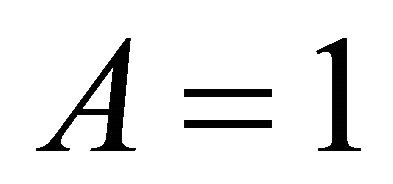 we achieve the numerical values
we achieve the numerical values
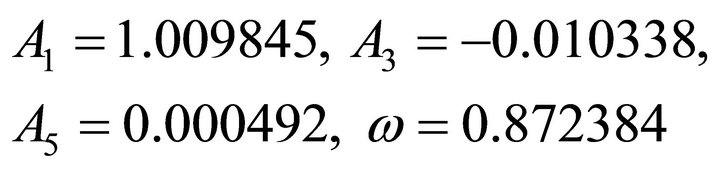 (31)
(31)
From Equation (14), we obtain the exact frequency for 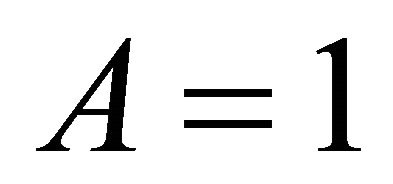 is
is
 (32)
(32)
The frequency-amplitude relationship of relativistic oscillator Equation (15) obtained by Zhao [18] and Beléndez et al. [19] by frequency-amplitude formulation (FAF) and homotopy perturbation method is given by
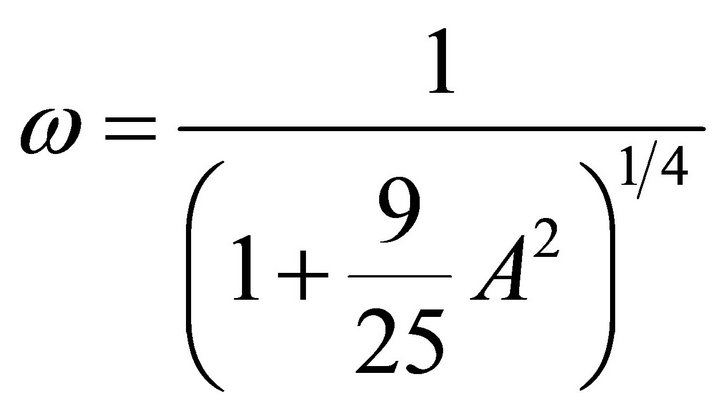 (33)
(33)
The frequency of Equation (15) found by Shen and Mo [17] using max-min approach is given as
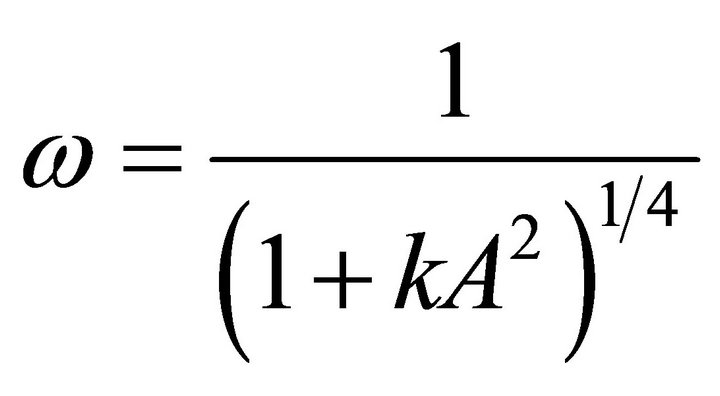 (34)
(34)
where

where  are the complete elliptic integral and elliptic integral of the first kind respectively. The accuracy of FAF/HPM reaches 0.332517%, the accuracy of max-min approach is 3.09685% and the accuracy of four parameter lower than 0.004816% for
are the complete elliptic integral and elliptic integral of the first kind respectively. The accuracy of FAF/HPM reaches 0.332517%, the accuracy of max-min approach is 3.09685% and the accuracy of four parameter lower than 0.004816% for . After comparison between the exact frequency with these methods, we conclude that the four parameter approach is better than the FAF, max-min approach and HPM.
. After comparison between the exact frequency with these methods, we conclude that the four parameter approach is better than the FAF, max-min approach and HPM.
3.2. Example for 
In this case, Equation (1) is reduces to the equation of motion of a mass attached to the center of a stretched elastic wire
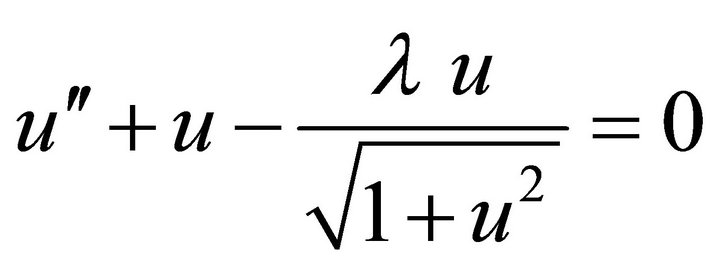 (35)
(35)
with initial conditions
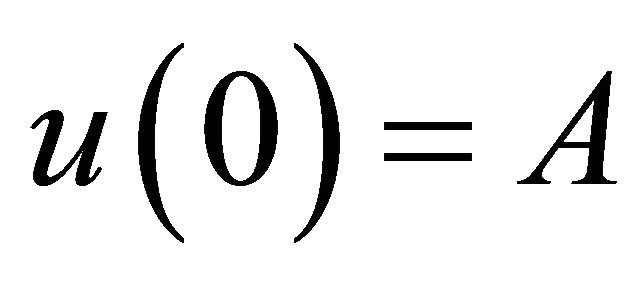 and
and  (36)
(36)
Multiplying both sides of Equation (35) by and integrating, taking into account the initial conditions, we get
 (37)
(37)
In MPM the solution of the problem is assumed to be
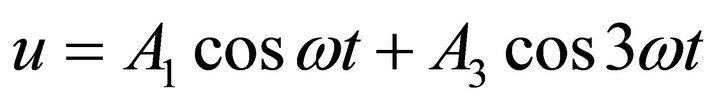 (38)
(38)
Differentiating Equaiton (38) leads to the results
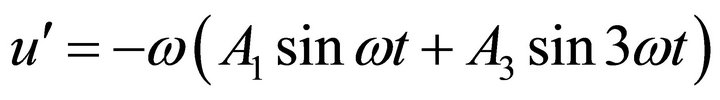 (39)
(39)
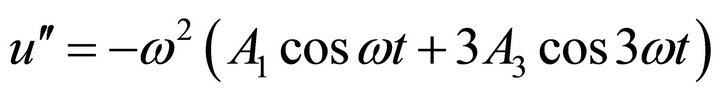 (40)
(40)
From the initial condition Equations (36) and (38), we have
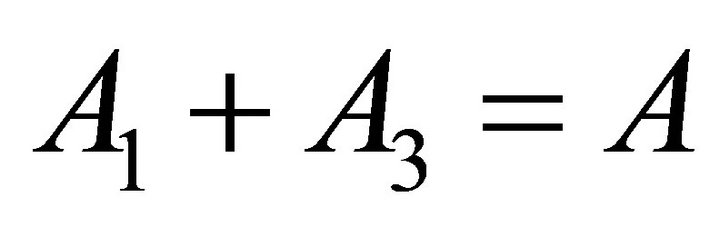 (41)
(41)
Substituting Equations (38) and (39) into Equation (37)
at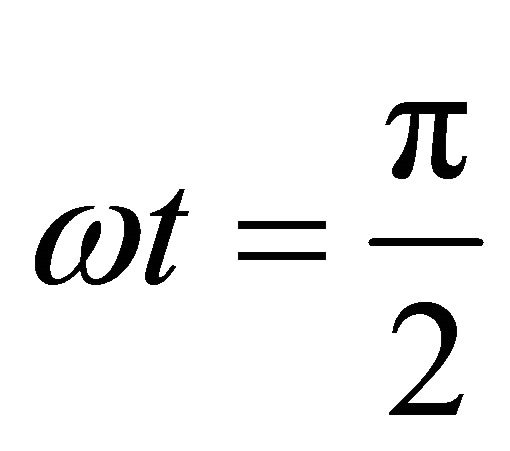 , we will find the following equation:
, we will find the following equation:
 (42)
(42)
Considering the acceleration at the time , from Equations (35) and (40), we get the following equation
, from Equations (35) and (40), we get the following equation
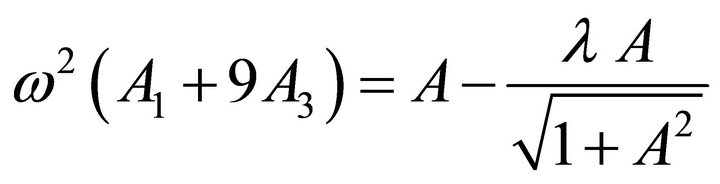 (43)
(43)
From, Equations (41)-(43), three unknowns 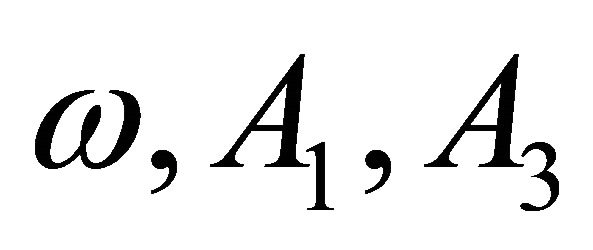 can be solved analytically/numerically (see Equation (44)).
can be solved analytically/numerically (see Equation (44)).
In order to find more accuracy of the solution the four parameters technique is introduce
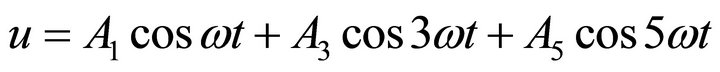 (45)
(45)
According to the initial conditions:
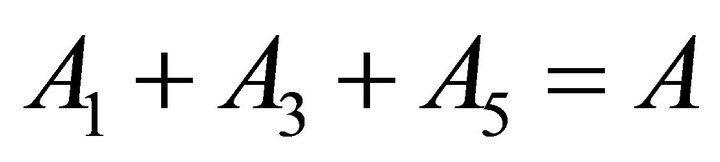 (46)
(46)
Substituting Equation (45) and its derivative at
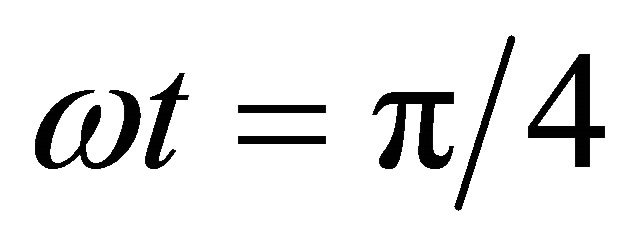
and 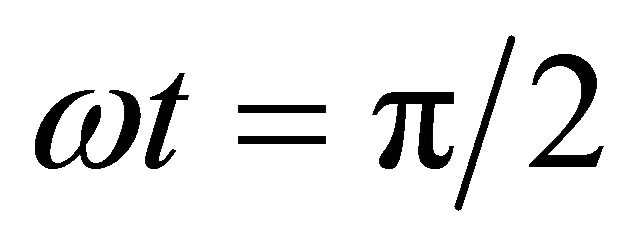 the following equations are obtained (see Equation (47)).
the following equations are obtained (see Equation (47)).
 (44)
(44)
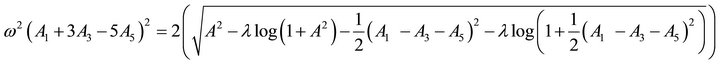 (47)
(47)
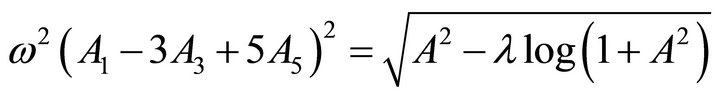 (48)
(48)
From Equation (45) and (36), we will find the following equation:
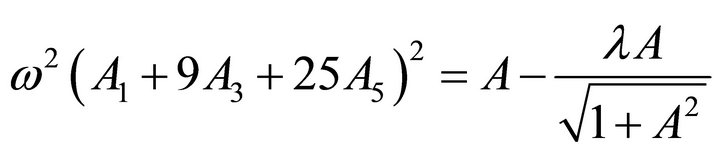 (49)
(49)
After some mathematical simplification with , we achieved the numerical values
, we achieved the numerical values
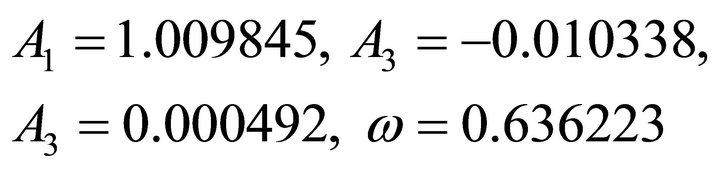 (50)
(50)
which is very close to the exact solution.
3.3. Example for 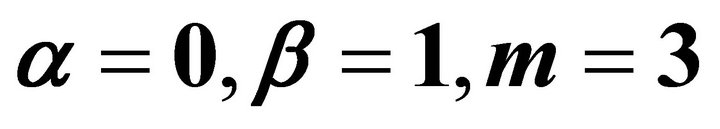
In this case, Equation (1) is reduces to the equation of a punctual charged ring, which is a free charge [21,22]
 (51)
(51)
with initial conditions
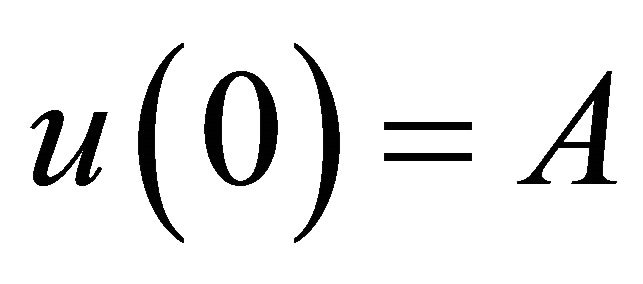 and
and  (52)
(52)
After utilizing the same procedure in the previous examples, we obtained the approximate solutions of the problem are portrayed in Figure 5.
4. Conclusion
The multiple parameter approach has proved to be a powerful mathematical tool to find an approximate analytical solution for relativistic harmonic oscillator, a mass attached of a stretched elastic wire and oscillation of a charged ring. Comparison of the results obtained with previous methods shows that the approximate solutions are accurate and valid for the whole solution domain, and very convenient and effective. It is also found the method gives the better results if the number of parameters will be increased. It is also observed that multiple parameter approach converts the original differential equation into system of nonlinear algebraic equations. It is found that an iterative procedure for solving the corresponding system of algebraic equations creates an extremely effective method for constructing periodic solutions for nonlinear oscillators. Figures 3-5 are plotted for three, four para-
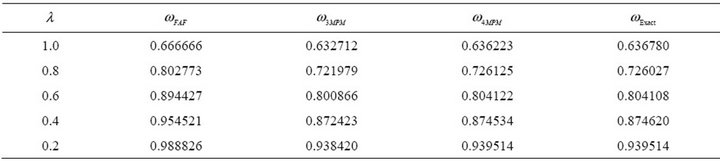
Table 1. Numerical comparison for frequency by present method and exact solution.
meters and exact trajectories and Table 1 shows the numerical comparisons for second examples.
5. Acknowledgements
The corresponding author is highly thankful for reviewers and the Dean faculty of Sciences for supporting this research work.