Reference Point Based TR-PSO for Multi-Objective Environmental/Economic Dispatch ()
1. Introduction
With the increase in the environmental awareness and the passage of environmental regulations, the environmental constraints are having a significant impact on the operation of power systems. Traditional economic dispatch to minimize the fuel cost is inadequate when environmental emissions are also to be included in the operation of power plants.
The purpose of EED problem is to figure out the optimal amount of the generated power for the fossil-based generating units in the system by minimizing the fuel cost and emission level simultaneously, subject to various equality and inequality constraints including the security measures of the power transmission/distribution. Various optimization techniques have been proposed by many researchers to deal with this multi-objective programming problem with varying degree of success.
Different techniques have been reported in the literature pertaining to EED problem. In Ref. [1] the problem has been reduced to a single objective problem by treating the emission as a constraint with a permissible limit. This formulation, however, has a severe difficulty in getting the trade off relations between cost and emission. Alternatively, minimizing the emission has been handled as another objective in addition to usual cost objective. A linear programming-based optimization procedure in which the objectives are considered one at a time was presented in Ref. [2]. Unfortunately, the EED problem is a highly non-linear and a multimodal optimization problem. Therefore, conventional optimization methods that make use of derivatives and gradients, in general, not able to locate or identify the global optimum. On the other hand, many mathematical assumptions such as analytic and differential objective functions have to be given to simplify the problem. Furthermore, this approach does not give any information regarding the trade-offs involved.
In other research direction, the multi-objective EED problem was converted to a single objective problem by linear combination of different objectives as a weighted sum [3-5]. The important aspect of this weighted sum method is that a set of Pareto-optimal solutions can be obtained by varying the weights. Unfortunately, this requires multiple runs as many times as the number of desired Pareto-optimal solutions. Furthermore, this method cannot be used to find Pareto-optimal solutions in problems having a non-convex Pareto-optimal front. In addition, there is no rational basis of determining adequate weights and the objective function so formed may lose significance due to combining non-commensurable objectives. To avoid this difficulty, the ε-constraint method for multi-objective optimization was presented in Ref. [6]. This method is based on optimization of the most preferred objective and considering the other objectives as constraints bounded by some allowable levels. These levels are then altered to generate the entire Pareto-optimal set. The most obvious weaknesses of this approach are that it is time-consuming and tends to find weakly non-dominated solutions.
Goal programming method was also proposed for multi-objective EED problem [7]. In this method, a target or a goal to be achieved for each objective is assigned and the objective function will then try to minimize the distance from the targets to the objectives. Although the method is computationally efficient, it will yield an inferior solution rather than a non-inferior one if the goal point is chosen in the feasible domain. Hence, the main drawback of this method is that it requires a priori knowledge about the shape of the problem search space.
The recent direction is to handle both objectives simultaneously as competing objectives instead of simplifying the multi-objective problem to a single objective problem [8-10]. The use and development of heuristicsbased multi-objective optimization techniques have significantly grown. Since they use a population of solutions in their search, multiple Pareto-optimal solutions can, in principle, be found in one single run. These models can be efficiently used to eliminate most of the difficulties of classical methods [11,12].
In this paper we present a reference point based multiobjective optimization using a combination between TR algorithm and PSO to solve the multi-objective EED problem. It is a new algorithm that performs TR as deterministic search and PSO as random search. TR method generate steps with the help of a quadratic model of the objective function, define a region around the current iterate within which they trust the model to be an adequate representation of the objective function, and then choose the step to be approximate minimizer of the model in this region. If a step is not acceptable, they reduce the size of the region and find a new minimize. In general, the direction of the step changes whenever the size of the TR is altered [13]. To see the idea of TR, consider the unconstrained optimization problem
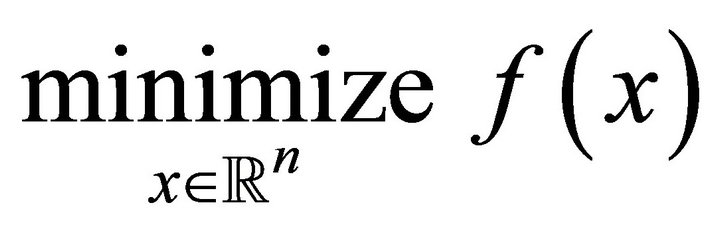 (1)
(1)
where  is a nonlinear continuous differentiable function in
is a nonlinear continuous differentiable function in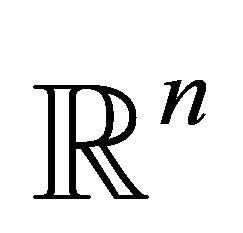 . For a known iterate
. For a known iterate  the TR method determines subsequent iterate using
the TR method determines subsequent iterate using
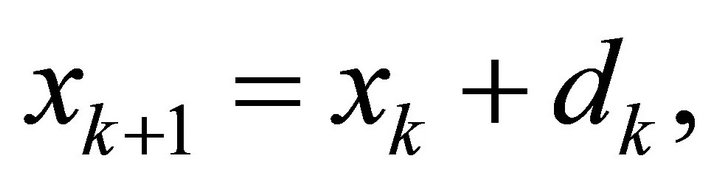 (2)
(2)
where  is trial step determined by minimizing a local quadratic (approximating) model of f at
is trial step determined by minimizing a local quadratic (approximating) model of f at  (TR subproblem) given by
(TR subproblem) given by
 (3)
(3)
where 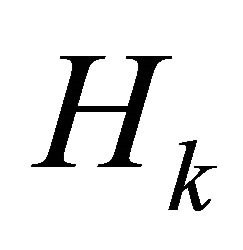 is Hessian of
is Hessian of 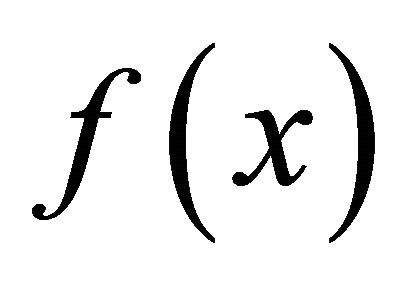 or approximate to it, and
or approximate to it, and  is the TR radius. Using the ratio
is the TR radius. Using the ratio
 (4)
(4)
traditional TR methods evaluate an agreement between the model and the objective function. The trial step 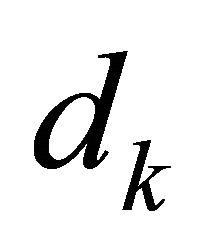 is accepted whenever
is accepted whenever  is greater than a positive constant. This leads us to the new point
is greater than a positive constant. This leads us to the new point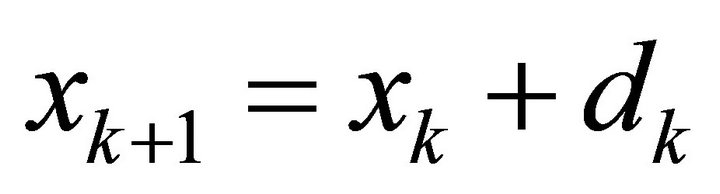 , and the TR radius is updated. Otherwise, the TR radius must be diminished and the sub-problem (3) must be solved again [14]. Figure 1 shows the mechanism of TR algorithm.
, and the TR radius is updated. Otherwise, the TR radius must be diminished and the sub-problem (3) must be solved again [14]. Figure 1 shows the mechanism of TR algorithm.
Because of the boundedness of the TR, TR algorithms can use non-convex approximate models. This is one of the advantages of TR algorithms comparing with line search algorithms. TR algorithms are reliable and robust, they can be applied to ill-conditioned problems, they have very strong convergence properties, and have been proven to be theoretically and practically effective and efficient for unconstrained and equality constrained optimization problems [15-17]. Also, the TR algorithm has proven to be a very successful globalization technique for nonlinear programming problems with equality and inequality constraints [18,19].
For multi-objective optimization problems, Kim and Ryu [20] developed an iterative algorithm for bi-objective stochastic optimization problems based on the TR method and investigated different sampling schemes. Their algorithm does not require any strong modeling
 New Solution
New Solution 
Figure 1. The mechanism of TR algorithm.
assumptions, and has great potential to work well in various real-world settings. El-Sobky [21] used the TR algorithm in solving an interactive approach for multiobjective optimization problems; where an active set strategy is used together with a reduced Hessian technique to convert the single objective optimization problem with quality and inequality constraints to equality constrained optimization problem and the computation of the trial step to two easy TR sub-problems similar to those for the unconstrained case.
PSO is an evolutionary computational (EC) model which is based on swarm intelligence. PSO is developed by Kennedy and Elberhart [22] who have been inspired by the research of the artificial livings. Similar to EC techniques, PSO is also an optimizer based on population. The system is initialized firstly in a set of randomly generated potential solutions, and then performs the search for the optimum one iteratively. Whereas the PSO does not possess the crossover and mutation processes used in EC, it finds the optimum solution by swarms following the best particle. Compared to EC, the PSO has much more profound intelligent background and could be performed more easily. Based on its advantages, the PSO is not only suitable for science research, but also engineering applications, in the fields of EC, optimization and many others.
The basic PSO algorithm is constructed as follows: consider a swarm of N particles or birds. For particle i, it is originally proposed that the position  is updated in the following manner:
is updated in the following manner:
 (7)
(7)
with the velocity  calculated as follows:
calculated as follows:
 (8)
(8)
Here, subscript t indicates a pseudo-time increment.  represents the best ever position of particle i at time t, with
represents the best ever position of particle i at time t, with  representing the global best ever position in the swarm at time t.
representing the global best ever position in the swarm at time t.  and
and  represent uniform random numbers between 0 and 1. Figure 2 shows the description of velocity and position updates of a particle for a two-dimensional parameter space.
represent uniform random numbers between 0 and 1. Figure 2 shows the description of velocity and position updates of a particle for a two-dimensional parameter space.
Multi-objective optimization has been one of the most studied application areas of PSO algorithms. Number of approaches have been utilized and/or designed to tackle multi-objective optimization problems using PSO. A comprehensive survey of the state-of-the-art in Multiobjective (MO) particle swarm optimizers can be found in [23] where different techniques reported in Multi-objective PSO development have been categorized and discussed.
From previous review, we want to integrate the merits of both TR and PSO in a new algorithm for solving EED problem; where TR has provided the initial set (close to

Figure 2. Description of velocity and position updates in particle swarm optimization for a two dimensional parameter space.
the Pareto set as possible and the reference point of the decision maker) followed by PSO to improve the quality of the solutions and get all the points on the Pareto frontier. Simulation results are presented for the standard IEEE 30-bus system. The effectiveness and potential of the proposed approach to solve the multi-objective EED problem are demonstrated.
2. Environmental/Economic Dispatch (EED)
The EED involves the simultaneous optimization of fuel cost and emission objectives which are conflicting ones. The deterministic problem is formulated as described below.
2.1. Objective Functions
2.1.1. Fuel Cost Objective
The classical EED problem of finding the optimal combination of power generation, which minimizes the total fuel cost while satisfying the total required demand can be mathematically stated as follows [5]:
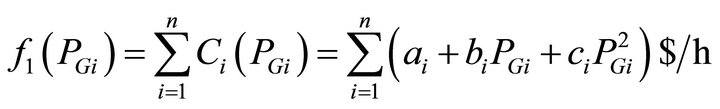 (9)
(9)
where : total fuel cost
: total fuel cost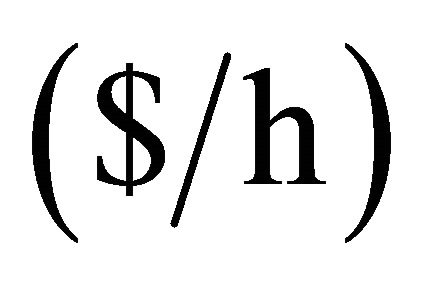 ,
,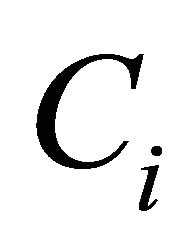 : is fuel cost of generator i,
: is fuel cost of generator i, : fuel cost coefficients of generator i,
: fuel cost coefficients of generator i, : power generated (p.u.) by generator i, and n: number of generators.
: power generated (p.u.) by generator i, and n: number of generators.
2.1.2. Emission Objective
The emission function can be presented as the sum of all types of emission considered, such as NOx, SO2, thermal emission, etc., with suitable pricing or weighting on each pollutant emitted. In the present study, only one type of emission NOx is taken into account without loss of generality. The amount of NOx emission is given as a function of generator output, that is, the sum of a quadratic and exponential function:
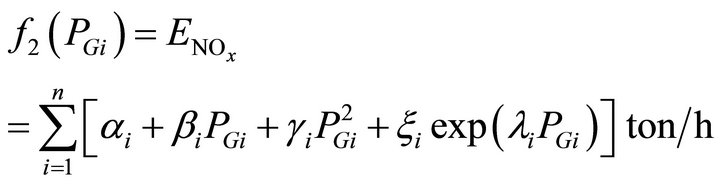 (10)
(10)
where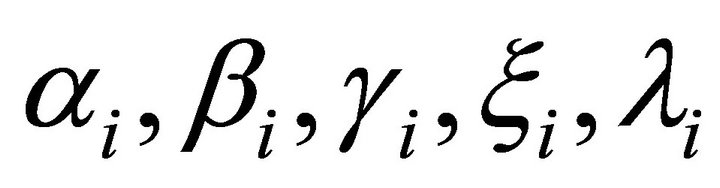 : coefficients of the ith generator’s NOx emission characteristic.
: coefficients of the ith generator’s NOx emission characteristic.
2.2. Constraints
The optimization problem is bounded by the following constraints.
2.2.1. Power Balance Constraint
The total power generated must supply the total load demand and the transmission losses:
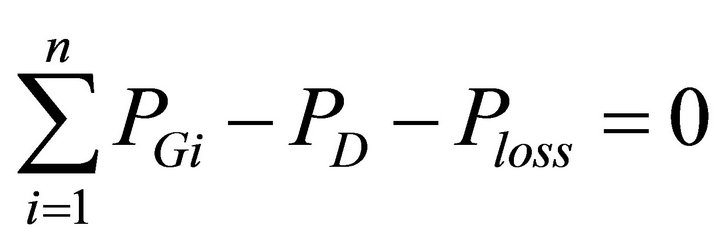 (11)
(11)
where
 : total load demand (p.u.), and
: total load demand (p.u.), and
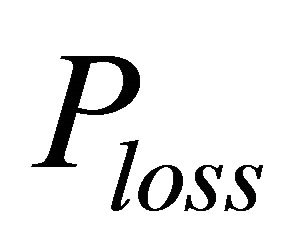 : transmission losses (p.u.).
: transmission losses (p.u.).
The transmission losses are given by [24]:
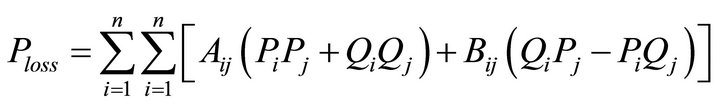 (12)
(12)
where

where n: number of buses;
Rij: series resistance connecting buses i and j;
Vi: voltage magnitude at bus i;
 : voltage angle at bus i;
: voltage angle at bus i;
Pi: real power injection at bus i, and Qi: reactive power injection bus i.
2.2.2. Maximum and Minimum Limits of Power Generation
The power generated PGi by each generator is constrained between its minimum and maximum limits, i.e.:
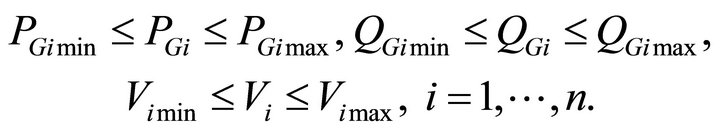
where PGi min: minimum power generated, and PGi max: maximum power generated.
2.2.3. Security Constraints
A mathematical formulation of the security constrained EELD problem would require a very large number of constraints to be considered. However, for typical systems the large proportion of lines has a rather small possibility of becoming overloaded. The EED problem should consider only the small proportion of lines in violation, or near violation of their respective security limits which are identified as the critical lines. We consider only the critical lines that are binding in the optimal solution. The detection of the critical lines is assumed done by the experiences of the decision maker. An improvement in the security can be obtained by minimizing the following objective function.
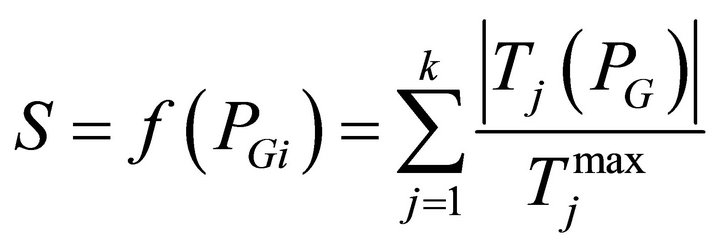 (13)
(13)
where Ti(PG): the real power flow;
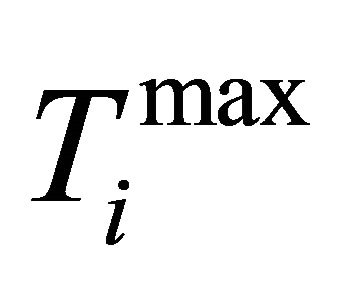 : the maximum limit of the real power flow of the jth line; and k: the number of monitored lines.
: the maximum limit of the real power flow of the jth line; and k: the number of monitored lines.
The line flow of the jth line is expressed in terms of the control variables PGs, by utilizing the generalized generation distribution factors (GGDF) [25] and is given below:
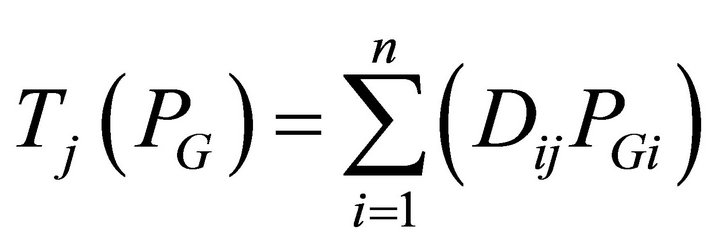 (14)
(14)
where Dij is the generalized GGDF for line j, due to generator i. For secure operation, the transmission line loading Sl is restricted by its upper limit as:

where nl is the number of transmission line.
3. Multi-Objective Optimization
Multi-objective optimization (also called multicriteria optimization, multiperformance or vector optimization) can be defined as the problem of finding a vector of decision variables which satisfies constraints and optimizes a vector function whose elements represent the objective functions. These functions form a mathematical description of performance criteria which are usually in conflict with each other. Hence, the term “optimize” means finding such a solution which would give the values of all the objective functions acceptable to the designer [26]. The general minimization problem of 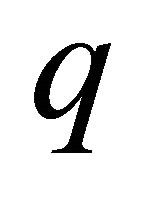 objectives can be mathematically stated as:
objectives can be mathematically stated as:
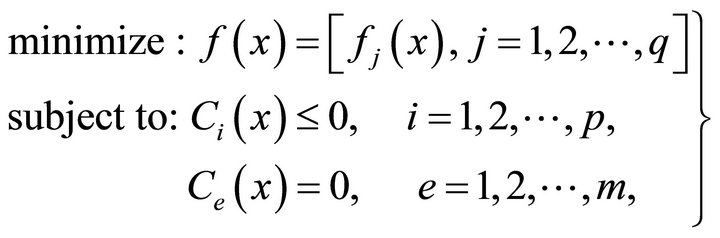 (15)
(15)
where fi(x) is the j-th objective function, Ci(x) is the i-th inequality constraint, Ce(x) is the e-th equality constraint and  is the vector of optimization or decision variables; where n is the dimension of the decision variable space. The multi-objective optimization problem then reduces to finding an x such that fi(x) is optimized. Since the notion of an optimum solution in multi-objective optimization problem is different compared to the single objective optimization problem, the concept of Pareto dominance is used for the evaluation of the solutions. This concept formulated by Vilfredo Pareto is defined as [27]:
is the vector of optimization or decision variables; where n is the dimension of the decision variable space. The multi-objective optimization problem then reduces to finding an x such that fi(x) is optimized. Since the notion of an optimum solution in multi-objective optimization problem is different compared to the single objective optimization problem, the concept of Pareto dominance is used for the evaluation of the solutions. This concept formulated by Vilfredo Pareto is defined as [27]:
Definition 1. (Dominance Criteria [28]). For a problem having more than one objective function (say,  ,
,  ,
, ), any two solution xa and xb can have one of two possibilities, one dominates the other or none dominates the other. A solution xa is said to dominate the other solution xb, if both the following condition are true
), any two solution xa and xb can have one of two possibilities, one dominates the other or none dominates the other. A solution xa is said to dominate the other solution xb, if both the following condition are true
• The solution xa is no worse (say the operator  denotes worse and
denotes worse and  denotes better) than xb in all objectives, or
denotes better) than xb in all objectives, or 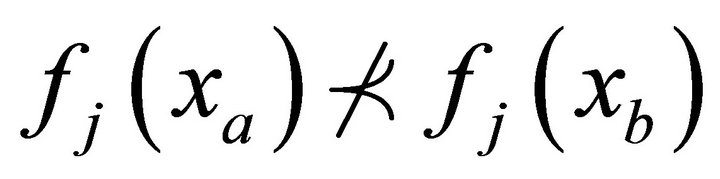 for all
for all 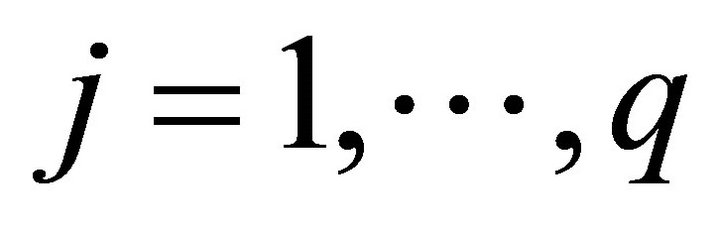 objectives.
objectives.
• The solution xa is strictly better than xb in at least one objective, or 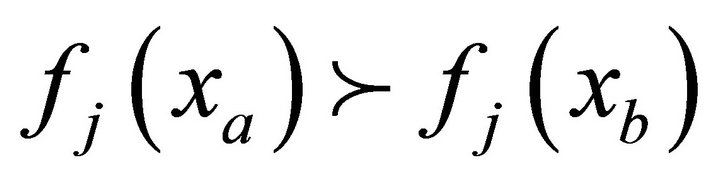 for at least one
for at least one  .
.
If any of the above condition is violated, the solution xa dose not dominates the solution xb.
Definition 2. (Pareto optimal solution). x* is said to be a Pareto optimal solution of multi-objective optimization problem if there exists no other feasible x such that, fi(x) ≤ fi(x*) for all  and fi(x) < fi(x*) for at least one objective function
and fi(x) < fi(x*) for at least one objective function .
.
4. Reference Point Based TR/PSO Approach
In this section, the proposed algorithm is presented. The proposed algorithm contains three stages initialization stage, TR stage (used to obtain a point on the Pareto frontier), and PSO stage (is applied to get all the points on the Pareto frontier). The mechanism of the proposed algorithm in the objective space is shown in Figure 3.
4.1. Initialization Stage
4.1.1. Initialization
Initialize N reference points in the search space, TR parameters, and PSO parameters.
4.1.2. Reference Point Method
The reference point interactive approach of Wierzbickiis [28] is very simple and practical for multi-objective optimization problems. Before the solution process starts, some information is given to the decision maker about the problem. The goal is to achieve Pareto-optimal solution closest to a supplied reference point. Moreover, the reference point approach works with only one reference point at a time [29]. However, the decision maker may be interested in exploring the preferred regions of Paretooptimality for multiple reference points simultaneously.

Figure 3. The mechanism of the proposed algorithm in the objective space.
With the above principles of reference point approaches and difficulties with the classical methods, we use a methodology by which a set of Pareto-optimal solutions near a supplied set of reference points will be found, thereby eliminating the need of any weight vector and the need of applying the methodologies again and again.
Given a reference point for a q-objective optimization problem of minimizing  with x belongs to the search space, the following optimization model is solved [28]:
with x belongs to the search space, the following optimization model is solved [28]:
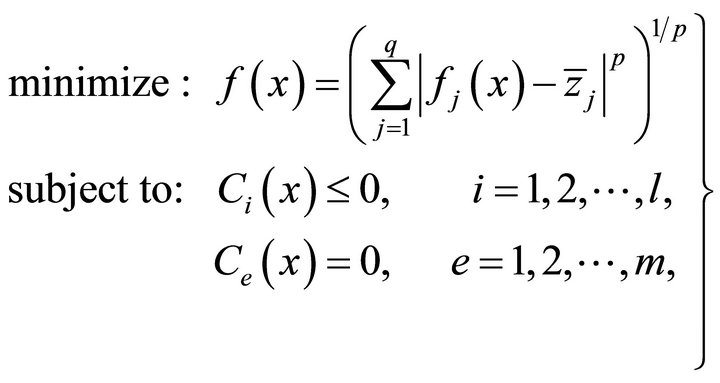 (16)
(16)
where the parameter p can take any value between 1 and ∞. When p = 2 is used, a Euclidean distance of any point in the objective space from the reference point  is minimized.
is minimized.
4.2. TR Stage
This section is devoted to presenting the detailed description of TR algorithm for solving problem (16). The proposed TR algorithm combines ideas from Byrd [30], Omojokun [31], and El Alem [32]. Following Dennis et al. [33], we define the indicator matrix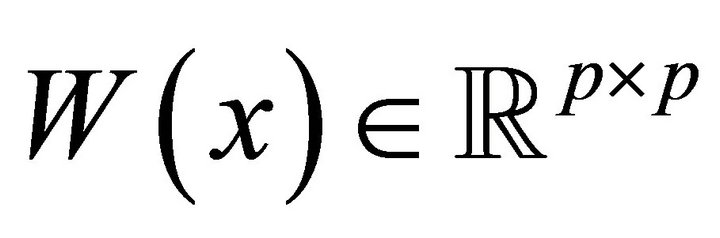 , whose diagonal entries are
, whose diagonal entries are
 (17)
(17)
Using this matrix, the Problem defined in Equation (16) can be transformed to the following equality constrained optimization problem:
 (18)
(18)
The above problem can be rewritten as:
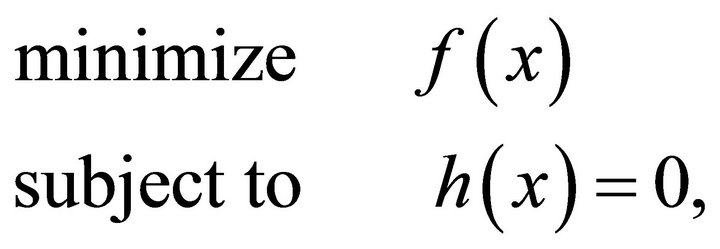 (19)
(19)
The Lagrangian function associated with problem defined in (19) is given by
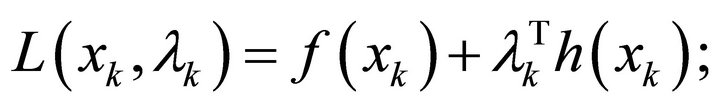 (20)
(20)
where  is the Lagrange multiplier vector associated with equality constraint
is the Lagrange multiplier vector associated with equality constraint .
.
The reduced Hessian approach is used to compute a trial step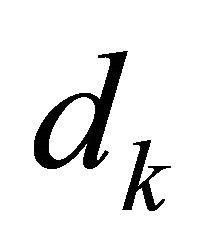 . In this approach, the trial step
. In this approach, the trial step  is decomposed into two orthogonal components; the normal component
is decomposed into two orthogonal components; the normal component  and the tangential component
and the tangential component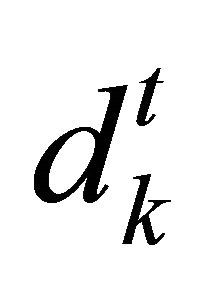 . The trial step
. The trial step  has the form
has the form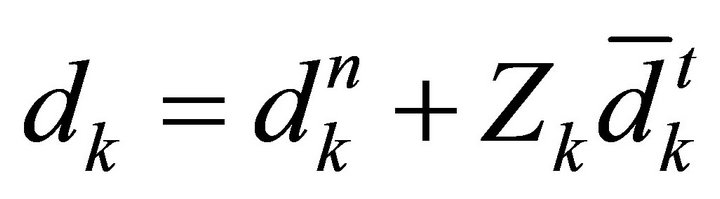 , where
, where  is a matrix whose columns form an orthonormal basis for the null space of
is a matrix whose columns form an orthonormal basis for the null space of .
.
We obtain the normal component 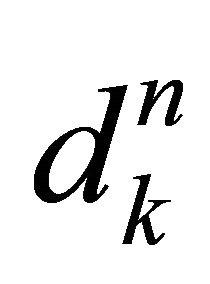 by solving the following TR sub-problem:
by solving the following TR sub-problem:
 (21)
(21)
for some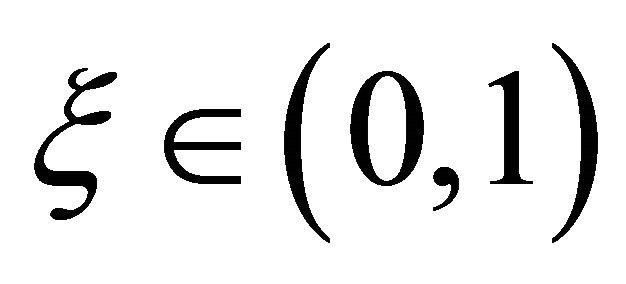 .
.
The tangential component is computed by solving the following TR sub-problem:
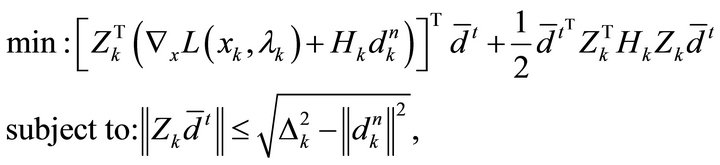 (22)
(22)
To test the step, we compare the actual reduction in moving from 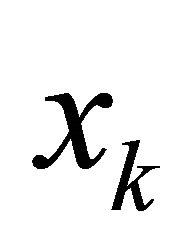 to
to 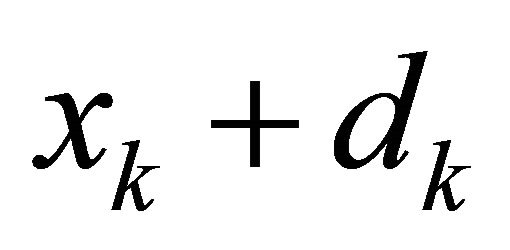 versus the predicted reduction. The actual reduction is defined as:
versus the predicted reduction. The actual reduction is defined as:
 (23)
(23)
The predicted reduction is defined as:
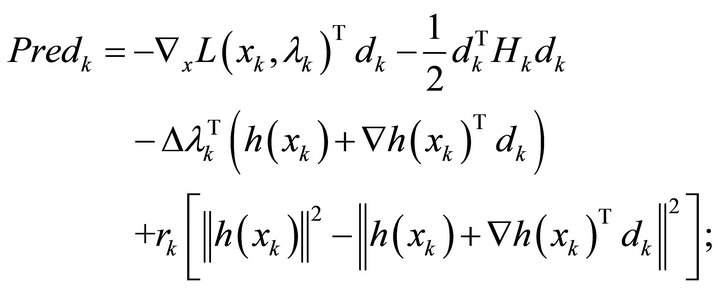 (24)
(24)
where  is a parameter usually called the penalty parameter, and
is a parameter usually called the penalty parameter, and 
If 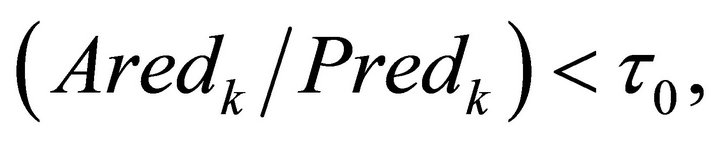 where
where 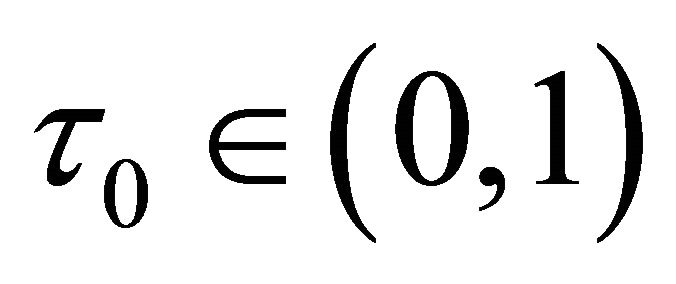 is a small fixed constant, then the step is rejected. In this case, the radius of the TR is decreased by setting
is a small fixed constant, then the step is rejected. In this case, the radius of the TR is decreased by setting , where
, where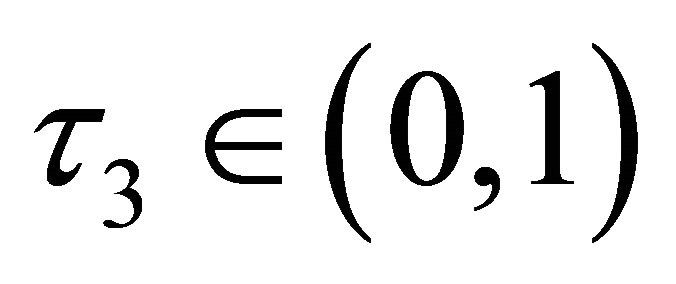 , and another trial step is computed.
, and another trial step is computed.
If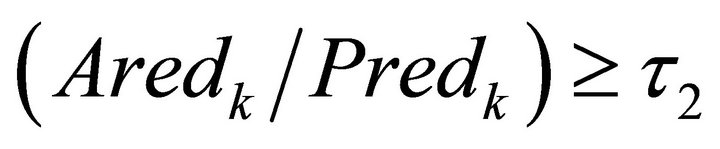 ; where
; where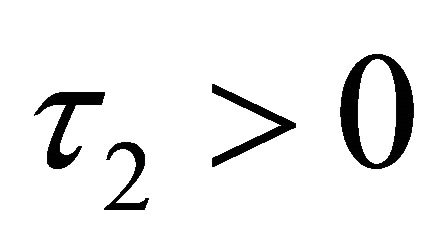 , then the step
, then the step 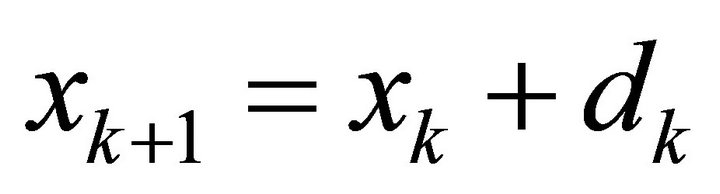 is accepted and set the TR as
is accepted and set the TR as
 ;
;
where 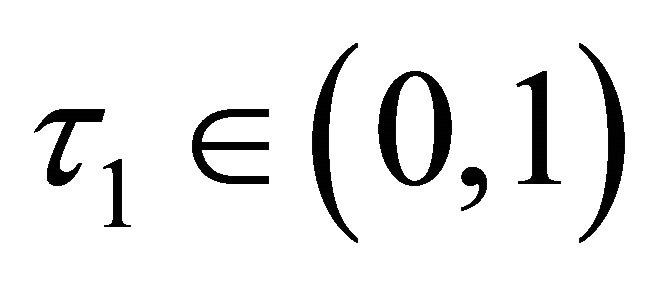 and another trial step is computed.
and another trial step is computed.
If 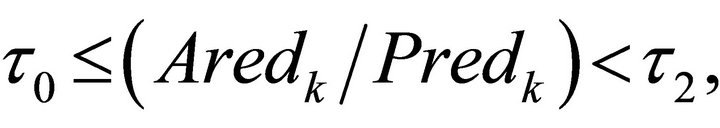 then the step
then the step  is accepted and set the TR as
is accepted and set the TR as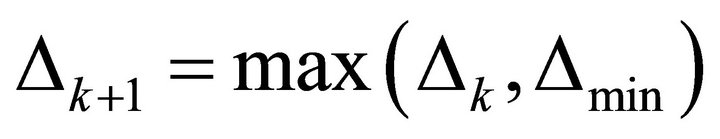 , and another trial step is computed.
, and another trial step is computed.
Finally, the algorithm is terminated when either  or
or  for some
for some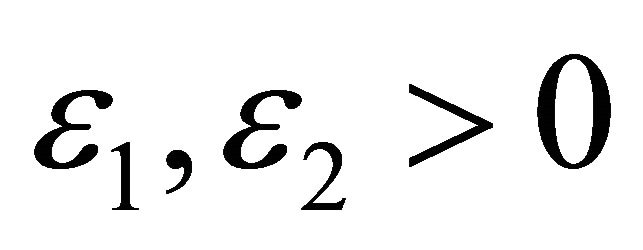 .
.
4.3. PSO Stage
In this stage a homogeneous PSO for multi-objective optimization problem (see [34]) is proposed with a decreasing constriction factor to restrict velocity of the particles and control it [35-37]. In homogeneous PSO one global repository concept is proposed for choosing pbest and gbest, this means that each particle has lost its own identity and treated simply as a member of social group. The procedure of the PSO stage is as follows.
Step 1: Initialization
All non-dominated points (which obtained by applying TR stage) chosen as particles position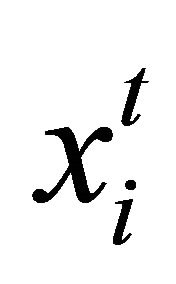 .
.
PSO parameters such as velocity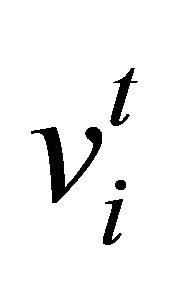 , inertia weight w and learning rates c1 and c2 are set up.
, inertia weight w and learning rates c1 and c2 are set up.
Store non-dominated particles in Pareto repository. If the specific constraint doesn’t exist for a repository, the size of the repository is unlimited.
Step 2: Evaluation
Evaluate the multi-objective fitness value of each particle and save it in a vector form.
Step 3: Floating
Two optimal solutions are chosen randomly for pbest and gbest from the repository.
Determine the new position of each particle with Equations (7) and (8).
Step 4: Repairing of particles
Where the particle i starts at position  with velocity
with velocity 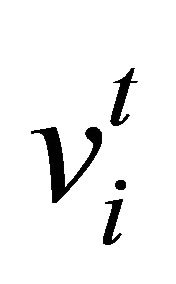 in the feasible space, the new position
in the feasible space, the new position  depends on velocity
depends on velocity , so we introduce a modified constriction factor (i.e., decreasing constriction factor)
, so we introduce a modified constriction factor (i.e., decreasing constriction factor)
 (25)
(25)
where,  is the age of the infeasible particle (i.e., how long it is still infeasible) and it is increased with the number of failed trials to keep the feasibility of the particle. The relation between the modified constriction factor and the age of the infeasible particle is shown in Figure 4.
is the age of the infeasible particle (i.e., how long it is still infeasible) and it is increased with the number of failed trials to keep the feasibility of the particle. The relation between the modified constriction factor and the age of the infeasible particle is shown in Figure 4.
The new modified positions of the particles are computed as:
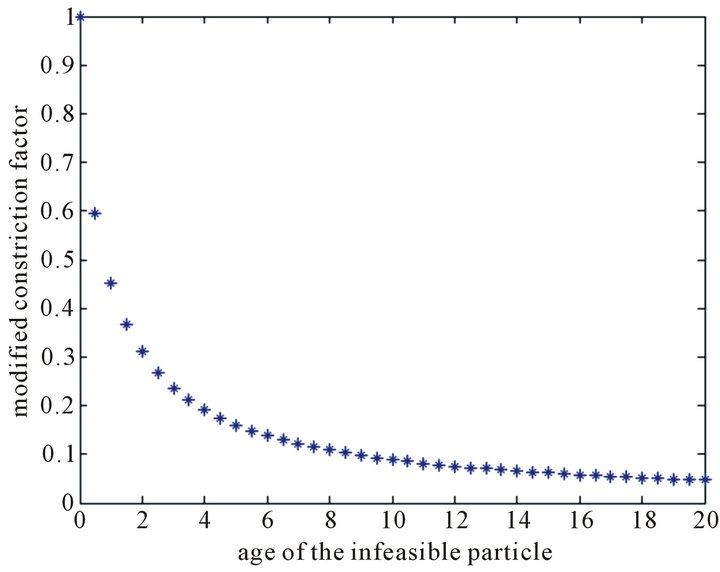
Figure 4. Relation between the modified constriction factor and the age of the infeasible particle.
 (26)
(26)
Step 5: Selection and update the repository
Check the Pareto optimality of each particle. If the fitness value of the particle is non-dominated when it compared to the Pareto optimal set in a repository, save it into the Pareto repository.
In the Pareto repository, if a particle is dominated from new one, then discard it.
Step 6: Repeat
Repeat again step 2 to step 5 until the number of generation reaches to given t. The pseudo code of the proposed algorithm showing in Figure 5.
5. Implementation of the Proposed Approach
Simulations were performed on the standard IEEE 30- bus 6-generator test system. The single-line diagram of this system is shown in Figure 6. The proposed algorithm have been implemented in MATLAB environment. We have kept the proposed approach parameters same in all problems as is shown in Table 1 (see [35,38]).
The power system is interconnected by 41 transmission lines and the total system demand for the 21 load buses is 2.834 p.u. Fuel cost and NOx emission coefficients for this system are given in Tables 2 and 3 respectively.
6. Results and Discussions
Figure 7 present the graphical results of our approach and ε-dominance based multi-objective genetic algorithm (MOGA) [39] for the EED problem after 200 generations.
From the figure, it can be deduced that the algorithm is capable of obtaining the Pareto front for the EED prob-

Figure 5. The pseudo code of the proposed algorithm.
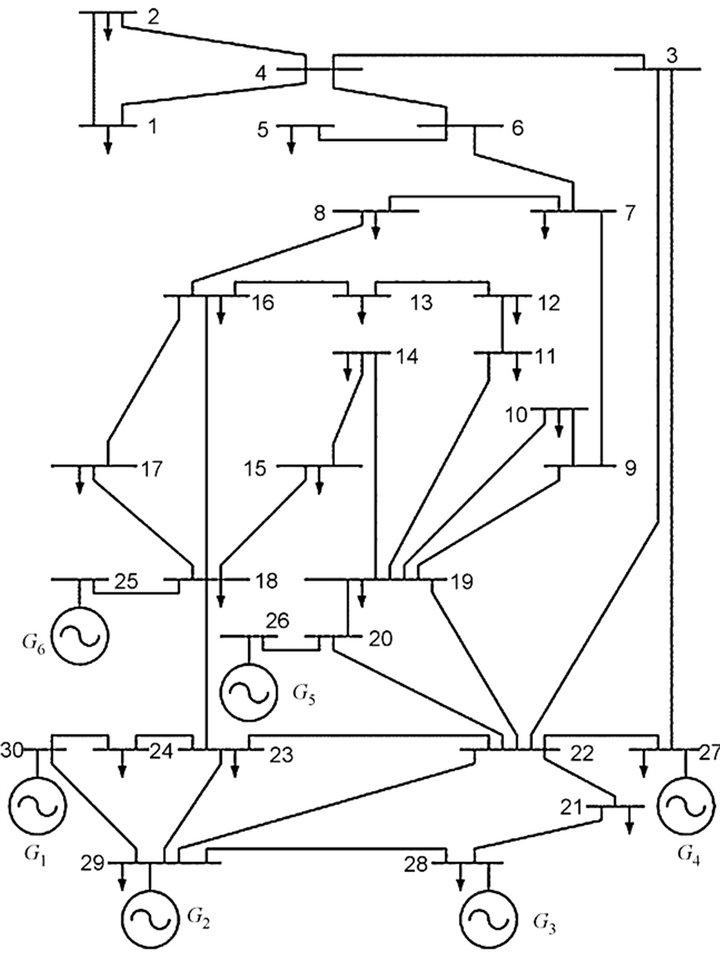
Figure 6. Single line diagram of IEEE 30-bus 6-generator test system.

Table 1. The parameter adopted in the implementation of the proposed algorithm.
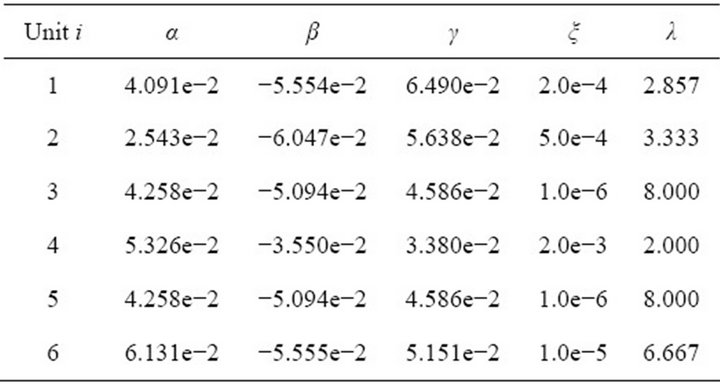
Table 3. NOx Emission coefficients.
lem as verified by the minimum of each objective and points obtained by ε-dominance based MOGA. In ε- dominance based MOGA. There are gaps between the nondominated solutions which make the curve nonsmooth. In other words, we can say that the proposed algorithm outperformed ε-dominance based MOGA in both distribution and spread.
The best fuel cost and best NOx emission obtained by the proposed approach as compared to non-dominated sorting genetic algorithm (NSGA) [8], niched Paretogenetic algorithm (NPGA) [9], strength Pareto-evolutionary algorithm (SPEA) [10], NSGA-II [40] and ε- dominance-based MOGA [39] are given in Tables 4 and 5. It is observed that the proposed approach finds better minimum fuel cost and emission level than the other
 ε-dominance based MOGA
ε-dominance based MOGA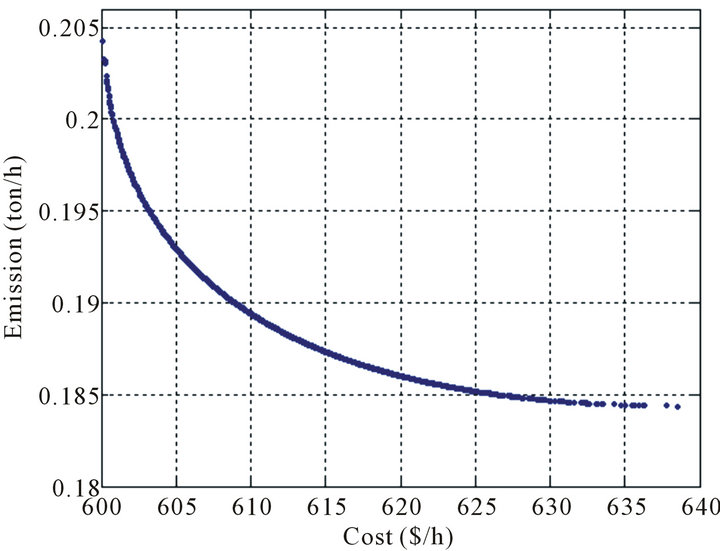 The proposed algorithm
The proposed algorithm
Figure 7. Pareto-optimal front for the EED problem.
evolutionary algorithms.
Table 6 reports the computational results, which declare that this work may be very valuable for on-line operation of power systems when environmental constraints are also need to be considered.
It has been shown that the proposed algorithm can obtain the Pareto front of the problem and it is therefore ideal for solving the multi-objective EED optimization problem which has conflicting objectives from the fact that the multi-objective approach yields multiple Paretooptimal solutions in a single simulation run whereas multiple runs are required for the single objective approach with weighted objectives. Another advantage is that the simulation results prove superiority of the proposed approach to those reported in the literature, where it completely covers and dominates all Pareto-set found by the other approaches. Finally, the reality of using the proposed approach to handle on-line problems of realistic dimensions has been approved due to small computational time.

Table 5. Best total ton/h NOx emission.

Table 6. Computation results for the proposed approach.
7. Conclusions
In this paper, the multi-objective EED problem has been solved using Reference Point Based TR/PSO approach. In this approach, we introduced an integration between TR and PSO to improve the quality of the founded solutions, and also to ensure faster convergence to the Pareto optimal solution. TR has provided the initial set (close to the Pareto set as possible and the reference point of the decision maker) followed by PSO to improve the quality of the solutions and get all the points on the Pareto frontier. The algorithm has been run on the standard IEEE 30-bus system.
The following are the significant contributions of this paper:
The proposed technique has been effectively applied to solve the EED considering two objectives simultaneously.
• Simulation results prove superiority of the proposed approach to those reported in the literature.
• The non-dominated solutions in the obtained Paretooptimal set are well distributed and have satisfactory diversity characteristics.
• The proposed algorithm does not have any restrictions on the number of the Pareto optimal solutions found; where it keeps track of all the feasible solutions found during the optimization.
• Also, the present work addresses an important task of combining TR methodology with PSO to not find a single optimal solution, but to find a set of solutions near the desired region of DM’s interest.
• The proposed approach is efficient for solving multiobjective optimization where multiple Pareto-optimal solutions can be found in one simulation run.
• The most important aspect of the proposed approach is that any number of objectives can be considered.
• The proposed approach is a new algorithm that performs TR as deterministic search and PSO as random search, where using the randomicity PSO and the high efficiency of TR method, can overcome the limitation of trust region method and solve efficiently a class of multi-objective applications.